Страница:
Другим примером направления, никак не связанного с вычислениями, – кстати, очень красивым направлением, – является проективная геометрия. Думаю, пример из этой области покажется вам занятным. В проективной геометрии вообще не рассматриваются метрические свойства, в ней не используются измерения. Понятие меры является основополагающим во всем, что касается количества, но проективная геометрия занимается описательными свойствами. Начертим две произвольные прямые и назовем их L и L’ (см. рис. 8).
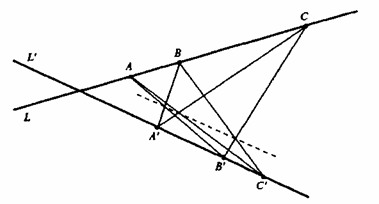Рис.8
Выберем на каждой прямой по три произвольных точки. Обозначим точки на прямой L буквами А, В и С, а точки на прямой L' -А', В' и С’. Теперь соединим отрезком точки Аи В', а также пару А' и В. Отметим место пересечения этих отрезков. После этого построим отрезки, соединяющие пары точек В и С', С и В', С и А' и, наконец, С' и А. Помните, что прямые и все точки были выбраны совершенно произвольно, мы не прибегали к каким-либо измерениям. Кроме того, прямые вообще бесконечны. В проективной геометрии все прямые имеют бесконечную длину, так как операции с ними не связаны с измерениями. Длины и углы не имеют никакого значения. Эта теорема (первым ее доказал Паскаль [17], и она является частным случаем более общей теоремы о конических сечениях) заключается в том, что три полученные точки пересечения построенных отрезков лежат на одной прямой. Математику такой результат кажется очень красивым -и не потому, что его можно увидеть воочию, а по той причине, что он оказывается полной неожиданностью. Вся изюминка в том, что это справедливо для любых, самых произвольных прямых. Точки также выбираются произвольным образом – вы можете поместить их куда пожелаете. Вы просто чертите прямые L и L', проводите три соединяющих их отрезка – и обнаруживаете, что полученные точки пересечения находятся на одной прямой. Если вы ощутили это, то получили определенное представление о той красоте, которую ценят математики. Это умозрительная красота. Она заключается в том, что между элементами, которые казались независимыми, разрозненными, внезапно возникает некое единство. Подобные переживания случаются часто, но обычно осознаются только при высоком уровне сосредоточенности, способном вызывать экстатическое состояние.
Более полное и точное определение математики приводится в «Словаре философии и психологии» Болдуина. Там сказано, что «математика представляет собой науку об абстрактных отношениях» [18]. В своей статье для девятой редакции «Британской энциклопедии» Уильямсон говорит, что «любая концепция, полностью описываемая конечным набором определений, является математическим понятием» [19]. Кроме того, Рассел сказал, что чистая математика представляет собой класс всех утверждений в форме «р влечет q», где р и q являются утверждениями, содержащими один и тот же набор переменных и не включающими в себя никаких постоянных, кроме логических констант.
Вернемся к неметрическим областям математики. Помимо алгебры логики и проективной геометрии, существует топология, которую иногда называют «геометрией на резиновой плоскости». Это чрезвычайно важное направление. Топология изучает те отношения, которые остаются неизменными при любых деформациях пространства. Скажем, плоскость можно растянуть таким образом, чтобы квадрат превратился в круг, а эллипс – в любую другую фигуру. Что же останется неизменным? Связность отдельных частей. Подобные опыты приводят ко множеству занятных построений – например, к созданию односторонней поверхности -ленты Мебиуса (см. рис. 9).
ЛЕНТА МЕБИУСА
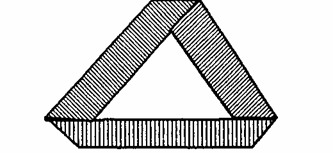Рис.9
Если вы перекрутите бумажную ленту ровно один раз, а затем склеите ее концы, то сможете, не отрывая карандаш от бумаги, провести вдоль центральной оси этой ленты одну прямую, которая протянется по обеим сторонам и вернется к исходной точке без необходимости изменения направления движения на обратное.
Порой люди занимаются исследованиями очень странных вещей, многие из которых чрезвычайно далеки от вопросов, связанных с измерениями.
Мы приближаемся к тому вопросу, который выходит за рамки любых определений, – к вопросу об основополагающей сущности математики. В ней выделяют три общепризнанные школы. Одна из них известна как логицизм, и самым видным ее представителем был Рассел. Логицисты считают, что математика – это только логика. Они придерживаются представления о том, что всю ныне известную математику и любые математические направления, которые могут возникнуть в будущем, можно свести к чисто логическому процессу (такому процессу, который можно использовать для программирования технических устройств). Сделать это пока не удалось. Логицизм сталкивается со множеством трудностей, с очень серьезными парадоксами. Например, представим себе множество всех множеств, которые не являются собственными элементами. Входит ли такое множество само в себя [20]? В свое время этот вопрос, то есть задача, был направлен в адрес Пеано [21], который только что завершил двухтомный труд по математической логике. Книга уже была в типографии, но этот вопрос полностью обесценивал ее содержание. Пеано сказал: «Как трудно смириться с тем, что после долгих лет, посвященных научным исследованиям, воздвигнутая вами башня разваливается в один миг». Вы можете сами убедиться в том, что на такой вопрос нельзя ответить ни «да», ни «нет». Этот парадокс возник в рамках самого взгляда на природу математики. Я задумываюсь о том, не попытались ли логицисты сделать ее чрезмерно чистой – в том смысле, что практически отказались от интуиции и свели математику к логическому процессу, который не пользуется интуицией и не испытывает в этом потребности.
Сейчас я попытаюсь подвести всему этому итог. Многие из вас еще не понимают, к чему я веду, но в действительности мы говорим о силах и слабостях, ограничениях чистого мышления, – а такое чистое мышление проявляется именно в математике. Поэтому я надеюсь, что вы не пожалеете о потраченном на понимание этих примеров времени – даже те из вас, у кого нет особых познаний в математике. Кроме того, подобные рассуждения отчасти подготовят нас к некоторым возможным трудностям.
Другой школой математики является формализм, связанный, в частности, с Гильбертом [22]. В отличие от школы Рассела, формализм уделяет особое внимание не логике, а необычным формам геометрии. Когда Евклид [23] писал свои труды по геометрии, он воспользовался рядом предположений, которые назвал «аксиомами», то есть «самоочевидными истинами», чем-то таким, в правильности чего никто не сомневается. В действительности, Евклид представил их в форме постулатов, а не обычных определений (аксиом) [24]. Он начал с этих положений и вывел из них все остальное. Пятая аксиома, известная как аксиома о параллельности [25], выглядит очень сложной. В ней утверждается: если сумма двух внутренних углов по одну и ту же сторону от некой прямой, пересекающей две заданные прямые, равна сумме двух прямых углов, то исходные прямые не пересекаются (см. рис. 10). Это утверждение кажется похожим на теорему, то есть на нечто требующее доказательства, но на самом деле это аксиома. В современных учебниках вы, вероятнее всего, встретите ее в такой формулировке (см. рис. 11): через точку С, не лежащую на прямой АВ, можно провести одну и только одну прямую, параллельную прямой АВ. Так ее описывают в наши дни, а первый вариант представляет собой формулировку Евклида. Поскольку она выглядит похожей на теорему, многие математики пытались доказать ее, опираясь на остальные аксиомы, но потерпели полную неудачу.
ПЯТАЯ АКСИОМА ЕВКЛИДА
Рис.10
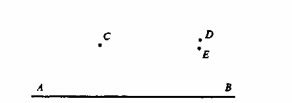Рис. 11
Следующим шагом стала попытка выдвинуть иные предположения. Лобачевский и Больяй [26] независимо друг от друга допустили, что через точку С, не лежащую на заданной прямой АВ, можно провести по меньшей мере две прямые, параллельные АВ. Это означает, что и прямая CD, и прямая СЕ могут не пересечь прямую АВ -нигде, кроме, быть может, бесконечности. Просто предположим, что это правильно. Быть может, мы так не думаем, но дело не в этом. Можно ли, пользуясь этой аксиомой, построить внутренне непротиворечивую геометрию? Да. И это было сделано. В геометрии Лобачевского многие, практически все, положения Евклида, опирающиеся на аксиому о параллельности, выглядят совершенно иначе. Например, все вы знакомы с утверждением о том, что сумма углов треугольника равна двум прямым углам, но в геометрии Лобачевского эта сумма всегда превышает сто восемьдесят градусов.
Другой математик, Риман [27], примерно в те же годы допустил, что через точку С невозможно провести ни одной прямой, параллельной заданной, то есть любая из них непременно пересечет выбранную прямую АВ на конечном расстоянии от точки С. Это уточнение очень важно. В геометрии Римана движение по любой прямой в одном направлении непременно заставит вас вернуться к исходной точке с другой стороны. Быть может, это противоречит интуитивным представлениям, но в построении такой геометрии тоже нет логических ошибок. Она внутренне непротиворечива.
По мнению Рассела, в математике допустимы любые внутренне непротиворечивые концепции. Это значит, что геометрии Лобачевского и Римана имеют право на существование. Через полсотни лет после Римана родился Эйнштейн, который развил общую теорию относительности. Обнаружив, что его концепция мироздания соответствует Римановой геометрии, Эйнштейн сказал: «Как могло случиться, что заточенного в башне из слоновой кости математика посещают совершенно правильные мысли о строении внешней вселенной?» Это очень хороший вопрос. Такого чистого математика, как Риман, интересует прежде всего, так сказать, интеллектуальное упражнение. Это относится ко всем чистым математикам. Подобно богам, они не руководствуются исключительно чувством долга. Математик делает нечто только во имя удовольствия. Такой образ жизни ведут все вольные души, и математики показывают нам огромное число примеров такой свободы. У вольной души нет обязанностей. Она делает что-то совершенно спонтанно, однако такие непреднамеренные действия почти всегда приводят к блестящим результатам. Да, чистый математик запирается в башне из слоновой кости и мыслит только ради удовольствия. После этого кто-то из проходящих мимо берет его результаты и обнаруживает, что они предлагают власть над той или иной сферой природы. Однако это вызывает у чистого математика боль, так как милая его сердцу чистота оказывается запятнанной практическим применением.
Рассказывают, что один математик, у которого возникла совершенно непрактичная идея, воскликнул: «Слава Богу, что эта мысль не имеет никаких вообразимых сфер приложения». Разве это странно? Что почувствует художник, если напишет прекрасную картину, а потом некто отберет ее и начнет использовать для продажи «кока-колы»? Те же чувства охватывают и чистого математика. Не все мы слеплены по одному образцу. Вот простой факт: практически все математические творения были созданы чистыми математиками, запиравшимися в башнях из слоновой кости; к тому же всем нам известно, что любые попытки творить ради практической пользы делают творчество невозможным. Единственным исключением стала развитая Ньютоном теория производных, то есть дифференциального исчисления. Ньютона занимали концепции мироздания, а математика оставалась для него лишь инструментом. То же самое можно сказать и о значении математики для Винера [28], одного из главных теоретиков в области создания вычислительных машин в наши дни. Он был склонен заниматься не чистой, а прикладной математикой.
Поговорим об этом подробнее. Вот история о Рамануджане [29], величайшем восточном (индийском) математике моего времени, и об английском ученом Харди [30]. Оба были чистыми теоретиками. На одной из своих лекций Харди рассказывал о том, как нанял кэб и отправился навестить Рамануджана, когда тот гостил в Англии. Появившись, Харди сказал: «Я приехал на кэбе номер 1729 – очень скучное число». Его друг-индиец возразил: «Напротив, это очень интересное число. Это минимальное из всех чисел, которые можно двумя различными способами представить в виде суммы двух кубов». Попробуйте самостоятельно найти решения этой задачи [31].
Дело в том, что вольная душа не трудится, а играет. Действия такого человека представляют собой спонтанное проявление радости, но такой подход приводит к величайшим открытиям. Что касается расцвета формализма, который начался после развития неевклидовых геометрий, то этот подъем стал подлинной революцией в представлениях о природе математики. Была низвергнута сама идея аксиом, то есть убежденность в существовании неких несомненных истин, на основе которых выстраиваются логические рассуждения. Вместо аксиом у математиков осталось только то, что можно назвать «основополагающими исходными посылками». Впоследствии это привело к созданию самых разнообразных экзотических геометрий. В качестве примера используем такие основополагающие исходные посылки (те, кому известны аксиомы Евклида, могут их не узнать):
Аксиома 1. Если а и b – различные элементы множества S, то существует по меньшей мере один класс L, одновременно содержащий в себе и а и b.
Аксиома 2. Если a и b – различные элементы множества S, то существует не более одного класса L, одновременно содержащего в себе и а и b.
Аксиома 3. Любые два класса L имеют по меньшей мере один общий элемент из множества S.
Аксиома 4. В множестве S существует по меньшей мере один класс L.
Аксиома 5. Любой класс L содержит по меньшей мере три элемента множества S.
Аксиома 6. Все элементы множества S не могут одновременно принадлежать одному классу L.
Аксиома 7. Ни один класс L не содержит более трех элементов множества S.
Обратимся к практическим приложениям этой геометрии. Предположим, существует некая банковская фирма, у которой есть семь совладельцев. Чтобы обеспечить правильное обращение с информацией, относящейся к вопросам ценных бумаг, совладельцы решили образовать семь комиссий, каждая из которых будет связана с определенной областью. Кроме того, партнеры договорились, что каждый из них должен стать председателем какой-либо комиссии и членом трех – ровно трех – комитетов в целом. Запишем названия комиссий и списки их членов; председателем подразделения является тот совладелец, чье имя указано первым:
Внутренние железные дороги: Адаме, Браун, Смит. Муниципальные долговые обязательства: Браун, Мерфи, Эллис.
Федеральные долговые обязательства: Мерфи, Смит, Джонс. Южноамериканские ценные бумаги: Смит, Эллис, Гордон. Национальная черная металлургия: Эллис, Джонс, Адаме. Континентальные ценные бумаги: Джонс, Гордон, Браун. Акции коммунальных предприятий: Гордон, Адаме, Мерфи.
Бесплотный дух Евклида! Вот чем становится современная геометрия! Этот список полностью соответствует нашим аксиомам. В прошлом слово «геометрия» обозначало землемерные работы, но теперь это понятие потеряло прежний смысл. Сейчас формалисты утверждают, что математика – это игра с формальными сущностями; подобно шахматам, она не несет никакого содержания, и все же люди играют в нее очень серьезно.
Лекция 3
Выберем на каждой прямой по три произвольных точки. Обозначим точки на прямой L буквами А, В и С, а точки на прямой L' -А', В' и С’. Теперь соединим отрезком точки Аи В', а также пару А' и В. Отметим место пересечения этих отрезков. После этого построим отрезки, соединяющие пары точек В и С', С и В', С и А' и, наконец, С' и А. Помните, что прямые и все точки были выбраны совершенно произвольно, мы не прибегали к каким-либо измерениям. Кроме того, прямые вообще бесконечны. В проективной геометрии все прямые имеют бесконечную длину, так как операции с ними не связаны с измерениями. Длины и углы не имеют никакого значения. Эта теорема (первым ее доказал Паскаль [17], и она является частным случаем более общей теоремы о конических сечениях) заключается в том, что три полученные точки пересечения построенных отрезков лежат на одной прямой. Математику такой результат кажется очень красивым -и не потому, что его можно увидеть воочию, а по той причине, что он оказывается полной неожиданностью. Вся изюминка в том, что это справедливо для любых, самых произвольных прямых. Точки также выбираются произвольным образом – вы можете поместить их куда пожелаете. Вы просто чертите прямые L и L', проводите три соединяющих их отрезка – и обнаруживаете, что полученные точки пересечения находятся на одной прямой. Если вы ощутили это, то получили определенное представление о той красоте, которую ценят математики. Это умозрительная красота. Она заключается в том, что между элементами, которые казались независимыми, разрозненными, внезапно возникает некое единство. Подобные переживания случаются часто, но обычно осознаются только при высоком уровне сосредоточенности, способном вызывать экстатическое состояние.
Более полное и точное определение математики приводится в «Словаре философии и психологии» Болдуина. Там сказано, что «математика представляет собой науку об абстрактных отношениях» [18]. В своей статье для девятой редакции «Британской энциклопедии» Уильямсон говорит, что «любая концепция, полностью описываемая конечным набором определений, является математическим понятием» [19]. Кроме того, Рассел сказал, что чистая математика представляет собой класс всех утверждений в форме «р влечет q», где р и q являются утверждениями, содержащими один и тот же набор переменных и не включающими в себя никаких постоянных, кроме логических констант.
Вернемся к неметрическим областям математики. Помимо алгебры логики и проективной геометрии, существует топология, которую иногда называют «геометрией на резиновой плоскости». Это чрезвычайно важное направление. Топология изучает те отношения, которые остаются неизменными при любых деформациях пространства. Скажем, плоскость можно растянуть таким образом, чтобы квадрат превратился в круг, а эллипс – в любую другую фигуру. Что же останется неизменным? Связность отдельных частей. Подобные опыты приводят ко множеству занятных построений – например, к созданию односторонней поверхности -ленты Мебиуса (см. рис. 9).
ЛЕНТА МЕБИУСА
Если вы перекрутите бумажную ленту ровно один раз, а затем склеите ее концы, то сможете, не отрывая карандаш от бумаги, провести вдоль центральной оси этой ленты одну прямую, которая протянется по обеим сторонам и вернется к исходной точке без необходимости изменения направления движения на обратное.
Порой люди занимаются исследованиями очень странных вещей, многие из которых чрезвычайно далеки от вопросов, связанных с измерениями.
Мы приближаемся к тому вопросу, который выходит за рамки любых определений, – к вопросу об основополагающей сущности математики. В ней выделяют три общепризнанные школы. Одна из них известна как логицизм, и самым видным ее представителем был Рассел. Логицисты считают, что математика – это только логика. Они придерживаются представления о том, что всю ныне известную математику и любые математические направления, которые могут возникнуть в будущем, можно свести к чисто логическому процессу (такому процессу, который можно использовать для программирования технических устройств). Сделать это пока не удалось. Логицизм сталкивается со множеством трудностей, с очень серьезными парадоксами. Например, представим себе множество всех множеств, которые не являются собственными элементами. Входит ли такое множество само в себя [20]? В свое время этот вопрос, то есть задача, был направлен в адрес Пеано [21], который только что завершил двухтомный труд по математической логике. Книга уже была в типографии, но этот вопрос полностью обесценивал ее содержание. Пеано сказал: «Как трудно смириться с тем, что после долгих лет, посвященных научным исследованиям, воздвигнутая вами башня разваливается в один миг». Вы можете сами убедиться в том, что на такой вопрос нельзя ответить ни «да», ни «нет». Этот парадокс возник в рамках самого взгляда на природу математики. Я задумываюсь о том, не попытались ли логицисты сделать ее чрезмерно чистой – в том смысле, что практически отказались от интуиции и свели математику к логическому процессу, который не пользуется интуицией и не испытывает в этом потребности.
Сейчас я попытаюсь подвести всему этому итог. Многие из вас еще не понимают, к чему я веду, но в действительности мы говорим о силах и слабостях, ограничениях чистого мышления, – а такое чистое мышление проявляется именно в математике. Поэтому я надеюсь, что вы не пожалеете о потраченном на понимание этих примеров времени – даже те из вас, у кого нет особых познаний в математике. Кроме того, подобные рассуждения отчасти подготовят нас к некоторым возможным трудностям.
Другой школой математики является формализм, связанный, в частности, с Гильбертом [22]. В отличие от школы Рассела, формализм уделяет особое внимание не логике, а необычным формам геометрии. Когда Евклид [23] писал свои труды по геометрии, он воспользовался рядом предположений, которые назвал «аксиомами», то есть «самоочевидными истинами», чем-то таким, в правильности чего никто не сомневается. В действительности, Евклид представил их в форме постулатов, а не обычных определений (аксиом) [24]. Он начал с этих положений и вывел из них все остальное. Пятая аксиома, известная как аксиома о параллельности [25], выглядит очень сложной. В ней утверждается: если сумма двух внутренних углов по одну и ту же сторону от некой прямой, пересекающей две заданные прямые, равна сумме двух прямых углов, то исходные прямые не пересекаются (см. рис. 10). Это утверждение кажется похожим на теорему, то есть на нечто требующее доказательства, но на самом деле это аксиома. В современных учебниках вы, вероятнее всего, встретите ее в такой формулировке (см. рис. 11): через точку С, не лежащую на прямой АВ, можно провести одну и только одну прямую, параллельную прямой АВ. Так ее описывают в наши дни, а первый вариант представляет собой формулировку Евклида. Поскольку она выглядит похожей на теорему, многие математики пытались доказать ее, опираясь на остальные аксиомы, но потерпели полную неудачу.
Рис.10
Следующим шагом стала попытка выдвинуть иные предположения. Лобачевский и Больяй [26] независимо друг от друга допустили, что через точку С, не лежащую на заданной прямой АВ, можно провести по меньшей мере две прямые, параллельные АВ. Это означает, что и прямая CD, и прямая СЕ могут не пересечь прямую АВ -нигде, кроме, быть может, бесконечности. Просто предположим, что это правильно. Быть может, мы так не думаем, но дело не в этом. Можно ли, пользуясь этой аксиомой, построить внутренне непротиворечивую геометрию? Да. И это было сделано. В геометрии Лобачевского многие, практически все, положения Евклида, опирающиеся на аксиому о параллельности, выглядят совершенно иначе. Например, все вы знакомы с утверждением о том, что сумма углов треугольника равна двум прямым углам, но в геометрии Лобачевского эта сумма всегда превышает сто восемьдесят градусов.
Другой математик, Риман [27], примерно в те же годы допустил, что через точку С невозможно провести ни одной прямой, параллельной заданной, то есть любая из них непременно пересечет выбранную прямую АВ на конечном расстоянии от точки С. Это уточнение очень важно. В геометрии Римана движение по любой прямой в одном направлении непременно заставит вас вернуться к исходной точке с другой стороны. Быть может, это противоречит интуитивным представлениям, но в построении такой геометрии тоже нет логических ошибок. Она внутренне непротиворечива.
По мнению Рассела, в математике допустимы любые внутренне непротиворечивые концепции. Это значит, что геометрии Лобачевского и Римана имеют право на существование. Через полсотни лет после Римана родился Эйнштейн, который развил общую теорию относительности. Обнаружив, что его концепция мироздания соответствует Римановой геометрии, Эйнштейн сказал: «Как могло случиться, что заточенного в башне из слоновой кости математика посещают совершенно правильные мысли о строении внешней вселенной?» Это очень хороший вопрос. Такого чистого математика, как Риман, интересует прежде всего, так сказать, интеллектуальное упражнение. Это относится ко всем чистым математикам. Подобно богам, они не руководствуются исключительно чувством долга. Математик делает нечто только во имя удовольствия. Такой образ жизни ведут все вольные души, и математики показывают нам огромное число примеров такой свободы. У вольной души нет обязанностей. Она делает что-то совершенно спонтанно, однако такие непреднамеренные действия почти всегда приводят к блестящим результатам. Да, чистый математик запирается в башне из слоновой кости и мыслит только ради удовольствия. После этого кто-то из проходящих мимо берет его результаты и обнаруживает, что они предлагают власть над той или иной сферой природы. Однако это вызывает у чистого математика боль, так как милая его сердцу чистота оказывается запятнанной практическим применением.
Рассказывают, что один математик, у которого возникла совершенно непрактичная идея, воскликнул: «Слава Богу, что эта мысль не имеет никаких вообразимых сфер приложения». Разве это странно? Что почувствует художник, если напишет прекрасную картину, а потом некто отберет ее и начнет использовать для продажи «кока-колы»? Те же чувства охватывают и чистого математика. Не все мы слеплены по одному образцу. Вот простой факт: практически все математические творения были созданы чистыми математиками, запиравшимися в башнях из слоновой кости; к тому же всем нам известно, что любые попытки творить ради практической пользы делают творчество невозможным. Единственным исключением стала развитая Ньютоном теория производных, то есть дифференциального исчисления. Ньютона занимали концепции мироздания, а математика оставалась для него лишь инструментом. То же самое можно сказать и о значении математики для Винера [28], одного из главных теоретиков в области создания вычислительных машин в наши дни. Он был склонен заниматься не чистой, а прикладной математикой.
Поговорим об этом подробнее. Вот история о Рамануджане [29], величайшем восточном (индийском) математике моего времени, и об английском ученом Харди [30]. Оба были чистыми теоретиками. На одной из своих лекций Харди рассказывал о том, как нанял кэб и отправился навестить Рамануджана, когда тот гостил в Англии. Появившись, Харди сказал: «Я приехал на кэбе номер 1729 – очень скучное число». Его друг-индиец возразил: «Напротив, это очень интересное число. Это минимальное из всех чисел, которые можно двумя различными способами представить в виде суммы двух кубов». Попробуйте самостоятельно найти решения этой задачи [31].
Дело в том, что вольная душа не трудится, а играет. Действия такого человека представляют собой спонтанное проявление радости, но такой подход приводит к величайшим открытиям. Что касается расцвета формализма, который начался после развития неевклидовых геометрий, то этот подъем стал подлинной революцией в представлениях о природе математики. Была низвергнута сама идея аксиом, то есть убежденность в существовании неких несомненных истин, на основе которых выстраиваются логические рассуждения. Вместо аксиом у математиков осталось только то, что можно назвать «основополагающими исходными посылками». Впоследствии это привело к созданию самых разнообразных экзотических геометрий. В качестве примера используем такие основополагающие исходные посылки (те, кому известны аксиомы Евклида, могут их не узнать):
Аксиома 1. Если а и b – различные элементы множества S, то существует по меньшей мере один класс L, одновременно содержащий в себе и а и b.
Аксиома 2. Если a и b – различные элементы множества S, то существует не более одного класса L, одновременно содержащего в себе и а и b.
Аксиома 3. Любые два класса L имеют по меньшей мере один общий элемент из множества S.
Аксиома 4. В множестве S существует по меньшей мере один класс L.
Аксиома 5. Любой класс L содержит по меньшей мере три элемента множества S.
Аксиома 6. Все элементы множества S не могут одновременно принадлежать одному классу L.
Аксиома 7. Ни один класс L не содержит более трех элементов множества S.
Обратимся к практическим приложениям этой геометрии. Предположим, существует некая банковская фирма, у которой есть семь совладельцев. Чтобы обеспечить правильное обращение с информацией, относящейся к вопросам ценных бумаг, совладельцы решили образовать семь комиссий, каждая из которых будет связана с определенной областью. Кроме того, партнеры договорились, что каждый из них должен стать председателем какой-либо комиссии и членом трех – ровно трех – комитетов в целом. Запишем названия комиссий и списки их членов; председателем подразделения является тот совладелец, чье имя указано первым:
Внутренние железные дороги: Адаме, Браун, Смит. Муниципальные долговые обязательства: Браун, Мерфи, Эллис.
Федеральные долговые обязательства: Мерфи, Смит, Джонс. Южноамериканские ценные бумаги: Смит, Эллис, Гордон. Национальная черная металлургия: Эллис, Джонс, Адаме. Континентальные ценные бумаги: Джонс, Гордон, Браун. Акции коммунальных предприятий: Гордон, Адаме, Мерфи.
Бесплотный дух Евклида! Вот чем становится современная геометрия! Этот список полностью соответствует нашим аксиомам. В прошлом слово «геометрия» обозначало землемерные работы, но теперь это понятие потеряло прежний смысл. Сейчас формалисты утверждают, что математика – это игра с формальными сущностями; подобно шахматам, она не несет никакого содержания, и все же люди играют в нее очень серьезно.
Лекция 3
С момента нашей прошлой встречи я большую часть времени был опьянен, но не тем вином, что делают из винограда, а совсем иным напитком – тем, который воспевают персидские мистики. Я окидывал взглядом танец мысли, представляемый на мировой сцене, я видел многих танцоров. Я видел Декарта [1], который валялся в постели до полудня, флиртуя с аналитической геометрией, – так и родилась современная мысль, математическая и философская. Я видел еще одного молодого человека в возрасте около двадцати четырех лет; он был так поглощен своими «Principia» [2], что забывал о еде и сне, но мышление этого человека стало тем ритмом, под который сегодня танцуют все инженеры. Этот молодой человек по имени Ньютон был настолько влюблен в свои «Principia», что однажды, как рассказывают, оставил у стола с поданным завтраком своего друга и сестру – она не имела над ним власти. Прошло несколько часов, друг Ньютона проголодался и решил немного поесть… а потом еще немного… и в конце концов съел все, что было на столе. А позже сэр Исаак Ньютон (впрочем, тогда он еще не был «сэром») спустился вниз, кивнул приятелю, сел за стол, посидел немного и сказал: «Мне казалось, что сегодня утром я еще не ел, но, должно быть, я ошибся». Такое случается со всеми танцорами мысли.
Еще одним человеком, который обладал всеми знаниями, известными миру Запада, – последним человеком, знавшим все, – был Лейбниц; он создал великую математику и великую философию. Кроме того, были Вейерш-трасси его чела Софья [3], которая стала величайшей женщиной-математиком. Был Гильберт, лучший математик своих дней. Однажды, читая лекцию студентам, он запнулся, так как не мог умножить 6 на 7. Один студент с готовностью выкрикнул: «41», а другой: «43». Гильберт ответил: «Господа, господа, я уверен, что существует единственный правильный ответ». Хорошее подтверждение тому, что математики редко умеют хорошо считать. Это две весьма различные способности.
Помимо того, я пересек мысленным взором весь мир и заглянул в чужие земли, чтобы увидеть Шанкару-математика из математиков, который еще мальчиком скитался по всей Индии и вызывал смятение у браминов; он уводил мужей от жен, так как те становились его саньясинами. По каким-то непонятным причинам женам это очень не нравилось, но выбора не было – оставалась только возможность примкнуть к рядам победителя. Взмахивая волшебной палочкой своей логики, этот человек заставил мир зримых проявлений исчезнуть, и на месте этого мира не осталось ничего, кроме Бога.
Вот пример его могущественной логики. Шанкара говорил, что, когда человек осознает иллюзорность определенного явления, это явление не только прекращает существование, но и лишается права на существование когда бы то ни было. Возможно, вам будет проще понять это, если такое переживание сравнить со зрелищем миража в пустыне. Путешествуя по пескам, вы видите прекрасное озеро. Иссушающая жара заставляет воду выглядеть особенно освежающей. Вы идете к озеру до тех пор, пока не замечаете некую странность, и тогда понимаете, что видите мираж. Что произошло с озером, когда оно было осознано как мираж? Оно просто исчезло в тот момент или же оно перестало быть когда бы то ни было? Вот еще один пример: вы идете по той же пустыне, замечаете змею и отпрыгиваете в сторону. Затем вы понимаете, что это просто палка, кусок веревки или какой-то другой похожий на змею предмет. Что случилось со змеей? Она просто исчезла в тот момент или перестала существовать во все времена? Подумайте об этом.
Вчера вечером я изложил вам две теории о природе математики. Одну называют логицизмом, а другую формализмом; первая связана с именем Рассела, вторая-со школой Гильберта. Существует и третья, современная теория, которую называют математическим интуиционизмом (хотя не очень ясно, почему она получила именно такое название). Это направление было развито, в первую очередь, Брауэром и Вейлем [4], которые заложили важнейшие основы современной математической мысли. Они сомневаются даже в допустимости приложения метода исключения к рассуждениям о бесконечности, хотя большая часть теории бесконечных множеств опиралась на определенные принципы, часто используемые в обычной математике [5]. Иногда случается так, что вы не можете непосредственно доказать некий факт, но при этом знаете, что существует ограниченное количество возможных вариантов -например, только два. Скажем, любое число может быть либо простым, либо не простым. Если не получается непосредственно доказать, что выбранное число является простым, то это можно сделать методом от противного, то есть показать, что оно не является не простым. Брауэр и Вейль считают, что этот принцип, подразумевающий суждение об исключении третьего, становится недопустимым в оценке бесконечных классов. В любом случае, подобное мнение может иметь достаточно важное значение. Однако я хочу показать вам, что среди самих математиков нет общего согласия в отношении окончательной природы того, с чем они имеют дело. То же относится и к логике: в ней все согласны с принципами подробного процесса, с тем, как следует подходить к рассматриваемому вопросу, но возникают расхождения во мнениях об окончательном содержании самого вопроса. Таким образом, мы сталкиваемся с различными взглядами на основополагающий характер самой математики.
Я не вполне уверен в том, что человек, занимающийся только математикой, имеет право на мнение о математике. Я уже цитировал слова Вейерштрасса о том, что математик, в котором нет ни капли поэта, – не настоящий математик. Лично я добавил бы, что математик, в котором нет ни капли философа, не имеет права судить о том, чем он занимается. Я хочу обратиться к тому человеку, который стал одним из двух величайших философов в истории. Я имею в виду Шпенглера, преподавателя математики в гимназии – даже не в университете. Он не был математиком-творцом. Этот человек написал знаменитую книгу «Закат Европы» [6], которая мгновенно подняла на ноги практически весь интеллектуальный мир. Первая после вступления глава его работы посвящена значению чисел, и, по моему мнению, содержание этого раздела проникает в основополагающую сущность математики намного глубже, чем все представленные до сих пор мнения.
Сейчас я зачитаю вам несколько отрывков из книги Шпенглера.
Чтобы наглядно показать тот способ, каким дупла стремится найти свое место в общей картине внешнего мира, – то есть для того, чтобы продемонстрировать, в какой мере Культура в состоянии своего «становления» проявляет или отражает представления о человеческом существовании, – я выбрал понятие числа, изначального элемента, на котором покоится любая математика. Я делаю это по той причине, что математика, доступная во всей своей глубине лишь немногим, занимает совершенно особое место среди всех порождений разума. Это наука самой строгой упорядоченности, и в этом она подобна логике, хотя и является более всеохватной и намного более полной; наряду со скульптурой и музыкой, это подлинное искусство, поскольку требует напутствующего вдохновения и развивается в рамках широких соглашений о формах; это, наконец, метафизика высочайшего уровня, что продемонстрировали Платон и, прежде всего, Лейбниц. Вследствие этого любая философия вырастает в тесном родстве с присущей ей математикой. Число представляет собой повседневно необходимый символ. Подобно концепции Бога, оно содержит в себе окончательный смысл мира как природы. Таким образом, существование чисел можно назвать загадкой, и религиозная мысль любой Культуры испытала на себе их влияние [7].
Итак, в числах как знаках завершенной отделенностн кроется сущность всего действительного, того, что распознано, очерчено четкими границами и становится сразу всем, – Пифагор и некоторые другие смогли увидеть это с полной внутренней убежденностью, вызванной могущественной и подлинно религиозной интуицией [8].
Таким образом, стиль любой зарождающейся математики полностью зависит от той культуры, в которой она возникает, от особенностей народа, над ней размышляющего [9].
Австралийские аборигены, которых относят по интеллектуальному уровню к грубым первобытным народам, обладают математическим инстинктом (или, что то же самое, способностью мыслить числами, еще не выраженными знаками или словами), намного превосходящим греческий в вопросах о толковании чистого пространства. Именно австралийцы изобрели бумеранг, и это можно объяснить только тем, что они владеют уверенным ощущением чисел того класса, для обращения с которым нам требуется прибегать в высшей геометрии [10].
Математика покидает сферу наблюдений и анализа. В минуты своих взлетов она нащупывает путь, опираясь на видения, а не на абстрактные рассуждения [11].
Таким образом, это толкование означает, что число представляет собой основную форму выражения духа культуры, что существует не единственная математика, а множество математик – и наши познания в этой области развивались отнюдь не по прямой линии, тянущейся от вавилонян через греков и арабов к современному миру с неизменными представлениями, с единственным содержанием. Вовсе нет! Шпенглер подчеркивает, что в каждой культуре числа получали особое, иное значение. Для греков они были чем-то похожим на четко разграниченные пространственные тела. Греков заботило не само пространство, а осязаемые, твердые поверхности, такие тела, которые можно ощутить, и потому их числа были, в основном, простыми целыми величинами и связанными с ними дробями. Так продолжалось вплоть до того нервного потрясения, которое пережил Пифагор [12]. Должно быть, вы помните его теорему (см. рис. 12) о том, что сумма квадратов катетов прямоугольного треугольника равна квадрату его гипотенузы (в наши дни любой плотник пользуется ею для разметки своих изделий).
Еще одним человеком, который обладал всеми знаниями, известными миру Запада, – последним человеком, знавшим все, – был Лейбниц; он создал великую математику и великую философию. Кроме того, были Вейерш-трасси его чела Софья [3], которая стала величайшей женщиной-математиком. Был Гильберт, лучший математик своих дней. Однажды, читая лекцию студентам, он запнулся, так как не мог умножить 6 на 7. Один студент с готовностью выкрикнул: «41», а другой: «43». Гильберт ответил: «Господа, господа, я уверен, что существует единственный правильный ответ». Хорошее подтверждение тому, что математики редко умеют хорошо считать. Это две весьма различные способности.
Помимо того, я пересек мысленным взором весь мир и заглянул в чужие земли, чтобы увидеть Шанкару-математика из математиков, который еще мальчиком скитался по всей Индии и вызывал смятение у браминов; он уводил мужей от жен, так как те становились его саньясинами. По каким-то непонятным причинам женам это очень не нравилось, но выбора не было – оставалась только возможность примкнуть к рядам победителя. Взмахивая волшебной палочкой своей логики, этот человек заставил мир зримых проявлений исчезнуть, и на месте этого мира не осталось ничего, кроме Бога.
Вот пример его могущественной логики. Шанкара говорил, что, когда человек осознает иллюзорность определенного явления, это явление не только прекращает существование, но и лишается права на существование когда бы то ни было. Возможно, вам будет проще понять это, если такое переживание сравнить со зрелищем миража в пустыне. Путешествуя по пескам, вы видите прекрасное озеро. Иссушающая жара заставляет воду выглядеть особенно освежающей. Вы идете к озеру до тех пор, пока не замечаете некую странность, и тогда понимаете, что видите мираж. Что произошло с озером, когда оно было осознано как мираж? Оно просто исчезло в тот момент или же оно перестало быть когда бы то ни было? Вот еще один пример: вы идете по той же пустыне, замечаете змею и отпрыгиваете в сторону. Затем вы понимаете, что это просто палка, кусок веревки или какой-то другой похожий на змею предмет. Что случилось со змеей? Она просто исчезла в тот момент или перестала существовать во все времена? Подумайте об этом.
Вчера вечером я изложил вам две теории о природе математики. Одну называют логицизмом, а другую формализмом; первая связана с именем Рассела, вторая-со школой Гильберта. Существует и третья, современная теория, которую называют математическим интуиционизмом (хотя не очень ясно, почему она получила именно такое название). Это направление было развито, в первую очередь, Брауэром и Вейлем [4], которые заложили важнейшие основы современной математической мысли. Они сомневаются даже в допустимости приложения метода исключения к рассуждениям о бесконечности, хотя большая часть теории бесконечных множеств опиралась на определенные принципы, часто используемые в обычной математике [5]. Иногда случается так, что вы не можете непосредственно доказать некий факт, но при этом знаете, что существует ограниченное количество возможных вариантов -например, только два. Скажем, любое число может быть либо простым, либо не простым. Если не получается непосредственно доказать, что выбранное число является простым, то это можно сделать методом от противного, то есть показать, что оно не является не простым. Брауэр и Вейль считают, что этот принцип, подразумевающий суждение об исключении третьего, становится недопустимым в оценке бесконечных классов. В любом случае, подобное мнение может иметь достаточно важное значение. Однако я хочу показать вам, что среди самих математиков нет общего согласия в отношении окончательной природы того, с чем они имеют дело. То же относится и к логике: в ней все согласны с принципами подробного процесса, с тем, как следует подходить к рассматриваемому вопросу, но возникают расхождения во мнениях об окончательном содержании самого вопроса. Таким образом, мы сталкиваемся с различными взглядами на основополагающий характер самой математики.
Я не вполне уверен в том, что человек, занимающийся только математикой, имеет право на мнение о математике. Я уже цитировал слова Вейерштрасса о том, что математик, в котором нет ни капли поэта, – не настоящий математик. Лично я добавил бы, что математик, в котором нет ни капли философа, не имеет права судить о том, чем он занимается. Я хочу обратиться к тому человеку, который стал одним из двух величайших философов в истории. Я имею в виду Шпенглера, преподавателя математики в гимназии – даже не в университете. Он не был математиком-творцом. Этот человек написал знаменитую книгу «Закат Европы» [6], которая мгновенно подняла на ноги практически весь интеллектуальный мир. Первая после вступления глава его работы посвящена значению чисел, и, по моему мнению, содержание этого раздела проникает в основополагающую сущность математики намного глубже, чем все представленные до сих пор мнения.
Сейчас я зачитаю вам несколько отрывков из книги Шпенглера.
Чтобы наглядно показать тот способ, каким дупла стремится найти свое место в общей картине внешнего мира, – то есть для того, чтобы продемонстрировать, в какой мере Культура в состоянии своего «становления» проявляет или отражает представления о человеческом существовании, – я выбрал понятие числа, изначального элемента, на котором покоится любая математика. Я делаю это по той причине, что математика, доступная во всей своей глубине лишь немногим, занимает совершенно особое место среди всех порождений разума. Это наука самой строгой упорядоченности, и в этом она подобна логике, хотя и является более всеохватной и намного более полной; наряду со скульптурой и музыкой, это подлинное искусство, поскольку требует напутствующего вдохновения и развивается в рамках широких соглашений о формах; это, наконец, метафизика высочайшего уровня, что продемонстрировали Платон и, прежде всего, Лейбниц. Вследствие этого любая философия вырастает в тесном родстве с присущей ей математикой. Число представляет собой повседневно необходимый символ. Подобно концепции Бога, оно содержит в себе окончательный смысл мира как природы. Таким образом, существование чисел можно назвать загадкой, и религиозная мысль любой Культуры испытала на себе их влияние [7].
Итак, в числах как знаках завершенной отделенностн кроется сущность всего действительного, того, что распознано, очерчено четкими границами и становится сразу всем, – Пифагор и некоторые другие смогли увидеть это с полной внутренней убежденностью, вызванной могущественной и подлинно религиозной интуицией [8].
Таким образом, стиль любой зарождающейся математики полностью зависит от той культуры, в которой она возникает, от особенностей народа, над ней размышляющего [9].
Австралийские аборигены, которых относят по интеллектуальному уровню к грубым первобытным народам, обладают математическим инстинктом (или, что то же самое, способностью мыслить числами, еще не выраженными знаками или словами), намного превосходящим греческий в вопросах о толковании чистого пространства. Именно австралийцы изобрели бумеранг, и это можно объяснить только тем, что они владеют уверенным ощущением чисел того класса, для обращения с которым нам требуется прибегать в высшей геометрии [10].
Математика покидает сферу наблюдений и анализа. В минуты своих взлетов она нащупывает путь, опираясь на видения, а не на абстрактные рассуждения [11].
Таким образом, это толкование означает, что число представляет собой основную форму выражения духа культуры, что существует не единственная математика, а множество математик – и наши познания в этой области развивались отнюдь не по прямой линии, тянущейся от вавилонян через греков и арабов к современному миру с неизменными представлениями, с единственным содержанием. Вовсе нет! Шпенглер подчеркивает, что в каждой культуре числа получали особое, иное значение. Для греков они были чем-то похожим на четко разграниченные пространственные тела. Греков заботило не само пространство, а осязаемые, твердые поверхности, такие тела, которые можно ощутить, и потому их числа были, в основном, простыми целыми величинами и связанными с ними дробями. Так продолжалось вплоть до того нервного потрясения, которое пережил Пифагор [12]. Должно быть, вы помните его теорему (см. рис. 12) о том, что сумма квадратов катетов прямоугольного треугольника равна квадрату его гипотенузы (в наши дни любой плотник пользуется ею для разметки своих изделий).