Большая Советская Энциклопедия (ДЛ)
дуги
— предел Д. вписанных в эту дугу ломаных, когда число звеньев неограниченно увеличивается и максимальная Д. звеньев стремится к нулю. 4) Д. непрерывной кривой, состоящей из конечного числа простых дуг, равна сумме Д. этих дуг. Например, Д. окружности может быть получена как предел периметров правильных вписанных многоугольников при неограниченном удвоении числа их сторон и равна 2p
R, где
R— радиус окружности. Всякая непрерывная кривая имеет Д. — конечную или бесконечную. Если её Д. конечна, то кривая называется спрямляемой. График функции (см.
рис.
)
даёт пример неспрямляемой кривой; здесь Д. вписанных ломаных неограниченно растут, когда Д. звеньев стремятся к нулю. Если уравнение плоской кривой в прямоугольных координатах имеет вид
у=
f(
x) (
aЈ
xЈ
b), причём функция
f(
x) имеет непрерывную производную
fў
(
x), то Д. кривой выражается интегралом
Аналогично выражается Д. кривой, заданной параметрически, и Д. пространственной кривой.
К вычислению Д. кривой при помощи предельного перехода из Д. ломаных прибегали по существу ещё математики древности. Для них, однако, этот предельный переход был лишь способом вычисления Д. кривой, а не определения понятия Д. кривой, т.к. последнее им представлялось, по-видимому, одним из первоначальных математических понятий. Необходимость определения Д. кривой стала ясной лишь в 1-й половине 19 в. Полное выяснение вопроса было достигнуто К.
Жорданом
. В
дифференциальной геометрии
определяется также Д. кривой на поверхности или в произвольном римановом пространстве. О единицах и технике измерения Д. см.
Меры длины
,
Измерение
.
Лит.:Лебег А., Об измерении величин, пер. с франц., 2 изд., М., 1960; Фихтенгольц Г. М., Курс дифференциального и интегрального исчисления, 7 изд., т. 2, М., 1969.
С. Б. Стечкин.
Рис. к ст. Длина.
волны
, находящимися в одинаковой
фазе
колебания. Д. в. l связана с периодом колебания
Ти скоростью
сраспространения волны соотношением l =
сТ.
эффективное поперечное сечение
молекулы. С повышением плотности газа (его давления) Д. с. п. уменьшается, т.к. растет число столкновений n в 1
сек. Повышение температуры (интенсивности движения молекул) приводит к некоторому уменьшению s и, следовательно, к росту `
l. Для обычных молекулярных газов в
нормальных условиях
(при атмосферном давлении и 20°С) `
l~ 10
-5
см, что примерно в 100 раз больше среднего расстояния между молекулами.
К частицам, движение и взаимодействие которых подчиняется законам
квантовой механики
, понятие Д. с. п. в ряде случаев также применимо (например, электроны проводимости в твёрдом теле,
нейтроны
в слабо поглощающих средах,
фотоны
в звёздах), но расчёт Д. с. п. для таких частиц более сложен.
волновое сопротивление
Wи скорость распространения
vэлектромагнитных волн вдоль неё. Мгновенные значения силы переменного тока и напряжения в любой точке Д. л. математически связаны между собой так называемыми телеграфными уравнениями. Д. л. называется однородной, если значения её параметров неизменны на всём протяжении; при отсутствии в ней электрических потерь, т. е.
R=
G= 0 (обычно на радиочастотах),
Входное сопротивление Д. л. имеет в общем случае комплексный характер (содержит активную и реактивную составляющие) и зависит от длины линии и характера электрической нагрузки на её конце (выходе). Входное сопротивление Д. л. бесконечной длины равно
W. Для максимальной передачи энергии от источника линии её входное сопротивление должно быть активным и равным внутреннему сопротивлению источника, т. е. согласованным с ним. Различают 3 режима работы Д. л.: режим бегущей волны, когда передаваемая энергия полностью поглощается нагрузкой (сопротивление нагрузки активное и равное
W); режим стоячей волны, когда передаваемая энергия полностью отражается от конца линии к источнику (короткозамкнутая или разомкнутая на конце Д. л.), и промежуточный режим (сопротивление нагрузки комплексное и не равное
W). Д. л. применяют для передачи информации в дальней телеграфно-телефонной связи, телевидении, радиолокации, а также для передачи энергии по проводам на далёкие расстояния (см.
Линия электропередачи
).
Лит.:Гарновский Н. Н., Теоретические основы электропроводной связи, ч. 2, М., 1959; Гоноровский И. С., Радиотехнические цепи и сигналы, ч. 2, М., 1967.
Ю. Б. Любченко.
балансомера
или
пиргеометра
. Методы измерения Д. и. в дневное время недостаточно совершенны из-за трудности отделения Д. и. от коротковолнового излучения, поэтому часто Д. и. определяют с помощью различных расчётных методов.
Лит.:Кондратьев К. Я., Актинометрия, Л., 1965.
К. Я. Кондратьев.
стрижи
и
колибри
. Из внешних признаков для Д. характерно строение крыла — очень длинного и узкого с укороченной плечевой костью и короткими второстепенными маховыми перьями, что обеспечивает Д. быстрый манёвренный полёт. В кладке 1—3 белых яйца. Птенцы вылупляются слепыми, родители кормят их, пока птенцы не начнут летать. Около 400 видов, распространённых в умеренном и особенно в тропических поясах.
двукрылых
; 2) отряд
прямокрылых
насекомых.
промышленного скрещивания
с крупной белой и др. породами. Основное поголовье длинноухих белых свиней и их помесей сосредоточено в РСФСР (Поволжье), Украинской ССР и Белорусской ССР.
Д. б. п. широко распространена в ГДР (немецкая вислоухая свинья), где составляет 75% поголовья свиней; пользуется большим международным спросом и экспортируется во многие страны.
Лит.:Руководство по разведению животных, [пер. с нем.], т. 3, кн. 2, М., 1965; Волкопялов Б. П., Свиноводство, 4 изд., Л., 1968.
А. И. Нетеса.
Матка длинноухой белой породы.
дифракции радиоволн
на сферической поверхности Земли на расстояния до 1—2 тыс.
км. На более далёкие расстояния Д. в. распространяются за счёт направляющего действия сферического атмосферного волновода, образованного поверхностью Земли и нижней границей ионосферы (см.
Распространение радиоволн
).
Польской рабочей партии
(1945), а затем членом ЦК
Польской объединённой рабочей партии
(1948). В 1945—48 работал главным редактором газеты «Глос люду» («GBos Ludu»). Д. — член Всемирного Совета Мира (с 1950), лауреат Международной Ленинской премии «За укрепление мира между народами» (1960).
О. Длуский.
даёт пример неспрямляемой кривой; здесь Д. вписанных ломаных неограниченно растут, когда Д. звеньев стремятся к нулю. Если уравнение плоской кривой в прямоугольных координатах имеет вид
у=
f(
x) (
aЈ
xЈ
b), причём функция
f(
x) имеет непрерывную производную
fў
(
x), то Д. кривой выражается интегралом
Аналогично выражается Д. кривой, заданной параметрически, и Д. пространственной кривой.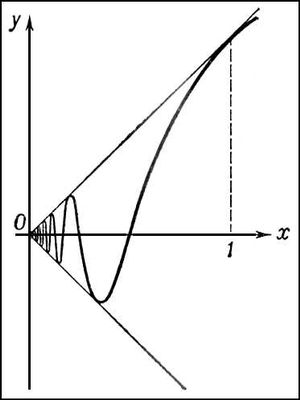
Рис. к ст. Длина.
