Страница:
Нет сомнений в том, что этот крестьянин, мужественно защищающий свою землю от пришельцев, и слыхом не слыхал о законах механики. Но в этой схватке он использует «кинетическую энергию» удара противника, он создает «опрокидывающий момент относительно точки опоры»… Словом, действует-то по законам механики! Так неужели мы, люди, вооруженные техническими знаниями, опираясь на боевой опыт предков, могли бы не заметить лежащего на поверхности вывода? А именно: необходимо перейти с интуитивного уровня на уровень осознанного применения, а точнее – учета законов механики в практике рукопашного боя. Это позволит нам в конечном счете успешно решить двуединую задачу: как возрождения самой системы рукопашного боя (притом на более высоком уровне), так и совершенствования существующей системы подготовки воина-рукопашника. Такой подход дает нам право говорить о новом стиле рукопашного боя. Именно о таком стиле, получившем название «русский рукопашный бой по системе выживания», идет речь.
Этот стиль прошел испытания в так называемых «горячих точках» и показал свою боеспособность, спасая жизнь тем, кто овладел этим искусством.
В приложении механики к рукопашному бою автор исповедует два подхода:
– применение законов механики в строгом научном изложении;
– представление законов механики на ассоциативном уровне.
Кто же он – настоящий рукопашник?
Часть 2
Человек как объект природы
Понятие о степенях свободы
Модельное представление человека
Кинематические пары
Этот стиль прошел испытания в так называемых «горячих точках» и показал свою боеспособность, спасая жизнь тем, кто овладел этим искусством.
В приложении механики к рукопашному бою автор исповедует два подхода:
– применение законов механики в строгом научном изложении;
– представление законов механики на ассоциативном уровне.
Кто же он – настоящий рукопашник?
Рукопашник – это человек, овладевший искусством рукопашного боя. Но одного этого мало. Настоящий рукопашник отличается многими дополнительными качествами. Так кто же он – настоящий рукопашник? Это, прежде всего, воин-христианин, хранитель Святой Веры и Отечества. Это высоконравственная, духовно богатая личность. Это хранитель традиций своих предков. И, наконец, это человек, сильный духом, готовый отдать жизнь за Веру и Отечество. Настоящий рукопашник:
– владеет всеми видами оружия, начиная с грубой палки и кончая утонченной шпагой, а также современным огнестрельным оружием;
– умеет вести огонь, не прицеливаясь, на звук и вспышку, по ноге от бедра;
– умеет, не обнаруживая себя, вести разведку;
– может так организовать ближний бой, чтобы без потерь перейти к рукопашной схватке;
– обладает психологической устойчивостью к действиям в экстремальных ситуациях. Настоящий рукопашник проявляет себя тогда, когда надо не просто действовать, а действовать правильно, наилучшим образом в непредсказуемой обстановке, когда нет времени задуматься и нельзя ошибиться. Настоящий рукопашник – человек дисциплинированный, обладающий чувством ответственности, умеющий мгновенно анализировать сложные ситуации боя, молниеносно принимающий единственно правильное решение и, не последнее, виртуозно владеющий своим телом.
– владеет всеми видами оружия, начиная с грубой палки и кончая утонченной шпагой, а также современным огнестрельным оружием;
– умеет вести огонь, не прицеливаясь, на звук и вспышку, по ноге от бедра;
– умеет, не обнаруживая себя, вести разведку;
– может так организовать ближний бой, чтобы без потерь перейти к рукопашной схватке;
– обладает психологической устойчивостью к действиям в экстремальных ситуациях. Настоящий рукопашник проявляет себя тогда, когда надо не просто действовать, а действовать правильно, наилучшим образом в непредсказуемой обстановке, когда нет времени задуматься и нельзя ошибиться. Настоящий рукопашник – человек дисциплинированный, обладающий чувством ответственности, умеющий мгновенно анализировать сложные ситуации боя, молниеносно принимающий единственно правильное решение и, не последнее, виртуозно владеющий своим телом.
«…Опираясь на автомат, из „Жигулей“ расслабленно-вяло вылез, поднялся во весь рост высокий, упакованный в набитую боеприпасами разгрузку бандит и удивленно, просто впиваясь глазами, словно желая запомнить, посмотрел на лежащего ничком Олега. Медлить было нельзя. Капитан Уфимцев снова открыл огонь, уничтожив боевика. Уже отползая от машины, Олег попал под автоматные очереди с двух отдаленных точек. Он не видел противника, уходя от пуль „нижней акробатикой“. Пули, разбиваясь о каменистую почву где-то рядом, мелкими осколками резали руки, лицо. А тридцативосьмилетний ученик великого наставника армейских спецназовцев Алексея Кадочникова, ведя ответный огонь, уходил от поражения…»
Журнал «Милиция», № 10, октябрь 2000 г.
Часть 2
Научные основы рукопашного боя
Человек как объект природы
Физика оперирует такими абстрактными понятиями, как материальная точка, абсолютно твердое тело, количество движения… По-видимому, по этой причине нередко говорят: «Физика – наука о неживой природе».[1]
Из этого как будто бы следует, что для живого мира, в том числе для человека, должны существовать какие-то особые законы.
Но еще в XVI веке Леонардо да Винчи утверждал, что «наука механика потому столь благородна и полезна более всех прочих наук, что, как оказывается, все живые тела, имеющие способность к движению, действуют по ее законам».
Действительно, ведь человек живет в мире, устроенном и функционирующем в соответствии с законами физики. Наравне с другими объектами природы он совершает перемещения, участвует в силовых взаимодействиях, подвергается влиянию физических полей разного рода.
Поэтому человек, хотя и относится к живой, осознающей себя материи, является полноправным объектом изучения физики. Более того, его следует рассматривать как сложную физическую систему, в которой функционирование отдельных частей и взаимодействие с окружающей средой определяются конкретными физическими законами.
И все-таки правомерно ли распространение законов классической механики на живые системы, в том числе на человека?
Ведь, во-первых, известно, что основные законы классической механики описывают движение абстрактных абсолютно твердых тел, то есть таких тел, которые не деформируются (не изменяют своей формы и размеров).[2]
Во-вторых, живые системы коренным образом отличаются от абсолютно твердых тел. Это отличие состоит в возможности существенного изменения не только формы и размеров, но и относительного расположения составных частей системы. Для человека, в частности, эти изменения характеризуются таким понятием как поза. То есть с точки зрения механики, тело человека является телом переменной конфигурации. Иногда и отдельные части живой системы (например, позвоночный столб, грудная клетка человека) также существенно деформируются.
Двигательная деятельность человека – одно из сложнейших явлений материального мира. Она сложна потому, что очень непросты функции органов движения. Она сложна и потому, что в ней участвует сознание как продукт наиболее организованной материи – мозга. Поэтому двигательная деятельность человека существенно отличается от двигательных действий животных. Сходство между движениями животных и человека имеется на чисто биологическом уровне.
В первую очередь речь идет об осознанной, целенаправленной, активной деятельности человека, о понимании ее смысла, о возможности контролировать и планомерно совершенствовать свои движения. При помощи двигательной деятельности человек активно преобразует мир, свою собственную природу, физически совершенствуется.
Двигательная деятельность человека складывается из его действий, всегда имеющих цель и определенный смысл. Двигательные действия осуществляются при помощи произвольных активных движений, совершаемых и управляемых работой мышц. Человек по собственной воле начинает движения, изменяет их и прекращает, когда цель достигнута.
Двигательные действия человека, в свою очередь, включают в себя механическое движение. Именно оно представляет непосредственную цель двигательного действия (переместиться самому, переместить противника или партнера).
Любое движение человека осуществляется при определяющем участии в двигательном действии более высоких биологических форм движения. Именно поэтому движения живых систем не только намного сложнее, но и, без сомнения, качественно отличаются от движений твердых тел. Движения человека происходят как под действием внешних сил (сил тяжести, трения, инерции и др.), так и под действием внутренних сил (сил тяги мышц). А поскольку мышцы управляют центральной нервной системой, то и развиваемые ими силы обусловлены физиологическими процессами. Поэтому для понимания сущности живого движения необходимо не только изучение собственно механики движений, но и рассмотрение биологической стороны.
То есть, применяя общие законы механики к живым объектам, необходимо учитывать их не только механические, но и биологические особенности. Такие, например, как приспособляемость движений к внешним условиям, подверженность живого организма утомлению, возможность совершенствования движений и целый ряд других.
Итак, следует знать, что не существует особых законов механики для объектов живого мира. Все живые системы подчиняются законам классической механики. Но насколько живые системы отличаются от абстрактных абсолютно твердых тел, настолько же движения существа сложнее движений абсолютно твердого тела. Природа движений рассматривается во взаимосвязи закономерностей механики и биологии с учетом роли человеческого сознания в целенаправленном управлении движениями.
Из этого как будто бы следует, что для живого мира, в том числе для человека, должны существовать какие-то особые законы.
Но еще в XVI веке Леонардо да Винчи утверждал, что «наука механика потому столь благородна и полезна более всех прочих наук, что, как оказывается, все живые тела, имеющие способность к движению, действуют по ее законам».
Действительно, ведь человек живет в мире, устроенном и функционирующем в соответствии с законами физики. Наравне с другими объектами природы он совершает перемещения, участвует в силовых взаимодействиях, подвергается влиянию физических полей разного рода.
Поэтому человек, хотя и относится к живой, осознающей себя материи, является полноправным объектом изучения физики. Более того, его следует рассматривать как сложную физическую систему, в которой функционирование отдельных частей и взаимодействие с окружающей средой определяются конкретными физическими законами.
И все-таки правомерно ли распространение законов классической механики на живые системы, в том числе на человека?
Ведь, во-первых, известно, что основные законы классической механики описывают движение абстрактных абсолютно твердых тел, то есть таких тел, которые не деформируются (не изменяют своей формы и размеров).[2]
Во-вторых, живые системы коренным образом отличаются от абсолютно твердых тел. Это отличие состоит в возможности существенного изменения не только формы и размеров, но и относительного расположения составных частей системы. Для человека, в частности, эти изменения характеризуются таким понятием как поза. То есть с точки зрения механики, тело человека является телом переменной конфигурации. Иногда и отдельные части живой системы (например, позвоночный столб, грудная клетка человека) также существенно деформируются.
Двигательная деятельность человека – одно из сложнейших явлений материального мира. Она сложна потому, что очень непросты функции органов движения. Она сложна и потому, что в ней участвует сознание как продукт наиболее организованной материи – мозга. Поэтому двигательная деятельность человека существенно отличается от двигательных действий животных. Сходство между движениями животных и человека имеется на чисто биологическом уровне.
Двигательная деятельность человека складывается из его действий, всегда имеющих цель и определенный смысл. Двигательные действия осуществляются при помощи произвольных активных движений, совершаемых и управляемых работой мышц. Человек по собственной воле начинает движения, изменяет их и прекращает, когда цель достигнута.
Двигательные действия человека, в свою очередь, включают в себя механическое движение. Именно оно представляет непосредственную цель двигательного действия (переместиться самому, переместить противника или партнера).
Любое движение человека осуществляется при определяющем участии в двигательном действии более высоких биологических форм движения. Именно поэтому движения живых систем не только намного сложнее, но и, без сомнения, качественно отличаются от движений твердых тел. Движения человека происходят как под действием внешних сил (сил тяжести, трения, инерции и др.), так и под действием внутренних сил (сил тяги мышц). А поскольку мышцы управляют центральной нервной системой, то и развиваемые ими силы обусловлены физиологическими процессами. Поэтому для понимания сущности живого движения необходимо не только изучение собственно механики движений, но и рассмотрение биологической стороны.
То есть, применяя общие законы механики к живым объектам, необходимо учитывать их не только механические, но и биологические особенности. Такие, например, как приспособляемость движений к внешним условиям, подверженность живого организма утомлению, возможность совершенствования движений и целый ряд других.
Итак, следует знать, что не существует особых законов механики для объектов живого мира. Все живые системы подчиняются законам классической механики. Но насколько живые системы отличаются от абстрактных абсолютно твердых тел, настолько же движения существа сложнее движений абсолютно твердого тела. Природа движений рассматривается во взаимосвязи закономерностей механики и биологии с учетом роли человеческого сознания в целенаправленном управлении движениями.
Понятие о степенях свободы
Человек изучает окружающий мир для того, чтобы приспособить его к себе, сделать безопасным для себя свое существование в нем. Поэтому процесс человеческого познания специфичен по целям, объекту и методам исследования.
Изучая какое-то явление природы, человек выделяет из всего многообразия связей и сторон этого явления то, что его больше всего интересует, и создает в своем сознании мысленный образ, идеальный объект. Этот объект можно считать некоей моделью, наблюдая за которой, изучают качественные и количественные закономерности ее поведения.
Таблица 1
Эксперименты с идеальным объектом позволяют обнаружить количественные взаимосвязи, так называемые физические законы.
Эти рассуждения можно представить в виде схемы (таблица 1).
В механике при изучении движения различных физических объектов используются следующие модельные представления: материальная точка, абсолютно твердое тело, система материальных точек или тел.
Простейшей моделью является материальная точка – тело, размерами которого в данных условиях движения можно пренебречь. В этом определении слова «в данных условиях движения» означают, что одно и то же тело при определенных его движениях можно считать точкой, а при других нельзя.
Понятие материальной точки абстрактное, но его введение облегчает решение многих практических задач. Например, океанский лайнер крайне мал по сравнению с протяженностью его рейса, и поэтому корабль можно считать точкой при описании движения в океане. Точно так же материальной точкой можно представить самолет или ракету, изучая их поступательное движение по заданным траекториям. Движение тел происходит в пространстве и во времени (t). Поэтому положение материальной точки определяется по отношению к какой-либо другой произвольно выбранной точке, называемой точкой отсчета или началом координат.
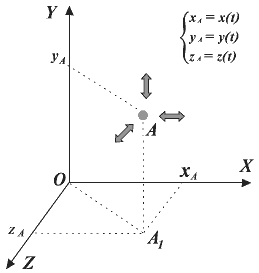
Пусть это будет точка О (рис. 1). Проведя через нее три взаимно перпендикулярные оси Ох, Оу и Oz, получим прямоугольную систему координат, в которой положение материальной точки А (например, положение самолета в воздухе) в данный момент времени характеризуется тремя координатами xA, yA, zA.
Число независимых координат, полностью определяющих положение точки в пространстве, называется числом степеней свободы.
Итак, если материальная точка (рис. 1) свободно движется в пространстве и изменяются ее координаты х, у, z, то она обладает тремя степенями свободы. Если точка В движется по некоторой поверхности (рис. 2) и изменяются ее координаты х, у, то она обладает двумя степенями свободы. Наконец, если точка С движется вдоль любой из осей координат, то она имеет одну степень свободы.
Кажется, к этому нечего добавить. Однако в действительности оказывается, что представление о степенях свободы складывается совсем не просто. Известный ученый-биолог Бернштейн Н. А, великолепно владевший умением рассказывать просто о сложных явлениях, в своей популярной книге о природе движения[3] пишет:
Н. А. Бернштейн
Утверждение об «одной единственной степени свободы» машины-автомата нуждается в оговорке.
Не стоит, по-видимому, говорить о подвижности машины-автомата вообще, в целом, а следует говорить только о подвижности какой-то движущейся детали этой машины.
И тогда здесь, на первый взгляд, обнаруживается некоторое противоречие. Если точка В (рис. 2) движется по дуге окружности в плоскости ХОY, то ее положение в каждый момент времени описывается двумя независимыми координатами xB, yB. Казалось бы, точка В имеет две степени свободы. Но это справедливо только для свободного движения. Если же движение является вынужденным, например, возвратно-поступательным, и «с этого пути движущаяся точка не сходит никогда», то эта точка имеет одну степень свободы.
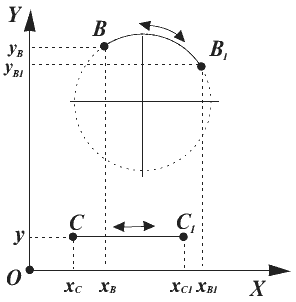Рис. 2
Вернемся к образным рассуждениям Бернштейна:
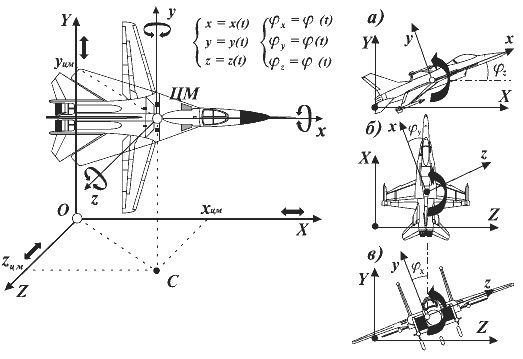Рис. 3
По этой причине в механике вводится еще одна модель – абсолютно твердое тело, то есть тело конечных размеров, которое ни при каких условиях не деформируется (не изменяет свою форму и размеры).
Эта модель существенно отличается от предыдущей. Она позволяет любое движение тела рассматривать как комбинацию поступательного и вращательного движений.
Следовательно, если твердое тело свободно движется в трехмерном пространстве, то оно получает дополнительные три степени свободы, а именно: свободы вращения (поворота) тела относительно каждой из осей координат. А это означает, что всякое твердое тело по сравнению с материальной точкой обладает шестью степенями свободы.
Перемещения тела при поступательном и вращательном движениях измеряются различно. При поступательном движении их можно определить по линейному перемещению любой точки тела, например, его центра масс (ЦМ), в неподвижной системе координат.[4] А при вращательном движении – по углу поворота тела относительно соответствующей координатной оси. Для измерения углов в центре масс тела помещают начало другой, подвижной системы координат, оси которой первоначально ориентированы так же, как и оси неподвижной системы. При повороте тела положение осей этой связанной системы координат относительно неподвижной системы определяется тремя углами.
Так, например, при изучении движения самолета в трехмерном пространстве (рис. 3) рассматривают:
• во-первых, движение его центра масс как материальной точки с массой, равной массе самолета, в неподвижной (земной) системе координат XYZ;
• во-вторых, поворот самолета как твердого тела конечных размеров относительно центра масс.
Положение осей связанной системы хyz, а следовательно, и повороты самолета в земной системе координат определяются тремя углами: φх, φy, φz.
И, наконец, в механике часто используется еще одно модельное представление: связанная система тел – совокупность материальных точек или тел – рассматриваемая как единое целое. Такая система имеет общий центр масс, а число степеней свободы системы обусловливается количеством связей между отдельными ее частями.
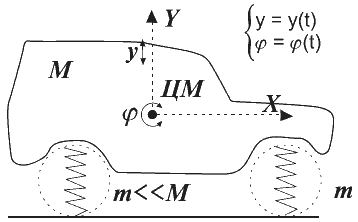Рис. 4
Житейским и понятным примером такой модели может служить автомобиль, кузов и колеса которого образуют взаимосвязанную механическую систему.
Рассмотрим самую простую схему двухосного агрегата, в которой кузов опирается на колесный ход через упругие устройства (например, цилиндрические пружины).
При движении по неровностям дороги возникают колебания автомобиля.
Кузов автомобиля (подрессоренная масса М) колеблется с некоторой частотой w в этих колебательных движениях и, как всякое твердое тело конечных размеров, имеет шесть степеней свободы. Колеса автомобиля (неподрессоренные массы m1) тоже колеблются, но с большей частотой (wk>w).
Если автомобиль имеет независимую подвеску колес, обеспечивающую только их вертикальные перемещения, то колеса имеют по одной степени свободы. Легко догадаться, что в рассматриваемом случае движущийся по неровной дороге четырехколесный автомобиль, рассматриваемый как колебательная механическая система тел, имеет десять степеней свободы.
Принятием дополнительных упрощающих допущений можно прийти к новому модельному представлению автомобиля – к плоской расчетной схеме (рис. 4), имеющей всего две степени свободы движения кузова относительно ЦМ.
Изучая какое-то явление природы, человек выделяет из всего многообразия связей и сторон этого явления то, что его больше всего интересует, и создает в своем сознании мысленный образ, идеальный объект. Этот объект можно считать некоей моделью, наблюдая за которой, изучают качественные и количественные закономерности ее поведения.
Таблица 1
Эти рассуждения можно представить в виде схемы (таблица 1).
В механике при изучении движения различных физических объектов используются следующие модельные представления: материальная точка, абсолютно твердое тело, система материальных точек или тел.
Простейшей моделью является материальная точка – тело, размерами которого в данных условиях движения можно пренебречь. В этом определении слова «в данных условиях движения» означают, что одно и то же тело при определенных его движениях можно считать точкой, а при других нельзя.
Понятие материальной точки абстрактное, но его введение облегчает решение многих практических задач. Например, океанский лайнер крайне мал по сравнению с протяженностью его рейса, и поэтому корабль можно считать точкой при описании движения в океане. Точно так же материальной точкой можно представить самолет или ракету, изучая их поступательное движение по заданным траекториям. Движение тел происходит в пространстве и во времени (t). Поэтому положение материальной точки определяется по отношению к какой-либо другой произвольно выбранной точке, называемой точкой отсчета или началом координат.
Пусть это будет точка О (рис. 1). Проведя через нее три взаимно перпендикулярные оси Ох, Оу и Oz, получим прямоугольную систему координат, в которой положение материальной точки А (например, положение самолета в воздухе) в данный момент времени характеризуется тремя координатами xA, yA, zA.
Число независимых координат, полностью определяющих положение точки в пространстве, называется числом степеней свободы.
Итак, если материальная точка (рис. 1) свободно движется в пространстве и изменяются ее координаты х, у, z, то она обладает тремя степенями свободы. Если точка В движется по некоторой поверхности (рис. 2) и изменяются ее координаты х, у, то она обладает двумя степенями свободы. Наконец, если точка С движется вдоль любой из осей координат, то она имеет одну степень свободы.
«Современная техника создала машины огромной сложности, способные совершенно самостоятельно, без участия человека, выполнять самые разнообразные и непростые операции. И самое поразительное, что все эти машины-автоматы при их сложности и изобилии подвижных частей имеют по одной-единственной степени свободы, т. е. обладают тем, что в технике называют вынужденным движением. Это значит, что каждая движущаяся точка в этих машинах, каждая деталь рычага, тяги или колеса движется все время по одному и тому же строго определенному пути. Форма этого пути может быть очень разнообразной: у одних точек – круговой, у других – прямолинейной, у третьих – овальной и т. д., но с этого пути движущаяся точка не сходит никогда. Таким образом, машины-автоматы в смысле своей подвижности принадлежат к числу самых простых систем, какие только могут существовать».
Утверждение об «одной единственной степени свободы» машины-автомата нуждается в оговорке.
Не стоит, по-видимому, говорить о подвижности машины-автомата вообще, в целом, а следует говорить только о подвижности какой-то движущейся детали этой машины.
И тогда здесь, на первый взгляд, обнаруживается некоторое противоречие. Если точка В (рис. 2) движется по дуге окружности в плоскости ХОY, то ее положение в каждый момент времени описывается двумя независимыми координатами xB, yB. Казалось бы, точка В имеет две степени свободы. Но это справедливо только для свободного движения. Если же движение является вынужденным, например, возвратно-поступательным, и «с этого пути движущаяся точка не сходит никогда», то эта точка имеет одну степень свободы.
Вернемся к образным рассуждениям Бернштейна:
«Если бы какая-нибудь часть такой машины получила вместо одной две степени свободы, это совсем не значило бы, что на ее долю вместо одного достались два или даже несколько возможных путей-траекторий. Нет, это означало бы, что даная часть машины получила возможность „разгуливать“ по какой-то поверхности. Если я возьму перо и стану водить им по поверхности листа бумаги, то, какие бы фигуры ни вздумалось мне им изображать, я нигде не превышу своих возможностей по части дозволенных кончику пера двух степеней свободы, пока буду водить его без отрыва от бумаги. Этот переход от одной степени свободы к двум означает, таким образом, огромный качественный скачок от одной-единственной, точно определенной дорожки-траектории к бесконечному и вполне произвольному разнообразию таких дорожек… Три степени свободы вместо двух дают еще больше, хотя на этот раз не происходит такого огромного качественного скачка, как при переходе от одной к двум степеням свободы… Для пояснения надо сказать, что совершенно ничем не связанная точка, например, вольно порхающая в воздухе снежинка, не может иметь больше трех степеней свободы».При решении практических задач очень часто оказывается, что в данных условиях движения никак нельзя пренебречь размерами тела. Тот же океанский лайнер при исследовании воздействия на него водной стихии (например, при бортовой и килевой качке) материальной точкой уже никак не назовешь, его следует рассматривать как тело конечных размеров.
По этой причине в механике вводится еще одна модель – абсолютно твердое тело, то есть тело конечных размеров, которое ни при каких условиях не деформируется (не изменяет свою форму и размеры).
Эта модель существенно отличается от предыдущей. Она позволяет любое движение тела рассматривать как комбинацию поступательного и вращательного движений.
Следовательно, если твердое тело свободно движется в трехмерном пространстве, то оно получает дополнительные три степени свободы, а именно: свободы вращения (поворота) тела относительно каждой из осей координат. А это означает, что всякое твердое тело по сравнению с материальной точкой обладает шестью степенями свободы.
Перемещения тела при поступательном и вращательном движениях измеряются различно. При поступательном движении их можно определить по линейному перемещению любой точки тела, например, его центра масс (ЦМ), в неподвижной системе координат.[4] А при вращательном движении – по углу поворота тела относительно соответствующей координатной оси. Для измерения углов в центре масс тела помещают начало другой, подвижной системы координат, оси которой первоначально ориентированы так же, как и оси неподвижной системы. При повороте тела положение осей этой связанной системы координат относительно неподвижной системы определяется тремя углами.
Так, например, при изучении движения самолета в трехмерном пространстве (рис. 3) рассматривают:
• во-первых, движение его центра масс как материальной точки с массой, равной массе самолета, в неподвижной (земной) системе координат XYZ;
• во-вторых, поворот самолета как твердого тела конечных размеров относительно центра масс.
Положение осей связанной системы хyz, а следовательно, и повороты самолета в земной системе координат определяются тремя углами: φх, φy, φz.
И, наконец, в механике часто используется еще одно модельное представление: связанная система тел – совокупность материальных точек или тел – рассматриваемая как единое целое. Такая система имеет общий центр масс, а число степеней свободы системы обусловливается количеством связей между отдельными ее частями.
Житейским и понятным примером такой модели может служить автомобиль, кузов и колеса которого образуют взаимосвязанную механическую систему.
Рассмотрим самую простую схему двухосного агрегата, в которой кузов опирается на колесный ход через упругие устройства (например, цилиндрические пружины).
При движении по неровностям дороги возникают колебания автомобиля.
Кузов автомобиля (подрессоренная масса М) колеблется с некоторой частотой w в этих колебательных движениях и, как всякое твердое тело конечных размеров, имеет шесть степеней свободы. Колеса автомобиля (неподрессоренные массы m1) тоже колеблются, но с большей частотой (wk>w).
Если автомобиль имеет независимую подвеску колес, обеспечивающую только их вертикальные перемещения, то колеса имеют по одной степени свободы. Легко догадаться, что в рассматриваемом случае движущийся по неровной дороге четырехколесный автомобиль, рассматриваемый как колебательная механическая система тел, имеет десять степеней свободы.
Принятием дополнительных упрощающих допущений можно прийти к новому модельному представлению автомобиля – к плоской расчетной схеме (рис. 4), имеющей всего две степени свободы движения кузова относительно ЦМ.
Модельное представление человека
Человека, как любое физическое тело, в зависимости от поставленных задач исследования можно рассматривать как материальную точку, как твердое тело или как связанную биомеханическую систему тел.
Как материальную точку человека рассматривают тогда, когда его перемещения намного больше собственных размеров тела и когда не исследуют движения отдельных частей тела и его вращение. Например, при прыжке с парашютом (рис. 5) парящий под куполом человек может рассматриваться как точка, положение которой в неподвижной системе координат XYZ определяется тремя независимыми координатами х1, у1, z1. То есть в данном случае человек обладает тремя степенями свободы.
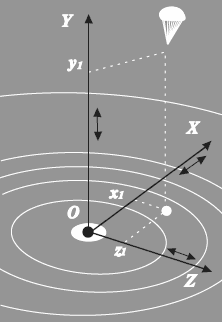Рис. 5
Человека рассматривают как твердое тело конечных размеров тогда, когда важно учитывать не только его местоположение в пространстве, но и ориентацию тела (в частности, при изучении условий статического равновесия человека, а также его вращения в постоянной позе). Так, парашютист, выполняющий в затяжном прыжке элементы воздушной акробатики, перемещается в пространстве относительно неподвижной (земной) системы координат ХYZ. При этом ось OY направлена по нормали к поверхности Земли, ось ОХ – по касательной к горизонту, ось OZ – перпендикулярно первым двум осям.
Положение осей связанной системы xyz, а следовательно, и повороты парашютиста в земной системе координат, определяются тремя углами: φх, φy, φz. То есть парашютист, выполняя акробатические фигуры, может совершать повороты вокруг каждой из осей.
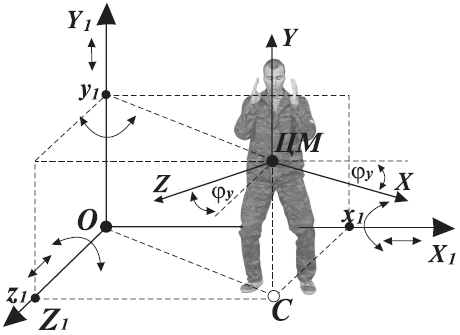Рис. 6
Например, при выполнении фигуры «сальто» вращение тела происходит относительно постоянно ориентированной в пространстве фронтальной оси тела ох (см. рис. 7).
При выполнении «сальто с поворотом» тело парашютиста вращается одновременно относительно, по меньшей мере, двух осей. Первая из них (например, ох) имеет постоянную ориентацию, вторая (к примеру, продольная ось тела оy) изменяет свою ориентацию в пространстве.
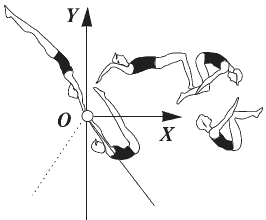Рис. 7
Итак, в свободном полете человек как твердое тело конечных размеров имеет шесть степеней свободы.
Линейные перемещения человека в рукопашном бою определяются изменением координат х1, у1, z1 его ЦМ (рис. 6) в неподвижной системе х1, у1, z1. Повороты тела относительно ЦМ измеряются тремя углами: φх, φy, φz. Так, например, положение осей ОХ и OZ связанной системы координат ХYZ на приведенном рисунке определяется поворотом тела человека вокруг вертикальной оси ОY на угол φy.
При отклонениях продольной оси тела от вертикали во фронтальной или глубинной плоскостях тела происходит поворот тела вокруг осей OZ1 или ОХ1 соответственно.
Опорная поверхность Х1OZ1 является связью, ограничивающей перемещения тела вдоль оси OY1.
Таким образом, рукопашник, стоящий на выпрямленных ногах, имеет пять степеней свободы: перемещения вдоль осей ОХ1, ОZ1 и вращения вокруг координатных осей ОХ1, ОY1, ОZ1. Согнув ноги в коленях (приняв боевую стойку), рукопашник приобретает дополнительную ограниченную степень свободы перемещения вдоль оси ОY1.
В общем случае в рукопашном бою каждая связь, ограничивающая перемещения тела, уменьшает число степеней свободы.
1. Фиксация одной точки тела противника сразу лишает его трех степеней свободы – линейных перемещений вдоль трех основных координатных осей.
2. Закрепление двух точек тела приводит к образованию оси, проходящей через эти точки. В этом случае у тела остается лишь одна степень свободы: вращение относительно данной оси.
3. Закрепление третьей точки, не лежащей на этой оси, полностью лишает противника свободы движений.
Число связей, а следовательно, число степеней свободы может изменяться в процессе выполнения двигательного действия! Например, гимнаст, выполняющий махи на перекладине (рис. 7), обладает всего лишь одной степенью свободы вынужденного движения относительно оси OZ – оси перекладины. При выполнении соскока «дугой с сальто» спортсмен имеет три степени свободы (дополнительные две – в плоскости ХОY). А при соскоке «сальто с поворотом» число степеней свободы возрастает до шести (в зависимости от сложности вращения).
И парашютист, выполняющий акробатические фигуры, и гимнаст, совершающий головоломный соскок, совершают сложные движения. Оба, управляя своим телом, меняют позу. Но в обоих случаях важно проследить за изменением ориентации тела в пространстве, не принимая во внимание взаимные перемещения частей тела. Этим оправдано модельное представление человека как твердого тела.
И, наконец, человека следует рассматривать как связанную систему тел, когда, кроме положения и ориентации человека в пространстве, важно знать взаимное расположение отдельных частей тела относительно друг друга. Это в одинаковой мере относится ко многим видам спортивной двигательной деятельности.
Описание выведения человека из состояния равновесия весьма затруднительно без учета движения всех частей тела. Тут уже, с точки зрения механики, речь идет о представлении тела человека как тела переменной конфигурации. При такой постановке вопроса для описания движений человека должно использоваться соответствующее модельное представление, которое учитывало бы особенности движения отдельных взаимосвязанных частей тела, влияющих на выполнение двигательного действия.
Такой моделью может служить рассматриваемая в дальнейшем связанная биомеханическая система тел.
Как материальную точку человека рассматривают тогда, когда его перемещения намного больше собственных размеров тела и когда не исследуют движения отдельных частей тела и его вращение. Например, при прыжке с парашютом (рис. 5) парящий под куполом человек может рассматриваться как точка, положение которой в неподвижной системе координат XYZ определяется тремя независимыми координатами х1, у1, z1. То есть в данном случае человек обладает тремя степенями свободы.
Человека рассматривают как твердое тело конечных размеров тогда, когда важно учитывать не только его местоположение в пространстве, но и ориентацию тела (в частности, при изучении условий статического равновесия человека, а также его вращения в постоянной позе). Так, парашютист, выполняющий в затяжном прыжке элементы воздушной акробатики, перемещается в пространстве относительно неподвижной (земной) системы координат ХYZ. При этом ось OY направлена по нормали к поверхности Земли, ось ОХ – по касательной к горизонту, ось OZ – перпендикулярно первым двум осям.
Положение осей связанной системы xyz, а следовательно, и повороты парашютиста в земной системе координат, определяются тремя углами: φх, φy, φz. То есть парашютист, выполняя акробатические фигуры, может совершать повороты вокруг каждой из осей.
Например, при выполнении фигуры «сальто» вращение тела происходит относительно постоянно ориентированной в пространстве фронтальной оси тела ох (см. рис. 7).
При выполнении «сальто с поворотом» тело парашютиста вращается одновременно относительно, по меньшей мере, двух осей. Первая из них (например, ох) имеет постоянную ориентацию, вторая (к примеру, продольная ось тела оy) изменяет свою ориентацию в пространстве.
Итак, в свободном полете человек как твердое тело конечных размеров имеет шесть степеней свободы.
Линейные перемещения человека в рукопашном бою определяются изменением координат х1, у1, z1 его ЦМ (рис. 6) в неподвижной системе х1, у1, z1. Повороты тела относительно ЦМ измеряются тремя углами: φх, φy, φz. Так, например, положение осей ОХ и OZ связанной системы координат ХYZ на приведенном рисунке определяется поворотом тела человека вокруг вертикальной оси ОY на угол φy.
При отклонениях продольной оси тела от вертикали во фронтальной или глубинной плоскостях тела происходит поворот тела вокруг осей OZ1 или ОХ1 соответственно.
Опорная поверхность Х1OZ1 является связью, ограничивающей перемещения тела вдоль оси OY1.
Таким образом, рукопашник, стоящий на выпрямленных ногах, имеет пять степеней свободы: перемещения вдоль осей ОХ1, ОZ1 и вращения вокруг координатных осей ОХ1, ОY1, ОZ1. Согнув ноги в коленях (приняв боевую стойку), рукопашник приобретает дополнительную ограниченную степень свободы перемещения вдоль оси ОY1.
В общем случае в рукопашном бою каждая связь, ограничивающая перемещения тела, уменьшает число степеней свободы.
1. Фиксация одной точки тела противника сразу лишает его трех степеней свободы – линейных перемещений вдоль трех основных координатных осей.
2. Закрепление двух точек тела приводит к образованию оси, проходящей через эти точки. В этом случае у тела остается лишь одна степень свободы: вращение относительно данной оси.
3. Закрепление третьей точки, не лежащей на этой оси, полностью лишает противника свободы движений.
Число связей, а следовательно, число степеней свободы может изменяться в процессе выполнения двигательного действия! Например, гимнаст, выполняющий махи на перекладине (рис. 7), обладает всего лишь одной степенью свободы вынужденного движения относительно оси OZ – оси перекладины. При выполнении соскока «дугой с сальто» спортсмен имеет три степени свободы (дополнительные две – в плоскости ХОY). А при соскоке «сальто с поворотом» число степеней свободы возрастает до шести (в зависимости от сложности вращения).
И парашютист, выполняющий акробатические фигуры, и гимнаст, совершающий головоломный соскок, совершают сложные движения. Оба, управляя своим телом, меняют позу. Но в обоих случаях важно проследить за изменением ориентации тела в пространстве, не принимая во внимание взаимные перемещения частей тела. Этим оправдано модельное представление человека как твердого тела.
И, наконец, человека следует рассматривать как связанную систему тел, когда, кроме положения и ориентации человека в пространстве, важно знать взаимное расположение отдельных частей тела относительно друг друга. Это в одинаковой мере относится ко многим видам спортивной двигательной деятельности.
Описание выведения человека из состояния равновесия весьма затруднительно без учета движения всех частей тела. Тут уже, с точки зрения механики, речь идет о представлении тела человека как тела переменной конфигурации. При такой постановке вопроса для описания движений человека должно использоваться соответствующее модельное представление, которое учитывало бы особенности движения отдельных взаимосвязанных частей тела, влияющих на выполнение двигательного действия.
Такой моделью может служить рассматриваемая в дальнейшем связанная биомеханическая система тел.
Кинематические пары
Искусственно созданную механическую систему тел, предназначенную для преобразования движения, называют механизмом. Главной особенностью всякого механизма является определенность движения его частей. Для того чтобы любое тело двигалось определенным образом, необходимо ограничить его подвижность другим телом.