Страница:
2. Факторы, которые входят в систему, должны быть не только необходимыми элементами формулы, но и находиться в причинно-следственной связи с изучаемыми показателями.
3. Все показатели факторной модели должны быть количественно измеримыми, т. е. иметь единицу измерения и необходимую информационную обеспеченность.
4. Факторная модель должна обеспечивать возможность измерения влияния отдельных факторов, т. е. в ней должна учитываться соразмерность изменений результативного и факторных показателей, а сумма влияния отдельных факторов должна равняться общему приросту результативного показателя.
В детерминированном анализе выделяют следующие типы наиболее часто встречающихся факторных моделей.
1. Аддитивные модели. Используются, когда результативный показатель представляет собой алгебраическую сумму нескольких факторных показателей.
2. Мультипликативные модели. Применяются, когда результативный показатель представляет собой произведение нескольких факторов.
3. Кратные модели. Используются, когда результативный показатель получают делением одного факторного показателя на величину другого.
4. Смешанные (комбинированные) модели – это сочетание в различных комбинациях предыдущих моделей.
Моделирование аддитивных факторных систем производится за счет расчленения одного или нескольких факторных показателей на составные элементы.
Моделирование мультипликативных факторных систем осуществляется путем последовательного расчленения факторов исходной системы на факторы-сомножители.
К классу кратных моделей применяют следующие способы их преобразования: удлинения, формального разложения, расширения и сокращения. Первый метод предусматривает удлинение числителя исходной модели путем замены одного или нескольких факторов на сумму однородных показателей. Способ формального разложения факторной системы предусматривает удлинение знаменателя исходной факторной модели путем замены одного или нескольких факторов на сумму или произведение однородных показателей. Метод расширения предусматривает расширение исходной факторной модели за счет умножения числителя и знаменателя дроби на один или несколько новых показателей. Способ сокращения представляет собой создание новой факторной модели путем деления числителя и знаменателя на один и тот же показатель.
Таким образом, результативные показатели могут быть разложены на составные элементы (факторы) различными способами и представлены в виде различных типов детерминированных моделей. Выбор способа моделирования зависит от объекта исследования, поставленной цели, а также от профессиональных знаний и навыков исследователя.
Процесс моделирования факторных систем – очень сложный и ответственный в анализе хозяйственной деятельности. От того, насколько реально и точно созданные модели отражают связь между исследуемыми показателями, зависят конечные результаты анализа.
8. Способы измерения влияния факторов в детерминированных моделях
9. Метод цепных подстановок
10. Индексный метод в факторном анализе
11. Интегральный метод факторного анализа
12. Метод выявления изолированного влияния факторов
13. Способы детерминированной комплексной оценки результатов деятельности
14. Эвристические приемы решения экономических задач
3. Все показатели факторной модели должны быть количественно измеримыми, т. е. иметь единицу измерения и необходимую информационную обеспеченность.
4. Факторная модель должна обеспечивать возможность измерения влияния отдельных факторов, т. е. в ней должна учитываться соразмерность изменений результативного и факторных показателей, а сумма влияния отдельных факторов должна равняться общему приросту результативного показателя.
В детерминированном анализе выделяют следующие типы наиболее часто встречающихся факторных моделей.
1. Аддитивные модели. Используются, когда результативный показатель представляет собой алгебраическую сумму нескольких факторных показателей.
2. Мультипликативные модели. Применяются, когда результативный показатель представляет собой произведение нескольких факторов.
3. Кратные модели. Используются, когда результативный показатель получают делением одного факторного показателя на величину другого.
4. Смешанные (комбинированные) модели – это сочетание в различных комбинациях предыдущих моделей.
Моделирование аддитивных факторных систем производится за счет расчленения одного или нескольких факторных показателей на составные элементы.
Моделирование мультипликативных факторных систем осуществляется путем последовательного расчленения факторов исходной системы на факторы-сомножители.
К классу кратных моделей применяют следующие способы их преобразования: удлинения, формального разложения, расширения и сокращения. Первый метод предусматривает удлинение числителя исходной модели путем замены одного или нескольких факторов на сумму однородных показателей. Способ формального разложения факторной системы предусматривает удлинение знаменателя исходной факторной модели путем замены одного или нескольких факторов на сумму или произведение однородных показателей. Метод расширения предусматривает расширение исходной факторной модели за счет умножения числителя и знаменателя дроби на один или несколько новых показателей. Способ сокращения представляет собой создание новой факторной модели путем деления числителя и знаменателя на один и тот же показатель.
Таким образом, результативные показатели могут быть разложены на составные элементы (факторы) различными способами и представлены в виде различных типов детерминированных моделей. Выбор способа моделирования зависит от объекта исследования, поставленной цели, а также от профессиональных знаний и навыков исследователя.
Процесс моделирования факторных систем – очень сложный и ответственный в анализе хозяйственной деятельности. От того, насколько реально и точно созданные модели отражают связь между исследуемыми показателями, зависят конечные результаты анализа.
8. Способы измерения влияния факторов в детерминированных моделях
После построения факторной модели необходимо определить способ оценки влияния факторов. Большинство способов измерения влияния факторов в детерминированных моделях основано на элиминировании. Элиминировать – значит устранить, исключить воздействие всех факторов на величину результативного показателя, кроме одного, исходя из того, что все факторы изменяются независимо друг от друга, т. е. сначала изменяется один фактор, а все остальные остаются без изменения, потом изменяются два при неизменности остальных и т. д.
Способ цепных подстановок заключается в определении ряда промежуточных значений обобщающего показателя путем последовательной замены базисных значений факторов на отчетные.
В общем виде применение способа цепных постановок можно описать следующим образом:
Y0 = а0⋅Ь0⋅С0; Yусл.1 = а1⋅Ь0⋅С0; Уа = Yусл.1– У0;
Yусл.2 = а1⋅Ь1⋅С0; YЬ = Yусл.2 – Yусл.1; Yф = а1⋅Ь1⋅С1
где а0,Ь0,С0 – базисные значения факторов, оказывающих влияние на обобщающий показатель Y; а1,Ь1,С1 – фактические значения факторов; Yусл.1, Yусл.2 – промежуточные значения результирующего показателя, связанные с изменением факторов а, b соответственно.
Общее изменение складывается из суммы изменений результирующего показателя за счет изменения каждого фактора при фиксированных значениях остальных факторов:
Yа + Yь + Yс = Yф – Y0.
Способ абсолютных разниц является модификацией способа цепной подстановки. Изменение результативного показателя за счет каждого фактора способом абсолютных разниц определяется как произведение отклонения изучаемого фактора на базисное или отчетное значение другого фактора в зависимости от выбранной последовательности подстановки:
Yа = ∆а⋅Ь0⋅С0; Yь = а1⋅ ∆Ь⋅ С0; Yс = а1 ⋅Ь1⋅∆с;
Yа + Yь + Yс = Yф – Y0.
Способ относительных разниц применяется для измерения влияния факторов на прирост результативного показателя в мультипликативных и смешанных моделях вида
Y = (а – Ь) – с.
Заключается в нахождении относительного отклонения каждого факторного показателя и определении направления и размера влияния факторов в % путем последовательного вычитания (из первого – всегда 100 %).
Способ сокращенных подстановок – показатели для расчета представляют собой промежуточные произведения с последовательным накоплением влияющих факторов 3, 3Ь, 3 Ьс. Производятся подстановки, а затем путем последовательного вычитания находятся размеры влияния факторов.
Интегральный метод позволяет достигнуть полного разложения результативного показателя по факторам и носит универсальный характер, т. е. применим к мультипликативным, кратным и смешанным моделям. Изменение результативного показателя измеряется на бесконечно малых отрезках времени, т. е. производится суммирование приращения результата, определяемого как частные произведения, умноженные на приращения факторов на бесконечно малых промежутках.
В специальной литературе имеются сформированные рабочие формулы для применения интегрального метода:
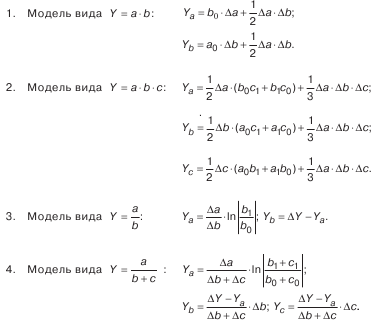
Способ цепных подстановок заключается в определении ряда промежуточных значений обобщающего показателя путем последовательной замены базисных значений факторов на отчетные.
В общем виде применение способа цепных постановок можно описать следующим образом:
Y0 = а0⋅Ь0⋅С0; Yусл.1 = а1⋅Ь0⋅С0; Уа = Yусл.1– У0;
Yусл.2 = а1⋅Ь1⋅С0; YЬ = Yусл.2 – Yусл.1; Yф = а1⋅Ь1⋅С1
где а0,Ь0,С0 – базисные значения факторов, оказывающих влияние на обобщающий показатель Y; а1,Ь1,С1 – фактические значения факторов; Yусл.1, Yусл.2 – промежуточные значения результирующего показателя, связанные с изменением факторов а, b соответственно.
Общее изменение складывается из суммы изменений результирующего показателя за счет изменения каждого фактора при фиксированных значениях остальных факторов:
Yа + Yь + Yс = Yф – Y0.
Способ абсолютных разниц является модификацией способа цепной подстановки. Изменение результативного показателя за счет каждого фактора способом абсолютных разниц определяется как произведение отклонения изучаемого фактора на базисное или отчетное значение другого фактора в зависимости от выбранной последовательности подстановки:
Yа = ∆а⋅Ь0⋅С0; Yь = а1⋅ ∆Ь⋅ С0; Yс = а1 ⋅Ь1⋅∆с;
Yа + Yь + Yс = Yф – Y0.
Способ относительных разниц применяется для измерения влияния факторов на прирост результативного показателя в мультипликативных и смешанных моделях вида
Y = (а – Ь) – с.
Заключается в нахождении относительного отклонения каждого факторного показателя и определении направления и размера влияния факторов в % путем последовательного вычитания (из первого – всегда 100 %).
Способ сокращенных подстановок – показатели для расчета представляют собой промежуточные произведения с последовательным накоплением влияющих факторов 3, 3Ь, 3 Ьс. Производятся подстановки, а затем путем последовательного вычитания находятся размеры влияния факторов.
Интегральный метод позволяет достигнуть полного разложения результативного показателя по факторам и носит универсальный характер, т. е. применим к мультипликативным, кратным и смешанным моделям. Изменение результативного показателя измеряется на бесконечно малых отрезках времени, т. е. производится суммирование приращения результата, определяемого как частные произведения, умноженные на приращения факторов на бесконечно малых промежутках.
В специальной литературе имеются сформированные рабочие формулы для применения интегрального метода:
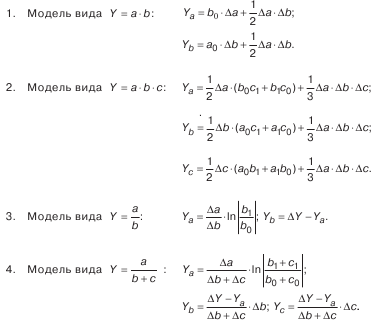
9. Метод цепных подстановок
Метод цепных подстановок является наиболее универсалы-ным из методов элиминирования. Он используется для расчета влияния факторов во всех типах детерминированных факторных моделей: аддитивные, мультипликативных, кратных и смешанных (комбинированных). Этот способ позволяет определить влияние отдельных факторов на изменение величины результативного показателя путем постепенной замены базисной величины каждого факторного показателя в объеме результативного показателя на фактическую в отчетном периоде. С этой целью определяют ряд условных величин результативного показателя, которые учитывают изменение одного, затем двух, трех и т д. факторов, допуская, что остальные не меняются. Сравнение величины результативного показателя до и после изменения уровня того или другого фактора позволяет элиминироваться от влияния всех факторов, кроме одного, и определить воздействие последнего на прирост результативного показателя.
Степень влияния того или иного показателя выявляется последовательным вычитанием: из второго расчета вычитается первый, из третьего – второй и т. д. В первом расчете все величины плановые, в последнем – фактические. В случае трехфакторной мультипликативной модели алгоритм расчета следующий:
Y0 = а0⋅Ь0⋅С0;
Yусл.1 = а1⋅Ь0⋅С0; Уа = Yусл.1 – У0;
Yусл.2 = а1⋅Ь1⋅С0; YЬ = Yусл.2 – Yусл.1;
Yф = а1⋅Ь1⋅С1; Yс = Yф – Yусл.2 и т. д.
Алгебраическая сумма влияния факторов обязательно должна быть равна общему приросту результативного показателя:
Yа + Yь + Yс = Yф – Y0.
Отсутствие такого равенства свидетельствует о допущенных ошибках в расчетах.
Отсюда вытекает правило, заключающееся в том, что число расчетов на единицу больше, чем число показателей расчетной формулы.
При использовании метода цепных подстановок очень важно обеспечить строгую последовательность подстановки, т. к. ее произвольное изменение может привести к неправильным результатам. В практике анализа в первую очередь выявляется влияние количественных показателей, а потом – качественных. Так, если требуется определить степень влияния численности работников и производительности труда на размер выпуска промышленной продукции, то прежде устанавливают влияние количественного показателя численности работников, а потом качественного производительности труда. Если выясняется влияние факторов количества и цен на объем реализованной промышленной продукции, то вначале исчисляется влияние количества, а потом влияние оптовых цен. Прежде чем приступить к расчетам, необходимо, во-первых, выявить четкую взаимосвязь между изучаемыми показателями, во-вторых, разграничить количественные и качественные показатели, в-третьих, правильно определить последовательность подстановки в тех случаях, когда имеется несколько количественных и качественных показателей (основных и производных, первичных и вторичных). Таким образом, применение способа цепной подстановки требует знания взаимосвязи факторов, их соподчиненности, умения правильно их классифицировать и систематизировать.
Произвольное изменение последовательности подстановки меняет количественную весомость того или иного показателя. Чем значительнее отклонение фактических показателей от плановых, тем больше и различий в оценке факторов, исчисленных при разной последовательности подстановки.
Метод цепной подстановки обладает существенным недостатком, суть которого сводится к возникновению неразложимого остатка, который присоединяется к числовому значению влияния последнего фактора. Этим объясняется разница в расчетах при изменении последовательности подстановки. Отмеченный недостаток устраняется при использовании в аналитических расчетах более сложного интегрального метода.
Степень влияния того или иного показателя выявляется последовательным вычитанием: из второго расчета вычитается первый, из третьего – второй и т. д. В первом расчете все величины плановые, в последнем – фактические. В случае трехфакторной мультипликативной модели алгоритм расчета следующий:
Y0 = а0⋅Ь0⋅С0;
Yусл.1 = а1⋅Ь0⋅С0; Уа = Yусл.1 – У0;
Yусл.2 = а1⋅Ь1⋅С0; YЬ = Yусл.2 – Yусл.1;
Yф = а1⋅Ь1⋅С1; Yс = Yф – Yусл.2 и т. д.
Алгебраическая сумма влияния факторов обязательно должна быть равна общему приросту результативного показателя:
Yа + Yь + Yс = Yф – Y0.
Отсутствие такого равенства свидетельствует о допущенных ошибках в расчетах.
Отсюда вытекает правило, заключающееся в том, что число расчетов на единицу больше, чем число показателей расчетной формулы.
При использовании метода цепных подстановок очень важно обеспечить строгую последовательность подстановки, т. к. ее произвольное изменение может привести к неправильным результатам. В практике анализа в первую очередь выявляется влияние количественных показателей, а потом – качественных. Так, если требуется определить степень влияния численности работников и производительности труда на размер выпуска промышленной продукции, то прежде устанавливают влияние количественного показателя численности работников, а потом качественного производительности труда. Если выясняется влияние факторов количества и цен на объем реализованной промышленной продукции, то вначале исчисляется влияние количества, а потом влияние оптовых цен. Прежде чем приступить к расчетам, необходимо, во-первых, выявить четкую взаимосвязь между изучаемыми показателями, во-вторых, разграничить количественные и качественные показатели, в-третьих, правильно определить последовательность подстановки в тех случаях, когда имеется несколько количественных и качественных показателей (основных и производных, первичных и вторичных). Таким образом, применение способа цепной подстановки требует знания взаимосвязи факторов, их соподчиненности, умения правильно их классифицировать и систематизировать.
Произвольное изменение последовательности подстановки меняет количественную весомость того или иного показателя. Чем значительнее отклонение фактических показателей от плановых, тем больше и различий в оценке факторов, исчисленных при разной последовательности подстановки.
Метод цепной подстановки обладает существенным недостатком, суть которого сводится к возникновению неразложимого остатка, который присоединяется к числовому значению влияния последнего фактора. Этим объясняется разница в расчетах при изменении последовательности подстановки. Отмеченный недостаток устраняется при использовании в аналитических расчетах более сложного интегрального метода.
10. Индексный метод в факторном анализе
В статистике, планировании и анализе хозяйственной деятельности основой для количественной оценки роли отдельных факторов в динамике изменений обобщающих показателей являются индексные модели. Индексный метод – один из приемов элиминирования. Основывается на относительных показателях динамики, пространственных сравнений, выполнении плана, выражающих отношение фактического уровня анализируемого показателя в отчетном периоде к его уровню в базисном периоде (или к плановому, или по другому объекту). Любой индекс исчисляется сопоставлением соизмеряемой (отчетной) величины с базисной. Индексы, выражающие соотношение непосредственно соизмеряемых величин, называются индивидуальными, а характеризующие соотношения сложных явлений – групповыми, или тотальными.
Статистика оперирует различными формами индексов (агрегатная, арифметическая, гармоническая и др.), используемыми в аналитической работе.
Агрегатный индекс является основной формой любого общего индекса; его можно преобразовать как в средний арифметический, так и в средний гармонический индексы. С помощью агрегатных индексов можно выявить влияние различных факторов на изменение уровня результативных показателей в мультипликативных и кратных моделях.
Корректность определения размера каждого фактора зависит от:
1) количества знаков после запятой (не менее четырех);
2) количества самих факторов (связь обратно пропорциональна).
Принципы построения индексов: изменение одного фактора при неизменном значении всех остальных, при этом если обобщающий экономический показатель представляет собой произведение количественного (объемного) и качественного показателей-факторов, то при определении влияния количественного фактора качественный показатель фиксируется на базисном уровне, а при определении влияния качественного фактора количественный показатель фиксируется на уровне отчетного периода.
Пусть Y = а⋅Ь⋅с⋅d. Тогда:

При этом: lY =la⋅lb⋅lc⋅ld.
Индексный метод позволяет провести разложение по факторам не только относительных, но и абсолютных отклонений обобщающего показателя. В этом случае влияние отдельных факторов определяется с помощью разности между числителем и знаменателем соответствующих индексов, т. е. также при расчете влияния одного фактора элиминируется влияние другого:
Пусть Y = а⋅Ь, где а – количественный фактор, ab – качественный. Тогда:
a1⋅b0 —a0⋅b0 – абсолютный прирост результирующего показателя за счет фактора а;
a1⋅b1 —a1⋅b0 – абсолютный прирост результирующего показателя за счет фактора b;
a1⋅b1 —a0⋅b0 – абсолютный прирост результирующего показателя за счет влияния всех факторов.
Данный принцип разложения абсолютного прироста (отклонения) обобщающего показателя по факторам пригоден для случая, когда число факторов равно двум (один из них количественный, другой – качественный), а анализируемый показатель представлен как их произведение.
Теория индексов не дает общего метода разложения абсолютных отклонений обобщающего показателя по факторам при числе факторов более двух. Для решения этой задачи используется метод цепных подстановок.
Статистика оперирует различными формами индексов (агрегатная, арифметическая, гармоническая и др.), используемыми в аналитической работе.
Агрегатный индекс является основной формой любого общего индекса; его можно преобразовать как в средний арифметический, так и в средний гармонический индексы. С помощью агрегатных индексов можно выявить влияние различных факторов на изменение уровня результативных показателей в мультипликативных и кратных моделях.
Корректность определения размера каждого фактора зависит от:
1) количества знаков после запятой (не менее четырех);
2) количества самих факторов (связь обратно пропорциональна).
Принципы построения индексов: изменение одного фактора при неизменном значении всех остальных, при этом если обобщающий экономический показатель представляет собой произведение количественного (объемного) и качественного показателей-факторов, то при определении влияния количественного фактора качественный показатель фиксируется на базисном уровне, а при определении влияния качественного фактора количественный показатель фиксируется на уровне отчетного периода.
Пусть Y = а⋅Ь⋅с⋅d. Тогда:

При этом: lY =la⋅lb⋅lc⋅ld.
Индексный метод позволяет провести разложение по факторам не только относительных, но и абсолютных отклонений обобщающего показателя. В этом случае влияние отдельных факторов определяется с помощью разности между числителем и знаменателем соответствующих индексов, т. е. также при расчете влияния одного фактора элиминируется влияние другого:
Пусть Y = а⋅Ь, где а – количественный фактор, ab – качественный. Тогда:
a1⋅b0 —a0⋅b0 – абсолютный прирост результирующего показателя за счет фактора а;
a1⋅b1 —a1⋅b0 – абсолютный прирост результирующего показателя за счет фактора b;
a1⋅b1 —a0⋅b0 – абсолютный прирост результирующего показателя за счет влияния всех факторов.
Данный принцип разложения абсолютного прироста (отклонения) обобщающего показателя по факторам пригоден для случая, когда число факторов равно двум (один из них количественный, другой – качественный), а анализируемый показатель представлен как их произведение.
Теория индексов не дает общего метода разложения абсолютных отклонений обобщающего показателя по факторам при числе факторов более двух. Для решения этой задачи используется метод цепных подстановок.
11. Интегральный метод факторного анализа
Элиминирование как способ детерминированного факторного анализа имеет важный недостаток. При его использовании исходят из того, что факторы изменяются независимо друг от друга, однако фактически они изменяются взаимосвязанно, в результате образуется некоторый неразложимый остаток, который прибавляется к величине влияния одного из факторов (как правило, последнего). В связи с этим величина влияния факторов на изменение результативного показателя колеблется в зависимости от места фактора в детерминированной модели. Чтобы избавиться от этого недостатка, в детерминированном факторном анализе используется интегральный метод, который применяется для определения влияния факторов в мультипликативных, кратных и смешанных моделях кратно-аддитивного вида.
Использование этого способа позволяет получить более точные результаты вычисления влияния факторов по сравнению со способами цепной подстановки, абсолютных и относительных разниц и избежать неоднозначной оценки влияния: в данном случае результаты не зависят от местоположения факторов в модели, а дополнительный прирост результативного показателя, возникающий из-за взаимодействия факторов, распределяется между ними поровну.
Для распределения дополнительного прироста недостаточно взять его часть, соответствующую количеству факторов, т. к. факторы могут действовать в разных направлениях. Поэтому изменение результативного показателя измеряется на бесконечно малых отрезках времени, т. е. производится суммирование приращения результата, определяемого как частные произведения, умноженные на приращения факторов на бесконечно малых промежутках. Операция вычисления определенного интеграла решается с помощью ПЭВМ и сводится к построению подынтегральных выражений, которые зависят от вида функции или модели факторной системы. В связи со сложностью вычисления некоторых определенных интегралов и дополнительные сложностей, связанных с возможным действием факторов в противоположных направлениях, на практике используются специально сформированные рабочие формулы, приводимые в специальной литературе:
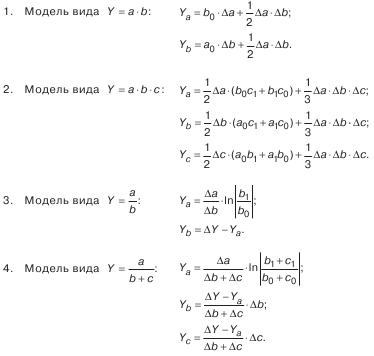
Таким образом, использование интегрального метода не нуждается в знании всего процесса интегрирования. Достаточно лишь в рабочие формулы подставить необходимые числовые данные и сделать подсчеты. При этом достигается более высокая точность расчетов.
Использование этого способа позволяет получить более точные результаты вычисления влияния факторов по сравнению со способами цепной подстановки, абсолютных и относительных разниц и избежать неоднозначной оценки влияния: в данном случае результаты не зависят от местоположения факторов в модели, а дополнительный прирост результативного показателя, возникающий из-за взаимодействия факторов, распределяется между ними поровну.
Для распределения дополнительного прироста недостаточно взять его часть, соответствующую количеству факторов, т. к. факторы могут действовать в разных направлениях. Поэтому изменение результативного показателя измеряется на бесконечно малых отрезках времени, т. е. производится суммирование приращения результата, определяемого как частные произведения, умноженные на приращения факторов на бесконечно малых промежутках. Операция вычисления определенного интеграла решается с помощью ПЭВМ и сводится к построению подынтегральных выражений, которые зависят от вида функции или модели факторной системы. В связи со сложностью вычисления некоторых определенных интегралов и дополнительные сложностей, связанных с возможным действием факторов в противоположных направлениях, на практике используются специально сформированные рабочие формулы, приводимые в специальной литературе:
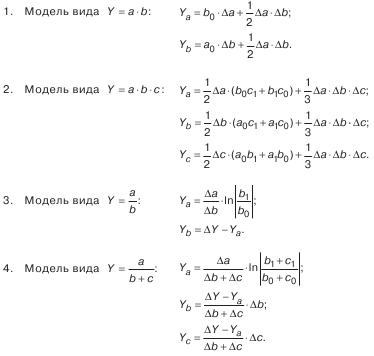
Таким образом, использование интегрального метода не нуждается в знании всего процесса интегрирования. Достаточно лишь в рабочие формулы подставить необходимые числовые данные и сделать подсчеты. При этом достигается более высокая точность расчетов.
12. Метод выявления изолированного влияния факторов
Сущность моделирования факторных систем заключается в том, что взаимосвязь исследуемого показателя с факторными передается в форме конкретного математического уравнения. В факторном анализе различают модели детерминированные (функциональные) и стохастические (корреляционные). С помощью детерминированных факторных моделей исследуется функциональная связь между результативным показателем (функцией) и факторами (аргументами).
Основная задача факторного анализа формируется как задача оценки влияния абсолютного изменения любого фактора на абсолютное изменение результативного показателя. Общая постановка данной задачи: пусть Y=f(x1 x2…., хп) – жестко детерминированная модель, характеризующая изменение результативного показателя Х от факторов (х1). Пусть Y получил приращение ∆Y за анализируемый период (в динамике или по сравнению с планом). Требуется определить, какой частью ∆Y обязано приращению каждого аргумента, т. е. представить его в следующем виде:
∆общ.Y = ∆x1Y + ∆x2Y + … + ∆xnY.
Одним из методов такой оценки является метод изолированного влияния факторов. Пусть результатный показатель Х определяется несколькими факторами: xv Х2, хп. Базовый период обозначим индексом 0, а отчетный – 1. Общее изменение результативного показателя, имевшее место за это время:
∆общ.Y = Y1 – Y2
Изменение, связанное с изменением лишь одного, х-го показателя, таким образом, составит:
∆x1=f(x10….,xi-10,xi0,xi+1…, хп0)−f(x10…., хп0)
Данной моделью выявляется изолированное влияние одного xi-го фактора.
Этот способ не относится к методам элиминирования и позволяет частично устранить главный недостаток совокупности этих методов. При использовании элиминирования основная гипотеза заключается в том, что факторы изменяются независимо друг от друга, однако фактически они изменяются взаимосвязанно, в результате образуется некоторый неразложимый остаток, который прибавляется к величине влияния одного из факторов (как правило, последнего). В связи с этим величина влияния факторов на изменение результативного показателя колеблется в зависимости от места фактора в детерминированной модели.
Очевидно, что для приема изолированного влияния факторов ∆общ.Y ≠ ∑∆xiY, т. к. при использовании данного метода неразложимый остаток отбрасывается полностью, не прибавляется ни к одному из значений влияния факторов. С одной стороны, не искажается степень абсолютного воздействия факторов на прирост результативного показателя; с другой стороны, полное разложение изменения результативного показателя на изменения факторов не достигается: сумма влияний всех факторов оказывается не равной общему приросту результативного показателя. Это является главным недостатком приема и причиной того, что он используется в тех случаях, когда не требуется высокая точность результата, а достаточно лишь приблизительно оценить степень влияния факторов.
Преимущества метода заключаются в том, что он является наиболее простым из специальных приемов факторного анализа и не требует установления очередности изменения факторов, которое вызывает много трудностей, например, при использовании метода цепных подстановок, и способно сильно исказить результат факторного анализа.
Основная задача факторного анализа формируется как задача оценки влияния абсолютного изменения любого фактора на абсолютное изменение результативного показателя. Общая постановка данной задачи: пусть Y=f(x1 x2…., хп) – жестко детерминированная модель, характеризующая изменение результативного показателя Х от факторов (х1). Пусть Y получил приращение ∆Y за анализируемый период (в динамике или по сравнению с планом). Требуется определить, какой частью ∆Y обязано приращению каждого аргумента, т. е. представить его в следующем виде:
∆общ.Y = ∆x1Y + ∆x2Y + … + ∆xnY.
Одним из методов такой оценки является метод изолированного влияния факторов. Пусть результатный показатель Х определяется несколькими факторами: xv Х2, хп. Базовый период обозначим индексом 0, а отчетный – 1. Общее изменение результативного показателя, имевшее место за это время:
∆общ.Y = Y1 – Y2
Изменение, связанное с изменением лишь одного, х-го показателя, таким образом, составит:
∆x1=f(x10….,xi-10,xi0,xi+1…, хп0)−f(x10…., хп0)
Данной моделью выявляется изолированное влияние одного xi-го фактора.
Этот способ не относится к методам элиминирования и позволяет частично устранить главный недостаток совокупности этих методов. При использовании элиминирования основная гипотеза заключается в том, что факторы изменяются независимо друг от друга, однако фактически они изменяются взаимосвязанно, в результате образуется некоторый неразложимый остаток, который прибавляется к величине влияния одного из факторов (как правило, последнего). В связи с этим величина влияния факторов на изменение результативного показателя колеблется в зависимости от места фактора в детерминированной модели.
Очевидно, что для приема изолированного влияния факторов ∆общ.Y ≠ ∑∆xiY, т. к. при использовании данного метода неразложимый остаток отбрасывается полностью, не прибавляется ни к одному из значений влияния факторов. С одной стороны, не искажается степень абсолютного воздействия факторов на прирост результативного показателя; с другой стороны, полное разложение изменения результативного показателя на изменения факторов не достигается: сумма влияний всех факторов оказывается не равной общему приросту результативного показателя. Это является главным недостатком приема и причиной того, что он используется в тех случаях, когда не требуется высокая точность результата, а достаточно лишь приблизительно оценить степень влияния факторов.
Преимущества метода заключаются в том, что он является наиболее простым из специальных приемов факторного анализа и не требует установления очередности изменения факторов, которое вызывает много трудностей, например, при использовании метода цепных подстановок, и способно сильно исказить результат факторного анализа.
13. Способы детерминированной комплексной оценки результатов деятельности
Комплексная оценка результатов хозяйственной деятельности организации или ее подразделений служит инструментом учета, анализа и планирования; индикатором научно-технического состояния хозяйственного объекта в изучаемой совокупности; критерием сравнительного оценивания коммерческой деятельности предприятий и их подразделений; показателем эффективности принятых ранее управленческих решений и полноты их реализации; основой выбора возможных вариантов развития производства и показателей ожидаемых результатов в будущем; стимулятором производства.
Отсюда возникает необходимость формирования комплексной оценки на базе системы показателей, агрегирование которых тем или иным способом позволит ранжировать результаты.
Конструирование интегрального показателя для обобщающей комплексной оценки может проводиться методами: сумм, средней геометрической, коэффициентов, суммы мест, расстояний и др.
Метод суммы основан на суммировании фактических абсолютных изменений показателей.
Недостатком метода сумм является возможность высокой оценки результатов по интегральному показателю при значительном отставании по какому-либо частному показателю, которое покрывается за счет высоких достижений по другим частным показателям.
Метод геометрической средней базируется на определении коэффициентов по частным показателям, когда за единицу принимается самое высокое значение данного индикатора. Этот метод целесообразно применять при относительно малом числе оцениваемых показателей и в случае, если большинство их значений близко к единице.
В некоторых случаях применим метод коэффициентов, т. е. оценка получается умножением соответствующих относительных показателей.
Метод суммы мест предполагает предварительное ранжирование каждого объекта анализа в зависимости от уровня исследуемых показателей. Число мест должно быть равно количеству анализируемых организаций. Чем меньше сумма мест, тем более высокий ранг присваивается анализируемому объекту.
Применение методов сумм, суммы мест, геометрической средней возможно только в случае однонаправленности влияния всех оцениваемых параметров на эффективность производства, т. е. увеличение (уменьшение) значения любого частного показателя расценивается как улучшение результатов хозяйственной деятельности (и наоборот). В противном случае при расчете показателя комплексной оценки в качестве критериев берутся обратные к исходным величинам показатели.
При использовании метода расстояний устанавливается близость объектов анализа к объекту-эталону по каждому из сравниваемых показателей. Вначале определяются коэффициенты по каждому показателю как отношение его значений к показателю-эталону с максимальным уровнем. В некоторых случаях типичным объектом считается такой, значения показателей которого равны средним арифметическим уровням показателей в изучаемой совокупности. Однако в совокупности экономических объектов, где преобладают асимметрические распределения, среднее арифметическое в качестве характеристики типичного, эталонного объекта утрачивает свое значение. Затем рассчитывается сумма квадратов полученных коэффициентов. Если есть возможность учесть сравнительную значимость индикаторов, то каждый квадрат умножается на соответствующий весовой коэффициент значимости. Затем из суммы квадратов извлекают квадратный корень.
Сведение ряда показателей в единый интегральный показатель позволяет определить отличие достигнутого состояния от базы сравнения в целом по группе выбранных показателей и, хотя оно не дает возможности измерить степень отличия, сделать однозначный вывод об улучшении (ухудшении) результатов работы за анализируемый промежуток времени. Однако конструирование интегрального показателя не означает, что для оценки используется лишь он один. Напротив, интегральный показатель предполагает исследование системы показателей, лежащих в основе оценки, а выводы, полученные только на базе интегрального показателя, носят лишь ориентировочный характер, выполняют вспомогательную (хотя и важную) роль определения характера изменений в результатах хозяйственной деятельности в целом по всем показателям.
Отсюда возникает необходимость формирования комплексной оценки на базе системы показателей, агрегирование которых тем или иным способом позволит ранжировать результаты.
Конструирование интегрального показателя для обобщающей комплексной оценки может проводиться методами: сумм, средней геометрической, коэффициентов, суммы мест, расстояний и др.
Метод суммы основан на суммировании фактических абсолютных изменений показателей.
Недостатком метода сумм является возможность высокой оценки результатов по интегральному показателю при значительном отставании по какому-либо частному показателю, которое покрывается за счет высоких достижений по другим частным показателям.
Метод геометрической средней базируется на определении коэффициентов по частным показателям, когда за единицу принимается самое высокое значение данного индикатора. Этот метод целесообразно применять при относительно малом числе оцениваемых показателей и в случае, если большинство их значений близко к единице.
В некоторых случаях применим метод коэффициентов, т. е. оценка получается умножением соответствующих относительных показателей.
Метод суммы мест предполагает предварительное ранжирование каждого объекта анализа в зависимости от уровня исследуемых показателей. Число мест должно быть равно количеству анализируемых организаций. Чем меньше сумма мест, тем более высокий ранг присваивается анализируемому объекту.
Применение методов сумм, суммы мест, геометрической средней возможно только в случае однонаправленности влияния всех оцениваемых параметров на эффективность производства, т. е. увеличение (уменьшение) значения любого частного показателя расценивается как улучшение результатов хозяйственной деятельности (и наоборот). В противном случае при расчете показателя комплексной оценки в качестве критериев берутся обратные к исходным величинам показатели.
При использовании метода расстояний устанавливается близость объектов анализа к объекту-эталону по каждому из сравниваемых показателей. Вначале определяются коэффициенты по каждому показателю как отношение его значений к показателю-эталону с максимальным уровнем. В некоторых случаях типичным объектом считается такой, значения показателей которого равны средним арифметическим уровням показателей в изучаемой совокупности. Однако в совокупности экономических объектов, где преобладают асимметрические распределения, среднее арифметическое в качестве характеристики типичного, эталонного объекта утрачивает свое значение. Затем рассчитывается сумма квадратов полученных коэффициентов. Если есть возможность учесть сравнительную значимость индикаторов, то каждый квадрат умножается на соответствующий весовой коэффициент значимости. Затем из суммы квадратов извлекают квадратный корень.
Сведение ряда показателей в единый интегральный показатель позволяет определить отличие достигнутого состояния от базы сравнения в целом по группе выбранных показателей и, хотя оно не дает возможности измерить степень отличия, сделать однозначный вывод об улучшении (ухудшении) результатов работы за анализируемый промежуток времени. Однако конструирование интегрального показателя не означает, что для оценки используется лишь он один. Напротив, интегральный показатель предполагает исследование системы показателей, лежащих в основе оценки, а выводы, полученные только на базе интегрального показателя, носят лишь ориентировочный характер, выполняют вспомогательную (хотя и важную) роль определения характера изменений в результатах хозяйственной деятельности в целом по всем показателям.
14. Эвристические приемы решения экономических задач
Круг экономико-математических моделей и методов, используемых в экономическом анализе, чрезвычайно широк, однако их применение сдерживается затрудненностью адекватного описания производственного процесса, получения решений в условиях высокой размерности задач, а также отсутствием необходимой для этого случая квалификации управленческого персонала. Методология экономического анализа, таким образом, должна быть расширена. Приемы исследования в экономическом анализе разделяют на две общие группы: качественные и количественные. Одним из видов качественных технических приемов являются эвристические.
Эвристика – приемы и методы принятия решений, использующие интуицию и опыт специалистов в решении аналогичных проблем.
Эвристические приемы экономического анализа представляют собой совокупность логических приемов и методических правил теоретического исследования и поиска приемлемого решения, которая опирается в определенной мере на изобретательность и творческий поиск и активно использует методику «наводящих» вопросов. Эвристические приемы можно разделить на три группы:
Эвристика – приемы и методы принятия решений, использующие интуицию и опыт специалистов в решении аналогичных проблем.
Эвристические приемы экономического анализа представляют собой совокупность логических приемов и методических правил теоретического исследования и поиска приемлемого решения, которая опирается в определенной мере на изобретательность и творческий поиск и активно использует методику «наводящих» вопросов. Эвристические приемы можно разделить на три группы:
