Страница:
Хотя резонанс 2:1 (a = 3,28 а.е.) способен доставлять некоторое количество материала в район орбиты Земли, средняя продолжительность существования тел на таких орбитах исчисляется всего сотней тысяч лет, поскольку Юпитер быстро преобразует их орбиты в гиперболические.
Помимо перечисленных наиболее мощных резонансов в поясе астероидов присутствует множество других резонансов, оказывающих менее существенное, но тем не менее заметное влияние на движение тел. Эти резонансы обусловлены соизмеримостями средних движений тел с Юпитером более высоких порядков (например, соизмеримостями 7:2, 7:3, 9:4, 10:3), соизмеримостями средних движений с Марсом, Землей, кратными соизмеримостями, когда резонансные соотношения связывают средние движения трех тел (например, Юпитера, Сатурна и астероида [Nesvorny and Morbidelli, 1998]), а также разного рода вековыми резонансами. В результате этого большая часть орбит астероидов Главного пояса обнаруживает слабую хаотичность. Правда, эффект этой хаотичности невелик. Большие полуоси орбит колеблются в узкой окрестности резонансов, а эксцентриситеты и наклоны хаотически диффундируют в сторону увеличения. Эти процессы также способствуют транспортировке вещества из внутренней части пояса (a < 2,5 а.е.) в район планет земной группы, а во внешней части пояса способствуют сближению тел с Юпитером, и, в конечном счете, выбросу их из Солнечной системы. Но время этой транспортировки крайне велико – от десятков миллионов до миллиардов лет. Тем не менее, именно эти слабые резонансы в основном ответственны за постоянное пополнение популяции астероидов, пересекающих орбиту Марса – «марс-кроссеров» (MC, Mars Crossers Asteroids) (1,3 < q < 1,67 а.е.), которая примерно в четыре раза более многочисленна, чем популяция АСЗ. Эта популяция не может поддерживаться за счет сильных резонансов, так как возрастание эксцентриситета в них происходит слишком быстро и при сближениях с Марсом в популяцию марс-кроссеров захватывается незначительное число астероидов. В области a 6 2,06 а.е. отсутствуют сильные резонансы, способные превратить орбиты, пересекающие орбиту Марса, в орбиты, пересекающие орбиты Земли и Венеры. Поэтому астероиды, попавшие в эту область под действием диффузных резонансов, надолго застревают в ней. Только случайные сближения с Марсом способны вернуть их в область сильных резонансов, где они могут быть преобразованы в АСЗ.
Хотя источники пополнения популяции АСЗ рассмотрены выше достаточно полно, остаются вопросы о том, каков вклад каждого источника в реально наблюдаемую популяцию и насколько сильно характеристики этой популяции искажены наблюдательной селекцией. Эффективным способом ответа на эти вопросы является построение динамической модели устойчивого состояния популяции [Bottke et al., 2002b]. В этой работе численным путем была прослежена эволюция многочисленных виртуальных астероидов, берущих начало в разных источниках: резонансах 3:1 и ν6, диффузных резонансах и в кометах семейства Юпитера. В ходе вычислений регистрировалось время, проведенное каждым астероидом в различных ячейках трехмерной сетки a, e, i за период существования частицы до того или иного финала. Если популяция находится в динамически устойчивом состоянии, то суммарное время, проведенное различными астероидами в отдельных ячейках трехмерного пространства, пропорционально орбитальному распределению тел. Общее распределение АСЗ было найдено как линейная комбинация взвешенного вклада каждого источника.
Из построенной модели следует, что 37 ± 8 % всех АСЗ с абсолютными звездными величинами в пределах 13m < H < 22m приходят из резонанса ν6, 23 ± 9 % – из резонанса 3:1, 33 ± 3 % – из многочисленных диффузных резонансов и 6 ± 4 % происходят из комет семейства Юпитера (кометы из облака Оорта не учитывались).
Таким образом, в настоящее время в основном известны механизмы транспортировки астероидного вещества из разных областей, прежде всего из резонансных зон ν6 и 3:1. Естественно возникает вопрос, каким образом происходит пополнение вещества в резонансных зонах пояса: без пополнения они давно были бы близки к полному истощению. Между тем, исследование распределения кратеров на поверхности Луны и Земли свидетельствует об относительном постоянстве темпа бомбардировки этих тел астероидами, кометами и их обломками в течение последних трех миллиардов лет [Grieve and Shoemaker, 1994; Иванов, 2005]. Потенциальные источники должны обеспечивать более или менее равномерный приток вещества в резонансные зоны, притом в нужном количестве.
Легко допустить, что поставщиком вещества в резонансные зоны может являться постоянное дробление вещества астероидов в соседних с этими зонами областях пояса в результате столкновений с более мелкими телами. Помимо этой составляющей в истории пояса имели место катастрофические столкновения тел, которые вели к образованию наиболее многочисленных семейств астероидов [Zappalá et al., 2002]. Такие события также могли эпизодически вбрасывать астероидное вещество в резонансные зоны. Существует, однако, ряд наблюдательных фактов, которые противоречат столь простому объяснению рассматриваемой проблемы.
Начать можно с того, что, согласно современным численным экспериментам [Gladman et al., 1997], вещество, вброшенное в область действия наиболее мощных резонансов, очень быстро достигает района планет земной группы, где оно также не может существовать длительное время. В результате средняя продолжительность пребывания вещества в открытом космическом пространстве, вне тел, из недр которых оно было выброшено, до его попадания на Землю должна составлять всего лишь около десяти миллионов лет. Но эта оценка находится в явном противоречии с космическими возрастами метеоритов, надежно определяемыми по относительному содержанию изотопов, образующихся в их телах под воздействием космических лучей. Для каменных метеоритов эти возрасты лежат преимущественно в диапазоне 1–100 млн лет с максимумами распределения в области 20 и 50 млн лет для разных групп метеоритов, а для железных они составляют несколько сотен миллионов лет с максимумом около 800–900 млн лет (рис. 3.12).
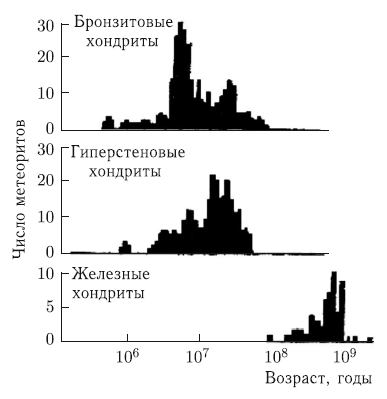Рис. 3.12. Космические возрасты каменных и железных метеоритов [Вуд, 1971]
Популяция АСЗ насчитывает около одной тысячи тел размером от одного километра и более. Для поддержания этой популяции в устойчивом состоянии динамического равновесия требуется, чтобы в поясе астероидов постоянно происходили катастрофические столкновения, так как только при таких столкновениях образующиеся тела километровых размеров могут получить достаточные по величине импульсы, чтобы достичь наиболее мощных резонансных зон. Но катастрофические столкновения – относительно редкие события. Возраст семейств, по общему мнению, составляет от нескольких сотен миллионов до нескольких миллиардов лет. Поскольку динамическое время жизни в окрестности мощных резонансов гораздо короче, память об этих событиях здесь давно стерлась. Таким образом, катастрофические столкновения не являются непосредственным поставщиком тел километровых размеров в резонансные зоны.
К этому можно добавить, что распределение тел по размерам среди АААА-астероидов, N(> D) = kD-b, имеет несколько иной характер, чем для осколков столкновений: показатель b интегрального степенного распределения тел по диаметру D в первом случае лежит в диапазоне 1,65–2,0 [Morbidelli and Vokrouhlicky, 2003; Stuart and Binzel, 2004], в то время как для осколков можно ожидать значение около 2,0–2,5.
Так что же является основным поставщиком астероидного материала в резонансные зоны? На сегодняшний день ответ на этот вопрос не вполне ясен, но наиболее правдоподобный ответ – эффект Ярковского.
3.6. Роль эффекта Ярковского в транспортировке вещества из пояса астероидов
3.7. Блеск, абсолютная звездная величина и альбедо астероидов
3.8. Диаметры астероидов
Помимо перечисленных наиболее мощных резонансов в поясе астероидов присутствует множество других резонансов, оказывающих менее существенное, но тем не менее заметное влияние на движение тел. Эти резонансы обусловлены соизмеримостями средних движений тел с Юпитером более высоких порядков (например, соизмеримостями 7:2, 7:3, 9:4, 10:3), соизмеримостями средних движений с Марсом, Землей, кратными соизмеримостями, когда резонансные соотношения связывают средние движения трех тел (например, Юпитера, Сатурна и астероида [Nesvorny and Morbidelli, 1998]), а также разного рода вековыми резонансами. В результате этого большая часть орбит астероидов Главного пояса обнаруживает слабую хаотичность. Правда, эффект этой хаотичности невелик. Большие полуоси орбит колеблются в узкой окрестности резонансов, а эксцентриситеты и наклоны хаотически диффундируют в сторону увеличения. Эти процессы также способствуют транспортировке вещества из внутренней части пояса (a < 2,5 а.е.) в район планет земной группы, а во внешней части пояса способствуют сближению тел с Юпитером, и, в конечном счете, выбросу их из Солнечной системы. Но время этой транспортировки крайне велико – от десятков миллионов до миллиардов лет. Тем не менее, именно эти слабые резонансы в основном ответственны за постоянное пополнение популяции астероидов, пересекающих орбиту Марса – «марс-кроссеров» (MC, Mars Crossers Asteroids) (1,3 < q < 1,67 а.е.), которая примерно в четыре раза более многочисленна, чем популяция АСЗ. Эта популяция не может поддерживаться за счет сильных резонансов, так как возрастание эксцентриситета в них происходит слишком быстро и при сближениях с Марсом в популяцию марс-кроссеров захватывается незначительное число астероидов. В области a 6 2,06 а.е. отсутствуют сильные резонансы, способные превратить орбиты, пересекающие орбиту Марса, в орбиты, пересекающие орбиты Земли и Венеры. Поэтому астероиды, попавшие в эту область под действием диффузных резонансов, надолго застревают в ней. Только случайные сближения с Марсом способны вернуть их в область сильных резонансов, где они могут быть преобразованы в АСЗ.
Хотя источники пополнения популяции АСЗ рассмотрены выше достаточно полно, остаются вопросы о том, каков вклад каждого источника в реально наблюдаемую популяцию и насколько сильно характеристики этой популяции искажены наблюдательной селекцией. Эффективным способом ответа на эти вопросы является построение динамической модели устойчивого состояния популяции [Bottke et al., 2002b]. В этой работе численным путем была прослежена эволюция многочисленных виртуальных астероидов, берущих начало в разных источниках: резонансах 3:1 и ν6, диффузных резонансах и в кометах семейства Юпитера. В ходе вычислений регистрировалось время, проведенное каждым астероидом в различных ячейках трехмерной сетки a, e, i за период существования частицы до того или иного финала. Если популяция находится в динамически устойчивом состоянии, то суммарное время, проведенное различными астероидами в отдельных ячейках трехмерного пространства, пропорционально орбитальному распределению тел. Общее распределение АСЗ было найдено как линейная комбинация взвешенного вклада каждого источника.
Из построенной модели следует, что 37 ± 8 % всех АСЗ с абсолютными звездными величинами в пределах 13m < H < 22m приходят из резонанса ν6, 23 ± 9 % – из резонанса 3:1, 33 ± 3 % – из многочисленных диффузных резонансов и 6 ± 4 % происходят из комет семейства Юпитера (кометы из облака Оорта не учитывались).
Таким образом, в настоящее время в основном известны механизмы транспортировки астероидного вещества из разных областей, прежде всего из резонансных зон ν6 и 3:1. Естественно возникает вопрос, каким образом происходит пополнение вещества в резонансных зонах пояса: без пополнения они давно были бы близки к полному истощению. Между тем, исследование распределения кратеров на поверхности Луны и Земли свидетельствует об относительном постоянстве темпа бомбардировки этих тел астероидами, кометами и их обломками в течение последних трех миллиардов лет [Grieve and Shoemaker, 1994; Иванов, 2005]. Потенциальные источники должны обеспечивать более или менее равномерный приток вещества в резонансные зоны, притом в нужном количестве.
Легко допустить, что поставщиком вещества в резонансные зоны может являться постоянное дробление вещества астероидов в соседних с этими зонами областях пояса в результате столкновений с более мелкими телами. Помимо этой составляющей в истории пояса имели место катастрофические столкновения тел, которые вели к образованию наиболее многочисленных семейств астероидов [Zappalá et al., 2002]. Такие события также могли эпизодически вбрасывать астероидное вещество в резонансные зоны. Существует, однако, ряд наблюдательных фактов, которые противоречат столь простому объяснению рассматриваемой проблемы.
Начать можно с того, что, согласно современным численным экспериментам [Gladman et al., 1997], вещество, вброшенное в область действия наиболее мощных резонансов, очень быстро достигает района планет земной группы, где оно также не может существовать длительное время. В результате средняя продолжительность пребывания вещества в открытом космическом пространстве, вне тел, из недр которых оно было выброшено, до его попадания на Землю должна составлять всего лишь около десяти миллионов лет. Но эта оценка находится в явном противоречии с космическими возрастами метеоритов, надежно определяемыми по относительному содержанию изотопов, образующихся в их телах под воздействием космических лучей. Для каменных метеоритов эти возрасты лежат преимущественно в диапазоне 1–100 млн лет с максимумами распределения в области 20 и 50 млн лет для разных групп метеоритов, а для железных они составляют несколько сотен миллионов лет с максимумом около 800–900 млн лет (рис. 3.12).
Популяция АСЗ насчитывает около одной тысячи тел размером от одного километра и более. Для поддержания этой популяции в устойчивом состоянии динамического равновесия требуется, чтобы в поясе астероидов постоянно происходили катастрофические столкновения, так как только при таких столкновениях образующиеся тела километровых размеров могут получить достаточные по величине импульсы, чтобы достичь наиболее мощных резонансных зон. Но катастрофические столкновения – относительно редкие события. Возраст семейств, по общему мнению, составляет от нескольких сотен миллионов до нескольких миллиардов лет. Поскольку динамическое время жизни в окрестности мощных резонансов гораздо короче, память об этих событиях здесь давно стерлась. Таким образом, катастрофические столкновения не являются непосредственным поставщиком тел километровых размеров в резонансные зоны.
К этому можно добавить, что распределение тел по размерам среди АААА-астероидов, N(> D) = kD-b, имеет несколько иной характер, чем для осколков столкновений: показатель b интегрального степенного распределения тел по диаметру D в первом случае лежит в диапазоне 1,65–2,0 [Morbidelli and Vokrouhlicky, 2003; Stuart and Binzel, 2004], в то время как для осколков можно ожидать значение около 2,0–2,5.
Так что же является основным поставщиком астероидного материала в резонансные зоны? На сегодняшний день ответ на этот вопрос не вполне ясен, но наиболее правдоподобный ответ – эффект Ярковского.
3.6. Роль эффекта Ярковского в транспортировке вещества из пояса астероидов
Суть эффекта Ярковского заключается в реакции отдачи, испытываемой нагретым телом в результате асимметричного переизлучения тепловой энергии.
Различают суточную и сезонную составляющие эффекта [Bottke et al., 2002a]. Cуточная составляющая зависит от вращения тела вокруг оси, не лежащей в плоскости его орбиты. При этом из-за тепловой инерции вещества вечерняя половина тела оказывается более нагретой лучами Солнца по сравнению с утренней. Наиболее высокая температура поверхности достигается не в точках, где Солнце находится в меридиане (т. е. не в полдень), а в точках, чей местный меридиан повернут относительно меридиана подсолнечной точки на некоторый угол к востоку или западу в зависимости от направления вращения тела. Нагретое тело излучает тепло. Тепловые фотоны, покидая тело, сообщают ему некоторый импульс. Если бы температура поверхности сферически симметричного тела была всюду одинаковой, то усредненный результирующий импульс был бы равен нулю. Из-за различия температур в различных точках результирующий импульс отличен от нуля, причем из-за вращения тела он направлен не в сторону, противоположную Солнцу, а под некоторым углом к этому направлению (рис. 3.13 а). Его действие аналогично реактивному эффекту истечения газов из ядра кометы при нагревании его солнечными лучами. В зависимости от направления вращения ядра по отношению к направлению орбитального движения эффект Ярковского, подобно негравитационному эффекту в движении кометы, может вызывать как ускорение орбитального движения тела (сокращение большой полуоси), так и замедление движения (увеличение большой полуоси).
Сезонная составляющая эффекта Ярковского связана с орбитальным движением тела и с неравномерностью нагрева летнего и зимнего полушарий тела, ось вращения которого сохраняет направление в пространстве, не перпендикулярное к плоскости его орбиты. Из-за тепловой инерции вещества наибольший нагрев летнего полушария достигается не в момент летнего солнцестояния, а спустя некоторое время. Из-за этого результирующий реактивный импульс имеет составляющую, направленную в сторону, противоположную направлению движения тела (рис. 3.13 б). Как всякий тормозящий эффект, сезонный эффект Ярковского вызывает ускорение орбитального движения тела, т. е. сокращение его большой полуоси. В отличие от суточной составляющей сезонная составляющая не зависит от направления вращения.
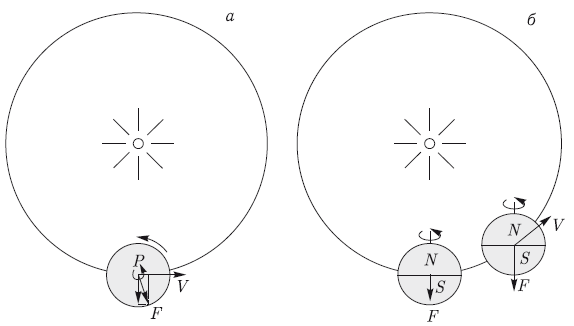Рис. 3.13. а) Суточный эффект Ярковского. Показан случай, когда ось вращения наклонена под углом 90° к плоскости орбиты. Максимальная температура поверхности достигается не в точках, где Солнце находится в меридиане (т. е. не в местный полдень), а в точках, чей меридиан повернут относительно меридиана подсолнечной точки на некоторый угол к востоку (при указанном направлении вращения). б) Сезонный эффект Ярковского. Показан случай, когда ось вращения астероида лежит в плоскости орбиты. Из-за тепловой инерции вещества наибольшая температура в северном полушарии (N) достигается не в момент, когда ось вращения направлена на Солнце, а в более поздний момент. Результирующий импульс F имеет составляющую, направленную против орбитальной скорости V
Величина каждой из составляющих эффекта Ярковского зависит от наклона оси вращения тела к плоскости его орбиты. Суточная составляющая максимальна, если ось вращения перпендикулярна к орбите, и обращается в нуль, если ось вращения лежит в плоскости орбиты. Сезонная составляющая, напротив, обращается в нуль в первом случае и максимальна во втором. В реальности обе составляющие действуют совместно, производя тот или иной эффект. На крупные тела (D > 20 км) эффект не оказывает заметного действия за приемлемые промежутки времени. То же самое можно сказать и об очень малых телах, в которых устанавливается постоянная температура. Для тел промежуточных размеров величина эффекта зависит от теплопроводности вещества, в особенности для тел размером 0,1–1,5 м.
Как показывают расчеты, выполненные при различных предположениях относительно размеров тел, их теплопроводности и других параметров, эффект Ярковского может обеспечить изменение больших полуосей тел, движущихся в поясе астероидов, на величины порядка 0,1–0,01 а.е. за время существования этих тел до их полного разрушения в результате катастрофических столкновений (от нескольких миллионов до примерно 2 млрд лет в зависимости от размеров).
Существуют вариации второго порядка в эффекте Ярковского – это YORP-эффект (название дано по первым буквам исследователей: Yarkovsky– O’Keefe – Radzievskii – Paddack). YORP-эффект состоит в изменении скорости вращения малых тел, таких как астероиды (см. рис. 3.14 на вклейке).
Радзиевский применил идеи эффекта Ярковского к вращающимся астероидам, основываясь на изменениях их альбедо за период вращения [Radzievskii, 1954]. В работах [Paddack, 1975; O’Keefe, 1976] было показано, что форма является фактором, от которого сильно зависит изменение скорости вращения тела, а также что YORP-эффект может быть причиной увеличения скорости вращения и выбрасывания из Солнечной системы небольших асимметричных тел. В 2007 г. было получено прямое подтверждение существования YORP-эффекта для небольших астероидов 54509 YORP (2000 PH5) и 1862 Apollo [Lowry et al., 2007; Kaasalainen et al., 2007].
Известно, что астероиды с диаметром более 125 км имеют максвелловское распределение скоростей вращения, в то время как астероиды с диаметрами от 50 до 125 км обладают немного асимметричным распределением, а для астероидов, размеры которых меньше 50 км, распределение оказалось смещенным относительно распределения для крупных астероидов в сторону либо более быстрого, либо более медленного вращения. В качестве объяснения причин этого явления предлагается несколько механизмов в зависимости от размеров объектов. YORP-эффект в основном может объяснить особенности распределения по скоростям вращения для тел различных размеров.
Как было указано выше, космические возрасты каменных и железных метеоритов находятся в противоречии с динамическими оценками времени их доставки из пояса астероидов на Землю. Эффект Ярковского позволяет привести эти оценки в согласие друг с другом. Осколки дробления астероидов, как правило, не попадают непосредственно в области активно действующих резонансов, но в течение длительных интервалов времени дрейфуют в направлении тех областей, где они подхватываются резонансами для дальнейшей транспортировки в район планет земной группы. За время дрейфа они успевают заметным образом состариться, причем из-за большей теплопроводности железных тел время их дрейфа оказывается в среднем на порядок большим, чем каменных. Таким образом, эффект Ярковского дает естественное объяснение большим космическим возрастам вещества метеоритов и разнице возрастов каменных и железных тел.
Ранее было также отмечено, что механизм катастрофических столкновений не может обеспечить равномерный приток тел километровых размеров в резонансные зоны и далее в район орбиты Земли. Напротив, эффект Ярковского способен обеспечить транспортировку тел до 20 км в диаметре из соседних достаточно обширных областей пояса в те области, откуда они перебрасываются к планетам земной группы. Действие эффекта сказывается на протяжении десятков и сотен миллионов лет, причем по-разному на тела различных размеров и различного состава. В результате в резонансные зоны достаточно равномерно поставляются тела различных размеров, являющиеся продуктами дробления тел различного состава. Эти особенности эффекта позволяют объяснить и равномерный характер притока вещества на Землю, и разнообразие минералогического состава вещества метеоритов, и распределение АСЗ по размерам.
Различают суточную и сезонную составляющие эффекта [Bottke et al., 2002a]. Cуточная составляющая зависит от вращения тела вокруг оси, не лежащей в плоскости его орбиты. При этом из-за тепловой инерции вещества вечерняя половина тела оказывается более нагретой лучами Солнца по сравнению с утренней. Наиболее высокая температура поверхности достигается не в точках, где Солнце находится в меридиане (т. е. не в полдень), а в точках, чей местный меридиан повернут относительно меридиана подсолнечной точки на некоторый угол к востоку или западу в зависимости от направления вращения тела. Нагретое тело излучает тепло. Тепловые фотоны, покидая тело, сообщают ему некоторый импульс. Если бы температура поверхности сферически симметричного тела была всюду одинаковой, то усредненный результирующий импульс был бы равен нулю. Из-за различия температур в различных точках результирующий импульс отличен от нуля, причем из-за вращения тела он направлен не в сторону, противоположную Солнцу, а под некоторым углом к этому направлению (рис. 3.13 а). Его действие аналогично реактивному эффекту истечения газов из ядра кометы при нагревании его солнечными лучами. В зависимости от направления вращения ядра по отношению к направлению орбитального движения эффект Ярковского, подобно негравитационному эффекту в движении кометы, может вызывать как ускорение орбитального движения тела (сокращение большой полуоси), так и замедление движения (увеличение большой полуоси).
Сезонная составляющая эффекта Ярковского связана с орбитальным движением тела и с неравномерностью нагрева летнего и зимнего полушарий тела, ось вращения которого сохраняет направление в пространстве, не перпендикулярное к плоскости его орбиты. Из-за тепловой инерции вещества наибольший нагрев летнего полушария достигается не в момент летнего солнцестояния, а спустя некоторое время. Из-за этого результирующий реактивный импульс имеет составляющую, направленную в сторону, противоположную направлению движения тела (рис. 3.13 б). Как всякий тормозящий эффект, сезонный эффект Ярковского вызывает ускорение орбитального движения тела, т. е. сокращение его большой полуоси. В отличие от суточной составляющей сезонная составляющая не зависит от направления вращения.
Величина каждой из составляющих эффекта Ярковского зависит от наклона оси вращения тела к плоскости его орбиты. Суточная составляющая максимальна, если ось вращения перпендикулярна к орбите, и обращается в нуль, если ось вращения лежит в плоскости орбиты. Сезонная составляющая, напротив, обращается в нуль в первом случае и максимальна во втором. В реальности обе составляющие действуют совместно, производя тот или иной эффект. На крупные тела (D > 20 км) эффект не оказывает заметного действия за приемлемые промежутки времени. То же самое можно сказать и об очень малых телах, в которых устанавливается постоянная температура. Для тел промежуточных размеров величина эффекта зависит от теплопроводности вещества, в особенности для тел размером 0,1–1,5 м.
Как показывают расчеты, выполненные при различных предположениях относительно размеров тел, их теплопроводности и других параметров, эффект Ярковского может обеспечить изменение больших полуосей тел, движущихся в поясе астероидов, на величины порядка 0,1–0,01 а.е. за время существования этих тел до их полного разрушения в результате катастрофических столкновений (от нескольких миллионов до примерно 2 млрд лет в зависимости от размеров).
Существуют вариации второго порядка в эффекте Ярковского – это YORP-эффект (название дано по первым буквам исследователей: Yarkovsky– O’Keefe – Radzievskii – Paddack). YORP-эффект состоит в изменении скорости вращения малых тел, таких как астероиды (см. рис. 3.14 на вклейке).
Радзиевский применил идеи эффекта Ярковского к вращающимся астероидам, основываясь на изменениях их альбедо за период вращения [Radzievskii, 1954]. В работах [Paddack, 1975; O’Keefe, 1976] было показано, что форма является фактором, от которого сильно зависит изменение скорости вращения тела, а также что YORP-эффект может быть причиной увеличения скорости вращения и выбрасывания из Солнечной системы небольших асимметричных тел. В 2007 г. было получено прямое подтверждение существования YORP-эффекта для небольших астероидов 54509 YORP (2000 PH5) и 1862 Apollo [Lowry et al., 2007; Kaasalainen et al., 2007].
Известно, что астероиды с диаметром более 125 км имеют максвелловское распределение скоростей вращения, в то время как астероиды с диаметрами от 50 до 125 км обладают немного асимметричным распределением, а для астероидов, размеры которых меньше 50 км, распределение оказалось смещенным относительно распределения для крупных астероидов в сторону либо более быстрого, либо более медленного вращения. В качестве объяснения причин этого явления предлагается несколько механизмов в зависимости от размеров объектов. YORP-эффект в основном может объяснить особенности распределения по скоростям вращения для тел различных размеров.
Как было указано выше, космические возрасты каменных и железных метеоритов находятся в противоречии с динамическими оценками времени их доставки из пояса астероидов на Землю. Эффект Ярковского позволяет привести эти оценки в согласие друг с другом. Осколки дробления астероидов, как правило, не попадают непосредственно в области активно действующих резонансов, но в течение длительных интервалов времени дрейфуют в направлении тех областей, где они подхватываются резонансами для дальнейшей транспортировки в район планет земной группы. За время дрейфа они успевают заметным образом состариться, причем из-за большей теплопроводности железных тел время их дрейфа оказывается в среднем на порядок большим, чем каменных. Таким образом, эффект Ярковского дает естественное объяснение большим космическим возрастам вещества метеоритов и разнице возрастов каменных и железных тел.
Ранее было также отмечено, что механизм катастрофических столкновений не может обеспечить равномерный приток тел километровых размеров в резонансные зоны и далее в район орбиты Земли. Напротив, эффект Ярковского способен обеспечить транспортировку тел до 20 км в диаметре из соседних достаточно обширных областей пояса в те области, откуда они перебрасываются к планетам земной группы. Действие эффекта сказывается на протяжении десятков и сотен миллионов лет, причем по-разному на тела различных размеров и различного состава. В результате в резонансные зоны достаточно равномерно поставляются тела различных размеров, являющиеся продуктами дробления тел различного состава. Эти особенности эффекта позволяют объяснить и равномерный характер притока вещества на Землю, и разнообразие минералогического состава вещества метеоритов, и распределение АСЗ по размерам.
3.7. Блеск, абсолютная звездная величина и альбедо астероидов
Астероиды, как и все тела Солнечной системы кроме центрального тела, светят отраженным светом Солнца. При наблюдении глаз регистрирует световой поток, рассеянный астероидом в направлении на Землю и проходящий через зрачок. Характеристикой субъективного ощущения светового потока различной интенсивности, приходящего от астероидов, является их блеск. Именно этот термин (а не яркость) рекомендуется использовать в научной литературе. Фактически глаз реагирует на освещенность сетчатки, т. е. на световой поток, приходящийся на единицу площади площадки, перпендикулярной лучу зрения, на расстоянии Земли. Освещенность обратно пропорциональна квадрату расстояния астероида от Земли. Учитывая, что рассеянный астероидом поток обратно пропорционален квадрату его расстояния от Солнца, можно заключить, что освещенность на Земле обратно пропорциональна квадрату расстояний от астероида до Солнца и до Земли. Таким образом, если обозначить освещенность, создаваемую астероидом, находящимся на расстоянии r от Солнца и Δ от Земли, посредством E, а посредством E1 – освещенность, создаваемую тем же телом, но находящимся на единичном расстоянии от Солнца и от Земли, то
E = E1r-2Δ-2. (3.2)
В астрономии освещенность принято выражать в звездных величинах. Интервалом освещенности в одну звездную величину называется отношение освещенностей, создаваемых двумя источниками, при котором освещенность от одного из них в 2,512 раза превосходит освещенность, создаваемую другим. В более общем случае имеет место формула Погсона:
Em1/Em2 = 2,512(m2-m1), (3.3)
где Em1 – освещенность от источника со звездной величиной m1, Em2 – освещенность от источника со звездной величиной m2 (освещенность тем меньше, чем больше звездная величина). Из этих формул вытекает зависимость блеска астероида m, выраженного в звездных величинах, от расстояния r от Солнца и Δ от Земли:
m = m0 + 5 lg(rΔ), (3.4)
где m0 – так называемая абсолютная звездная величина астероида, численно равная звездной величине, которую имел бы астероид, находясь на расстоянии 1 а.е. от Солнца и Земли и при нулевом угле фазы (напомним, что углом фазы называется угол при астероиде между направлениями на Землю и на Солнце). Очевидно, что в природе подобная конфигурация трех тел осуществиться не может.
Формула (3.4) не полностью описывает изменение блеска астероида при его орбитальном движении. Фактически блеск астероида зависит не только от его расстояний от Солнца и Земли, но и от угла фазы. Эта зависимость связана, с одной стороны, с наличием ущерба (неосвещенной Солнцем части астероида) при наблюдении с Земли при ненулевом фазовом угле, с другой, – от микро– и макроструктуры поверхности.
Надо иметь в виду, что астероиды Главного пояса могут наблюдаться лишь при относительно небольших фазовых углах, приблизительно до 30°.
До 80-х гг. XX в. считалось, что добавление в формулу (3.4) слагаемого, пропорционального величине фазового угла, позволяет достаточно хорошо учесть изменение блеска в зависимости от угла фазы:
m = m0 + 5 lg(rΔ) + kβ, (3.5)
где β – угол фазы. Коэффициент пропорциональности k, хотя и отличается для разных астероидов, варьируется в основном в пределах 0,01–0,05 m/°.
Возрастание звездной величины m с ростом угла фазы согласно формуле (3.5) имеет линейный характер, m0 есть ордината точки пересечения фазовой кривой (фактически прямой) с вертикалью при r = Δ = 1 и β = 0°.
Более поздние исследования показали, что фазовая кривая астероидов имеет сложный характер. Линейный спад блеска (увеличение звездной величины объекта) с ростом фазового угла имеет место лишь в диапазоне приблизительно от 7° до 40°, после чего начинается нелинейный спад. С другой стороны, при углах фазы, меньших 7°, имеет место так называемый оппозиционный эффект – нелинейное нарастание блеска с уменьшением фазового угла (рис. 3.15).
Рис. 3.15. Зависимость звездной величины от угла фазы для астероида (1862) Apollo [Bowell et al., 1989]
С 1986 г. для вычислений видимой звездной величины астероидов в лучах V (визуальная полоса спектра фотометрической системы UBV) применяется более сложная полуэмпирическая формула, которая позволяет более точно описать изменение блеска в диапазоне фазовых углов от 0° до 120° [Bowell et al., 1989]. Формула имеет вид
V = H + 5 lg(rΔ) – 2,5 lg[(1 – G)Φ1 + GΦ2]. (3.6)
Здесь H – абсолютная звездная величина астероида в лучах V, G – так называемый параметр наклона, Φ1 и Φ2 – функции угла фазы, определяемые следующими выражениями:
Φi = exp { – Ai[tg(β/2)]Bi}, i = 1, 2,
A1 = 3,33, A2 = 1,87, B1 = 0,63, B2 = 1,22.
После того как элементы орбиты определены и, следовательно, r, Δ и β могут быть вычислены, формула (3.6) позволяет найти абсолютную звездную величину, если имеются наблюдения видимой звездной величины. Для определения параметра G требуются наблюдения видимой звездной величины при различных углах фазы. В настоящее время значение параметра G определено из наблюдений только для 114 астероидов, в том числе для нескольких АСЗ. Найденные значения G варьируются в пределах от –0,12 до 0,60. Для прочих астероидов значение G принимается равным 0,15.
Поток лучистой энергии Солнца в диапазоне длин волн видимого света, падающий на поверхность астероида, обратно пропорционален квадрату его расстояния от Солнца и зависит от размеров астероида. Этот поток частично поглощается поверхностью астероида, нагревая ее, а частично рассеивается по всем направлениям. Отношение величины рассеянного по всем направлениям потока к падающему потоку называется сферическим альбедо A. Оно характеризует отражательную способность поверхности астероида.
Сферическое альбедо принято представлять в виде произведения двух сомножителей:
A = pq.
Первый сомножитель p, называемый геометрическим альбедо, есть отношение блеска реального небесного тела при нулевом угле фазы к блеску абсолютно белого диска того же радиуса, что и небесное тело, расположенного перпендикулярно к солнечным лучам на том же расстоянии от Солнца и Земли, что и само небесное тело. Второй сомножитель q, называемый фазовым интегралом, зависит от формы поверхности.
В противоречии со своим названием геометрическое альбедо определяет зависимость рассеяния падающего потока не от геометрии тела, а от физических свойств поверхности. Значения именно геометрического альбедо приводят в таблицах и имеют в виду, когда говорят об отражательной способности поверхностей астероидов.
Альбедо не зависит от размеров тела. Оно тесным образом связано с минералогическим составом и микроструктурой поверхностных слоев астероида и может быть использовано для классификации астероидов и определения их размеров. Для разных астероидов альбедо варьируется в пределах от 0,02 (очень темные объекты, отражающие только 2 % падающего света Солнца) до 0,5 и более (очень светлые).
Для дальнейшего важно установить связь между радиусом астероида, его альбедо и абсолютной звездной величиной. Очевидно, что чем больше радиус астероида и чем больше его альбедо, тем больший световой поток он отражает в заданном направлении при прочих равных условиях. Освещенность, которую астероид создает на Земле, зависит также от его расстояния от Солнца и Земли и потока лучистой энергии Солнца, который может быть выражен через звездную величину Солнца.
Если обозначить освещенность, создаваемую Солнцем на Земле, как E⊙, освещенность, создаваемую астероидом, – как E, расстояния от астероида до Солнца и Земли – как r и Δ, а радиус астероида (в а.е.) – как ρ, то для вычисления геометрического альбедо p можно использовать следующее выражение:
Если прологарифмировать это соотношение и заменить логарифм отношения E/E⊙ по формуле Погсона (3.3), то найдем
lg p = 0,4(m⊙ – m) + 2(lg r + lg Δ – lg ρ),
где m⊙ – видимая звездная величина Солнца. Заменим теперь m по формуле (3.4), тогда
lg p = 0,4(m⊙ – m0) – 2 lg ρ,
или, выражая диаметр D в километрах и полагая видимую звездную величину Солнца в лучах V равной –26,77 [Герелс, 1974], получим
lg D = 3,122 – 0,5 lg p – 0,2H, (3.7)
где H – абсолютная звездная величина астероида в лучах V.
E = E1r-2Δ-2. (3.2)
В астрономии освещенность принято выражать в звездных величинах. Интервалом освещенности в одну звездную величину называется отношение освещенностей, создаваемых двумя источниками, при котором освещенность от одного из них в 2,512 раза превосходит освещенность, создаваемую другим. В более общем случае имеет место формула Погсона:
Em1/Em2 = 2,512(m2-m1), (3.3)
где Em1 – освещенность от источника со звездной величиной m1, Em2 – освещенность от источника со звездной величиной m2 (освещенность тем меньше, чем больше звездная величина). Из этих формул вытекает зависимость блеска астероида m, выраженного в звездных величинах, от расстояния r от Солнца и Δ от Земли:
m = m0 + 5 lg(rΔ), (3.4)
где m0 – так называемая абсолютная звездная величина астероида, численно равная звездной величине, которую имел бы астероид, находясь на расстоянии 1 а.е. от Солнца и Земли и при нулевом угле фазы (напомним, что углом фазы называется угол при астероиде между направлениями на Землю и на Солнце). Очевидно, что в природе подобная конфигурация трех тел осуществиться не может.
Формула (3.4) не полностью описывает изменение блеска астероида при его орбитальном движении. Фактически блеск астероида зависит не только от его расстояний от Солнца и Земли, но и от угла фазы. Эта зависимость связана, с одной стороны, с наличием ущерба (неосвещенной Солнцем части астероида) при наблюдении с Земли при ненулевом фазовом угле, с другой, – от микро– и макроструктуры поверхности.
Надо иметь в виду, что астероиды Главного пояса могут наблюдаться лишь при относительно небольших фазовых углах, приблизительно до 30°.
До 80-х гг. XX в. считалось, что добавление в формулу (3.4) слагаемого, пропорционального величине фазового угла, позволяет достаточно хорошо учесть изменение блеска в зависимости от угла фазы:
m = m0 + 5 lg(rΔ) + kβ, (3.5)
где β – угол фазы. Коэффициент пропорциональности k, хотя и отличается для разных астероидов, варьируется в основном в пределах 0,01–0,05 m/°.
Возрастание звездной величины m с ростом угла фазы согласно формуле (3.5) имеет линейный характер, m0 есть ордината точки пересечения фазовой кривой (фактически прямой) с вертикалью при r = Δ = 1 и β = 0°.
Более поздние исследования показали, что фазовая кривая астероидов имеет сложный характер. Линейный спад блеска (увеличение звездной величины объекта) с ростом фазового угла имеет место лишь в диапазоне приблизительно от 7° до 40°, после чего начинается нелинейный спад. С другой стороны, при углах фазы, меньших 7°, имеет место так называемый оппозиционный эффект – нелинейное нарастание блеска с уменьшением фазового угла (рис. 3.15).
С 1986 г. для вычислений видимой звездной величины астероидов в лучах V (визуальная полоса спектра фотометрической системы UBV) применяется более сложная полуэмпирическая формула, которая позволяет более точно описать изменение блеска в диапазоне фазовых углов от 0° до 120° [Bowell et al., 1989]. Формула имеет вид
V = H + 5 lg(rΔ) – 2,5 lg[(1 – G)Φ1 + GΦ2]. (3.6)
Здесь H – абсолютная звездная величина астероида в лучах V, G – так называемый параметр наклона, Φ1 и Φ2 – функции угла фазы, определяемые следующими выражениями:
Φi = exp { – Ai[tg(β/2)]Bi}, i = 1, 2,
A1 = 3,33, A2 = 1,87, B1 = 0,63, B2 = 1,22.
После того как элементы орбиты определены и, следовательно, r, Δ и β могут быть вычислены, формула (3.6) позволяет найти абсолютную звездную величину, если имеются наблюдения видимой звездной величины. Для определения параметра G требуются наблюдения видимой звездной величины при различных углах фазы. В настоящее время значение параметра G определено из наблюдений только для 114 астероидов, в том числе для нескольких АСЗ. Найденные значения G варьируются в пределах от –0,12 до 0,60. Для прочих астероидов значение G принимается равным 0,15.
Поток лучистой энергии Солнца в диапазоне длин волн видимого света, падающий на поверхность астероида, обратно пропорционален квадрату его расстояния от Солнца и зависит от размеров астероида. Этот поток частично поглощается поверхностью астероида, нагревая ее, а частично рассеивается по всем направлениям. Отношение величины рассеянного по всем направлениям потока к падающему потоку называется сферическим альбедо A. Оно характеризует отражательную способность поверхности астероида.
Сферическое альбедо принято представлять в виде произведения двух сомножителей:
A = pq.
Первый сомножитель p, называемый геометрическим альбедо, есть отношение блеска реального небесного тела при нулевом угле фазы к блеску абсолютно белого диска того же радиуса, что и небесное тело, расположенного перпендикулярно к солнечным лучам на том же расстоянии от Солнца и Земли, что и само небесное тело. Второй сомножитель q, называемый фазовым интегралом, зависит от формы поверхности.
В противоречии со своим названием геометрическое альбедо определяет зависимость рассеяния падающего потока не от геометрии тела, а от физических свойств поверхности. Значения именно геометрического альбедо приводят в таблицах и имеют в виду, когда говорят об отражательной способности поверхностей астероидов.
Альбедо не зависит от размеров тела. Оно тесным образом связано с минералогическим составом и микроструктурой поверхностных слоев астероида и может быть использовано для классификации астероидов и определения их размеров. Для разных астероидов альбедо варьируется в пределах от 0,02 (очень темные объекты, отражающие только 2 % падающего света Солнца) до 0,5 и более (очень светлые).
Для дальнейшего важно установить связь между радиусом астероида, его альбедо и абсолютной звездной величиной. Очевидно, что чем больше радиус астероида и чем больше его альбедо, тем больший световой поток он отражает в заданном направлении при прочих равных условиях. Освещенность, которую астероид создает на Земле, зависит также от его расстояния от Солнца и Земли и потока лучистой энергии Солнца, который может быть выражен через звездную величину Солнца.
Если обозначить освещенность, создаваемую Солнцем на Земле, как E⊙, освещенность, создаваемую астероидом, – как E, расстояния от астероида до Солнца и Земли – как r и Δ, а радиус астероида (в а.е.) – как ρ, то для вычисления геометрического альбедо p можно использовать следующее выражение:
lg p = 0,4(m⊙ – m) + 2(lg r + lg Δ – lg ρ),
где m⊙ – видимая звездная величина Солнца. Заменим теперь m по формуле (3.4), тогда
lg p = 0,4(m⊙ – m0) – 2 lg ρ,
или, выражая диаметр D в километрах и полагая видимую звездную величину Солнца в лучах V равной –26,77 [Герелс, 1974], получим
lg D = 3,122 – 0,5 lg p – 0,2H, (3.7)
где H – абсолютная звездная величина астероида в лучах V.
3.8. Диаметры астероидов
Абсолютная звездная величина H – важная характеристика астероида, которая позволяет оценить его линейные размеры, если найдено или из каких-либо соображений принято значение альбедо. Формула (3.7) связывает диаметр астероида, выраженный в километрах, его абсолютную звездную величину и геометрическое альбедо p. Данная формула позволяет достаточно надежно оценивать диаметры астероидов, имеющих значительные по величине альбедо (более 0,05). При меньших альбедо относительная ошибка может быть весьма большой.
Поскольку альбедо зависит от длины волны света, то в формуле (3.7) предполагается использование альбедо в тех же лучах V, в которых оценивалась звездная величина Солнца и величина H (обозначается как pV).
Для АСЗ усредненное значение альбедо равно 0,14 [Stuart and Binzel, 2004]. Если при данном значении альбедо подставить в формулу (3.7) значение H = 17,75m, то найдем, что данному значению звездной величины отвечает значение диаметра, равное 1 км.
Для оценки фотометрического значения диаметра астероида по его абсолютной звездной величине можно воспользоваться таблицей, опубликованной на сайте Центра малых планет (табл. 3.5). Таблица дает величины диаметров для значений альбедо 0,5, 0,25 и 0,05. Для значений H из левой колонки диаметры приводятся в километрах, для значений H из правой колонки – в метрах (как показывает формула (3.7), значения H, различающиеся на 15 звездных величин, при одном и том же значении альбедо дают значения диаметров, различающиеся ровно в тысячу раз).
Поскольку альбедо зависит от длины волны света, то в формуле (3.7) предполагается использование альбедо в тех же лучах V, в которых оценивалась звездная величина Солнца и величина H (обозначается как pV).
Для АСЗ усредненное значение альбедо равно 0,14 [Stuart and Binzel, 2004]. Если при данном значении альбедо подставить в формулу (3.7) значение H = 17,75m, то найдем, что данному значению звездной величины отвечает значение диаметра, равное 1 км.
Для оценки фотометрического значения диаметра астероида по его абсолютной звездной величине можно воспользоваться таблицей, опубликованной на сайте Центра малых планет (табл. 3.5). Таблица дает величины диаметров для значений альбедо 0,5, 0,25 и 0,05. Для значений H из левой колонки диаметры приводятся в километрах, для значений H из правой колонки – в метрах (как показывает формула (3.7), значения H, различающиеся на 15 звездных величин, при одном и том же значении альбедо дают значения диаметров, различающиеся ровно в тысячу раз).