Страница:
Схема отношения (обозначается S) определяется как конечное множество атрибутов с уникальными именами, т. е.:
Количество атрибутов в схеме отношений определяет степень этого отношения и обозначается как мощность множества: |S|.
Схема отношений может ассоциироваться с именем схемы отношений.
В табличной форме представления отношений, как нетрудно заметить, схема отношения – это не что иное, как строка заголовков столбцов.
 S = {a1, a2, a3, a4} – схема отношений этой таблицы.
S = {a1, a2, a3, a4} – схема отношений этой таблицы.
Имя отношения изображается как схематический заголовок таблицы.
В текстовой же форме представления схема отношений может быть представлена как именованный список имен атрибутов, например:
Из определения следует, что схема отношения может быть и пустой (S = ∅). Правда, возможно это только в теории, так как на практике система управления базами данных никогда не допустит создания пустой схемы отношения.
Именованное значение кортежа на атрибуте (обозначается t(a))определяется по аналогии с атрибутом как упорядоченная пара, состоящая из имени атрибута и значения атрибута, т. е.:
В табличной форме представления отношения каждое именованное значение кортежа на атрибуте – это соответствующая ячейка таблицы:
 Здесь t(a1), t(a2), t(a3) – именованные значения кортежа t на атрибутах а1, а2, а3.
Здесь t(a1), t(a2), t(a3) – именованные значения кортежа t на атрибутах а1, а2, а3.
Простейшие примеры именованных значений кортежей на атрибутах:
4. Кортежи. Типы кортежей
5. Отношения. Типы отношений
Лекция № 4. Реляционная алгебра. Унарные операции
1. Унарная операция выборки
2. Унарная операция проекции
3. Унарная операция переименования
4. Свойства унарных операций
Лекция № 5. Реляционная алгебра. Бинарные операции
1. Операции объединения, пересечения, разности
2. Операции декартового произведения и естественного соединения
S = {a | a ∈ S};В каждой таблице, представляющей отношение, все заголовки столбцов (все атрибуты) объединяются в схему этого отношения.
Количество атрибутов в схеме отношений определяет степень этого отношения и обозначается как мощность множества: |S|.
Схема отношений может ассоциироваться с именем схемы отношений.
В табличной форме представления отношений, как нетрудно заметить, схема отношения – это не что иное, как строка заголовков столбцов.

Имя отношения изображается как схематический заголовок таблицы.
В текстовой же форме представления схема отношений может быть представлена как именованный список имен атрибутов, например:
Студенты (№ зачетной книжки, Фамилия, Имя, Отчество, Дата рождения).Здесь, как и в табличной форме представления, домены атрибутов не указываются, но подразумеваются.
Из определения следует, что схема отношения может быть и пустой (S = ∅). Правда, возможно это только в теории, так как на практике система управления базами данных никогда не допустит создания пустой схемы отношения.
Именованное значение кортежа на атрибуте (обозначается t(a))определяется по аналогии с атрибутом как упорядоченная пара, состоящая из имени атрибута и значения атрибута, т. е.:
t(a) = (name(a) : x), x ∈ dom(a);Видим, что значение атрибута берется из домена атрибута.
В табличной форме представления отношения каждое именованное значение кортежа на атрибуте – это соответствующая ячейка таблицы:

Простейшие примеры именованных значений кортежей на атрибутах:
(Курс: 5), (Балл: 5);Здесь соответственно Курс и Балл – имена двух атрибутов, а 5 – это одно из их значений, взятое из их доменов. Разумеется, хоть эти значения в обоих случаях равны друг другу, семантически они различны, так как множества этих значений в обоих случаях отличаются друг от друга.
4. Кортежи. Типы кортежей
Понятие кортежа в системах управления базами данных может быть интуитивно найдено уже из предыдущего пункта, когда мы говорили об именованном значении кортежа на различных атрибутах. Итак, кортеж (обозначается t, от англ. tuple – «кортеж») со схемой отношения S определяется как множество именованных значений этого кортежа на всех атрибутах, входящих в данную схему отношений S. Другими словами, атрибуты берутся из области определения кортежа, def(t), т. е.:
В табличной форме записи отношения кортежем будет любая строка таблицы, т. е.:
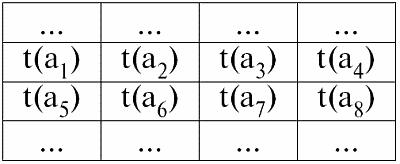
Здесь t1(S) = {t(a1), t(a2), t(a3), t(a4)} и t2(S) = {t(a5), t(a6), t(a7), t(a8)} – кортежи.
Кортежи в СУБД различаются по типам в зависимости от своей области определения. Кортежи называются:
1) частичными, если их область определения включается или совпадает со схемой отношения, т. е. def(t) ⊆ S.
Это общий случай в практике баз данных;
2) полными, в том случае если их область определения полностью совпадает, равна схеме отношения, т. е. def(t) = S;
3) неполными, если область определения полностью включается в схему отношений, т. е. def(t) ⊂ S;
4) нигде не определенными, если их область определения равна пустому множеству, т. е. def(t) = ∅.
Поясним на примере. Пусть у нас имеется отношение, заданное следующей таблицей.
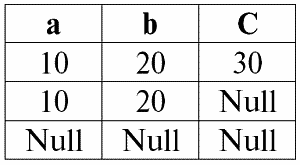
Пусть здесь t1 = {10, 20, 30}, t2 = {10, 20, Null}, t3 = {Null, Null, Null}. Тогда легко заметить, что кортеж t1 – полный, так как его область определения def(t1) = { a, b, c} = S.
Кортеж t2 – неполный, def(t2) = { a, b} ⊂ S. И, наконец, кортеж t3 – нигде не определенный, так как его def(t3) = ∅.
Надо заметить, что нигде не определенный кортеж – это пустое множество, тем не менее ассоциируемое со схемой отношений. Иногда нигде не определенный кортеж обозначается: ∅(S). Как мы уже видели в приведенном примере, такой кортеж представляет собой строку таблицы, состоящую только из Null-значений.
Интересно, что сравнимыми, т. е. возможно равными, являются только кортежи с одной и той же схемой отношений. Поэтому, например, два нигде не определенных кортежа с различными схемами отношений не будут равными, как могло ожидаться. Они будут различными так же, как их схемы отношений.
t ≡ t(S) = {t(a) | a ∈ def(t) ⊆ S;.Важно, что одному имени атрибута обязательно должно соответствовать не более одного значения атрибута.
В табличной форме записи отношения кортежем будет любая строка таблицы, т. е.:

Здесь t1(S) = {t(a1), t(a2), t(a3), t(a4)} и t2(S) = {t(a5), t(a6), t(a7), t(a8)} – кортежи.
Кортежи в СУБД различаются по типам в зависимости от своей области определения. Кортежи называются:
1) частичными, если их область определения включается или совпадает со схемой отношения, т. е. def(t) ⊆ S.
Это общий случай в практике баз данных;
2) полными, в том случае если их область определения полностью совпадает, равна схеме отношения, т. е. def(t) = S;
3) неполными, если область определения полностью включается в схему отношений, т. е. def(t) ⊂ S;
4) нигде не определенными, если их область определения равна пустому множеству, т. е. def(t) = ∅.
Поясним на примере. Пусть у нас имеется отношение, заданное следующей таблицей.

Пусть здесь t1 = {10, 20, 30}, t2 = {10, 20, Null}, t3 = {Null, Null, Null}. Тогда легко заметить, что кортеж t1 – полный, так как его область определения def(t1) = { a, b, c} = S.
Кортеж t2 – неполный, def(t2) = { a, b} ⊂ S. И, наконец, кортеж t3 – нигде не определенный, так как его def(t3) = ∅.
Надо заметить, что нигде не определенный кортеж – это пустое множество, тем не менее ассоциируемое со схемой отношений. Иногда нигде не определенный кортеж обозначается: ∅(S). Как мы уже видели в приведенном примере, такой кортеж представляет собой строку таблицы, состоящую только из Null-значений.
Интересно, что сравнимыми, т. е. возможно равными, являются только кортежи с одной и той же схемой отношений. Поэтому, например, два нигде не определенных кортежа с различными схемами отношений не будут равными, как могло ожидаться. Они будут различными так же, как их схемы отношений.
5. Отношения. Типы отношений
И наконец дадим определение отношению, как некой вершине пирамиды, состоящей из всех предыдущих понятий. Итак, отношение (обозначается r, от англ. relation – «отношение») со схемой отношений S определяется как обязательно конечное множество кортежей, имеющих ту же схему отношения S. Таким образом:
Отношения, как и кортежи, различаются по типам. Итак, отношения называются:
1) частичными, если для любого входящего в отношение кортежа выполняется следующее условие: [def(t) ⊆ S].
Это (как и с кортежами) общий случай;
2) полными, в том случае если ∀t ∈ r(S) выполняется: [def(t) = S];
3) неполными, если ∃t ∈ r(S) def(t) ⊂ S;
4) нигде не определенными, если ∀t ∈ r(S) [def(t) = ∅].
Обратим отдельное внимание на нигде не определенные отношения. В отличие от кортежей работа с такими отношениями включает в себя небольшую тонкость. Дело в том, что нигде не определенные отношения могут быть двух видов: они могут быть либо пустыми, либо могут содержать единственный нигде не определенный кортеж (такие отношения обозначаются {∅(S)}).
Сравнимыми (по аналогии с кортежами), т. е., возможно равными, являются лишь отношения с одной и той же схемой отношения. Поэтому отношения с различными схемами отношений являются различными.
В табличной форме представления, отношение – это тело таблицы, которому соответствует строка – заголовок столбцов, т. е. буквально – вся таблица, вместе с первой строкой, содержащей заголовки.
r ≡ r(S) = {t(S) | t ∈r};По аналогии со схемами отношений количество кортежей в отношении называют мощностью отношений и обозначают как мощность множества: |r|.
Отношения, как и кортежи, различаются по типам. Итак, отношения называются:
1) частичными, если для любого входящего в отношение кортежа выполняется следующее условие: [def(t) ⊆ S].
Это (как и с кортежами) общий случай;
2) полными, в том случае если ∀t ∈ r(S) выполняется: [def(t) = S];
3) неполными, если ∃t ∈ r(S) def(t) ⊂ S;
4) нигде не определенными, если ∀t ∈ r(S) [def(t) = ∅].
Обратим отдельное внимание на нигде не определенные отношения. В отличие от кортежей работа с такими отношениями включает в себя небольшую тонкость. Дело в том, что нигде не определенные отношения могут быть двух видов: они могут быть либо пустыми, либо могут содержать единственный нигде не определенный кортеж (такие отношения обозначаются {∅(S)}).
Сравнимыми (по аналогии с кортежами), т. е., возможно равными, являются лишь отношения с одной и той же схемой отношения. Поэтому отношения с различными схемами отношений являются различными.
В табличной форме представления, отношение – это тело таблицы, которому соответствует строка – заголовок столбцов, т. е. буквально – вся таблица, вместе с первой строкой, содержащей заголовки.
Лекция № 4. Реляционная алгебра. Унарные операции
Реляционная алгебра, как нетрудно догадаться, – это особая разновидность алгебры, в которой все операции производятся над реляционными моделями данных, т. е. над отношениями.
В табличных терминах отношение включает в себя строки, столбцы и строку – заголовок столбцов. Поэтому естественными унарными операциями являются операции выбора определенных строк или столбцов, а также смены заголовков столбцов – переименования атрибутов.
В табличных терминах отношение включает в себя строки, столбцы и строку – заголовок столбцов. Поэтому естественными унарными операциями являются операции выбора определенных строк или столбцов, а также смены заголовков столбцов – переименования атрибутов.
1. Унарная операция выборки
Первой унарной операцией, которую мы рассмотрим, является операция выборки – операция выбора строк из таблицы, представляющей отношение, по какому-либо принципу, т. е. выбор строк-кортежей, удовлетворяющих определенному условию или условиям.
Оператор выборки обозначается σ<P>, условие выборки – P<S>, т. е., оператор σ берется всегда с определенным условием на кортежи P, а само условие P записывается зависящим от схемы отношения S. С учетом всего этого сама операция выборки над схемой отношения S применительно к отношению r будет выглядеть следующим образом:
Чтобы лучше понять принцип работы этой операции, приведем пример. Пусть дана следующая схема отношения:
Пусть также дан следующий кортеж из этого отношения:
А вообще результатом этой конкретной выборки
Оператор выборки обозначается σ<P>, условие выборки – P<S>, т. е., оператор σ берется всегда с определенным условием на кортежи P, а само условие P записывается зависящим от схемы отношения S. С учетом всего этого сама операция выборки над схемой отношения S применительно к отношению r будет выглядеть следующим образом:
σ<P>r(S) ≡ σ<P>r = {t(S) |t ∈ r & P<S>t} = {t(S) |t ∈ r & IfNull(P<S>t, False};Результатом этой операции будет новое отношение с той же схемой отношения S, состоящее из тех кортежей t(S) исходного отношения-операнда, которые удовлетворяют условию выборки P<S>t. Понятно, что для того, чтобы применить какое-то условие к кортежу, необходимо подставить значения атрибутов кортежа вместо имен атрибутов.
Чтобы лучше понять принцип работы этой операции, приведем пример. Пусть дана следующая схема отношения:
S: Сессия (№ зачетной книжки, Фамилия, Предмет, Оценка).Условие выборки возьмем такое:
P<S> = (Предмет = ‘Информатика’ and Оценка > 3).Нам необходимо из исходного отношения-операнда выделить те кортежи, в которых содержится информация о студентах, сдавших предмет «Информатика» не ниже, чем на три балла.
Пусть также дан следующий кортеж из этого отношения:
t0(S) ∈ r(S): {(№ зачетной книжки: 100), (Фамилия: ‘Иванов’), (Предмет: ‘Базы данных’), (Оценка: 5)};Применяем наше условие выборки к кортежу t0, получаем:
P<S>t0 = (‘Базы данных’ = ‘Информатика’ and 5 > 3);На данном конкретном кортеже условие выборки не выполняется.
А вообще результатом этой конкретной выборки
σ<Предмет = 'Информатика' and Оценка > 3 > Сессиябудет таблица «Сессия», в которой оставлены строки, удовлетворяющие условию выборки.
2. Унарная операция проекции
Еще одна стандартная унарная операция, которую мы изучим, – это операция проекции. Операция проекции – это операция выбора столбцов из таблицы, представляющей отношение, по какому-либо признаку. А именно машина выбирает те атрибуты (т. е. буквально те столбцы) исходного отношения-операнда, которые были указаны в проекции.
Оператор проекции обозначается [S'] или π<S'>. Здесь S' – подсхема исходной схемы отношения S, т. е. ее некоторые столбцы. Что это означает? Это означает, что у S’ атрибутов меньше, чем у S, потому что в S' остались только те из них, для которых выполнилось условие проекции. А в таблице, представляющей отношение r(S' ), строк столько же, сколько их у таблицы r(S), а столбцов – меньше, так как остались только соответствующие оставшимся атрибутам. Таким образом, оператор проекции π< S'> применительно к отношению r(S) дает в результате новое отношение с другой схемой отношения r(S' ), состоящее из проекций t(S) [S' ] кортежей исходного отношения. Как определяются эти проекции кортежей? Проекция любого кортежа t(S) исходного отношения r(S) на подсхему S' определяется следующей формулой:
С учетом всего вышесказанного, операция проекции в терминах систем управления базами данных будет выглядеть следующим образом:
Пусть дано отношение «Сессия» и схема этого отношения:
Далее, пусть нам дан кортеж t0(S) из исходного отношения:
Оператор проекции обозначается [S'] или π<S'>. Здесь S' – подсхема исходной схемы отношения S, т. е. ее некоторые столбцы. Что это означает? Это означает, что у S’ атрибутов меньше, чем у S, потому что в S' остались только те из них, для которых выполнилось условие проекции. А в таблице, представляющей отношение r(S' ), строк столько же, сколько их у таблицы r(S), а столбцов – меньше, так как остались только соответствующие оставшимся атрибутам. Таким образом, оператор проекции π< S'> применительно к отношению r(S) дает в результате новое отношение с другой схемой отношения r(S' ), состоящее из проекций t(S) [S' ] кортежей исходного отношения. Как определяются эти проекции кортежей? Проекция любого кортежа t(S) исходного отношения r(S) на подсхему S' определяется следующей формулой:
t(S) [S’] = {t(a)|a ∈ def(t) ∩ S’}, S' ⊆S.Важно заметить, что дубликаты кортежей из результата исключаются, т. е. в таблице, представляющей новое, результирующее отношение повторяющихся строк не будет.
С учетом всего вышесказанного, операция проекции в терминах систем управления базами данных будет выглядеть следующим образом:
π<S'>r(S) ≡ π<S’>r ≡ r(S) [S’] ≡ r [S' ] = {t(S) [S’] | t ∈ r };Рассмотрим пример, иллюстрирующий принцип работы операции выборки.
Пусть дано отношение «Сессия» и схема этого отношения:
S: Сессия (№ зачетной книжки, Фамилия, Предмет, Оценка);Нас будут интересовать только два атрибута из этой схемы, а именно «№ зачетной книжки» и «Фамилия» студента, поэтому подсхема S' будет выглядеть следующим образом:
S' : (№ зачетной книжки, Фамилия).Нужно исходное отношение r(S) спроецировать на подсхему S'.
Далее, пусть нам дан кортеж t0(S) из исходного отношения:
t0(S) ∈ r(S): {(№ зачетной книжки: 100), (Фамилия: ‘Иванов’), (Предмет: ‘Базы данных’), (Оценка: 5)};Значит, проекция этого кортежа на данную подсхему S' будет выглядеть следующим образом:
t0(S) S': {(№ зачетной книжки: 100), (Фамилия: ‘Иванов’)};Если говорить об операции проекции в терминах таблиц, то проекция Сессия [№ зачетной книжки, Фамилия] исходного отношения – это таблица Сессия, из которой вычеркнуты все столбцы, кроме двух: № зачетной книжки и Фамилия. Кроме того, все дублирующиеся строки также удалены.
3. Унарная операция переименования
И последняя унарная операция, которую мы рассмотрим, – это операция переименования атрибутов. Если говорить об отношении как о таблице, то операция переименования нужна для того, чтобы поменять названия всех или некоторых столбцов.
Оператор переименования выглядит следующим образом: ρ<φ>, здесь φ — функция переименования.
Эта функция устанавливает взаимно-однозначное соответствие между именами атрибутов схем S и Ŝ, где соответственно S — схема исходного отношения, а Ŝ — схема отношения с переименованными атрибутами. Таким образом, оператор ρ<φ> в применении к отношению r(S) дает новое отношение со схемой Ŝ, состоящее из кортежей исходного отношения только с переименованными атрибутами.
Запишем операцию переименования атрибутов в терминах систем управления базами данных:
Рассмотрим уже знакомое нам отношение Сессия, со схемой:
В табличных терминах отношение
Оператор переименования выглядит следующим образом: ρ<φ>, здесь φ — функция переименования.
Эта функция устанавливает взаимно-однозначное соответствие между именами атрибутов схем S и Ŝ, где соответственно S — схема исходного отношения, а Ŝ — схема отношения с переименованными атрибутами. Таким образом, оператор ρ<φ> в применении к отношению r(S) дает новое отношение со схемой Ŝ, состоящее из кортежей исходного отношения только с переименованными атрибутами.
Запишем операцию переименования атрибутов в терминах систем управления базами данных:
ρ<φ> r(S) ≡ ρ<φ>r = {ρ<φ> t(S)| t ∈ r};Приведем пример использования этой операции:
Рассмотрим уже знакомое нам отношение Сессия, со схемой:
S: Сессия (№ зачетной книжки, Фамилия, Предмет, Оценка);Введем новую схему отношения Ŝ, с другими именами атрибутов, которые мы бы хотели видеть вместо имеющихся:
Ŝ : (№ ЗК, Фамилия, Предмет, Балл);Например, заказчик базы данных захотел в вашем готовом отношении видеть другие названия. Чтобы воплотить в жизнь этот заказ, необходимо спроектировать следующую функцию переименования:
φ : (№ зачетной книжки, Фамилия, Предмет, Оценка) → (№ ЗК, Фамилия, Предмет, Балл);Фактически, требуется поменять имя только у двух атрибутов, поэтому законно будет записать следующую функцию переименования вместо имеющейся:
φ : (№ зачетной книжки, Оценка) → (№ ЗК, Балл);Далее, пусть дан также уже знакомый нам кортеж принадлежащий отношению Сессия:
t0(S) ∈ r(S): {(№ зачетной книжки: 100), (Фамилия: ‘Иванов’), (Предмет: ‘Базы данных’), (Оценка: 5)};Применим оператор переименования к этому кортежу:
ρ<φ> t0(S): {(№ ЗК: 100), (Фамилия: ‘Иванов’), (Предмет: ‘Базы данных’), (Балл: 5)};Итак, это один из кортежей нашего отношения, у которого переименовали атрибуты.
В табличных терминах отношение
ρ < № зачетной книжки, Оценка → «№ ЗК, Балл > Сессия —это новая таблица, полученная из таблицы отношения «Сессия», переименованием указанных атрибутов.
4. Свойства унарных операций
У унарных операций, как и у любых других, есть определенные свойства. Рассмотрим наиболее важные из них.
Первым свойством унарных операций выборки, проекции и переименования является свойство, характеризующее соотношение мощностей отношений. (Напомним, что мощность – это количество кортежей в том или ином отношении.) Понятно, что здесь рассматривается соответственно отношение исходное и отношение, полученное в результате применения той или иной операции.
Заметим, что все свойства унарных операций следуют непосредственно из их определений, поэтому их можно легко объяснить и даже при желании вывести самостоятельно.
Итак:
1) соотношение мощностей:
а) для операции выборки: | σ<P>r |≤ |r|;
б) для операции проекции: | r[S'] | ≤ |r|;
в) для операции переименования: | ρ<φ>r | = |r|;
Итого, мы видим, что для двух операторов, а именно для оператора выборки и оператора проекции, мощность исходных отношений – операндов больше, чем мощность отношений, получаемых из исходных применением соответствующих операций. Это происходит потому, что при выборе, сопутствующему действию этих двух операций выборки и проекции, происходит исключение некоторых строк или столбцов, не удовлетворивших условиям выбора. В том случае, когда условиям удовлетворяют все строки или столбцы, уменьшения мощности (т. е. количества кортежей) не происходит, поэтому в формулах неравенство нестрогое.
В случае же операции переименования, мощность отношения не изменяется, за счет того, что при смене имен никакие кортежи из отношения не исключаются;
2) свойство идемпотентности:
а) для операции выборки: σ<P> σ<P>r = σ<P>;
б) для операции проекции: r [S’] [S’] = r [S'];
в) для операции переименования в общем случае свойство идемпотентности неприменимо.
Это свойство означает, что двойное последовательное применение одного и того же оператора к какому-либо отношению равносильно его однократному применению.
Для операции переименования атрибутов отношения, вообще говоря, это свойство может быть применено, но обязательно со специальными оговорками и условиями.
Свойство идемпотентности очень часто используется для упрощения вида выражения и приведения его к более экономичному, актуальному виду.
И последнее свойство, которое мы рассмотрим, – это свойство монотонности. Интересно заметить, что при любых условиях все три оператора монотонны;
3) свойство монотонности:
а) для операции выборки: r1 ⊆ r2 ⇒ σ<P> r1 ⇒ σ <P>r2;
б) для операции проекции: r1 ⊆ r2 ⇒ r1[S'] ⊆ r2 [S'];
в) для операции переименования: r1 ⊆ r2 ⇒ ρ<φ>r1 ⊆ ρ <φ>r2;
Понятие монотонности в реляционной алгебре аналогично этому же понятию из алгебры обычной, общей. Поясним: если изначально отношения r1 и r2 были связаны между собой таким образом, что r ⊆ r2, то и после применения любого их трех операторов выборки, проекции или переименования это соотношение сохранится.
Первым свойством унарных операций выборки, проекции и переименования является свойство, характеризующее соотношение мощностей отношений. (Напомним, что мощность – это количество кортежей в том или ином отношении.) Понятно, что здесь рассматривается соответственно отношение исходное и отношение, полученное в результате применения той или иной операции.
Заметим, что все свойства унарных операций следуют непосредственно из их определений, поэтому их можно легко объяснить и даже при желании вывести самостоятельно.
Итак:
1) соотношение мощностей:
а) для операции выборки: | σ<P>r |≤ |r|;
б) для операции проекции: | r[S'] | ≤ |r|;
в) для операции переименования: | ρ<φ>r | = |r|;
Итого, мы видим, что для двух операторов, а именно для оператора выборки и оператора проекции, мощность исходных отношений – операндов больше, чем мощность отношений, получаемых из исходных применением соответствующих операций. Это происходит потому, что при выборе, сопутствующему действию этих двух операций выборки и проекции, происходит исключение некоторых строк или столбцов, не удовлетворивших условиям выбора. В том случае, когда условиям удовлетворяют все строки или столбцы, уменьшения мощности (т. е. количества кортежей) не происходит, поэтому в формулах неравенство нестрогое.
В случае же операции переименования, мощность отношения не изменяется, за счет того, что при смене имен никакие кортежи из отношения не исключаются;
2) свойство идемпотентности:
а) для операции выборки: σ<P> σ<P>r = σ<P>;
б) для операции проекции: r [S’] [S’] = r [S'];
в) для операции переименования в общем случае свойство идемпотентности неприменимо.
Это свойство означает, что двойное последовательное применение одного и того же оператора к какому-либо отношению равносильно его однократному применению.
Для операции переименования атрибутов отношения, вообще говоря, это свойство может быть применено, но обязательно со специальными оговорками и условиями.
Свойство идемпотентности очень часто используется для упрощения вида выражения и приведения его к более экономичному, актуальному виду.
И последнее свойство, которое мы рассмотрим, – это свойство монотонности. Интересно заметить, что при любых условиях все три оператора монотонны;
3) свойство монотонности:
а) для операции выборки: r1 ⊆ r2 ⇒ σ<P> r1 ⇒ σ <P>r2;
б) для операции проекции: r1 ⊆ r2 ⇒ r1[S'] ⊆ r2 [S'];
в) для операции переименования: r1 ⊆ r2 ⇒ ρ<φ>r1 ⊆ ρ <φ>r2;
Понятие монотонности в реляционной алгебре аналогично этому же понятию из алгебры обычной, общей. Поясним: если изначально отношения r1 и r2 были связаны между собой таким образом, что r ⊆ r2, то и после применения любого их трех операторов выборки, проекции или переименования это соотношение сохранится.
Лекция № 5. Реляционная алгебра. Бинарные операции
1. Операции объединения, пересечения, разности
У любых операций есть свои правила применимости, которые необходимо соблюдать, чтобы выражения и действия не теряли смысла. Бинарные теоретико-множественные операции объединения, пересечений и разности могут быть применены только к двум отношениям обязательно с одной и той же схемой отношения. Результатом таких бинарных операций будут являться отношения, состоящие из кортежей, удовлетворяющих условиям операций, но с такой же схемой отношения, как и у операндов.
1. Результатом операции объединения двух отношений r1(S) и r2(S) будет новое отношение r3(S), состоящее из тех кортежей отношений r1(S) и r2(S), которые принадлежат хотя бы одному из исходных отношений и с такой же схемой отношения.
Таким образом, пересечение двух отношений – это:
Пусть даны два отношения:
r1(S):
r2(S):

Мы видим, что схемы первого и второго отношений одинаковы, только имеют различной количество кортежей. Объединением этих двух отношений будет отношение r3(S), которому будет соответствовать следующая таблица:
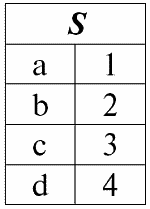
Итак, схема отношения S не изменилась, только выросло количество кортежей.
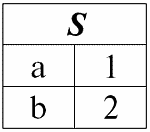
2. Перейдем к рассмотрению следующей бинарной операции – операции пересечения двух отношений. Как мы знаем еще из школьной геометрии, в результирующее отношение войдут только те кортежи исходных отношений, которые присутствуют одновременно в обоих отношениях r1(S) и r2(S) (снова обращаем внимание на одинаковую схему отношения).
Операция пересечения двух отношений будет выглядеть следующим образом:
r1(S):
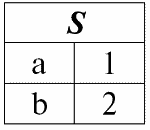
r2(S):

Согласно определению операции пересечением отношений r1(S) и r2(S) будет новое отношение r4(S), табличное представление которого будет выглядеть следующим образом:
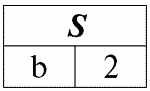
Действительно, если посмотреть на кортежи первого и второго исходного отношений, общий среди них только один: {b, 2}. Он и стал единственным кортежем нового отношения r4(S).
3. Операция разности двух отношений определяется аналогичным с предыдущими операциями образом. Отношения-операнды, так же, как и в предыдущих операциях, должны иметь одинаковые схемы отношения, тогда в результирующее отношение войдут все те кортежи первого отношения, которых нет во втором, т. е.:
r1(S):
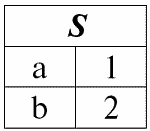
r2(S):

Мы рассмотрим как операнды в операции пересечения двух отношений. Тогда, следуя данному определению, результирующее отношение r5(S) будет выглядеть следующим образом:
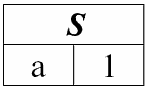
Рассмотренные бинарные операции являются базовыми, на них основываются другие операции, более сложные.
1. Результатом операции объединения двух отношений r1(S) и r2(S) будет новое отношение r3(S), состоящее из тех кортежей отношений r1(S) и r2(S), которые принадлежат хотя бы одному из исходных отношений и с такой же схемой отношения.
Таким образом, пересечение двух отношений – это:
r3(S) = r1(S) ∪ r2(S) = {t(S) | t ∈r1 ∪t ∈r2};Для наглядности, приведем пример в терминах таблиц:
Пусть даны два отношения:
r1(S):

r2(S):

Мы видим, что схемы первого и второго отношений одинаковы, только имеют различной количество кортежей. Объединением этих двух отношений будет отношение r3(S), которому будет соответствовать следующая таблица:
r3(S) = r1(S) ∪ r2(S):

Итак, схема отношения S не изменилась, только выросло количество кортежей.
2. Перейдем к рассмотрению следующей бинарной операции – операции пересечения двух отношений. Как мы знаем еще из школьной геометрии, в результирующее отношение войдут только те кортежи исходных отношений, которые присутствуют одновременно в обоих отношениях r1(S) и r2(S) (снова обращаем внимание на одинаковую схему отношения).
Операция пересечения двух отношений будет выглядеть следующим образом:
r4(S) = r1(S) ∩ r2(S) = {t(S) | t ∈ r1 & t ∈ r2};И снова рассмотрим действие этой операции над отношениями, представленными в виде таблиц:
r1(S):

r2(S):

Согласно определению операции пересечением отношений r1(S) и r2(S) будет новое отношение r4(S), табличное представление которого будет выглядеть следующим образом:
r4(S) = r1(S) ∩ r2(S):

Действительно, если посмотреть на кортежи первого и второго исходного отношений, общий среди них только один: {b, 2}. Он и стал единственным кортежем нового отношения r4(S).
3. Операция разности двух отношений определяется аналогичным с предыдущими операциями образом. Отношения-операнды, так же, как и в предыдущих операциях, должны иметь одинаковые схемы отношения, тогда в результирующее отношение войдут все те кортежи первого отношения, которых нет во втором, т. е.:
r5(S) = r1(S) \ r2(S) = {t(S) | t ∈ r1 & t ∉ r2};Уже хорошо знакомые нам отношения r1(S) и r2(S), в табличном представлении выглядящие следующим образом:
r1(S):

r2(S):

Мы рассмотрим как операнды в операции пересечения двух отношений. Тогда, следуя данному определению, результирующее отношение r5(S) будет выглядеть следующим образом:
r5(S) = r1(S) \ r2(S):
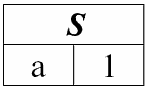
Рассмотренные бинарные операции являются базовыми, на них основываются другие операции, более сложные.
2. Операции декартового произведения и естественного соединения
Операция декартового произведения и операция естественного соединения являются бинарными операциями типа произведения и основываются на операции объединения двух отношений, которую мы рассматривали ранее.
Хотя действие операции декартова произведения многим может показаться знакомым, начнем мы все-таки с операции естественного произведения, так как она является более общим случаем, нежели первая операция.
Итак, рассмотрим операцию естественного соединения. Следует сразу заметить, что операндами этого действия могут являться отношения с разными схемами в отличие от трех бинарных операций объединения, пересечения и переименования.
Если рассмотреть два отношения с различными схемами отношений r1(S1) и r2(S2), то их естественным соединением будет новое отношение r3(S3), которое будет состоять только из тех кортежей операндов, которые совпадают на пересечении схем отношений. Соответственно, схема нового отношения будет больше любой из схем отношений исходных, так как является их соединением, «склеиванием». Кстати, кортежи, одинаковые в двух отношениях-операндах, по которым и происходит это «склеивание», называются соединимыми.
Запишем определение операции естественного соединения на языке формул систем управления базами данных:
r1(S1):
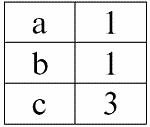
r2(S2):
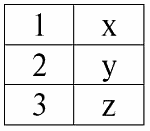
Мы видим, что у этих отношений присутствуют кортежи, совпадающие при пересечении схем S1 и S2 отношений. Перечислим их:
1) кортеж {a, 1} отношения r1(S1) совпадает с кортежем {1, x} отношения r2(S2);
2) кортеж {b, 1} из r1(S1) также совпадает с кортежем {1, x} из r2(S2);
3) кортеж {c, 3} совпадает с кортежем {3, z}.
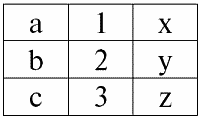
Значит, при естественном соединении новое отношение r3(S3) получается «склеиванием» именно на этих кортежах. Таким образом, r3(S3) в табличном представлении будет выглядеть следующим образом:
Хотя действие операции декартова произведения многим может показаться знакомым, начнем мы все-таки с операции естественного произведения, так как она является более общим случаем, нежели первая операция.
Итак, рассмотрим операцию естественного соединения. Следует сразу заметить, что операндами этого действия могут являться отношения с разными схемами в отличие от трех бинарных операций объединения, пересечения и переименования.
Если рассмотреть два отношения с различными схемами отношений r1(S1) и r2(S2), то их естественным соединением будет новое отношение r3(S3), которое будет состоять только из тех кортежей операндов, которые совпадают на пересечении схем отношений. Соответственно, схема нового отношения будет больше любой из схем отношений исходных, так как является их соединением, «склеиванием». Кстати, кортежи, одинаковые в двух отношениях-операндах, по которым и происходит это «склеивание», называются соединимыми.
Запишем определение операции естественного соединения на языке формул систем управления базами данных:
r3(S3) = r1(S1) × r2(S2) = {t(S1 ∪S2) | t[S1] ∈ r1 & t(S2) ∈ r2};Рассмотрим пример, хорошо иллюстрирующий работу естественного соединения, его «склеивание». Пусть дано два отношения r1(S1) и r2(S2), в табличной форме представления соответственно равные:
r1(S1):

r2(S2):
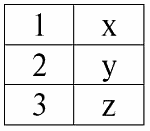
Мы видим, что у этих отношений присутствуют кортежи, совпадающие при пересечении схем S1 и S2 отношений. Перечислим их:
1) кортеж {a, 1} отношения r1(S1) совпадает с кортежем {1, x} отношения r2(S2);
2) кортеж {b, 1} из r1(S1) также совпадает с кортежем {1, x} из r2(S2);
3) кортеж {c, 3} совпадает с кортежем {3, z}.
Значит, при естественном соединении новое отношение r3(S3) получается «склеиванием» именно на этих кортежах. Таким образом, r3(S3) в табличном представлении будет выглядеть следующим образом:
r3(S3) = r1(S1) × r2(S2):

