Страница:
Коллектив авторов
Концепции современного естествознания: Шпаргалка
1. ПОНЯТИЕ ЕСТЕСТВОЗНАНИЯ
Естествознание – это совокупность наук о явлениях и законах природы. Само слово «естествознание» образовано из двух слов: «естество» (природа) и «знание», что означает буквально знание природы. В настоящее время в области естествознания накоплен огромный научный материал, изложить который в одной учебной дисциплине не представляется возможным. В связи с этим ограничимся лишь рассмотрением концепций современного естествознания. Концепция (от лат. conceptio – понимание, система) – это определенный способ понимания, трактовки каких-либо явлений, основная точка зрения, руководящая идея для их освещения. Концептуальный подход позволяет с единых позиций интегрировать разрозненные знания о неживой и живой природе и человеческом обществе в целостную естественнонаучную картину мира. Он полезен не только для понимания истории развития естествознания, сути изучаемых им явлений и законов природы, но и для ознакомления с важнейшими достижениями естествознания.
В процессе получения нового знания исследователь всегда пользуется определенной методологией. Слово «методология» происходит от греческих слов «методос» (путь познания) – метод и «логос» – учение и означает учение о методах. В современном понимании методология – учение о структуре, логической организации, методах и средствах деятельности. Метод – это способ достижения какой-либо цели, включающий совокупность приемов практической или теоретической деятельности. Метод вооружает человека наиболее рациональными способами проведения исследований и тем самым оптимизирует его деятельность. Один из основоположников научной методологии английский философ Ф. Бэкон (1561–1626) считал, что научный метод подобен фонарю, освещающему дорогу бредущему в темноте путнику.
В процессе получения нового знания исследователь всегда пользуется определенной методологией. Слово «методология» происходит от греческих слов «методос» (путь познания) – метод и «логос» – учение и означает учение о методах. В современном понимании методология – учение о структуре, логической организации, методах и средствах деятельности. Метод – это способ достижения какой-либо цели, включающий совокупность приемов практической или теоретической деятельности. Метод вооружает человека наиболее рациональными способами проведения исследований и тем самым оптимизирует его деятельность. Один из основоположников научной методологии английский философ Ф. Бэкон (1561–1626) считал, что научный метод подобен фонарю, освещающему дорогу бредущему в темноте путнику.
2. АТОМИСТИЧЕСКИЕ КОНЦЕПЦИИ ДО 20 в
В основе представлений о микромире лежит атомистическая концепция о строении материи, которая впервые была выдвинута древнегреческим философом Левкиппом (ок. 500–440 до н. э.). Он ввел такие понятия, как «атом» и «пустота». Атомистические представления Левкиппа были конкретизированы, дополнены и развиты другим великим древнегреческим философом – Демокритом (ок. 460–370 до н. э.). Согласно гипотезе Демокрита, в абсолютной пустоте окружающего пространства существует бесконечное число мельчайших неделимых частиц – атомов, которые имеют разнообразную форму и движутся в пустоте беспорядочно, иногда они сталкиваются и отскакивают друг от друга, но иногда сцепляются в разных положениях и сочетаниях, что означает образование вещей с разным качеством. Эпикур (341–270 до н. э.) наделил атомы еще свойством тяжести. Атомы вечны, а вещи, образованные из них, гибнут (разъединяются), но сами атомы остаются, они далее могут сцепляться в новых сочетаниях с образованием новых вещей и т. д. Так возникают из атомов не только обычные вещи, но и Земля, звезды, космические миры в бесконечном пространстве.
Концепция атомизма получила дальнейшее развитие в XVIII веке в работах Дж. Дальтона (17661844), который принял атомный вес водорода за единицу и сопоставил с ним атомные веса других газов. Благодаря этому стали изучаться физико-химические свойства атомов. В XIX веке Д.И. Менделеев (1834–1907) построил систему химических элементов, основанную на их атомном весе.
Систематические исследования строения атомов начались в 1897 году благодаря открытию Дж. Томсоном (1856–1940) электрона – отрицательно заряженной частицы, входящей в состав всех атомов. В 1903 году Дж. Томсон, развивая идеи У. Томсона (лорда Кельвина) (1824–1907) о строении атома (У. Томсон в 1902 году предложил первую модель атома, согласно которой положительный заряд в атоме распределен в достаточно большой области, а электроны вкраплены в него, как «изюм в пудинг»), усовершенствовал модель атома. Атом, по Дж. Томсону, представлял собой положительно заряженный шар с вкрапленными в него электронами, суммарный отрицательный заряд которых по модулю равен положительному заряду шара (модель атома Томсона). Поскольку масса электрона приблизительно в 2000 раз меньше массы атома водорода, то предполагалось, что почти вся масса атома определяется массой положительного заряда.
Концепция атомизма получила дальнейшее развитие в XVIII веке в работах Дж. Дальтона (17661844), который принял атомный вес водорода за единицу и сопоставил с ним атомные веса других газов. Благодаря этому стали изучаться физико-химические свойства атомов. В XIX веке Д.И. Менделеев (1834–1907) построил систему химических элементов, основанную на их атомном весе.
Систематические исследования строения атомов начались в 1897 году благодаря открытию Дж. Томсоном (1856–1940) электрона – отрицательно заряженной частицы, входящей в состав всех атомов. В 1903 году Дж. Томсон, развивая идеи У. Томсона (лорда Кельвина) (1824–1907) о строении атома (У. Томсон в 1902 году предложил первую модель атома, согласно которой положительный заряд в атоме распределен в достаточно большой области, а электроны вкраплены в него, как «изюм в пудинг»), усовершенствовал модель атома. Атом, по Дж. Томсону, представлял собой положительно заряженный шар с вкрапленными в него электронами, суммарный отрицательный заряд которых по модулю равен положительному заряду шара (модель атома Томсона). Поскольку масса электрона приблизительно в 2000 раз меньше массы атома водорода, то предполагалось, что почти вся масса атома определяется массой положительного заряда.
3. АТОМИСТИЧЕСКИЕ КОНЦЕПЦИИ 20 в.: Э. РЕЗЕРФОРД И Н. БОР
В 1908 году Х. Гейгер и Э. Марсден, сотрудники лаборатории Э. Резерфорда (1871–1937), провели опыты по прохождению альфа-частиц через тонкие фольги из золота и других металлов и обнаружили, что почти все они проходят через фольгу, будто нет препятствия, и только 1/10000 из них испытывает сильное отклонение. С помощью модели Дж. Томсона это объяснить не удалось, но Резерфорд нашел выход. Он обратил внимание на то, что большая часть частиц отклоняется на малый угол, а малая – до 150°. Резерфорд пришел к выводу, что они взаимодействуют с каким-то массивным объектом малого размера, этот объект представляет собой ядро атома – положительно заряженную микрочастицу, размер которой (10-12 см) очень мал по сравнению с размерами атома (10-8 см), но в нем почти полностью сосредоточена масса атома.
В 1911 году Резерфорд предложил модель атома, которая напоминала Солнечную систему: в центре находится атомное ядро, а вокруг него по своим орбитам движутся электроны. Однако эта модель содержала неразрешимое противоречие, заключавшееся в том, что электроны по круговым орбитам движутся с ускорением, а следовательно, согласно законам электродинамики они обязаны излучать электромагнитную энергию. В этом случае электроны очень быстро потеряли бы свою энергию и упали бы на ядро, но опыт показывает, что этого не происходит.
В 1913 году датскому физику Н. Бору (1885–1962) удалось усовершенствовать планетарную модель атома Резерфорда и тем самым разрешить имеющиеся в ней противоречия. Для этого Бору потребовалось ввести два постулата, совершенно несовместимые с классической физикой:
1) из бесчисленного множества электронных орбит, возможных с точки зрения классической механики, осуществляются в действительности только некоторые дискретные круговые орбиты, удовлетворяющие определенным квантовым условиям. Электрон, находящийся на одной из этих орбит, несмотря на то, что он движется с ускорением, обусловленным изменением направления вектора скорости, не излучает электромагнитных волн (света);
2) излучение испускается или поглощается атомом в виде порции (кванта) энергии при переходе электрона из одного стационарного (устойчивого) состояния в другое, т. е. при переходе с одной стационарной орбиты на другую.
В 1911 году Резерфорд предложил модель атома, которая напоминала Солнечную систему: в центре находится атомное ядро, а вокруг него по своим орбитам движутся электроны. Однако эта модель содержала неразрешимое противоречие, заключавшееся в том, что электроны по круговым орбитам движутся с ускорением, а следовательно, согласно законам электродинамики они обязаны излучать электромагнитную энергию. В этом случае электроны очень быстро потеряли бы свою энергию и упали бы на ядро, но опыт показывает, что этого не происходит.
В 1913 году датскому физику Н. Бору (1885–1962) удалось усовершенствовать планетарную модель атома Резерфорда и тем самым разрешить имеющиеся в ней противоречия. Для этого Бору потребовалось ввести два постулата, совершенно несовместимые с классической физикой:
1) из бесчисленного множества электронных орбит, возможных с точки зрения классической механики, осуществляются в действительности только некоторые дискретные круговые орбиты, удовлетворяющие определенным квантовым условиям. Электрон, находящийся на одной из этих орбит, несмотря на то, что он движется с ускорением, обусловленным изменением направления вектора скорости, не излучает электромагнитных волн (света);
2) излучение испускается или поглощается атомом в виде порции (кванта) энергии при переходе электрона из одного стационарного (устойчивого) состояния в другое, т. е. при переходе с одной стационарной орбиты на другую.
4. ФУНДАМЕНТАЛЬНЫЕ ВЗАИМОДЕЙСТВИЯ В ПРИРОДЕ: СИЛЬНОЕ, ЭЛЕКТРОМАГНИТНОЕ И СЛАБОЕ
В настоящее время известны четыре вида фундаментальных взаимодействий в природе: сильное, электромагнитное, слабое и гравитационное. Сильное взаимодействие обеспечивает связь нуклонов в ядре и определяет ядерные силы. Предполагается, что ядерные силы возникают при обмене между нуклонами кварками. Кварк, принадлежащий одному нуклону, переходит в другой нуклон, кварк которого в свою очередь переходит в первый нуклон. Этот обмен эквивалентен обмену между нуклонами виртуальной парой «кварк – антикварк», которую иногда называют пионом, и говорят, что сильное взаимодействие между нуклонами в ядре осуществляется за счет обмена между ними виртуальными пионами. Виртуальными частицами называют такие частицы, экспериментально обнаружить которые в ходе обменного процесса невозможно. Сильное взаимодействие между нуклонами действует на расстоянии ~10-13 см, т. е. практически в пределах ядра. Энергия связи между нуклонами является чрезвычайно большой, например, для ядра гелия она равна 7,1 МэВ/нуклон, а для ядра цинка – 8,7 МэВ/нуклон. Это является причиной высокой устойчивости ядер.
Электромагнитное взаимодействие связано с электрическими и магнитными полями. Носителями электромагнитного взаимодействия являются виртуальные фотоны – кванты электромагнитного поля, которыми обмениваются заряды. Электрическое поле возникает при наличии электрических зарядов, а магнитное поле – при их движении. Электромагнитное взаимодействие описывается фундаментальными законами электростатики и электродинамики: законом Кулона, законом Ампера, законом Фарадея – Максвелла и др. Его более общее описание дает электромагнитная теория Дж. Максвелла (1831–1879), основанная на фундаментальных уравнениях, связывающих электрическое и магнитное поля. В процессе электромагнитного взаимодействия электроны и атомные ядра соединяются в атомы, атомы – в молекулы. Различные агрегатные состояния вещества (твердое, жидкое, газообразное, плазменное), явление трения, упругие и другие свойства вещества определяются преимущественно силами межмолекулярного взаимодействия, которое по своей природе является электромагнитным.
Слабое взаимодействие несет ответственность за некоторые виды ядерных процессов. Слабое взаимодействие между частицами осуществляется посредством обмена так называемыми промежуточными бозонами. Оно простирается на расстояние ~10-22-10-16 см и связано главным образом с распадом частиц, например, с происходящими в атомном ядре превращениями нейтрона в протон, электрон и антинейтрино. В соответствии с современным уровнем знаний большинство частиц нестабильны именно благодаря слабому взаимодействию.
Электромагнитное взаимодействие связано с электрическими и магнитными полями. Носителями электромагнитного взаимодействия являются виртуальные фотоны – кванты электромагнитного поля, которыми обмениваются заряды. Электрическое поле возникает при наличии электрических зарядов, а магнитное поле – при их движении. Электромагнитное взаимодействие описывается фундаментальными законами электростатики и электродинамики: законом Кулона, законом Ампера, законом Фарадея – Максвелла и др. Его более общее описание дает электромагнитная теория Дж. Максвелла (1831–1879), основанная на фундаментальных уравнениях, связывающих электрическое и магнитное поля. В процессе электромагнитного взаимодействия электроны и атомные ядра соединяются в атомы, атомы – в молекулы. Различные агрегатные состояния вещества (твердое, жидкое, газообразное, плазменное), явление трения, упругие и другие свойства вещества определяются преимущественно силами межмолекулярного взаимодействия, которое по своей природе является электромагнитным.
Слабое взаимодействие несет ответственность за некоторые виды ядерных процессов. Слабое взаимодействие между частицами осуществляется посредством обмена так называемыми промежуточными бозонами. Оно простирается на расстояние ~10-22-10-16 см и связано главным образом с распадом частиц, например, с происходящими в атомном ядре превращениями нейтрона в протон, электрон и антинейтрино. В соответствии с современным уровнем знаний большинство частиц нестабильны именно благодаря слабому взаимодействию.
5. ГРАВИТАЦИОННОЕ ВЗАИМОДЕЙСТВИЕ
Гравитационное взаимодействие характерно для всех материальных объектов вне зависимости от их природы. Оно заключается во взаимном притяжении тел и определяется фундаментальным законом всемирного тяготения: между двумя точечными телами действует сила притяжения, прямо пропорциональная произведению их масс и обратно пропорциональная квадрату расстояния между ними. Гравитационным взаимодействием определяется падение тел в поле сил тяготения Земли. Законом всемирного тяготения описывается, например, движение планет Солнечной системы, а также других макрообъектов. Предполагается, что гравитационное взаимодействие обусловлено некими элементарными частицами – гравитонами, существование которых к настоящему времени экспериментально не подтверждено.
Гравитационное взаимодействие – самое слабое, не учитываемое в теории элементарных частиц, поскольку на характерных для них расстояниях ~10-13 см оно дает чрезвычайно малые эффекты. Однако на ультрамалых расстояниях (~10-33 см) и при ультрабольших энергиях гравитация приобретает существенное значение. Здесь начинают проявляться необычные свойства физического вакуума. Сверхтяжелые виртуальные частицы создают вокруг себя заметное гравитационное поле, которое начинает искажать геометрию пространства. В космических масштабах гравитационное взаимодействие имеет решающее значение. Радиус его действия не ограничен.
От силы взаимодействия зависит время, в течение которого совершается превращение элементарных частиц. Ядерные реакции, связанные с сильными взаимодействиями, происходят в течение 10-24-10-23 с. Приблизительно это тот кратчайший интервал времени, за который частица, ускоренная до высоких энергий, когда ее скорость близка к скорости света, пролетает расстояние ~10-13 см. Изменения, обусловленные электромагнитными взаимодействиями, осуществляются в течение 10-21-10-19 с, а слабыми (например, распад элементарных частиц) – в основном в течение 10-10 с. По времени различных превращений можно судить о силе связанных с ним взаимодействий.
Гравитационное взаимодействие – самое слабое, не учитываемое в теории элементарных частиц, поскольку на характерных для них расстояниях ~10-13 см оно дает чрезвычайно малые эффекты. Однако на ультрамалых расстояниях (~10-33 см) и при ультрабольших энергиях гравитация приобретает существенное значение. Здесь начинают проявляться необычные свойства физического вакуума. Сверхтяжелые виртуальные частицы создают вокруг себя заметное гравитационное поле, которое начинает искажать геометрию пространства. В космических масштабах гравитационное взаимодействие имеет решающее значение. Радиус его действия не ограничен.
От силы взаимодействия зависит время, в течение которого совершается превращение элементарных частиц. Ядерные реакции, связанные с сильными взаимодействиями, происходят в течение 10-24-10-23 с. Приблизительно это тот кратчайший интервал времени, за который частица, ускоренная до высоких энергий, когда ее скорость близка к скорости света, пролетает расстояние ~10-13 см. Изменения, обусловленные электромагнитными взаимодействиями, осуществляются в течение 10-21-10-19 с, а слабыми (например, распад элементарных частиц) – в основном в течение 10-10 с. По времени различных превращений можно судить о силе связанных с ним взаимодействий.
6. ЗАКОНЫ НЬЮТОНА
В качестве первого закона Ньютон (1643–1727) принял закон инерции, открытый еще Г. Галилеем
(1564–1642): тело (материальная точка), не подверженное внешним воздействиям, либо находится в покое, либо движется прямолинейно и равномерно. Такое тело называется свободным, а его движение – свободным или движением по инерции. Первый закон Ньютона – Галилея фактически постулирует, что существует система отсчета, в которой все свободные тела движутся прямолинейно и равномерно. Такая система называется инерциальной системой отсчета. Под системой отсчета понимается совокупность тела отсчета, системы координат и часов.
Второй закон Ньютона: ускорение движущегося тела прямо пропорционально действующей на него силе, обратно пропорционально массе тела и направлено по прямой, по которой эта сила действует, т. е.
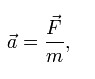
где a – ускорение тела; F – сила; m – масса тела.
Сила есть действие, производимое над телом, чтобы изменить его состояние покоя или равномерного и прямолинейного движения. Масса тела выступает как коэффициент пропорциональности между силой, действующей на тело, и ускорением (F = ma) и характеризует инертность тела, т. е. степень неподатливости изменению состояния движения.
Третий закон Ньютона: силы взаимодействия двух материальных точек равны по величине, противоположно направлены и действуют вдоль прямой, соединяющей эти материальные точки, т. е.
где F12 – сила, действующая на первое тело со стороны второго; F21 – сила, действующая на второе тело со стороны первого.
Выдающейся заслугой Ньютона было открытие закона всемирного тяготения: два точечных тела притягивают друг друга с силой, прямо пропорциональной произведению их масс, обратно пропорциональной квадрату расстояния между ними и направленной вдоль соединяющей их прямой, т. е.
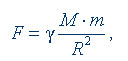
где γ = 6,7 10-11 м3/(кг • с2) – гравитационная постоянная; m1 и m2 – массы тел; r – расстояние между телами.
(1564–1642): тело (материальная точка), не подверженное внешним воздействиям, либо находится в покое, либо движется прямолинейно и равномерно. Такое тело называется свободным, а его движение – свободным или движением по инерции. Первый закон Ньютона – Галилея фактически постулирует, что существует система отсчета, в которой все свободные тела движутся прямолинейно и равномерно. Такая система называется инерциальной системой отсчета. Под системой отсчета понимается совокупность тела отсчета, системы координат и часов.
Второй закон Ньютона: ускорение движущегося тела прямо пропорционально действующей на него силе, обратно пропорционально массе тела и направлено по прямой, по которой эта сила действует, т. е.
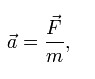
где a – ускорение тела; F – сила; m – масса тела.
Сила есть действие, производимое над телом, чтобы изменить его состояние покоя или равномерного и прямолинейного движения. Масса тела выступает как коэффициент пропорциональности между силой, действующей на тело, и ускорением (F = ma) и характеризует инертность тела, т. е. степень неподатливости изменению состояния движения.
Третий закон Ньютона: силы взаимодействия двух материальных точек равны по величине, противоположно направлены и действуют вдоль прямой, соединяющей эти материальные точки, т. е.
где F12 – сила, действующая на первое тело со стороны второго; F21 – сила, действующая на второе тело со стороны первого.
Выдающейся заслугой Ньютона было открытие закона всемирного тяготения: два точечных тела притягивают друг друга с силой, прямо пропорциональной произведению их масс, обратно пропорциональной квадрату расстояния между ними и направленной вдоль соединяющей их прямой, т. е.
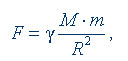
где γ = 6,7 10-11 м3/(кг • с2) – гравитационная постоянная; m1 и m2 – массы тел; r – расстояние между телами.
7. ПРИНЦИПЫ ОТНОСИТЕЛЬНОСТИ ГАЛИЛЕЯ
Во всех инерциальных системах отсчета законы классической механики (законы Ньютона) имеют одинаковую форму; в этом сущность механического принципа относительности – принципа относительности Галилея. Он означает, что уравнения динамики при переходе от одной инерциальной системы отсчета к другой не изменяются, т. е. инвариантны по отношению к преобразованиям координат.
x′ = x – vt, y′ = y, z′ =z, t′ = t,
где x, y, z и t; x′, y′, z′ и t′– координаты тела и время в неподвижной и подвижной системах отсчета соответственно; v – скорость подвижной системы отсчета.
Эти формулы называются преобразованиями Галилея.
Легко показать, что законы динамики Ньютона инвариантны относительно преобразований Галилея. Это объясняется тем, что силы и массы тел одинаковы во всех инерциальных системах отсчета и ускорения тел, которые определяются двойным дифференцированием координат по времени, также одинаковы
(a = d2x/dt2 = d2x'/dt2 = a').
Инвариантами, т. е. величинами, численное значение которых не изменяется при преобразовании координат по Галилею, являются длины и интервалы времени. Покажем это.
Пусть в подвижной системе координат находится неподвижный стержень, координаты концов которого (x´1, y1´, z´1) и (x´2, y´2, z´2). Это означает, что длина стержня в подвижной системе
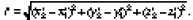
Тогда относительно неподвижной системы отсчета стержень движется поступательно и все его точки имеют скорость v. Длиной движущегося стержня, по определению, называется расстояние между координатами его концов в некоторый момент времени. Таким образом, для измерения длины движущегося стержня необходимо одновременно, т. е. при одинаковых показаниях часов неподвижной системы отсчета, расположенных в соответствующих точках, отметить положение концов стержня. Пусть засечки положения концов движущегося стержня сделаны в неподвижной системе координат в момент времени t и характеризуются координатами (х1, у1, z1) и (х2, у2, z2). Тогда для длины стержня в неподвижной системе отсчета будем иметь
т. е. длина стержня в обеих системах координат одинакова. Это позволяет утверждать, что длина является инвариантом преобразований Галилея.
x′ = x – vt, y′ = y, z′ =z, t′ = t,
где x, y, z и t; x′, y′, z′ и t′– координаты тела и время в неподвижной и подвижной системах отсчета соответственно; v – скорость подвижной системы отсчета.
Эти формулы называются преобразованиями Галилея.
Легко показать, что законы динамики Ньютона инвариантны относительно преобразований Галилея. Это объясняется тем, что силы и массы тел одинаковы во всех инерциальных системах отсчета и ускорения тел, которые определяются двойным дифференцированием координат по времени, также одинаковы
(a = d2x/dt2 = d2x'/dt2 = a').
Инвариантами, т. е. величинами, численное значение которых не изменяется при преобразовании координат по Галилею, являются длины и интервалы времени. Покажем это.
Пусть в подвижной системе координат находится неподвижный стержень, координаты концов которого (x´1, y1´, z´1) и (x´2, y´2, z´2). Это означает, что длина стержня в подвижной системе
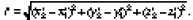
Тогда относительно неподвижной системы отсчета стержень движется поступательно и все его точки имеют скорость v. Длиной движущегося стержня, по определению, называется расстояние между координатами его концов в некоторый момент времени. Таким образом, для измерения длины движущегося стержня необходимо одновременно, т. е. при одинаковых показаниях часов неподвижной системы отсчета, расположенных в соответствующих точках, отметить положение концов стержня. Пусть засечки положения концов движущегося стержня сделаны в неподвижной системе координат в момент времени t и характеризуются координатами (х1, у1, z1) и (х2, у2, z2). Тогда для длины стержня в неподвижной системе отсчета будем иметь
т. е. длина стержня в обеих системах координат одинакова. Это позволяет утверждать, что длина является инвариантом преобразований Галилея.
8. ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА
В 1904 году Лоренц предложил формулы для преобразования координат, которые обеспечивают инвариантность уравнений Максвелла при переходе от одной инерциальной системы отсчета к другой:
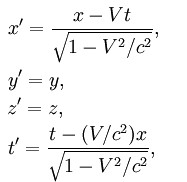
где с – скорость света в вакууме.
Формулы были названы Пуанкаре преобразованиями Лоренца.
Инвариантным относительно преобразований Лоренца является так называемый пространственно-временной интервал, или просто интервал. Пусть события произошли в точке х1, у1, z1 в момент времени t1 и в точке х2, у2, z2 в момент времени t2. Интервалом между событиями, или, как говорят, интервалом между точками х1, у1, z1, t1 и х2, у2, z2, t2, называется величина s, квадрат которой определяется формулой
S2 = С2 (t2 – t1)2 – (Х2 – Х1)2 – (У2 – У1)2 – (Z2 – Z1)2. (1)
В подвижной системе отсчета квадрат интервала S записывается в виде
Подставляя формулу (1) в (2), убедимся, что s2 = s'2 = inv. Впервые понятие интервала ввел Пуанкаре, и он же показал, что интервал является инвариантом при преобразованиях Лоренца.
Из преобразований Лоренца следует сокращение длины движущегося стержня, а именно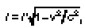
где l = x2 – x1 и l' = x'2 – x1, и замедление хода движущихся часов, а именно
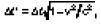, где Δt = t2– t1 и Δt' = = t'2-t' 1.
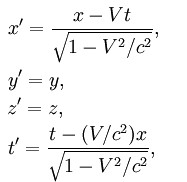
где с – скорость света в вакууме.
Формулы были названы Пуанкаре преобразованиями Лоренца.
Инвариантным относительно преобразований Лоренца является так называемый пространственно-временной интервал, или просто интервал. Пусть события произошли в точке х1, у1, z1 в момент времени t1 и в точке х2, у2, z2 в момент времени t2. Интервалом между событиями, или, как говорят, интервалом между точками х1, у1, z1, t1 и х2, у2, z2, t2, называется величина s, квадрат которой определяется формулой
S2 = С2 (t2 – t1)2 – (Х2 – Х1)2 – (У2 – У1)2 – (Z2 – Z1)2. (1)
В подвижной системе отсчета квадрат интервала S записывается в виде
Подставляя формулу (1) в (2), убедимся, что s2 = s'2 = inv. Впервые понятие интервала ввел Пуанкаре, и он же показал, что интервал является инвариантом при преобразованиях Лоренца.
Из преобразований Лоренца следует сокращение длины движущегося стержня, а именно
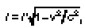где l = x2 – x1 и l' = x'2 – x1, и замедление хода движущихся часов, а именно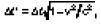, где Δt = t2– t1 и Δt' = = t'2-t' 1.
9. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
В основе специальной теории относительности, созданной Лоренцем, Пуанкаре и Эйнштейном и представляющей собой фактически физическую теорию пространства и времени, лежат два постулата: принцип относительности; принцип постоянства скорости света.
Принцип относительности утверждает, что все тождественные физические явления в любых инерциальных системах отсчета при одинаковых начальных и граничных условиях протекают одинаково. Другими словами, все законы природы инвариантны по отношению к переходу от одной инерциальной системы отсчета к другой, т. е. уравнения, выражающие законы природы, имеют одинаковый вид во всех инерциальных системах отсчета. Несмотря на то что приведенная формулировка принципа относительности отличается от той, что дал Пуанкаре, в физическом смысле обе формулировки тождественны. Этот постулат распространяет принцип относительности Галилея на все физические явления природы. Это означает, что все инерциальные системы отсчета равноправны и никакие опыты (механические, электромагнитные и т. п.), проведенные в данной инерциальной системе отсчета, не дают возможности обнаружить, покоится ли эта система или движется равномерно и прямолинейно.
Принцип постоянства скорости света гласит, что скорость света в вакууме одинакова во всех инерциальных системах отсчета и не зависит от движения источников и приемников света. Специальная теория относительности объединила пространство и время в единый континуум «пространство-время», (см. преобразования Лоренца) причем она, как и классическая ньютоновская механика, предполагает, что время однородно, а пространство однородно и изотропно.
Принцип относительности утверждает, что все тождественные физические явления в любых инерциальных системах отсчета при одинаковых начальных и граничных условиях протекают одинаково. Другими словами, все законы природы инвариантны по отношению к переходу от одной инерциальной системы отсчета к другой, т. е. уравнения, выражающие законы природы, имеют одинаковый вид во всех инерциальных системах отсчета. Несмотря на то что приведенная формулировка принципа относительности отличается от той, что дал Пуанкаре, в физическом смысле обе формулировки тождественны. Этот постулат распространяет принцип относительности Галилея на все физические явления природы. Это означает, что все инерциальные системы отсчета равноправны и никакие опыты (механические, электромагнитные и т. п.), проведенные в данной инерциальной системе отсчета, не дают возможности обнаружить, покоится ли эта система или движется равномерно и прямолинейно.
Принцип постоянства скорости света гласит, что скорость света в вакууме одинакова во всех инерциальных системах отсчета и не зависит от движения источников и приемников света. Специальная теория относительности объединила пространство и время в единый континуум «пространство-время», (см. преобразования Лоренца) причем она, как и классическая ньютоновская механика, предполагает, что время однородно, а пространство однородно и изотропно.
10. ОБЩАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ ЭЙНШТЕЙНА
Дальнейшее развитие представлений о пространстве и времени было сделано Эйнштейном в 1915 году в общей теории относительности, называемой иногда теорией тяготения. В ней Эйнштейн расширил принцип относительности, распространив его на неинерциальные системы отсчета, и использовал принцип эквивалентности инертной и гравитационной масс (отношение инертной массы к гравитационной одинаково для всех тел), который непосредственно следует из установленного еще Галилеем факта одинаковости ускорения различных тел при их свободном падении.
Используя законы классической механики, покажем, что отношение инертной mин и гравитационной mгр масс одинаково для всех тел. Предположим, что вниз одновременно начинают падать два разных тела. На каждое из тел действует сила тяжести. На первое тело действует сила тяжести, равная F1 = mгр1g, а на второе – F2 = mгр2g, где g – ускорение свободного падения. Согласно второму закону Ньютона, под действием этих сил тела будут двигаться с ускорениями соответственно a1 и a2, причем в качестве коэффициентов пропорциональностей между силами и ускорениями будут выступать их инертные массы mин1 и mин2: F1 = mин1a1 и F2 = mин2a2. Из этих рассуждений непосредственно следует, что mгр1g = mин1a1 и mгр2g = mин2a2. Галилей экспериментально показал, что все тела при отсутствии сопротивления падают с одинаковым ускорением, т.е. отношение ускорений равно единице, или a1/a2 = (mгр1/mин1)(mин2 /mгр2) = 1.
Это возможно только при пропорциональности инертной и гравитационной масс. Последние эксперименты подтверждают равенство mин = mгр с высокой точностью (относительная ошибка измерений не превышает 10-11).
Общая теория относительности объяснила сущность тяготения, состоящую в изменении геометрических свойств, искривлении четырехмерного пространства-времени вокруг тел, которые образуют поле тяготения. В рамках общей теории относительности Эйнштейну удалось получить уравнение, описывающее поле тяготения.
Для проверки своей теории Эйнштейн предложил три эффекта:
• искривление светового луча в поле тяготения Солнца;
• смещение перигелия Меркурия;
• гравитационное красное смещение.
Эти эффекты, как показали последующие эксперименты, действительно существуют и количественно правильно предсказывались ОТО (с приемлемой на тот исторический момент времени погрешностью).
Используя законы классической механики, покажем, что отношение инертной mин и гравитационной mгр масс одинаково для всех тел. Предположим, что вниз одновременно начинают падать два разных тела. На каждое из тел действует сила тяжести. На первое тело действует сила тяжести, равная F1 = mгр1g, а на второе – F2 = mгр2g, где g – ускорение свободного падения. Согласно второму закону Ньютона, под действием этих сил тела будут двигаться с ускорениями соответственно a1 и a2, причем в качестве коэффициентов пропорциональностей между силами и ускорениями будут выступать их инертные массы mин1 и mин2: F1 = mин1a1 и F2 = mин2a2. Из этих рассуждений непосредственно следует, что mгр1g = mин1a1 и mгр2g = mин2a2. Галилей экспериментально показал, что все тела при отсутствии сопротивления падают с одинаковым ускорением, т.е. отношение ускорений равно единице, или a1/a2 = (mгр1/mин1)(mин2 /mгр2) = 1.
Это возможно только при пропорциональности инертной и гравитационной масс. Последние эксперименты подтверждают равенство mин = mгр с высокой точностью (относительная ошибка измерений не превышает 10-11).
Общая теория относительности объяснила сущность тяготения, состоящую в изменении геометрических свойств, искривлении четырехмерного пространства-времени вокруг тел, которые образуют поле тяготения. В рамках общей теории относительности Эйнштейну удалось получить уравнение, описывающее поле тяготения.
Для проверки своей теории Эйнштейн предложил три эффекта:
• искривление светового луча в поле тяготения Солнца;
• смещение перигелия Меркурия;
• гравитационное красное смещение.
Эти эффекты, как показали последующие эксперименты, действительно существуют и количественно правильно предсказывались ОТО (с приемлемой на тот исторический момент времени погрешностью).
11. ИСКРИВЛЕНИЕ СВЕТОВОГО ЛУЧА В ПОЛЕ ТЯГОТЕНИЯ СОЛНЦА
Предположим, что свет от звезды S проходит непосредственно вблизи поверхности Солнца. Тогда солнечное тяготение наиболее сильно искривляет его траекторию (рис. 1). Земному наблюдателю будет казаться, что звезда находится в направлении S'. В соответствии с ОТО угол, на который отклоняется луч света, можно рассчитать по формуле
где φ – угол отклонения луча света; MC – масса Солнца; Rc – радиус Солнца.
Рис. 1. Отклонение луча света гравитационным полем Солнца
Угол отклонения луча света полем тяготения Солнца, рассчитанный по формуле (1), равен 1,75». Значение угла j экспериментально определяют, сравнивая положения звезд, близких к Солнцу, во время полного солнечного затмения и во время, когда Солнце находится далеко от данного участка звездного неба. Многократно проведенные измерения показали, что экспериментальные значения угла отклонения луча света полем тяготения Солнца в пределах 10 % совпадают с его теоретическим значением.
где φ – угол отклонения луча света; MC – масса Солнца; Rc – радиус Солнца.
Рис. 1. Отклонение луча света гравитационным полем Солнца
Угол отклонения луча света полем тяготения Солнца, рассчитанный по формуле (1), равен 1,75». Значение угла j экспериментально определяют, сравнивая положения звезд, близких к Солнцу, во время полного солнечного затмения и во время, когда Солнце находится далеко от данного участка звездного неба. Многократно проведенные измерения показали, что экспериментальные значения угла отклонения луча света полем тяготения Солнца в пределах 10 % совпадают с его теоретическим значением.
12. ГРАВИТАЦИОННОЕ КРАСНОЕ СМЕЩЕНИЕ
Предположим, что фотон с энергией ε = hν (h – постоянная Планка; ν – частота) покидает поверхность звезды. Покидая поверхность звезды, фотон будет совершать работу, связанную с преодолением действия гравитационного поля звезды. Эта работа будет совершена за счет убыли энергии фотона.
Можно показать, что энергия фотона на достаточно большом удалении от звезды, когда гравитационное взаимодействие становится ничтожно малым, оказывается равной
где Мзв и Rзв – масса и радиус звезды соответственно; с – скорость света; γ – гравитационная постоянная.
Это означает, что фотон частоты v, покидающий звезду и уходящий в бесконечность, будет восприниматься в бесконечности с частотой
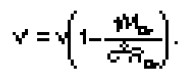
Уменьшение частоты фотона означает, что если фотон принадлежит к голубой области спектра, то он испытывает смещение по частоте в сторону красной границы видимого спектра, вследствие чего этот эффект и известен под названием «гравитационное красное смещение». Его не следует смешивать с доплеровским красным смещением далеких звезд, приписываемым их кажущемуся радиальному движению в направлении от Земли. Гравитационное красное смещение хорошо подтверждается экспериментально. Так, для звезды Сириус В вычисленное относительное смещение составляет:
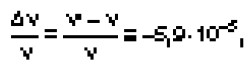
а измеренное равно -6,6 10-5. Расхождение не выходит за пределы возможной ошибки, связанной с неопределенностью значений Мзв и Rзв.
Можно показать, что энергия фотона на достаточно большом удалении от звезды, когда гравитационное взаимодействие становится ничтожно малым, оказывается равной
где Мзв и Rзв – масса и радиус звезды соответственно; с – скорость света; γ – гравитационная постоянная.
Это означает, что фотон частоты v, покидающий звезду и уходящий в бесконечность, будет восприниматься в бесконечности с частотой
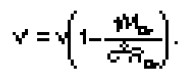
Уменьшение частоты фотона означает, что если фотон принадлежит к голубой области спектра, то он испытывает смещение по частоте в сторону красной границы видимого спектра, вследствие чего этот эффект и известен под названием «гравитационное красное смещение». Его не следует смешивать с доплеровским красным смещением далеких звезд, приписываемым их кажущемуся радиальному движению в направлении от Земли. Гравитационное красное смещение хорошо подтверждается экспериментально. Так, для звезды Сириус В вычисленное относительное смещение составляет:
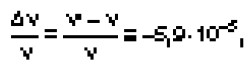
а измеренное равно -6,6 10-5. Расхождение не выходит за пределы возможной ошибки, связанной с неопределенностью значений Мзв и Rзв.
13. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ
Величина
(1) называется кинетической энергией материальной точки (m и v – масса и скорость).
(1) называется кинетической энергией материальной точки (m и v – масса и скорость).