Применению симметричных криптографических алгоритмов присущ ряд проблем. Во-первых, где гарантия, что отправитель и получатель используют один и тот же ключ для зашифровки и расшифровки сообщений? Обычно для обеспечения идентичности ключей отправителя и получателя пользуются услугами курьерской службы или каким-либо другим средством пересылки ключей. Во-вторых, что делать, если у получателя не окажется ключа, которым были зашифрованы принимаемые данные? Например, представьте себе ситуацию, когда ключ симметричной криптосистемы, реализованной аппаратными средствами, изменяется каждое утро в 4.00 на приемном и передающем конце. Что произойдет, если на одном из концов «забудут» изменить ключ в нужное время (вне зависимости от того, как это будет реализовано: при помощи полоски ленты, дополнительной аппаратуры или каким-либо другим способом) и передадут зашифрованные старым ключом данные, а на приемной стороне ключ будет изменен? Получатель, используя правильный ключ, не сможет расшифровать принятые данные. В результате во время кризиса могут возникнуть проблемы. Особенно если старый ключ был удален. Этот простой пример показывает, к чему может привести использование получателем и отправителем разных ключей шифрования.
Асимметричные криптосистемы – относительно новое направление в криптографии, возможно, более известное под синонимом криптография с открытым ключом. В асимметричных криптосистемах используются два различных ключа: открытый ключ – для зашифровки сообщения и секретный (личный) – для расшифровки. Уитфилд Диффи (Whitfield Diffie) и Мартин Хеллман (Martin Hellman) первыми заявили о криптографии с открытым ключом в 1976 году, опубликовав метод обмена ключами в системе с секретными ключами. Опубликованный ими алгоритм, впоследствии названный алгоритмом Диффи-Хеллмана (DH-алгоритмом), будет рассмотрен в этой главе. Хотя большинство считает В. Диффи и М. Хеллмана авторами криптографии с открытым ключом, тем не менее некоторые отдают приоритет английской разведке BSS (British Secret Service), поскольку якобы за несколько лет до публикации В. Диффи и М. Хеллмана BSS уже знал об аналогичном методе. Правда, предполагается, что BSS после изобретения алгоритма нигде его не использовал. Подробнее об этом читатель сможет узнать по адресу: www.wired.com/wired/archive/7.04/crypto_pr.html.
Некоторое время спустя криптография с открытым ключом стала популярной благодаря Филу Зиммерману (Phil Zimmerman), который в августе 1991 года выпустил версию 1.0 программы «Pretty Good Privacy» (PGP) для DOS. В 1993 году, после выпуска версии 2.3 программы PGP, была добавлена поддержка других платформ, в том числе UNIX и Amiga. С течением времени программа PGP была усовершенствована и распространялась многочисленными фирмами, включая ViaCrypt и PGP, Inc., которые в настоящее время вошли в состав Network Associates. Доступны как коммерческие, так и свободно распространяемые (для некоммерческого использования) версии программы PGP. Жители Соединенных Штатов и Канады могут получить свободно распространяемую версию программы с сайта http://web.mit.edu/network/pgp.html. Коммерческая версия может быть куплена на сайте Network Associates www.pgp.com.
Стандарты алгоритмов шифрования
Симметричные алгоритмы
Асимметричные алгоритмы
«Грубая сила»
Основы метода «грубой силы»
Асимметричные криптосистемы – относительно новое направление в криптографии, возможно, более известное под синонимом криптография с открытым ключом. В асимметричных криптосистемах используются два различных ключа: открытый ключ – для зашифровки сообщения и секретный (личный) – для расшифровки. Уитфилд Диффи (Whitfield Diffie) и Мартин Хеллман (Martin Hellman) первыми заявили о криптографии с открытым ключом в 1976 году, опубликовав метод обмена ключами в системе с секретными ключами. Опубликованный ими алгоритм, впоследствии названный алгоритмом Диффи-Хеллмана (DH-алгоритмом), будет рассмотрен в этой главе. Хотя большинство считает В. Диффи и М. Хеллмана авторами криптографии с открытым ключом, тем не менее некоторые отдают приоритет английской разведке BSS (British Secret Service), поскольку якобы за несколько лет до публикации В. Диффи и М. Хеллмана BSS уже знал об аналогичном методе. Правда, предполагается, что BSS после изобретения алгоритма нигде его не использовал. Подробнее об этом читатель сможет узнать по адресу: www.wired.com/wired/archive/7.04/crypto_pr.html.
Некоторое время спустя криптография с открытым ключом стала популярной благодаря Филу Зиммерману (Phil Zimmerman), который в августе 1991 года выпустил версию 1.0 программы «Pretty Good Privacy» (PGP) для DOS. В 1993 году, после выпуска версии 2.3 программы PGP, была добавлена поддержка других платформ, в том числе UNIX и Amiga. С течением времени программа PGP была усовершенствована и распространялась многочисленными фирмами, включая ViaCrypt и PGP, Inc., которые в настоящее время вошли в состав Network Associates. Доступны как коммерческие, так и свободно распространяемые (для некоммерческого использования) версии программы PGP. Жители Соединенных Штатов и Канады могут получить свободно распространяемую версию программы с сайта http://web.mit.edu/network/pgp.html. Коммерческая версия может быть куплена на сайте Network Associates www.pgp.com.
Стандарты алгоритмов шифрования
Почему так много алгоритмов шифрования? Почему не стандартизируют один из них? Учитывая большое количество алгоритмов шифрования, следует признать, что на этот вопрос нельзя дать простой ответ. Максимум, что возможно, – это достичь компромисса между безопасностью, скоростью и удобством применения. В данном случае под безопасностью алгоритма понимается его способность противостоять как современным атакам, так и атакам в будущем. Скорость алгоритма характеризует его возможности по обработке данных и выражается временем, которое необходимо затратить на зашифровку и расшифровку сообщений. И наконец, под удобством применения понимается удобство реализации алгоритма программным или аппаратным способом. Каждый алгоритм хорош по-своему и ни один из них не идеален. В этой главе будут рассмотрены пять алгоритмов, с которыми чаще всего приходится иметь дело: стандарт шифрования данных DES (Data Encryption Standard), улучшенный стандарт шифрования AES [Rijndael], международный алгоритм шифрования данных IDEA (International Data Encryption Algorithm), алгоритм Диффи-Хеллмана и алгоритм RSA. Но знайте, что есть и другие алгоритмы, которые ничем не уступают названным.
Симметричные алгоритмы
В этой секции будет рассмотрено несколько наиболее типичных представителей класса симметричных алгоритмов: DES, его преемник AES и Европейский стандарт IDEA. Имейте в виду, что криптостойкость симметричных алгоритмов определяется прежде всего размером используемых в алгоритме ключей и числом циклов алгоритма. Все симметричные алгоритмы теоретически уязвимы к атакам «грубой силы», в основе которых лежит перебор всех возможных ключей. Но часто подобные атаки технически неосуществимы. Детально они будут обсуждены далее в главе.
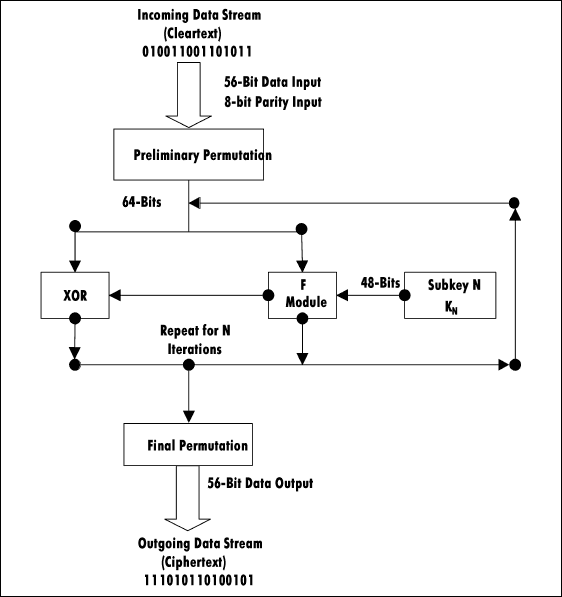Рис. 6.1. Схема алгоритма шифрования DES
В каждом раунде выполняются подстановка, во время которой биты данных заменяются битами ключа, и перестановка, во время которой замененные данные переставляются (перемешиваются). Операции перестановки, которые иногда называют перемешиванием, выполняются в S-блоках, а операции перестановки, иногда называемые операциями рассеивания, – в P-блоках. Два названных класса операций реализованы в «F-модуле» диаграммы. Безопасность DES чаще основывается на том, что операции перестановки нелинейные, поэтому зашифрованный текст ничем не напоминает исходное сообщение. Поэтому методы языкового анализа зашифрованного текста, которые обсуждаются далее в этой главе, не приводят к положительному результату. Операции перестановки повышают безопасность, дополнительно шифруя уже частично зашифрованное сообщение.
На продолжительности жизни DES сказалась сравнительно малая длина ключа – существенный конструктивный недостаток алгоритма. Чем меньше длина используемых в алгоритме ключей, тем сильнее он подвержен атакам «грубой силы». Уитфилд Диффи (Whitfield Diffie) и Мартин Хеллман (Martin Hellman) были первыми, кто обратили внимание на недостаточную длину ключей DES, и уже в 1979 году предсказали алгоритму забвение через 10 лет. Несмотря на это, никто до 1997 года не смог публично взломать алгоритм DES атакой «грубой силы».
Первая известная успешная атака «грубой силы» на алгоритм DES заняла 4 месяца работы большой вычислительной сети. В 1998 году специалисты EFF (Electronic Frontier Foundation – Фонд электронной защиты) взломали DES менее чем за три дня, используя специально разработанный для этой цели компьютер под кодовым именем «Deep Crack» («Искусный взломщик»). Расходы на его разработку и производство составили чуть меньше $250 000. Рекорд взлома алгоритма DES за 22 ч принадлежит Distributed.net, которая использовала для этой цели компьютерную сеть из нескольких тысяч машин, работающих параллельно, в том числе и компьютер «Deep Crack». Осталось только добавить, что Брюс Шнейер (Bruce Schneier) теоретически обосновал возможность создания за 10 млн долл. компьютера, способного взломать DES приблизительно за 6 мин. Теперь становится понятна озабоченность NIST по поводу достойной замены DES новым алгоритмом.
• подобно DES, он должен быть симметричным блочным алгоритмом с секретным ключом;
• его криптостойкость и скорость зашифрования и расширования данных должны быть выше, чем у алгоритма 3-DES;
• время жизни нового стандарта должно быть, по крайней мере, 20–30 лет;
• он должен поддерживать ключи длиной 128, 192 и 256 бит;
• он должен удовлетворять условиям свободного распространения, не должен быть запатентован, и на него нельзя предъявить права собственности.
В течение нескольких месяцев NIST рассмотрел 15 различных заявок, шесть из которых были отклонены почти немедленно как не удовлетворяющие предъявляемым требованиям. К 1999 году NIST сузил число претендентов до пяти финалистов: MARS, RC6, Rijndael, Serpent и Twofish.
Отбор кандидатов занял еще один год, потому что нужно было тщательно протестировать каждого кандидата и удостовериться, что он удовлетворяет требованиям работы при различных условиях эксплуатации. Ведь AES должен был работать везде, начиная с портативных кредитных карточек с микропроцессором и обычных 32-разрядных настольных компьютеров и до 64-разрядных высококачественных оптимизированных компьютеров. Поскольку все из финалистов удовлетворяли требованиям безопасности, то решающим критерием выбора стала скорость обработки данных и удобство реализации алгоритма (которое в этом случае предполагало объем используемой памяти).
В конечном счете в октябре 2000 года победителем был объявлен алгоритм Rijndael («рейн-долл»). Прежде всего по причине высокой производительности программной или аппаратной реализации и невысоких требований к памяти. Алгоритм Rijndael был предложен бельгийскими криптографами докторами Джоаном Дименом (Joan Daemen) и Винсентом Риджменом (Vincent Rijmen). Ожидается, что он стоек к перспективным атакам будущего.
Как работает AES/Rijndael? Вместо использования циклов Фейстеля в каждом раунде, как это сделано в DES, в Rijndael, как и в IDEA, используются повторяющиеся раунды (алгоритм IDEA обсуждается в следующей секции). Данные разбиваются на блоки по 128 бит, которые группируются в 4 группы по 4 байта в каждом. Число раундов алгоритма зависит от размеров ключа. При ключе длиной 128 бит выполняется 9 раундов, 192 бит – 11 раундов и 256 бит – 13 раундов. Каждый раунд состоит из шага побитовой подстановки в S-блоках порции данных и следующим за ним шагом псевдоперестановки, в котором биты перетасовываются между группами. Затем каждая группа перемножается как матрица и результат складывается с подключом этого раунда.
Насколько AES быстрее, чем 3-DES? Ответить на это вопрос трудно, потому что скорость шифрования изменяется в широких пределах в зависимости от типа используемого процессора и от того, на каких средствах выполняется шифрование: на программных или аппаратных, специально для этого разработанных. Но при одинаковой реализации AES всегда быстрее алгоритма 3-DES. Тестирование, выполненное Брайоном Гладманом (Brian Gladman), показало, что на Pentium Pro 200 с оптимизированным кодом на языке C AES (Rijndael) может зашифровать и расшифровать сообщения со средней скоростью 70.2 Mbps, в то время как скорость работы DES при соблюдении этих же условий – только 28 M6/c Другие результаты исследователя можно найти по адресу fp.gladman.plus.com/cryptography_technology/aes.
Алгоритм IDEA появился не только позднее DES. Он также значительно быстрее и безопаснее DES. Скорость работы IDEA возросла благодаря более простым операциям (операции исключающего ИЛИ – XOR, логического дополнения и умножения), используемым в каждом раунде, по сравнению с операциями цикла Фейстеля в DES. Используемые в IDEA операции проще реализовать программным способом, чем выполнить подстановку и перестановку в DES.
Алгоритм IDEA оперирует с 64-битовыми блоками открытого текста, и его ключ имеет длину 128 бит. Процесс зашифрования / расшифрования состоит из восьми раундов, в каждом из которых используется шесть 16-битных подключей. Алгоритм IDEA запатентован в США и Европе, но разрешено его свободное некоммерческое использование.
Алгоритм DES
Стандарт шифрования данных (алгоритм) DES – один из старых и наиболее известных алгоритмов шифрования, который был изобретен корпорацией IBM и был американским правительственным стандартом с 1976 до 2001 года. В значительной степени DES основан на алгоритме Люцифер (Lucifer) Хорста Фейстеля (Horst Feistel), который не получил широкого распространения. Существенно то, что в алгоритме DES используется единственный 64-битовый ключ: 56 бит значащие и 8 бит – проверочные биты для контроля на четность. Алгоритм обрабатывает блоки данных порциями по 64 бита. Ключ разбивается на 16 отдельных 48-битовых подключей по одному на каждый раунд, который называется циклом Фейстеля (Feistel cycles). На рисунке 6.1 показана схема работы алгоритма DES.В каждом раунде выполняются подстановка, во время которой биты данных заменяются битами ключа, и перестановка, во время которой замененные данные переставляются (перемешиваются). Операции перестановки, которые иногда называют перемешиванием, выполняются в S-блоках, а операции перестановки, иногда называемые операциями рассеивания, – в P-блоках. Два названных класса операций реализованы в «F-модуле» диаграммы. Безопасность DES чаще основывается на том, что операции перестановки нелинейные, поэтому зашифрованный текст ничем не напоминает исходное сообщение. Поэтому методы языкового анализа зашифрованного текста, которые обсуждаются далее в этой главе, не приводят к положительному результату. Операции перестановки повышают безопасность, дополнительно шифруя уже частично зашифрованное сообщение.
Служба компьютерной безопасности предупреждает!Каждые пять лет, начиная с 1976 и до 2001 года, Национальный институт стандартов и технологий (NIST – National Institute of Standards and Technology) подтверждал статус DES как стандарта шифрования для американских государственных учреждений. С 1990 года стареющий алгоритм начал подавать признаки надвигающейся кончины, несмотря на то что новые методы, которые, по мнению экспертов, были способны взломать DES, на практике пока еще не могли это сделать, как, например, предложенный в начале девяностых метод дифференциального криптоанализа.
Как добиться еще большей безопасности от симметричных алгоритмов типа DES? Теоретически возможны два пути. Увеличить, во-первых, длину ключа, а во-вторых, число раундов алгоритма шифрования. Оба решения требуют повышения производительности алгоритма и ведут к замедлению зашифровки и расшифровки сообщений из-за увеличения числа математических операций. Примерами модификации алгоритма DES служат алгоритмы 3-DES (известный также под названием тройной DES) и DESX. В алгоритме 3-DES применяется 168-битовый ключ, который состоит из отдельных ключей по 56 бит в каждом. Хотя иногда первый и третий ключи совпадают. При этом достигаемая безопасность такова, как если бы использовался один 112-битовый ключ. В алгоритме DESX используется дополнительный 64-битовый ключ. Появление модификаций 3-DES и DESX вызвано необходимостью повышения криптостойкости алгоритма DES-атакам методом «грубой силы».
На продолжительности жизни DES сказалась сравнительно малая длина ключа – существенный конструктивный недостаток алгоритма. Чем меньше длина используемых в алгоритме ключей, тем сильнее он подвержен атакам «грубой силы». Уитфилд Диффи (Whitfield Diffie) и Мартин Хеллман (Martin Hellman) были первыми, кто обратили внимание на недостаточную длину ключей DES, и уже в 1979 году предсказали алгоритму забвение через 10 лет. Несмотря на это, никто до 1997 года не смог публично взломать алгоритм DES атакой «грубой силы».
Первая известная успешная атака «грубой силы» на алгоритм DES заняла 4 месяца работы большой вычислительной сети. В 1998 году специалисты EFF (Electronic Frontier Foundation – Фонд электронной защиты) взломали DES менее чем за три дня, используя специально разработанный для этой цели компьютер под кодовым именем «Deep Crack» («Искусный взломщик»). Расходы на его разработку и производство составили чуть меньше $250 000. Рекорд взлома алгоритма DES за 22 ч принадлежит Distributed.net, которая использовала для этой цели компьютерную сеть из нескольких тысяч машин, работающих параллельно, в том числе и компьютер «Deep Crack». Осталось только добавить, что Брюс Шнейер (Bruce Schneier) теоретически обосновал возможность создания за 10 млн долл. компьютера, способного взломать DES приблизительно за 6 мин. Теперь становится понятна озабоченность NIST по поводу достойной замены DES новым алгоритмом.
Алгоритм AES (Rijndael)
В 1997 году, когда низвержение DES стало очевидным, NIST объявил о конкурсе на поиск преемника DES – улучшенного стандарта шифрования (Advanced Encryption Standard – AES). Многие криптографы с мировым именем представили на рассмотрение свои алгоритмы. Среди требований к алгоритму AES были следующие:• подобно DES, он должен быть симметричным блочным алгоритмом с секретным ключом;
• его криптостойкость и скорость зашифрования и расширования данных должны быть выше, чем у алгоритма 3-DES;
• время жизни нового стандарта должно быть, по крайней мере, 20–30 лет;
• он должен поддерживать ключи длиной 128, 192 и 256 бит;
• он должен удовлетворять условиям свободного распространения, не должен быть запатентован, и на него нельзя предъявить права собственности.
В течение нескольких месяцев NIST рассмотрел 15 различных заявок, шесть из которых были отклонены почти немедленно как не удовлетворяющие предъявляемым требованиям. К 1999 году NIST сузил число претендентов до пяти финалистов: MARS, RC6, Rijndael, Serpent и Twofish.
Отбор кандидатов занял еще один год, потому что нужно было тщательно протестировать каждого кандидата и удостовериться, что он удовлетворяет требованиям работы при различных условиях эксплуатации. Ведь AES должен был работать везде, начиная с портативных кредитных карточек с микропроцессором и обычных 32-разрядных настольных компьютеров и до 64-разрядных высококачественных оптимизированных компьютеров. Поскольку все из финалистов удовлетворяли требованиям безопасности, то решающим критерием выбора стала скорость обработки данных и удобство реализации алгоритма (которое в этом случае предполагало объем используемой памяти).
В конечном счете в октябре 2000 года победителем был объявлен алгоритм Rijndael («рейн-долл»). Прежде всего по причине высокой производительности программной или аппаратной реализации и невысоких требований к памяти. Алгоритм Rijndael был предложен бельгийскими криптографами докторами Джоаном Дименом (Joan Daemen) и Винсентом Риджменом (Vincent Rijmen). Ожидается, что он стоек к перспективным атакам будущего.
Как работает AES/Rijndael? Вместо использования циклов Фейстеля в каждом раунде, как это сделано в DES, в Rijndael, как и в IDEA, используются повторяющиеся раунды (алгоритм IDEA обсуждается в следующей секции). Данные разбиваются на блоки по 128 бит, которые группируются в 4 группы по 4 байта в каждом. Число раундов алгоритма зависит от размеров ключа. При ключе длиной 128 бит выполняется 9 раундов, 192 бит – 11 раундов и 256 бит – 13 раундов. Каждый раунд состоит из шага побитовой подстановки в S-блоках порции данных и следующим за ним шагом псевдоперестановки, в котором биты перетасовываются между группами. Затем каждая группа перемножается как матрица и результат складывается с подключом этого раунда.
Насколько AES быстрее, чем 3-DES? Ответить на это вопрос трудно, потому что скорость шифрования изменяется в широких пределах в зависимости от типа используемого процессора и от того, на каких средствах выполняется шифрование: на программных или аппаратных, специально для этого разработанных. Но при одинаковой реализации AES всегда быстрее алгоритма 3-DES. Тестирование, выполненное Брайоном Гладманом (Brian Gladman), показало, что на Pentium Pro 200 с оптимизированным кодом на языке C AES (Rijndael) может зашифровать и расшифровать сообщения со средней скоростью 70.2 Mbps, в то время как скорость работы DES при соблюдении этих же условий – только 28 M6/c Другие результаты исследователя можно найти по адресу fp.gladman.plus.com/cryptography_technology/aes.
Алгоритм IDEA
IDEA – Европейский коллега алгоритма DES. Существование алгоритма IDEA доказывает, что американцы не монополисты качественной криптографии. Первоначальное название алгоритма IDEA – предлагаемый стандарт шифрования (Proposed Encryption Standard — PES). В 1990 году он был предложен криптографами Джеймсом Мэсси (James Massey) и Кседжой Лей (Xuejia Lai) как итог совместного научно-исследовательского проекта Ascom и Швейцарского федерального института технологии. Прежде чем алгоритм PES получил широкое распространение, в 1991 году авторы усилили его против атак на основе использования дифференциального криптоанализа и изменили название алгоритма на улучшенный предлагаемый стандарт шифрования (Improved PES – IPES). Наконец, в 1992 году он стал называться международным алгоритмом шифрования данных (International Data Encryption Algorithm – IDEA).Алгоритм IDEA появился не только позднее DES. Он также значительно быстрее и безопаснее DES. Скорость работы IDEA возросла благодаря более простым операциям (операции исключающего ИЛИ – XOR, логического дополнения и умножения), используемым в каждом раунде, по сравнению с операциями цикла Фейстеля в DES. Используемые в IDEA операции проще реализовать программным способом, чем выполнить подстановку и перестановку в DES.
Алгоритм IDEA оперирует с 64-битовыми блоками открытого текста, и его ключ имеет длину 128 бит. Процесс зашифрования / расшифрования состоит из восьми раундов, в каждом из которых используется шесть 16-битных подключей. Алгоритм IDEA запатентован в США и Европе, но разрешено его свободное некоммерческое использование.
Асимметричные алгоритмы
В отличие от симметричных алгоритмов асимметричные используют два ключа – открытый и секретный (возможны алгоритмы и с большим количеством ключей). Вместо используемых в симметричных алгоритмах операций подстановки и перемешивания асимметричные алгоритмы основаны на использовании математических проблем больших целых чисел. Для большинства из них легко решается прямая задача, но сложно получить решение обратной задачи. Например, легко решить прямую задачу – перемножить два числа, но обратная задача – найти делители большого целого числа, особенно если оно состоит из сотни десятичных цифр, – практически неразрешима. Вообще говоря, безопасность асимметричных алгоритмов зависит не от возможностей атак «грубой силы», а от способности решить сложную обратную задачу и прогресса в математике, который сможет предложить новые эффективные методы их решения. В этой секции будут рассмотрены алгоритмы RSA и Диффи-Хеллмана (Diffie-Hellman) – два наиболее популярных алгоритма в настоящее время.
До алгоритма Диффи-Хеллмана (Diffie-Hellman) было сложно совместно использовать зашифрованные данные из-за проблем хранения ключей и передачи информации. Подробнее об этом будет еще сказано. В большинстве случаев передача информации по каналам связи небезопасна, потому что сообщение может пройти десятки систем, прежде чем оно достигнет потенциального адресата, и нет никаких гарантий, что по пути никто не сможет взломать секретный ключ. Уитфилд Диффи (Whitfield Diffie) и Мартин Хеллман (Martin Hellman) предложили зашифровывать секретный ключ DES по алгоритму Диффи-Хеллмана на передающей стороне и пересылать его вместе с сообщением, зашифрованным с использованием DES. Тогда на другом конце его сможет расшифровать только получатель сообщения.
На практике обмен ключами по алгоритму Диффи-Хеллмана происходит по следующей схеме.
1. Два участника обмена договариваются о двух числах. Один выбирает большое простое число, а другой – целое число, меньшее числа первого участника. Переговоры они могут вести открыто, и это никак не отразится на безопасности.
2. Каждый из двух участников, независимо друг от друга, генерит другое число, которое они будут хранить в тайне. Эти числа выполняют роль секретного ключа. Далее в вычислениях используются секретный ключ и два предыдущих целых числа. Результат вычислений посылается участнику обмена, и он играет роль открытого ключа.
3. Участники обмена обмениваются открытыми ключами. Далее они, используя собственный секретный ключ и открытый ключ партнера, конфиденциально вычисляют ключ сессии. Каждый партер вычисляет один и тот же ключ сессии.
4. Ключ сессии может использоваться как секретный ключ для другого алгоритма шифрования, например DES. Никакое третье лицо, контролирующее обмен, не сможет вычислить ключ сессии, не зная один из секретных ключей.
Самое сложное в алгоритме Диффи-Хеллмана обмена ключами – это понять, что в нем фактически два различных независимых цикла шифрования. Алгоритм Диффи-Хеллмана применяется для обработки небольших сообщений от отправителя получателю. Но в этом маленьком сообщении передается секретный ключ для расшифровки большого сообщения.
Сильная сторона алгоритма Диффи-Хеллмана заключается в том, что никто не сможет скомпрометировать секретное сообщение, зная один или даже два открытых ключа получателя и отправителя. В качестве секретных и открытых ключей используются очень большие целые числа. Алгоритм Диффи-Хеллмана основан на полезных для криптографии свойствах дискретных логарифмов. Безопасность алгоритма основана на значительной сложности вычисления дискретных логарифмов по сравнению с возведением в степень натуральных чисел. Несмотря на то что несколько лет назад срок действия патента истек, алгоритм широко используется. Особенно в протоколе IPSec, где алгоритм Диффи-Хеллмана применяется совместно с алгоритмом аутентификации RSA для обмена ключом сессии, который используется для шифрования трафика по туннелю IPSec.
Алгоритм Диффи-Хеллмана
В 1976 году после публичной критики алгоритма DES и указания на сложность обработки секретных ключей Уитфилд Диффи (Whitfield Diffie) и Мартин Хеллман (Martin Hellman) опубликовали свой алгоритм обмена ключами. Это была первая публикация на тему криптографии с открытым ключом и, возможно, самый большой шаг вперед в области криптографии, сделанный когда-либо. Из-за невысокого быстродействия, свойственного асимметричным алгоритмам, алгоритм Диффи-Хеллмана не предназначен для шифрования данных. Он был ориентирован на передачу секретных ключей DES или других подобных алгоритмов через небезопасную среду. В большинстве случаев алгоритм Диффи-Хеллмана (Diffie-Hellman) не используется для шифрования сообщений, потому что он, в зависимости от реализации, от 10 до 1000 раз медленнее алгоритма DES.До алгоритма Диффи-Хеллмана (Diffie-Hellman) было сложно совместно использовать зашифрованные данные из-за проблем хранения ключей и передачи информации. Подробнее об этом будет еще сказано. В большинстве случаев передача информации по каналам связи небезопасна, потому что сообщение может пройти десятки систем, прежде чем оно достигнет потенциального адресата, и нет никаких гарантий, что по пути никто не сможет взломать секретный ключ. Уитфилд Диффи (Whitfield Diffie) и Мартин Хеллман (Martin Hellman) предложили зашифровывать секретный ключ DES по алгоритму Диффи-Хеллмана на передающей стороне и пересылать его вместе с сообщением, зашифрованным с использованием DES. Тогда на другом конце его сможет расшифровать только получатель сообщения.
На практике обмен ключами по алгоритму Диффи-Хеллмана происходит по следующей схеме.
1. Два участника обмена договариваются о двух числах. Один выбирает большое простое число, а другой – целое число, меньшее числа первого участника. Переговоры они могут вести открыто, и это никак не отразится на безопасности.
2. Каждый из двух участников, независимо друг от друга, генерит другое число, которое они будут хранить в тайне. Эти числа выполняют роль секретного ключа. Далее в вычислениях используются секретный ключ и два предыдущих целых числа. Результат вычислений посылается участнику обмена, и он играет роль открытого ключа.
3. Участники обмена обмениваются открытыми ключами. Далее они, используя собственный секретный ключ и открытый ключ партнера, конфиденциально вычисляют ключ сессии. Каждый партер вычисляет один и тот же ключ сессии.
4. Ключ сессии может использоваться как секретный ключ для другого алгоритма шифрования, например DES. Никакое третье лицо, контролирующее обмен, не сможет вычислить ключ сессии, не зная один из секретных ключей.
Самое сложное в алгоритме Диффи-Хеллмана обмена ключами – это понять, что в нем фактически два различных независимых цикла шифрования. Алгоритм Диффи-Хеллмана применяется для обработки небольших сообщений от отправителя получателю. Но в этом маленьком сообщении передается секретный ключ для расшифровки большого сообщения.
Сильная сторона алгоритма Диффи-Хеллмана заключается в том, что никто не сможет скомпрометировать секретное сообщение, зная один или даже два открытых ключа получателя и отправителя. В качестве секретных и открытых ключей используются очень большие целые числа. Алгоритм Диффи-Хеллмана основан на полезных для криптографии свойствах дискретных логарифмов. Безопасность алгоритма основана на значительной сложности вычисления дискретных логарифмов по сравнению с возведением в степень натуральных чисел. Несмотря на то что несколько лет назад срок действия патента истек, алгоритм широко используется. Особенно в протоколе IPSec, где алгоритм Диффи-Хеллмана применяется совместно с алгоритмом аутентификации RSA для обмена ключом сессии, который используется для шифрования трафика по туннелю IPSec.
Алгоритм RSA
Спустя год после появления алгоритма Диффи-Хеллмана Рон Ривест (Ron Rivest), Ади Шамир (Adi Shamir) и Леонард Адлеман (Leonard Adleman) предложили другой вариант построения криптографической системы с открытым ключом. Их предложение теперь известно как алгоритм RSA. Имя алгоритма образовано из первых букв фамилий авторов алгоритма. RSA очень похож на алгоритм Диффи-Хеллмана тем, что он основан на факторизации (разложении числа на сомножители) и перемножении больших целых чисел. Но RSA работает значительно быстрее алгоритма Диффи-Хеллмана. Благодаря RSA асимметричные криптосистемы разделись на два класса: системы распределения открытых ключей (Public Key Distribution Systems – PKDS) и системы шифрования с открытым ключом (PublicKey Encryption – PKE). К первому классу (классу PKDS) относятся системы, основанные на алгоритме Диффи-Хеллмана и ему подобных, а ко второму (классу PKE) – алгоритм RSA и его модификации. Системы PKDS используются для обмена ключей сессий, в то время как системы PKE считаются достаточно быстрыми для шифрования разумно маленьких сообщений. Однако PKE-системы не считаются достаточно быстрыми для шифровки большого объема данных в файловых системах или высокоскоростных линий передачи данных.ПримечаниеИз-за прежних ограничений патентного права алгоритм RSA не получил широкого распространения и до середины 1990-х годов применялся в основном в разработках компании RSA Security. Но сейчас можно встретить много программ, широко использующих алгоритм RSA. Прежде всего это программы PGP и Secure Shell (SSH). Сведения об алгоритме RSA были полностью раскрыты за две недели до истечения срока действия патента в сентябре 2000 года. Ныне алгоритм RSA свободно распространяется для любых целей.
В алгоритмах RSA, Диффи-Хеллмана и других асимметричных алгоритмах криптографии используются ключи намного большей длины, чем в симметричных криптоалгоритмах. Чаще всего размер ключа составляет 1024 или 2048 бит. Необходимость использования таких длинных ключей обусловлена тем, что операция факторизации (разложения числа на сомножители) на современных компьютерах выполняется быстрее, чем перебор ключей симметричных алгоритмов. Относительная медлительность криптографических систем с открытым ключом – отчасти следствие использования длинных ключей. Поскольку большинство компьютеров могут обрабатывать только 32-разрядные числа, то для эмуляции операций над целыми числами длиной 1024 или 2048 бит нужны хитроумные алгоритмы. Но дополнительное время обработки 2048-битных ключей оправдано тем, что такой ключ «навсегда» обеспечит безопасность зашифрованных им сообщений, если только исследования математических алгоритмов факторизации не приведут к экспоненциальному росту их производительности.
«Грубая сила»
Насколько безопасны зашифрованные файлы и пароли? Считается, что существует два способа взлома алгоритмов шифрования – «грубая сила» и разнообразные «разумные» методы криптоанализа (методы дешифровки сообщений). Для разных алгоритмов шифрования найдены различные методы криптоанализа. Возможно, что для некоторых алгоритмов методов криптоанализа не существует. Зачастую они сложны, их всегда трудно придумать и эффективно использовать. Напротив, метод «грубой силы» всегда под рукой, им легко воспользоваться. Метод «грубой силы» основан на исчерпывающем переборе всевозможных ключей до тех пор, пока не будет найден ключ или комбинация паролей, позволяющих расшифровать сообщение.
Основы метода «грубой силы»
В качестве примера рассмотрим велосипедный замок, который открывается набором ключевой комбинации из трех цифр. Каждая цифра – это число от 0 до 9. Открыть замок нетрудно, если располагать временем и если ключевая комбинация во время вскрытия замка не изменяется. Общее число всевозможных комбинаций (ключей) – 10 3 , или 1000. Предположив, что велосипедный вор способен перебирать 30 комбинаций в минуту, определим, что в худшем для него случае он откроет замок приблизительно через 1000: 30 = 33 мин. При этом имейте в виду, что после выбора очередной комбинации число возможных комбинаций (ключевое пространство) уменьшается, а шансы угадать ключевую комбинацию на следующем шаге увеличиваются.
Метод «грубой силы» всегда приводит к успеху, потому что ключевое пространство, как бы велико оно ни было, всегда конечно. Противостоять «грубой силе» можно, увеличивая длину ключа и тем самым время расшифровки сообщения. В случае примера с велосипедным замком три цифры ключевого пространства позволят велосипедному вору украсть велосипед максимум за 33 мин. Поэтому для велосипедного вора в данном случае метод «грубой силы» выглядит привлекательным. Рассмотрим велосипедный замок с ключевой комбинацией из пяти цифр, для которого число возможных комбинаций равно 100 000. Теперь для подбора ключевой комбинации методом «грубой силы» потребуется 55,5 ч. Ясно, что большинство воров отказалось бы от этой затеи и искало бы более легкую добычу.
Метод «грубой силы» всегда приводит к успеху, потому что ключевое пространство, как бы велико оно ни было, всегда конечно. Противостоять «грубой силе» можно, увеличивая длину ключа и тем самым время расшифровки сообщения. В случае примера с велосипедным замком три цифры ключевого пространства позволят велосипедному вору украсть велосипед максимум за 33 мин. Поэтому для велосипедного вора в данном случае метод «грубой силы» выглядит привлекательным. Рассмотрим велосипедный замок с ключевой комбинацией из пяти цифр, для которого число возможных комбинаций равно 100 000. Теперь для подбора ключевой комбинации методом «грубой силы» потребуется 55,5 ч. Ясно, что большинство воров отказалось бы от этой затеи и искало бы более легкую добычу.