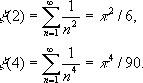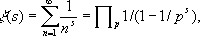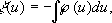автор:

А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Э Ю Я [A-Z] [0-9]

книга:

А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Э Ю Я [A-Z] [0-9]

серия:

А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Э Ю Я [A-Z] [0-9]

• Главная
• Жанры
• Контакты

TheLib.Ru » Энциклопедии » БСЭ » Большая Советская Энциклопедия (ДЗ) » онлайн-чтение (стр. 2)

 

 

Страница:

• << Первая
• « Предыдущая
• 1
• 2
• Следующая »
• Последняя >>

     Соч.: ХорхSссжг. Радзырдтж, Сталинир, 1959; Алагираг сатана, Орджоникидзе, 1967; Фыййауы сагжс, Орджоникидзе, 1970.
     Лит.:Джусойты Н., Кудзаг Дзесов, в кн.: Очерки истории осетинской советской литературы, Орджоникидзе, 1967.
      Н. Д. Гаглоев.

Эйлер (1737), а для комплексных sвпервые изучал немецкий математик Б. Риман (1859), поэтому её часто называют дзета-функцией Римана. После трудов Л. Эйлера (1748, 1749), П. Л. Чебышева (1848) и Б. Римана выяснилась глубокая связь между свойствами Д.-ф. и свойствами простых чисел.
     Эйлер вычислил значения x(2 s) для любого натурального s. В частности

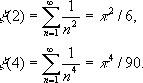   Далее он вывел тождество (тождество Эйлера)

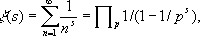   где произведение распространяется на все простые числа р= 2, 3, 5,...
     Первостепенное значение для теории простых чисел имеет распределение нулей Д.-ф. Известно, что Д.-ф. имеет нули в точках s= —2 n, где n= 1, 2, ... (эти нули принято называть тривиальными) и что все остальные (так называемые нетривиальные) нули Д.-ф. находятся в полосе 0 < s< 1, называемой критической полосой. Риман высказал предположение, что все нетривиальные нули Д.-ф. расположены на прямой s= ¹/ ₂. Эта гипотеза Римана до сих пор не доказана и не опровергнута. Важные результаты о распределении нулей Д.-ф. получены при помощи созданного советским математиком И. М. Виноградовым нового метода в аналитической теории чисел.
     Лит.:Эйлер Л., Введение в анализ бесконечных, пер. с латин., 2 изд., т. 1, М., 1961; Уиттекер Э. Т., Ватсон Дж. Н., Курс современного анализа, пер. с англ., 2 изд., ч. 2, М., 1963; Титчмарш Е. К., Дзета-функция Римана, пер. с англ., М., 1947; Ингам А. Е., Распределение простых чисел, пер. с англ., М. — Л., 1936; Янке Е., Эмде Ф., Таблицы функций с формулами и кривыми, пер. с нем., М. — Л., 1948; Прахар К., Распределение простых чисел, пер. с нем., М., 1967.
     2) В теории эллиптических функций встречается Д.-ф. Вейерштрасса

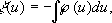   где Г( u) — эллиптическая функция Вейерштрасса. Эту Д.-ф. не следует смешивать с Д.-ф. Римана.

Аматэрасу . Предание о походе Дзимму с острова Кюсю в провинцию Ямато на острове Хонсю (667—660 до н. э.) и основании им японского государства (660 до н. э.) отражает, по-видимому, процессы миграции японских племён и складывания племенного союза, относимые современной наукой к началу н. э. С 1873 по 1948 день 11 февраля (день, когда, согласно мифам, Д. в 660 до н. э. вступил на престол) ежегодно отмечался как праздник основания империи (кигэнсэцу). В декабре 1966 решением японского правительства день кигэнсэцу восстановлен в качестве национального праздника.

Юрмала .

«Минкэн ундо» .

Мицуи ), связанной с помещиками. В июне 1898 Д. объединилась с Симпото (партией крупной буржуазии) в партию Кэнсэйто. В 1900 Кэнсэйто послужила основой для создания помещичье-буржуазной партии Сэйюкай .

дерево-земляных огневых сооружений .

буддизма . Само слово «Д.» — японское произношение китайской иероглифической транскрипции санскритского термина дхьяна (медитация, самоуглубление), китайское произношение — чань. Д. сложился в Китае в 6—7 вв. под сильным влиянием даосизма , у которого Д. заимствовал пренебрежение к знанию, убеждение в том, что истина не выразима в словах и её можно постичь лишь путём внутреннего скачка, освободив сознание не только от проторённых путей, которыми движется мысль, но и от мысли вообще. Для Д. характерны отказ от установленных норм разумного и морального, любовь к парадоксу, интуитивизм, непосредственность. Основа понятийного и художественного языка Д. — лаконичный намёк и ритмическая пауза. На первое место выдвигается импровизация, действие по наитию, без плана. Эти черты Д. могут быть поняты как выражение «свободы духа» в обществе, где свободное мыслимо только как нечаянное, необдуманное, юродское.
     Первым патриархом Д. в Китае считается индийский проповедник Бодхидхарма (начало 6 в.), но решающую роль сыграли шестой патриарх Хуэй-нэн (638—713), а также Шэнь-сю (605—706). Период расцвета Д. в Китае продолжался до 9 в.; в Японии Д. появился в 12—13 вв.; он продолжает оказывать серьёзное воздействие на культуру и идеологию вплоть до настоящего времени. Д., в котором творческий акт интерпретируется как религиозный, оказал огромное влияние на китайскую живопись, каллиграфию и поэзию и на японскую культуру, особенно начиная с периода Муромати (14—16 вв.).
     Своеобразный (вульгаризированный) вариант Д. процветает среди битников, понимающих Д. как идеологию отказа от цивилизации.
     Лит.:Померанц Г., Дзэн и его наследие, «Народы Азии и Африки», 1964, № 4; Завадская Е. В., Пятигорский А. М., Отзвуки культуры Востока в произведениях Дж. Д. Сэлинджера, там же, 1966, № 3; Suzuki D. Т., Essays in Zen Buddhism, ser. 1—3, L., 1953; Watts A., Way of Zen, N. Y., 1957; Blyth R. Н., Zen and zen classics, v. 1—5, Tokyo, 1960—66.
      Г. С. Померанц.

джиу-джицу , превращённое в спорт, возникло в Японии в 1882; создателем Д.-д. считается профессор Д. Кано (1860—1938). При борьбе стоя с помощью различных приёмов (подножек, подсечек, бросков и др.) борцы стремятся бросить друг друга на ковёр, при борьбе лёжа, применяя различные захваты, — удержать противника прижатым спиной к ковру в течение 30 секили, применяя болевые приёмы на руку и удушающие захваты, заставить его признать себя побеждённым. Борцы выступают в кимоно со свободным поясом, без обуви. Схватки проводятся на ковре, составленном из циновок «татами», изготовленных из прессованной соломы, и продолжаются от 4 до 15 минбез перерыва — в зависимости от значимости соревнований и возраста борцов. В Японии в 1970 Д.-д. занималось свыше 4,5 млн. чел.; Д.-д. включено как обязательный предмет в школьную программу.
     С конца 19 — начала 20 вв. культивируется в странах Европы, Азии и Америки; наибольшее развитие этот вид борьбы получил в США, Франции, Нидерландах, ФРГ, КНДР, ГДР и др. В 1956 создана Международная федерация Д.-д. (МФД — IFD), объединяющая 5 континентальных союзов — Европейский, Азиатский, Панамериканский, Африканский и Океанский, в которые входит свыше 80 стран.
     Чемпионаты мира по Д.-д. проводятся 1 раз в 2 года, чемпионаты континентальных союзов — ежегодно. В 1964 Д.-д. включено в программу Олимпийских игр . С 1967 официальные международные соревнования проводятся в 5 весовых категориях: лёгкой — до 63 кг, полусредней — до 70 кг, средней — до 80 кг, полутяжёлой — до 93 кг, тяжёлой — свыше 93 кги абсолютной — без веса.
     В СССР борьба Д.-д. не получила широкого распространения (значительное развитие имеет борьба самбо , в которой применяются почти все приёмы, разрешённые в Д.-д.), однако советские спортсмены являются сильнейшими в мире вслед за дзюдоистами Японии. В 1962 созданная при федерации самбо СССР секция Д.-Д. вступила в МФД. В 1963—70 советские спортсмены завоевали на чемпионатах Европы по Д.-д. 51 золотую медаль, на чемпионатах мира и Олимпийских играх — 13 серебряных и бронзовых медалей. Сборная Команда СССР — чемпион Европы по Д.-д. 1963—66 и 1970; широко известны имена заслуженных мастеров спорта А. Боголюбова, А Киброцашвили, А. Кикнадзе, В. Покатаева, О. Степанова, С. Суслина.
      В. М. Андреев.

Дзялошинский Игорь Ехисльевич