Страница:
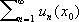
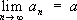 ; С. ряда
; С. ряда
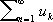 —конечного предела (называемого суммой ряда) у последовательности его частичных сумм
—конечного предела (называемого суммой ряда) у последовательности его частичных сумм
 ,
,
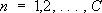 ; С. бесконечного произведения
b
1b
2... b
n—конечного предела, не равного нулю, у последовательности конечных произведений
p
n= b
1b
2... b
n, n =1, 2,...;
С. интеграла
; С. бесконечного произведения
b
1b
2... b
n—конечного предела, не равного нулю, у последовательности конечных произведений
p
n= b
1b
2... b
n, n =1, 2,...;
С. интеграла
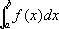 от функции
f(
x)
,интегрируемой по любому конечному отрезку [
а, b]
,—конечного предела у интегралов при
b® +µ, называется
несобственным интегралом
от функции
f(
x)
,интегрируемой по любому конечному отрезку [
а, b]
,—конечного предела у интегралов при
b® +µ, называется
несобственным интегралом
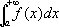
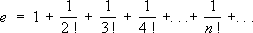
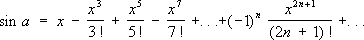
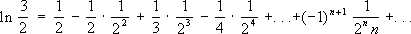 ,
,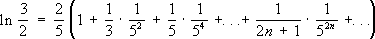 .
. и
и
 ,и
,и
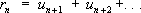 ,
,
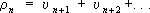 . —их остатки, то 1-й ряд называется сходящимся быстрее 2-го ряда, если
. —их остатки, то 1-й ряд называется сходящимся быстрее 2-го ряда, если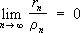 .
.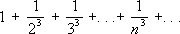
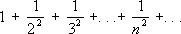 .
.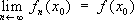 для каждой точки
X
0(из
М)
,то говорят о С. в каждой точке [если это равенство не имеет места лишь для точек, образующих множество меры нуль (см.
Мера множества
)
,то говорят о С. почти всюду]. Несмотря на свою естественность, понятие С. в каждой точке обладает многими нежелательными особенностями [например, последовательность непрерывных функций может сходиться в каждой точке к разрывной функции; из С. функций
f
n(
x) к
f(
x)
в каждой точке не следует, вообще говоря, С. интегралов от функций
f
n(
x) к интегралу от
f(
x) и т. д.]. В связи с этим было введено понятие равномерной С., свободное от этих недостатков: последовательность {
f
n(
x)} называется равномерно сходящейся к
f(
x) на множестве
М,если
для каждой точки
X
0(из
М)
,то говорят о С. в каждой точке [если это равенство не имеет места лишь для точек, образующих множество меры нуль (см.
Мера множества
)
,то говорят о С. почти всюду]. Несмотря на свою естественность, понятие С. в каждой точке обладает многими нежелательными особенностями [например, последовательность непрерывных функций может сходиться в каждой точке к разрывной функции; из С. функций
f
n(
x) к
f(
x)
в каждой точке не следует, вообще говоря, С. интегралов от функций
f
n(
x) к интегралу от
f(
x) и т. д.]. В связи с этим было введено понятие равномерной С., свободное от этих недостатков: последовательность {
f
n(
x)} называется равномерно сходящейся к
f(
x) на множестве
М,если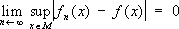
 (
х) по формуле
(
х) по формуле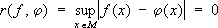
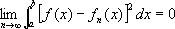 .
.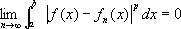 .
.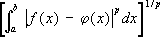 .
.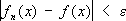 ,стремится к нулю с возрастанием
n',слабая С.:
,стремится к нулю с возрастанием
n',слабая С.: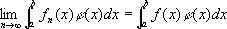
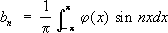 ряда Фурье стремятся к нулю).
ряда Фурье стремятся к нулю).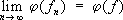 для всех линейных функционалов; введённая выше слабая С. функций соответствует рассмотрению нормы
для всех линейных функционалов; введённая выше слабая С. функций соответствует рассмотрению нормы
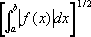 . В современной математике рассматривается также С. по частично упорядоченным множествам (см.
Упорядоченные и частично упорядоченные множества
)
.В теории вероятностей для последовательности случайных величин употребляются понятия С. с вероятностью 1 и С. по вероятности.
. В современной математике рассматривается также С. по частично упорядоченным множествам (см.
Упорядоченные и частично упорядоченные множества
)
.В теории вероятностей для последовательности случайных величин употребляются понятия С. с вероятностью 1 и С. по вероятности.