Страница:
но иразрушила представление о гравитации как о силе. Общая теория относительности уверенно провозгласила, что гравитация представляет собой геометрию искривленного пространства. Таким образом, Эйнштейн свел само понятие гравитации к чистой геометрии. На смену представлению об ускорении в пространстве пришло представление об искривлении пространства.
Теория Эйнштейна ознаменовала столь важный прогресс в понимании природы, что уже вскоре стал неизбежным пересмотр взглядов и на другие силы природы. В это время единственной “другой” силой, существование которой было твердо установлено, являлось электромагнитное взаимодействие. Однако внешне оно совершенно не походило на гравитацию. Более того, за несколько десятков лет до создания теории гравитации Эйнштейна электромагнетизм успешно описала теория Максвелла, и не было никаких оснований сомневаться в справедливости этой теории.
На протяжении всей жизни Эйнштейн мечтал о создании единой теории поля, в'которой все силы природы сливались бы воедино на основе чистой геометрии. Поискам такой схемы Эйнштейн посвятил большую часть своей жизни после создания общей теории относительности. Однако по иронии судьбы ближе всех к реализации мечты Эйнштейна подошел малоизвестный польский физик Теодор Калуца, который еще в 1921 г. заложил основы нового и неожиданного подхода к объединению физики, до сих пор поражающего воображение своей дерзостью.
Калуца был вдохновлен способностью геометрии описать гравитацию; он задался целью обобщить теорию Эйнштейна, включив электромагнетизм в геометрическую формулировку теории поля. Это следовало сделать не нарушая “священных” уравнений теории электромагнетизма Максвелла. То, что удалось сделать Калуце, — классический пример проявления творческого воображения и физической интуиции. Калуца понимал, что теорию Максвелла невозможно сформулировать на языке чистой геометрии (в том смысле, как мы ее обычно понимаем), даже допуская наличие искривленного пространства. Он нашел удивительно простое решение, обобщив геометрию так, чтобы она “вместила в себя” теорию Максвелла. Чтобы выйти из затруднения, Калуца нашел весьма необычный, но вместе с тем неожиданно убедительный способ. Калуца показал, что электромагнетизм является своего рода “гравитацией”, но не обычной, а “гравитацией” в ненаблюдаемых измерениях пространства.
Физики долю привыкали к тому, чтобы пользоваться временем как четвертым измерением. Теория относительности установила, что пространство и время сами по себе не являются универсальными физическими понятиями, так как они неизбежно сливаются в единую четырехмерную структуру, называемую “пространство-время”. Калуца фактически сделал следующий шаг: он постулировал, что существует еще дополнительное пространственное измерение и общее число измерений пространства равно четырем, а всего пространство-время насчитывает пять измерений. Если принять это допущение, то, как показал Калуца, произойдет своего рода математическое чудо. Гравитационное поле в таком пятимерном мире проявляет себя в виде обычного гравитационного поля плюс электромагнитное поле Максвелла — если наблюдать этот мир из пространства-времени, ограниченного четырьмя измерениями. Своей смелой гипотезой Калуца по существу утверждал, что если мы расширим свое представление о мире до пяти измерений, то в нем будет существовать лишь единственное силовое поле — гравитация. То, что мы называем электромагнетизмом, — всего лишь часть гравитационного поля, которая действует в пятом дополнительном измерении пространства, которое мы не в состоянии наглядно представить.
Теория Калуцы не только позволила соединить гравитацию и электромагнетизм в единой схеме, но и дала основанное на геометрии описание обоих силовых полей. Так, электромагнитная волна (например, радиоволна) в этой теории не что иное, как пульсации пятого измерения. Особенности движения электрически заряженных частиц в электрических и магнитных полях прекрасно объясняются, если предположить, что частицы пребывают в дополнительном пятом измерении. Если принять эту точку зрения, то вообще нет никаких сил — существует только геометрия искривленного пятимерного пространства, а частицы свободно “кочуют” по наделенной структурой пустоте.
Математически гравитационное поле Эйнштейна в пространстве пяти измерений в точности и полностью эквивалентно обычной гравитации плюс электромагнетизм в пространстве четырех измерений; разумеется, это нечто большее, чем просто случайное совпадение. Однако в таком случае теория Калуцы остается загадочной в том отношении, что столь важное четвертое измерение пространства вообще не воспринимается нами. Пространство, доступное нашему непосредственному восприятию, с полной очевидностью и неизменностью остается трехмерным. Если четвертое измерение пространства существует, то где же оно? Прежде чем ответить на этот вопрос, следует также выяснить, что мы в действительности понимаем под размерностью пространства.
Однако интерес к проблеме размерности пространства возник задолго до появления фантастики. Древние греки остро чувствовали ее значение для развития науки геометрии. Непосредственно столкнуться с проблемой размерности их заставил любопытный случай, связанный со свойствами правильных многоугольников (замкнутых плоских фигур со сторонами равной длины, например квадратов, правильных пяти-, восьмиугольников и т. п.). Количество различных правильных многоугольников безгранично — могут существовать правильные многоугольники с любым числом сторон. Однако существует всего лишь пять типов различных правильных многогранников (замкнутых объемных фигур, грани которых образованы правильными многоугольниками). Грекам было свойственно наделять геометрию глубоким мистическим смыслом, а Птолемей даже написал исследование на тему о размерности, в котором утверждалось, что в природе вообще не может существовать более трех пространственных измерений.
В дальнейшем математики, в частности Риман, систематически изучали свойства многомерных пространств с чисто математических позиций. При этом основная проблема заключалась в формулировке последовательного определения размерности. Это было совершенно необходимо для доказательства строгих теорем относительно пространств с различным числом измерений.
Интуитивно все геометрические структуры мы подразделяем на одно-, двух- и трехмерные в соответствии с их протяженностью. Так, не имеющей протяженности точке соответствует нулевая размерность. Линия является одномерной, поверхность — двумерной, объем — трехмерным. Вряд ли нам удастся лучше сформулировать эти определения, чем это сделал сам Евклид почти за 300 лет до н. э.
Точка — это то, что не имеет частей. Линия — длина, лишенная ширины.
Плоскость — это то, что имеет только длину и ширину. Объем — это то, что имеет длину, ширину и глубину.
Далее Евклид уточнял, что границами линии служат точки, границами поверхности — линии, а границей объемного тела — поверхность. Возникла мысль определить размерность по иерархической схеме, начиная с нулевой размерности точки, а затем шаг за шагом увеличивая ее на единицу. Тогда одномерным будет объект, у которого началом и концом служат точки, т.е. линия. Двигаясь далее, мы по индукции придем к определению четырехмерной структуры как ограниченной трехмерным объемом. Число измерений, которые можно логически ввести таким способом, не ограниченно, однако сама процедура не содержит каких" либо указаний на реальную физическую ситуацию.
Более наглядное и ясное представление о трехмерности можно получить с помощью другой схемы, основанной на указании местоположения точек в пространстве. Представьте себе, что вам необходимо встретиться с приятелем в заранее обусловленном месте. В этом случае можно указать географическую широту и долготу выбранного места; пусть это будет, например, Эмпайрстейт билдинг. Но в этом случае остается еще одна неопределенная величина — высота. На каком этаже должна состояться встреча? Итак, в общей сложности необходимо указать три независимых числа для того, чтобы однозначно определить положение точки в пространстве. По этой причине такое пространство называют трехмерным.
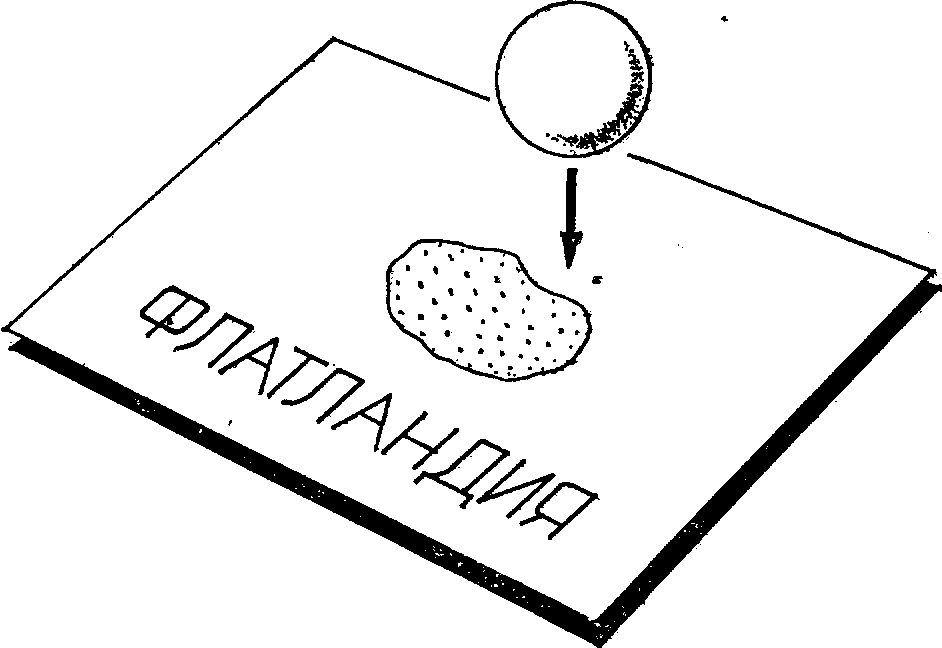
Рис. 23. Двумерная вселенная. Плоское существо, живущее во Флатландии, не имеет представления о “верхе” и “низе”. Шар, пронизывающий плоский мир, воспринимается этим существом как двумерный объект, меняющий свою форму.
Теория относительности обнаружила, что пространство переплетено со временем, поэтому в действительности следует говорить не об одном только пространстве, а о пространстве-времени. В какой день.вы собираетесь встретиться с приятелем в здании Эмпайр-стейт-билдннг? Указание времени события требует задать единственное число (“дату”), так что время одномерно. Объединяя пространство и время, мы приходим к четырехмерному пространству-времени.
Когда мы пытаемся наглядно представить дополнительные измерения, например, четвертое пространственное измерение (в этом случае полное пространство-время насчитывает пять измерений), нашей интуиции оказывается недостаточно. Для облегчения задачи можно обратиться к аналогии. Вообразим двумерное “блинообразное” создание, которое обречено существовать только на поверхности; у него отсутствуют представления о “верхе” и о “низе”. На рис. 23 изображена такая плоская вселенная. Мы можем догадываться, что эта поверхность в действительности “вложена” в трехмерное пространство, однако обитатель плоского мира не в состоянии понять эту более широкую точку зрения. Он воспринимает только события, происходящие на самой поверхности.
Возникает вопрос: а что будет наблюдать это создание, когда поверхность пересекается трехмерным объектом? Поверхность рассечет этот объект, причем размеры и форма сечения будут в общем случае изменяться по мере прохождения объекта. Так, сечение сферы в первый момент будет выглядеть как точка, которая, постепенно “расплываясь”, превратится в круг все увеличивающегося радиуса; достигнув максимального радиуса, круг начнет уменьшаться в размерах, напоследок снова превратившись в точку. Более сложные объекты будут создавать при прохождении следы более сложного сечения.
Рассуждая далее, по аналогии можно предположить, что четыре измерения пространства-времени “вложены” во вселенную, имеющую пять или даже большее число измерений. Геометрию такой вселенной трудно вообразить, однако с помощью математики можно построить законченное логическое описание ее. Математики уже давно обобщили законы геометрии на случай пространства с произвольным числом измерений (включая бесконечно большое). Поэтому смысл многомерных пространств вполне можно понять, хотя непосредственному восприятию доступно лишь триизмерения.
Какие особенности присущи четырехмерному пространству? Один из аспектов размерности касается числа взаимно перпендикулярных направлений, которые существуют в данном пространстве. Например, пространство этой страницы двумерно. Если положить ее на стол, то в любом из углов края страницы образуют две прямые линии, перпендикулярные друг к другу. Из того же угла невозможно провести третью прямую, лежащую в плоскости страницы и перпендикулярную обоим ее краям. Однако направление такой прямой удастся найти, если выйти из плоскости страницы и начертить вертикальную линию. Таким образом, в трехмерном пространстве в отличие от двумерной поверхности страницы существует три взаимно перпендикулярных направления.
В четырехмерном пространстве удалось бы найти четыре взаимно перпендикулярных направления. На рис. 24 изображен случай трех измерений: три взаимно перпендикулярные прямые исчерпывают максимально возможное число таких прямых. Как бы мы ни старались, мы никогда не найдем в обычном пространстве прямую, перпендикулярную всем трем. Любая прямая, перпендикулярная трем названным, должна идти в направлении, не принадлежащем нашему пространству. И хотя мы не в состоянии представить какпроходит подобная прямая, очевидно, что формальноона могла бы существовать. Ее можно описать, а именно вычислить и систематизировать ее геометрические параметры.
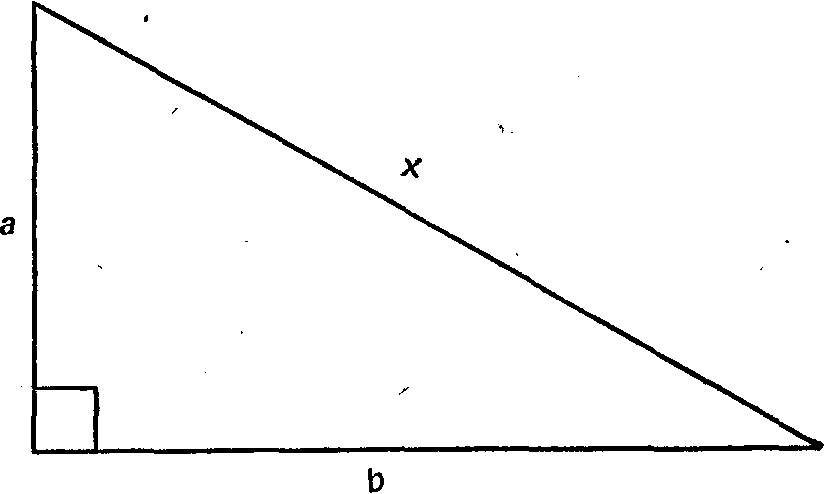
Рис. 24. Вершины прямоугольного параллелепипеда образованы тремя взаимно перпендикулярными прямыми линиями. В трехмерном пространстве из вершины нельзя провести ни одной прямой, которая была бы перпендикулярна всем трем ребрам.

Рис. 25. Знаменитая теорема Пифагора, связывающая между собой длины сторон прямоугольного треугольника, а, b, х, без труда обобщается на случай больших размерностей.
Простым примером сказанного может служить знаменитая геометрическая теорема древнегреческого геометра Пифагора, которая знакома любому школьнику. Эта теорема относится к прямоугольным треугольникам; на рис. 25 длины сторон такого треугольника обозначены соответственно а, b , х.Теорема Пифагора утверждает, что эти величины связаны между собой простой формулой х^2= а^2+b^2. Если положить для удобства а = 3, b = 4, то х= 5, поскольку 52 = З2 + 42.
Треугольник, изображенный на рис. 25, является, очевидно, двумерным объектом, однако теорему Пифагора можно без труда обобщить на случай трех измерений. На рис. 26 изображен прямоугольный ящик (параллелепипед) со сторонами а, b, с.Теорема Пифагора в этом случае относится к длине хдиагонали, проведенной между противоположными вершинами ящика. Соответствующая формула имеет вид х^2 = а^2+b^2+с^2, очень сходный с двумерным случаем; однако теперь для вычисления длины диагонали нам необходимо знать длины трех взаимно перпендикулярных сторон.
В четырехмерном пространстве для нахождения длины диагонали пришлось бы использовать длины четырех взаимно перпендикулярных сторон, а, Ь, с и а. В этом случае формула имела бы вид x^2 = а^2 + b^2 + с^2 + d^2. Таким образом, хотя нам и не удается вообразить четырехмерный ящик, мы в состоянии детально проанализировать его геометрические свойства. ,
Однако при всей важности подобных геометрических рассмотрении такие построения остаются не более чем карточным домиком. И этот домик рухнул с наступлением в конце прошлого века эры современной математики, ознаменовавшейся развитием могущественного раздела математики —теории множеств. Одно из сильнейших потрясений, испытанных математиками, было связано с открытием Георга Кантора. Оно заключалось в том, что линия насчитывает столько же точек, сколько и поверхность. Интуитивное представление, что на поверхности в бесконечное число раз больше точек, чем в проведенной на ней линии, было полностью опровергнуто. Это утверждение было встречено скептически весьма уважаемыми математиками. Некоторые отвергали открытие Кантора, объявив его безумным. Шарль Эрмит писал: “Чтение писаний Кантора напоминает настоящую пытку... Отображение линии на поверхности совершенно неубедительно... подобный произвол... Автору следовало бы подождать с этим...” — и далее в том же духе.
Лишь на рубеже нынешнего столетия справедливость восторжествовала и удалось дать удовлетворительное определение размерности. Благодаря важным работам Л. Е. Дж. Брауэра, Рене Лебега и других была в конце концов найдена надежная процедура сравнения двух пространств с целью сопоставления их размерностей. Соответствующие методы и доказательства основаны на тонких абстрактных понятиях теории множеств, весьма далеких от наших интуитивных представлений. Лишь подобная тщательность и внимание к деталям позволили закрепить формальные основы нашей науки и нашего повседневного опыта.
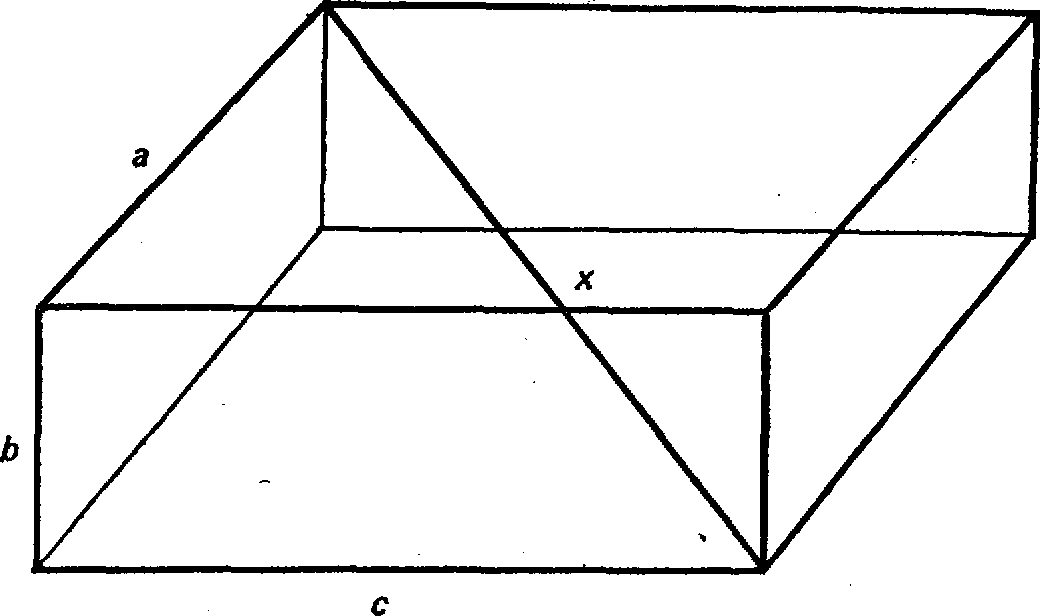
Рис. 26. Длину диагонали прямоугольного параллелепипеда можно выразить через длины его ребер а, Ь и с, просто обобщив теорему Пифагора. Нетрудно перенести это обобщение и на случай четырех или большего числа измерений пространства.
В 1917 г. физик Пауль Эренфест написал статью под названием “Каким образом в фундаментальных законах физики отражается тот факт, что пространство трехмерно?”. Эренфест обратил внимание на факт существования устойчивых орбит —типа тех, по каким планеты движутся вокруг Солнца или электроны вокруг атомного ядра. В физике широко распространен закон “обратных квадратов”, описывающий характер изменения различных сил с расстоянием. В гл. 5 мы узнали, что этому закону следуют гравитационные, электрические и магнитные силы. Еще в 1747 г. Иммануил Кант осознал глубокую связь между этим законом и трехмерностью пространства. Уравнения, описывающие гравитационное или электрическое поле точечного источника, можно легко обобщить на случай пространства с другим числом измерений и найти их решения для этого случая. Из этих решений видно, что в пространстве с n измерениями мы приходим к закону обратной степени n —1. В частности, в трехмерном пространстве n —1=2 и справедлив закон “обратных квадратов”; в четырехмерном пространстве n —1=3 (закон “обратных кубов”) и т.д. Нетрудно показать, что если бы гравитационное поле Солнца действовало на планеты, например, по закону “обратных кубов”, то планеты, двигаясь по спиральным траекториям, довольно быстро упали бы на Солнце и оно поглотило бы их.
Аналогичная картина наблюдается и в мире атомов. Оказывается, что, даже если принять во внимание квантовые эффекты, у электронов не будет устойчивых орбит в пространстве с числом измерений больше трех. А без устойчивых атомных орбит не было бы химических процессов, а следовательно, и жизни.
От размерности пространства существенно зависит еще одно явление — распространение волн. Нетрудно показать, что в пространствах с четным числом измерений не могут распространяться “чистые” волны. За волной обязательно возникают возмущения, которые вызывают реверберацию. Именно поэтому четко сформированные сигналы нельзя передавать по двумерной поверхности (например, по резиновому покрытию). Анализируя этот вопрос, математик Г. Дж. Уитроу в 1955 г. пришел к выводу, что высшие формы жизни были бы невозможны в пространствах чётной размерности, поскольку живым организмам для согласованных действий необходимы эффективная передача и 'обработка информации.
Эти исследования отнюдь не доказывают невозможность другого числа измерений пространства; они лишь говорят о том, что в мире с числом измерений, отличным от трех, физика была бы совершенно другой и, возможно, такой мир был бы значительно менее упорядочен по сравнению с тем, который мы реально воспринимаем.
Как совместить все это с теорией Калуцы, в которой вселенная имеет четыре пространственных измерения? Одна возможность состоит в том, чтобы рассматривать дополнительное, невидимое измерение исключительно как формальный математический прием, не имеющий физического смысла. Однако более привлекательная идея была высказана вскоре после публикации Калуцей первоначального варианта теории.
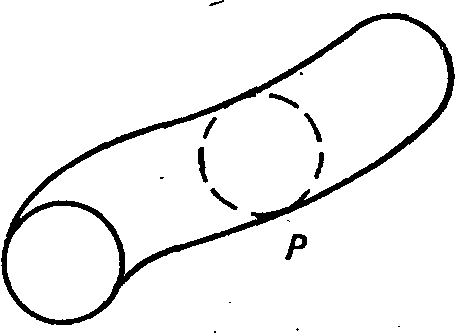
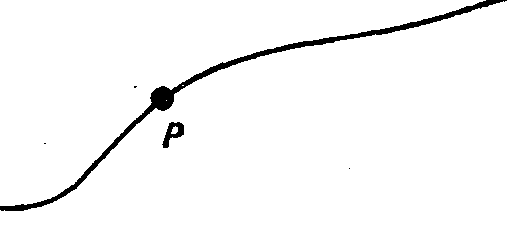
Рис. 27. С большого расстояния трубка кажется волнистой линией. При ближайшем рассмотрении точка Р на этой линии оказывается окружностью поверхности трубки. Возможно, что объект, обычно воспринимаемый нами как точка в трехмерном пространстве, в действительности представляет собой крошечную окружность в других измерениях пространства. Эта идея лежит в основе теории Ка-луцы—Клейна, объединяющей электромагнитное и гравитационное взаимодействия.
Клейн вычислил периметр петель вокруг пятого измерения, используя известное значение элементарного электрического заряда электрона и других частиц, а также величину гравитационного взаимодействия между частицами. Он оказался равным 10^-32 см, т.е. в 10^20 раз меньше размера атомного ядра. Поэтому неудивительно, что мы не замечаем пятого измерения: оно скручено в масштабах, которые значительно меньше размеров любой из известных нам структур, даже в физике субъядерных частиц. Очевидно, в таком случае не возникает вопроса о движении, скажем, атома в пятом измерении. Скорее это измерение следует представлять себе как нечто находящееся внутри атома.
Несмотря на ее неординарность теория Калуцы — Клейна на протяжении более полувека оставалась по существу не более чем математическим курьезом. С открытием в 30-е годы нашего столетия слабых и сильных взаимодействий идеи объединения гравитации и электромагнетизма в значительной мере потеряли свою привлекательность. Последовательная единая теория поля должна была включить в себя уже не две, а четыре силы. Очевидно, это нельзя было сделать, не достигнув глубокого понимания слабых и сильных взаимодействий. В конце 70-х годов благодаря свежему ветру, принесенному теориями Великого объединения (ТВО) и супергравитацией, вспомнили старую теорию Калуцы — Клейна. С нее стряхнули нафталин, сдули пыль, приодели по моде и включили в нее все известные на сегодня взаимодействия.
В ТВО теоретикам удалось собрать в рамках одной концепции три очень различных вида взаимодействий; как мы узнали из предыдущих глав, это обусловлено тем, что все три взаимодействия могут быть описаны с помощью калибровочных полей. Основное свойство калибровочных полей состоит в существовании абстрактных симметрий, благодаря которым этот подход обретает элегантность и открывает широкие возможности. Наличие симметрий силовых полей достаточно определенно указывает на проявление некоторой скрытой геометрии. В возвращенной к жизни теории Калуцы — Клейна симметрии калибровочных полей приобретают конкретность — это геометрические симметрии, связанные с до-волнительными измерениями пространства.
Как и в первоначальном варианте, взаимодействия вводятся в теории путем присоединения к пространству-времени дополни-тельных пространственных измерений. Однако, поскольку теперь надо дать пристанище взаимодействиям- трех типов, приходится вводить несколько дополнительных измерений. Простой подсчет количества операций симметрии, входящих в ТВО, приводит к теории с семью дополнительными пространственными измерениями (так что их общее число достигает десяти); если же учесть время, то всего пространство-время насчитывает одиннадцатьизмерений. Таким образом, современный вариант теории Ка-луцы — Клейна постулирует одиннадцатимерную вселенную.
Теория Эйнштейна ознаменовала столь важный прогресс в понимании природы, что уже вскоре стал неизбежным пересмотр взглядов и на другие силы природы. В это время единственной “другой” силой, существование которой было твердо установлено, являлось электромагнитное взаимодействие. Однако внешне оно совершенно не походило на гравитацию. Более того, за несколько десятков лет до создания теории гравитации Эйнштейна электромагнетизм успешно описала теория Максвелла, и не было никаких оснований сомневаться в справедливости этой теории.
На протяжении всей жизни Эйнштейн мечтал о создании единой теории поля, в'которой все силы природы сливались бы воедино на основе чистой геометрии. Поискам такой схемы Эйнштейн посвятил большую часть своей жизни после создания общей теории относительности. Однако по иронии судьбы ближе всех к реализации мечты Эйнштейна подошел малоизвестный польский физик Теодор Калуца, который еще в 1921 г. заложил основы нового и неожиданного подхода к объединению физики, до сих пор поражающего воображение своей дерзостью.
Калуца был вдохновлен способностью геометрии описать гравитацию; он задался целью обобщить теорию Эйнштейна, включив электромагнетизм в геометрическую формулировку теории поля. Это следовало сделать не нарушая “священных” уравнений теории электромагнетизма Максвелла. То, что удалось сделать Калуце, — классический пример проявления творческого воображения и физической интуиции. Калуца понимал, что теорию Максвелла невозможно сформулировать на языке чистой геометрии (в том смысле, как мы ее обычно понимаем), даже допуская наличие искривленного пространства. Он нашел удивительно простое решение, обобщив геометрию так, чтобы она “вместила в себя” теорию Максвелла. Чтобы выйти из затруднения, Калуца нашел весьма необычный, но вместе с тем неожиданно убедительный способ. Калуца показал, что электромагнетизм является своего рода “гравитацией”, но не обычной, а “гравитацией” в ненаблюдаемых измерениях пространства.
Физики долю привыкали к тому, чтобы пользоваться временем как четвертым измерением. Теория относительности установила, что пространство и время сами по себе не являются универсальными физическими понятиями, так как они неизбежно сливаются в единую четырехмерную структуру, называемую “пространство-время”. Калуца фактически сделал следующий шаг: он постулировал, что существует еще дополнительное пространственное измерение и общее число измерений пространства равно четырем, а всего пространство-время насчитывает пять измерений. Если принять это допущение, то, как показал Калуца, произойдет своего рода математическое чудо. Гравитационное поле в таком пятимерном мире проявляет себя в виде обычного гравитационного поля плюс электромагнитное поле Максвелла — если наблюдать этот мир из пространства-времени, ограниченного четырьмя измерениями. Своей смелой гипотезой Калуца по существу утверждал, что если мы расширим свое представление о мире до пяти измерений, то в нем будет существовать лишь единственное силовое поле — гравитация. То, что мы называем электромагнетизмом, — всего лишь часть гравитационного поля, которая действует в пятом дополнительном измерении пространства, которое мы не в состоянии наглядно представить.
Теория Калуцы не только позволила соединить гравитацию и электромагнетизм в единой схеме, но и дала основанное на геометрии описание обоих силовых полей. Так, электромагнитная волна (например, радиоволна) в этой теории не что иное, как пульсации пятого измерения. Особенности движения электрически заряженных частиц в электрических и магнитных полях прекрасно объясняются, если предположить, что частицы пребывают в дополнительном пятом измерении. Если принять эту точку зрения, то вообще нет никаких сил — существует только геометрия искривленного пятимерного пространства, а частицы свободно “кочуют” по наделенной структурой пустоте.
Математически гравитационное поле Эйнштейна в пространстве пяти измерений в точности и полностью эквивалентно обычной гравитации плюс электромагнетизм в пространстве четырех измерений; разумеется, это нечто большее, чем просто случайное совпадение. Однако в таком случае теория Калуцы остается загадочной в том отношении, что столь важное четвертое измерение пространства вообще не воспринимается нами. Пространство, доступное нашему непосредственному восприятию, с полной очевидностью и неизменностью остается трехмерным. Если четвертое измерение пространства существует, то где же оно? Прежде чем ответить на этот вопрос, следует также выяснить, что мы в действительности понимаем под размерностью пространства.
Что такое размерность?
В научной фантастике уже давно обыгрываются преимущества, связанные с дополнительными измерениями пространства. Авторы часто обращаются к ним, чтобы перемещать своих персонажей из одного места Вселенной в другое, избегая утомительных путешествий со скоростью света или около того — в общем черепашьим шагом — по обычному трехмерному пространству. Так, в книге Артура Кларка “Космическая Одиссея: 2001" экспедиция на Сатурн завершается рискованным проникновением в дополнительное измерение на одном из спутников Сатурна.Однако интерес к проблеме размерности пространства возник задолго до появления фантастики. Древние греки остро чувствовали ее значение для развития науки геометрии. Непосредственно столкнуться с проблемой размерности их заставил любопытный случай, связанный со свойствами правильных многоугольников (замкнутых плоских фигур со сторонами равной длины, например квадратов, правильных пяти-, восьмиугольников и т. п.). Количество различных правильных многоугольников безгранично — могут существовать правильные многоугольники с любым числом сторон. Однако существует всего лишь пять типов различных правильных многогранников (замкнутых объемных фигур, грани которых образованы правильными многоугольниками). Грекам было свойственно наделять геометрию глубоким мистическим смыслом, а Птолемей даже написал исследование на тему о размерности, в котором утверждалось, что в природе вообще не может существовать более трех пространственных измерений.
В дальнейшем математики, в частности Риман, систематически изучали свойства многомерных пространств с чисто математических позиций. При этом основная проблема заключалась в формулировке последовательного определения размерности. Это было совершенно необходимо для доказательства строгих теорем относительно пространств с различным числом измерений.
Интуитивно все геометрические структуры мы подразделяем на одно-, двух- и трехмерные в соответствии с их протяженностью. Так, не имеющей протяженности точке соответствует нулевая размерность. Линия является одномерной, поверхность — двумерной, объем — трехмерным. Вряд ли нам удастся лучше сформулировать эти определения, чем это сделал сам Евклид почти за 300 лет до н. э.
Точка — это то, что не имеет частей. Линия — длина, лишенная ширины.
Плоскость — это то, что имеет только длину и ширину. Объем — это то, что имеет длину, ширину и глубину.
Далее Евклид уточнял, что границами линии служат точки, границами поверхности — линии, а границей объемного тела — поверхность. Возникла мысль определить размерность по иерархической схеме, начиная с нулевой размерности точки, а затем шаг за шагом увеличивая ее на единицу. Тогда одномерным будет объект, у которого началом и концом служат точки, т.е. линия. Двигаясь далее, мы по индукции придем к определению четырехмерной структуры как ограниченной трехмерным объемом. Число измерений, которые можно логически ввести таким способом, не ограниченно, однако сама процедура не содержит каких" либо указаний на реальную физическую ситуацию.
Более наглядное и ясное представление о трехмерности можно получить с помощью другой схемы, основанной на указании местоположения точек в пространстве. Представьте себе, что вам необходимо встретиться с приятелем в заранее обусловленном месте. В этом случае можно указать географическую широту и долготу выбранного места; пусть это будет, например, Эмпайрстейт билдинг. Но в этом случае остается еще одна неопределенная величина — высота. На каком этаже должна состояться встреча? Итак, в общей сложности необходимо указать три независимых числа для того, чтобы однозначно определить положение точки в пространстве. По этой причине такое пространство называют трехмерным.

Рис. 23. Двумерная вселенная. Плоское существо, живущее во Флатландии, не имеет представления о “верхе” и “низе”. Шар, пронизывающий плоский мир, воспринимается этим существом как двумерный объект, меняющий свою форму.
Теория относительности обнаружила, что пространство переплетено со временем, поэтому в действительности следует говорить не об одном только пространстве, а о пространстве-времени. В какой день.вы собираетесь встретиться с приятелем в здании Эмпайр-стейт-билдннг? Указание времени события требует задать единственное число (“дату”), так что время одномерно. Объединяя пространство и время, мы приходим к четырехмерному пространству-времени.
Когда мы пытаемся наглядно представить дополнительные измерения, например, четвертое пространственное измерение (в этом случае полное пространство-время насчитывает пять измерений), нашей интуиции оказывается недостаточно. Для облегчения задачи можно обратиться к аналогии. Вообразим двумерное “блинообразное” создание, которое обречено существовать только на поверхности; у него отсутствуют представления о “верхе” и о “низе”. На рис. 23 изображена такая плоская вселенная. Мы можем догадываться, что эта поверхность в действительности “вложена” в трехмерное пространство, однако обитатель плоского мира не в состоянии понять эту более широкую точку зрения. Он воспринимает только события, происходящие на самой поверхности.
Возникает вопрос: а что будет наблюдать это создание, когда поверхность пересекается трехмерным объектом? Поверхность рассечет этот объект, причем размеры и форма сечения будут в общем случае изменяться по мере прохождения объекта. Так, сечение сферы в первый момент будет выглядеть как точка, которая, постепенно “расплываясь”, превратится в круг все увеличивающегося радиуса; достигнув максимального радиуса, круг начнет уменьшаться в размерах, напоследок снова превратившись в точку. Более сложные объекты будут создавать при прохождении следы более сложного сечения.
Рассуждая далее, по аналогии можно предположить, что четыре измерения пространства-времени “вложены” во вселенную, имеющую пять или даже большее число измерений. Геометрию такой вселенной трудно вообразить, однако с помощью математики можно построить законченное логическое описание ее. Математики уже давно обобщили законы геометрии на случай пространства с произвольным числом измерений (включая бесконечно большое). Поэтому смысл многомерных пространств вполне можно понять, хотя непосредственному восприятию доступно лишь триизмерения.
Какие особенности присущи четырехмерному пространству? Один из аспектов размерности касается числа взаимно перпендикулярных направлений, которые существуют в данном пространстве. Например, пространство этой страницы двумерно. Если положить ее на стол, то в любом из углов края страницы образуют две прямые линии, перпендикулярные друг к другу. Из того же угла невозможно провести третью прямую, лежащую в плоскости страницы и перпендикулярную обоим ее краям. Однако направление такой прямой удастся найти, если выйти из плоскости страницы и начертить вертикальную линию. Таким образом, в трехмерном пространстве в отличие от двумерной поверхности страницы существует три взаимно перпендикулярных направления.
В четырехмерном пространстве удалось бы найти четыре взаимно перпендикулярных направления. На рис. 24 изображен случай трех измерений: три взаимно перпендикулярные прямые исчерпывают максимально возможное число таких прямых. Как бы мы ни старались, мы никогда не найдем в обычном пространстве прямую, перпендикулярную всем трем. Любая прямая, перпендикулярная трем названным, должна идти в направлении, не принадлежащем нашему пространству. И хотя мы не в состоянии представить какпроходит подобная прямая, очевидно, что формальноона могла бы существовать. Ее можно описать, а именно вычислить и систематизировать ее геометрические параметры.

Рис. 24. Вершины прямоугольного параллелепипеда образованы тремя взаимно перпендикулярными прямыми линиями. В трехмерном пространстве из вершины нельзя провести ни одной прямой, которая была бы перпендикулярна всем трем ребрам.

Рис. 25. Знаменитая теорема Пифагора, связывающая между собой длины сторон прямоугольного треугольника, а, b, х, без труда обобщается на случай больших размерностей.
Простым примером сказанного может служить знаменитая геометрическая теорема древнегреческого геометра Пифагора, которая знакома любому школьнику. Эта теорема относится к прямоугольным треугольникам; на рис. 25 длины сторон такого треугольника обозначены соответственно а, b , х.Теорема Пифагора утверждает, что эти величины связаны между собой простой формулой х^2= а^2+b^2. Если положить для удобства а = 3, b = 4, то х= 5, поскольку 52 = З2 + 42.
Треугольник, изображенный на рис. 25, является, очевидно, двумерным объектом, однако теорему Пифагора можно без труда обобщить на случай трех измерений. На рис. 26 изображен прямоугольный ящик (параллелепипед) со сторонами а, b, с.Теорема Пифагора в этом случае относится к длине хдиагонали, проведенной между противоположными вершинами ящика. Соответствующая формула имеет вид х^2 = а^2+b^2+с^2, очень сходный с двумерным случаем; однако теперь для вычисления длины диагонали нам необходимо знать длины трех взаимно перпендикулярных сторон.
В четырехмерном пространстве для нахождения длины диагонали пришлось бы использовать длины четырех взаимно перпендикулярных сторон, а, Ь, с и а. В этом случае формула имела бы вид x^2 = а^2 + b^2 + с^2 + d^2. Таким образом, хотя нам и не удается вообразить четырехмерный ящик, мы в состоянии детально проанализировать его геометрические свойства. ,
Однако при всей важности подобных геометрических рассмотрении такие построения остаются не более чем карточным домиком. И этот домик рухнул с наступлением в конце прошлого века эры современной математики, ознаменовавшейся развитием могущественного раздела математики —теории множеств. Одно из сильнейших потрясений, испытанных математиками, было связано с открытием Георга Кантора. Оно заключалось в том, что линия насчитывает столько же точек, сколько и поверхность. Интуитивное представление, что на поверхности в бесконечное число раз больше точек, чем в проведенной на ней линии, было полностью опровергнуто. Это утверждение было встречено скептически весьма уважаемыми математиками. Некоторые отвергали открытие Кантора, объявив его безумным. Шарль Эрмит писал: “Чтение писаний Кантора напоминает настоящую пытку... Отображение линии на поверхности совершенно неубедительно... подобный произвол... Автору следовало бы подождать с этим...” — и далее в том же духе.
Лишь на рубеже нынешнего столетия справедливость восторжествовала и удалось дать удовлетворительное определение размерности. Благодаря важным работам Л. Е. Дж. Брауэра, Рене Лебега и других была в конце концов найдена надежная процедура сравнения двух пространств с целью сопоставления их размерностей. Соответствующие методы и доказательства основаны на тонких абстрактных понятиях теории множеств, весьма далеких от наших интуитивных представлений. Лишь подобная тщательность и внимание к деталям позволили закрепить формальные основы нашей науки и нашего повседневного опыта.

Рис. 26. Длину диагонали прямоугольного параллелепипеда можно выразить через длины его ребер а, Ь и с, просто обобщив теорему Пифагора. Нетрудно перенести это обобщение и на случай четырех или большего числа измерений пространства.
Почему три?
Какова бы ни была действительная размерность пространства, несомненно, что нашему восприятию непосредственно доступны лишь три измерения. Многие ученые задавались вопросом, можно ли объяснить, почему природа “выбрала” именно число три и является ли это число в определенном смысле выделенным.В 1917 г. физик Пауль Эренфест написал статью под названием “Каким образом в фундаментальных законах физики отражается тот факт, что пространство трехмерно?”. Эренфест обратил внимание на факт существования устойчивых орбит —типа тех, по каким планеты движутся вокруг Солнца или электроны вокруг атомного ядра. В физике широко распространен закон “обратных квадратов”, описывающий характер изменения различных сил с расстоянием. В гл. 5 мы узнали, что этому закону следуют гравитационные, электрические и магнитные силы. Еще в 1747 г. Иммануил Кант осознал глубокую связь между этим законом и трехмерностью пространства. Уравнения, описывающие гравитационное или электрическое поле точечного источника, можно легко обобщить на случай пространства с другим числом измерений и найти их решения для этого случая. Из этих решений видно, что в пространстве с n измерениями мы приходим к закону обратной степени n —1. В частности, в трехмерном пространстве n —1=2 и справедлив закон “обратных квадратов”; в четырехмерном пространстве n —1=3 (закон “обратных кубов”) и т.д. Нетрудно показать, что если бы гравитационное поле Солнца действовало на планеты, например, по закону “обратных кубов”, то планеты, двигаясь по спиральным траекториям, довольно быстро упали бы на Солнце и оно поглотило бы их.
Аналогичная картина наблюдается и в мире атомов. Оказывается, что, даже если принять во внимание квантовые эффекты, у электронов не будет устойчивых орбит в пространстве с числом измерений больше трех. А без устойчивых атомных орбит не было бы химических процессов, а следовательно, и жизни.
От размерности пространства существенно зависит еще одно явление — распространение волн. Нетрудно показать, что в пространствах с четным числом измерений не могут распространяться “чистые” волны. За волной обязательно возникают возмущения, которые вызывают реверберацию. Именно поэтому четко сформированные сигналы нельзя передавать по двумерной поверхности (например, по резиновому покрытию). Анализируя этот вопрос, математик Г. Дж. Уитроу в 1955 г. пришел к выводу, что высшие формы жизни были бы невозможны в пространствах чётной размерности, поскольку живым организмам для согласованных действий необходимы эффективная передача и 'обработка информации.
Эти исследования отнюдь не доказывают невозможность другого числа измерений пространства; они лишь говорят о том, что в мире с числом измерений, отличным от трех, физика была бы совершенно другой и, возможно, такой мир был бы значительно менее упорядочен по сравнению с тем, который мы реально воспринимаем.
Как совместить все это с теорией Калуцы, в которой вселенная имеет четыре пространственных измерения? Одна возможность состоит в том, чтобы рассматривать дополнительное, невидимое измерение исключительно как формальный математический прием, не имеющий физического смысла. Однако более привлекательная идея была высказана вскоре после публикации Калуцей первоначального варианта теории.
Теория Калуцы — Клейна
В 1926 г. шведский физик Оскар Клейн предложил блестящий по простоте ответ на вопрос о том, куда же исчезло пятое измерение Калуцы. Клейн предположил, что мы не замечаем дополнительного измерения потому, что оно в некотором смысле “свернулось” до очень малых размеров. Поясним это на примере шланга для полива. Издали он выглядит просто как извилистая линия. При близком рассмотрении то, что мы принимали за точку на линии, оказывается окружностью (рис. 27). Клейн предположил, что Вселенная устроена'аналогичным образом. То, что мы обычно Считаем точкой в трехмерном пространстве, в действительности является крохотной окружностью в четвертом пространственном измерении. Из каждой точки пространства в направлении ни вверх, ни вниз, ни вбок, ни куда-либо еще в воспринимаемом нами пространстве выходит небольшая “петелька”. Мы не замечаем всех этих “петель” вследствие крайней малости их размеров. Чтобы свыкнуться с идеей Клейна, требуется время. Вопервых, мы не можем представить себе, где же свертываются эти петли? Ведь они находятся не а пространстве, а расширяют его, Подобно тому, как кривая, многократно описывая петлю за петлей, вырисовывает трубку. Мы без труда представляем себе это в двух измерениях, но не в четырех. Однако предположение Клейна все-таки сохраняет смысл. При этом не возникает проблемы ни с устойчивостью орбит, ни с распространенней волн. Дело в том, что ни вещество, ни поля (в виде волн) не могут неограниченно перемещаться в дополнительном измерении. Наличие пятого измерения допустимо, однако ничто не может ускользнуть из него сколь-нибудь далеко. Тем самым теория Калуцы — Клейна, увы, не оставляет никаких надежд фантастам использовать ее для сокращения пути в пространстве.

Рис. 27. С большого расстояния трубка кажется волнистой линией. При ближайшем рассмотрении точка Р на этой линии оказывается окружностью поверхности трубки. Возможно, что объект, обычно воспринимаемый нами как точка в трехмерном пространстве, в действительности представляет собой крошечную окружность в других измерениях пространства. Эта идея лежит в основе теории Ка-луцы—Клейна, объединяющей электромагнитное и гравитационное взаимодействия.
Клейн вычислил периметр петель вокруг пятого измерения, используя известное значение элементарного электрического заряда электрона и других частиц, а также величину гравитационного взаимодействия между частицами. Он оказался равным 10^-32 см, т.е. в 10^20 раз меньше размера атомного ядра. Поэтому неудивительно, что мы не замечаем пятого измерения: оно скручено в масштабах, которые значительно меньше размеров любой из известных нам структур, даже в физике субъядерных частиц. Очевидно, в таком случае не возникает вопроса о движении, скажем, атома в пятом измерении. Скорее это измерение следует представлять себе как нечто находящееся внутри атома.
Несмотря на ее неординарность теория Калуцы — Клейна на протяжении более полувека оставалась по существу не более чем математическим курьезом. С открытием в 30-е годы нашего столетия слабых и сильных взаимодействий идеи объединения гравитации и электромагнетизма в значительной мере потеряли свою привлекательность. Последовательная единая теория поля должна была включить в себя уже не две, а четыре силы. Очевидно, это нельзя было сделать, не достигнув глубокого понимания слабых и сильных взаимодействий. В конце 70-х годов благодаря свежему ветру, принесенному теориями Великого объединения (ТВО) и супергравитацией, вспомнили старую теорию Калуцы — Клейна. С нее стряхнули нафталин, сдули пыль, приодели по моде и включили в нее все известные на сегодня взаимодействия.
В ТВО теоретикам удалось собрать в рамках одной концепции три очень различных вида взаимодействий; как мы узнали из предыдущих глав, это обусловлено тем, что все три взаимодействия могут быть описаны с помощью калибровочных полей. Основное свойство калибровочных полей состоит в существовании абстрактных симметрий, благодаря которым этот подход обретает элегантность и открывает широкие возможности. Наличие симметрий силовых полей достаточно определенно указывает на проявление некоторой скрытой геометрии. В возвращенной к жизни теории Калуцы — Клейна симметрии калибровочных полей приобретают конкретность — это геометрические симметрии, связанные с до-волнительными измерениями пространства.
Как и в первоначальном варианте, взаимодействия вводятся в теории путем присоединения к пространству-времени дополни-тельных пространственных измерений. Однако, поскольку теперь надо дать пристанище взаимодействиям- трех типов, приходится вводить несколько дополнительных измерений. Простой подсчет количества операций симметрии, входящих в ТВО, приводит к теории с семью дополнительными пространственными измерениями (так что их общее число достигает десяти); если же учесть время, то всего пространство-время насчитывает одиннадцатьизмерений. Таким образом, современный вариант теории Ка-луцы — Клейна постулирует одиннадцатимерную вселенную.
