Страница:
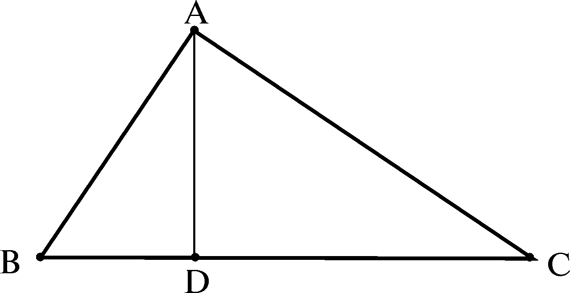
АВ2 = BC'BD и АС2 = ВС'DC
Сложив эти уравнения, получаем:АВ2 + АС2 = BC(BD + DC); АВ2 + АС2 = ВС2
Пифагор создал учение о четных и нечетных числах. Он дал определения этим видам чисел и исследовал их свойства. Историки математики считают, что приведенные ниже утверждения из 9-й книги «Начал» Евклида восходят к Пифагору и переданы практически в неизмененном виде.21. Если складывается сколько угодно четных чисел, то целое будет четным.
22. Если складывается сколько угодно нечетных чисел, количество же их будет четным, то целое будет четным.
23. Если складывается сколько угодно нечетных чисел, количество же их будет нечетным, то и целое будет нечетным.
24. Если от четного числа отнимается четное, то остаток будет четным.
25. Если от четного числа отнимается нечетное, то остаток будет нечетным.
26. Если от нечетного числа отнимается нечетное, то остаток будет четным.
27. Если от нечетного числа отнимается четное, то остаток будет нечетным.
28. Если нечетное число, умножая четное, производит что-то, то возникающее будет четным.
29. Если нечетное число, умножая нечетное число, производит что-то, то возникающее будет нечетным.
30. Если нечетное число измеряет (является делителем) четное число, то оно будет измерять и его половину.
31. Если нечетное число по отношению к некоторому числу будет первым, то оно будет первым и по отношению к его удвоенному.
32. Из чисел, получаемых удвоением от двойки, каждое будет только четно-четным (см. ниже).
33. Если число имеет нечетную половину, то оно будет только четно-нечетным.
34. Если число не будет из получаемых удвоением от двойки и не имеет нечетную половину, то оно будет и четно-четным и четно-нечетным.
Терминология, используемая Евклидом, изложена в начале 7-й книги. Часть из используемых определений, по всей видимости, тоже восходит к Пифагору.
6. Четное число есть делящееся пополам.
7. Нечетное же – не делящееся пополам или отличающееся на единицу от четного числа.
8. Четно-четное число – есть четным числом, измеряемое четным числом (раз).
9. Четно же нечетное есть четным числом, измеряемое нечетное число (раз).
10. Нечетно-четное число есть нечетным числом, измеряемое четное число (раз).
11. Нечетно-нечетное число есть нечетным числом, измеряемое нечетное число (раз).
О том, что именно Пифагор занимался изучением свойств четных и нечетных чисел, свидетельствуют Аристотель и Аристоксен. Едва ли можно предположить, что эти ученые приписывали Пифагору «честь» открытия вполне очевидных истин. Здесь, как и в случае с теоремой Пифагора, заслугой, безусловно, является доказательства приведенных утверждений. Следовательно, ученый впервые применил дедуктивный подход к арифметике.
Единственное незначительное отличие, содержащееся в книге Евклида, состоит в способе доказательства приведенных утверждений. Евклид в данном фрагменте представляет числа в виде отрезков, а Пифагор и его последователи пользовались счетными камешками (псефами). В остальном доказательства, приводимые Евклидом, скорее всего, сходны с доказательствами Пифагора. Интересно, что в восходящем к Пифагору фрагменте «Начал» для некоторых положений даже применяется такой метод, как доказательство от противного. Открытие этого метода также вполне можно приписать Пифагору.
Исследования свойств четных и нечетных чисел стали первыми исследованиями в области теории чисел. Таким образом, нашего героя с полным правом можно назвать основателем этого раздела математики.
Во времена Пифагора и, скорее всего, им самим, также была разработана теория фигурных чисел. Эта теория стала результатом попыток найти взаимосвязь между числами и геометрическими фигурами. Здесь следует несколько подробнее рассмотреть методы счета, используемые пифагорейцами. Для вычислений, как мы уже говорили, они использовали счетные камешки. Их выкладывали на песке, а позже – на счетной доске (абаке) в виде геометрических фигур. Кстати, некоторые источники приписывают изобретение абака Пифагору. Интересно, что при таком взгляде на числа невозможно было представить ноль. Даже единицу считали не числом, а «числовым атомом», а другие числа считали множеством единиц, что и нашло свое отображение в пифагорейской философии.
Рассматривая фигуры, которые образовывали выложенные на песке псефы, Пифагор обнаружил несколько типов фигурных чисел.
Квадратные числа – сумма ряда нечетных чисел, начиная с единицы: 1 + 3 + 5+… + (2n – 1) = n2.
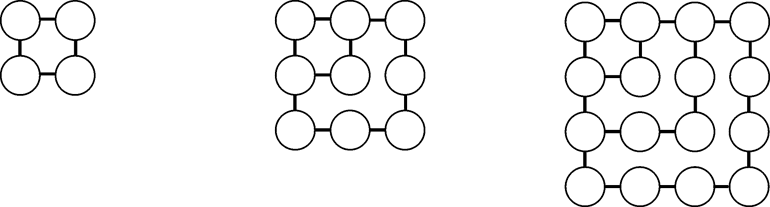
Треугольные числа:
Такой способ вычисления вполне мог стать толчком для открытия некоторых математических закономерностей. Возможно, именно так, еще в допифагорейский период, было установлено, что площадь прямоугольника равна произведению его сторон. С помощью псефов можно легко вывести и продемонстрировать справедливость многих арифметических правил, например ab = bа
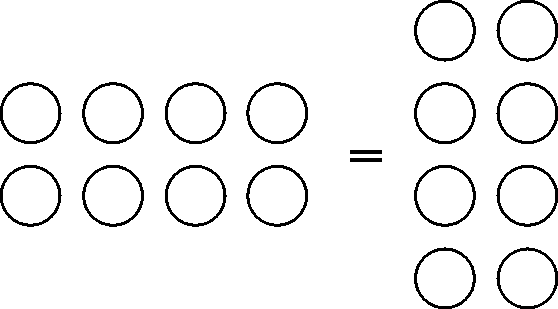
(а + b)с = ас + bc
К сожалению, теория фигурных чисел не вошла в «Начала» Евклида, хотя в определениях к 7-й книге «Начал» есть описания «плоскостных», «телесных», «квадратных» и «кубических» чисел. Более подробно теория фигурных чисел описана у Никомаха – философа II века нашей эры, но этот источник не содержит доказательств. Тем не менее, было бы странно предположить, что, исследуя свойства четных и нечетных чисел, Пифагор доказывал вполне очевидные вещи и при этом оставил недоказанными гораздо более сложные положения теории фигурных чисел. Так же как для теоремы Пифагора, ученые реконструируют возможные способы доказательств этих положений.
Считается, что с помощью теории фигурных чисел Пифагор вывел метод нахождения неограниченного количества так называемых «пифагоровых троек» – целочисленных длин сторон прямоугольного треугольника. Числа, составляющие пифагоровы тройки, должны укладываться в равенство а2 + b2 = с2. Как видим, эта формула соответствует теореме Пифагора. Пифагор открыл, что числа эти должны иметь следующий вид:
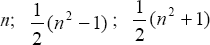
Есть сведения о том, что, изучая делимость чисел, Пифагор открыл дружественные и совершенные числа. Дружественные числа – пары чисел, каждое из которых равно сумме делителей другого. Например: 220 и 284. Совершенные числа равны сумме собственных делителей: 6 (1 + 2 + 3 = 6), 28 (1 + 2 + 4 + 7 + 14 = 28). Об открытии Пифагором дружественных чисел пишет Ямвлих. А описание способа нахождения совершенных чисел есть и у Никомаха, и в «Началах» Евклида. В последнем источнике описание этого способа и доказательство его справедливости расположены в непосредственной близости от описания свойств четных и нечетных чисел (36-я глава 9-й книги). Таким образом, можно предположить, что они тоже восходят к Пифагору.
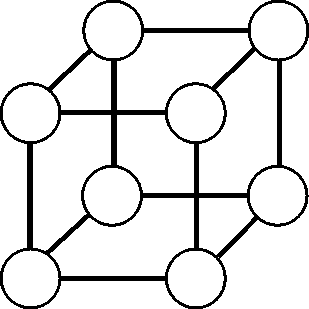
Как мы уже писали выше, ему приписывают и построение «космических тел» – правильных многогранников – тетраэдра, куба, додекаэдра, октаэдра и икосаэдра. То, что Пифагор не мог открыть все пять правильных многоугольников, достоверно известно. Два последних открыл Теэтет – ученый IV века до нашей эры. Некоторые источники утверждают, что додекаэдр построил Гиппас – математик-пифагореец V века до нашей эры. Таким образом, Пифагору может принадлежать только честь построения двух первых многогранников – тетраэдра и куба.
Также есть сведения о том, что Пифагор открыл и доказал иррациональность
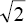. Но эта информация вызывает серьезные сомнения. Многие источники свидетельствуют о том, что иррациональные величины открыл Гиппас.Роль Пифагора в становлении и развитии математики, естественно, заключается не только в тех открытиях, которые он сам совершил. Гиппас и другие математики – члены пифагорейских общин – продолжили дело своего учителя. Пользуясь дедуктивным методом, разработанным Фалесом и Пифагором, они заложили прочный фундамент теоретической математики. К сожалению, сведений о том, какие именно открытия принадлежат тому или иному ученому, практически нет. Только о Гиппасе известно, что он открыл способ построения додекаэдра, вписанного в шар, открыл иррациональные величины, работал над теорией пропорций и продолжил изыскания Пифагора в области математической теории музыки.
В целом же о масштабах достижений пифагорейских математиков можно судить только косвенно по развитию математики за тот период времени, когда ею занимались практически только пифагорейцы. Считается, что представителями школы Пифагора к середине V века до нашей эры были найдены все математические положения, изложенные в 2-й и 4-й книгах «Начал» Евклида. 2-я книга содержит основы геометрической алгебры, а 4-я посвящена правильным многоугольникам. К ним же восходит основная масса материала, изложенного в 1-й и 3-й книгах. 1-я книга содержит 23 определения геометрических понятий. Вот несколько примеров этих определений: точка – то, что не имеет частей; линия – длина без ширины; прямая – линия, одинаково расположенная относительно всех своих точек; параллельные прямые – прямые, которые лежат в одной плоскости и не встречаются, сколь угодно продолженные. Дальше содержатся аксиомы и постулаты, рассматриваются свойства основных фигур планиметрии: треугольника, прямоугольника, параллелограмма[16], приводится теорема о сумме углов треугольника и теорема Пифагора. 3-я книга описывает свойства круга, его касательных и хорд. К этому же времени был в том или ином виде создан тот кусок 9-й книги «Начал», о котором мы писали выше, и часть 13-й книги, описывающая построения тетраэдра, куба и додекаэдра. Также есть основания предполагать, что пифагорейцам принадлежит авторство 7-й книги «Начал», представляющей собой введение в арифметику.
Кроме математики пифагорейцы занимались и астрономическими исследованиями. К сожалению, установить авторство тех или иных астрономических открытий и теорий того времени еще сложнее, чем математических. Поэтому мы ограничимся только перечислением тех достижений астрономии, которые предположительно восходят к Пифагору и его ближайшим последователям. Так, Пифагору приписывается авторство идеи о шарообразности Земли. Возможно, именно он установил, что Фосфор и Геспер, звезды, которые наблюдали утром и вечером, на самом деле являются Венерой, а также осуществил разделение Земли на зоны: арктическую, летнюю, экваториальную, зимнюю и антарктическую. В такой зональности отражено более раннее разделение на пояса небесной сферы. Так, Арктика получила свое название от созвездия Большой Медведицы.[17] Разделение на пояса небесной сферы тоже приписывается Пифагору. Считается, что он ввел и само слово «космос».
Пифагор и его ученики проводили астрономические наблюдения. Им приписывается отделение планет от звезд и обнаружение попятного движения планет[18]. Пифагорейцы, скорее всего, открыли все пять планет, видимые невооруженным глазом: Меркурий, Венеру, Марс, Юпитер и Сатурн. Они же установили и порядок расположения планет: Луна, Солнце, Венера, Меркурий, Марс, Юпитер, Сатурн (Луна и Солнце ставились в один ряд с планетами). Этот порядок был выведен из скорости движения небесных тел и их яркости. При этом ошибка в определении относительного положения Венеры и Меркурия связана именно с выводами, сделанными из яркости этих небесных тел. Пифагорейцы знали о том, что Луна светит отраженным светом. Скорее всего, они также пришли к выводу о круговом движении планет и высказали идею геоцентризма.
Пифагорейцы считали, что движение небесных тел подчиняется законам так называемой гармонии небесных сфер. Вот краткое описание пифагорейской модели мира, вернее, того варианта этой модели, который дошел до нас. Земля имеет форму шара. Она находится в центре космоса. Вокруг Земли с запада на восток вращаются Солнце, Луна, Венера, Меркурий, Марс, Юпитер и Сатурн. Каждое тело вращается по своей сфере. С востока на запад вращается сфера неподвижных звезд. Каждая сфера движется равномерно и при этом издает свой звук. Расстояние между сферами, скорость их движения и звуки, которые они издают, соответствуют музыкальным гармоническим интервалам. Почему человек не слышит звуки, издаваемые вращающимися сферами, объяснялось по-разному. Например, одним из вариантов объяснения был такой: человек с рождения находится в среде, где звук небесной музыки присутствует, привыкает к нему и уже не замечает, подобно кузнецам, которые со временем перестают замечать грохот молотов.
Авторы этой системы, скорее всего, вполне сознательно не учли факты, не укладывающиеся в нее. Так, уже упомянутое попятное движение планет не может быть объяснено в рамках такой модели. Пифагорейцы просто пренебрегали уже известными им неудобными данными в угоду своим теоретическим выкладкам. Очевидно, что, ища и находя строгие математические закономерности в музыке, пифагорейцы придали им некую универсальность. Они старались перенести эти закономерности и на свою модель мира, не пытаясь искать собственные законы для описания движения небесных тел. Тем не менее, существование этой модели сыграло важную роль в развитии астрономии через две с лишним тысячи лет. Пытаясь найти математические закономерности в скоростях движения планет и расстоянии до них, Иоганн Кеплер открыл законы движения планет. Естественно, что при этом он уже не задумывался о звуках, которые якобы издают небесные тела при движении. Но книгу, в которой Кеплер в 1619 году опубликовал свои законы, он совсем не случайно назвал «Гармонией мира».
Объединив воедино арифметику, геометрию, музыку и астрономию, Пифагор и его последователи заложили свод наук, впоследствии превратившийся в средневековый квадривиум – повышенный цикл семи свободных искусств.
Последняя область научной деятельности пифагорейцев, которой мы уделим внимание, – медицина. Достоверных данных, касающихся теории и практики медицины ранних пифагорейцев, не много. Но абсолютно очевидно, что они занимались врачеванием. Биографы пишут, что сам Пифагор лечил своих учеников. Конечно, можно было бы сомневаться в этих свидетельствах, как в утверждениях об исцеляющей силе святых, но о врачебной практике Пифагора пишут не только Диоген, Порфирий и Ямвлих, но и авторы, непосредственно занимавшиеся медициной. К сожалению, эти свидетельства очень отрывочны. Известно, что Пифагор пытался применять для лечения музыку. Знаменитый врач и ученый II века нашей эры Гален писал, что Пифагор является автором теории критических дней, согласно которой в каждой болезни периодически наступают дни кризиса. Правда, и здесь Пифагор пытался подогнать действительные данные под свои философские умозаключения. Он говорил, что критические дни чаще всего бывают нечетными.
С гораздо большей уверенностью можно сказать, что Пифагор серьезно интересовался вопросом профилактики болезней. Он проповедовал здоровый образ жизни, большое внимание уделял правильному распорядку дня, чередованию видов деятельности, физическим упражнениям, правильному питанию, заложил основы диетологии. Эти методы применялись при подготовке кротонских атлетов, которые во времена расцвета пифагореизма считались фаворитами спортивных состязаний.
На основе пифагорейского учения в конце V – начале IV века до нашей эры возникла кротонская школа медицины. К этой школе относились самые знаменитые врачи того времени, и большинство из них были пифагорейцами. Занятия медициной врачи Кротона совмещали с изучением наук, неразрывно связанных с медициной: анатомией, физиологией, ботаникой.
В заключение хочется добавить еще несколько общих слов. Мы не знаем, насколько велики научные достижения Пифагора. Трудно сказать, какие именно принадлежат ему, какие его ученикам, а к каким они не имеют отношения. Но с уверенностью можно утверждать, что имя Пифагора неразрывно связано со становлением античной науки и сыграло в нем значительную роль.
Аристотель
«Какой бы области человеческих знаний он ни касался, он производит впечатление специалиста, занимающегося только ею».
Сент-Илер[19] об Аристотеле
Введение
Жила-была восьминогая муха. И долго жила. Больше 1000 лет. Нет, не то чтобы жила, и не то чтобы была, но все же… Аристотель якобы написал в одном из трактатов, что у мухи 8 ног. И на протяжении тысячи лет никто не сомневался в восьминогости этого, мягко говоря, довольно распространенного животного. И только по прошествии многих веков кто-то удосужился посчитать количество лапок у самого известного «источника заразы». Возможно, что и раньше кто-то другой посчитать не поленился, но, обнаружив несоответствие с мнением авторитета, просто побоялся поделиться с современниками своим «открытием»…Принято считать, что этот общеизвестный анекдот хорошо иллюстрирует роль Аристотеля в средневековой науке. Действительно, можно сказать, что на протяжении многих веков авторитет этого ученого был непререкаем. Конечно, восьминогая муха – это плохо, конечно, плохо, что никто не пересчитал, но возникают закономерные вопросы: как один человек смог добиться такого отношения к себе, что у многих поколений потомков не вызывали сомнения даже такие абсурдные его свидетельства? Почему этот язычник в средневековой христианской Европе стал непререкаемым авторитетом в большинстве областей человеческих знаний? Какие заслуги привели к тому, что мнение Аристотеля могло соперничать с простейшей, если можно так выразиться, зооарифметикой? Мы попробуем ответить на эти вопросы, показать масштаб влияния Аристотеля на становление научного мировоззрения и познакомить читателя с этим в высшей степени интересным человеком.
Биография
Происхождение
Аристотель родился в 1-й год 99-й Олимпиады (384 год до нашей эры), предположительно в июле-сентябре. Местом его рождения стал город Стагир (Стагира, Стагиры), поэтому Аристотеля иногда называют Стагирским или Стагиритом. Этот город находился на полуострове Халкидики на юге Македонии (по другой информации – во Фракии). Стагир был основан выходцами с острова Андрос. На Андросе родился и отец Аристотеля Никомах.Никомах был врачом. И врачом не простым. Согласно легенде, переданной Диогеном Лаэртием, отец Аристотеля был потомком Никомаха, сына Махаона и внука самого Асклепия. Махаон упоминается в «Илиаде». В поэме Гомера Махаон лечит раненного стрелой Менелая: извлекает стрелу, выжимает кровь и прикладывает к ране лекарство, секрет которого унаследовал от отца (Асклепия), а тот – от мудрого кентавра Хирона. Асклепий же, основатель рода, был сыном Аполлона и почитался как бог врачевания. Так же, согласно «Илиаде», когда сам Махаон был ранен, Нестор (царь Пилоса) увез его из гущи сражения на колеснице и лично позаботился о нем, поскольку: «Опытный врач драгоценнее многих других человеков».
О матери Аристотеля известно только то, что ее звали Фестида, и что ее род происходил с острова Эвбеи. Таким образом, несмотря на то что родиной Аристотеля была Македония, по происхождению он был греком. У Аристотеля также была старшая сестра Аримнеста и младший брат Аримнест.
Биографы сообщают, что Аристотель не отличался привлекательной наружностью. Он был чрезмерно худощав, имел тонкие ноги, маленькие глаза и к тому же шепелявил. Но при этом следил за своей внешностью: любил богато одеваться, носил дорогие перстни и уделял большое внимание прическе.
Отец Аристотеля был придворным медиком и, возможно, другом македонского царя Амниты II. Есть предположение, что прежде, чем занять должность царского врачевателя, Никомах практиковал как странствующий врач, а сын странствовал вместе с ним. При дворе Аристотель стал товарищем по играм и другом царского сына Филиппа, будущего царя Македонии.
Конечно же, Никомах хотел передать сыну тайны искусства врачевания. Но судьба распорядилась иначе. Когда Аристотелю было около 15 лет, Никомах умер. Аристотель и его младший брат были взяты под опеку Проксеном, мужем их сестры Аримнесты. Проксен жил в Стагире и был образованным человеком. По некоторым сведениям, он лично знал Платона. Возможно, не только Никомах, но и Проксен привил своему воспитаннику интерес к изучению природы. Опекун позаботился и о том, чтобы Аристотель получил лучшее по тем временам образование. Этому способствовало и немалое состояние, которое Аристотель получил в наследство от отца. Когда юноше было 18 лет (367/366 год до нашей эры), он отправился в Афины в Академию Платона. Нам, безусловно, следует уделить внимание и учебному заведению, в котором Аристотель провел следующие 20 лет своей жизни, и его основателю.
Платон и академия
Платон основал академию примерно в 387 году до нашей эры. Собственно слово «академия» восходит к школе Платона. После смерти своего учителя Сократа[20] Платон много странствовал. В частности, особое внимание он уделял греческим колониям в Южной Италии, где сохранились пифагорейские общины или, по крайней мере, еще жили отдельные философы-пифагорейцы. Основной целью философа, по-видимому, было знакомство с пифагорейцами и их учением. С этой же целью Платон, скорее всего, и посетил Сицилию, хотя Диоген Лаэртий полагает, что целью путешествия было «посмотреть остров и на вулканы». В Сиракузах Платон познакомился и подружился с Дионом, зятем тирана[21] Дионисия I. Следует сказать, что за время своих странствий Платон, ученик знаменитого Сократа, стал популярен как философ. Дион считал себя последователем его идей.К слову сказать, именно с Дионисием Старшим связана легенда о Дамокловом мече. Дамокл, фаворит тирана, считал, что Дионисий счастливейший из смертных, так как он облечен неограниченной властью. Тогда тиран на один день предложил престол Дамоклу. А на пышном пиру, состоявшемся в этот день, Дамокл увидел над собой обнаженный меч, подвешенный на конском волосе. Этим Дионисий хотел продемонстрировать эфемерность благополучия тирана.
Тиран Дионисий заставил философа жить при его дворе. По некоторым сведениям, Платон, используя знакомство с Дионом, сам пытался сойтись с тираном для того, чтобы оказать на него благотворное влияние и попытаться с его помощью реализовать на практике свои идеи об идеальном государственном строе. Философ открыто высказывался против тиранической власти Дионисия, в личных беседах смело называл своего нежеланного покровителя тираном и критиковал его поступки. Придворные, особенно молодежь, восхищались речами Платона, и его влияние при дворе быстро росло. Разгневанный Дионисий не проявил мудрости, продемонстрированной в отношениях с Дамоклом. Он решил казнить Платона, и только вмешательство Диона спасло философу жизнь. Тем не менее, в наказание Платон был продан в рабство спартанцу Поллиду. По другим версиям, Дион, понимая, что Платон играет с огнем, решил отправить его из Сиракуз и посадил на корабль к спартанскому послу Поллиду. Спартанец же получил от Дионисия тайный приказ убить Платона, как только корабль выйдет в море. Поллид не решился убить знаменитого философа, но, опасаясь гнева сиракузского тирана, решил продать его в рабство.