Страница:
Единственный ответ, который можно дать на эти вопросы, основан на принципе естественного отбора Дарвина. В любой популяции самовоспроизводящихся организмов неизбежны вариации в генетическом веществе и воспитании различных особей. Эти различия подразумевают, что некоторые индивидуумы способны вернее других судить об окружающем мире и действовать в соответствии со своими суждениями. Подобные индивидуумы с большей вероятностью выживут и дадут потомство, а стало быть, их поведение и образ мышления станет доминировать. Не подлежит сомнению, что в прошлом то, что мы называем интеллектом и научным мышлением, давало преимущества в борьбе за выживание. Не совсем ясно, однако, дают ли они подобное преимущество сегодня. Наши научные открытия способны уничтожить всех нас, и, даже если этого не произойдет, полная объединенная теория не увеличит наших шансов на выживание. Однако, если Вселенная развивалась по определенным законам, мы могли бы ожидать, что способность к мышлению, которой наделил нас естественный отбор, поможет нам также в поисках полной объединенной теории и не приведет нас в конечном счете к ложным заключениям.
Частные теории, которыми мы уже располагаем, достаточны для того, чтобы делать точные предсказания во всех ситуациях, за исключением самых экстремальных. Поэтому поиск окончательной теории Вселенной, похоже, трудно оправдать соображениями практической пользы. (Стоит отметить тем не менее, что подобный аргумент мог использоваться и против теории относительности и квантовой механики, а они дали нам ядерную энергию и микроэлектронную революцию!) Открытие полной объединенной теории может и не помочь выживанию человеческого рода. Оно может даже не отразиться на нашем образе жизни. Но с самого зарождения цивилизации люди отказывались считать явления лишенными взаимосвязей и необъяснимыми. Они жаждали постичь лежащий в основе всего миропорядок. Сегодня мы все еще стремимся узнать, откуда и каким образом появились мы в этом мире. Фундаментальная тяга человечества к знанию — достаточное основание для продолжения поисков. И мы не удовольствуемся меньшим, чем полное постижение Вселенной, в которой мы живем.
Глава четвертая
Глава пятая
Частные теории, которыми мы уже располагаем, достаточны для того, чтобы делать точные предсказания во всех ситуациях, за исключением самых экстремальных. Поэтому поиск окончательной теории Вселенной, похоже, трудно оправдать соображениями практической пользы. (Стоит отметить тем не менее, что подобный аргумент мог использоваться и против теории относительности и квантовой механики, а они дали нам ядерную энергию и микроэлектронную революцию!) Открытие полной объединенной теории может и не помочь выживанию человеческого рода. Оно может даже не отразиться на нашем образе жизни. Но с самого зарождения цивилизации люди отказывались считать явления лишенными взаимосвязей и необъяснимыми. Они жаждали постичь лежащий в основе всего миропорядок. Сегодня мы все еще стремимся узнать, откуда и каким образом появились мы в этом мире. Фундаментальная тяга человечества к знанию — достаточное основание для продолжения поисков. И мы не удовольствуемся меньшим, чем полное постижение Вселенной, в которой мы живем.
Глава четвертая
ВСЕЛЕННАЯ НЬЮТОНА
Наши нынешние представления о движении тел восходят к Галилею и Ньютону. До них люди верили Аристотелю, утверждавшему, что естественное состояние тела — покой, а движется оно только под влиянием силы или импульса. Отсюда следовало, что тяжелое тело должно падать быстрее легкого, потому что оно сильнее притягивается к Земле.
Аристотелевская традиция провозглашала также, что все законы, управляющие Вселенной, можно вывести путем чистого умозрения, без экспериментальной проверки. Поэтому до Галилея никто не дал себе труда удостовериться, действительно ли тела различной массы падают с разной скоростью.
Говорят, что Галилей демонстрировал ложность утверждения Аристотеля, бросая предметы с накренившейся башни в итальянском городе Пиза. Эта история, скорее всего, выдумана, но Галилей все же делал нечто подобное: он скатывал шары разной массы по гладкой наклонной плоскости. Это аналогично вертикальному падению тел, но благодаря меньшим скоростям в подобном эксперименте легче выполнять наблюдения.
Измерения Галилея показали, что скорость движения тел возрастала одинаково независимо от их массы. Например, если вы пустите шар по наклонной плоскости, которая понижается на один метр каждые десять метров, то независимо от массы через секунду он будет двигаться со скоростью примерно один метр в секунду, через две секунды — два метра в секунду и так далее.
Конечно, тело из свинца падает быстрее перышка, но только потому, что падение пера замедляется сопротивлением воздуха. Два тела, не испытывающих существенного воздушного сопротивления, например два свинцовых груза разной массы, будут падать с одним и тем же ускорением. (Мы скоро узнаем почему.) На Луне, где нет воздуха, замедляющего падение, астронавт Дэвид Р. Скотт провел эксперимент, бросая перышко и кусок свинца, и убедился, что они одновременно упали на грунт.
Ньютон положил измерения Галилея в основание своих законов движения. В экспериментах Галилея тело скатывалось с наклонной плоскости под действием постоянной силы, придававшей ему постоянное ускорение. Этим демонстрировалось, что реальный эффект от действия силы — изменение скорости тела, а не приведение его в движение, как считалось ранее. Также отсюда следовало, что, пока тело не подвергается действию какой-либо силы, оно перемещается по прямой линии с постоянной скоростью. Данная идея, впервые отчетливо высказанная в «Началах» (1687), известна как первый закон Ньютона[6].
Поведение тела под действием силы описывается вторым законом Ньютона. Он утверждает, что тело будет ускоряться, то есть изменять свою скорость в темпе, пропорциональном величине приложенной силы. (Например, ускорение увеличится вдвое, если вдвое возрастет сила.) Кроме того, ускорение тела тем меньше, чем больше его масса, то есть количество вещества. (Одна и та же сила, действующая на тело вдвое большей массы, дает половинное ускорение.) Всем, кто имел дело с автомобилями, известно: чем мощнее двигатель, тем больше ускорение, а при одной и той же мощности двигателя более тяжелая машина ускоряется медленнее.
В дополнение к законам движения, описывающим реакцию тел на действие сил, ньютоновская теория тяготения описывает, как определить величину одного конкретного вида сил — гравитации. Как уже было сказано, согласно этой теории любые два тела притягиваются друг к другу с силой, пропорциональной их массам. То есть сила притяжения между двумя телами возрастает вдвое, если удвоить массу одного из тел, например тела А (рис. 4). Это вполне естественно, поскольку можно рассматривать новое тело А как два тела, каждое из которых обладает первоначальной массой и притягивает тело В с первоначальной силой. Таким образом, полная сила взаимного притяжения тел А и В будет вдвое больше первоначальной. А если бы масса одного из тел возросла в шесть раз, или масса одного вдвое, а другого — втрое, то сила притяжения между ними выросла бы в шесть раз.
Теперь можно понять, почему все тела падают с одинаковым ускорением. Согласно закону всемирного тяготения то из двух тел, чья масса вдвое больше, вдвое сильнее притягивается Землей. Но в соответствии со вторым законом Ньютона из-за вдвое большей массы его ускорение окажется вдвое меньше на единицу силы. Таким образом, эти два эффекта компенсируют друг друга, и ускорение свободного падения не зависит от массы тела.
Закон тяготения Ньютона также гласит, что чем дальше друг от друга находятся тела, тем слабее их притяжение. По Ньютону, тяготение далекой звезды будет ровно вчетверо слабее притяжения такой же звезды, находящейся вдвое ближе. Этот закон позволяет с высочайшей точностью предсказывать траектории движения Земли, Луны и планет. Если бы гравитационное притяжение звезды уменьшалось с расстоянием быстрее или медленнее, орбиты планет не были бы эллиптическими, а имели бы форму спирали, сходящейся к Солнцу или расходящейся от него.
Важнейшее различие между учением Аристотеля и идеями Галилея и Ньютона состоит в том, что Аристотель считал покой естественным состоянием любого тела, к которому оно стремится, если не испытывает действия некоей силы или импульса. В частности, Аристотель полагал, что Земля пребывает в состоянии покоя. Но из законов Ньютона следует, что нет никакого уникального стандарта покоя.
Можно сказать, что тело А находится в состоянии покоя, а тело В перемещается относительно него с постоянной скоростью, или что тело В пребывает в покое, а тело А перемещается, и оба утверждения будут одинаково верны.
Например, если забыть на мгновение, что Земля вращается вокруг своей оси и обращается вокруг Солнца, то в равной мере можно говорить, что Земля находится в состоянии покоя, а поезд движется по ней на север со скоростью девяносто миль в час или что поезд находится в состоянии покоя, а Земля движется на юг со скоростью девяносто миль в час.
Если провести в поезде эксперименты с движущимися телами, все законы Ньютона подтвердятся. Например, играя в пинг-понг в вагоне поезда, убеждаешься, что шарик повинуется законам Ньютона точно так же, как и шарик на столе у дороги. Так что невозможно узнать, что именно движется — поезд или Земля.
Как проверить, кто прав — Ньютон или Аристотель? Вот один из возможных экспериментов. Вообразите, что вы находитесь внутри закрытого контейнера и не знаете, стоит ли он на полу вагона в движущемся поезде или на твердой поверхности Земли, стандарте покоя согласно Аристотелю. Можно ли определить, где вы? Если можно, Аристотель, вероятно, был прав: состояние покоя на Земле является особым. Однако это невозможно. Эксперименты, выполненные внутри контейнера в движущемся поезде, будут протекать точно так же, как и те, что проделаны внутри контейнера на «неподвижном» перроне (мы считаем, что поезд не испытывает толчков, не поворачивает и не тормозит). Играя в пинг-понг в вагоне поезда, можно обнаружить, что шарик ведет себя точно так же, как и шарик на столе у дороги. И если, находясь внутри контейнера, вы играете в пинг-понг, при разных скоростях поезда относительно Земли — 0,50 или 90 миль в час — шарик всегда будет вести себя одинаково. Так устроен мир, что и отражено в уравнениях законов Ньютона: не существует способа узнать, что движется — поезд или Земля. Понятие движения имеет смысл, только если оно задано относительно других объектов.
Действительно ли существенно, кто прав — Аристотель или Ньютон? Идет ли речь о различии взглядов, философских систем, или это проблема, важная для науки? Отсутствие абсолютного стандарта покоя имеет в физике далеко идущие последствия: из него вытекает, что нельзя определить, случились ли два события, которые имели место в разное время, в одном и том же месте.
Чтобы уяснить это, давайте предположим, что некто в поезде вертикально бросает теннисный шарик на стол. Шарик отскакивает вверх и через секунду снова ударяет в то же место на поверхности стола. Для человека, бросившего шарик, расстояние между точками первого и второго касания будет равно нулю. Но для того, кто стоит снаружи вагона, два касания будут разделены приблизительно сорока метрами, потому что именно столько пройдет поезд между двумя отскоками шарика (рис. 5). Согласно Ньютону оба человека имеют равное право считать, что находятся в состоянии покоя, так что обе точки зрения одинаково приемлемы. Ни один из них не имеет преимущества перед другим, в противоположность тому, что считал Аристотель. Места, где наблюдаются события, и расстояния между ними различны для человека в поезде и человека на платформе, и нет никаких причин предпочесть одно наблюдение другому.
Ньютона очень беспокоило отсутствие абсолютных положений, или абсолютного пространства, как принято было говорить, поскольку это не согласовывалось с его идеей абсолютного Бога. Фактически он отказался принять отсутствие абсолютного пространства, несмотря на то что его законы подразумевали это. За эту иррациональную веру его критиковали многие, особенно епископ Беркли, философ, полагавший, что все материальные тела, пространство и время — иллюзия. Когда знаменитого доктора Джонсона ознакомили с мнением Беркли, он вскричал: «Я опровергаю это так!» — и ударил ногой по большому камню.
И Аристотель, и Ньютон верили в абсолютное время. То есть полагали, что можно однозначно измерить интервал времени между двумя событиями и полученное значение будет одним и тем же, кто бы его ни измерял, если использовать точные часы. В отличие от абсолютного пространства, абсолютное время согласовывалось с законами Ньютона. И большинство людей считает, что это соответствует здравому смыслу.
Тем не менее в двадцатом столетии физики были вынуждены пересмотреть представления о времени и пространстве. Как мы убедимся в дальнейшем, ученые обнаружили, что интервал времени между двумя событиями, подобно расстоянию между отскоками теннисного шарика, зависит от наблюдателя. Физики также открыли, что время не является совершенно независимым от пространства.
Ключом к прозрению стало новое понимание свойств света. Свойства эти, казалось бы, противоречат нашему опыту, но наш здравый смысл, исправно служащий нам, когда мы имеем дело с яблоками или планетами, которые движутся сравнительно медленно, перестает работать в мире околосветовых скоростей.
Аристотелевская традиция провозглашала также, что все законы, управляющие Вселенной, можно вывести путем чистого умозрения, без экспериментальной проверки. Поэтому до Галилея никто не дал себе труда удостовериться, действительно ли тела различной массы падают с разной скоростью.
Говорят, что Галилей демонстрировал ложность утверждения Аристотеля, бросая предметы с накренившейся башни в итальянском городе Пиза. Эта история, скорее всего, выдумана, но Галилей все же делал нечто подобное: он скатывал шары разной массы по гладкой наклонной плоскости. Это аналогично вертикальному падению тел, но благодаря меньшим скоростям в подобном эксперименте легче выполнять наблюдения.
Измерения Галилея показали, что скорость движения тел возрастала одинаково независимо от их массы. Например, если вы пустите шар по наклонной плоскости, которая понижается на один метр каждые десять метров, то независимо от массы через секунду он будет двигаться со скоростью примерно один метр в секунду, через две секунды — два метра в секунду и так далее.
Конечно, тело из свинца падает быстрее перышка, но только потому, что падение пера замедляется сопротивлением воздуха. Два тела, не испытывающих существенного воздушного сопротивления, например два свинцовых груза разной массы, будут падать с одним и тем же ускорением. (Мы скоро узнаем почему.) На Луне, где нет воздуха, замедляющего падение, астронавт Дэвид Р. Скотт провел эксперимент, бросая перышко и кусок свинца, и убедился, что они одновременно упали на грунт.
Ньютон положил измерения Галилея в основание своих законов движения. В экспериментах Галилея тело скатывалось с наклонной плоскости под действием постоянной силы, придававшей ему постоянное ускорение. Этим демонстрировалось, что реальный эффект от действия силы — изменение скорости тела, а не приведение его в движение, как считалось ранее. Также отсюда следовало, что, пока тело не подвергается действию какой-либо силы, оно перемещается по прямой линии с постоянной скоростью. Данная идея, впервые отчетливо высказанная в «Началах» (1687), известна как первый закон Ньютона[6].
Поведение тела под действием силы описывается вторым законом Ньютона. Он утверждает, что тело будет ускоряться, то есть изменять свою скорость в темпе, пропорциональном величине приложенной силы. (Например, ускорение увеличится вдвое, если вдвое возрастет сила.) Кроме того, ускорение тела тем меньше, чем больше его масса, то есть количество вещества. (Одна и та же сила, действующая на тело вдвое большей массы, дает половинное ускорение.) Всем, кто имел дело с автомобилями, известно: чем мощнее двигатель, тем больше ускорение, а при одной и той же мощности двигателя более тяжелая машина ускоряется медленнее.
В дополнение к законам движения, описывающим реакцию тел на действие сил, ньютоновская теория тяготения описывает, как определить величину одного конкретного вида сил — гравитации. Как уже было сказано, согласно этой теории любые два тела притягиваются друг к другу с силой, пропорциональной их массам. То есть сила притяжения между двумя телами возрастает вдвое, если удвоить массу одного из тел, например тела А (рис. 4). Это вполне естественно, поскольку можно рассматривать новое тело А как два тела, каждое из которых обладает первоначальной массой и притягивает тело В с первоначальной силой. Таким образом, полная сила взаимного притяжения тел А и В будет вдвое больше первоначальной. А если бы масса одного из тел возросла в шесть раз, или масса одного вдвое, а другого — втрое, то сила притяжения между ними выросла бы в шесть раз.
Теперь можно понять, почему все тела падают с одинаковым ускорением. Согласно закону всемирного тяготения то из двух тел, чья масса вдвое больше, вдвое сильнее притягивается Землей. Но в соответствии со вторым законом Ньютона из-за вдвое большей массы его ускорение окажется вдвое меньше на единицу силы. Таким образом, эти два эффекта компенсируют друг друга, и ускорение свободного падения не зависит от массы тела.
Закон тяготения Ньютона также гласит, что чем дальше друг от друга находятся тела, тем слабее их притяжение. По Ньютону, тяготение далекой звезды будет ровно вчетверо слабее притяжения такой же звезды, находящейся вдвое ближе. Этот закон позволяет с высочайшей точностью предсказывать траектории движения Земли, Луны и планет. Если бы гравитационное притяжение звезды уменьшалось с расстоянием быстрее или медленнее, орбиты планет не были бы эллиптическими, а имели бы форму спирали, сходящейся к Солнцу или расходящейся от него.
Рис. 4. Гравитационное притяжение составных тел.
Если масса одного из тел возрастает в два раза, удваивается и сила притяжения между телами.Можно сказать, что тело А находится в состоянии покоя, а тело В перемещается относительно него с постоянной скоростью, или что тело В пребывает в покое, а тело А перемещается, и оба утверждения будут одинаково верны.
Например, если забыть на мгновение, что Земля вращается вокруг своей оси и обращается вокруг Солнца, то в равной мере можно говорить, что Земля находится в состоянии покоя, а поезд движется по ней на север со скоростью девяносто миль в час или что поезд находится в состоянии покоя, а Земля движется на юг со скоростью девяносто миль в час.
Если провести в поезде эксперименты с движущимися телами, все законы Ньютона подтвердятся. Например, играя в пинг-понг в вагоне поезда, убеждаешься, что шарик повинуется законам Ньютона точно так же, как и шарик на столе у дороги. Так что невозможно узнать, что именно движется — поезд или Земля.
Как проверить, кто прав — Ньютон или Аристотель? Вот один из возможных экспериментов. Вообразите, что вы находитесь внутри закрытого контейнера и не знаете, стоит ли он на полу вагона в движущемся поезде или на твердой поверхности Земли, стандарте покоя согласно Аристотелю. Можно ли определить, где вы? Если можно, Аристотель, вероятно, был прав: состояние покоя на Земле является особым. Однако это невозможно. Эксперименты, выполненные внутри контейнера в движущемся поезде, будут протекать точно так же, как и те, что проделаны внутри контейнера на «неподвижном» перроне (мы считаем, что поезд не испытывает толчков, не поворачивает и не тормозит). Играя в пинг-понг в вагоне поезда, можно обнаружить, что шарик ведет себя точно так же, как и шарик на столе у дороги. И если, находясь внутри контейнера, вы играете в пинг-понг, при разных скоростях поезда относительно Земли — 0,50 или 90 миль в час — шарик всегда будет вести себя одинаково. Так устроен мир, что и отражено в уравнениях законов Ньютона: не существует способа узнать, что движется — поезд или Земля. Понятие движения имеет смысл, только если оно задано относительно других объектов.
Действительно ли существенно, кто прав — Аристотель или Ньютон? Идет ли речь о различии взглядов, философских систем, или это проблема, важная для науки? Отсутствие абсолютного стандарта покоя имеет в физике далеко идущие последствия: из него вытекает, что нельзя определить, случились ли два события, которые имели место в разное время, в одном и том же месте.
Чтобы уяснить это, давайте предположим, что некто в поезде вертикально бросает теннисный шарик на стол. Шарик отскакивает вверх и через секунду снова ударяет в то же место на поверхности стола. Для человека, бросившего шарик, расстояние между точками первого и второго касания будет равно нулю. Но для того, кто стоит снаружи вагона, два касания будут разделены приблизительно сорока метрами, потому что именно столько пройдет поезд между двумя отскоками шарика (рис. 5). Согласно Ньютону оба человека имеют равное право считать, что находятся в состоянии покоя, так что обе точки зрения одинаково приемлемы. Ни один из них не имеет преимущества перед другим, в противоположность тому, что считал Аристотель. Места, где наблюдаются события, и расстояния между ними различны для человека в поезде и человека на платформе, и нет никаких причин предпочесть одно наблюдение другому.
Рис. 5. Относительность расстояния.
Расстояние, которое преодолевает тело, — и его путь — могут по-разному оцениваться разными наблюдателями.И Аристотель, и Ньютон верили в абсолютное время. То есть полагали, что можно однозначно измерить интервал времени между двумя событиями и полученное значение будет одним и тем же, кто бы его ни измерял, если использовать точные часы. В отличие от абсолютного пространства, абсолютное время согласовывалось с законами Ньютона. И большинство людей считает, что это соответствует здравому смыслу.
Тем не менее в двадцатом столетии физики были вынуждены пересмотреть представления о времени и пространстве. Как мы убедимся в дальнейшем, ученые обнаружили, что интервал времени между двумя событиями, подобно расстоянию между отскоками теннисного шарика, зависит от наблюдателя. Физики также открыли, что время не является совершенно независимым от пространства.
Ключом к прозрению стало новое понимание свойств света. Свойства эти, казалось бы, противоречат нашему опыту, но наш здравый смысл, исправно служащий нам, когда мы имеем дело с яблоками или планетами, которые движутся сравнительно медленно, перестает работать в мире околосветовых скоростей.
Глава пятая
ОТНОСИТЕЛЬНОСТЬ
Тот факт, что свет распространяется с конечной, хотя и очень высокой, скоростью, был обнаружен в 1676 г . датским астрономом Оле Христиансеном Рёмером. Наблюдая за спутниками Юпитера, можно заметить, что время от времени они исчезают из виду, проходя позади гигантской планеты. Такие затмения в системе спутников Юпитера должны происходить с одинаковыми интервалами, однако Рёмер установил, что промежутки между ними различны. Может быть, скорость движения спутников по орбите то уменьшается, то увеличивается? Рёмер нашел другое объяснение.
Если бы свет распространялся с бесконечной скоростью, то на Земле эти затмения наблюдались бы через равные интервалы времени, в те самые моменты, когда они происходят, — подобно тиканью космических часов. Приближение Юпитера к Земле или его удаление не имело бы никакого значения, так как свет любое расстояние преодолевал бы моментально.
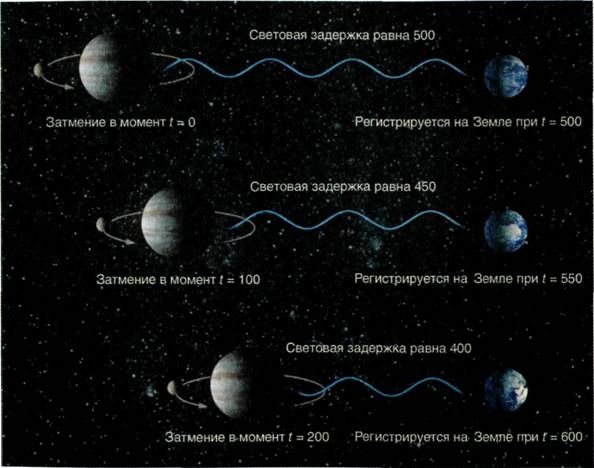
Теперь представим, что свет распространяется с конечной скоростью. Тогда затмения должны наблюдаться спустя некоторое время после их наступления. Эта задержка зависит от скорости света и от расстояния до Юпитера. Если бы расстояние между Юпитером и Землей оставалось неизменным, то и затмения отмечались бы всегда через равные интервалы. Однако, когда расстояние между Землей и Юпитером сокращается, «сигнал» о каждом следующем затмении преодолевает все меньшее и меньшее расстояние и достигает нашей планеты со все большим «опережением графика». По той же причине, когда Юпитер удаляется от Земли, мы видим, что затмения все больше запаздывают (рис. 6). Величина опережения и запаздывания зависит от скорости света, что позволяет ее измерить.
Именно это и сделал Рёмер. Он заметил, что во время сближения Земли и Юпитера затмения наступают раньше, а во время их удаления друг от друга — позже, и использовал эту разницу для вычисления скорости света. Однако его оценки изменения расстояния от Земли до Юпитера были не очень точными, из-за чего он получил величину скорости света 225 тысяч километров в секунду, отличную от современной — 300 тысяч километров в секунду. И все же достижение Рёмера достойно восхищения. Ведь он не только установил, что скорость света конечна, и вычислил ее величину, но и сделал это за одиннадцать лет до публикации «Начал» Ньютона.
Удовлетворительной теории распространения света не существовало до 1865 г ., когда английский физик Максвелл сумел объединить до того обособленные описания электрических и магнитных сил. Уравнения Максвелла предсказывали возможность волнообразных возмущений сущности, которую он назвал электромагнитным полем. Они должны были распространяться с постоянной скоростью, подобно ряби на поверхности пруда. Вычислив эту скорость, Максвелл обнаружил, что она точно совпадает со скоростью света!
Сегодня мы знаем, что волны Максвелла воспринимаются человеческим глазом как видимый свет, если их длина находится в интервале от сорока до восьмидесяти миллионных долей сантиметра. [Длиной волны называют расстояние между двумя ее гребнями или впадинами (рис. 7).] Волны, длина которых короче, чем у видимого света, теперь называют ультрафиолетовым, рентгеновским и гамма-излучением. Волны, превосходящие по длине видимый свет, — это радиоволны (метр или больше), микроволны (несколько сантиметров) и инфракрасное излучение (больше десятитысячной доли сантиметра).
Вытекающее из теории Максвелла положение о том, что радио— и световые волны распространяются с некоторой постоянной скоростью, было трудно согласовать с теорией Ньютона. В отсутствие абсолютного стандарта покоя не может быть и никакого универсального соглашения о скорости объекта. Чтобы понять это, снова представьте себя играющим в пинг-понг в поезде. Если вы направляете шарик к противнику со скоростью 10 миль в час , то для наблюдателя на платформе скорость шарика составит 100 миль в час: 10 — скорость шарика относительно поезда плюс 90 — скорость поезда относительно платформы. Какова скорость шарика — 10 или 100 миль в час? А как вы будете ее определять? Относительно поезда? Относительно Земли? Без абсолютного стандарта покоя вы не можете определить абсолютную скорость шарика. Одному и тому же шарику можно приписать любую скорость в зависимости от того, относительно какой системы отсчета она измеряется (рис. 8). Согласно теории Ньютона то же самое должно относиться и к свету. Так какой же тогда смысл несет в себе утверждение теории Максвелла о том, что световые волны всегда распространяются с одинаковой скоростью?
Чтобы примирить теорию Максвелла с законами Ньютона, была принята гипотеза о том, что повсюду, даже в вакууме, в «пустом» пространстве, существует некая среда, получившая название «эфир». Идея эфира имела особую привлекательность для тех ученых, которые считали, что, подобно морским волнам, требующим воды, или звуковым колебаниям, требующим воздуха, волнам электромагнитной энергии нужна некая среда, в которой они могли бы распространяться. С этой точки зрения световые волны распространяются в эфире так же, как звуковые волны в воздухе, и их скорость, выводимая из уравнений Максвелла, должна измеряться относительно эфира. В таком случае разные наблюдатели фиксировали бы разные значения скорости света, но относительно эфира она оставалась бы постоянной.
Эту идею можно проверить. Представьте себе свет, испускаемый неким источником. Согласно теории эфира свет распространяется в эфире с постоянной скоростью. Если вы движетесь сквозь эфир в сторону источника, скорость, с которой к вам приближается свет, будет складываться из скорости движения света в эфире и вашей скорости относительно эфира. Свет будет приближаться к вам быстрее, чем если бы вы были неподвижны или, например, двигались в каком-то другом направлении. Однако это различие в скорости очень трудно измерить из-за того, что скорость света многократно больше той скорости, с которой вы могли бы двигаться навстречу источнику.
В 1887 г. Альберт Майкельсон (который впоследствии стал первым американским лауреатом Нобелевской премии по физике) и Эдвард Морли выполнили очень тонкий и трудный эксперимент в Школе прикладных наук в Кливленде. Они решили воспользоваться тем, что раз Земля обращается вокруг Солнца со скоростью около 30 километров в секунду, то и их лаборатория должна двигаться сквозь эфир с этой относительно высокой скоростью. Конечно, никто не знал, перемещается ли эфир относительно Солнца, а если да, то в каком направлении и с какой скоростью. Но, повторяя измерения в разное время года, когда Земля находится в различных точках своей орбиты, они надеялись учесть этот неизвестный фактор. Майкельсон и Морли разработали эксперимент, в котором скорость света в направлении движения Земли через эфир (когда мы движемся в сторону источника света) сравнивалась со скоростью света под прямым углом к этому направлению (когда мы не приближаемся к источнику). К несказанному их удивлению, они обнаружили, что скорость в обоих направлениях в точности одинакова!
Между 1887 и 1905 гг. было предпринято несколько попыток спасти теорию эфира. Наиболее интересными оказались работы голландского физика Хендрика Лоренца, который попробовал объяснить результат эксперимента Майкельсона—Морли сжатием предметов и замедлением хода часов при передвижении сквозь эфир. Однако в 1905 г . доселе неизвестный сотрудник швейцарского патентного бюро Альберт Эйнштейн показал, что всякая надобность в эфире отпадает, если отказаться от идеи абсолютного времени (вы скоро узнаете почему). Ведущий французский математик Анри Пуанкаре высказал похожие соображения несколькими неделями позже. Аргументы Эйнштейна были ближе к физике, чем выкладки Пуанкаре, который рассматривал проблему как чисто математическую и до последнего своего дня не принимал эйнштейновскую интерпретацию теории.
Фундаментальный постулат Эйнштейна, именуемый принципом относительности, гласит, что все законы физики должны быть одинаковыми для всех свободно движущихся наблюдателей независимо от их скорости. Это было верно для законов движения Ньютона, но теперь Эйнштейн распространил эту идею также и на теорию Максвелла. Другими словами, раз теория Максвелла объявляет скорость света постоянной, то любой свободно движущийся наблюдатель должен фиксировать одно и то же значение независимо от скорости, с которой он приближается к источнику света или удаляется от него. Конечно, эта простая идея объяснила — без привлечения эфира или иной привилегированной системы отсчета — смысл появления скорости света в уравнениях Максвелла, однако из нее также вытекал ряд удивительных следствий, которые зачастую противоречили интуиции.
Например, требование, чтобы все наблюдатели сошлись в оценке скорости света, вынуждает изменить концепцию времени. Согласно теории относительности наблюдатель, едущий на поезде, и тот, что стоит на платформе, разойдутся в оценке расстояния, пройденного светом. А поскольку скорость есть расстояние, деленное на время, единственный способ для наблюдателей прийти к согласию относительно скорости света — это разойтись также и в оценке времени. Другими словами, теория относительности положила конец идее абсолютного времени! Оказалось, что каждый наблюдатель должен иметь свою собственную меру времени и что идентичные часы у разных наблюдателей не обязательно будут показывать одно и то же время.
Теория относительности не нуждается в эфире, присутствие которого, как показал эксперимент Майкельсона—Морли, невозможно обнаружить. Вместо этого теория относительности заставляет нас существенно изменить представления о пространстве и времени. Мы должны признать, что время не полностью отделено от пространства, но составляет с ним некую общность — пространство-время. Понять это нелегко. Даже сообществу физиков понадобились годы, чтобы принять теорию относительности. Она — свидетельство богатого воображения Эйнштейна, его способности к построению теорий, его доверия к собственной логике, благодаря которому он делал выводы, не пугаясь тех, казалось бы, странных заключений, которые порождала теория.
Всем хорошо известно, что положение точки в пространстве можно описать тремя числами, или координатами. Например, можно сказать, что некая точка в комнате находится в семи футах от одной стены, в трех футах от другой и на высоте пяти футов над полом. Или мы можем указать точку, задав ее географические широту и долготу, а также высоту над уровнем моря (рис. 9).
Можно использовать любые три подходящие координаты, однако каждая система координат имеет ограниченную область применения. Не слишком-то удобно определять положение Луны относительно центра Лондона — столько-то миль на север и столько-то к западу от площади Пиккадилли и на столько-то футов выше уровня моря. Вместо этого можно задать положение Луны, указав ее расстояние от Солнца, удаление от плоскости планетных орбит, а также угол между прямой Луна—Солнце и линией, соединяющей Солнце с ближайшей к нам звездой, Проксимой Центавра. Но даже эти координаты не особенно удобны для указания местоположения Солнца в нашей Галактике или самой Галактики в Местной группе галактик. На самом деле Вселенную можно описывать в терминах своего рода перекрывающихся «заплат». В пределах каждой заплаты для задания положения точки правомерно использовать свою систему координат.
В пространстве-времени теории относительности любое событие — то есть нечто случающееся в определенной точке пространства в определенное время — можно задать четырьмя координатами. Выбор координат опять-таки произволен: можно использовать любые три четко заданные пространственные координаты и любой способ измерения времени. Но в теории относительности нет принципиального различия между пространственными и временными координатами, как нет его между любыми двумя пространственными координатами. Можно выбрать новую систему координат, в которой, скажем, первая пространственная координата будет неким сочетанием прежних первой и второй пространственных координат.
Если бы свет распространялся с бесконечной скоростью, то на Земле эти затмения наблюдались бы через равные интервалы времени, в те самые моменты, когда они происходят, — подобно тиканью космических часов. Приближение Юпитера к Земле или его удаление не имело бы никакого значения, так как свет любое расстояние преодолевал бы моментально.
Теперь представим, что свет распространяется с конечной скоростью. Тогда затмения должны наблюдаться спустя некоторое время после их наступления. Эта задержка зависит от скорости света и от расстояния до Юпитера. Если бы расстояние между Юпитером и Землей оставалось неизменным, то и затмения отмечались бы всегда через равные интервалы. Однако, когда расстояние между Землей и Юпитером сокращается, «сигнал» о каждом следующем затмении преодолевает все меньшее и меньшее расстояние и достигает нашей планеты со все большим «опережением графика». По той же причине, когда Юпитер удаляется от Земли, мы видим, что затмения все больше запаздывают (рис. 6). Величина опережения и запаздывания зависит от скорости света, что позволяет ее измерить.
Рис. 6. Скорость света и моменты затмений спутников Юпитера.
Наблюдаемые моменты затмений спутников Юпитера зависят как от действительного времени затмений, так и от времени, в течение которого свет преодолевает расстояние от Юпитера до Земли. Так, создается впечатление, будто затмения случаются чаще, когда Юпитер сближается с Землей, и реже — когда удаляется от нее. Этот эффект здесь преувеличен для наглядности.Удовлетворительной теории распространения света не существовало до 1865 г ., когда английский физик Максвелл сумел объединить до того обособленные описания электрических и магнитных сил. Уравнения Максвелла предсказывали возможность волнообразных возмущений сущности, которую он назвал электромагнитным полем. Они должны были распространяться с постоянной скоростью, подобно ряби на поверхности пруда. Вычислив эту скорость, Максвелл обнаружил, что она точно совпадает со скоростью света!
Сегодня мы знаем, что волны Максвелла воспринимаются человеческим глазом как видимый свет, если их длина находится в интервале от сорока до восьмидесяти миллионных долей сантиметра. [Длиной волны называют расстояние между двумя ее гребнями или впадинами (рис. 7).] Волны, длина которых короче, чем у видимого света, теперь называют ультрафиолетовым, рентгеновским и гамма-излучением. Волны, превосходящие по длине видимый свет, — это радиоволны (метр или больше), микроволны (несколько сантиметров) и инфракрасное излучение (больше десятитысячной доли сантиметра).
Рис. 7. Длина волны.
Длиной волны называют расстояние между двумя ее гребнями или впадинами.Чтобы примирить теорию Максвелла с законами Ньютона, была принята гипотеза о том, что повсюду, даже в вакууме, в «пустом» пространстве, существует некая среда, получившая название «эфир». Идея эфира имела особую привлекательность для тех ученых, которые считали, что, подобно морским волнам, требующим воды, или звуковым колебаниям, требующим воздуха, волнам электромагнитной энергии нужна некая среда, в которой они могли бы распространяться. С этой точки зрения световые волны распространяются в эфире так же, как звуковые волны в воздухе, и их скорость, выводимая из уравнений Максвелла, должна измеряться относительно эфира. В таком случае разные наблюдатели фиксировали бы разные значения скорости света, но относительно эфира она оставалась бы постоянной.
Эту идею можно проверить. Представьте себе свет, испускаемый неким источником. Согласно теории эфира свет распространяется в эфире с постоянной скоростью. Если вы движетесь сквозь эфир в сторону источника, скорость, с которой к вам приближается свет, будет складываться из скорости движения света в эфире и вашей скорости относительно эфира. Свет будет приближаться к вам быстрее, чем если бы вы были неподвижны или, например, двигались в каком-то другом направлении. Однако это различие в скорости очень трудно измерить из-за того, что скорость света многократно больше той скорости, с которой вы могли бы двигаться навстречу источнику.
В 1887 г. Альберт Майкельсон (который впоследствии стал первым американским лауреатом Нобелевской премии по физике) и Эдвард Морли выполнили очень тонкий и трудный эксперимент в Школе прикладных наук в Кливленде. Они решили воспользоваться тем, что раз Земля обращается вокруг Солнца со скоростью около 30 километров в секунду, то и их лаборатория должна двигаться сквозь эфир с этой относительно высокой скоростью. Конечно, никто не знал, перемещается ли эфир относительно Солнца, а если да, то в каком направлении и с какой скоростью. Но, повторяя измерения в разное время года, когда Земля находится в различных точках своей орбиты, они надеялись учесть этот неизвестный фактор. Майкельсон и Морли разработали эксперимент, в котором скорость света в направлении движения Земли через эфир (когда мы движемся в сторону источника света) сравнивалась со скоростью света под прямым углом к этому направлению (когда мы не приближаемся к источнику). К несказанному их удивлению, они обнаружили, что скорость в обоих направлениях в точности одинакова!
Рис. 8. Различные скорости теннисного шарика.
Согласно теории относительности различающиеся результаты измерений скорости тела, полученные разными наблюдателями, одинаково справедливы.Фундаментальный постулат Эйнштейна, именуемый принципом относительности, гласит, что все законы физики должны быть одинаковыми для всех свободно движущихся наблюдателей независимо от их скорости. Это было верно для законов движения Ньютона, но теперь Эйнштейн распространил эту идею также и на теорию Максвелла. Другими словами, раз теория Максвелла объявляет скорость света постоянной, то любой свободно движущийся наблюдатель должен фиксировать одно и то же значение независимо от скорости, с которой он приближается к источнику света или удаляется от него. Конечно, эта простая идея объяснила — без привлечения эфира или иной привилегированной системы отсчета — смысл появления скорости света в уравнениях Максвелла, однако из нее также вытекал ряд удивительных следствий, которые зачастую противоречили интуиции.
Например, требование, чтобы все наблюдатели сошлись в оценке скорости света, вынуждает изменить концепцию времени. Согласно теории относительности наблюдатель, едущий на поезде, и тот, что стоит на платформе, разойдутся в оценке расстояния, пройденного светом. А поскольку скорость есть расстояние, деленное на время, единственный способ для наблюдателей прийти к согласию относительно скорости света — это разойтись также и в оценке времени. Другими словами, теория относительности положила конец идее абсолютного времени! Оказалось, что каждый наблюдатель должен иметь свою собственную меру времени и что идентичные часы у разных наблюдателей не обязательно будут показывать одно и то же время.
Теория относительности не нуждается в эфире, присутствие которого, как показал эксперимент Майкельсона—Морли, невозможно обнаружить. Вместо этого теория относительности заставляет нас существенно изменить представления о пространстве и времени. Мы должны признать, что время не полностью отделено от пространства, но составляет с ним некую общность — пространство-время. Понять это нелегко. Даже сообществу физиков понадобились годы, чтобы принять теорию относительности. Она — свидетельство богатого воображения Эйнштейна, его способности к построению теорий, его доверия к собственной логике, благодаря которому он делал выводы, не пугаясь тех, казалось бы, странных заключений, которые порождала теория.
Всем хорошо известно, что положение точки в пространстве можно описать тремя числами, или координатами. Например, можно сказать, что некая точка в комнате находится в семи футах от одной стены, в трех футах от другой и на высоте пяти футов над полом. Или мы можем указать точку, задав ее географические широту и долготу, а также высоту над уровнем моря (рис. 9).
Рис. 9. Координаты в пространстве.
Говоря, что пространство имеет три измерения, мы подразумеваем, что положение точки в нем можно передать с помощью трех чисел — координат. Если мы введем в наше описание время, то получим четырехмерное пространство-время.В пространстве-времени теории относительности любое событие — то есть нечто случающееся в определенной точке пространства в определенное время — можно задать четырьмя координатами. Выбор координат опять-таки произволен: можно использовать любые три четко заданные пространственные координаты и любой способ измерения времени. Но в теории относительности нет принципиального различия между пространственными и временными координатами, как нет его между любыми двумя пространственными координатами. Можно выбрать новую систему координат, в которой, скажем, первая пространственная координата будет неким сочетанием прежних первой и второй пространственных координат.
Конец бесплатного ознакомительного фрагмента