Страница:
Здесь ряд х, у, z… означает объем, а ряд а, Ь, с… – содержание сложного понятия; поэтому на основании этих формул могут быть представлены также и все вообще отношения между объемом и содержанием (понятий).
На основании этих отношений, а главным образом отношений подчинения понятий, становится ясным значение понятий подчиняющих, соподчиненных и подчиненных, тождественных, равнозначащих, перекрещивающихся, разобщенных и несоединимых, а также деление понятий по родам и видам, равно как и правила определения, т. е. важнейшие учения школьной логики о понятии (см. особенно Ubeiweg-Meyer, System der Logik).
§ 12. Количество суждения и количественный синтез
§ 13. Качество суждения и качественный синтез
§ 14. Главные формы умозаключения
1) общеутвердительные с частноотрицательными (а-о),
2) общеотрицательные с частноутвердительными (e-i) находятся в отношении противоречия, т. е. с признанием одного – другое всегда отрицается, с отрицанием одного – другое всегда признается, tertuim поп datur,
3) общеутвердительные с общеотрицательными (а – е)
находятся в отношении противной противоположности, т. е. с признанием одного – другое отрицается, но отрицанием одного – еще не признается другое, tertuim datur,
4) частноутвердительные с частноотрицательными (i – о) находятся в отношении подпротивности, т. е. с отрицанием одного – другое признается, но признанием одного – еще не отрицается другое. Из этих отношений возникает первый род непосредственного умозаключения, заключение по противоположности (Opposition); при этом субъект данного суждения повторяется в качестве субъекта, а предикат – в качестве предиката заключения. Напротив, если понятие субъекта и понятие предиката меняются в заключении своими ролями, то получается заключение через обращение (Konversion). Таким образом, в порядке обращения:
1) из общеутвердительного суждения получается частноутвердительное (а – i),
2) из частноутвердительного суждения получается частноутвердительное (i – i),
3) из общеотрицательного суждения получается общеотрицательное (е-е),
тогда как при частноотрицательном суждении (о) обращение не приводит ни к какому результату. Заключение по противопоставлению получается в том случае, когда кроме положительных понятий данного суждения принимаются во внимание и противоположные им отрицательные понятия. Основной случай (а-е), например: все люди смертны, следовательно, то, что не смертно, не есть человек.

В пределах каждой фигуры умозаключение строится неодинаково в зависимости от того, какую из четырех форм – а, е, i, о — имеют посылки. Соответственно этому в каждой фигуре силлогизма могло бы, собственно говоря, быть 4 x 4 = 16 комбинаций. Из них многие, однако, отпадают, так как 1) из одних только отрицательных и одних только частных посылок, равно как из частной большей посылки и отрицательной меньшей, никоим образом нельзя получить правильного заключения, вследствие чего выпадают уже восемь самих по себе возможных комбинаций;
2) к этому в пределах отдельных фигур присоединяются еще дальнейшие ограничения. Среди остающихся и имеющих значение умозаключений самыми важными являются четыре способа умозаключения или Modi первой фигуры, представляемые в следующем мнемоническом стихе:
(Primae) Barbara Celarent Darii Ferioque,
где три гласные всегда указывают на характер обеих посылок и вывода. Из них в науке чаще всего употребляется первый модус:
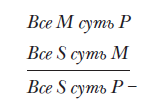
единственная форма силлогизма, приводящая к общеутвердительному выводу, между тем как все четыре модуса второй фигуры -
Cesare Camestres Festino Barocco (secundae) -
дают лишь отрицательные заключения; все шесть модусов третьей фигуры -
(tertia) Darapti Felapton Disamis Datisi Bocardo Ferison -
дают лишь частные заключения, и наконец пять малоупотребительных и легко могущих быть избегнутыми модусов четвертой фигуры ведут только к общеотрицательным, частноутвердительным или частноотрицательным выводам.
§ 15. Индукция и умозаключение по аналогии
§ 16. Метод научного познания
В. Основные положения теории познания
§ 17. Проблема предмета
§ 18. Основные законы чувственности. Пространство и время
§ 19. Объективирование чувственного материала сообразно основным законам количества и качества
На основании этих отношений, а главным образом отношений подчинения понятий, становится ясным значение понятий подчиняющих, соподчиненных и подчиненных, тождественных, равнозначащих, перекрещивающихся, разобщенных и несоединимых, а также деление понятий по родам и видам, равно как и правила определения, т. е. важнейшие учения школьной логики о понятии (см. особенно Ubeiweg-Meyer, System der Logik).
§ 12. Количество суждения и количественный синтез
Исходя из основной функции синтетического единства можно понять смысл количества и качества суждения. Синтетическое единство есть единство многообразного, основывающееся на единстве той точки зрения, с которой это многообразное воспринимается и связывается. Многообразное, мыслимое только как таковое, представляет собой множество. Это последнее предполагает единство в смысле единичности, потому что оно выражает повторяющееся полагание одного, еще одного и т. д. Но этот ряд полаганий, сам по себе допускающий неопределенную продолжаемость, требует соответственно самой природе синтетического единства, как единства определения, завершения в некотором новом единстве. Так получается третий способ количественного постижения многообразного – (составная) общность (Allheit) или сумма, объединяющая многие единицы в одном множестве. Этим трем ступеням количественного синтеза (единичность, множество, общность в смысле суммы) соответствуют три рода суждений: единичные, множественные и всеобщие (правильнее – суммативные) суждения.
Закономерная деятельность количественного синтеза получила совершенно своеобразное научное выражение в числе, основывающемся на тех же трех моментах: на полагании численно единого, на возможности неограниченного перехода от одного к еще одному и т. д., т. е. на неопределенном множестве, и на образовании замкнутого числа или определенного множества. Но так как деятельность счисления, состоящая в получении количества (Quantum) через объединение многих единиц в одно множество, коренится в основной функции синтетического единства и только выражает саму эту функцию в отношении количества (т. е. того многообразного, которое в нем подлежит объединению), то эта деятельность находится в нашем распоряжении не на один или на несколько раз, но раз навсегда и, следовательно, представляет собой один из безусловно основных методов познания. Это особенно выражается в бесконечности и бесконечной делимости числа. Но из этого способа выведения числа вытекает в то же время и его прерывность (дискретность числа), т. е. невозможность мыслить переход от количества (Quantum) к количеству в непрерывной связи, потому что именно указанным способом, т. е. лишь через суммирование единств, в свою очередь заключающих в себе множественность, происходит этот переход в бесконечность, другими словами – переход этот совершается скачками, не непрерывно.
Закономерная деятельность количественного синтеза получила совершенно своеобразное научное выражение в числе, основывающемся на тех же трех моментах: на полагании численно единого, на возможности неограниченного перехода от одного к еще одному и т. д., т. е. на неопределенном множестве, и на образовании замкнутого числа или определенного множества. Но так как деятельность счисления, состоящая в получении количества (Quantum) через объединение многих единиц в одно множество, коренится в основной функции синтетического единства и только выражает саму эту функцию в отношении количества (т. е. того многообразного, которое в нем подлежит объединению), то эта деятельность находится в нашем распоряжении не на один или на несколько раз, но раз навсегда и, следовательно, представляет собой один из безусловно основных методов познания. Это особенно выражается в бесконечности и бесконечной делимости числа. Но из этого способа выведения числа вытекает в то же время и его прерывность (дискретность числа), т. е. невозможность мыслить переход от количества (Quantum) к количеству в непрерывной связи, потому что именно указанным способом, т. е. лишь через суммирование единств, в свою очередь заключающих в себе множественность, происходит этот переход в бесконечность, другими словами – переход этот совершается скачками, не непрерывно.
§ 13. Качество суждения и качественный синтез
Подобно тому, как количество основывается на свойстве синтетического единства объединять многообразное, так и качество имеет своим основанием некоторое единство многообразного, устанавливаемое объединяющим умственным взором нашего духа. Непосредственным выражением единства синтеза по его качественному значению служит понятие тождества. И именно постольку тождество есть принцип всякого вообще суждения, а не только аналитического. Тождеству противостоит понятие различия. Оба эти понятия относятся друг к другу в области качества так же, как единство и множество – в области количества. А тождественно с В – это значит, что А и В суть одно и то же; А отлично от В, – что это два разных качества. Тождество и различие выражаются также в утвердительном и в отрицательном суждении: А есть В, А не есть В. Но подобно тому, как в области количества из объединения множества в одном новом количественном единстве возникает сложная общность, так и в области качества из объединения различного (т. е. качественно многого) в некотором новом качественном единстве получается новая логическая категория, служащая основанием единства различных видов в одном роде. Так родовое понятие треугольника не только количественно обнимает всю совокупность треугольников, но вместе с тем и качественно – все виды треугольников или вообще всевозможные треугольники, какие только существуют. На трех ступенях качественного синтеза основывается также и способ определения через указание на род и видообразующее отличие. Равным образом из законов качественного синтеза становится понятным и значение противоречащей и противной противоположности.
Подобно количественному, и качественный синтез может охватывать в некотором единстве не только всякую данную множественность, но и бесконечность различий. Но в отличие от количественного качественный синтез состоит не во внешнем только – периферическом, но во внутреннем центральном объединении бесконечного; он выражает единство внутренней связи (Komprehension), а не простого складывания (Komposition). Качественный синтез мыслится как источник или первоначальное основание, из которого множественность качественных различий неисчерпаемо порождается все вновь и вновь. Эта особенность качественного синтеза в силу необходимого соответствия между количеством и качеством находит себе выражение также и в области величины, именно в непрерывности. Последняя коренится, следовательно, не в одном количестве самом по себе, а во взаимоотношении количественного и качественного синтеза; но вследствие неустранимости этого взаимоотношения она распространяется на количество вообще, следовательно, также и на число как общее выражение количества.
Подобно количественному, и качественный синтез может охватывать в некотором единстве не только всякую данную множественность, но и бесконечность различий. Но в отличие от количественного качественный синтез состоит не во внешнем только – периферическом, но во внутреннем центральном объединении бесконечного; он выражает единство внутренней связи (Komprehension), а не простого складывания (Komposition). Качественный синтез мыслится как источник или первоначальное основание, из которого множественность качественных различий неисчерпаемо порождается все вновь и вновь. Эта особенность качественного синтеза в силу необходимого соответствия между количеством и качеством находит себе выражение также и в области величины, именно в непрерывности. Последняя коренится, следовательно, не в одном количестве самом по себе, а во взаимоотношении количественного и качественного синтеза; но вследствие неустранимости этого взаимоотношения она распространяется на количество вообще, следовательно, также и на число как общее выражение количества.
§ 14. Главные формы умозаключения
А. Непосредственное умозаключение
На количественных и качественных отношениях суждений основываются общие правила вывода новых суждений из данных, т. е. правила умозаключений. При этом непосредственными умозаключениями называются такие, которые выводят новое суждение из одного какого-нибудь данного суждения, а посредственными – такие, где вывод делается из двух или большего числа суждений. При установлении правил умозаключения неизбежно возникает вопрос, являются ли сравниваемые суждения по количеству общими или частными, а по качеству – утвердительными или отрицательными. Отсюда и получаются четыре класса суждений: общеутвердительные (а), общеотрицательные (е), частноутвердительные (i) и частноотрицательные (о). Из них:1) общеутвердительные с частноотрицательными (а-о),
2) общеотрицательные с частноутвердительными (e-i) находятся в отношении противоречия, т. е. с признанием одного – другое всегда отрицается, с отрицанием одного – другое всегда признается, tertuim поп datur,
3) общеутвердительные с общеотрицательными (а – е)
находятся в отношении противной противоположности, т. е. с признанием одного – другое отрицается, но отрицанием одного – еще не признается другое, tertuim datur,
4) частноутвердительные с частноотрицательными (i – о) находятся в отношении подпротивности, т. е. с отрицанием одного – другое признается, но признанием одного – еще не отрицается другое. Из этих отношений возникает первый род непосредственного умозаключения, заключение по противоположности (Opposition); при этом субъект данного суждения повторяется в качестве субъекта, а предикат – в качестве предиката заключения. Напротив, если понятие субъекта и понятие предиката меняются в заключении своими ролями, то получается заключение через обращение (Konversion). Таким образом, в порядке обращения:
1) из общеутвердительного суждения получается частноутвердительное (а – i),
2) из частноутвердительного суждения получается частноутвердительное (i – i),
3) из общеотрицательного суждения получается общеотрицательное (е-е),
тогда как при частноотрицательном суждении (о) обращение не приводит ни к какому результату. Заключение по противопоставлению получается в том случае, когда кроме положительных понятий данного суждения принимаются во внимание и противоположные им отрицательные понятия. Основной случай (а-е), например: все люди смертны, следовательно, то, что не смертно, не есть человек.
В. Силлогизм
Виды посредственного умозаключения составляют: 1) силлогизм, 2) индукция и 3) умозаключение по аналогии. Силлогизм заключает от общего к частному, индукция – от частного к общему, аналогия – от одного частного к другому частному того же рода. Для простого силлогизма, т. е. такого, который из двух данных суждений (предшествующих положений или посылок) выводит новое (вывод или заключение), требуется – 1) чтобы в одной посылке (propositio major, большая посылка) предикат, в другой (propositio minor, меньшая посылка) – субъект вывода встречались в качестве субъекта или предиката; 2) чтобы другое понятие в обеих посылках было одним и тем же. Так как это понятие служит посредствующим звеном для связи обоих понятий вывода, то оно называется средним термином (terminus medius). Если буквами 5 и Р обозначить субъект и предикат вывода, а буквою М – средний термин, то большая посылка должна, следовательно, содержать в себе понятия P u М, а меньшая посылка – понятия S и М. Три понятия Р, S u М называются элементами или терминами силлогизма. По их положению в обеих посылках в качестве субъекта или предиката различают четыре фигуры силлогизма. Возможны именно четыре положения:
В пределах каждой фигуры умозаключение строится неодинаково в зависимости от того, какую из четырех форм – а, е, i, о — имеют посылки. Соответственно этому в каждой фигуре силлогизма могло бы, собственно говоря, быть 4 x 4 = 16 комбинаций. Из них многие, однако, отпадают, так как 1) из одних только отрицательных и одних только частных посылок, равно как из частной большей посылки и отрицательной меньшей, никоим образом нельзя получить правильного заключения, вследствие чего выпадают уже восемь самих по себе возможных комбинаций;
2) к этому в пределах отдельных фигур присоединяются еще дальнейшие ограничения. Среди остающихся и имеющих значение умозаключений самыми важными являются четыре способа умозаключения или Modi первой фигуры, представляемые в следующем мнемоническом стихе:
(Primae) Barbara Celarent Darii Ferioque,
где три гласные всегда указывают на характер обеих посылок и вывода. Из них в науке чаще всего употребляется первый модус:
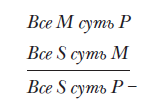
единственная форма силлогизма, приводящая к общеутвердительному выводу, между тем как все четыре модуса второй фигуры -
Cesare Camestres Festino Barocco (secundae) -
дают лишь отрицательные заключения; все шесть модусов третьей фигуры -
(tertia) Darapti Felapton Disamis Datisi Bocardo Ferison -
дают лишь частные заключения, и наконец пять малоупотребительных и легко могущих быть избегнутыми модусов четвертой фигуры ведут только к общеотрицательным, частноутвердительным или частноотрицательным выводам.
§ 15. Индукция и умозаключение по аналогии
Индукция заключает от единичного или частного к общему. Оправдание такого умозаключения нельзя дать, опираясь на чисто субъективную основу ассоциации, которая побуждает нас при сходных условиях ожидать и сходных последствий; дать такое оправдание возможно, лишь опираясь на логическую связь отдельных данных нам случаев, определяемую выражением какого-нибудь закона; это выражение и дает тогда большую посылку, которая, – если применять ее все к новым и новым отдельным случаям, представляющим собою меньшие посылки, – приводит к заключениям, совпадение или несовпадение которых с заведомо установленными фактами служит пробным камнем истинности большей посылки, принятой сначала лишь предварительно в качестве «гипотезы». Правда и эта проверка на фактах всегда остается незавершимой, однако здесь обнаруживается лишь тот характер бесконечности, который вообще присущ опытному познанию. Индукция есть незавершимый процесс, потому что таков вообще характер опыта. Уже в так называемой полной индукции, т. е. такой, которая на основании исчерпывающего деления всецело охватывает объем понятия, о котором в выводе нечто высказывается всеобщим образом, – даже в такой индукции связывание отдельных данных в общее познание основывается не на простом суммировании единичных познаний, а на убеждении в тождественности того основания, которое в применении ко всем возможным случаям приводит к одному и тому же результату. Но точно таким же образом и неполная индукция, т. е. заключение от ограниченного числа данных случаев, для которых установлено известное тождественное отношение, ко всем однородным случаям, является оправданной лишь постольку, поскольку закономерная связь искомого отношения может быть предположена на основании общих соображений в качестве имеющей значение для всех мыслимых случаев того же рода. Таким образом, индукция всегда основывается на предположении некоторой закономерной связи, каковое общее предположение и подлежит затем оправданию посредством проверки на фактах. Но свое последнее основание такое предположение имеет в общих основоположениях возможного опыта вообще и прежде всего в законе причинности (§ 20). Сами эти основоположения, напротив, уже не могут быть доказаны посредством индукции, а требуют совсем другого рода оправдания («трансцендентальной дедукции»).
Умозаключение по аналогии идет от частного не к общему, но к другому частному такого же рода. Оно не основывается на каком-либо новом принципе сравнительно с индукцией и отличается от последней лишь по форме результата, а не по существу своего основания.
Умозаключение по аналогии идет от частного не к общему, но к другому частному такого же рода. Оно не основывается на каком-либо новом принципе сравнительно с индукцией и отличается от последней лишь по форме результата, а не по существу своего основания.
§ 16. Метод научного познания
Из указанных выше составных частей слагается метод научного познания. Основывается он главным образом на доказательстве, т. е. на выведении посредством умозаключения истинности одного какого-нибудь положения из ранее установленной истинности других положений. Доказательство есть поэтому главное средство для связывания между собой отдельных положений в единство научного целого или системы. Это связывание происходит частью дедуктивно (синтетически, прогрессивно), частью индуктивно (аналитически, регрессивно). Синтетический метод шаг за шагом конструктивно развивает из наиболее простых основных истин истины более сложного характера, между тем как аналитический метод сводит более сложные истины к их простейшим основаниям или разлагает их на простые истины. Чистейший пример синтетического или дедуктивного метода представляет математика в ее известных отделах, а также теоретическая механика. И даже там, где (как это нередко бывает и в математике) применяется регрессивный (аналитический) метод, последний однако всегда имеет в виду построение (Konstruktion) на основании возможно более простых предположений, как они формулируются в аксиомах и определениях. В противоположность математике естественные науки в преобладающей своей части пользуются преимущественно индуктивным, т. е. аналитическим, методом. Процессы природы непосредственно доступны нам большею частью лишь в очень сложном виде, из которого аналитическим путем еще только впервые требуется получить простую основную форму действий природы. Исходным пунктом служат здесь поэтому не аксиомы и определения, но факты восприятия, как они отчасти сами нам навязываются, отчасти отыскиваются планомерным наблюдением или впервые создаются при помощи эксперимента; приобретенные так или иначе факты служат затем для проверки объясняющей теории, которая, предвосхищая закон, выставляет его первоначально только как гипотезу. Целью однако всегда является при этом дедуктивное развитие фактов из закона. При завершении науки исчезла бы противоположность между дедуктивным и индуктивным методами, и систематическое единство познания, составляющее самую сущность науки, ясно выступило бы тогда и в форме самого метода.
В. Основные положения теории познания
§ 17. Проблема предмета
Познание есть понятие и суждение о предмете (§ 9). Но определить, что такое предмет, можно, только принимая во внимание его отношение к основному закону познания (§ 7). Основной закон познания есть закон синтетического единства, т. е. определения того, что само в себе неопределенно подлежит бесконечному определению, или, – что то же самое, – это есть закон определения чувственно данного (§ 10). Но определение того, что еще только должно быть определено, и есть познание того, что подлежит познанию, т. е. познание предмета. Определять то, что есть, значит познавать предмет. Следует однако различать два значения термина «предмет». Он может обозначать: 1) искомый, еще не познанный предмет. В этом смысле он совпадает с чувственно данным, т. е. с тем, что еще только подлежит определению, но вместе с тем уже дано, как нечто = х. Или 2) он обозначает познанный предмет, следовательно, уже достигнутое определение чувственно данного в понятии и суждении, как в таких формах, в которых предмет только и может быть мыслим. Соответственно этому предмет, с одной стороны, как только данный основывается на чувственном материале; с другой стороны, как только мыслимый – на интеллектуальной форме познания (понятии). Но такой только данный или только мыслимый предмет становится познанным предметом лишь через взаимодействие обоих факторов, формального и материального, или интеллектуального и чувственного. Однако материю познания никогда нельзя при этом всецело разрешить в чистую форму, и, следовательно, ни данный, ни мыслимый предмет никогда не могут превратиться в познанный предмет без всякого остатка; напротив, предмет навсегда сохранит за собой значение задачи. Абсолютное определение того, что подлежит определению, или, что то же, абсолютный предмет («вещь в себе» – Канта) имеет для нашего познания лишь значение последней границы, к которой оно, правда, бесконечно приближается, но которой оно никогда не достигает. При этом «вещь в себе» является, однако, лишь абсолютным выражением задачи нашего познания, а не каким-либо особенным, самим по себе существующим предметом для какого-то познания, отличного от нашего. В этом понятии наше познание ограничивается не как в чем-то, что противостоит ему, но лишь как в своем собственном последнем законе.
§ 18. Основные законы чувственности. Пространство и время
Познание предмета основывается (§ 17) на соотношении (Korrelation) чувственного и интеллектуального факторов. Чувственное содержание познания было определено как последнее многообразное (т. е. как многое и различимое), которое должно быть охвачено в единстве и тождестве понятия. В качестве многообразного оно прежде всего должно быть мыслимо как подлежащее анализу: количественному и качественному. Отсюда получилось у нас (§ 10) понятие ощущения как элемента чувственно данного. С другой стороны, многообразное необходимо мыслить как способное к соединению. Но двумя первоначальными, общими и в то же время друг от друга неотделимыми способами непосредственной связи чувственно данного служат, как известно, время и пространство. Они должны, следовательно, быть первоначальной основой всякого синтеза многообразного и, значит, также всякого понятия и всякого познания предметов. Они отличаются друг от друга лишь по способу полагания элементарных содержаний в сознании. Посредством времени эти элементарные содержания сознания полагаются вне друг друга, каждый раз как бы в обособленном сознании; посредством пространства, напротив, – рядом друг с другом, т. е. как связанные или находящиеся вместе. Поэтому пространственное многообразие нельзя сознать в качестве многообразного (т. е. в качестве раздельного) иначе, как через посредство времени, и равным образом временную последовательность (длительность) нельзя представить себе в виде связного целого иначе, как через посредство пространства. Указанное различение во времени возможно лишь в одном измерении совершенно так же, как и первоначальная деятельность счисления, соответствующая этому различению в качестве логической функции; напротив, пространственная связь возможна в нескольких направлениях, аналогично сложному числу. Внешняя и внутренняя бесконечность пространства и времени служат основанием для признания их за общие, допускающие безграничное применение способы деятельности сознания в полагании чувственного содержания (познания). Однако пространство и время не суть только формальные функции мышления, но сохраняют непосредственное отношение к чувственной материи. В качестве форм данности каждая из них (т. е. и пространство и время) существует всегда только в единственном числе, точно так же, как сама данность всегда может быть мыслима только как одна данность, а не как множество (кантовское понятие «созерцания»). При этом формы пространства и времени сохраняют самое непосредственное отношение к ощущению, поскольку оно есть то последнее, что подлежит определению, а они (формы времени и пространства) – основные способы определяемое™. Ощущение всегда обозначает поэтому какой-нибудь данный в пространстве и времени пункт («теперь» и «здесь»), и, с другой стороны, каждый такой временный или пространственный пункт, в свою очередь, никогда не дается иначе, как через ощущение. Сами по себе время и пространство пусты, и без содержания, которое дает им ощущение, они ничто. И тем не менее они не ощущения, а способы распорядка или роды полагания ощущений. Они обладают, следовательно, одновременно и чувственной и формальной природой и потому составляют посредствующее звено между ощущением и функцией понятия как чисто формального фактора познания.
§ 19. Объективирование чувственного материала сообразно основным законам количества и качества
1. Количество. Многообразное чувственного содержания, мыслимое только как многообразное, создает условие для усвоения его (§ 12) посредством основного понятия количества в трех последовательных ступенях его: единичности, множественности и общности (сложного единства или суммы). Поэтому все чувственное, как данное в «созерцании» (т. е. во времени и пространстве), необходимо должно быть объективировано как величина, и, наоборот, величина, как нечто предметное, необходимо должна быть представлена в созерцании, т. е. не просто в абстрактном числе, а в пространстве и во времени (первое основоположение Канта). Согласно этому основоположению чистые понятия величин в математике, в которых наше мышление прежде всего систематически развивает лишь образ действия (Denkverfahren) количественного синтеза, находят самое точное применение ко всему, что дано или только когда-нибудь может быть дано в пространстве и времени. Этим обеспечивается строгое объективное значение первой науки – математики, поскольку ее определения чисто количественные (см. ниже 2). Правда, данное в чувственном созерцании подчиняется чистым понятиям математики всегда лишь условно, однако обращение с этими понятиями остается тем не менее вполне точным и в своей строгой точности не перестает быть масштабом для объективирования всего чувственно данного. Но чтобы было возможно беспредельное приспособление этих понятий к бесконечной определяемости чувственно данного, необходимо, чтобы самый способ обращения мысли с этими понятиями допускал беспредельное развитие, что в действительности и оправдывается на понятиях математического бесконечного. Понятия пространственных и временных величин именно поэтому всегда относительны, но как раз в этой своей относительности они и удовлетворяют требованиям опыта как такого рода познания, предметность которого сама лишь относительна.
2. Качество. Если в количестве объективируется прежде всего «созерцание», то в качестве объективированию подвергается ощущение. В самом деле, ощущение выражает не только данное место в пространстве и времени, но также содержание, его наполняющее, – нечто, что занимает или наполняет пространство и время, т. е. нечто «реальное». Но образ действия мысли, которым нечто полагается и в этом полагании не только отличается от другого, но и вновь объединяется с ним в некотором единстве («компрегенсивном» или родовом единстве), и есть функция качества (§ 13). Для качества не существует особенного математического выражения, соответственно числу, как выражению количества, но зато тот образ действия мышления, выражением которого является число, сам способен испытывать такое расширение и углубление, что он одновременно делается пригодным и для выражения качества. В самом деле, уже для того, чтобы определить простое качество ощущения (Quale), нет никакого другого способа, кроме расположения ощущений в ряд и различения мест в этом ряду, т. е. счисления. Примененное таким образом к качеству число называется «степенью». Но качество есть именно то, что первоначально и лежит в основании; никакое счисление не было бы возможно без счисляемого, т. е. подлежащего качественному различению. Однако измеряется качество только через посредство количества. Качество не обосновывает, следовательно, какой-либо новой науки наряду и в соответствии с математикой, но вследствие неустранимого соответствия между качеством и количеством оно служит обоснованием самой математики не только в ее применимости к пространству и времени как чистым формам созерцания, но и к тому, что составляет содержание пространства и времени. Качество обосновывает вместе с тем основное свойство математической величины, которое не может быть понято на основании одного только количества, именно «непрерывность» (ср. § 13); более того, оно вообще впервые обосновывает самое понятие «величины» как чего-то, относительно чего высказываются различные «величины» (Das So-und-so-gross, количество), но что остается, несмотря на все эти изменчивые определения, всегда тем же самым («переменная» величина); что как бы выражает род, видоизменяющийся в единичные дискретные величины. (У Канта эта как бы выражающая род величина называется интенсивной, а единичные дискретные величины – экстенсивными; в математике величина первого рода называется бесконечно малой (infinitesimale), а величины второго рода – конечными. – Второе основоположение Канта.)
2. Качество. Если в количестве объективируется прежде всего «созерцание», то в качестве объективированию подвергается ощущение. В самом деле, ощущение выражает не только данное место в пространстве и времени, но также содержание, его наполняющее, – нечто, что занимает или наполняет пространство и время, т. е. нечто «реальное». Но образ действия мысли, которым нечто полагается и в этом полагании не только отличается от другого, но и вновь объединяется с ним в некотором единстве («компрегенсивном» или родовом единстве), и есть функция качества (§ 13). Для качества не существует особенного математического выражения, соответственно числу, как выражению количества, но зато тот образ действия мышления, выражением которого является число, сам способен испытывать такое расширение и углубление, что он одновременно делается пригодным и для выражения качества. В самом деле, уже для того, чтобы определить простое качество ощущения (Quale), нет никакого другого способа, кроме расположения ощущений в ряд и различения мест в этом ряду, т. е. счисления. Примененное таким образом к качеству число называется «степенью». Но качество есть именно то, что первоначально и лежит в основании; никакое счисление не было бы возможно без счисляемого, т. е. подлежащего качественному различению. Однако измеряется качество только через посредство количества. Качество не обосновывает, следовательно, какой-либо новой науки наряду и в соответствии с математикой, но вследствие неустранимого соответствия между качеством и количеством оно служит обоснованием самой математики не только в ее применимости к пространству и времени как чистым формам созерцания, но и к тому, что составляет содержание пространства и времени. Качество обосновывает вместе с тем основное свойство математической величины, которое не может быть понято на основании одного только количества, именно «непрерывность» (ср. § 13); более того, оно вообще впервые обосновывает самое понятие «величины» как чего-то, относительно чего высказываются различные «величины» (Das So-und-so-gross, количество), но что остается, несмотря на все эти изменчивые определения, всегда тем же самым («переменная» величина); что как бы выражает род, видоизменяющийся в единичные дискретные величины. (У Канта эта как бы выражающая род величина называется интенсивной, а единичные дискретные величины – экстенсивными; в математике величина первого рода называется бесконечно малой (infinitesimale), а величины второго рода – конечными. – Второе основоположение Канта.)
