Страница:
Решения Паскаля жюри признало наилучшими, и в декабре 1658 года он сочинил «Письмо Амоса Деттонвилля к господину де Каркави», в котором изложил свои результаты и приводящие к ним методы. В следующем году оно пополнилось еще несколькими трактатами, и в печати появляются «Письма Амоса Деттонвилля, содержащие некоторые из его открытий в области геометрии».
О том, что суд жюри был действительно справедливым, свидетельствуют сами результаты и методы Паскаля, всеобщее одобрение и восхищение, которое они вызвали среди европейских ученых. Так, например, в феврале 1659 года Гюйгенс писал Блезу, что хотел бы называться его учеником в науке, где Паскаль продемонстрировал свое явное превосходство над многими. А в июне того же года, характеризуя «Письмо к Каркави», Гюйгенс сообщал Слюзу: «Работа выполнена столь тонко, что к ней нельзя ничего добавить». Действительно, отвечал Слюз знаменитому голландцу, «нельзя отрицать, что прекрасные, изобретательные и тонкие идеи, содержащиеся в этой книге, могут продвинуть вперед геометрию».
И Слюз был прав. Приемы и обобщения анализа бесконечно малых, которые Паскаль использовал в своих трудах по циклоиде, вели к изобретению дифференциального и интегрального исчисления.
Оно открыло целую эпоху в развитии естествознания и стало применяться не только во всех математических дисциплинах, но и повлияло на создание ряда новых разделов математики. Благодаря дифференциальному и интегральному исчислению математика стала гораздо шире проникать в область естественных наук и техники. Таким образом, в истории науки XVII века открытие этого исчисления было важнейшим событием, которое возникло как раз на основе методов исчисления бесконечно малых.
2
3
«Мысли»
1
2
О том, что суд жюри был действительно справедливым, свидетельствуют сами результаты и методы Паскаля, всеобщее одобрение и восхищение, которое они вызвали среди европейских ученых. Так, например, в феврале 1659 года Гюйгенс писал Блезу, что хотел бы называться его учеником в науке, где Паскаль продемонстрировал свое явное превосходство над многими. А в июне того же года, характеризуя «Письмо к Каркави», Гюйгенс сообщал Слюзу: «Работа выполнена столь тонко, что к ней нельзя ничего добавить». Действительно, отвечал Слюз знаменитому голландцу, «нельзя отрицать, что прекрасные, изобретательные и тонкие идеи, содержащиеся в этой книге, могут продвинуть вперед геометрию».
И Слюз был прав. Приемы и обобщения анализа бесконечно малых, которые Паскаль использовал в своих трудах по циклоиде, вели к изобретению дифференциального и интегрального исчисления.
Оно открыло целую эпоху в развитии естествознания и стало применяться не только во всех математических дисциплинах, но и повлияло на создание ряда новых разделов математики. Благодаря дифференциальному и интегральному исчислению математика стала гораздо шире проникать в область естественных наук и техники. Таким образом, в истории науки XVII века открытие этого исчисления было важнейшим событием, которое возникло как раз на основе методов исчисления бесконечно малых.
2
Своеобразие и эволюцию новых методов можно проследить, например, по исследованиям Кеплера и Кавальери. Так, Кеплер при определении целесообразной формы... винных бочек, когда при наименьшей затрате материала требуется получить наибольшую вместимость, разбивал идеальную поверхность изучаемого тела на элементарные части, суммировал их и тем самым непосредственно вводил бесконечно малые величины. Он применял способы исчисления бесконечно малых и в астрономических исследованиях.
Если использование этих способов у Кеплера ограничено конкретными задачами, возникавшими в ходе его научной деятельности, то в поисках более общих и систематизированных принципов образования и измерения поверхностей и тел Кавальери ввел и исследовал абстрактное понятие «неделимых». (Подобно Кавальери и независимо от него стал применять неделимые и Роберваль.) Неделимые у Кавальери — это элементы, из которых состоит площадь или объем того или иного геометрического объекта и размерность которых на единицу меньше размерности рассматриваемого объекта. Так, точка является неделимым для линии, прямая — для плоскости и т. д. При этом, например, площадь какой-то плоской фигуры определялась через уже известную площадь другой фигуры в результате сравнения отрезков прямых линий (неделимых), которыми эти фигуры покрывались.
Торричелли, отмечая особое воздействие метода неделимых на развитие математики, писал: «Несомненно, что геометрия Кавальери есть удивительное по своей экономии средство для нахождения теорем и дает возможность разрешить огромное число, казалось бы, неразрешимых теорем краткими, прямыми, наглядными доказательствами, что невозможно сделать по методу древних. Это — истинно царская дорога среди зарослей математического терновника... Метод Кавальери является действительно научным способом доказательства, всегда идущим путем прямым и свойственным самой природе. Жаль мне древней геометрии, что она либо не знала, либо не хотела признавать учения о неделимых...»
Однако, по замечанию советского историка математики Л. С. Фреймана, метод Кавальери страдал существенными логическими противоречиями: «Одним из таких противоречий является то, что неделимое (линия) имеет на одно измерение меньше числа измерений у площади, а совокупность неделимых уже имеет столько же измерений, сколько площадь!» Действительно, при наложении, скажем, друг на друга плоскостей, толщина которых равна нулю, нельзя получить какой-то объем определенной толщины — суммирование нулей дает в итоге нулевой результат.
В своих исследованиях Паскаль преодолел подобные противоречия: он рассматривал неделимые как однородные с измеряемым объектом бесконечно малые величины, из которых и составлялись интегральные суммы. Для демонстрации приемов Паскаля приведем простой пример, упоминаемый французским исследователем его научного творчества Умбертом. Предположим, что необходимо определить площадь криволинейной трапеции АВСД, составленной прямой AB, перпендикулярами к ней АС и ВД и кривой линией СД (см. рис. 4).
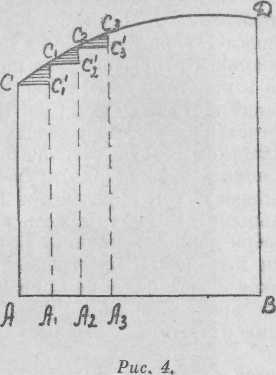На оси AB берется ряд близко расположенных друг к другу точек A1, A2, A3..., из которых проводятся перпендикуляры к AB до пересечения с СД в точках C1, С2, С3... Из этих точек проводятся отрезки CC'1, С1С'2, С2С'3..., параллельные AB. Если подсчитать и просуммировать площади прямоугольников ACC'1A1, A1C1C'2A2, А2С2С'3А3..., то получится приближенное значение искомой площади, отличающееся от нее на сумму площадей криволинейных треугольников CC1C'1, С1С2С'2, С2С3С'3... (заштрихованных на чертеже). Если же предположить, что точки разделения A1, A2, A3... на AB будут бесконечно увеличиваться в количестве и, следовательно, все более сближаться друг с другом, то получаемые бесконечно узкие прямоугольники и будут неделимыми Паскаля (маленькие заштрихованные треугольники в данном случае уменьшаются и как бы стремятся «раствориться» в кривой СД).
Но Паскаль, пишет Умберт, не удовлетворяется простым интуитивным решением: «Он доказывает строгими методами, что сумма площадей этих маленьких треугольников совсем не влияет на общий результат и ею можно пренебречь, ибо она бесконечно мала по сравнению с суммой площадей прямоугольников. Следовательно, для определения искомой поверхности следует подсчитать сумму площадей этих прямоугольников. Каждая из них в отдельности является бесконечно малой величиной (так как основание каждого прямоугольника бесконечно мало), но число прямоугольников бесконечно велико. Таким образом, речь идет о подсчете сумм бесконечно большого количества бесконечно малых величин, то есть о том, что современные математики называют интегрированием. Интегральное исчисление, по крайней мере в своем начале, было искусством подсчета этих сумм и вычисления с их помощью площадей и объемов».
В работах, связанных с циклоидой, Паскаль сделал шаг вперед по сравнению со своими предшественниками на пути дальнейшего совершенствования и обобщения методов интегрирования. Он преобразовал понятие совокупности Кавальери в понятие суммы. При этом, как пишет известный немецкий историк математики Вилейтнер, Паскаль проводил отчетливое различие между неделимыми и элементарными частями и «существенно более общим образом толковал понятие равенства фигур, чем это позволяло употребительное до того определение Евклида. Именно он считал равными две фигуры, если различие между ними меньше любой данной величины. Паскаль с полной ясностью проник в существо интеграционного процесса, заметив, что всякое интегрирование приводится к определению некоторых арифметических сумм. Паскаль подошел к определению интеграла ближе всех своих современников».
Применяя метод неделимых к различным величинам, преобразуя одни виды суммирования в другие, Паскаль в геометрической форме получил фундаментальные результаты, относящиеся к так называемым криволинейным в двойным интегралам, с помощью наглядных конкретных примеров и ясных доказательств, искусного использования приемов современной ему и античной математики упорядочил многие интеграционные проблемы, освободив их от нечетких и приблизительных решений. До прямого открытия интегрального исчисления Паскалю оставалось сделать лишь шаг — определить формальные операции интегрирования и дать его особый вычислительный алгоритм. Но Паскаль этого шага не сделал. Как и прежде, помешали его «геометризм» и антиалгебраическая настроенность, использование прямых конкретных методов. Поэтому славу первооткрывателей интегрального и дифференциального исчисления делят между собой Ньютон и Лейбниц, хотя некоторые исследователи и причисляют Паскаля к ним, исходя из возможности легкого перевода исключительно геометрических рассуждений Блеза на абстрактный язык анализа бесконечно малых.
О возможности такого перевода и извлечения алгоритма из математических трудов Паскаля свидетельствует и признание Лейбница, которое относится к «Трактату о синусах четверти круга» Блеза, связанному с исследованием циклоиды. В 1673 году по совету Гюйгенса немецкий философ познакомился с этим трактатом и, как он сам замечает, был внезапно озарен новым светом. Особое внимание Лейбница привлек чертеж с бесконечно малым треугольником, используемым Блезом для преобразования интегральных сумм. Лейбниц назвал этот треугольник характеристическим, увидев в нем один из основных элементов дифференциального исчисления, и с его помощью подошел к формулировке самих принципов этого исчисления.
Пусть нам дана, пишет Паскаль в лемме «Трактата...», четверть круга ABC (см. рис. 5),
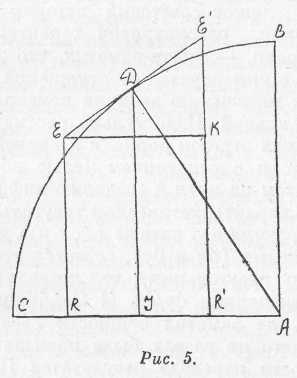где радиус AB рассматривается как ось, а радиус АС — как основание. Возьмем на дуге окружности произвольную точку Д, из которой на основание проводится линия синуса ДI и радиус АД и через которую проходит также касательная ЕЕ'. Из точек E и E' на основание АС опускаются перпендикуляры ER и E'R'. Затем Паскаль строит треугольник ЕКЕ' (данный треугольник Лейбниц и назвал характеристическим), который подобен треугольнику ДIА. Это подобие дает ему пропорцию:
AD/DI= EE1/ЕК,
в которой отношение бесконечно малых величин (EE1/EK) выражено отношением конечных величин AD/DI, и равенство:
ДIxЕЕ' = АДxЕК, илиДIxЕЕ' = АДxRR'.
Если же разделить какую-либо дугу четверти круга на малые части и заменить отрезки касательных эквивалентными им при переходе к пределу малыми дугами, то при интегрировании обеих частей этого равенства получается теорема, которая в «Трактате...» Паскаля звучит так: «Сумма синусов какой-либо дуги четверти круга равна отрезку основания между крайними синусами, умноженному на радиус».
«Лейбниц, — пишет советский историк математики И. Б. Погребысский, рассматривая характеристический треугольник Паскаля, — сразу заметил, что это построение и связанный с ним переход от отношения бесконечно малых величин к отношению величин конечных справедливы для любой кривой. Надо только рассматривать АД не как радиус, а как отрезок нормали к кривой, проведенный до пересечения с основанием (осью абсцисс). Это было важным шагом на пути к созданию дифференциального исчисления: характеристический треугольник при переходе к пределу, когда его катеты (^ х и ^ у) становятся бесконечно малыми (dx и dy), остается все время подобным конечному треугольнику, что позволяет уверенно действовать с отношением dy/dx. И Лейбница удивляло, как это Паскаль не заметил общности своего построения, „словно у него на глазах была повязка“.
О естественности перевода результатов Паскаля при решении задач в связи с циклоидой на терминологию специальных понятий и абстрактной символики интегрального исчисления, а также о четкости его мышления и ясности языка можно судить и по высказыванию известных французских математиков, выступивших под псевдонимом Н. Бурбаки: «Валлис в 1655 году и Паскаль в 1658 году составили каждый для своего употребления языки алгебраического характера, в которых, не записывая ни единой формулы, они дают формулировки, которые можно немедленно, как только будет понят их механизм, записать в формулах интегрального исчисления. Язык Паскаля особенно ясен и точен; и если не всегда понятно, почему он отказался от применения алгебраических обозначений не только Декарта, но и Виета, все же нельзя не восхищаться его мастерством, которое могло проявиться лишь на основе совершенного владения языком».
Если использование этих способов у Кеплера ограничено конкретными задачами, возникавшими в ходе его научной деятельности, то в поисках более общих и систематизированных принципов образования и измерения поверхностей и тел Кавальери ввел и исследовал абстрактное понятие «неделимых». (Подобно Кавальери и независимо от него стал применять неделимые и Роберваль.) Неделимые у Кавальери — это элементы, из которых состоит площадь или объем того или иного геометрического объекта и размерность которых на единицу меньше размерности рассматриваемого объекта. Так, точка является неделимым для линии, прямая — для плоскости и т. д. При этом, например, площадь какой-то плоской фигуры определялась через уже известную площадь другой фигуры в результате сравнения отрезков прямых линий (неделимых), которыми эти фигуры покрывались.
Торричелли, отмечая особое воздействие метода неделимых на развитие математики, писал: «Несомненно, что геометрия Кавальери есть удивительное по своей экономии средство для нахождения теорем и дает возможность разрешить огромное число, казалось бы, неразрешимых теорем краткими, прямыми, наглядными доказательствами, что невозможно сделать по методу древних. Это — истинно царская дорога среди зарослей математического терновника... Метод Кавальери является действительно научным способом доказательства, всегда идущим путем прямым и свойственным самой природе. Жаль мне древней геометрии, что она либо не знала, либо не хотела признавать учения о неделимых...»
Однако, по замечанию советского историка математики Л. С. Фреймана, метод Кавальери страдал существенными логическими противоречиями: «Одним из таких противоречий является то, что неделимое (линия) имеет на одно измерение меньше числа измерений у площади, а совокупность неделимых уже имеет столько же измерений, сколько площадь!» Действительно, при наложении, скажем, друг на друга плоскостей, толщина которых равна нулю, нельзя получить какой-то объем определенной толщины — суммирование нулей дает в итоге нулевой результат.
В своих исследованиях Паскаль преодолел подобные противоречия: он рассматривал неделимые как однородные с измеряемым объектом бесконечно малые величины, из которых и составлялись интегральные суммы. Для демонстрации приемов Паскаля приведем простой пример, упоминаемый французским исследователем его научного творчества Умбертом. Предположим, что необходимо определить площадь криволинейной трапеции АВСД, составленной прямой AB, перпендикулярами к ней АС и ВД и кривой линией СД (см. рис. 4).
Но Паскаль, пишет Умберт, не удовлетворяется простым интуитивным решением: «Он доказывает строгими методами, что сумма площадей этих маленьких треугольников совсем не влияет на общий результат и ею можно пренебречь, ибо она бесконечно мала по сравнению с суммой площадей прямоугольников. Следовательно, для определения искомой поверхности следует подсчитать сумму площадей этих прямоугольников. Каждая из них в отдельности является бесконечно малой величиной (так как основание каждого прямоугольника бесконечно мало), но число прямоугольников бесконечно велико. Таким образом, речь идет о подсчете сумм бесконечно большого количества бесконечно малых величин, то есть о том, что современные математики называют интегрированием. Интегральное исчисление, по крайней мере в своем начале, было искусством подсчета этих сумм и вычисления с их помощью площадей и объемов».
В работах, связанных с циклоидой, Паскаль сделал шаг вперед по сравнению со своими предшественниками на пути дальнейшего совершенствования и обобщения методов интегрирования. Он преобразовал понятие совокупности Кавальери в понятие суммы. При этом, как пишет известный немецкий историк математики Вилейтнер, Паскаль проводил отчетливое различие между неделимыми и элементарными частями и «существенно более общим образом толковал понятие равенства фигур, чем это позволяло употребительное до того определение Евклида. Именно он считал равными две фигуры, если различие между ними меньше любой данной величины. Паскаль с полной ясностью проник в существо интеграционного процесса, заметив, что всякое интегрирование приводится к определению некоторых арифметических сумм. Паскаль подошел к определению интеграла ближе всех своих современников».
Применяя метод неделимых к различным величинам, преобразуя одни виды суммирования в другие, Паскаль в геометрической форме получил фундаментальные результаты, относящиеся к так называемым криволинейным в двойным интегралам, с помощью наглядных конкретных примеров и ясных доказательств, искусного использования приемов современной ему и античной математики упорядочил многие интеграционные проблемы, освободив их от нечетких и приблизительных решений. До прямого открытия интегрального исчисления Паскалю оставалось сделать лишь шаг — определить формальные операции интегрирования и дать его особый вычислительный алгоритм. Но Паскаль этого шага не сделал. Как и прежде, помешали его «геометризм» и антиалгебраическая настроенность, использование прямых конкретных методов. Поэтому славу первооткрывателей интегрального и дифференциального исчисления делят между собой Ньютон и Лейбниц, хотя некоторые исследователи и причисляют Паскаля к ним, исходя из возможности легкого перевода исключительно геометрических рассуждений Блеза на абстрактный язык анализа бесконечно малых.
О возможности такого перевода и извлечения алгоритма из математических трудов Паскаля свидетельствует и признание Лейбница, которое относится к «Трактату о синусах четверти круга» Блеза, связанному с исследованием циклоиды. В 1673 году по совету Гюйгенса немецкий философ познакомился с этим трактатом и, как он сам замечает, был внезапно озарен новым светом. Особое внимание Лейбница привлек чертеж с бесконечно малым треугольником, используемым Блезом для преобразования интегральных сумм. Лейбниц назвал этот треугольник характеристическим, увидев в нем один из основных элементов дифференциального исчисления, и с его помощью подошел к формулировке самих принципов этого исчисления.
Пусть нам дана, пишет Паскаль в лемме «Трактата...», четверть круга ABC (см. рис. 5),
AD/DI= EE1/ЕК,
в которой отношение бесконечно малых величин (EE1/EK) выражено отношением конечных величин AD/DI, и равенство:
ДIxЕЕ' = АДxЕК, илиДIxЕЕ' = АДxRR'.
Если же разделить какую-либо дугу четверти круга на малые части и заменить отрезки касательных эквивалентными им при переходе к пределу малыми дугами, то при интегрировании обеих частей этого равенства получается теорема, которая в «Трактате...» Паскаля звучит так: «Сумма синусов какой-либо дуги четверти круга равна отрезку основания между крайними синусами, умноженному на радиус».
«Лейбниц, — пишет советский историк математики И. Б. Погребысский, рассматривая характеристический треугольник Паскаля, — сразу заметил, что это построение и связанный с ним переход от отношения бесконечно малых величин к отношению величин конечных справедливы для любой кривой. Надо только рассматривать АД не как радиус, а как отрезок нормали к кривой, проведенный до пересечения с основанием (осью абсцисс). Это было важным шагом на пути к созданию дифференциального исчисления: характеристический треугольник при переходе к пределу, когда его катеты (^ х и ^ у) становятся бесконечно малыми (dx и dy), остается все время подобным конечному треугольнику, что позволяет уверенно действовать с отношением dy/dx. И Лейбница удивляло, как это Паскаль не заметил общности своего построения, „словно у него на глазах была повязка“.
О естественности перевода результатов Паскаля при решении задач в связи с циклоидой на терминологию специальных понятий и абстрактной символики интегрального исчисления, а также о четкости его мышления и ясности языка можно судить и по высказыванию известных французских математиков, выступивших под псевдонимом Н. Бурбаки: «Валлис в 1655 году и Паскаль в 1658 году составили каждый для своего употребления языки алгебраического характера, в которых, не записывая ни единой формулы, они дают формулировки, которые можно немедленно, как только будет понят их механизм, записать в формулах интегрального исчисления. Язык Паскаля особенно ясен и точен; и если не всегда понятно, почему он отказался от применения алгебраических обозначений не только Декарта, но и Виета, все же нельзя не восхищаться его мастерством, которое могло проявиться лишь на основе совершенного владения языком».
3
Научные открытия, сделанные Паскалем весенней ночью, — последний всплеск его математической фантазии, а радость победы вскоре омрачается горечью угрызения совести. Блез искренне мучается оттого, что неистребимое libido sciendi, a вместе с ним и опьяняющее libido dominandi вновь проснулись в его душе. Действительно, в конкурсе с циклоидой горделивое тщеславие и нетерпимость к слабостям соперников опять выявляются в его поведении, как уже случалось в годы молодости. Конкурс был организован с намерением показать, что ни один европейский математик не способен соревноваться с Паскалем, и потому Блез так неумолим в отношении краткости его сроков, резко и нетерпеливо реагирует на всякие возражения, подчеркивает достоинство своих трудов и свысока относится к попыткам конкурентов.
Задумываясь над всем этим, он теперь начинает догадываться, что путь к нравственному совершенству не имеет остановок, где можно передохнуть или даже слегка развлечься, что каждый шаг на этом пути в чем-то сложнее предыдущего и что необходимы постоянные новые усилия, чтобы продолжить начатое.
Такому устремлению способствует и новый кризис в состоянии здоровья Паскаля, начавшийся зимой 1659 года. По словам Каркави, Блез находится в изнеможении всех своих сил и любое занятие, требующее хоть малейшего внимания, причиняет ему невероятную боль. Лечение бульонами и молоком ослицы, которое прописали врачи, не помогает, и больной даже не может прочитать присланную ему Слюзом научную брошюру. Когда родные и близкие принимаются жалеть его, Паскаль отвечает, что жалобы тут ни к чему, что он рад своим страданиям и боится вылечиться, что хорошо знает опасность здоровья и «преимущества» болезни: «с ее помощью мы пребываем в таком положении, в каком должны бы находиться всегда — в страдании, горестях, в лишении всех благ и чувственных удовольствий, без всяких страстей и честолюбия, без скупости и в постоянном ожидании смерти».
Жильберта вспоминала, что брат так стойко переносил любые недомогания, как мало кто был способен это делать. Это отношение к собственным страданиям, угрызения совести, новый подъем религиозной ревностности в душе Паскаля необыкновенно ярко проявляются в его покаянном «Молитвенном размышлении об обращении во благо болезней», чрезвычайно важном для понимания последних лет жизни Блеза.
Вот некоторые фрагменты из него:
«Господи... ты даровал мне здоровье на служение Тебе, а я истратил его для суетных целей. Теперь Ты посылаешь мне болезнь, чтобы исправить меня: не допусти же меня прогневать Тебя моим нетерпением. Я злоупотребил своим здоровьем, и Ты справедливо покарал меня. Помоги мне извлечь должную пользу из Твоего наказания... Если сердце мое было полно привязанности к миру, пока в нем была некоторая сила, — уничтожь эту силу для моего спасения и сделай меня неспособным наслаждаться миром: ослабив ли мое тело или возбудив во мне пыл любви к ближним, чтобы наслаждаться мне одним Тобою... Отверзи сердце мое, Господи, войди в это мятежное место, занятое пороками. Они держат его в своей власти. Войди в него, как в жилище укрепившегося; но свяжи сначала крепкого и сильного врага, который им владеет, и тогда возьми лежащие в нем сокровища... Да пожелаю отныне здоровья и жизни только для того, чтобы пользоваться ими и окончить ее для Тебя, с Тобою и в Тебе».
В разные времена и у разных читателей это душеизлияние Паскаля вызывало целую гамму чувств — от восхищения и сопереживания до саркастической насмешки. В Паскалевой «молитве» слышали отзвук библейских псалмов с их поэтикой покаянности и исповедальной обнаженности сердца и предельное выражение аскетической самоизолированности.
Блез, как видим, горько сожалеет, что когда-то считал здоровье благом и использовал его на вкушение «гибельных удовольствий жизни». Он надеется, что телесные страдания окажут врачующее воздействие на его душевные недуги, величайший из которых состоит в неспособности души ощущать свою собственную нищету и неустанно раскаиваться в сделанных ею согрешениях. Теперь он лучше, чем когда-либо, видит пределы человеческих возможностей и вносит поправки в основной труд своей жизни.
Задумываясь над всем этим, он теперь начинает догадываться, что путь к нравственному совершенству не имеет остановок, где можно передохнуть или даже слегка развлечься, что каждый шаг на этом пути в чем-то сложнее предыдущего и что необходимы постоянные новые усилия, чтобы продолжить начатое.
Такому устремлению способствует и новый кризис в состоянии здоровья Паскаля, начавшийся зимой 1659 года. По словам Каркави, Блез находится в изнеможении всех своих сил и любое занятие, требующее хоть малейшего внимания, причиняет ему невероятную боль. Лечение бульонами и молоком ослицы, которое прописали врачи, не помогает, и больной даже не может прочитать присланную ему Слюзом научную брошюру. Когда родные и близкие принимаются жалеть его, Паскаль отвечает, что жалобы тут ни к чему, что он рад своим страданиям и боится вылечиться, что хорошо знает опасность здоровья и «преимущества» болезни: «с ее помощью мы пребываем в таком положении, в каком должны бы находиться всегда — в страдании, горестях, в лишении всех благ и чувственных удовольствий, без всяких страстей и честолюбия, без скупости и в постоянном ожидании смерти».
Жильберта вспоминала, что брат так стойко переносил любые недомогания, как мало кто был способен это делать. Это отношение к собственным страданиям, угрызения совести, новый подъем религиозной ревностности в душе Паскаля необыкновенно ярко проявляются в его покаянном «Молитвенном размышлении об обращении во благо болезней», чрезвычайно важном для понимания последних лет жизни Блеза.
Вот некоторые фрагменты из него:
«Господи... ты даровал мне здоровье на служение Тебе, а я истратил его для суетных целей. Теперь Ты посылаешь мне болезнь, чтобы исправить меня: не допусти же меня прогневать Тебя моим нетерпением. Я злоупотребил своим здоровьем, и Ты справедливо покарал меня. Помоги мне извлечь должную пользу из Твоего наказания... Если сердце мое было полно привязанности к миру, пока в нем была некоторая сила, — уничтожь эту силу для моего спасения и сделай меня неспособным наслаждаться миром: ослабив ли мое тело или возбудив во мне пыл любви к ближним, чтобы наслаждаться мне одним Тобою... Отверзи сердце мое, Господи, войди в это мятежное место, занятое пороками. Они держат его в своей власти. Войди в него, как в жилище укрепившегося; но свяжи сначала крепкого и сильного врага, который им владеет, и тогда возьми лежащие в нем сокровища... Да пожелаю отныне здоровья и жизни только для того, чтобы пользоваться ими и окончить ее для Тебя, с Тобою и в Тебе».
В разные времена и у разных читателей это душеизлияние Паскаля вызывало целую гамму чувств — от восхищения и сопереживания до саркастической насмешки. В Паскалевой «молитве» слышали отзвук библейских псалмов с их поэтикой покаянности и исповедальной обнаженности сердца и предельное выражение аскетической самоизолированности.
Блез, как видим, горько сожалеет, что когда-то считал здоровье благом и использовал его на вкушение «гибельных удовольствий жизни». Он надеется, что телесные страдания окажут врачующее воздействие на его душевные недуги, величайший из которых состоит в неспособности души ощущать свою собственную нищету и неустанно раскаиваться в сделанных ею согрешениях. Теперь он лучше, чем когда-либо, видит пределы человеческих возможностей и вносит поправки в основной труд своей жизни.
«Мысли»
1
Один из современных западных исследователей творчества Паскаля, оценивая вклад французского мыслителя в мировую культуру, пишет: «На свете великое множество тех, кто любит Паскаля. Но кто любит Декарта? И кто любит Канта?»
В этой полемической заостренности есть известная доля правоты. Дело не только в обстоятельствах личной жизни названных мыслителей, но прежде всего в характере их мыслительной деятельности. Паскаля невозможно отнести к категории философов-профессионалов, создателей философских систем. Само это слово «философ» в его словаре имеет смысл несовершенного, ограниченного знания. И хотя о Паскале вполне можно говорить как об историке философии (вспомним его критику стоицизма, скептицизма и эпикуреизма), хотя можно говорить об оригинальной теории познания Паскаля, но в первую очередь о нем должно говорить как о создателе своеобразнейшей этики. Человековедение Паскаля выражало себя в традиционных для его времени понятиях и рамках религиозности. В этом смысле он мало чем отличался от большинства, причем подавляющего большинства ученых умов эпохи: вспомним хотя бы нашего Ломоносова, кстати, очень высоко отзывавшегося о Пасхалии (так транскрибировалась фамилия Блеза в России XVIII века).
Да, Паскаль-моралист говорил на языке своей эпохи, но сумел выразить с помощью этого языка, иногда для нас, людей XX столетия, уже отчасти невнятного, требующего пояснений, великие общечеловеческие истины, которые остаются насущными и по сей день. В этом смысле к Паскалю безусловно применимы известные ленинские слова о том, что «исторические заслуги судятся не по тому, чего не дали исторические деятели сравнительно с современными требованиями, а по тому, что они дали нового сравнительно с своими предшественниками»[24].
Паскаль, как уже упоминалось, оказался в центре «переворачивания» средневековой картины мира, когда теоцентризм уступал место антропоцентризму, утверждавшему человека мерой всей, целиком от его деятельности и планов зависимой, действительности, а религиозные догматы стали замещаться истинами, основанными на опытных данных и рациональном анализе. Этот антропологический поворот способствовал атеистическому сдвигу в сознании людей. Паскаль ясно представляет себе все аспекты подобного сдвига, что заметно, в частности, по «Письмам к провинциалу», и относится к нему весьма неравнодушно.
По мнению Паскаля, провозглашенное возрожденцами величие независимого человека есть в некотором роде преувеличение, опасный крен в сторону его самообожествления. Возрожденческое миропонимание полагает, что в неистощимой плодовитости самой природы, которая мыслится здоровой и не нуждающейся в изменении и восстановлении, подобный человек сможет найти объяснение всем фактам своего бытия, собственной мудростью определить и исполнить свое предназначение, обеспечить полное развитие своих способностей и сил, а в конечном итоге полностью завоевать и подчинить эту природу.
Паскаль счел необходимым обсудить подобные положения, показав границы идеалов «жизни по природе». Но он не был бы самим собой, если бы задался только подобной умозрительной целью. Почти все его научные, философские и полемические труды, как мы помним, вытекали из конкретных обстоятельств его жизни. В этом отношении не является исключением и задуманное им сочинение.
XVII столетие во Франции было не только «веком святых», но веком вольнодумцев. Так, например, Мерсенн в одном Париже насчитывал около пятидесяти тысяч атеистов. Против них в это время принимались суровые меры наказания (отрезание губ, языка, сожжение). Паскаль считает, что подобные меры могут породить только страх, а не уважение к религии. Вольнодумцы (буквально «сильные умы» — esprits forts) заявляют о своей вере лишь в то, что можно увидеть и потрогать. «Атеизм является признаком ума, — соглашается Паскаль, — но только до известной степени»: можно ли гордиться положением вещей, ведущих человека к «ожиданию безнадежного уничтожения среди непроницаемого мрака»? Так, вероятно, вопрошал Паскаль вольнодумцев из Пуату, с которыми ему пришлось столкнуться в 1652 году. К этой дате и восходит, видимо, первый замысел «Апологии...», который долгое время остается невоплощенным и меняется с течением времени, ориентируясь на внимательно изучаемую им в эти годы светскую среду. «Порядочные люди» были не то чтобы враждебны, но глубоко безразличны к религии, считая ее вслед за Макиавелли удобным орудием в руках политиков, не задумывались о последних целях своего существования и «собирали розы жизни», отдаваясь удовольствиям, заключая, как советовал Монтень, «брак между необходимостью и наслаждением». Поэтому одна из главных целей апологии заключается в том, чтобы нарушить безразличное спокойствие людей и способствовать изменению состояния их духа. Для выполнения этой цели Паскаль считает бесполезным доказывать существование бога через произведения природы. Не намеревается он использовать и метафизические доказательства схоластиков и философов наподобие Декартовых, которые отдалены от обычных рассуждений большинства людей, удовлетворяют только ученый ум и ведут к деизму. В своей апологии Паскаль настроен полемически по отношению к такой позиции.
Отправляясь от радикального методологического сомнения во всем существующем, Декарт, как известно, приходил к одному неоспоримому, на его взгляд, положению: существование человека достоверно постольку, поскольку он сомневается, то есть мыслит. «Следовательно, я, строго говоря, — только мыслящая вещь...» С такой же ясностью и отчетливостью перед «мыслящей вещью» предстает и то, что в человеке, как существе сомневающемся, то есть конечном и несовершенном, врожденно присутствует идея существа бесконечного и совершенного. В самом факте присутствия в нас этой идеи Декарт видел следствие существования совершенной надчеловеческой реальности, «бесконечной субстанции». Таким образом, бог Декарта является, как сказал бы Паскаль, «Богом философов и ученых», творцом геометрических истин, санкционирующим познание мира и не вмешивающимся в его дела.
Паскаль считает подобные доказательства существования «бесконечной субстанции» малодейственными: «Не только невозможно, но и бесполезно знать Бога без Иисуса Христа». В своей апологии Паскаль хочет как раз выделить и подчеркнуть отсутствующие у Декарта доказательства.
Но чтобы расположить души «порядочных людей» к восприятию этих доказательств, он пытается найти с ними общий язык, прибегая к близким для них понятиям и проблемам (разум, счастье, справедливость, собственный интерес, самолюбие, привычка и т. д.). Для этого он использует выделенный Возрождением антропологический принцип, то есть исходит из общего рассмотрения человеческой природы, из наблюдений (их каждый может проверить) над сложным богатством конкретной внутренней жизни людей, над неизгладимыми противоречиями и напряжениями в любом срезе живой действительности. Именно это движение, а не систему, неизбежный переход от одного плана к другому, осуществляемый при участии не только интеллекта «мыслящей вещи», как у Декарта, а всех присущих человеку сил и способностей (сердца, разума, воли и т. д.), и хочет навязать Паскаль вниманию «порядочных людей».
Материалы для апологии Блезу дает прежде всего изучаемая им жизнь современников, опыт собственных сомнений, колебаний и внутренних поворотов (и в известном отношении апология носит автобиографический характер).
В этой полемической заостренности есть известная доля правоты. Дело не только в обстоятельствах личной жизни названных мыслителей, но прежде всего в характере их мыслительной деятельности. Паскаля невозможно отнести к категории философов-профессионалов, создателей философских систем. Само это слово «философ» в его словаре имеет смысл несовершенного, ограниченного знания. И хотя о Паскале вполне можно говорить как об историке философии (вспомним его критику стоицизма, скептицизма и эпикуреизма), хотя можно говорить об оригинальной теории познания Паскаля, но в первую очередь о нем должно говорить как о создателе своеобразнейшей этики. Человековедение Паскаля выражало себя в традиционных для его времени понятиях и рамках религиозности. В этом смысле он мало чем отличался от большинства, причем подавляющего большинства ученых умов эпохи: вспомним хотя бы нашего Ломоносова, кстати, очень высоко отзывавшегося о Пасхалии (так транскрибировалась фамилия Блеза в России XVIII века).
Да, Паскаль-моралист говорил на языке своей эпохи, но сумел выразить с помощью этого языка, иногда для нас, людей XX столетия, уже отчасти невнятного, требующего пояснений, великие общечеловеческие истины, которые остаются насущными и по сей день. В этом смысле к Паскалю безусловно применимы известные ленинские слова о том, что «исторические заслуги судятся не по тому, чего не дали исторические деятели сравнительно с современными требованиями, а по тому, что они дали нового сравнительно с своими предшественниками»[24].
Паскаль, как уже упоминалось, оказался в центре «переворачивания» средневековой картины мира, когда теоцентризм уступал место антропоцентризму, утверждавшему человека мерой всей, целиком от его деятельности и планов зависимой, действительности, а религиозные догматы стали замещаться истинами, основанными на опытных данных и рациональном анализе. Этот антропологический поворот способствовал атеистическому сдвигу в сознании людей. Паскаль ясно представляет себе все аспекты подобного сдвига, что заметно, в частности, по «Письмам к провинциалу», и относится к нему весьма неравнодушно.
По мнению Паскаля, провозглашенное возрожденцами величие независимого человека есть в некотором роде преувеличение, опасный крен в сторону его самообожествления. Возрожденческое миропонимание полагает, что в неистощимой плодовитости самой природы, которая мыслится здоровой и не нуждающейся в изменении и восстановлении, подобный человек сможет найти объяснение всем фактам своего бытия, собственной мудростью определить и исполнить свое предназначение, обеспечить полное развитие своих способностей и сил, а в конечном итоге полностью завоевать и подчинить эту природу.
Паскаль счел необходимым обсудить подобные положения, показав границы идеалов «жизни по природе». Но он не был бы самим собой, если бы задался только подобной умозрительной целью. Почти все его научные, философские и полемические труды, как мы помним, вытекали из конкретных обстоятельств его жизни. В этом отношении не является исключением и задуманное им сочинение.
XVII столетие во Франции было не только «веком святых», но веком вольнодумцев. Так, например, Мерсенн в одном Париже насчитывал около пятидесяти тысяч атеистов. Против них в это время принимались суровые меры наказания (отрезание губ, языка, сожжение). Паскаль считает, что подобные меры могут породить только страх, а не уважение к религии. Вольнодумцы (буквально «сильные умы» — esprits forts) заявляют о своей вере лишь в то, что можно увидеть и потрогать. «Атеизм является признаком ума, — соглашается Паскаль, — но только до известной степени»: можно ли гордиться положением вещей, ведущих человека к «ожиданию безнадежного уничтожения среди непроницаемого мрака»? Так, вероятно, вопрошал Паскаль вольнодумцев из Пуату, с которыми ему пришлось столкнуться в 1652 году. К этой дате и восходит, видимо, первый замысел «Апологии...», который долгое время остается невоплощенным и меняется с течением времени, ориентируясь на внимательно изучаемую им в эти годы светскую среду. «Порядочные люди» были не то чтобы враждебны, но глубоко безразличны к религии, считая ее вслед за Макиавелли удобным орудием в руках политиков, не задумывались о последних целях своего существования и «собирали розы жизни», отдаваясь удовольствиям, заключая, как советовал Монтень, «брак между необходимостью и наслаждением». Поэтому одна из главных целей апологии заключается в том, чтобы нарушить безразличное спокойствие людей и способствовать изменению состояния их духа. Для выполнения этой цели Паскаль считает бесполезным доказывать существование бога через произведения природы. Не намеревается он использовать и метафизические доказательства схоластиков и философов наподобие Декартовых, которые отдалены от обычных рассуждений большинства людей, удовлетворяют только ученый ум и ведут к деизму. В своей апологии Паскаль настроен полемически по отношению к такой позиции.
Отправляясь от радикального методологического сомнения во всем существующем, Декарт, как известно, приходил к одному неоспоримому, на его взгляд, положению: существование человека достоверно постольку, поскольку он сомневается, то есть мыслит. «Следовательно, я, строго говоря, — только мыслящая вещь...» С такой же ясностью и отчетливостью перед «мыслящей вещью» предстает и то, что в человеке, как существе сомневающемся, то есть конечном и несовершенном, врожденно присутствует идея существа бесконечного и совершенного. В самом факте присутствия в нас этой идеи Декарт видел следствие существования совершенной надчеловеческой реальности, «бесконечной субстанции». Таким образом, бог Декарта является, как сказал бы Паскаль, «Богом философов и ученых», творцом геометрических истин, санкционирующим познание мира и не вмешивающимся в его дела.
Паскаль считает подобные доказательства существования «бесконечной субстанции» малодейственными: «Не только невозможно, но и бесполезно знать Бога без Иисуса Христа». В своей апологии Паскаль хочет как раз выделить и подчеркнуть отсутствующие у Декарта доказательства.
Но чтобы расположить души «порядочных людей» к восприятию этих доказательств, он пытается найти с ними общий язык, прибегая к близким для них понятиям и проблемам (разум, счастье, справедливость, собственный интерес, самолюбие, привычка и т. д.). Для этого он использует выделенный Возрождением антропологический принцип, то есть исходит из общего рассмотрения человеческой природы, из наблюдений (их каждый может проверить) над сложным богатством конкретной внутренней жизни людей, над неизгладимыми противоречиями и напряжениями в любом срезе живой действительности. Именно это движение, а не систему, неизбежный переход от одного плана к другому, осуществляемый при участии не только интеллекта «мыслящей вещи», как у Декарта, а всех присущих человеку сил и способностей (сердца, разума, воли и т. д.), и хочет навязать Паскаль вниманию «порядочных людей».
Материалы для апологии Блезу дает прежде всего изучаемая им жизнь современников, опыт собственных сомнений, колебаний и внутренних поворотов (и в известном отношении апология носит автобиографический характер).
2
С тех пор как Паскаль задумал свое сочинение, до начала практической работы над ним прошло несколько лет. Хотя он в это время и размышлял над его проблемами, но почти ничего не записывал из-за недостатка времени, отнимаемого болезнями, деятельностью в Пор-Рояле и полемикой с иезуитами. Лишь с середины 1657 года Блез вплотную занялся основным трудом своей жизни, рассчитывая затратить на него около десяти лет. Записи он делает на больших листах, распределяя на них различные фрагменты в зависимости от соответствующей темы. Однако новый кризис здоровья, начавшийся зимой 1659 года, не позволяет ему производить дальнейшую классификацию. Более того, отныне он с трудом записывает свои мысли на первом попавшемся клочке бумаги, не развивая и не дополняя их, а лишь намечая основную проблему. Спустя какое-то время он обнаружил, что не в состоянии даже диктовать, и вовсе прекратил работу над апологией.