Будем рассматривать только тот случай, когда все множества A∑, B∑,D∑, E∑, F∑, S∑ конечны. Пересечение каждой пары множеств А∑, В∑, D∑, Е∑, F∑, S∑ представляет собой конечное пустое множество.
Модель полной системы.
● Полной системой S назовем совокупность взаимосвязанных элементов a ∈ A, е ∈ Е (A ⊆ A∑, , E ⊆ E∑) и осуществляемых ими элементарных процессов в ∈ В, d ∈ D (B ⊆ В∑ D ⊆ D∑), предназначенную для достижения цели F, связанной с выпуском определенного изделия (продукта) SF, SF ⊆ SF∑, F ⊆ F∑.
Модель полной системы (математическую модель полной системы) S определим, как конечную алгебраическую систему
S= < { A, В, D, Е }, W, Φ >, (3.3.1)
состоящую из множества-носителя {А, B, D, Е}, множества операций W={W1, W2, …, Wl } и множества предикатов Φ={Φ1, Φ2, …, Φr}.
Для описания всех необходимых взаимосвязей в модели системы (3.3.1) используем два множества: W∑ и Φ∑. Множество W∑ является множеством всех операций, используемых при анализе и синтезе всех моделей S из множества S∑. Множество операций W используется для определенной модели S. Множество S∑ – это множество моделей системы S, причем каждая модель S отражает одну технологию изготовления одного изделия, выпуска одного продукта (или его модификации). Множество W∑ может содержать теоретико-множественные операции объединения, пересечения и другие.
Множество Φ∑ содержит предикаты, используемые для описания отношений на множествах-носителях всех моделей системы. Множество главных предикатов Φ содержит предикаты Φ1-Φr, определяющие отношения связи на {A, В, D, E}, которые должны соответствовать цели F изготовления «изделия SF», F ⊆ F∑, SF ⊆ SF∑ . Переход от модели системы S для одной технологии изготовления изделия к модели другой технологии осуществляется путем замены одной совокупности A,B,D,E,W,Φ на другую. Используя эти совокупности для технологий изготовления всех изделий, можно составить множество S∑ всех моделей S данной системы, S ⊆ S∑..
* В модели (3.3.1) для конкретной реализации системы S, значение предиката Φj ⊂ Φ равно 1 (истинно), если взаимосвязи между элементами множества-носителя соответствуют выбранной технологии изготовления изделия. Множество главных предикатов Φ описывает взаимосвязи, необходимые для конкретной реализации S. Минимально необходим, независимо от природы системы, набор предикатов, устанавливающих такое подмножество отношений взаимосвязи, которое можно представить связным подграфом, без петель, покрывающим все вершины графа отношений. Кроме того, с помощью элементов множества Φ и введения дополнительных предикатов можно описать различные технологические маршруты изготовления узлов и блоков, сборки изделия, подготовки документов, разработки проектов, изготовления управленческого решения и т.д. Переход от модели изготовления изделия F к модели для изготовления другого изделия осуществляется путем замены множества главных предикатов Φ на другое. Реализовать необходимые переходы от одной модели к другой можно установлением набора состояний «взаимодействие разрешено» и «взаимодействие исключено» в элементах е ∈ Е.
* В процессе формирования конкретной модели системы используются операции множества W (напр. при декомпозиции системы), состав которого определяется в зависимости от задач анализа и синтеза системы. Во многих важных приложениях достаточно, если множество-носитель образуете с W решетку или алгебру Кантора.
Формирование конкретной модели системы с определенным набором элементов из {A, B, D, E} и множества Φ может производиться следующим образом. Будем считать, что множества A∑, B∑, D∑, E∑ определены, как наборы элементов, пригодных для всех возможных конкретных реализаций S.
Вначале устанавливается некоторое отношение на множестве B∑, т.е. выбираются и упорядочиваются процессы b ∈ В, B ⊆ B∑. Тем самым упорядочивается набор элементарных процессов достижения цели, который должен обеспечить системный процесс достижения цели, для реализации которого, в данном случае, нужна система S. Одновременно устанавливается необходимость обеспечения взаимодействий для пар процессов из В∑, определяются требования к элементарным взаимодействиям со стороны каждого процесса b, b ∈ В∑.
Затем устанавливается отношение на паре множеств В∑, A∑, определяются и упорядочиваются основные элементы из А∑, обеспечивающие выбранный набор процессов из В∑, А ⊆ А∑, В ⊆ В∑.
Параллельно устанавливается некоторое отношение на паре множеств В∑, D∑ и определяется набор элементарных процессов взаимодействия d∈ D, D ⊆ D∑ , обеспечивающих взаимодействие между элементарными процессами b, b ∈ В. При этом, для учета ограничений на элементарные процессы d ∈ D со стороны элементов множества А, устанавливается отношение на паре A, D.
И, наконец, устанавливаются отношения на паре D∑, Е∑, позволяющие сформировать набор элементов е ∈ Е, E ⊆ E∑ ,которые войдут в данную реализацию системы. Для учета ограничений на элементы е ∈ Е со стороны элементов множеств А и В должны быть установлены соответствующие отношения на парах А, Е и В, D.
* В процессе формирования модели конкретной реализации S описанная последовательность многократно повторяется и образует, в конечном счете, системный процесс достижения цели (модель которого описана в разделе 4.1) в некоторой системе-субъекте по созданию системы S. В качестве ресурсов выступают описания возможностей использования различных видов ресурсов для достижения некоторой глобальной цели, поставленной перед создаваемой системой; в качестве методов выступают описания различных процессов, которые можно реализовать для достижения цели.
Вначале описывается глобальная цель создания системы (этап 1), затем возможные виды ресурсов для построения элементов системы (этап 2), далее – процессы использования ресурсов (этап 3), которые можно реализовать в системе и ограничения (этап 4), накладываемые на цель, ресурсы, процессы. Затем выбирается конкретный процесс использования ресурсов для достижения цели (этап 7), процесс апробируется (этап 5), оценивается (этап 6). Если не возникает необходимости создания системы, то найденный процесс используется для достижения глобальной цели. Но в большинстве случаев оказывается, что имеющиеся ресурсы позволяют достичь глобальную цель только в виде процесса последовательного достижения ряда частных целей. Поэтому на следующих циклах производится преобразование глобальной цели в систему F локальных (на уровне подсистем) и, далее, элементарных целей (на уровне элементов) (этап 1); тогда этапы 2,3,4 будут заключаться в создании системы S на множествах элементов из имеющихся ресурсов и элементарных процессов с учетом ограничений, этапы 5,6,7 будут заключаться в анализе вариантов конкретной реализации системы. В результате на некотором уровне элементарности будут сформированы множества типа {А, B, D, Е}, описывающие модели конкретных реализаций системы для различных целей, соответствующих различным возможным изделиям и продуктам системы.
* В соответствии с принципом системности можно определить, в данном случае, что создаваемая система S является системой-объектом S0, система целей F, описывающая изделие системы, является системой-результатом SF Для моделирования системы-объекта и системы-результата должна использоваться одна модель общей системы (3.3.1).
Таким образом, предлагаемый подход позволяет проводить исследование F и S по отдельности, учитывая отношения взаимосвязи, которые устанавливает между ними создающая система – субъект Sc .
Отношения взаимосвязи, которые установятся в результате, между элементами систем F и S, обозначим через ψi и ψi-1, I ∈ {A, B, D, E}.
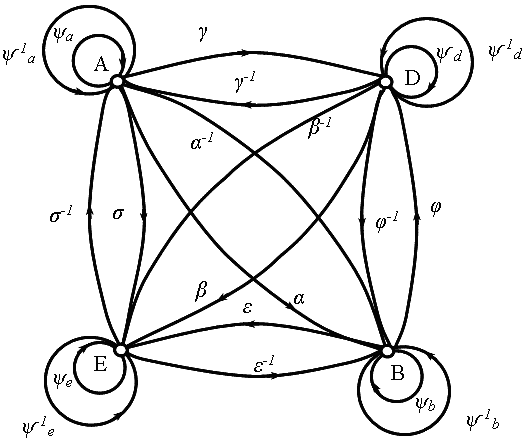
* Модели F и S и множества A, B, D, E описывают ряд взаимосвязей, которые некоторая создающая система устанавливает для конкретной реализации S. Они в обобщенной форме показаны и обозначены на рис.3.1 а,б в виде графов, вершинами которых являются множества A, B, D, E , F, а ребрами – отношения взаимосвязи. Так, через α обозначено отношение α, α ⊆ A × B, описывающее тот факт, что каждый элемент системы аi, ai ⊆ A, реализует один и только один элементарный процесс достижения цели bi, bi ∈В. В свою очередь, отношение α-1 описывает взаимосвязи такого вида: элементарный процесс достижения цели bi ∈ B, реализуется одним элементом ai ∈A. Аналогичным образом описываются все остальные взаимосвязи.
Для наглядности ориентированный граф отношений показан на рис. 3.1а, 3.1б, в виде двух подграфов. Вершины графа – множества, ребра – отношения между ними. Ребра без весов отражают отношения включения множеств.
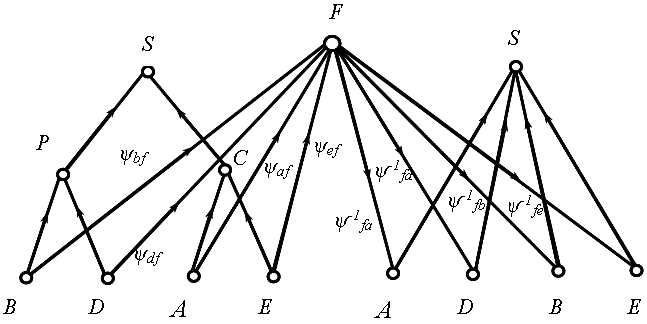
* Каждый путь на этом графе, проходящий множества А, В, D , E, F, P, С в какой-либо последовательности, отражает определенный порядок действий при осуществлении какой-либо деятельности (исследование или проектирование системы, технологический процесс изготовления изделия) и может описываться каким-либо дополнительным или главным предикатом. В свою очередь, каждое минимальное покрытие всех вершин графа определений описывает режим системы,
отвечающий решению отдельных задач. Так, путь F – B – A – D – E на графе определений и отношений отражают простейшую последовательность формирования системы, создаваемую для реализации процесса достижения цели, описанную в начале раздела, путь А – F – D – F – B – F отражает последовательность прохождения предмета труда в технологическом процессе и т.д.
 a)
a)
 б)
б)
 в)
в)
Рис. 3.1. Графы отношениий.
Модели процесса и структуры.
* В общем случае каждому элементу ai из А соответствует некоторое подмножество элементарных процессов взаимодействия Di ⊂ D, через которые ai воздействует на другие элементы множества А. Каждому элементу aj из А соответствует также некоторое множество элементарных процессов взаимодействия Dj ⊂ D, через которые aj подвергается воздействию других элементов из А. Пересечение Di ⋂ Dj = Dij множество элементарных процессов взаимодействия, через которые ai воздействует на aj (для упрощения в дальнейшем примем, что Dij — одноэлементные множества: Dij = {dij}). В противном случае соответствующее обстоятельство будем специально оговаривать. Будем считать, что аналогичным образом выделены подмножества элементов Ei, Ej, Eij, обеспечивающие, соответственно, множества процессов взаимодействия Di, Dj, Dij.
* Будем считать, что главным предикатам Φ1-Φr соответствуют отношения ψA, ψB, ψD, ψE строгого частичного порядка и отношения α, α-1, β, β-1, σ, σ-1, φ, φ-1, ψAF, ψ-1AF, ψ-1BF, ψDF, ψ-1DF, ψEF, ψ-1EF. Предположим, что на всех моделях, как полной системы, так и ее частей (основная и дополнительная системы, структура и процесс системы) сохраняются главные операции W.
* Сформулируем теперь модели процесса и структуры системы. Далее, если это не требует специальных разъяснений, все дальнейшее изложение будем вести для модели конкретной реализации системы с набором главных предикатов Φ; множества А, В, D, Е линейно упорядочены; для описания связей выберем отношения α, β, σ, φ, ψв, , и, соответственно , α-1, β-1, σ-1, φ-1, ψ-1в. Для описания взаимосвязи с F выберем отношение ψ вf. Выбор такого набора отношений соответствует наиболее распространенной схеме формирования системы, уже описанной в начале раздела в виде процесса достижения цели, когда для достижения системы целей F формируется множество элементарных процессов В. Будем считать, что главные предикаты Φ1 ÷ Φr описывают только выбранные бинарные отношения. Можно выбрать и другой набор отношений; при любом наборе отношений, устанавливающих взаимосвязи между всеми множествами А, В, D, E, F, будут справедливы результаты, полученные ниже.
* Модели процесса и структуры системы определим в следующем виде.
Процесс Р системы S (назовем его также полным системным процессом) – это множество взаимосвязанных элементарных процессов:
P = < {B, D}, W, Φp >; Φр ⊂ Φ. (3.3.2)
Структура С системы S (назовем ее также полной системной структурой) – это множество взаимосвязанных элементов системы:
С = < {A, E}, W, Φc >; Φс ⊂ Φ. (3.3.3)
* В соответствии с принятыми исходными положениями моделирования системы имеет место взаимнооднозначное соответствие между элементами множеств А и В. Взаимнооднозначное соответствие имеет место также между элементами множеств E и D; следовательно, имеет место взaимнооднoзначное соответствие между элементами множеств-носителей в (3.3.2) и (3.3.3). Имеется также взаимнооднозначное соответствие между каждыми двумя упорядоченными парами (аi, ej ) и (вi, dj), что однозначно следует из исходных положений описания с помощью сигнатуры Φ целенаправленного процесса формирования модели (3.3.1). Следовательно, имеется взаимнооднозначное соответствие между элементами сигнатур Φр и Φс , Φр ⇔ Φс. Далее, любая операция из Wc, например, объединение элементов а, а ∈ А и е, е ∈ E, взаимнооднозначно соответствует такой же операции из Wp, т.е., в данном случае, объединению процессов в, в ∈ B и d, d ∈ D. Следовательно, Wp = Wc. Но так как Wp ⊂ Wc , Wc ⊂ W и W \ {Wp ⋃ Wc} = ∅, то Wp = Wc = W. Итак, доказана следующая
Теорема 3.1. Для модели системы S модели процесса Р и структуры С изоморфны.
* Модели полных, основных и дополнительных системных объектов.
На основе (3.3.1)–(3.3.3) сформулируем следующий результат.
Теорема 3.2. Модель полной системы S – это совокупность моделей процесса Р и структуры С:
S = < P,C,Φ(α),Φ(α-1),Φ(β),Φ(β-1)> (3.3.4)
* Полный процесс системы Р мы представляем как объединение основного процесса достижения цели Рa и системного процесса взаимодействия Ре. Хотя нами рассматриваются системы, создаваемые для реализации процесса, все результаты системной технологии могут быть применены для систем, предназначенных для реализации структуры. В системах, предназначенных для реализации системного процесса достижения цели, основные элементы системы а реализуют элементарные процессы достижения цели в. Но элементарные процессы достижения цели не могут объединяться в системный процесс Pа, минуя элементарные процессы взаимодействия d. Следовательно, необходимо описать вклад, вносимый элементарными процессами взаимодействия, в системный процесс достижения цели. Это участие не является целенаправленным, как в случае элементарных процессов достижения цели в, и, как правило, приводит к некоторому ухудшению Pa. Допустимое влияние элементарного процесса взаимодействия должно, видимо, заключаться в том, чтобы вносить какие-либо допустимые изменения в процесс достижения цели Pa при «передаче» предмета труда от одного элементарного процесса достижения цели вi к некоторому другому элементарному процессу достижения цели вj. Обозначим это допустимое изменение δd — изменение результатов некоторого элементарного процесса вi при «передаче» предмета труда к некоторому другому «следующему» элементарному процессу вj. Множество этих изменений обозначим Δd, т.е. δd ∈ Δd. Отсюда вытекает следующая теорема.
Теорема 3.3. Каждый элементарный процесс взаимодействия d, d ∈ D, между некоторыми двумя элементарными процессами достижения цели вi и вj (вi, вj ∈ В) объединяет в себе собственно элементарный процесс взаимодействия d0 и элементарный процесс обеспечения ограничения δd:
d = { d0, δd }; d0 ∈ D0; δd ∈ Δd; D = { D0, Δd }. (3.3.5)
Системный процесс взаимодействия Рe, в свою очередь, реализуется в системе элементами взаимодействия е. Но элементарные процессы взаимодействия d, которые ими реализуются, не могут быть объединены в системный процесс взаимодействия Pе без участия элементарных процессов достижения цели в. Участие элементарных процессов достижения цели в в процессе Pe (аналогично учету участия элементарных процессов d в процессе Pa) должно быть учтено введением ограничений δв на изменение характеристик элементарных процессов взаимодействия при «переходе» через некоторый элементарный процесс из В («обеспечение взаимодействия между элементарными взаимодействиями»). Множество этих ограничений обозначим Δв, т.е. δв ∈ Δв.
Отсюда следует
Теорема 3.4. Каждый элементарный процесс в, в ∈ В, реализуемый элементом а ∈ А, объединяет в себе собственно элементарный процесс достижения цели в0 и элементарный процесс обеспечения ограничения δв:
в = {в0 , δв }; в0 ∈ В0 ; δв ∈ Δв , В = { В0 , Δв }. (3.3.6)
Пересечения D0 ⋂ Δd и В0 ⋂ Δв не обязательно пустые множества.
* Полученные результаты и наличие взаимнооднозначных соответствий между элементами множеств А и В, а также между элементами множеств Е и D, соответственно, позволяют сформулировать следующую теорему.
Теорема 3.5. Элементы а и е разложимы на части, реализующие части процессов в и d:
а = {а0, δa}; а0 ∈ A0; δa ∈ Δa; А = {A0 , Δa};
e = { e0, δе }; e0 ∈ E0; δе ∈ Δe; E= { E0, Δe}; (3.3.7)
* В качестве обобщения сформулируем следующий результат.
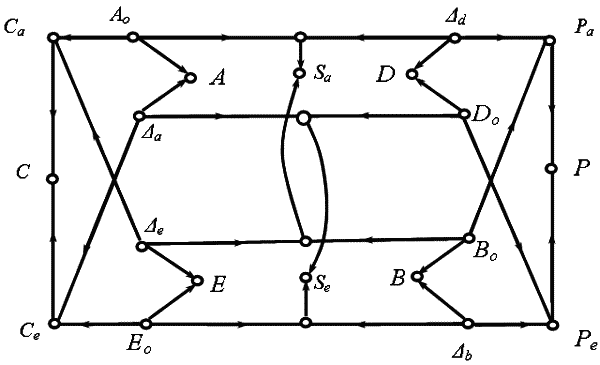
Теорема 3.6. Элементы а, е (а ∈ А, е ∈ Е) и элементарные процессы в, d (в ∈ В, d ∈ D) в модели системы S разложимы на части, образующие структуры Ca, Ce и процессы Рa, Ре основной Sa и дополнительной Sе систем.
Следуя доказанному, сформулируем следующие результаты.
* Системный процесс достижения цели Рa представит собой объединения элементарных процессов достижения цели в0 и процессов обеспечения ограничений на допустимое изменение результатов элементарных процессов достижения цели δd при передаче результатов одного элементарного процесса достижения цели к другому. Отсюда следует, что
Модель основного системного процесса Рa имеет вид:
Рa = < { B0, Δd }, W, Φp >. (3.3.8а)
* Системный процесс взаимодействия, в свою очередь, представит собой объединение элементарных процессов взаимодействия d0 и процессов обеспечения ограничений на допустимое изменение характеристик взаимодействия δв при «передаче взаимодействия» через процессы достижения цели. Отсюда следует, что
Модель дополнительного системного процесса Ре имеет вид:
Ре =< { D0, Δa }, W, Φp >. (3.3.8b)
* Следуя (3.3.7) и (3.3.8), можно сформулировать следующие определения структур.
Модель основной системной структуры Ca имеет вид:
Ca = < { A0, Δe }, W, Φc >. (3.3.9а)
Модель дополнительной системной структуры Сe имеет вид:
Сe = < {Δa, E0 }, W, Φc >. (3.3.9b)
• Исходя из (3.3.4), где доказано, что система – это объединение процесса и структуры, определим основную и дополнительную системы.
Модель основной системы Sa имеет вид:
Sa = <{Pa, Ca }, W, Φ>; Sa = <{A0, B0, Δd, Δe}, W,Φ>. (3.3.10)
Модель дополнительной системы Se имеет вид:
Se= <{Pe, Ce}, W, Φ>; Se = <{Δa, Δв , D0, E0}, W, Φ>. (3.3.11)
* Другими словами, полная система S — это объединение полного системного процесса Р и полной системной структуры С, основная система Sa — это объединение системного процесса достижения цели Pa и структуры для его реализации Сa, а дополнительная система Se — это объединение системного процесса взаимодействия Pe и структуры для его реализации Ce.
Модель полной системы.
● Полной системой S назовем совокупность взаимосвязанных элементов a ∈ A, е ∈ Е (A ⊆ A∑, , E ⊆ E∑) и осуществляемых ими элементарных процессов в ∈ В, d ∈ D (B ⊆ В∑ D ⊆ D∑), предназначенную для достижения цели F, связанной с выпуском определенного изделия (продукта) SF, SF ⊆ SF∑, F ⊆ F∑.
Модель полной системы (математическую модель полной системы) S определим, как конечную алгебраическую систему
S= < { A, В, D, Е }, W, Φ >, (3.3.1)
состоящую из множества-носителя {А, B, D, Е}, множества операций W={W1, W2, …, Wl } и множества предикатов Φ={Φ1, Φ2, …, Φr}.
Для описания всех необходимых взаимосвязей в модели системы (3.3.1) используем два множества: W∑ и Φ∑. Множество W∑ является множеством всех операций, используемых при анализе и синтезе всех моделей S из множества S∑. Множество операций W используется для определенной модели S. Множество S∑ – это множество моделей системы S, причем каждая модель S отражает одну технологию изготовления одного изделия, выпуска одного продукта (или его модификации). Множество W∑ может содержать теоретико-множественные операции объединения, пересечения и другие.
Множество Φ∑ содержит предикаты, используемые для описания отношений на множествах-носителях всех моделей системы. Множество главных предикатов Φ содержит предикаты Φ1-Φr, определяющие отношения связи на {A, В, D, E}, которые должны соответствовать цели F изготовления «изделия SF», F ⊆ F∑, SF ⊆ SF∑ . Переход от модели системы S для одной технологии изготовления изделия к модели другой технологии осуществляется путем замены одной совокупности A,B,D,E,W,Φ на другую. Используя эти совокупности для технологий изготовления всех изделий, можно составить множество S∑ всех моделей S данной системы, S ⊆ S∑..
* В модели (3.3.1) для конкретной реализации системы S, значение предиката Φj ⊂ Φ равно 1 (истинно), если взаимосвязи между элементами множества-носителя соответствуют выбранной технологии изготовления изделия. Множество главных предикатов Φ описывает взаимосвязи, необходимые для конкретной реализации S. Минимально необходим, независимо от природы системы, набор предикатов, устанавливающих такое подмножество отношений взаимосвязи, которое можно представить связным подграфом, без петель, покрывающим все вершины графа отношений. Кроме того, с помощью элементов множества Φ и введения дополнительных предикатов можно описать различные технологические маршруты изготовления узлов и блоков, сборки изделия, подготовки документов, разработки проектов, изготовления управленческого решения и т.д. Переход от модели изготовления изделия F к модели для изготовления другого изделия осуществляется путем замены множества главных предикатов Φ на другое. Реализовать необходимые переходы от одной модели к другой можно установлением набора состояний «взаимодействие разрешено» и «взаимодействие исключено» в элементах е ∈ Е.
* В процессе формирования конкретной модели системы используются операции множества W (напр. при декомпозиции системы), состав которого определяется в зависимости от задач анализа и синтеза системы. Во многих важных приложениях достаточно, если множество-носитель образуете с W решетку или алгебру Кантора.
Формирование конкретной модели системы с определенным набором элементов из {A, B, D, E} и множества Φ может производиться следующим образом. Будем считать, что множества A∑, B∑, D∑, E∑ определены, как наборы элементов, пригодных для всех возможных конкретных реализаций S.
Вначале устанавливается некоторое отношение на множестве B∑, т.е. выбираются и упорядочиваются процессы b ∈ В, B ⊆ B∑. Тем самым упорядочивается набор элементарных процессов достижения цели, который должен обеспечить системный процесс достижения цели, для реализации которого, в данном случае, нужна система S. Одновременно устанавливается необходимость обеспечения взаимодействий для пар процессов из В∑, определяются требования к элементарным взаимодействиям со стороны каждого процесса b, b ∈ В∑.
Затем устанавливается отношение на паре множеств В∑, A∑, определяются и упорядочиваются основные элементы из А∑, обеспечивающие выбранный набор процессов из В∑, А ⊆ А∑, В ⊆ В∑.
Параллельно устанавливается некоторое отношение на паре множеств В∑, D∑ и определяется набор элементарных процессов взаимодействия d∈ D, D ⊆ D∑ , обеспечивающих взаимодействие между элементарными процессами b, b ∈ В. При этом, для учета ограничений на элементарные процессы d ∈ D со стороны элементов множества А, устанавливается отношение на паре A, D.
И, наконец, устанавливаются отношения на паре D∑, Е∑, позволяющие сформировать набор элементов е ∈ Е, E ⊆ E∑ ,которые войдут в данную реализацию системы. Для учета ограничений на элементы е ∈ Е со стороны элементов множеств А и В должны быть установлены соответствующие отношения на парах А, Е и В, D.
* В процессе формирования модели конкретной реализации S описанная последовательность многократно повторяется и образует, в конечном счете, системный процесс достижения цели (модель которого описана в разделе 4.1) в некоторой системе-субъекте по созданию системы S. В качестве ресурсов выступают описания возможностей использования различных видов ресурсов для достижения некоторой глобальной цели, поставленной перед создаваемой системой; в качестве методов выступают описания различных процессов, которые можно реализовать для достижения цели.
Вначале описывается глобальная цель создания системы (этап 1), затем возможные виды ресурсов для построения элементов системы (этап 2), далее – процессы использования ресурсов (этап 3), которые можно реализовать в системе и ограничения (этап 4), накладываемые на цель, ресурсы, процессы. Затем выбирается конкретный процесс использования ресурсов для достижения цели (этап 7), процесс апробируется (этап 5), оценивается (этап 6). Если не возникает необходимости создания системы, то найденный процесс используется для достижения глобальной цели. Но в большинстве случаев оказывается, что имеющиеся ресурсы позволяют достичь глобальную цель только в виде процесса последовательного достижения ряда частных целей. Поэтому на следующих циклах производится преобразование глобальной цели в систему F локальных (на уровне подсистем) и, далее, элементарных целей (на уровне элементов) (этап 1); тогда этапы 2,3,4 будут заключаться в создании системы S на множествах элементов из имеющихся ресурсов и элементарных процессов с учетом ограничений, этапы 5,6,7 будут заключаться в анализе вариантов конкретной реализации системы. В результате на некотором уровне элементарности будут сформированы множества типа {А, B, D, Е}, описывающие модели конкретных реализаций системы для различных целей, соответствующих различным возможным изделиям и продуктам системы.
* В соответствии с принципом системности можно определить, в данном случае, что создаваемая система S является системой-объектом S0, система целей F, описывающая изделие системы, является системой-результатом SF Для моделирования системы-объекта и системы-результата должна использоваться одна модель общей системы (3.3.1).
Таким образом, предлагаемый подход позволяет проводить исследование F и S по отдельности, учитывая отношения взаимосвязи, которые устанавливает между ними создающая система – субъект Sc .
Отношения взаимосвязи, которые установятся в результате, между элементами систем F и S, обозначим через ψi и ψi-1, I ∈ {A, B, D, E}.
* Модели F и S и множества A, B, D, E описывают ряд взаимосвязей, которые некоторая создающая система устанавливает для конкретной реализации S. Они в обобщенной форме показаны и обозначены на рис.3.1 а,б в виде графов, вершинами которых являются множества A, B, D, E , F, а ребрами – отношения взаимосвязи. Так, через α обозначено отношение α, α ⊆ A × B, описывающее тот факт, что каждый элемент системы аi, ai ⊆ A, реализует один и только один элементарный процесс достижения цели bi, bi ∈В. В свою очередь, отношение α-1 описывает взаимосвязи такого вида: элементарный процесс достижения цели bi ∈ B, реализуется одним элементом ai ∈A. Аналогичным образом описываются все остальные взаимосвязи.
Для наглядности ориентированный граф отношений показан на рис. 3.1а, 3.1б, в виде двух подграфов. Вершины графа – множества, ребра – отношения между ними. Ребра без весов отражают отношения включения множеств.
* Каждый путь на этом графе, проходящий множества А, В, D , E, F, P, С в какой-либо последовательности, отражает определенный порядок действий при осуществлении какой-либо деятельности (исследование или проектирование системы, технологический процесс изготовления изделия) и может описываться каким-либо дополнительным или главным предикатом. В свою очередь, каждое минимальное покрытие всех вершин графа определений описывает режим системы,
отвечающий решению отдельных задач. Так, путь F – B – A – D – E на графе определений и отношений отражают простейшую последовательность формирования системы, создаваемую для реализации процесса достижения цели, описанную в начале раздела, путь А – F – D – F – B – F отражает последовательность прохождения предмета труда в технологическом процессе и т.д.



Рис. 3.1. Графы отношениий.
Модели процесса и структуры.
* В общем случае каждому элементу ai из А соответствует некоторое подмножество элементарных процессов взаимодействия Di ⊂ D, через которые ai воздействует на другие элементы множества А. Каждому элементу aj из А соответствует также некоторое множество элементарных процессов взаимодействия Dj ⊂ D, через которые aj подвергается воздействию других элементов из А. Пересечение Di ⋂ Dj = Dij множество элементарных процессов взаимодействия, через которые ai воздействует на aj (для упрощения в дальнейшем примем, что Dij — одноэлементные множества: Dij = {dij}). В противном случае соответствующее обстоятельство будем специально оговаривать. Будем считать, что аналогичным образом выделены подмножества элементов Ei, Ej, Eij, обеспечивающие, соответственно, множества процессов взаимодействия Di, Dj, Dij.
* Будем считать, что главным предикатам Φ1-Φr соответствуют отношения ψA, ψB, ψD, ψE строгого частичного порядка и отношения α, α-1, β, β-1, σ, σ-1, φ, φ-1, ψAF, ψ-1AF, ψ-1BF, ψDF, ψ-1DF, ψEF, ψ-1EF. Предположим, что на всех моделях, как полной системы, так и ее частей (основная и дополнительная системы, структура и процесс системы) сохраняются главные операции W.
* Сформулируем теперь модели процесса и структуры системы. Далее, если это не требует специальных разъяснений, все дальнейшее изложение будем вести для модели конкретной реализации системы с набором главных предикатов Φ; множества А, В, D, Е линейно упорядочены; для описания связей выберем отношения α, β, σ, φ, ψв, , и, соответственно , α-1, β-1, σ-1, φ-1, ψ-1в. Для описания взаимосвязи с F выберем отношение ψ вf. Выбор такого набора отношений соответствует наиболее распространенной схеме формирования системы, уже описанной в начале раздела в виде процесса достижения цели, когда для достижения системы целей F формируется множество элементарных процессов В. Будем считать, что главные предикаты Φ1 ÷ Φr описывают только выбранные бинарные отношения. Можно выбрать и другой набор отношений; при любом наборе отношений, устанавливающих взаимосвязи между всеми множествами А, В, D, E, F, будут справедливы результаты, полученные ниже.
* Модели процесса и структуры системы определим в следующем виде.
Процесс Р системы S (назовем его также полным системным процессом) – это множество взаимосвязанных элементарных процессов:
P = < {B, D}, W, Φp >; Φр ⊂ Φ. (3.3.2)
Структура С системы S (назовем ее также полной системной структурой) – это множество взаимосвязанных элементов системы:
С = < {A, E}, W, Φc >; Φс ⊂ Φ. (3.3.3)
* В соответствии с принятыми исходными положениями моделирования системы имеет место взаимнооднозначное соответствие между элементами множеств А и В. Взаимнооднозначное соответствие имеет место также между элементами множеств E и D; следовательно, имеет место взaимнооднoзначное соответствие между элементами множеств-носителей в (3.3.2) и (3.3.3). Имеется также взаимнооднозначное соответствие между каждыми двумя упорядоченными парами (аi, ej ) и (вi, dj), что однозначно следует из исходных положений описания с помощью сигнатуры Φ целенаправленного процесса формирования модели (3.3.1). Следовательно, имеется взаимнооднозначное соответствие между элементами сигнатур Φр и Φс , Φр ⇔ Φс. Далее, любая операция из Wc, например, объединение элементов а, а ∈ А и е, е ∈ E, взаимнооднозначно соответствует такой же операции из Wp, т.е., в данном случае, объединению процессов в, в ∈ B и d, d ∈ D. Следовательно, Wp = Wc. Но так как Wp ⊂ Wc , Wc ⊂ W и W \ {Wp ⋃ Wc} = ∅, то Wp = Wc = W. Итак, доказана следующая
Теорема 3.1. Для модели системы S модели процесса Р и структуры С изоморфны.
* Модели полных, основных и дополнительных системных объектов.
На основе (3.3.1)–(3.3.3) сформулируем следующий результат.
Теорема 3.2. Модель полной системы S – это совокупность моделей процесса Р и структуры С:
S = < P,C,Φ(α),Φ(α-1),Φ(β),Φ(β-1)> (3.3.4)
* Полный процесс системы Р мы представляем как объединение основного процесса достижения цели Рa и системного процесса взаимодействия Ре. Хотя нами рассматриваются системы, создаваемые для реализации процесса, все результаты системной технологии могут быть применены для систем, предназначенных для реализации структуры. В системах, предназначенных для реализации системного процесса достижения цели, основные элементы системы а реализуют элементарные процессы достижения цели в. Но элементарные процессы достижения цели не могут объединяться в системный процесс Pа, минуя элементарные процессы взаимодействия d. Следовательно, необходимо описать вклад, вносимый элементарными процессами взаимодействия, в системный процесс достижения цели. Это участие не является целенаправленным, как в случае элементарных процессов достижения цели в, и, как правило, приводит к некоторому ухудшению Pa. Допустимое влияние элементарного процесса взаимодействия должно, видимо, заключаться в том, чтобы вносить какие-либо допустимые изменения в процесс достижения цели Pa при «передаче» предмета труда от одного элементарного процесса достижения цели вi к некоторому другому элементарному процессу достижения цели вj. Обозначим это допустимое изменение δd — изменение результатов некоторого элементарного процесса вi при «передаче» предмета труда к некоторому другому «следующему» элементарному процессу вj. Множество этих изменений обозначим Δd, т.е. δd ∈ Δd. Отсюда вытекает следующая теорема.
Теорема 3.3. Каждый элементарный процесс взаимодействия d, d ∈ D, между некоторыми двумя элементарными процессами достижения цели вi и вj (вi, вj ∈ В) объединяет в себе собственно элементарный процесс взаимодействия d0 и элементарный процесс обеспечения ограничения δd:
d = { d0, δd }; d0 ∈ D0; δd ∈ Δd; D = { D0, Δd }. (3.3.5)
Системный процесс взаимодействия Рe, в свою очередь, реализуется в системе элементами взаимодействия е. Но элементарные процессы взаимодействия d, которые ими реализуются, не могут быть объединены в системный процесс взаимодействия Pе без участия элементарных процессов достижения цели в. Участие элементарных процессов достижения цели в в процессе Pe (аналогично учету участия элементарных процессов d в процессе Pa) должно быть учтено введением ограничений δв на изменение характеристик элементарных процессов взаимодействия при «переходе» через некоторый элементарный процесс из В («обеспечение взаимодействия между элементарными взаимодействиями»). Множество этих ограничений обозначим Δв, т.е. δв ∈ Δв.
Отсюда следует
Теорема 3.4. Каждый элементарный процесс в, в ∈ В, реализуемый элементом а ∈ А, объединяет в себе собственно элементарный процесс достижения цели в0 и элементарный процесс обеспечения ограничения δв:
в = {в0 , δв }; в0 ∈ В0 ; δв ∈ Δв , В = { В0 , Δв }. (3.3.6)
Пересечения D0 ⋂ Δd и В0 ⋂ Δв не обязательно пустые множества.
* Полученные результаты и наличие взаимнооднозначных соответствий между элементами множеств А и В, а также между элементами множеств Е и D, соответственно, позволяют сформулировать следующую теорему.
Теорема 3.5. Элементы а и е разложимы на части, реализующие части процессов в и d:
а = {а0, δa}; а0 ∈ A0; δa ∈ Δa; А = {A0 , Δa};
e = { e0, δе }; e0 ∈ E0; δе ∈ Δe; E= { E0, Δe}; (3.3.7)
* В качестве обобщения сформулируем следующий результат.
Теорема 3.6. Элементы а, е (а ∈ А, е ∈ Е) и элементарные процессы в, d (в ∈ В, d ∈ D) в модели системы S разложимы на части, образующие структуры Ca, Ce и процессы Рa, Ре основной Sa и дополнительной Sе систем.
Следуя доказанному, сформулируем следующие результаты.
* Системный процесс достижения цели Рa представит собой объединения элементарных процессов достижения цели в0 и процессов обеспечения ограничений на допустимое изменение результатов элементарных процессов достижения цели δd при передаче результатов одного элементарного процесса достижения цели к другому. Отсюда следует, что
Модель основного системного процесса Рa имеет вид:
Рa = < { B0, Δd }, W, Φp >. (3.3.8а)
* Системный процесс взаимодействия, в свою очередь, представит собой объединение элементарных процессов взаимодействия d0 и процессов обеспечения ограничений на допустимое изменение характеристик взаимодействия δв при «передаче взаимодействия» через процессы достижения цели. Отсюда следует, что
Модель дополнительного системного процесса Ре имеет вид:
Ре =< { D0, Δa }, W, Φp >. (3.3.8b)
* Следуя (3.3.7) и (3.3.8), можно сформулировать следующие определения структур.
Модель основной системной структуры Ca имеет вид:
Ca = < { A0, Δe }, W, Φc >. (3.3.9а)
Модель дополнительной системной структуры Сe имеет вид:
Сe = < {Δa, E0 }, W, Φc >. (3.3.9b)
• Исходя из (3.3.4), где доказано, что система – это объединение процесса и структуры, определим основную и дополнительную системы.
Модель основной системы Sa имеет вид:
Sa = <{Pa, Ca }, W, Φ>; Sa = <{A0, B0, Δd, Δe}, W,Φ>. (3.3.10)
Модель дополнительной системы Se имеет вид:
Se= <{Pe, Ce}, W, Φ>; Se = <{Δa, Δв , D0, E0}, W, Φ>. (3.3.11)
* Другими словами, полная система S — это объединение полного системного процесса Р и полной системной структуры С, основная система Sa — это объединение системного процесса достижения цели Pa и структуры для его реализации Сa, а дополнительная система Se — это объединение системного процесса взаимодействия Pe и структуры для его реализации Ce.
Конец бесплатного ознакомительного фрагмента
