Страница:

Илья Ветров
Курс Го для новичков на основе правил по стандарту AGA
http://okruzhor.narod.ru/AGA_66/index.htm#SUMM
Посвящается Галине с благодарностью за идею, помощь и поддержку.
"Мастера выплетали узоры из каменных кружев"
– Д.Кедрин "Зодчие"
Облавные шашки 6*6
Перед Вами рассказ о чрезвычайно древней логической игре. В Японии она называется Го, в Корее – Бадук, в Китае – Вейчи (буквально – облавные шашки).
По разным оценкам ее возраст – от двух до четырех тысяч лет.
Несколько последних столетий японские профессиональные игроки были сильнейшими в мире, но в 20-м веке их догнали профессионалы из Китая и Кореи.
Люди многих поколений развлекались этой игрой и при этом учились ловить удачу и исправлять ошибки, строить планы и оценивать риск, искать золотую середину и жертвовать хорошим ради лучшего, воевать и торговать. Го тренирует память и внимание, интуицию и логику.
Сегодня, как и всегда, Го – современная игра. Можно гордиться человеческим разумом, который научил машину обыгрывать человека в шахматы. Но еще более удивительно, что существует логическая игра, в которой человеческий ум намного сильнее искусственного интеллекта.
У каждого игрока в Го – свой индивидуальный стиль игры, который постепенно развивается вместе с личностью. Играя и тренируясь, Вы сможете пробуждать и укреплять свои способности, решать внутренние проблемы и переживать богатейшую гамму эмоций. Го всегда будет с Вами, пока Вы этого хотите – в детстве и в старости, в бедности и в богатстве. Никогда не станет одиноким человек, способный через увлекательную игру общаться с современными и древними игроками.
Более 40 лет Го развивается в России.
Во многих городах открыты школы и клубы, проходят турниры. Наши игроки успешно выступают на европейских первенствах. Нас много на игровых серверах Го в интернете. Приходите, вам будут рады!
По разным оценкам ее возраст – от двух до четырех тысяч лет.
Несколько последних столетий японские профессиональные игроки были сильнейшими в мире, но в 20-м веке их догнали профессионалы из Китая и Кореи.
Люди многих поколений развлекались этой игрой и при этом учились ловить удачу и исправлять ошибки, строить планы и оценивать риск, искать золотую середину и жертвовать хорошим ради лучшего, воевать и торговать. Го тренирует память и внимание, интуицию и логику.
Сегодня, как и всегда, Го – современная игра. Можно гордиться человеческим разумом, который научил машину обыгрывать человека в шахматы. Но еще более удивительно, что существует логическая игра, в которой человеческий ум намного сильнее искусственного интеллекта.
У каждого игрока в Го – свой индивидуальный стиль игры, который постепенно развивается вместе с личностью. Играя и тренируясь, Вы сможете пробуждать и укреплять свои способности, решать внутренние проблемы и переживать богатейшую гамму эмоций. Го всегда будет с Вами, пока Вы этого хотите – в детстве и в старости, в бедности и в богатстве. Никогда не станет одиноким человек, способный через увлекательную игру общаться с современными и древними игроками.
Более 40 лет Го развивается в России.
Во многих городах открыты школы и клубы, проходят турниры. Наши игроки успешно выступают на европейских первенствах. Нас много на игровых серверах Го в интернете. Приходите, вам будут рады!
Глава 1. Обзор правил игры
Правила Го просты и естественны, но сильно отличаются от правил других игр. Сегодня в мире существует несколько версий правил Го. Различия между ними относятся в основном к началу и окончанию игры и редко проявляются в тактике.
Большинство турниров проходит по японским правилам, но здесь описывается более простая и логичная система – правила AGA (Американской Ассоциации Го).
– В Го играют вдвоем на доске с квадратной сеткой. Игровыми пунктами считаются не клетки, а точки пересечения линий, в том числе на сторонах и в углах сетки. В стандартном комплекте на доске начерчены 19 вертикальных и 19 горизонтальных линий, которые дают 361 игровой пункт. Тренироваться можно и на доске с меньшим числом точек, например 13*13 или 9*9. В этом курсе применяется формат 6*6.
– Каждый игрок имеет чашу с запасом одинаковых камней, у одного игрока черные камни, у другого белые. В стандартном комплекте 181 черный камень и 180 белых.
– Игроки ходят по очереди, выставляя камни из своих чаш на свободные точки доски. Начинают черные.
– Цель игры – вплотную окружать камни противника и снимать их с доски, а также окружать пустые территории.
– Можно ставить собственные камни в полное окружение, только если при этом снимаются чужие камни. Нельзя повторять позицию, бывшую раньше в той же партии.
– Игра закончена, если черные и белые подряд пропустили ход. Затем нужно подсчитать съеденные (то есть снятые с доски) камни, точки окруженных территорий и пропущенные ходы и по итогам определить победителя. При равенстве очков побеждают белые.
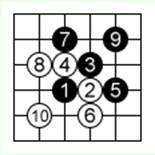 Диаграммa 1.
Диаграммa 1.
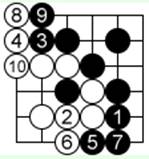 Диаграммa 2.
Диаграммa 2.
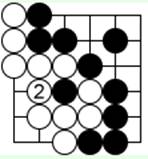 Диаграммa 3.
Диаграммa 3.
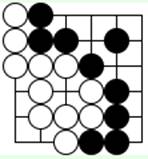 Диаграммa 4.
Диаграммa 4.
Диаграммы 1…4 показывают учебную партию на доске 6*6. Ходы 21, 23 и 24 пропущены – игроки сделали пасы.
Ход 6: иначе черные займут эту точку и снимут камень 2.
Ход 9: гарантирует соединение 3 черных камней (3, 5 и 7).
Ход 10: ловит черный камень 1 и укрепляет белые камни.
Ход 11: угрожает группе из 2 белых камней (2 и 6).
Ходы 13…19: оформление границ территорий.
Ход 20: спасает 2 белых камня (14 и 18).
Ход 22: снятие черного камня.
Партия завершилась двумя пасами подряд (вместо ходов 23 и 24). Черные не сняли с доски ни одного белого камня, окружили 11 пустых точек и пропустили 2 хода (21 и 23). Белые сняли 1 черный камень, окружили 5 точек территории и пропустили 1 ход (24-й). Каждый пас – потеря 1 очка.
Результат: черные выиграли (0+11+1) – (1+5+2) = 4 очка.
Большинство турниров проходит по японским правилам, но здесь описывается более простая и логичная система – правила AGA (Американской Ассоциации Го).
– В Го играют вдвоем на доске с квадратной сеткой. Игровыми пунктами считаются не клетки, а точки пересечения линий, в том числе на сторонах и в углах сетки. В стандартном комплекте на доске начерчены 19 вертикальных и 19 горизонтальных линий, которые дают 361 игровой пункт. Тренироваться можно и на доске с меньшим числом точек, например 13*13 или 9*9. В этом курсе применяется формат 6*6.
– Каждый игрок имеет чашу с запасом одинаковых камней, у одного игрока черные камни, у другого белые. В стандартном комплекте 181 черный камень и 180 белых.
– Игроки ходят по очереди, выставляя камни из своих чаш на свободные точки доски. Начинают черные.
– Цель игры – вплотную окружать камни противника и снимать их с доски, а также окружать пустые территории.
– Можно ставить собственные камни в полное окружение, только если при этом снимаются чужие камни. Нельзя повторять позицию, бывшую раньше в той же партии.
– Игра закончена, если черные и белые подряд пропустили ход. Затем нужно подсчитать съеденные (то есть снятые с доски) камни, точки окруженных территорий и пропущенные ходы и по итогам определить победителя. При равенстве очков побеждают белые.




Диаграммы 1…4 показывают учебную партию на доске 6*6. Ходы 21, 23 и 24 пропущены – игроки сделали пасы.
Ход 6: иначе черные займут эту точку и снимут камень 2.
Ход 9: гарантирует соединение 3 черных камней (3, 5 и 7).
Ход 10: ловит черный камень 1 и укрепляет белые камни.
Ход 11: угрожает группе из 2 белых камней (2 и 6).
Ходы 13…19: оформление границ территорий.
Ход 20: спасает 2 белых камня (14 и 18).
Ход 22: снятие черного камня.
Партия завершилась двумя пасами подряд (вместо ходов 23 и 24). Черные не сняли с доски ни одного белого камня, окружили 11 пустых точек и пропустили 2 хода (21 и 23). Белые сняли 1 черный камень, окружили 5 точек территории и пропустили 1 ход (24-й). Каждый пас – потеря 1 очка.
Результат: черные выиграли (0+11+1) – (1+5+2) = 4 очка.
Глава 2. Взятие одиночного камня
Задачи:
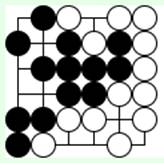 Задача 1 (ход черных)
Задача 1 (ход черных)
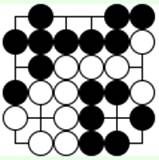 Задача 2 (ход белых)
Задача 2 (ход белых)
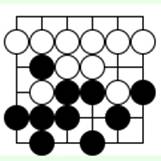 Задача 3 (ход черных)
Задача 3 (ход черных)
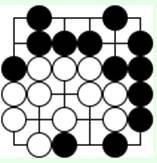 Задача 4 (ход белых)
Задача 4 (ход белых)
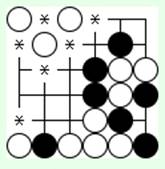 Диаграмма 5
Диаграмма 5
Около каждого одиночного камня на доске должны быть соседние (по вертикали или горизонтали) свободные точки – ДАМЭ. У камня в углу может быть 1 или 2 дамэ, на стороне – от 1 до 3 дамэ, в других точках от 1 до 4 дамэ. Состояние камня с единственным дамэ называется АТАРИ.
На 5-й диаграмме все дамэ одиночных белых камней отмечены (*). Белый камень в левом нижнем углу находится в атари. А сколько здесь черных камней в положении атари?
Если Вы заняли последнее дамэ чужого камня, тогда сразу же снимите этот камень с доски и храните его у себя. В конце игры нужно будет сосчитать все снятые камни.
Одним ходом можно окружить и снять несколько камней. Могут ли белые на 5-й диаграмме сделать такой ход?
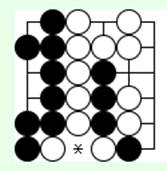 Диаграмма 6
Диаграмма 6
Вы можете поставить свой камень в окружение, если при этом окружаете один или несколько чужих камней, потому что чужие камни Вы снимете этим же ходом, и у поставленного камня появятся дамэ.
На 6-й диаграмме (*) отмечает возможный ход черных со снятием белых камней, а на 7-й виден результат этого хода. Как нужно играть белым при своем ходе на 6-й диаграмме?
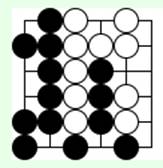 Диаграмма 7
Диаграмма 7
Запрещено делать ход, после которого свой камень оказался бы окруженным. Ставить свой камень в атари можно, иногда жертва бывает выгодной.
Запрещено делать ход, после которого повторилась бы прежняя расстановка всех камней на доске, бывшая когда-либо раньше в партии при той же очереди хода.
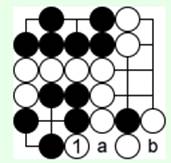 Диаграмма 8
Диаграмма 8
На 8-й диаграмме (ход черных) отмечены запрещенные ходы после того, как белые ходом '1' съели черный камень в точке 'a'.
Если теперь черные пойдут в точку 'a', повторится расстановка перед предыдущим ходом, и очередь хода снова будет у белых. Такой повтор запрещен.
Если же черные пойдут в точку 'b', их камень окажется окруженным, а все белые камни останутся на доске. Такое самоубийство запрещено.





Около каждого одиночного камня на доске должны быть соседние (по вертикали или горизонтали) свободные точки – ДАМЭ. У камня в углу может быть 1 или 2 дамэ, на стороне – от 1 до 3 дамэ, в других точках от 1 до 4 дамэ. Состояние камня с единственным дамэ называется АТАРИ.
На 5-й диаграмме все дамэ одиночных белых камней отмечены (*). Белый камень в левом нижнем углу находится в атари. А сколько здесь черных камней в положении атари?
Если Вы заняли последнее дамэ чужого камня, тогда сразу же снимите этот камень с доски и храните его у себя. В конце игры нужно будет сосчитать все снятые камни.
Одним ходом можно окружить и снять несколько камней. Могут ли белые на 5-й диаграмме сделать такой ход?

Вы можете поставить свой камень в окружение, если при этом окружаете один или несколько чужих камней, потому что чужие камни Вы снимете этим же ходом, и у поставленного камня появятся дамэ.
На 6-й диаграмме (*) отмечает возможный ход черных со снятием белых камней, а на 7-й виден результат этого хода. Как нужно играть белым при своем ходе на 6-й диаграмме?

Запрещено делать ход, после которого свой камень оказался бы окруженным. Ставить свой камень в атари можно, иногда жертва бывает выгодной.
Запрещено делать ход, после которого повторилась бы прежняя расстановка всех камней на доске, бывшая когда-либо раньше в партии при той же очереди хода.

На 8-й диаграмме (ход черных) отмечены запрещенные ходы после того, как белые ходом '1' съели черный камень в точке 'a'.
Если теперь черные пойдут в точку 'a', повторится расстановка перед предыдущим ходом, и очередь хода снова будет у белых. Такой повтор запрещен.
Если же черные пойдут в точку 'b', их камень окажется окруженным, а все белые камни останутся на доске. Такое самоубийство запрещено.
Ответы на задачи 1-4.

Если черные съедят 1 камень, белые спасут 2 своих, и у черных на 1 трофейный камень меньше, чем при правильном ответе.

После хода белых 'b' и хода черных 'a' белые получают на 1 камень меньше, чем черные.
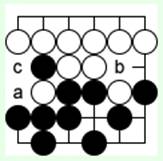
После черного 'b' и белого 'c' оба съели поровну.

После белого 'b' и черного 'a' белые получат на один камень меньше, чем при правильном ответе.
Глава 3. Окружение групп
Задачи:
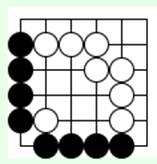 Задача 5 (ход черных)
Задача 5 (ход черных)
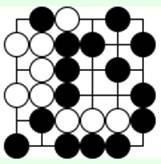 Задача 6 (ход белых)
Задача 6 (ход белых)
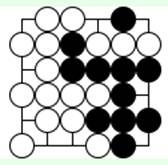 Задача 7 (ход черных)
Задача 7 (ход черных)
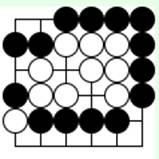 Задача 8 (ход белых)
Задача 8 (ход белых)
 Диаграмма 9
Диаграмма 9
ГРУППА – это камни одного цвета, стоящие вплотную друг к другу. На 9-й диаграмме показаны 2 черные группы (из 3 и из 12 камней) и 3 белые группы (из 2, 4 и 10 камней).
Для окружения группы противник должен занять все ее дамэ, то есть соседние свободные точки, в том числе внутренние.
На той же 9-й диаграмме все дамэ черных групп отмечены (*). Какая из этих групп находится в состоянии атари? В какую из отмеченных точек лучше пойти белым при своем ходе и какой ход для них запрещен?
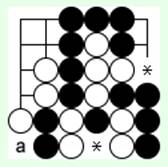 Диаграмма 10
Диаграмма 10
Правила окружения групп и запреты остаются такими же, как для одиночных камней. На 10-й диаграмме 'a' отмечает запрещенный ход черных, а (*) – возможные ходы черных со снятием белых групп. Какой из двух этих ходов лучше?
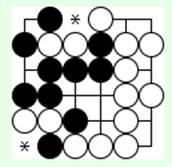 Диаграмма 11
Диаграмма 11
На 11-й диаграмме (ход белых) обе белые группы в положении атари обречены, захвачены. Если белые займут последнее дамэ (*), их группа останется под атари и может быть съедена следующим ходом черных (каким?).
В 5-й главе описаны ситуации, когда группа может жить вечно при любых атаках противника, а также когда группа обречена даже при наличии множества дамэ.
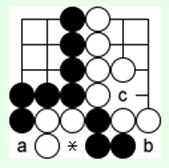 Диаграмма 12
Диаграмма 12
На 12-й диаграмме показана схватка между черной и белой группой из трех камней. Обе группы имеют по 2 дамэ, и здесь выиграет тот, чья очередь ходить. Обычно лучше начинать окружение снаружи и лишь потом занимать общие дамэ. Черные при своем ходе должны идти в 'a', белые при своем ходе – в 'b'. А что будет, если начать с хода (*)?
Интересно, что если бы на той же 12-й диаграмме в точке 'c' стоял черный камень, то в ответ на ход белых 'b' черные съели бы слишком смелую белую группу в углу. Поэтому благодаря своему обреченному камню 'c' черные выиграли бы даже при ходе белых!





ГРУППА – это камни одного цвета, стоящие вплотную друг к другу. На 9-й диаграмме показаны 2 черные группы (из 3 и из 12 камней) и 3 белые группы (из 2, 4 и 10 камней).
Для окружения группы противник должен занять все ее дамэ, то есть соседние свободные точки, в том числе внутренние.
На той же 9-й диаграмме все дамэ черных групп отмечены (*). Какая из этих групп находится в состоянии атари? В какую из отмеченных точек лучше пойти белым при своем ходе и какой ход для них запрещен?

Правила окружения групп и запреты остаются такими же, как для одиночных камней. На 10-й диаграмме 'a' отмечает запрещенный ход черных, а (*) – возможные ходы черных со снятием белых групп. Какой из двух этих ходов лучше?

На 11-й диаграмме (ход белых) обе белые группы в положении атари обречены, захвачены. Если белые займут последнее дамэ (*), их группа останется под атари и может быть съедена следующим ходом черных (каким?).
В 5-й главе описаны ситуации, когда группа может жить вечно при любых атаках противника, а также когда группа обречена даже при наличии множества дамэ.

На 12-й диаграмме показана схватка между черной и белой группой из трех камней. Обе группы имеют по 2 дамэ, и здесь выиграет тот, чья очередь ходить. Обычно лучше начинать окружение снаружи и лишь потом занимать общие дамэ. Черные при своем ходе должны идти в 'a', белые при своем ходе – в 'b'. А что будет, если начать с хода (*)?
Интересно, что если бы на той же 12-й диаграмме в точке 'c' стоял черный камень, то в ответ на ход белых 'b' черные съели бы слишком смелую белую группу в углу. Поэтому благодаря своему обреченному камню 'c' черные выиграли бы даже при ходе белых!
Ответы на задачи 5-8.
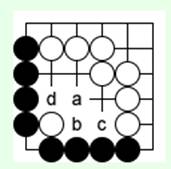
Если черные сделают атари, тогда белый камень спасется, например черные 'd', белые 'b', черные 'c', белые 'a'.
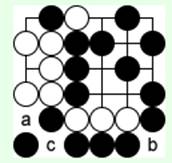
При любом другом первом ходе белых черные соединятся в 'c' и спасут свои камни.
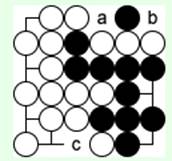
На взятие черных 'c' белые соединяются 'a'.
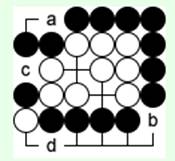
При любом другом первом ходе белых черные соединятся 'a'. Теперь обе белые группы обречены.
Глава 4. Территория
Задачи:
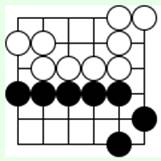 Задача 9 (ход черных)
Задача 9 (ход черных)
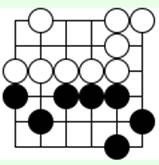 Задача 10 (ход белых)
Задача 10 (ход белых)
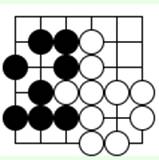 Задача 11 (ход черных)
Задача 11 (ход черных)
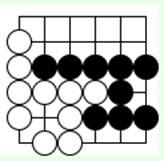 Задача 12 (ход белых)
Задача 12 (ход белых)
После окончания партии нужно выяснить, сколько точек удалось окружить каждому игроку.
ТЕРРИТОРИЯ – это пустая область доски, окруженная (по вертикали и горизонтали) камнями только одного цвета.
Зона, которая соприкасается и с черными, и с белыми камнями, считается нейтральной и никому не приносит очков.
Во 2-й главе на 4-й диаграмме закончена учебная партия. Территория черных состоит из 11 точек. В территории белых 2 части – из 4 точек и 1 точки, всего 5 очков.
Вся партия на диаграммах 1-4 показывает постепенное оцепление зоны черных вверху справа и зоны белых внизу слева. Примерно к 13-му ходу доска уже разделена на две зоны, которые еще не совсем ограничены, но хорошо видны.
В конце партии игроки достраивают границы зон и оформляют территории, а затем занимают ничейные точки.
Для окружения чужих обреченных камней в своей зоне Вам придется играть внутри этой зоны, каждым ходом уничтожая точку своей будущей территории. Поэтому занимайтесь этим в самом конце игры (ход 22 в партии), когда сделаны все полезные ходы (1…20 в партии) и заполнены нейтральные точки. Тогда противник будет (так же как и Вы) играть в своей территории или пропускать ходы (21-й в партии), платя по одному очку за каждый пас.
Если Вы вторглись в чужую территорию, и Ваш десант был разбит, но противник был вынужден ходить в свою зону в ответ на каждый Ваш ход, тогда баланс очков сохранился. Вы потеряли несколько камней, а противник на столько же точек уменьшил свою территорию. Если же Ваше вторжение будет успешным, Вы получите большую выгоду.
Даже если Вы полностью окружили свою зону, и все чужие камни внутри нее мертвы, противник часто может уменьшить Ваши владения, угрожая снаружи Вашим пограничным камням.
Камни важнее точек. Если Вы теряете группу, тогда противник обычно получает по 2 очка за каждый Ваш камень (1 очко за сам камень и 1 за точку под ним), по 2 очка за каждую точку территории (которая была Вашей и перешла к противнику) и по 2 очка за каждый внутренний камень противника (который должен был принести Вам 2 очка). Но камень или группа может быть еще дороже из-за своей роли (связь своих сил, разрезание или блокировка противника и так далее).




После окончания партии нужно выяснить, сколько точек удалось окружить каждому игроку.
ТЕРРИТОРИЯ – это пустая область доски, окруженная (по вертикали и горизонтали) камнями только одного цвета.
Зона, которая соприкасается и с черными, и с белыми камнями, считается нейтральной и никому не приносит очков.
Во 2-й главе на 4-й диаграмме закончена учебная партия. Территория черных состоит из 11 точек. В территории белых 2 части – из 4 точек и 1 точки, всего 5 очков.
Вся партия на диаграммах 1-4 показывает постепенное оцепление зоны черных вверху справа и зоны белых внизу слева. Примерно к 13-му ходу доска уже разделена на две зоны, которые еще не совсем ограничены, но хорошо видны.
В конце партии игроки достраивают границы зон и оформляют территории, а затем занимают ничейные точки.
Для окружения чужих обреченных камней в своей зоне Вам придется играть внутри этой зоны, каждым ходом уничтожая точку своей будущей территории. Поэтому занимайтесь этим в самом конце игры (ход 22 в партии), когда сделаны все полезные ходы (1…20 в партии) и заполнены нейтральные точки. Тогда противник будет (так же как и Вы) играть в своей территории или пропускать ходы (21-й в партии), платя по одному очку за каждый пас.
Если Вы вторглись в чужую территорию, и Ваш десант был разбит, но противник был вынужден ходить в свою зону в ответ на каждый Ваш ход, тогда баланс очков сохранился. Вы потеряли несколько камней, а противник на столько же точек уменьшил свою территорию. Если же Ваше вторжение будет успешным, Вы получите большую выгоду.
Даже если Вы полностью окружили свою зону, и все чужие камни внутри нее мертвы, противник часто может уменьшить Ваши владения, угрожая снаружи Вашим пограничным камням.
Камни важнее точек. Если Вы теряете группу, тогда противник обычно получает по 2 очка за каждый Ваш камень (1 очко за сам камень и 1 за точку под ним), по 2 очка за каждую точку территории (которая была Вашей и перешла к противнику) и по 2 очка за каждый внутренний камень противника (который должен был принести Вам 2 очка). Но камень или группа может быть еще дороже из-за своей роли (связь своих сил, разрезание или блокировка противника и так далее).
Ответы на задачи 9-12.
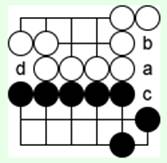
Нейтральный ход 'd' делать рано, белые ходом 'a' делают точку 'b' своей территорией и получают за нее 1 очко.
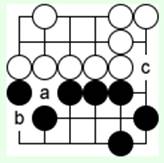
Начиная ходом 'c', белые теряют темп. Угрозы черным нет, и они соединяются в 'a', получая на 1 очко больше, чем при правильном ходе белых.

На ход черных 'e' белые отвечают комбинацией (белые 'c' – черные 'f', белые 'a'). Результат на 3 очка хуже правильного.

Глава 5. Бессмертные группы
Задачи:
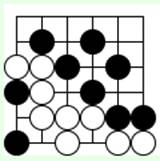 Задача 13 (ход черных)
Задача 13 (ход черных)
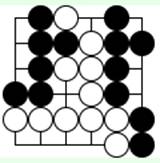 Задача 14 (ход белых)
Задача 14 (ход белых)
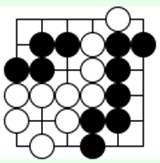 Задача 15 (ход черных)
Задача 15 (ход черных)
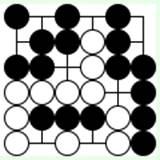 Задача 16 (ход белых)
Задача 16 (ход белых)
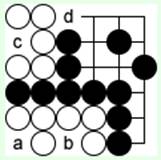 Диаграмма 13
Диаграмма 13
На 13-й диаграмме черным запрещено ходить в 'a', 'b' и 'c' (почему?). Черные могут сначала пойти в 'd', а затем (после любого хода белых) завершить окружение верхней белой группы ходом в 'c'. Но они никогда не смогут пойти в 'a' или в 'b'. Поэтому нижнюю белую группу нельзя съесть, она бессмертна.
Каждая отдельная точка внутри группы называется ГЛАЗ. Если группа имеет 2 глаза, она неуязвима.
Будет ли жить группа с 3 глазами?
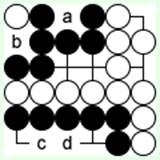 Диаграмма 14
Диаграмма 14
На 14-й диаграмме обе черные группы живы, хотя прямо сейчас у них нет 2 глаз.
Белый камень внутри верхней черной группы обречен. Эту форму обычно называют глазом черной группы, потому что белые никогда не займут ни 'a', ни 'b'.
Территория нижней черной группы состоит из 4 точек в линию. Черные всегда могут разгородить ее ходом 'c' или 'd' и таким образом построить глаза. На ход белых 'c' надо будет ответить 'd' и наоборот. А что случится, если белые займут и 'c', и 'd'?
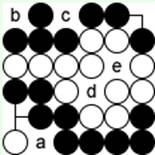 Диаграмма 15
Диаграмма 15
На 15-й диаграмме все черные группы мертвы.
Черная группа внизу была бы неуязвимой, если бы черные сами заняли угловую точку. Но теперь белые могут сыграть 'a', делая атари черной группе, затем после снятия 2 белых камней белые снова пойдут в 'a' и после съедения 1 камня снимут черную группу тем же ходом 'a'. Поэтому черным незачем сопротивляться, но и белым незачем спешить. Обреченные камни и группы съедаются в конце игры.
Черная группа вверху на той же диаграмме обречена, хотя сейчас белым нельзя ходить ни в 'b', ни в 'c'. Дело в том, что 'c' – не внутренняя точка группы, она граничит с двумя группами (из 4 и из 2 камней).
После окружения снаружи белые пойдут в 'c' или заставят черных занять 'c', а позже снимут черную группу. Поэтому точка 'c' называется ложным глазом.
А вот обе белые группы на 15-й диаграмме живы независимо от слабостей соседних черных групп. Очевидно, что даже сейчас, при полном внешнем окружении, черным запрещено идти в 'd' и в 'e'.
Поэтому такую пару групп одного цвета с двумя общими глазами обычно считают одной группой.
Надо ли белым соединяться ходом 'd' или 'e'?
 Диаграмма 16
Диаграмма 16
Может ли жить группа без двух глаз? На 16-й диаграмме все белые и черные группы живут в такой ситуации – СЭКИ.
В сэки всегда есть общие дамэ, они отмечены (*). Тот, кто займет точку (*), потеряет группу, на месте которой противник сможет достроить глаза.
Обычно в сэки участвует 1 черная и 1 белая группа.





На 13-й диаграмме черным запрещено ходить в 'a', 'b' и 'c' (почему?). Черные могут сначала пойти в 'd', а затем (после любого хода белых) завершить окружение верхней белой группы ходом в 'c'. Но они никогда не смогут пойти в 'a' или в 'b'. Поэтому нижнюю белую группу нельзя съесть, она бессмертна.
Каждая отдельная точка внутри группы называется ГЛАЗ. Если группа имеет 2 глаза, она неуязвима.
Будет ли жить группа с 3 глазами?

На 14-й диаграмме обе черные группы живы, хотя прямо сейчас у них нет 2 глаз.
Белый камень внутри верхней черной группы обречен. Эту форму обычно называют глазом черной группы, потому что белые никогда не займут ни 'a', ни 'b'.
Территория нижней черной группы состоит из 4 точек в линию. Черные всегда могут разгородить ее ходом 'c' или 'd' и таким образом построить глаза. На ход белых 'c' надо будет ответить 'd' и наоборот. А что случится, если белые займут и 'c', и 'd'?

На 15-й диаграмме все черные группы мертвы.
Черная группа внизу была бы неуязвимой, если бы черные сами заняли угловую точку. Но теперь белые могут сыграть 'a', делая атари черной группе, затем после снятия 2 белых камней белые снова пойдут в 'a' и после съедения 1 камня снимут черную группу тем же ходом 'a'. Поэтому черным незачем сопротивляться, но и белым незачем спешить. Обреченные камни и группы съедаются в конце игры.
Черная группа вверху на той же диаграмме обречена, хотя сейчас белым нельзя ходить ни в 'b', ни в 'c'. Дело в том, что 'c' – не внутренняя точка группы, она граничит с двумя группами (из 4 и из 2 камней).
После окружения снаружи белые пойдут в 'c' или заставят черных занять 'c', а позже снимут черную группу. Поэтому точка 'c' называется ложным глазом.
А вот обе белые группы на 15-й диаграмме живы независимо от слабостей соседних черных групп. Очевидно, что даже сейчас, при полном внешнем окружении, черным запрещено идти в 'd' и в 'e'.
Поэтому такую пару групп одного цвета с двумя общими глазами обычно считают одной группой.
Надо ли белым соединяться ходом 'd' или 'e'?

Может ли жить группа без двух глаз? На 16-й диаграмме все белые и черные группы живут в такой ситуации – СЭКИ.
В сэки всегда есть общие дамэ, они отмечены (*). Тот, кто займет точку (*), потеряет группу, на месте которой противник сможет достроить глаза.
Обычно в сэки участвует 1 черная и 1 белая группа.
Ответы на задачи 13-16.

Ходом 'c' черные съедают 2 белых камня, но белые ходом 'a' спасают большую группу.
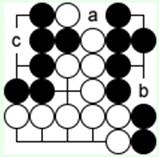
Если белые атакуют лишь одну крупную черную группу, например съедая 2 камня ходом 'b', тогда черные соединяются ходом 'a', съедая белый камень, и спасают обе большие группы.
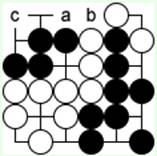
Иначе белые захватят черных слева вверху.
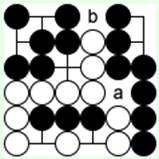
В ответ на слишком агрессивный ход белых 'b' черные разрушают сэки ходом 'a'. Два белых камня внизу гибнут, поэтому черные камни внизу спасаются, и все белые группы обречены.
Глава 6. Циклические процессы
Задачи:
 Задача 17 (ход черных)
Задача 17 (ход черных)
 Задача 18 (ход белых)
Задача 18 (ход белых)
 Задача 19 (ход черных)
Задача 19 (ход черных)
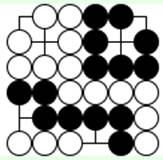
 Задача 20 (ход белых)
Задача 20 (ход белых)
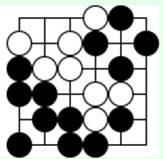
 Диаграмма 17
Диаграмма 17
У белой группы два глаза. Черные вверху могут построить два глаза. Белые атакуют нижнюю черную группу ходом 'a', черные пытаются выжить 'b', но белые съедают 'c'.
Черным нельзя есть ходом 'b' из-за повторения предыдущей ситуации.
Если белые соединятся 'b', черные останутся с одним глазом. Могут ли черные соединить свои группы?
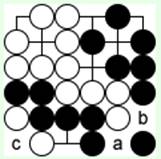 Диаграмма 18
Диаграмма 18
(продолжение 17-й). Черные ходом 'a' угрожают соединиться в 'b', белые режут 'b', и
черные едят 'c', потому что позиция на доске изменилась. Теперь белые не могут есть сразу, а тоже только через ход.
Если черные съедят еще раз, у них будет два глаза. У белых нет способа помешать черным выжить.
 Диаграмма 19
Диаграмма 19
(продолжение 18-й). Белые ходом 'a' угрожают верхней группе черных. Если теперь черные спасут эту группу ходом 'c', тогда белые ходом 'd' захватят нижнюю группу, которая больше верхней. Поэтому черные строят два глаза ходом 'b' и прекращают поочередное взятие камня, а белые ходом 'c' разрушают глаз верхней черной группы.
Правило, которое запрещает повторять расстановку камней при той же очереди хода, называется КО. Если позиция в некоторой части доски повторяется, хотя позиция на всей доске обязательно меняется, такой процесс называется ко-борьбой. При этом каждый игрок использует так называемые ко-угрозы, чтобы помешать противнику закончить ко-борьбу. Каким был бы итог борьбы, если белые на 17-й диаграмме сразу напали бы на верхнюю правую группу черных?
Ко-борьба состоит из одного или нескольких циклов (раундов). Цикл обычно начинается со взятия одного камня (диаграмма 17 'c'). Другой игрок использует ко-угрозу (18 'a') и после ответа на нее (18 'b') сам берет "горячий" камень (18 'c') и так далее. Наконец очередная ко-угроза против игрока (19 'a') оказывается слишком слабой, игрок ее игнорирует и завершает (выигрывает) ко-борьбу (19 'b'), а противник реализует (доигрывает) свою ко-угрозу (19 'c').
Ко-борьбу выигрывает тот, у кого оказалось больше сильных ко-угроз, а при равенстве угроз – тот, кто совершил первое взятие в этой борьбе.
Особенно важны так называемые местные ко-угрозы (18 'a' в отличие от 19 'a'), которые делают бессмысленным завершение ко-борьбы.
Игрок, проигравший ко, получает некоторую компенсацию, реализуя ко-угрозу.
Подумайте, почему на 18-й диаграмме ход черных 'a' лучше, чем 'b'?
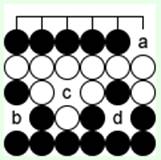 Диаграмма 20
Диаграмма 20
Здесь показано "тройное ко" – один из более сложных циклических процессов. Черные делают атари ходом 'a', белые 'b' и так далее, наконец черным нельзя брать белый камень в точке 'd' из-за повтора ситуации, бывшей шесть ходов назад. Черным нужна ко-угроза, но ее нет, они пасуют, а белые доедают черную группу.





У белой группы два глаза. Черные вверху могут построить два глаза. Белые атакуют нижнюю черную группу ходом 'a', черные пытаются выжить 'b', но белые съедают 'c'.
Черным нельзя есть ходом 'b' из-за повторения предыдущей ситуации.
Если белые соединятся 'b', черные останутся с одним глазом. Могут ли черные соединить свои группы?

(продолжение 17-й). Черные ходом 'a' угрожают соединиться в 'b', белые режут 'b', и
черные едят 'c', потому что позиция на доске изменилась. Теперь белые не могут есть сразу, а тоже только через ход.
Если черные съедят еще раз, у них будет два глаза. У белых нет способа помешать черным выжить.

(продолжение 18-й). Белые ходом 'a' угрожают верхней группе черных. Если теперь черные спасут эту группу ходом 'c', тогда белые ходом 'd' захватят нижнюю группу, которая больше верхней. Поэтому черные строят два глаза ходом 'b' и прекращают поочередное взятие камня, а белые ходом 'c' разрушают глаз верхней черной группы.
Правило, которое запрещает повторять расстановку камней при той же очереди хода, называется КО. Если позиция в некоторой части доски повторяется, хотя позиция на всей доске обязательно меняется, такой процесс называется ко-борьбой. При этом каждый игрок использует так называемые ко-угрозы, чтобы помешать противнику закончить ко-борьбу. Каким был бы итог борьбы, если белые на 17-й диаграмме сразу напали бы на верхнюю правую группу черных?
Ко-борьба состоит из одного или нескольких циклов (раундов). Цикл обычно начинается со взятия одного камня (диаграмма 17 'c'). Другой игрок использует ко-угрозу (18 'a') и после ответа на нее (18 'b') сам берет "горячий" камень (18 'c') и так далее. Наконец очередная ко-угроза против игрока (19 'a') оказывается слишком слабой, игрок ее игнорирует и завершает (выигрывает) ко-борьбу (19 'b'), а противник реализует (доигрывает) свою ко-угрозу (19 'c').
Ко-борьбу выигрывает тот, у кого оказалось больше сильных ко-угроз, а при равенстве угроз – тот, кто совершил первое взятие в этой борьбе.
Особенно важны так называемые местные ко-угрозы (18 'a' в отличие от 19 'a'), которые делают бессмысленным завершение ко-борьбы.
Игрок, проигравший ко, получает некоторую компенсацию, реализуя ко-угрозу.
Подумайте, почему на 18-й диаграмме ход черных 'a' лучше, чем 'b'?

Здесь показано "тройное ко" – один из более сложных циклических процессов. Черные делают атари ходом 'a', белые 'b' и так далее, наконец черным нельзя брать белый камень в точке 'd' из-за повтора ситуации, бывшей шесть ходов назад. Черным нужна ко-угроза, но ее нет, они пасуют, а белые доедают черную группу.
Ответы на задачи 17-20.
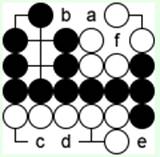

Ситуация в левом нижнем углу похожа на сэки, но белые могут начать здесь ко-борьбу.
Ходом 'a' они отдают свою "кривую четверку", черные едят 'e', белые вбрасывают 'c', черные ходом 'b' пытаются разгородить глаза, но белые едят 'a', начиная ко-борьбу.
Ко-угроз нет (их обычно и не бывает в самом конце партии), поэтому черные пасуют, а белые доедают ходом 'd'.
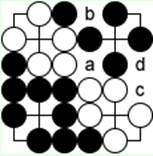
нельзя выиграть две ко-борьбы сразу. Рано или поздно черные съедают какую-нибудь белую группу.
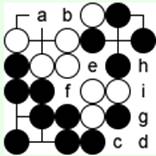
Обойтись без ко-борьбы нельзя. Варианты (белые 'b' – черные 'e', 'f'-'a', 'g'-'c', 'h'-'i') и (белые 'e' – черные 'b', белые 'a', черные соединяются) ведут к потерям белых.
Глава 7. Начало и конец партии
Право первого хода дает черным преимущество в игре. Для компенсации черные платят белым несколько очков – КОМИ.
В партиях игроков с большой разницей в силе можно применять ФОРУ. Более слабый играет черными без коми и перед началом партии ставит на доску сразу несколько своих камней в специальные форовые точки. Затем ходят белые. Минимальная фора – игра черными без коми, как в учебной партии на диаграммах 1-4 главы 2.
Игрок в любой момент может сдаться, иначе игра продолжается до 2 пасов подряд.
Пропуская ход, игрок платит 1 очко, то есть отдает противнику камень из своей чаши.
Затем каждый игрок указывает на обреченные камни противника. Если возражений нет, все эти камни (черные и белые) снимаются с доски и прибавляются к съеденным. Если игрок возражает, он сам указывает на свою спорную группу. Тогда все камни (даже бесспорно мертвые) остаются на доске, а игра продолжается с сохранением очереди хода.
Таким образом игра может останавливаться и возобновляться много раз до полного согласия игроков. Если согласие так и не было достигнуто, игра окончательно завершается после 4 пасов подряд, и тогда все оставшиеся на доске камни считаются живыми.
В партиях игроков с большой разницей в силе можно применять ФОРУ. Более слабый играет черными без коми и перед началом партии ставит на доску сразу несколько своих камней в специальные форовые точки. Затем ходят белые. Минимальная фора – игра черными без коми, как в учебной партии на диаграммах 1-4 главы 2.
Игрок в любой момент может сдаться, иначе игра продолжается до 2 пасов подряд.
Пропуская ход, игрок платит 1 очко, то есть отдает противнику камень из своей чаши.
Затем каждый игрок указывает на обреченные камни противника. Если возражений нет, все эти камни (черные и белые) снимаются с доски и прибавляются к съеденным. Если игрок возражает, он сам указывает на свою спорную группу. Тогда все камни (даже бесспорно мертвые) остаются на доске, а игра продолжается с сохранением очереди хода.
Таким образом игра может останавливаться и возобновляться много раз до полного согласия игроков. Если согласие так и не было достигнуто, игра окончательно завершается после 4 пасов подряд, и тогда все оставшиеся на доске камни считаются живыми.
