Страница:
Первым человеком, кто привлек математику для решения проблемы темноты ночного неба, был друг Ньютона английский астроном, математик и геофизик Эдмонд Галлей. Надо заметить, что Ньютон отличался довольно неуживчивым нравом, и Галлей был одним из немногих друзей, сохранявшим с ним хорошие отношения на протяжении нескольких десятилетий. Эдмонд Галлей, чье имя обычно помнят только из-за яркой кометы, орбиту которой он рассчитал и предсказал ее возвращение к Солнцу в 1758 году (комета Галлея), внес большой вклад в самые разные области – например, он открыл собственные движения звезд, составил первый каталог звезд южного неба, заложил основы геофизики и научной демографии. Не менее важной заслугой Галлея перед наукой является и то, что он убедил Ньютона написать «Математические начала натуральной философии», выполнил всю редакторскую работу и издал книгу за свой счет.

Рис. 10. Эдмонд Галлей (1656–1742)
Как ни странно, можно, по-видимому, назвать точную дату, когда Галлей заинтересовался проблемой ночного неба. Скорее всего, это произошло утром 23 февраля 1721 года во время совместного завтрака Ньютона, Галлея и Вильяма Стакли (1687–1765) (английского археолога, одного из первых исследователей Стоунхенджа). Разговор за завтраком шел на астрономические темы и Стакли скорее всего упомянул свои соображения о том, что звезды распределены в пространстве не однородно, как это требуется по космологии Ньютона, а в виде «гигантского меридиана», делящего бесконечное пространство на две части. Если бы это было не так, то, согласно Стакли, все небо должно было бы быть столь же ярким как Млечный Путь.
Эта беседа, вероятно, подтолкнула Галлея к собственным размышлениям и всего через две недели после этого завтрака – 9 марта 1721 года – он представил на заседании Королевского общества статью «О бесконечности сферы неподвижных звезд», в которой Галлей упомянул, не называя его по имени, и аргументацию Стакли. Вскоре – 16 марта – Галлей зачитал и вторую небольшую работу («О числе, порядке и свете неподвижных звезд») на ту же тему.
В своих работах Галлей сначала приводит аргументы в поддержку того, что система звезд бесконечна: чем более мощный телескоп используется при наблюдениях, тем больше звезд в него видно; кроме того, если система звезд конечна, то звезды под действием гравитации должны были сжаться в единый объект в центре (аргумент, использованный ранее Ньютоном). Затем Галлей обсуждает два возражения против бесконечности Вселенной. Одно из них чисто терминологическое, а второе – это, по сути, возражение Стакли, которое перекликается и с мнением Кеплера (см. ранее).
Для того, чтобы преодолеть это затруднение, Галлей вводит идею концентрических слоев одинаковой толщины (рис. 1), подсчитывает количество звезд в слое и создаваемую каждой из этих звезд освещенность по мере увеличения радиуса. Добравшись до звезд сотого слоя, освещенность от каждой из которых в 10 000 меньше, чем от звезды в первом слое, он заключает, что эта освещенность столь мала, что человеческий глаз даже в телескоп просто не увидит этих звезд.
Следовательно, для решения фотометрического парадокса Галлей использует тот же аргумент, что и Томас Диггес за полтора столетия до него – далекие звезды слишком слабы, чтобы быть увиденными. Галлей не догадался просуммировать вклад далеких звезд и убедиться, что им нельзя пренебречь. (Как видно из формулы (2), вклад каждого слоя одинаковой толщины одинаков – падение освещенностей от индивидуальных звезд точно компенсируется увеличением их числа).
Журнал Королевского общества зафиксировал еще один довод Галлея, сводящийся к тому, что освещенность от далеких звезд спадает быстрее, чем по закону обратных квадратов (см. формулу (1) в параграфе 1.2): «свет не делится до бесконечности и, следовательно, когда звезды находятся на очень больших расстояниях, их излучение слабеет быстрее, чем по общему правилу». Это предположение может решить фотометрический парадокс, но оно, конечно, неверно.
Ньютон председательствовал на заседаниях Королевского общества во время выступлений Галлея, однако его реакция на результаты Галлея осталась неизвестной. Возможно, пожилой Ньютон просто проспал выступления своего друга, что, судя по воспоминаниям современников, с ним нередко случалось на разных заседаниях.
Заметки Галлея были опубликованы в журнале Королевского общества «Philosophical Transactions» и, по-видимому, они стимулировали работу швейцарского астронома и физика Шезо, который в 1744 году выполнил первый корректный математический анализ парадокса.
1.5. Шезо и Ольберс
Жан-Филипп Луи де Шезо родился вблизи Лозанны в семье обеспеченного землевладельца. Он очень рано проявил интерес к астрономии и построил собственную обсерваторию, оборудованную парой небольших телескопов. Ранние работы Шезо по физике распространения звука, о торможении пушечных ядер воздухом и пр. привлекли к нему широкое внимание, и российская императрица Елизавета Петровна даже приглашала его на работу в Санкт-Петербург. По причине слабого здоровья Шезо не смог воспользоваться этим предложением.
В декабре 1743 года Шезо открыл комету (практически одновременно она была также обнаружена датчанином Дирком Клинкенбергом) и наблюдал ее до марта 1744 года. Комета была очень яркой, ярче Юпитера, и в одну из ночей продемонстрировала целых 6 хвостов. Через несколько месяцев после исчезновения кометы Шезо опубликовал о ней книгу. Книга содержала восемь приложений, посвященных разным вопросам астрономии. Второе приложение – «О силе света, его прохождении через эфир и расстоянии до неподвижных звезд» – содержало математический анализ загадки ночного неба.
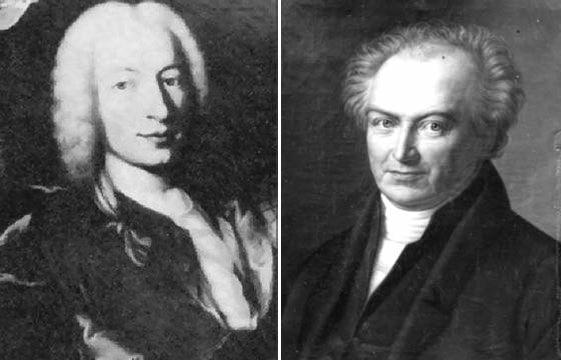
Рис. 11. Жан-Филипп Луи де Шезо (1718–1751) и Генрих Вильгельм Ольберс (1758–1840)
Анализ Шезо был, по сути, эквивалентен приведенному ранее в параграфе 1.2 этой книги. Так же как и Галлей, Шезо рассматривает окружающие Солнце концентрические слои одинаковой толщины и в предположении однородного распределения звезд в пространстве находит, что освещенность от каждого слоя одинакова. Если звездное пространство бесконечно или даже просто очень велико, то любой участок небесной сферы должен сиять как Солнце (он предположил, что все звезды по размерам и по светимости подобны Солнцу), поскольку звезды перекроют своими видимыми дисками весь небосвод. Шезо оценил, что вся доступная наблюдениям полусфера в этом случае должна сиять в 91 850 раз ярче Солнца. (Эта оценка примерно равна отношению площади полусферы к площади солнечного диска.)
«Громадное несоответствие между этим заключением и опытом свидетельствует, что либо сфера неподвижных звезд не бесконечна…, либо освещенность спадает быстрее, чем по закону обратных квадратов», – пишет Шезо. Он считает, что второе допущение более правдоподобно и предполагает, что межзвездное пространство может быть заполнено разреженной средой, задерживающей излучение звезд. Он полагает, что даже ничтожное поглощение в межзвездной среде, постепенно накапливаясь, может объяснить темноту ночного неба. Решение, предложенное Шезо, выглядит правдоподобно, но, как будет показано, далее, неверно – межзвездное поглощение не может решить фотометрический парадокс.
В работе Шезо содержатся еще два примечательных результата. Во-первых, он оказался одним из первых исследователей, правильно оценивших масштаб межзвездных расстояний. Этой задачей пытались заниматься многие (например, Гук, Пикар, Флемстид, Брадлей, Вильям Гершель и другие), однако прямая оценка расстояний методом годичного параллакса из-за несовершенства используемых инструментов и методов обработки не давала результатов вплоть до XIX века.
В качестве альтернативного и, конечно, очень грубого подхода можно использовать видимый блеск звезды в сравнении с Солнцем. Если считать, что все звезды, включая Солнце, имеют одинаковую светимость, то, сравнивая освещенности от какой-либо звезды и от Солнца, можно оценить, во сколько раз звезда дальше от нас, чем Солнце. Используя этот метод, голландский физик, математик и астроном Христиан Гюйгенс (1629–1695) оценил, что Сириус находится в 28 000 раз дальше Солнца, то есть на расстоянии около 0.14 пк[6].
Для того, чтобы получить этот результат, Гюйгенсу пришлось сравнивать яркость освещенного Солнцем отверстия в темной комнате с воспоминанием о яркости Сириуса ночью. Естественно, сделать это очень сложно, что и привело к заниженному почти в 20 раз расстоянию (расстояние до Сириуса равно 2.7 пк или 8.7 световых лет). Этот результат Гюйгенса был опубликован уже после его смерти – в 1698 году.
Однако еще раньше – в 1668 году – шотландский математик, астроном и оптик Джеймс Грегори (1638–1675) опубликовал замечательную модификацию фотометрического метода. Грегори предложил не сравнивать яркости звезд и Солнца, что на практике очень сложно, а использовать в качестве промежуточного стандарта яркость планет. Суть его метода очень проста – ночью можно сравнить яркость какой-либо звезды с яркостью внешней планеты (Марса, Юпитера, Сатурна), а затем, зная расстояние этой планеты от Солнца и ее угловой диаметр, можно рассчитать ее яркость по сравнению с яркостью Солнца (предполагая, конечно, что планета светит отраженным светом и задавая определенный коэффициент отражения). Применив этот метод к Сириусу, и используя наблюдения Сатурна, Грегори получил, что эта звезда находится в 80000 раз дальше Солнца – результат гораздо лучший, чем у Гюйгенса, хотя все еще существенно заниженный.
Во второй части работы о фотометрическом парадоксе Шезо использует метод Грегори для определения расстояний до ярчайших звезд (Сириуса и Регула) на основе сравнения их блеска с Сатурном, Юпитером и Марсом. Он заключает, что расстояние до ярчайших звезд примерно в 240 000 раз превышает расстояние от Земли до Солнца. Эта оценка составляет около 4 световых лет или чуть больше 1 пк. Учитывая грубость используемого метода, результат можно признать просто превосходным!
Однако Шезо не был первым человеком, правильно оценившим масштаб межзвездных расстояний. Как оказалось, это было сделано Исааком Ньютоном в «De mundi systemate» («Система мира») – дополнении к «Началам», написанном еще в 1680-х годах и опубликованном в 1728 году, уже после его смерти. В этой работе Ньютон методом Грегори нашел, что расстояние до звезд первой величины примерно в 100 000 раз превышает расстояние от Сатурна до Солнца, что составляет ~ 1 000 000 астрономических единиц (4.8 пк)[7].
Еще один интересный результат небольшой работы Шезо о фотометрическом парадоксе – корректная математическая оценка доступной наблюдениям области Вселенной. Если предположить, что все звезды подобны Солнцу и что они равномерно распределены в пространстве со средним взаимным расстоянием 4 световых года, то в пределах сферы радиусом 3×1015 световых лет звезды перекроют своими дисками всю небесную сферу. Свет от более далеких звезд будет экранирован дисками более близких объектов и внешняя часть Вселенной останется ненаблюдаемой.
Британский космолог Эдвард Харрисон считает, что, возможно, именно огромность, несоизмеримость этих масштабов могла подтолкнуть Шезо к идее межзвездного поглощения – ведь даже ничтожная непрозрачность межзвездной среды на столь больших расстояниях способна полностью скрыть далекие объекты и, тем самым, сделать ночное небо темным.
Следующий исследователь, внесший вклад в исследование парадокса, названного позднее его именем, – это немецкий врач и астроном-любитель Генрих Ольберс. Ольберс был дипломированным медиком, но, горячо увлекаясь астрономией, он в течение многих лет сочетал оба занятия. Днем он был солидным бременским врачом, а ночью проводил наблюдения в частной обсерватории на верхнем этаже собственного дома. Лишь после смерти дочери и второй жены он оставил врачебную практику и с 1820 года полностью посвятил себя астрономии. В биографическом очерке, включенном в книгу С. Ньюкомба и Р. Энгельмана «Астрономия в общепонятном изложении» (опубликована на русском языке в 1896 году), об Ольберсе было написано так: «Едва ли можно назвать другого любителя, которому астрономия была бы так много обязана, как Ольберсу; и мало было специалистов по астрономии, которые обладали столь обширными познаниями в ней, как этот любитель».
Основные результаты Ольберса посвящены наблюдениям комет (он открыл их 7 штук) и расчетам их орбит (им разработан метод определения орбит комет по трем наблюдениям). В 1802 году Ольберс переоткрыл первую малую планету (Цереру)[8], которая вскоре после ее открытия в 1801 году итальянским астрономом Пиацци была потеряна. В том же 1802 году он открыл вторую малую планету (Палладу), а в 1807 – четвертую (Весту).
В 1823 году, почти через 80 лет после работы Шезо, Генрих Ольберс опубликовал статью «О прозрачности пространства». В своей статье Ольберс анализирует фотометрический парадокс – более пространно и в более качественном стиле по сравнению с кратким изложением Шезо – и предполагает, что учет поглощения света далеких звезд в межзвездном пространстве может решить эту проблему.
Изложение Ольберса в целом оригинально и вводит в обсуждение парадокса несколько новых идей. Например, Ольберс допускает, что звезды не обязательно должны быть однородно распределены в пространстве, а могут группироваться в системы, подобные Млечному Пути, то есть в галактики. Такое скучивание не избавляет от парадокса, поскольку любой луч зрения все равно рано или поздно должен упереться в диск какой-либо звезды. Ольберс считает, что полная прозрачность межзвездного пространства «в высокой степени невероятна» и обосновывает существование поглощающей среды тем, что вещество кометных хвостов рассеивается, пополняя окружающее пространство, а также существованием зодиакального света. (Строго говоря, это говорит лишь о межпланетной среде, но отсюда уже один шаг до признания существования и межзвездного вещества.)
Любопытен «научно-фантастический» пассаж Ольберса о том, что даже в случае, если бы вся небесная сфера сияла как поверхность Солнца, можно было бы вообразить живые организмы, приспособившиеся и к таким экстремальным условиям. Он отмечает, что астрономия у разумных существ такой планеты находилась бы в примитивном состоянии – обитателям ничего не было бы известно о звездах, о существовании Солнца можно было бы узнать лишь по наблюдениям его пятен, а Луна и планеты обнаруживались бы лишь как темные пятна на сверкающем фоне. (Соображения Ольберса отчасти перекликаются с высказанными в п. 1.1 этой книги.)
В своей статье Ольберс цитирует Галлея, но ни разу не упоминает работу Шезо. Знал ли он о ней, и повлияла ли она как-нибудь на его собственную работу? Вопрос не праздный, поскольку подход Ольберса и предложенное им решение фотометрического парадокса в целом похожи на то, что сделал Шезо задолго до него. Кроме того, оказалось, что в библиотеке Ольберса была книга Шезо 1744 года, посвященная знаменитой шестихвостой комете, в приложении к которой Шезо описал свое решение фотометрического парадокса. Более того, Ольберс, несомненно, читал эту книгу – американский историк астрономии Стенли Яки обнаружил, что в записных книжках, относящихся к 1782–96 годам, Ольберс тщательно законспектировал часть книги Шезо, в которой тот описывает предложенный им метод определения кометных орбит.
Так что же произошло? Яки, да и не только он, считает, что речь не может идти о плагиате, поскольку это в сильнейшей степени противоречит тому, что известно об Ольберсе, о его характере и научных работах. Скорее всего, к 1823 году, когда Ольберс написал свою статью, он забыл или полузабыл о короткой заметке Шезо, которую он, возможно, читал тридцать или сорок лет назад в поисках информации о столь любимых им кометах. Как полагает Эдвард Харрисон, люди забывают об источниках своих идей гораздо чаще, чем обычно считают.
Какова дальнейшая судьба идеи Шезо и Ольберса о межзвездном поглощении как о возможном решении фотометрического парадокса? Идея эта, конечно, не верна, поскольку в заполненной звездами безграничной и вечной Вселенной само поглощающее вещество (межзвездная пыль и газ) начнет нагреваться до тех пор, пока не установится тепловое равновесие между поглощающей средой и излучением звезд, а тогда среда станет излучать столько же, сколько поглотит. Первым это понял, по-видимому, английский астроном Джон Гершель (1792–1871), знаменитый сын еще более знаменитого отца – Вильяма Гершеля (1738–1822).
В 1848 году Джон Гершель опубликовал рецензию на недавно появившийся первый том «Космоса» Александра фон Гумбольдта. Гершель упоминает Ольберса и идею поглощения света, а затем пишет, что, действительно, свет легко поглощается, однако поглощенный свет нагревает поглощающую материю и она должна начать излучать, отдавая через излучение столько же энергии, сколько поглотила. Гершель использовал немного другие слова, но суть его комментария именно в этом. Очень примечательно, что это было написано тогда, когда недавно открытый закон сохранения энергии еще не стал широко известным и общепринятым.
Джон Гершель предложил и свой вариант решения фотометрического парадокса. Будучи наблюдателем, он был уверен, что в некоторых направлениях на небе он и в самом деле видит пустое пространство за пределами нашей звездной системы. С другой стороны, он имел хорошую математическую подготовку и догадывался, что можно придумать такое пространственное распределение объектов, что даже при бесконечном числе звезд ночное небо будет оставаться темным: «…легко представить устройство вселенной, которая будет оставаться в точном смысле слова бесконечной, и в которой произвольное количество лучей зрения не будут пересекаться со звездами». Гершель коротко описал такое устройство – звезды распределены самоподобным образом на всех уровнях, – то, что позднее стали называть иерархическим или фрактальным распределением. Идея иерархического строения Вселенной позднее развивалась многими исследователями – например, Ричардом Проктором, Карлом Шарлье, Фурнье д’Альбе. Эта идея, действительна, способна решить фотометрический парадокс, однако она противоречит наблюдаемой на больших масштабах однородности нашей Вселенной (см. следующую главу).
1.6. Динамическая Вселенная Эдгара По
Появление имени знаменитого поэта, писателя, классика и родоначальника сразу нескольких жанров литературы, может показаться странным в книге по астрономии. Однако что не было странным в жизни этого человека?
Эдгар Аллан По рано остался без родителей и воспитывался в доме богатого коммерсанта из Ричмонда Джона Аллана. Вместе с приемной семьей Эдгар По пять лет прожил в Англии, где учился в дорогом пансионе в Лондоне. После возвращения Алланов в США Эдгар закончил колледж в Ричмонде, в 1826 году поступил в недавно открытый Университет штата Вирджиния. Проучился в университете лишь год, вынужден был его бросить, записался добровольцем в армию, пытался закончить элитную военную академию в Вест-Пойнте, но был отчислен. Дальше – работа в нескольких журналах, богемная жизнь, личные и семейные драмы, нервное перенапряжение, болезни, запои, и на фоне всего этого – многочисленные стихи, рассказы, новеллы… И смерть в 40 лет в унизительной бедности и горячечном бреду. Биография, разительнейшим образом отличающаяся от жизни остальных героев этой книги.

Рис. 12. Дагерротип Эдгара Аллана По (1809–1849), изготовленный незадолго до смерти поэта.
Парадоксально, что именно этот парадоксальный человек предложил первое правильное, хотя и качественное, решение загадки темноты ночного неба. Даже более – Эдгара По можно назвать, пусть и с некоторой натяжкой, одним из идейных предшественников современной космологии в целом. Это не было случайностью – он очень интересовался наукой и, в особенности, астрономией, изучал книги классиков физики и астрономии (например, Ньютона, Лапласа, Вильяма и Джона Гершелей, Гумбольдта). Когда Эдгару было 16 лет, опекун подарил ему маленький телескоп и Эдгар По наблюдал в него Луну и звезды.
Рассказ «Необыкновенное приключение некоего Ганса Пфааля» (опубликован в 1835 году) по признанию самого Эдгара По был вдохновлен «Курсом астрономии» Джона Гершеля, американское издание которого вышло лишь годом ранее. Открываем это рассказ и находим в нем массу научной информации – параметры лунной орбиты, детальное описание вида Земли из космоса, сведения о кометах и зодиакальном свете, ссылки на великих ученых прошлого. Эдгар По так старался убедить читателей в подлинности фантастического путешествия на воздушном шаре на Луну, что превратил свой рассказ почти в научно-популярный астрономический очерк.
3 февраля 1848 года Эдгар По выступил в Общественной библиотеке Нью-Йорка с лекцией «О космогонии Вселенной». Аншлага не было – на лекцию пришло около 60 слушателей, большинству из которых лекция показалась скучной, затянутой и малопонятной. Затем По переработал лекцию и в том же году тиражом в 500 экземпляров выпустил ее расширенную версию под названием «Эврика. Поэма в прозе» (По хотел напечатать 50 000 экземпляров, издатель уменьшил тираж в сто раз). Эдгар По считал, что этой поэмой он «революционизирует мир физических и метафизических наук». Революции не произошло – «Эврика» на многие годы оказалась забытой и на развитие науки она уж точно никакого влияния не оказала. По словам Эдварда Харрисона, «ее наука была слишком метафизической, а ее метафизика – слишком научной».
Среди немногочисленных читателей «Эврики», высоко оценивших ее содержание, были в основном поэты – например, Шарль Бодлер (автор французского перевода), Поль Валери, Константин Бальмонт, переведший поэму на русский язык. Дочь знаменитого французского поэта Теофиля Готье – Юдит Готье – в 1864 году (ей было тогда только 15 лет!) написала о только что вышедшей на французском языке «Эврике»: «Было бы ошибочно думать, что Эдгар По, создавая «Эврику», ставил своей целью только написать поэму; он был абсолютно убежден, что открыл великий секрет Вселенной, и он использовал всю мощь своего таланта для развития своей идеи».
Рассмотрим нарисованную в «Эврике» картину Вселенной (все последующие цитаты взяты из перевода К. Бальмонта). Согласно По, пространство бесконечно, а «звездная Вселенная» или «Вселенная звезд», то есть заполненная материей часть бесконечного пространства, конечна во времени и в пространстве. В этой бесконечной «метавселенной» наша Вселенная не единственна —»существует некая беспредельная последовательность Вселенных, более или менее подобных той, о которой мы имеем осведомленность…» Каждая из этих Вселенных имеет свои собственные законы, и эти Вселенные никак друг с другом не взаимодействуют – «не имея доли в нашем происхождении, они не имеют доли в наших законах. Ни они не притягивают нас, ни мы их… Между ними и нами… нет влияний взаимных…» (Нарисованная Эдгаром По картина очень напоминает современную концепцию Мультивселенной (Multiverse) – см. следующую главу.)

Рис. 10. Эдмонд Галлей (1656–1742)
Как ни странно, можно, по-видимому, назвать точную дату, когда Галлей заинтересовался проблемой ночного неба. Скорее всего, это произошло утром 23 февраля 1721 года во время совместного завтрака Ньютона, Галлея и Вильяма Стакли (1687–1765) (английского археолога, одного из первых исследователей Стоунхенджа). Разговор за завтраком шел на астрономические темы и Стакли скорее всего упомянул свои соображения о том, что звезды распределены в пространстве не однородно, как это требуется по космологии Ньютона, а в виде «гигантского меридиана», делящего бесконечное пространство на две части. Если бы это было не так, то, согласно Стакли, все небо должно было бы быть столь же ярким как Млечный Путь.
Эта беседа, вероятно, подтолкнула Галлея к собственным размышлениям и всего через две недели после этого завтрака – 9 марта 1721 года – он представил на заседании Королевского общества статью «О бесконечности сферы неподвижных звезд», в которой Галлей упомянул, не называя его по имени, и аргументацию Стакли. Вскоре – 16 марта – Галлей зачитал и вторую небольшую работу («О числе, порядке и свете неподвижных звезд») на ту же тему.
В своих работах Галлей сначала приводит аргументы в поддержку того, что система звезд бесконечна: чем более мощный телескоп используется при наблюдениях, тем больше звезд в него видно; кроме того, если система звезд конечна, то звезды под действием гравитации должны были сжаться в единый объект в центре (аргумент, использованный ранее Ньютоном). Затем Галлей обсуждает два возражения против бесконечности Вселенной. Одно из них чисто терминологическое, а второе – это, по сути, возражение Стакли, которое перекликается и с мнением Кеплера (см. ранее).
Для того, чтобы преодолеть это затруднение, Галлей вводит идею концентрических слоев одинаковой толщины (рис. 1), подсчитывает количество звезд в слое и создаваемую каждой из этих звезд освещенность по мере увеличения радиуса. Добравшись до звезд сотого слоя, освещенность от каждой из которых в 10 000 меньше, чем от звезды в первом слое, он заключает, что эта освещенность столь мала, что человеческий глаз даже в телескоп просто не увидит этих звезд.
Следовательно, для решения фотометрического парадокса Галлей использует тот же аргумент, что и Томас Диггес за полтора столетия до него – далекие звезды слишком слабы, чтобы быть увиденными. Галлей не догадался просуммировать вклад далеких звезд и убедиться, что им нельзя пренебречь. (Как видно из формулы (2), вклад каждого слоя одинаковой толщины одинаков – падение освещенностей от индивидуальных звезд точно компенсируется увеличением их числа).
Журнал Королевского общества зафиксировал еще один довод Галлея, сводящийся к тому, что освещенность от далеких звезд спадает быстрее, чем по закону обратных квадратов (см. формулу (1) в параграфе 1.2): «свет не делится до бесконечности и, следовательно, когда звезды находятся на очень больших расстояниях, их излучение слабеет быстрее, чем по общему правилу». Это предположение может решить фотометрический парадокс, но оно, конечно, неверно.
Ньютон председательствовал на заседаниях Королевского общества во время выступлений Галлея, однако его реакция на результаты Галлея осталась неизвестной. Возможно, пожилой Ньютон просто проспал выступления своего друга, что, судя по воспоминаниям современников, с ним нередко случалось на разных заседаниях.
Заметки Галлея были опубликованы в журнале Королевского общества «Philosophical Transactions» и, по-видимому, они стимулировали работу швейцарского астронома и физика Шезо, который в 1744 году выполнил первый корректный математический анализ парадокса.
1.5. Шезо и Ольберс
Пустота чудовищно вместительна.
Станислав Ежи Лец
Жан-Филипп Луи де Шезо родился вблизи Лозанны в семье обеспеченного землевладельца. Он очень рано проявил интерес к астрономии и построил собственную обсерваторию, оборудованную парой небольших телескопов. Ранние работы Шезо по физике распространения звука, о торможении пушечных ядер воздухом и пр. привлекли к нему широкое внимание, и российская императрица Елизавета Петровна даже приглашала его на работу в Санкт-Петербург. По причине слабого здоровья Шезо не смог воспользоваться этим предложением.
В декабре 1743 года Шезо открыл комету (практически одновременно она была также обнаружена датчанином Дирком Клинкенбергом) и наблюдал ее до марта 1744 года. Комета была очень яркой, ярче Юпитера, и в одну из ночей продемонстрировала целых 6 хвостов. Через несколько месяцев после исчезновения кометы Шезо опубликовал о ней книгу. Книга содержала восемь приложений, посвященных разным вопросам астрономии. Второе приложение – «О силе света, его прохождении через эфир и расстоянии до неподвижных звезд» – содержало математический анализ загадки ночного неба.
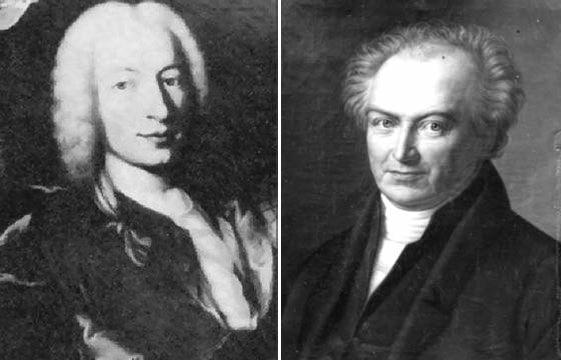
Рис. 11. Жан-Филипп Луи де Шезо (1718–1751) и Генрих Вильгельм Ольберс (1758–1840)
Анализ Шезо был, по сути, эквивалентен приведенному ранее в параграфе 1.2 этой книги. Так же как и Галлей, Шезо рассматривает окружающие Солнце концентрические слои одинаковой толщины и в предположении однородного распределения звезд в пространстве находит, что освещенность от каждого слоя одинакова. Если звездное пространство бесконечно или даже просто очень велико, то любой участок небесной сферы должен сиять как Солнце (он предположил, что все звезды по размерам и по светимости подобны Солнцу), поскольку звезды перекроют своими видимыми дисками весь небосвод. Шезо оценил, что вся доступная наблюдениям полусфера в этом случае должна сиять в 91 850 раз ярче Солнца. (Эта оценка примерно равна отношению площади полусферы к площади солнечного диска.)
«Громадное несоответствие между этим заключением и опытом свидетельствует, что либо сфера неподвижных звезд не бесконечна…, либо освещенность спадает быстрее, чем по закону обратных квадратов», – пишет Шезо. Он считает, что второе допущение более правдоподобно и предполагает, что межзвездное пространство может быть заполнено разреженной средой, задерживающей излучение звезд. Он полагает, что даже ничтожное поглощение в межзвездной среде, постепенно накапливаясь, может объяснить темноту ночного неба. Решение, предложенное Шезо, выглядит правдоподобно, но, как будет показано, далее, неверно – межзвездное поглощение не может решить фотометрический парадокс.
В работе Шезо содержатся еще два примечательных результата. Во-первых, он оказался одним из первых исследователей, правильно оценивших масштаб межзвездных расстояний. Этой задачей пытались заниматься многие (например, Гук, Пикар, Флемстид, Брадлей, Вильям Гершель и другие), однако прямая оценка расстояний методом годичного параллакса из-за несовершенства используемых инструментов и методов обработки не давала результатов вплоть до XIX века.
В качестве альтернативного и, конечно, очень грубого подхода можно использовать видимый блеск звезды в сравнении с Солнцем. Если считать, что все звезды, включая Солнце, имеют одинаковую светимость, то, сравнивая освещенности от какой-либо звезды и от Солнца, можно оценить, во сколько раз звезда дальше от нас, чем Солнце. Используя этот метод, голландский физик, математик и астроном Христиан Гюйгенс (1629–1695) оценил, что Сириус находится в 28 000 раз дальше Солнца, то есть на расстоянии около 0.14 пк[6].
Для того, чтобы получить этот результат, Гюйгенсу пришлось сравнивать яркость освещенного Солнцем отверстия в темной комнате с воспоминанием о яркости Сириуса ночью. Естественно, сделать это очень сложно, что и привело к заниженному почти в 20 раз расстоянию (расстояние до Сириуса равно 2.7 пк или 8.7 световых лет). Этот результат Гюйгенса был опубликован уже после его смерти – в 1698 году.
Однако еще раньше – в 1668 году – шотландский математик, астроном и оптик Джеймс Грегори (1638–1675) опубликовал замечательную модификацию фотометрического метода. Грегори предложил не сравнивать яркости звезд и Солнца, что на практике очень сложно, а использовать в качестве промежуточного стандарта яркость планет. Суть его метода очень проста – ночью можно сравнить яркость какой-либо звезды с яркостью внешней планеты (Марса, Юпитера, Сатурна), а затем, зная расстояние этой планеты от Солнца и ее угловой диаметр, можно рассчитать ее яркость по сравнению с яркостью Солнца (предполагая, конечно, что планета светит отраженным светом и задавая определенный коэффициент отражения). Применив этот метод к Сириусу, и используя наблюдения Сатурна, Грегори получил, что эта звезда находится в 80000 раз дальше Солнца – результат гораздо лучший, чем у Гюйгенса, хотя все еще существенно заниженный.
Во второй части работы о фотометрическом парадоксе Шезо использует метод Грегори для определения расстояний до ярчайших звезд (Сириуса и Регула) на основе сравнения их блеска с Сатурном, Юпитером и Марсом. Он заключает, что расстояние до ярчайших звезд примерно в 240 000 раз превышает расстояние от Земли до Солнца. Эта оценка составляет около 4 световых лет или чуть больше 1 пк. Учитывая грубость используемого метода, результат можно признать просто превосходным!
Однако Шезо не был первым человеком, правильно оценившим масштаб межзвездных расстояний. Как оказалось, это было сделано Исааком Ньютоном в «De mundi systemate» («Система мира») – дополнении к «Началам», написанном еще в 1680-х годах и опубликованном в 1728 году, уже после его смерти. В этой работе Ньютон методом Грегори нашел, что расстояние до звезд первой величины примерно в 100 000 раз превышает расстояние от Сатурна до Солнца, что составляет ~ 1 000 000 астрономических единиц (4.8 пк)[7].
Еще один интересный результат небольшой работы Шезо о фотометрическом парадоксе – корректная математическая оценка доступной наблюдениям области Вселенной. Если предположить, что все звезды подобны Солнцу и что они равномерно распределены в пространстве со средним взаимным расстоянием 4 световых года, то в пределах сферы радиусом 3×1015 световых лет звезды перекроют своими дисками всю небесную сферу. Свет от более далеких звезд будет экранирован дисками более близких объектов и внешняя часть Вселенной останется ненаблюдаемой.
Британский космолог Эдвард Харрисон считает, что, возможно, именно огромность, несоизмеримость этих масштабов могла подтолкнуть Шезо к идее межзвездного поглощения – ведь даже ничтожная непрозрачность межзвездной среды на столь больших расстояниях способна полностью скрыть далекие объекты и, тем самым, сделать ночное небо темным.
Следующий исследователь, внесший вклад в исследование парадокса, названного позднее его именем, – это немецкий врач и астроном-любитель Генрих Ольберс. Ольберс был дипломированным медиком, но, горячо увлекаясь астрономией, он в течение многих лет сочетал оба занятия. Днем он был солидным бременским врачом, а ночью проводил наблюдения в частной обсерватории на верхнем этаже собственного дома. Лишь после смерти дочери и второй жены он оставил врачебную практику и с 1820 года полностью посвятил себя астрономии. В биографическом очерке, включенном в книгу С. Ньюкомба и Р. Энгельмана «Астрономия в общепонятном изложении» (опубликована на русском языке в 1896 году), об Ольберсе было написано так: «Едва ли можно назвать другого любителя, которому астрономия была бы так много обязана, как Ольберсу; и мало было специалистов по астрономии, которые обладали столь обширными познаниями в ней, как этот любитель».
Основные результаты Ольберса посвящены наблюдениям комет (он открыл их 7 штук) и расчетам их орбит (им разработан метод определения орбит комет по трем наблюдениям). В 1802 году Ольберс переоткрыл первую малую планету (Цереру)[8], которая вскоре после ее открытия в 1801 году итальянским астрономом Пиацци была потеряна. В том же 1802 году он открыл вторую малую планету (Палладу), а в 1807 – четвертую (Весту).
В 1823 году, почти через 80 лет после работы Шезо, Генрих Ольберс опубликовал статью «О прозрачности пространства». В своей статье Ольберс анализирует фотометрический парадокс – более пространно и в более качественном стиле по сравнению с кратким изложением Шезо – и предполагает, что учет поглощения света далеких звезд в межзвездном пространстве может решить эту проблему.
Изложение Ольберса в целом оригинально и вводит в обсуждение парадокса несколько новых идей. Например, Ольберс допускает, что звезды не обязательно должны быть однородно распределены в пространстве, а могут группироваться в системы, подобные Млечному Пути, то есть в галактики. Такое скучивание не избавляет от парадокса, поскольку любой луч зрения все равно рано или поздно должен упереться в диск какой-либо звезды. Ольберс считает, что полная прозрачность межзвездного пространства «в высокой степени невероятна» и обосновывает существование поглощающей среды тем, что вещество кометных хвостов рассеивается, пополняя окружающее пространство, а также существованием зодиакального света. (Строго говоря, это говорит лишь о межпланетной среде, но отсюда уже один шаг до признания существования и межзвездного вещества.)
Любопытен «научно-фантастический» пассаж Ольберса о том, что даже в случае, если бы вся небесная сфера сияла как поверхность Солнца, можно было бы вообразить живые организмы, приспособившиеся и к таким экстремальным условиям. Он отмечает, что астрономия у разумных существ такой планеты находилась бы в примитивном состоянии – обитателям ничего не было бы известно о звездах, о существовании Солнца можно было бы узнать лишь по наблюдениям его пятен, а Луна и планеты обнаруживались бы лишь как темные пятна на сверкающем фоне. (Соображения Ольберса отчасти перекликаются с высказанными в п. 1.1 этой книги.)
В своей статье Ольберс цитирует Галлея, но ни разу не упоминает работу Шезо. Знал ли он о ней, и повлияла ли она как-нибудь на его собственную работу? Вопрос не праздный, поскольку подход Ольберса и предложенное им решение фотометрического парадокса в целом похожи на то, что сделал Шезо задолго до него. Кроме того, оказалось, что в библиотеке Ольберса была книга Шезо 1744 года, посвященная знаменитой шестихвостой комете, в приложении к которой Шезо описал свое решение фотометрического парадокса. Более того, Ольберс, несомненно, читал эту книгу – американский историк астрономии Стенли Яки обнаружил, что в записных книжках, относящихся к 1782–96 годам, Ольберс тщательно законспектировал часть книги Шезо, в которой тот описывает предложенный им метод определения кометных орбит.
Так что же произошло? Яки, да и не только он, считает, что речь не может идти о плагиате, поскольку это в сильнейшей степени противоречит тому, что известно об Ольберсе, о его характере и научных работах. Скорее всего, к 1823 году, когда Ольберс написал свою статью, он забыл или полузабыл о короткой заметке Шезо, которую он, возможно, читал тридцать или сорок лет назад в поисках информации о столь любимых им кометах. Как полагает Эдвард Харрисон, люди забывают об источниках своих идей гораздо чаще, чем обычно считают.
Какова дальнейшая судьба идеи Шезо и Ольберса о межзвездном поглощении как о возможном решении фотометрического парадокса? Идея эта, конечно, не верна, поскольку в заполненной звездами безграничной и вечной Вселенной само поглощающее вещество (межзвездная пыль и газ) начнет нагреваться до тех пор, пока не установится тепловое равновесие между поглощающей средой и излучением звезд, а тогда среда станет излучать столько же, сколько поглотит. Первым это понял, по-видимому, английский астроном Джон Гершель (1792–1871), знаменитый сын еще более знаменитого отца – Вильяма Гершеля (1738–1822).
В 1848 году Джон Гершель опубликовал рецензию на недавно появившийся первый том «Космоса» Александра фон Гумбольдта. Гершель упоминает Ольберса и идею поглощения света, а затем пишет, что, действительно, свет легко поглощается, однако поглощенный свет нагревает поглощающую материю и она должна начать излучать, отдавая через излучение столько же энергии, сколько поглотила. Гершель использовал немного другие слова, но суть его комментария именно в этом. Очень примечательно, что это было написано тогда, когда недавно открытый закон сохранения энергии еще не стал широко известным и общепринятым.
Джон Гершель предложил и свой вариант решения фотометрического парадокса. Будучи наблюдателем, он был уверен, что в некоторых направлениях на небе он и в самом деле видит пустое пространство за пределами нашей звездной системы. С другой стороны, он имел хорошую математическую подготовку и догадывался, что можно придумать такое пространственное распределение объектов, что даже при бесконечном числе звезд ночное небо будет оставаться темным: «…легко представить устройство вселенной, которая будет оставаться в точном смысле слова бесконечной, и в которой произвольное количество лучей зрения не будут пересекаться со звездами». Гершель коротко описал такое устройство – звезды распределены самоподобным образом на всех уровнях, – то, что позднее стали называть иерархическим или фрактальным распределением. Идея иерархического строения Вселенной позднее развивалась многими исследователями – например, Ричардом Проктором, Карлом Шарлье, Фурнье д’Альбе. Эта идея, действительна, способна решить фотометрический парадокс, однако она противоречит наблюдаемой на больших масштабах однородности нашей Вселенной (см. следующую главу).
1.6. Динамическая Вселенная Эдгара По
Наука! ты – дитя Седых Времен!
Меняя все вниманьем глаз прозрачных,
Зачем тревожишь ты поэта сон,
О коршун! крылья чьи – взмах истин мрачных!
Эдгар По
Появление имени знаменитого поэта, писателя, классика и родоначальника сразу нескольких жанров литературы, может показаться странным в книге по астрономии. Однако что не было странным в жизни этого человека?
Эдгар Аллан По рано остался без родителей и воспитывался в доме богатого коммерсанта из Ричмонда Джона Аллана. Вместе с приемной семьей Эдгар По пять лет прожил в Англии, где учился в дорогом пансионе в Лондоне. После возвращения Алланов в США Эдгар закончил колледж в Ричмонде, в 1826 году поступил в недавно открытый Университет штата Вирджиния. Проучился в университете лишь год, вынужден был его бросить, записался добровольцем в армию, пытался закончить элитную военную академию в Вест-Пойнте, но был отчислен. Дальше – работа в нескольких журналах, богемная жизнь, личные и семейные драмы, нервное перенапряжение, болезни, запои, и на фоне всего этого – многочисленные стихи, рассказы, новеллы… И смерть в 40 лет в унизительной бедности и горячечном бреду. Биография, разительнейшим образом отличающаяся от жизни остальных героев этой книги.

Рис. 12. Дагерротип Эдгара Аллана По (1809–1849), изготовленный незадолго до смерти поэта.
Парадоксально, что именно этот парадоксальный человек предложил первое правильное, хотя и качественное, решение загадки темноты ночного неба. Даже более – Эдгара По можно назвать, пусть и с некоторой натяжкой, одним из идейных предшественников современной космологии в целом. Это не было случайностью – он очень интересовался наукой и, в особенности, астрономией, изучал книги классиков физики и астрономии (например, Ньютона, Лапласа, Вильяма и Джона Гершелей, Гумбольдта). Когда Эдгару было 16 лет, опекун подарил ему маленький телескоп и Эдгар По наблюдал в него Луну и звезды.
Рассказ «Необыкновенное приключение некоего Ганса Пфааля» (опубликован в 1835 году) по признанию самого Эдгара По был вдохновлен «Курсом астрономии» Джона Гершеля, американское издание которого вышло лишь годом ранее. Открываем это рассказ и находим в нем массу научной информации – параметры лунной орбиты, детальное описание вида Земли из космоса, сведения о кометах и зодиакальном свете, ссылки на великих ученых прошлого. Эдгар По так старался убедить читателей в подлинности фантастического путешествия на воздушном шаре на Луну, что превратил свой рассказ почти в научно-популярный астрономический очерк.
3 февраля 1848 года Эдгар По выступил в Общественной библиотеке Нью-Йорка с лекцией «О космогонии Вселенной». Аншлага не было – на лекцию пришло около 60 слушателей, большинству из которых лекция показалась скучной, затянутой и малопонятной. Затем По переработал лекцию и в том же году тиражом в 500 экземпляров выпустил ее расширенную версию под названием «Эврика. Поэма в прозе» (По хотел напечатать 50 000 экземпляров, издатель уменьшил тираж в сто раз). Эдгар По считал, что этой поэмой он «революционизирует мир физических и метафизических наук». Революции не произошло – «Эврика» на многие годы оказалась забытой и на развитие науки она уж точно никакого влияния не оказала. По словам Эдварда Харрисона, «ее наука была слишком метафизической, а ее метафизика – слишком научной».
Среди немногочисленных читателей «Эврики», высоко оценивших ее содержание, были в основном поэты – например, Шарль Бодлер (автор французского перевода), Поль Валери, Константин Бальмонт, переведший поэму на русский язык. Дочь знаменитого французского поэта Теофиля Готье – Юдит Готье – в 1864 году (ей было тогда только 15 лет!) написала о только что вышедшей на французском языке «Эврике»: «Было бы ошибочно думать, что Эдгар По, создавая «Эврику», ставил своей целью только написать поэму; он был абсолютно убежден, что открыл великий секрет Вселенной, и он использовал всю мощь своего таланта для развития своей идеи».
Рассмотрим нарисованную в «Эврике» картину Вселенной (все последующие цитаты взяты из перевода К. Бальмонта). Согласно По, пространство бесконечно, а «звездная Вселенная» или «Вселенная звезд», то есть заполненная материей часть бесконечного пространства, конечна во времени и в пространстве. В этой бесконечной «метавселенной» наша Вселенная не единственна —»существует некая беспредельная последовательность Вселенных, более или менее подобных той, о которой мы имеем осведомленность…» Каждая из этих Вселенных имеет свои собственные законы, и эти Вселенные никак друг с другом не взаимодействуют – «не имея доли в нашем происхождении, они не имеют доли в наших законах. Ни они не притягивают нас, ни мы их… Между ними и нами… нет влияний взаимных…» (Нарисованная Эдгаром По картина очень напоминает современную концепцию Мультивселенной (Multiverse) – см. следующую главу.)
Конец бесплатного ознакомительного фрагмента
