Страница:
Между прочим, случилась одна вещь, которая удивила меня. Помните, я говорил вам, что в самом начале моего путешествия, раньше, чем машина времени понеслась с огромной скоростью, через лабораторию прошла миссис Уатчет, как мне тогда показалось, промелькнувшая мимо меня с мгновенностью ракеты. На возвратном пути мой аппарат, понятно, опять пронес меня через ту же минуту; я снова увидел мою экономку, и все ее движения повторились, но в противоположном направлении. Дверь из сада отворилась; миссис Уатчет спокойно скользнула через комнату, спиной вперед, и исчезла за той дверью, через которую она тогда вошла.
Машина остановилась. Я был в моей давно знакомой мне лаборатории. Мои инструменты, мои приборы, все я нашел в том виде, в каком оставил. Я спустился с седла совершенно разбитый и сел на скамейку. Я услышал ваши голоса, звон посуды и, уловив обонянием запах мяса, открыл дверь в столовую. Остальное вы знаете. Я умылся, пообедал, а теперь рассказываю вам о моих странствиях.
– Я страшно занят, – сказал он, – знаете, опять той вещью… там.
– Вы действительно путешествовали во времени?
– Действительно и реально, – был его ответ. Он посмотрел мне в глаза ясным правдивым взглядом. Несколько мгновений Путешественник колебался, обводя комнату глазами, наконец прибавил: – Дайте мне только полчаса времени. На столе несколько журналов; займитесь ими. Если вы останетесь позавтракать со мной, я окончательно рассею ваше сомнение относительно моих странствий. А теперь позвольте мне покинуть вас на короткое время.
Я согласился, не вполне, впрочем, понимая, о чем он говорит. Путешественник же, кивнув мне головой, ушел по коридору в свою лабораторию. Я слышал, как за ним закрылась дверь; сев в кресло, я взял газету. Что собирался он сделать до завтрака? Случайно на глаза мне попалось одно объявление и напомнило, что я обещался в два часа побывать у издателя Ричардсона; посмотрев же на часы, я понял, что у меня на это осталось мало времени, а потому поднялся с места и пошел по коридору; я собирался сказать Путешественнику, что мне не придется завтракать у него.
В ту минуту, когда я взялся за ручку двери в лабораторию, прозвучало странно оборвавшееся восклицание; послышался звон и стук. Через растворенную дверь на меня хлынул порыв воздуха; в ту же секунду я услыхал звон разбитого стекла, осколки которого сыпались на пол. Путешественника в комнате не было. Передо мною на мгновение мелькнула призрачная сидячая человеческая фигура, еле различимая в хаосе вращающейся черной тени и отблесков меди, – фигура такая прозрачная, что сквозь нее отлично была видна скамейка, заваленная листами чертежей. Через мгновение все пропало. Едва я протер глаза, призрак как бы растаял. Машина времени исчезла. Я был поражен. Я понимал, что произошло нечто необыкновенное, но не мог сообразить, что именно. Я стоял, как окаменелый, широко открыв глаза; в эту минуту садовая дверь открылась и в лабораторию вошел лакей Путешественника.
Мы посмотрели друг на друга, и мало-помалу мои мысли начали приходить в порядок.
– Скажите, он прошел через эту дверь? – спросил я.
– Нет, в сад никто не прошел. Я думал, что застану его здесь, – был ответ.
Я все понял. Я остался ждать Путешественника, а также и второго, может быть, еще более удивительного рассказа. Но я начинаю бояться, что мне придется ждать всю жизнь.
Путешественник во времени исчез три года тому назад и, как все теперь знают, не вернулся.
Чтобы уяснить себе это, перенесемся мысленно из знакомого нам мира трех измерений в мир двух измерений. Таким двухмерным миром, имеющим длину и ширину, но вовсе не имеющим толщины, является плоскость. Вообразим же себе, что весь пространственный мир сплющился в одну плоскость и что в таком мире обитают разумные существа, – конечно, также двухмерные. Для двухмерных обитателей существуют только двухмерные вещи. Всякая линия, пересекающая их плоский мир, должна представляться им в виде точки, так как они могут из всей линии воспринять только одну точку – именно ту, в которой эта линия встречает плоскость. Двухмерные существа могли бы исследовать всю эту линию только в том случае, если бы их плоский мир двигался в третьем измерении, – например, по перпендикулярному направлению. Наделим этот мир таким движением. Следя тогда за тем, как изменяется положение точки встречи линии с их плоскостью, двухмерные мыслители могли бы составить себе некоторое понятие о всей трехмерной линии. Но, конечно, они не могли бы так наглядно, как мы, представить себе, какое положение занимает в трехмерном мире эта линия: все трехмерное не укладывается в сознании существа двухмерного. Двухмерный мыслитель высказался бы об этом в других выражениях: он сказал бы, что исследуемая им точка изменяет свое положение во «времени». То, что для нас является движением двухмерного мира (плоскости) в трехмерном пространстве, то для обитателя двухмерного мира представлялось бы, как «течение времени». То, что для нас существует одновременно в пространстве трех измерений, – для них появляется последовательно в пространстве двух измерений.
Рассмотрим еще пример. Двухмерный мир (плоскость), двигаясь в трехмерном пространстве, наткнулся на тело в форме двойного конуса (см. рис.). Двухмерный обитатель плоскости, конечно, не может воспринять этот конус как тело; не может даже и вообразить его себе.
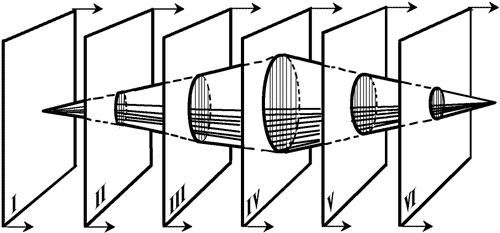Что же будет он видеть и думать, когда мир его наткнется на подобное трехмерное тело и оно пройдет сквозь плоский мир? Проследим за этим. Сначала в двухмерном мире появится точка – вершина конуса. Затем, по мере дальнейшего продвижения плоского мира в направлении третьего измерения (т. е. «с течением времени», как сказал бы двухмерный мыслитель), точка превратится в небольшой кружок или эллипс – сечение конуса плоскостью двухмерного мира. Кружок будет расти, расширяться и, достигнув наибольшего размера, станет сокращаться, постепенно превратится в точку и вновь исчезнет. Двухмерный исследователь наблюдал историю зарождения, развития, увядания и исчезновения «кружка», между тем как мы, существа трехмерные, воспринимаем ту же вещь сразу, одновременно в форме трех измерений. Для них он существовал в цепи последовательно воспринимаемых плоских сечений, для нас – весь целиком, как трехмерное тело. Движение плоскости в третьем измерении знакомого нам пространства переживается двухмерным существом как течение времени. Для него «прошедшее» конуса – это те его части, которые лежат по одну сторону его плоского мира (по ту, откуда плоскость движется); «будущее» конуса – те его части, которые расположены по другую сторону, а «настоящее» – пересечение конуса с двухмерным миром.
Приложим теперь те же рассуждения к миру трехмерному. Когда мы описываем историю изменений какой-нибудь вещи в нашем трехмерном пространстве, не даем ли мы последовательные изображения этой вещи во времени? Если так, то можно рассматривать время как четвертое измерение мира, измерение, в котором движется наш трехмерный мир; каждое явление, наблюдаемое в трехмерном мире – есть одно из последовательных «пересечений» нашего трехмерного мира с четырехмерною вещью. Существо четырех измерений могло бы сразу охватить всю историю вещи, всю ее «жизнь» в виде некоторого четырехмерного объекта, недоступного нашему воображению.
Само собою разумеется, что фантастическая мысль Уэллса – придумать механизм для произвольного движения в четвертом измерении – не свободна от внутренних противоречий и должна быть принимаема не иначе как чисто художественный прием, удобный для успешного развития интриги фантастической повести.
На комете
Однажды – 27 июня – профессор Розетт бомбой влетел в общую залу, где собрались капитан Сервадак, лейтенант Прокофьев, Тимашев и ординарец Бен-Зуф.
– Лейтенант Прокофьев, – крикнул он, – отвечайте без обиняков и лишних разговоров на вопрос, который я вам задам.
– Я и не имею обыкновения… – начал было лейтенант.
– И отлично! – перебил профессор, обращавшийся с лейтенантом, как учитель с учеником. – Отвечайте: вы объехали на вашей шхуне «Добрыне» кругом Галлии почти по экватору, иначе говоря – по ее большому кругу. Да или нет?
– Да, – ответил лейтенант, которому Тимашев подал знак не противоречить раздраженному ученому.
– Хорошо. А измерили вы при этом путь, пройденный шхуной «Добрыней»?
– Приблизительно, т. е. с помощью лага[10] и буссоли[11], но не измеряя высоты солнца и звезд, которую невозможно было определить,
– И что же вы узнали?
– Что окружность Галлии составляет около 2.323[12] километров, а следовательно, ее диаметр равен 740 километрам.
– Да, – сказал профессор, словно про себя, – диаметр в 17 раз меньшеземногодиаметра, равного 12.735[13] километрам.
Сервадак и его спутники смотрели на ученого, не понимая, куда он ведет.
– Так вот, – сказал профессор, – для завершения моего изучения Галлии мне остается определить ее поверхность, объем, массу, плотность и напряжение тяжести на ней.
– Что касается поверхности и объема, – ответил Прокофьев, – то раз мы знаем диаметр Галлии, нет ничего легче, как определить их.
– А я говорю разве, что это трудно? – воскликнул профессор. – Ученик Сервадак, возьмите перо. Зная длину большого круга Галлии, определите величину ее поверхности.
– Вот, – ответил Сервадак, решивший держаться примерным учеником. – Множим окружность 2.323 километра на диаметр, т. е. на 740.
– Скорее же, – торопил профессор, – пора бы уже иметь результат. Ну!
– Так вот, – ответил Сервадак, – я получил в произведении 1.719.020 квадратных километров. Это и есть поверхность Галлии.
– Ну, – продолжал профессор, разгорячаясь, – а теперь, каков же объем Галлии?
– Объем… – замялся Сервадак.
– Ученик Сервадак, неужели вы не можете вычислить объем шара, раз вам известна его поверхность?
– Но, профессор, вы не даете мне времени вздохнуть…
– При вычислениях не дышат, сударь, не дышат!
Слушатели с большим трудом удерживались от смеха.
– Мы когда-нибудь кончим с этим? – спросил профессор – Объем шара равен…
– Произведению поверхности на…
– На треть радиуса, сударь, на треть радиуса! – гремел профессор. – Кончили?
– Почти. Треть радиуса Галлии равна 123,33.
– Ну?
– Произведение 1.719.020 на 123,33 составляет 212.006.737 кубических километров.
– Итак, – сказал профессор, – мы знаем теперь диаметр, окружность, поверхность и объем Галлии. Это уже нечто, но еще не все. Я намерен определить ее массу, плотность и напряжение тяжести на ее поверхности.
– Это будет трудно, – сказал Тимашев.
– Все равно. Я желаю знать, сколько весит моя комета, и узнаю это!
– Задача не легкая, – заметил лейтенант Прокофьев. – Ведь нам неизвестен состав вещества Галлии.
– Вам неизвестен ее состав? – спросил профессор.
– Неизвестен, – сказал Тимашев, – и если вы нам поможете…
– Пустяки, – заметил ученый, – я решу свою задачу и без этого.
– Мы всегда к вашим услугам, – сказал капитан Сервадак.
Сервадак, Тимашев и Прокофьев боялись пропустить свидание, назначенное вспыльчивым ученым. С утра все собрались в большой зале. Профессор, по-видимому, не был в дурном настроении, – но день только начался.
Все знают, что такое напряжение тяжести. Это сила притяжения, проявляемая Землей по отношению к телу, масса которого равна единице. Галлийцам было известно, что это притяжение на Галлии ослаблено, – откуда и возрастание мускульной силы галлийцев. Но они не знали, на сколько именно тяжесть ослабела.
Итак, первый вопрос, подлежавший разрешению, был: как велико напряжение тяжести на поверхности Галлии?
Второй вопрос: какова масса Галлии, а следовательно, и ее вес?
Третий вопрос: какую массу заключает вещество Галлии в единице объема? Другими словами: какова ее плотность?
– Сегодня, – начал профессор, – мы закончим определение элементов моей кометы. Когда мы определим напряжение тяжести на ее поверхности, ее массу и плотность, для нас не будет больше тайн на Галлии. В результате мы взвесим Галлию.
Ординарец Бен-Зуф как раз при этих последних словах вошел в залу. Он тотчас же молча вышел, но вскоре появился вновь и сказал лукаво:
– Я обшарил кладовую, но не нашел весов, подходящих для взвешивания кометы. Да я и не знаю, куда бы мы их привесили.
При этом Бен-Зуф выглянул наружу, словно ища гвоздя на небе.
Взгляд, брошенный на него профессором, и жест Сервадака заставили шутника замолчать.
– Прежде всего, – сказал профессор, – нужно узнать, сколько весит на Галлии земной килограмм. Так как масса Галлии меньше массы Земли, то все тела на ее поверхности весят меньше, чем на Земле[15]. Но на сколько именно – вот это необходимо знать.
– Совершенно верно, – ответил Прокофьев. – Но обыкновенные весы, если бы мы их даже имели, не годились бы для этого, так как обе их чашки одинаково подвержены притяжению Галлии и не указали бы нам соотношения весов галлийского и земного.
– Действительно, – подхватил Тимашев, – килограмм, которым мы будем пользоваться, потеряет в своем весе столько же, сколько и взвешиваемая вещь, и…
– Если вы говорите все это в назидание мне, – объявил профессор, – то напрасно теряете время. Прошу вас, позвольте мне продолжать курс.
Профессор держал себя, словно на кафедре.
– Есть ли у вас пружинные весы и гиря в один килограмм? – продолжал он. – Это необходимо. В пружинных весах вес тела определяется степенью растяжения пружины, обусловленного ее упругостью. Поэтому, если я подвешу груз в 1 килограмм к пружинным весам, указатель покажет в точности, сколько весит 1 килограмм на Галлии. Повторяю: имеются у вас пружинные весы?
Слушатели смотрели друг на друга. Сервадак обратился к Бен-Зуфу, хорошо знавшему весь инвентарь колонии.
– У нас нет ни пружинных весов, ни гирь, – ответил ординарец.
Профессор выразил свою досаду, энергично топнув ногой.
– Но, – продолжал Бен-Зуф, – я, кажется, знаю, где есть пружинные весы, а пожалуй, и гири.
– Где?
– У Хаккабута[16].
– Так надо пойти за ними, – сказал капитан.
– Иду, – ответил ординарец.
– Я с тобой, – сказал капитан. – Хаккабут не особенно сговорчив, когда дело доходит до того, чтобы ссудить что-нибудь.
– Пойдемте все, – предложил Тимашев. – Посмотрим, как устроился он на своей тартане[17].
Когда все выходили, профессор сказал Тимашеву:
– Не может ли кто-нибудь из ваших людей обтесать осколок каменистой массы, чтобы получился в точности кубический дециметр?
– Наш механик сделает это без труда, но при одном условии: если его снабдить метром, необходимым для точного отмеривания.
– Разве у вас нет метра? – спросил профессор.
В кладовых не было метра: это удостоверил Бен-Зуф.
– Но, – прибавил он, – весьма возможно, что метр найдется у Хаккабута.
– Так идемте же, – торопил профессор, поспешно направляясь в коридор.
– Хозяин Исаак, – сказал капитан, – мы пришли к вам, чтобы попросить об услуге.
– Услуге?
– Одним словом: можете ли вы ссудить нам пружинные весы?
– Вы просите меня ссудить вам…
– Только на один день, – вмешался профессор, – всего на один день. Вам возвратят их.
– Но это очень деликатный инструмент; пружина может сломаться на таком холоде… Вам понадобится, может быть, взвешивать что-нибудь очень тяжелое?
– Уж не думаешь ли ты, – сказал ординарец – что мы будем вешать гору?
– Больше чем гору, – заметил профессор. – Мы взвесим Галлию.
– Помилуйте! – воскликнул Хаккабут.
– Хозяин, – вмешался капитан, – пружинные весы нам нужны, чтобы взвесить вещь, не тяжелее килограмма.
– Еще меньше килограмма, вследствие ослабления тяжести на Галлии. Словом, вам нечего опасаться за свои весы.
– А вы внесете мне залог?
– Да. Сто франков. Весы стоят двадцать. Достаточно?
– А плата за пользование?
– Двадцать франков.
Торг был заключен. Хаккабут принес инструмент. Это были пружинные весы с крючком, на который навешивался груз. Стрелка на циферблате показывала вес. Предназначенный для взвешивания земных предметов, инструмент был градуирован на Земле. Но каковы будут его показания на Галлии?
Посетители встали, чтобы покинуть тартану, когда профессор задержал всех:
– Нам надо еще взять у него метр и гирю в один килограмм.
– К сожалению, невозможно, – ответил Хаккабут, – я рад был бы их дать вам…
На этот раз он говорил искренно, утверждая, что у него нет ни метра, ни гири и что он охотно дал бы их в пользование: сделка была бы выгодная.
– Придется как-нибудь обойтись без них, – сказал раздосадованный профессор.
Не успели посетители сойти с тартаны, как из каюты донесся звон монет: Хаккабут пересчитывал золото в своих ящиках.
Услышав этот звук, профессор кинулся назад к лестнице, все с недоумением смотрели на него, не зная, чему приписать его стремительность.
– У вас есть деньги? – крикнул профессор, хватая торговца за платье.
– У меня… деньги!.. – шептал Хаккабут, словно на него напал грабитель.
– Французские монеты! – продолжал профессор.
– Пятифранковые монеты!
Профессор наклонился над ящиком.
– Это французские монеты, – заявил он, – и они мне нужны.
– Никогда!.. – кричал торговец.
– Они мне нужны, говорю тебе, и они у меня будут!
Сервадак видел, что пришло время вмешаться.
– Вам нужны деньги? – спросил он профессора. – Определенное число монет для ваших исследований?
– Да, сорок монет.
– Двести франков! – шептал торговец.
– И кроме того, десять монет в два франка и двадцать монет по 50 сантимов.
– Тридцать франков! – жалобно стонал Хаккабут.
– Хорошо, – сказал капитан, обращаясь к Тимашеву,
– есть у вас что дать Хаккабуту в обеспечение займа?
– Двести рублей кредитными билетами.
Тимашев бросил на стол деньги. Французские монеты, потребованные профессором, были ему вручены, и он с видимым довольством спрятал их в карман.
Через несколько минут капитан и его спутники покинули тартану.
– Это не двести тридцать франков, – воскликнул профессор, – это то, из чего мы изготовим в точности и метр, и килограмм!
Профессор распорядился расчистить место на столе. Деньги, занятые у торговца, были рассортированы по их достоинству, образовав два столбика в 20 монет по пяти франков, один – из 10 монет по два франка и еще один – из 20 монет по 50 сантимов.
Профессор начал с удовлетворенным видом:
– Так как при столкновении с кометой мы не догадались запастись метром и гирей в один килограмм, то я вынужден был придумать способ заменить эти предметы, необходимые мне для определения напряжения тяжести, массы и плотности моей кометы.
Никто не прерывал этого странного вступления.
– Я убедился, – продолжал профессор, – что монеты эти почти новы, нисколько не изношены, не потерты. Они как раз в таком состоянии, какое необходимо, чтобы разрешить нашу задачу с надлежащею точностью.
Сервадак и его товарищи угадали намерения профессора, прежде чем он изложил их до конца. Но ординарец взирал на него, как на фокусника, готовящегося выполнить очередной «номер».
Вот на чем основывал ученый свою первую операцию, идея которой возникла в его уме, когда он услышал звон монет в ящике торговца.
Известно, что монеты Франции заготовляются по десятичной системе, включающей в пределах от сантима до ста франков: 1) медные монеты в 1, в 2, в 3 и в 10 сантимов; 2) серебряные – в 20 и в 50 сантимов, в 1, в 2 и в 5 франков; 3) золотые – в 5, в 10, в 20, в 50 и в 100 франков.
Для профессора Розетта важно было то, что диаметры этих монет были строго определены законом. Так, диаметр пятифранковой монеты равен 37 миллиметрам, двухфранковой – 27 миллиметрам, полуфранковой – 18 миллиметрам. Нельзя ли поэтому, прикладывая друг к другу монеты различного достоинства, получить точно длину метра?
Вполне возможно, и профессор знал это; вот почему он выбрал 10 монет по пяти франков, десять по два франка и 20 монет по 50 сантимов.
В самом деле: набросав быстро на клочке бумаги следующий расчет, он представил его слушателям:
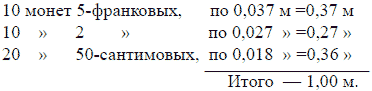– Прекрасно, дорогой профессор, – сказал Сервадак. – Остается лишь тщательно выложить эти 40 монет в одну прямую линию, чтобы получить точную длину метра.
– О, – воскликнул ординарец. – Быть ученым, я вижу, совсем неплохо!
– Он называет это быть ученым, – заметил профессор, пожимая плечами.
Десять пятифранковых монет были выложены в один ряд, одна к другой так, чтобы центры их были на одной прямой; к ним примыкали десять двухфранковых монет и двадцать полуфранковых. Границы составившейся длины были отмечены черточками.
– Вот, – объявил профессор, – точная длина метра.
Операция была выполнена с крайней тщательностью. Полученная длина была циркулем разделена на десять частей, т. е. на дециметры, и брусок соответствующей длины был вручен судовому механику.
Тот уже раздобыл обломок неизвестной горной породы, из которой составлена была масса Галлии, и оставалось лишь, как требовал профессор, обтесать его в форме кубического дециметра.
Метр был получен. Теперь надо было изготовить гирю в один килограмм.
Это было более легким делом. Действительно, французские монеты имеют не только строго определенный диаметр, но и установленный законом вес. Пятифранковая монета весит ровно 25 граммов, что составляет вес пяти монет по одному франку[18]. Достаточно поэтому взять 40 серебряных монет по 5 франков, чтобы получился вес в 1 килограмм.
– Как вижу я, – сказал ординарец, – быть ученым все же недостаточно, надо еще…
– Что еще? – спросил Сервадак.
– Быть богатым.
Замечание было встречено дружным хохотом.
Через несколько часов механик доставил профессору тщательно выточенный кубик из горной породы. Теперь ученый имел все необходимое.
– Должен напомнить вам, – начал профессор, – на случай, если вы забыли или не знали, знаменитый закон Ньютона, согласно которому сила притяжения прямо пропорциональна произведению масс и обратно пропорциональна квадрату расстояния. Прошу всегда твердо помнить этот закон.
Машина остановилась. Я был в моей давно знакомой мне лаборатории. Мои инструменты, мои приборы, все я нашел в том виде, в каком оставил. Я спустился с седла совершенно разбитый и сел на скамейку. Я услышал ваши голоса, звон посуды и, уловив обонянием запах мяса, открыл дверь в столовую. Остальное вы знаете. Я умылся, пообедал, а теперь рассказываю вам о моих странствиях.
XVI. ПОСЛЕ РАССКАЗА
Почти всю ночь я не спал, раздумывая о слышанном, и на следующий день решился повидаться с Путешественником во времени. Когда я пришел к нему, мне сказали, что он в лаборатории, и я отправился туда же. Однако лаборатория оказалась пустой. Я посмотрел на машину времени и даже потрогал один из рычагов. Я вернулся в курильную; там меня встретил Путешественник, который, видимо, собрался куда-то. В одной руке он держал маленькую фотографическую камеру, в другой – дорожную сумку. Завидев меня, Путешественник засмеялся и для рукопожатия подал мне локоть.– Я страшно занят, – сказал он, – знаете, опять той вещью… там.
– Вы действительно путешествовали во времени?
– Действительно и реально, – был его ответ. Он посмотрел мне в глаза ясным правдивым взглядом. Несколько мгновений Путешественник колебался, обводя комнату глазами, наконец прибавил: – Дайте мне только полчаса времени. На столе несколько журналов; займитесь ими. Если вы останетесь позавтракать со мной, я окончательно рассею ваше сомнение относительно моих странствий. А теперь позвольте мне покинуть вас на короткое время.
Я согласился, не вполне, впрочем, понимая, о чем он говорит. Путешественник же, кивнув мне головой, ушел по коридору в свою лабораторию. Я слышал, как за ним закрылась дверь; сев в кресло, я взял газету. Что собирался он сделать до завтрака? Случайно на глаза мне попалось одно объявление и напомнило, что я обещался в два часа побывать у издателя Ричардсона; посмотрев же на часы, я понял, что у меня на это осталось мало времени, а потому поднялся с места и пошел по коридору; я собирался сказать Путешественнику, что мне не придется завтракать у него.
В ту минуту, когда я взялся за ручку двери в лабораторию, прозвучало странно оборвавшееся восклицание; послышался звон и стук. Через растворенную дверь на меня хлынул порыв воздуха; в ту же секунду я услыхал звон разбитого стекла, осколки которого сыпались на пол. Путешественника в комнате не было. Передо мною на мгновение мелькнула призрачная сидячая человеческая фигура, еле различимая в хаосе вращающейся черной тени и отблесков меди, – фигура такая прозрачная, что сквозь нее отлично была видна скамейка, заваленная листами чертежей. Через мгновение все пропало. Едва я протер глаза, призрак как бы растаял. Машина времени исчезла. Я был поражен. Я понимал, что произошло нечто необыкновенное, но не мог сообразить, что именно. Я стоял, как окаменелый, широко открыв глаза; в эту минуту садовая дверь открылась и в лабораторию вошел лакей Путешественника.
Мы посмотрели друг на друга, и мало-помалу мои мысли начали приходить в порядок.
– Скажите, он прошел через эту дверь? – спросил я.
– Нет, в сад никто не прошел. Я думал, что застану его здесь, – был ответ.
Я все понял. Я остался ждать Путешественника, а также и второго, может быть, еще более удивительного рассказа. Но я начинаю бояться, что мне придется ждать всю жизнь.
Путешественник во времени исчез три года тому назад и, как все теперь знают, не вернулся.
Примечание редактора
ВРЕМЯ КАК ЧЕТВЕРТОЕ ИЗМЕРЕНИЕ
Полезно остановиться подробнее на высказанном Уэллсом своеобразном понимании в р е м е н и как четвертого измерения пространства.Чтобы уяснить себе это, перенесемся мысленно из знакомого нам мира трех измерений в мир двух измерений. Таким двухмерным миром, имеющим длину и ширину, но вовсе не имеющим толщины, является плоскость. Вообразим же себе, что весь пространственный мир сплющился в одну плоскость и что в таком мире обитают разумные существа, – конечно, также двухмерные. Для двухмерных обитателей существуют только двухмерные вещи. Всякая линия, пересекающая их плоский мир, должна представляться им в виде точки, так как они могут из всей линии воспринять только одну точку – именно ту, в которой эта линия встречает плоскость. Двухмерные существа могли бы исследовать всю эту линию только в том случае, если бы их плоский мир двигался в третьем измерении, – например, по перпендикулярному направлению. Наделим этот мир таким движением. Следя тогда за тем, как изменяется положение точки встречи линии с их плоскостью, двухмерные мыслители могли бы составить себе некоторое понятие о всей трехмерной линии. Но, конечно, они не могли бы так наглядно, как мы, представить себе, какое положение занимает в трехмерном мире эта линия: все трехмерное не укладывается в сознании существа двухмерного. Двухмерный мыслитель высказался бы об этом в других выражениях: он сказал бы, что исследуемая им точка изменяет свое положение во «времени». То, что для нас является движением двухмерного мира (плоскости) в трехмерном пространстве, то для обитателя двухмерного мира представлялось бы, как «течение времени». То, что для нас существует одновременно в пространстве трех измерений, – для них появляется последовательно в пространстве двух измерений.
Рассмотрим еще пример. Двухмерный мир (плоскость), двигаясь в трехмерном пространстве, наткнулся на тело в форме двойного конуса (см. рис.). Двухмерный обитатель плоскости, конечно, не может воспринять этот конус как тело; не может даже и вообразить его себе.
Приложим теперь те же рассуждения к миру трехмерному. Когда мы описываем историю изменений какой-нибудь вещи в нашем трехмерном пространстве, не даем ли мы последовательные изображения этой вещи во времени? Если так, то можно рассматривать время как четвертое измерение мира, измерение, в котором движется наш трехмерный мир; каждое явление, наблюдаемое в трехмерном мире – есть одно из последовательных «пересечений» нашего трехмерного мира с четырехмерною вещью. Существо четырех измерений могло бы сразу охватить всю историю вещи, всю ее «жизнь» в виде некоторого четырехмерного объекта, недоступного нашему воображению.
Само собою разумеется, что фантастическая мысль Уэллса – придумать механизм для произвольного движения в четвертом измерении – не свободна от внутренних противоречий и должна быть принимаема не иначе как чисто художественный прием, удобный для успешного развития интриги фантастической повести.
На комете
Жюля Верна[9]
– Лейтенант Прокофьев, – крикнул он, – отвечайте без обиняков и лишних разговоров на вопрос, который я вам задам.
– Я и не имею обыкновения… – начал было лейтенант.
– И отлично! – перебил профессор, обращавшийся с лейтенантом, как учитель с учеником. – Отвечайте: вы объехали на вашей шхуне «Добрыне» кругом Галлии почти по экватору, иначе говоря – по ее большому кругу. Да или нет?
– Да, – ответил лейтенант, которому Тимашев подал знак не противоречить раздраженному ученому.
– Хорошо. А измерили вы при этом путь, пройденный шхуной «Добрыней»?
– Приблизительно, т. е. с помощью лага[10] и буссоли[11], но не измеряя высоты солнца и звезд, которую невозможно было определить,
– И что же вы узнали?
– Что окружность Галлии составляет около 2.323[12] километров, а следовательно, ее диаметр равен 740 километрам.
– Да, – сказал профессор, словно про себя, – диаметр в 17 раз меньшеземногодиаметра, равного 12.735[13] километрам.
Сервадак и его спутники смотрели на ученого, не понимая, куда он ведет.
– Так вот, – сказал профессор, – для завершения моего изучения Галлии мне остается определить ее поверхность, объем, массу, плотность и напряжение тяжести на ней.
– Что касается поверхности и объема, – ответил Прокофьев, – то раз мы знаем диаметр Галлии, нет ничего легче, как определить их.
– А я говорю разве, что это трудно? – воскликнул профессор. – Ученик Сервадак, возьмите перо. Зная длину большого круга Галлии, определите величину ее поверхности.
– Вот, – ответил Сервадак, решивший держаться примерным учеником. – Множим окружность 2.323 километра на диаметр, т. е. на 740.
– Скорее же, – торопил профессор, – пора бы уже иметь результат. Ну!
– Так вот, – ответил Сервадак, – я получил в произведении 1.719.020 квадратных километров. Это и есть поверхность Галлии.
– Ну, – продолжал профессор, разгорячаясь, – а теперь, каков же объем Галлии?
– Объем… – замялся Сервадак.
– Ученик Сервадак, неужели вы не можете вычислить объем шара, раз вам известна его поверхность?
– Но, профессор, вы не даете мне времени вздохнуть…
– При вычислениях не дышат, сударь, не дышат!
Слушатели с большим трудом удерживались от смеха.
– Мы когда-нибудь кончим с этим? – спросил профессор – Объем шара равен…
– Произведению поверхности на…
– На треть радиуса, сударь, на треть радиуса! – гремел профессор. – Кончили?
– Почти. Треть радиуса Галлии равна 123,33.
– Ну?
– Произведение 1.719.020 на 123,33 составляет 212.006.737 кубических километров.
– Итак, – сказал профессор, – мы знаем теперь диаметр, окружность, поверхность и объем Галлии. Это уже нечто, но еще не все. Я намерен определить ее массу, плотность и напряжение тяжести на ее поверхности.
– Это будет трудно, – сказал Тимашев.
– Все равно. Я желаю знать, сколько весит моя комета, и узнаю это!
– Задача не легкая, – заметил лейтенант Прокофьев. – Ведь нам неизвестен состав вещества Галлии.
– Вам неизвестен ее состав? – спросил профессор.
– Неизвестен, – сказал Тимашев, – и если вы нам поможете…
– Пустяки, – заметил ученый, – я решу свою задачу и без этого.
– Мы всегда к вашим услугам, – сказал капитан Сервадак.
* * *
62-го галлийского апреля[14] на имя капитана Сервадака пришла краткая записка от профессора. Розетт сообщал, что в этот день предлагает выполнить работы, необходимые для определения массы, плотности кометы и напряжения тяжести на ее поверхности.Сервадак, Тимашев и Прокофьев боялись пропустить свидание, назначенное вспыльчивым ученым. С утра все собрались в большой зале. Профессор, по-видимому, не был в дурном настроении, – но день только начался.
Все знают, что такое напряжение тяжести. Это сила притяжения, проявляемая Землей по отношению к телу, масса которого равна единице. Галлийцам было известно, что это притяжение на Галлии ослаблено, – откуда и возрастание мускульной силы галлийцев. Но они не знали, на сколько именно тяжесть ослабела.
Итак, первый вопрос, подлежавший разрешению, был: как велико напряжение тяжести на поверхности Галлии?
Второй вопрос: какова масса Галлии, а следовательно, и ее вес?
Третий вопрос: какую массу заключает вещество Галлии в единице объема? Другими словами: какова ее плотность?
– Сегодня, – начал профессор, – мы закончим определение элементов моей кометы. Когда мы определим напряжение тяжести на ее поверхности, ее массу и плотность, для нас не будет больше тайн на Галлии. В результате мы взвесим Галлию.
Ординарец Бен-Зуф как раз при этих последних словах вошел в залу. Он тотчас же молча вышел, но вскоре появился вновь и сказал лукаво:
– Я обшарил кладовую, но не нашел весов, подходящих для взвешивания кометы. Да я и не знаю, куда бы мы их привесили.
При этом Бен-Зуф выглянул наружу, словно ища гвоздя на небе.
Взгляд, брошенный на него профессором, и жест Сервадака заставили шутника замолчать.
– Прежде всего, – сказал профессор, – нужно узнать, сколько весит на Галлии земной килограмм. Так как масса Галлии меньше массы Земли, то все тела на ее поверхности весят меньше, чем на Земле[15]. Но на сколько именно – вот это необходимо знать.
– Совершенно верно, – ответил Прокофьев. – Но обыкновенные весы, если бы мы их даже имели, не годились бы для этого, так как обе их чашки одинаково подвержены притяжению Галлии и не указали бы нам соотношения весов галлийского и земного.
– Действительно, – подхватил Тимашев, – килограмм, которым мы будем пользоваться, потеряет в своем весе столько же, сколько и взвешиваемая вещь, и…
– Если вы говорите все это в назидание мне, – объявил профессор, – то напрасно теряете время. Прошу вас, позвольте мне продолжать курс.
Профессор держал себя, словно на кафедре.
– Есть ли у вас пружинные весы и гиря в один килограмм? – продолжал он. – Это необходимо. В пружинных весах вес тела определяется степенью растяжения пружины, обусловленного ее упругостью. Поэтому, если я подвешу груз в 1 килограмм к пружинным весам, указатель покажет в точности, сколько весит 1 килограмм на Галлии. Повторяю: имеются у вас пружинные весы?
Слушатели смотрели друг на друга. Сервадак обратился к Бен-Зуфу, хорошо знавшему весь инвентарь колонии.
– У нас нет ни пружинных весов, ни гирь, – ответил ординарец.
Профессор выразил свою досаду, энергично топнув ногой.
– Но, – продолжал Бен-Зуф, – я, кажется, знаю, где есть пружинные весы, а пожалуй, и гири.
– Где?
– У Хаккабута[16].
– Так надо пойти за ними, – сказал капитан.
– Иду, – ответил ординарец.
– Я с тобой, – сказал капитан. – Хаккабут не особенно сговорчив, когда дело доходит до того, чтобы ссудить что-нибудь.
– Пойдемте все, – предложил Тимашев. – Посмотрим, как устроился он на своей тартане[17].
Когда все выходили, профессор сказал Тимашеву:
– Не может ли кто-нибудь из ваших людей обтесать осколок каменистой массы, чтобы получился в точности кубический дециметр?
– Наш механик сделает это без труда, но при одном условии: если его снабдить метром, необходимым для точного отмеривания.
– Разве у вас нет метра? – спросил профессор.
В кладовых не было метра: это удостоверил Бен-Зуф.
– Но, – прибавил он, – весьма возможно, что метр найдется у Хаккабута.
– Так идемте же, – торопил профессор, поспешно направляясь в коридор.
* * *
Исаак Хаккабут стоял в углу с видом человека, ожидающего приговора суда.– Хозяин Исаак, – сказал капитан, – мы пришли к вам, чтобы попросить об услуге.
– Услуге?
– Одним словом: можете ли вы ссудить нам пружинные весы?
– Вы просите меня ссудить вам…
– Только на один день, – вмешался профессор, – всего на один день. Вам возвратят их.
– Но это очень деликатный инструмент; пружина может сломаться на таком холоде… Вам понадобится, может быть, взвешивать что-нибудь очень тяжелое?
– Уж не думаешь ли ты, – сказал ординарец – что мы будем вешать гору?
– Больше чем гору, – заметил профессор. – Мы взвесим Галлию.
– Помилуйте! – воскликнул Хаккабут.
– Хозяин, – вмешался капитан, – пружинные весы нам нужны, чтобы взвесить вещь, не тяжелее килограмма.
– Еще меньше килограмма, вследствие ослабления тяжести на Галлии. Словом, вам нечего опасаться за свои весы.
– А вы внесете мне залог?
– Да. Сто франков. Весы стоят двадцать. Достаточно?
– А плата за пользование?
– Двадцать франков.
Торг был заключен. Хаккабут принес инструмент. Это были пружинные весы с крючком, на который навешивался груз. Стрелка на циферблате показывала вес. Предназначенный для взвешивания земных предметов, инструмент был градуирован на Земле. Но каковы будут его показания на Галлии?
Посетители встали, чтобы покинуть тартану, когда профессор задержал всех:
– Нам надо еще взять у него метр и гирю в один килограмм.
– К сожалению, невозможно, – ответил Хаккабут, – я рад был бы их дать вам…
На этот раз он говорил искренно, утверждая, что у него нет ни метра, ни гири и что он охотно дал бы их в пользование: сделка была бы выгодная.
– Придется как-нибудь обойтись без них, – сказал раздосадованный профессор.
Не успели посетители сойти с тартаны, как из каюты донесся звон монет: Хаккабут пересчитывал золото в своих ящиках.
Услышав этот звук, профессор кинулся назад к лестнице, все с недоумением смотрели на него, не зная, чему приписать его стремительность.
– У вас есть деньги? – крикнул профессор, хватая торговца за платье.
– У меня… деньги!.. – шептал Хаккабут, словно на него напал грабитель.
– Французские монеты! – продолжал профессор.
– Пятифранковые монеты!
Профессор наклонился над ящиком.
– Это французские монеты, – заявил он, – и они мне нужны.
– Никогда!.. – кричал торговец.
– Они мне нужны, говорю тебе, и они у меня будут!
Сервадак видел, что пришло время вмешаться.
– Вам нужны деньги? – спросил он профессора. – Определенное число монет для ваших исследований?
– Да, сорок монет.
– Двести франков! – шептал торговец.
– И кроме того, десять монет в два франка и двадцать монет по 50 сантимов.
– Тридцать франков! – жалобно стонал Хаккабут.
– Хорошо, – сказал капитан, обращаясь к Тимашеву,
– есть у вас что дать Хаккабуту в обеспечение займа?
– Двести рублей кредитными билетами.
Тимашев бросил на стол деньги. Французские монеты, потребованные профессором, были ему вручены, и он с видимым довольством спрятал их в карман.
Через несколько минут капитан и его спутники покинули тартану.
– Это не двести тридцать франков, – воскликнул профессор, – это то, из чего мы изготовим в точности и метр, и килограмм!
* * *
Спустя четверть часа посетители тартаны вновь собрались в общей зале, и последние слова профессора получили свое объяснение.Профессор распорядился расчистить место на столе. Деньги, занятые у торговца, были рассортированы по их достоинству, образовав два столбика в 20 монет по пяти франков, один – из 10 монет по два франка и еще один – из 20 монет по 50 сантимов.
Профессор начал с удовлетворенным видом:
– Так как при столкновении с кометой мы не догадались запастись метром и гирей в один килограмм, то я вынужден был придумать способ заменить эти предметы, необходимые мне для определения напряжения тяжести, массы и плотности моей кометы.
Никто не прерывал этого странного вступления.
– Я убедился, – продолжал профессор, – что монеты эти почти новы, нисколько не изношены, не потерты. Они как раз в таком состоянии, какое необходимо, чтобы разрешить нашу задачу с надлежащею точностью.
Сервадак и его товарищи угадали намерения профессора, прежде чем он изложил их до конца. Но ординарец взирал на него, как на фокусника, готовящегося выполнить очередной «номер».
Вот на чем основывал ученый свою первую операцию, идея которой возникла в его уме, когда он услышал звон монет в ящике торговца.
Известно, что монеты Франции заготовляются по десятичной системе, включающей в пределах от сантима до ста франков: 1) медные монеты в 1, в 2, в 3 и в 10 сантимов; 2) серебряные – в 20 и в 50 сантимов, в 1, в 2 и в 5 франков; 3) золотые – в 5, в 10, в 20, в 50 и в 100 франков.
Для профессора Розетта важно было то, что диаметры этих монет были строго определены законом. Так, диаметр пятифранковой монеты равен 37 миллиметрам, двухфранковой – 27 миллиметрам, полуфранковой – 18 миллиметрам. Нельзя ли поэтому, прикладывая друг к другу монеты различного достоинства, получить точно длину метра?
Вполне возможно, и профессор знал это; вот почему он выбрал 10 монет по пяти франков, десять по два франка и 20 монет по 50 сантимов.
В самом деле: набросав быстро на клочке бумаги следующий расчет, он представил его слушателям:
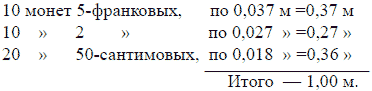
– О, – воскликнул ординарец. – Быть ученым, я вижу, совсем неплохо!
– Он называет это быть ученым, – заметил профессор, пожимая плечами.
Десять пятифранковых монет были выложены в один ряд, одна к другой так, чтобы центры их были на одной прямой; к ним примыкали десять двухфранковых монет и двадцать полуфранковых. Границы составившейся длины были отмечены черточками.
– Вот, – объявил профессор, – точная длина метра.
Операция была выполнена с крайней тщательностью. Полученная длина была циркулем разделена на десять частей, т. е. на дециметры, и брусок соответствующей длины был вручен судовому механику.
Тот уже раздобыл обломок неизвестной горной породы, из которой составлена была масса Галлии, и оставалось лишь, как требовал профессор, обтесать его в форме кубического дециметра.
Метр был получен. Теперь надо было изготовить гирю в один килограмм.
Это было более легким делом. Действительно, французские монеты имеют не только строго определенный диаметр, но и установленный законом вес. Пятифранковая монета весит ровно 25 граммов, что составляет вес пяти монет по одному франку[18]. Достаточно поэтому взять 40 серебряных монет по 5 франков, чтобы получился вес в 1 килограмм.
– Как вижу я, – сказал ординарец, – быть ученым все же недостаточно, надо еще…
– Что еще? – спросил Сервадак.
– Быть богатым.
Замечание было встречено дружным хохотом.
Через несколько часов механик доставил профессору тщательно выточенный кубик из горной породы. Теперь ученый имел все необходимое.
– Должен напомнить вам, – начал профессор, – на случай, если вы забыли или не знали, знаменитый закон Ньютона, согласно которому сила притяжения прямо пропорциональна произведению масс и обратно пропорциональна квадрату расстояния. Прошу всегда твердо помнить этот закон.