Страница:
Базовые положения его концепции гласят: «Средства регуляции агрессии: ритуализация и социосозидательные функции ритуализованных действий» (гл. 2), «Средства регуляции психических реальностей. Переход от реагирования к моделированию» (гл. 3). Среди важных тезисных пунктов: «Агрессия во зло» и «Агрессия во благо» в связи с работами Конрада Лоренца.
Во многом сходные положения И. Н. Черкасовой—Цвергер основаны на ее личном опыте работы с французско—русскими текстами, связанными с событиями в европейском ареале, такими как «Молодежная революция» 1968 г. и 2005 г. в Парижском районе, поджоги автомобилей, – откуда и название темы «Парижский синдром», – а также на опыте исследования отношения французов к событиям в России (травля Б. Пастернака, изгнание А. И. Солженицына).
И. Н. Черкасова—Цвергер (в имеющемся у меня тексте в кн. [Гуманитарная наука сегодня 2006]) говорит о том, что она называет «псевдо—специализацией дискурса»: «В описываемый нами (ею. – Ю. С.) период, период тоталитаризма в России, принадлежность к определенному комплексу идей определяет видовую принадлежность человека. Точно так же, как в животном царстве (выше мы уже подчеркнули от себя аналогию между дискурсом и ценозом. – Ю. С.) видовая принадлежность определяется морфологией и ритуализованным типом поведения».
Таким образом, понятия «дискурсы» и «ценозы», возникшие в нашей и з о– теме 2, оказываются связанными и в этом, в известной мере заключительном, ее пункте.
Здесь мы кратко остановимся на узловых пунктах книги Ю. В. Монича. Он справедливо напоминает, что еще в 1865 г. Парижское лингвистическое общество прописало в своем уставе, что оно отказывается от принятия к рассмотрению каких бы то ни было работ, касающихся проблемы происхождения языка. Тогда это было вынужденной мерой, призванной оградить науку от захлестывающего ее потока разнообразных, большей частью полуфантастических спекуляций на эту тему, не имевших под собой хоть сколь—либо надежной эмпирической базы. Хотя Парижское общество вовсе не ставило перед собой цели предписать свое локальное «табу» всему ученому миру, оно все же было молча принято к исполнению фактически всеми прогрессивными научными школами, ясно осознававшими, что наука еще не созрела для решения подобных проблем. И далее он четко формулирует научную ситуацию.
Естественно, в рамках нашей данной книги мы можем остановиться лишь выборочно на некоторых фрагментах исследования названных «массовидных объектов».
В сфере этологии Ю. В. Монич основывается главным образом на работах Конрада Лоренца (прежде всего, на книге «Агрессия (так называемое „зло“)». Пер. с нем. М., 1994). В сфере лингвистики Ю. В. Монич опирается на свои собственные, но подкрепленные исследованиями других авторов, положения. Главное из них – н е с л у ч а й н о е р а с п р е д е л е н и е ф о р м о о б р а з у ю щ и х т и п о в з в у к о в, особенно сонорных (сонантовных), в индоевропейских языках.
Ограничимся некоторыми примерами этих сфер, указанными Ю. В. Моничем.
Из раздела этологии по Ю. В. Моничу:
Ю. В. Монич продолжает:
П р и ло же н ие к тексту Ю. В. Монича (текст его)
Таблица 1 (соотношение между типом формы и типом грамматического значения)

r = +0,074; а = 0,0006 ([r = +0,058; а = 0,007], [r = +0,041; а = 0,054], [r = +0,026; а = 0,22])
Таблица 2 (соотношение между типом значения и деривацией)

r = -0,21; а = 1,310 –22 ([r = -0,20; а = 3,0–10 –20], [r = -0,19; а = 9,1–10» -20], [r = -0,18; а = 1,4–10» -17])
Таблица 3 (соотношение между типом формы и деривацией)

r = +0,30; а = 4,8–10» -45 ([r = +0,27; а = 1,110 –37], [r = +0,25; а = 1,9–10» -32], [r = +0,23; а = 1,5–10» -27])
Коэффициент корреляции, полученный по данным таблицы 2, отчетливо демонстрирует, что деривационные процессы явно тяготеют к образованию имен, а отнюдь не глаголов. В то же время корреляционный показатель по таблице 3 недвусмысленно говорит о том, что звучащее завершение корня находится в вовсе не случайной связи с деривационной активностью, которая превосходит таковую у оппонентов более чем в 4 раза.
[.] Думается, из сказанного со всей очевидностью вытекает, что коэффициент корреляции говорит только о том, что существует некоторая доля случаев, связанных какой—то причинно—следственной связью, но конкретный характер этой связи в нем, разумеется, никоим образом не эксплицируется. Это уже сфера исследовательских допущений.
Заканчивая здесь, по необходимости, это длинное Приложение, от себя подчеркнем лишь, что данные Ю. В. Монича доказательно разрешают один из «вечных», «роковых» вопросов лингвистики как части гуманитарной науки, – о чем свидетельствует нижеследующая итоговая таблица —
Соотношение между типом формы и типом значения (по Ю. В. Моничу)
Таблица 4 (простые корни)

r = +0,035; а = 0,29 ([r = +0,03; а = 0,37], [r = +0,025; а = 0,44], [r = +0,019; а = 0,56])
Таблица 5 (расширенные корни)

r = +0,27; а = 3,5–Ю» -21 ([r = +0,20; а = 6,910 –13], [r = +0,16; а = 1,5–10» -8], [r = +0,11; а = 3,8–10 –5])
8. Изотема 8
9. Изотема 9
Во многом сходные положения И. Н. Черкасовой—Цвергер основаны на ее личном опыте работы с французско—русскими текстами, связанными с событиями в европейском ареале, такими как «Молодежная революция» 1968 г. и 2005 г. в Парижском районе, поджоги автомобилей, – откуда и название темы «Парижский синдром», – а также на опыте исследования отношения французов к событиям в России (травля Б. Пастернака, изгнание А. И. Солженицына).
И. Н. Черкасова—Цвергер (в имеющемся у меня тексте в кн. [Гуманитарная наука сегодня 2006]) говорит о том, что она называет «псевдо—специализацией дискурса»: «В описываемый нами (ею. – Ю. С.) период, период тоталитаризма в России, принадлежность к определенному комплексу идей определяет видовую принадлежность человека. Точно так же, как в животном царстве (выше мы уже подчеркнули от себя аналогию между дискурсом и ценозом. – Ю. С.) видовая принадлежность определяется морфологией и ритуализованным типом поведения».
Таким образом, понятия «дискурсы» и «ценозы», возникшие в нашей и з о– теме 2, оказываются связанными и в этом, в известной мере заключительном, ее пункте.
Здесь мы кратко остановимся на узловых пунктах книги Ю. В. Монича. Он справедливо напоминает, что еще в 1865 г. Парижское лингвистическое общество прописало в своем уставе, что оно отказывается от принятия к рассмотрению каких бы то ни было работ, касающихся проблемы происхождения языка. Тогда это было вынужденной мерой, призванной оградить науку от захлестывающего ее потока разнообразных, большей частью полуфантастических спекуляций на эту тему, не имевших под собой хоть сколь—либо надежной эмпирической базы. Хотя Парижское общество вовсе не ставило перед собой цели предписать свое локальное «табу» всему ученому миру, оно все же было молча принято к исполнению фактически всеми прогрессивными научными школами, ясно осознававшими, что наука еще не созрела для решения подобных проблем. И далее он четко формулирует научную ситуацию.
Несмотря на то, что с тех пор прошло уже почти полтора века, за которые как лингвистика, так и смежные с ней дисциплины существенно продвинулись вперед в своем развитии, отмеченная проблематика так и находится на самой отдаленной периферии круга приоритетности стоящих перед лингвистикой задач. До сих пор еще исследования в этом направлении носят факультативный характер и рассматриваются скорее как упражнения в философствовании, позволительные только для состоявшихся авторитетов. Такое маргинальное положение проблемы языковых истоков, разумеется, обусловлено отнюдь не отсутствием к ней интереса: вопросы, связанные с происхождением языка, всегда были и остаются в числе самых животрепещущих для стремящегося к познанию собственных истоков человеческого мышления. Однако происхождение языка – проблема комплексная, и достичь каких—либо успехов в ее решении можно лишь адекватной ее комплексности консолидацией усилий, исходящих из различных областей знания.Ю. В. Моничу, естественно, оказывается необходимым сделать еще несколько общих утверждений типа преамбул:
Все наблюдающиеся на сегодняшний день в лингвистике гипотезы о происхождении языка характеризуются тем, что они ограничиваются общими схемами относительно того, как и в каких условиях язык мог бы зародиться, тогда как эмпирическая сторона коммуникации – как языковой, так и предшествующей языку – обычно остается вне всякого анализа. И в отечественных, и в зарубежных публикациях на эту тему наблюдаются лишь отсылки к наборам сигналов у животных наряду с поверхностным скольжением по некоторым экспериментальным данным, почерпнутым из зоопсихологии и сравнительной психологии и касающимся преимущественно проблем эволюции когнитивных способностей. Этологической ветви внимание уделяется только в зарубежной литературе, тогда как у нас она оказывается чуть ли не в полном небрежении. Исключением здесь является лишь, пожалуй, недавно вышедшая в свет работа А. Н. Барулина [Барулин 2002], где, впрочем, как и в зарубежной литературе, хотя и отдается должное этологическому подходу, дальше построения общих схем и разговоров о том, какие он сулит перспективы для сопоставления с языком, дело, к сожалению, не идет.Существо концепции самого Ю. В. Монича заключается не в отдельных «примерах», а в том, что он оперирует м а с с о в и д н ы м и объектами – он связывает типы агрессии у гуманоидов с типами их биологического языкового поведения, последнее же позволяет уже констатировать наблюдаемые научные факты – типы языковых форм реакций, в частности словесных, «словных» форм реакций, зафиксированных в этимологических и исторических словарях. (Использован и предварительно лингвистически проанализирован знаменитый многотомный словарь Ю. Покорного [Pokorny 1951].)
Казалось бы, для понимания данной проблемы явно недостаточно только отстраненного ретроспективного взгляда. О каких истоках языка или же преобразованиях в сфере коммуникации вообще может идти речь, если просто оказывается невозможным элементарное сопоставление языка с тем, что ему предшествовало, так как лингвист, замкнувшийся в своем предмете, даже не предпринимает никаких попыток осмысления внутренней структуры предъязыковой системы коммуникации? Но для этого, очевидно, как бы ни страшны были опасения вокруг вероятной «зооморфизации» человека или, наоборот, «антропоморфизации» животного, нужно так или иначе погружаться в мир последнего.
Естественно, в рамках нашей данной книги мы можем остановиться лишь выборочно на некоторых фрагментах исследования названных «массовидных объектов».
В сфере этологии Ю. В. Монич основывается главным образом на работах Конрада Лоренца (прежде всего, на книге «Агрессия (так называемое „зло“)». Пер. с нем. М., 1994). В сфере лингвистики Ю. В. Монич опирается на свои собственные, но подкрепленные исследованиями других авторов, положения. Главное из них – н е с л у ч а й н о е р а с п р е д е л е н и е ф о р м о о б р а з у ю щ и х т и п о в з в у к о в, особенно сонорных (сонантовных), в индоевропейских языках.
Ограничимся некоторыми примерами этих сфер, указанными Ю. В. Моничем.
Из раздела этологии по Ю. В. Моничу:
1.3. Агрессия в этологии(Напомним здесь от себя, что речь идет об основной работе: Konrad Lorenz. Das sogennante Bose. Zur Naturgeschichte der Aggression. Borotha – Schoeler Verlag. Wien, 1963; имеется русский перевод (по изд. Taschenbuch Verlag, Munchen) – [Лоренц 1994]. Российские издатели в своей аннотации на данную книгу трактуют, на наш взгляд, идею К. Лоренца искаженно, говоря, что он «выделяет внутривидовую агрессию, как наибольшую опасность, грозящую человечеству в современных условиях». В действительности у него (как и у Ю. В. Монича) речь идет о «регуляции» массовых коллективных действий. В русском переводе имеется другая выдающаяся работа К. Лоренца – «Эволюция ритуала в биологической и культурной сферах» // Природа, № 11, 1969. С. 42–51, к которой восходит ключевой термин «р и т у а л и з а ц и я» у Ю. В. Монича, И. Н. Черкасовой—Цвергер и др.)
Полемизирующий с несуществующими призраками Э. Фромм, см. [Фромм 1998] и его сторонники с удивительной то ли ловкостью, то ли слепотой проходят мимо тех положений книги К. Лоренца, которые, казалось бы, манифестированы самым очевиднейшим образом и вполне внятно говорят о том, что этологическая концепция в первую очередь имеет дело с механизмами регуляции агрессии, в то время как сама агрессия является не более чем фоном, – грубым биологическим полотном, на котором эволюция ткет тонкие и изящные формы ритуализованного поведения.
Ю. В. Монич продолжает:
Саму же агрессию Лоренц, видимо, посчитал в своей работе излишним представлять в «анатомированном» виде. Но, возможно, ему бы следовало это сделать хотя бы для того, чтобы показать, из каких комбинаций стимулов и реакций строятся формы агрессивного поведения и где в них – хотя бы в грубом приближении – заканчивается врожденное и начинается приобретенное. Тогда, может быть, некоторым читателям и перестали бы мерещиться ужасы записанного в человеческих генах кровожадного вандализма.Из раздела лингвистики, по Ю. В. Моничу, необходимо выделить данные о связи т и п а п о с т р о е н и я г л а г о л ь н о г о к о р н я (его деривации) с его семантикой. Ниже цитируем Приложение – текст Ю. В. Монича (заметим, что для не—специалиста чтение этих страниц, разумеется, не является необходимым, но они призваны свидетельствовать по крайней мере о наличии данных).
Подразумеваемый Лоренцем облик агрессии можно было бы попытаться восстановить из анализа форм ее регуляции. Однако проще будет пойти иным путем, опираясь на общепринятый в биологии тезис о свойственной всему живому фундаментальной тенденции к росту и размножению, из которой и произрастают все формы агрессии. Рассматриваемая в этом ракурсе защитная агрессия оказывается отнюдь не первичным, как считает Фромм, а вторичным продуктом, так как всегда является реакцией на агрессию вторжения. Поэтому, думается, если вести речь об изначальной природе агрессии, то ее все—таки более целесообразно было бы рассматривать как функцию роста. И здесь – как бы ни была неприятна «гидравлическая модель» Лоренца Фромму – она как раз и работает.
Истоки же механизма, обеспечивающего кроющееся за этой моделью накопление заряда экспансии, лежат на тех уровнях организации живой материи, при описании которых термин «агрессия» еще не может употребляться. В какой—то мере уже клеточная мембрана может быть представлена как сдерживающий «агрессию» роста фактор, поскольку она не только защищает клетку от неблагоприятных внешних воздействий, но призвана также сдерживать ее центробежные тенденции, задавая рамку для протекания внутренних процессов. Когда же эти тенденции больше не поддаются сдерживанию, вступает в силу механизм деления, порождающий уже две немедленно стремящиеся к росту клетки, и т. д.
П р и ло же н ие к тексту Ю. В. Монича (текст его)
Таблица 1 (соотношение между типом формы и типом грамматического значения)

r = +0,074; а = 0,0006 ([r = +0,058; а = 0,007], [r = +0,041; а = 0,054], [r = +0,026; а = 0,22])
Таблица 2 (соотношение между типом значения и деривацией)

r = -0,21; а = 1,310 –22 ([r = -0,20; а = 3,0–10 –20], [r = -0,19; а = 9,1–10» -20], [r = -0,18; а = 1,4–10» -17])
Таблица 3 (соотношение между типом формы и деривацией)

r = +0,30; а = 4,8–10» -45 ([r = +0,27; а = 1,110 –37], [r = +0,25; а = 1,9–10» -32], [r = +0,23; а = 1,5–10» -27])
Коэффициент корреляции, полученный по данным таблицы 2, отчетливо демонстрирует, что деривационные процессы явно тяготеют к образованию имен, а отнюдь не глаголов. В то же время корреляционный показатель по таблице 3 недвусмысленно говорит о том, что звучащее завершение корня находится в вовсе не случайной связи с деривационной активностью, которая превосходит таковую у оппонентов более чем в 4 раза.
[.] Думается, из сказанного со всей очевидностью вытекает, что коэффициент корреляции говорит только о том, что существует некоторая доля случаев, связанных какой—то причинно—следственной связью, но конкретный характер этой связи в нем, разумеется, никоим образом не эксплицируется. Это уже сфера исследовательских допущений.
Заканчивая здесь, по необходимости, это длинное Приложение, от себя подчеркнем лишь, что данные Ю. В. Монича доказательно разрешают один из «вечных», «роковых» вопросов лингвистики как части гуманитарной науки, – о чем свидетельствует нижеследующая итоговая таблица —
Соотношение между типом формы и типом значения (по Ю. В. Моничу)
Таблица 4 (простые корни)

r = +0,035; а = 0,29 ([r = +0,03; а = 0,37], [r = +0,025; а = 0,44], [r = +0,019; а = 0,56])
Таблица 5 (расширенные корни)

r = +0,27; а = 3,5–Ю» -21 ([r = +0,20; а = 6,910 –13], [r = +0,16; а = 1,5–10» -8], [r = +0,11; а = 3,8–10 –5])
8. Изотема 8
Гармоникология
Гармонический (формантный) анализ в лингвистике &
Гармонические ряды; ряды Фурье в математике &
Второй закон термодинамики & Понятие энтропии
Термин «конфликтология» как название дисциплины, отрасли науки возник недавно – чего, естественно, и следовало ждать – и где же еще, как не в современной России, пронизанной конфликтами. Термин же «гармоникология» – под нашим пером, только для противопоставления предшествующему «конфликтологии». Вообще же понятие гармонизации всякого рода, конечно, одно из древнейших в мировой культуре. Писатель Бальзак, как считают, открыл, при хорошем обеде, один из важнейших компонентов в нем – понятие ферментов [Степанов 1971: 12].
Для культуролога естественно начать здесь с «чего—то культурологического». Начну с собственного учебного пособия, по которому в течение многих лет преподавал лингвистику студентам (книга «Основы языкознания» [Степанов 1966: 189–192]), а в нем – с единицы звучания естественной человеческой речи – импульса
Акустические характеристики (параметры) импульса. До сравнительно недавнего времени физиологи исходили из понятия звука как колебательного синусоидального движения. Приближенным его изображением считалась синусоида, представляющая размах колебаний, – д и а п а з о н. Однако, как показали более точные исследования, в природе вообще, а в речи и подавно, не встречается синусоидальных звуков. Прерывистая структура речи и наличие огромного числа обертонов не позволяют сводить речевые звуки к синусоидам.
При анализе звуков речи и голоса допустимо представлять их как совокупность простых синусоид, но это представление остается математической абстракцией, а не физической реальностью.
В современной физиологии речи принято поэтому понятие зв уко в о го импульса. Рассмотренный с акустической стороны, импульс представляет со—бой сложную (комплексную) звуковую волну, не сводимую к простой сумме элементарных колебательных движений. Она воздействует на орган восприятия – ухо – всей своей сложностью. Рассмотренный со стороны восприятия, импульс представляет собой минимальную предельную единицу ощущения (квант). Хотя возможны и сложные импульсы, но предельный импульс, импульс—единица неразложим. Подобные единицы ощущения обнаруживаются не только в процессе восприятия звука, но и при всех других восприятиях (цвета, обоняния и т. д.). То, что звуковой импульс неразложим, означает, что орган чувства (в данном случае ухо) реагирует на него также неразложимой единицей ощущения и физических соответствий по отдельности между элементами звукового импульса – частотой, интенсивностью и длительностью и элементами импульса восприятия – нет. Однако теоретически, как уже было сказано, для некоторых целей можно представлять импульс состоящим из более простых физических качеств – параметров. Основными параметрами звукового импульса являются интенсивность (размах колебания, сила звука), частота и длительность.
Для наглядного схематического изображения этих качеств на бумаге (т. е. в пространстве двухмерном) необходимо представлять их всегда попарно, в системе координат.
Схема № 1
Интенсивность в зависимости от времени
(Горизонтальная линия (ось абсцисс) изображает время, вертикальная – интенсивность. Синусоиды А, В, С – элементарные колебания, диапазоны; фигура AВС – их сумма, дающая звуковой импульс.)
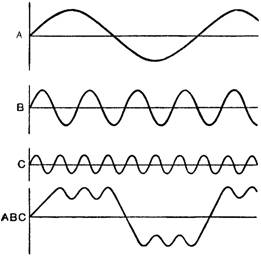
Схема № 2
Частота и интенсивность
(Вертикальные линии изображают интенсивность колебаний, представленных выше (А, В, С), горизонтальная линия изображает частоту (F); каждая вертикальная линия (интенсивность) помещена в той точке горизонтальной, которой соответствует частота этой интенсивности, или период. Эта схема представляет спектр звука в данный момент времени.)
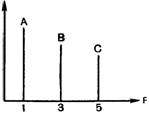
Схема № 3
(Время (Т) и частота (F). В данном случае частота остается постоянной во времени, поэтому все линии частоты параллельны линии времени. Эта схема представляет гармонический анализ в течение некоторого времени.)
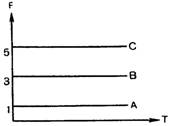
На приведенных схемах рассматривался простейший, так называемый квадратный импульс (ср. фиг. ABC на схеме № 1). Если этот импульс воспроизводится периодически и длится каждый раз время t, а от начала одного импульса до начала другого проходит время Т, то Т представляет период. Величина 1/Т называется ритмом. Например, если T = 1/10 сек., то ритм – 10 импульсов в секунду.
Эта сложная кривая (AEG) может быть теоретически разложена на простые частоты. Основная частота (обозначаемая F1) равна ритму, т. е. обратна периоду: F1 = 1/T. Другие частоты гармонируют с первой («дают обертоны»).
Обертоны более частые, чем 1/T, имеют очень слабую интенсивность, поэтому при описании ими можно пренебречь. Если мы отсекаем эту часть спектра за пределами 1 /Т, то на графике углы квадрата округляются. В физиологии приходится иметь дело только с такими импульсами. То или иное изменение теоретического квадратного импульса принято называть ф о р м о й и м п у л ь с а.
Приборы для изучения речи. В современных акустических исследованиях речи применяются в основном три вида приборов.
Магнитофон, позволяющий легко записывать речь на ферромагнитную пленку и тотчас после записи воспроизводить ее. Пленку можно запускать на различной скорости, менять скорость воспроизведения по сравнению со скоростью записи и т. п., а также разрезать ее, что дает возможность воспроизводить изолированно отдельные моменты звучания.
Спектрографы различного типа, например, сонограф, или аппарат так называемой «видимой речи». Он дает спектрограмму звуков, т. е. график того типа, который приведен на схеме № 2. Кроме спектра частот, этот аппарат также указывает их интенсивность, давая тем более густые штрихи, чем она больше.
Аппарат синтетической речи, или синтезатор, сравнительно недавнее изобретение, основанное на достижениях электроники. Синтезатор позволяет искусственно производить гласные и до известной степени согласные, а также связные куски звучания, полностью подобные человеческой речи. Программой для работы синтезатора служат графики «видимой речи» или рисованные графики, полученные самыми различными путями. Электронное устройство считывает их и преобразует в звук.
Лучшие типы синтезаторов могут воспроизводить одновременно несколько переменных характеристик (параметров) речи:
1. основную частоту гортани – «тон»;
2. интенсивность этого тона – «громкость»;
3. интенсивность шипения – «фрикативный шум» (для согласных);
4. частоту первой форманты – F1;
5. частоту второй форманты – F2;
6. частоту третьей форманты – F3 —
и, кроме того, получать одновременные сдвиги основных параметров, дающие «детский тон», «женский тон» и т. п., в наборе из 8 черт.[1] Синтезаторы позволяют производить весьма важные и доказательные эксперименты (см. § 78).
По—видимому, не часто бывает так, чтобы понятия, увлекающие человека, заинтересованного не столько гармонией, сколько звуками, связали его с наукой. Понятие «сферических гармоник», как мы только что видели (Изотема 5), использовал в сравнительно недавнее время А. Тьюринг.
Представления о естественной речи человека – импульсе звука и о его естественном механическом инструменте – струне издревле пронизывают все зачастую весьма сложные математические понятия. Задача о колебаниях струны в XVIII веке – веке Амати и Страдивари – увлекла многих великих математиков. Струна при ее делении на 2, 3, 4… и т. д. равные части дает звуки, гармонирующие с основным тоном. Л. Эйлер (1707–1783) в одной из своих 15 статей, посвященных этой задаче о колебании струны, дал решение одного из частных случаев. Д. Бернулли через пять лет предложил общее решение, исходя из физического соображения, что звук, издаваемый колеблющейся струной, слагается из основного тона и бесконечного множества обертонов. Именно:
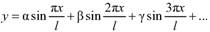
(l – длина струны, а = a(t), β = β(t), γ = γ(t)…) – (по работе: К. А. Рыбников. История математики. М., 1974. С. 207).
Более точным математическим анализом может служить понятие «гармонического ряда». Название связано с тем, что струна при делении ее на 2, 3, 4, равные части дает звуки, гармонирующие с основным тоном («Справочник по высшей математике» [Выгодский 1995: 536]).
(Культурологу здесь может быть необходимо, как нам думается, целое математическое п р и м е ч а н и е, для которого просто указываем соответствующую страницу названной книги М. Я. Выгодского (с. 532–533).)
Мы продолжаем историческое изложение К. А. Рыбникова. «Однако Эйлер выступил против такой трактовки общего решения, так как, по его мнению, функция, предложенная Д. Бернулли, являлась недостаточно общей. В самом деле, она непрерывная, нечетная, периодическая. Поэтому, по Эйлеру, она могла выражать лишь частное решение, в крайнем случае – класс частных решений. Возникший спор привел к задаче: выяснить объем класса функций, представи—мых тригонометрическими рядами.
В 1807 г. (опубликовано в 1822) Фурье в работах по аналитической теории тепла показал, что [.] все эйлеровские связанные кривые, начерченные свободным движением руки, оказались охваченными аналитическим аппаратом тригонометрических рядов» [Рыбников 1974: 207].
Мы продолжаем изложение К. А. Рыбникова (с. 209, 354). В 1822 г. Фурье опубликовал «аналитическую теорию тепла», оказавшую огромное влияние на развитие математики, в дальнейшем математические методы, ведущие свое начало от Фурье, в соединении с соображениями о законах сохранения энергии (С. Карно, 1824; Р. Майер; Г. Гельмгольц; Дж. Джоуль – 1840–е; Р. Клаузиус, 1850; У. Томсон—Кельвин, 1851) привели к формулировке второго начала термодинамики и установлению понятия энтропии.
Однако сейчас для развития нашей темы нам важны не столько общие принципы вроде начал термодинамики, энтропии и т. п., сколько более конкретные исследовательские понятия, в частности, понятие функции. Это понятие очень популярно у современных исследователей разных областей науки. Математик и культуролог А. Н. П а р ш и н исследовал «числа как функции» [Паршин 2002: 7 и сл. ] (культурологам, в частности, будет интересно «рисунчатое, движением руки, изображение» кривой и знака функции).
Необходимые К. А. Рыбникову для его «Истории математики» (с. 354) ссылки на Л. Больцмана и, самое главное, на развитие понятия функции (с. 200, 206 и сл.) оказываются параллельными (как «изотемы») ссылкам автора данной книги для его истории культуры (например, в работе «Язык и метод. К современной философии языка» [Степанов 1998: 332, 495]; в работе «Функции и глубинное» [Степанов 2002] и др.). По этой причине последнюю изотему мы подчеркнем отдельно – в следующем разделе.
Для культуролога естественно начать здесь с «чего—то культурологического». Начну с собственного учебного пособия, по которому в течение многих лет преподавал лингвистику студентам (книга «Основы языкознания» [Степанов 1966: 189–192]), а в нем – с единицы звучания естественной человеческой речи – импульса
Акустические характеристики (параметры) импульса. До сравнительно недавнего времени физиологи исходили из понятия звука как колебательного синусоидального движения. Приближенным его изображением считалась синусоида, представляющая размах колебаний, – д и а п а з о н. Однако, как показали более точные исследования, в природе вообще, а в речи и подавно, не встречается синусоидальных звуков. Прерывистая структура речи и наличие огромного числа обертонов не позволяют сводить речевые звуки к синусоидам.
При анализе звуков речи и голоса допустимо представлять их как совокупность простых синусоид, но это представление остается математической абстракцией, а не физической реальностью.
В современной физиологии речи принято поэтому понятие зв уко в о го импульса. Рассмотренный с акустической стороны, импульс представляет со—бой сложную (комплексную) звуковую волну, не сводимую к простой сумме элементарных колебательных движений. Она воздействует на орган восприятия – ухо – всей своей сложностью. Рассмотренный со стороны восприятия, импульс представляет собой минимальную предельную единицу ощущения (квант). Хотя возможны и сложные импульсы, но предельный импульс, импульс—единица неразложим. Подобные единицы ощущения обнаруживаются не только в процессе восприятия звука, но и при всех других восприятиях (цвета, обоняния и т. д.). То, что звуковой импульс неразложим, означает, что орган чувства (в данном случае ухо) реагирует на него также неразложимой единицей ощущения и физических соответствий по отдельности между элементами звукового импульса – частотой, интенсивностью и длительностью и элементами импульса восприятия – нет. Однако теоретически, как уже было сказано, для некоторых целей можно представлять импульс состоящим из более простых физических качеств – параметров. Основными параметрами звукового импульса являются интенсивность (размах колебания, сила звука), частота и длительность.
Для наглядного схематического изображения этих качеств на бумаге (т. е. в пространстве двухмерном) необходимо представлять их всегда попарно, в системе координат.
Схема № 1
Интенсивность в зависимости от времени
(Горизонтальная линия (ось абсцисс) изображает время, вертикальная – интенсивность. Синусоиды А, В, С – элементарные колебания, диапазоны; фигура AВС – их сумма, дающая звуковой импульс.)

Схема № 2
Частота и интенсивность
(Вертикальные линии изображают интенсивность колебаний, представленных выше (А, В, С), горизонтальная линия изображает частоту (F); каждая вертикальная линия (интенсивность) помещена в той точке горизонтальной, которой соответствует частота этой интенсивности, или период. Эта схема представляет спектр звука в данный момент времени.)

Схема № 3
(Время (Т) и частота (F). В данном случае частота остается постоянной во времени, поэтому все линии частоты параллельны линии времени. Эта схема представляет гармонический анализ в течение некоторого времени.)

На приведенных схемах рассматривался простейший, так называемый квадратный импульс (ср. фиг. ABC на схеме № 1). Если этот импульс воспроизводится периодически и длится каждый раз время t, а от начала одного импульса до начала другого проходит время Т, то Т представляет период. Величина 1/Т называется ритмом. Например, если T = 1/10 сек., то ритм – 10 импульсов в секунду.
Эта сложная кривая (AEG) может быть теоретически разложена на простые частоты. Основная частота (обозначаемая F1) равна ритму, т. е. обратна периоду: F1 = 1/T. Другие частоты гармонируют с первой («дают обертоны»).
Обертоны более частые, чем 1/T, имеют очень слабую интенсивность, поэтому при описании ими можно пренебречь. Если мы отсекаем эту часть спектра за пределами 1 /Т, то на графике углы квадрата округляются. В физиологии приходится иметь дело только с такими импульсами. То или иное изменение теоретического квадратного импульса принято называть ф о р м о й и м п у л ь с а.
Приборы для изучения речи. В современных акустических исследованиях речи применяются в основном три вида приборов.
Магнитофон, позволяющий легко записывать речь на ферромагнитную пленку и тотчас после записи воспроизводить ее. Пленку можно запускать на различной скорости, менять скорость воспроизведения по сравнению со скоростью записи и т. п., а также разрезать ее, что дает возможность воспроизводить изолированно отдельные моменты звучания.
Спектрографы различного типа, например, сонограф, или аппарат так называемой «видимой речи». Он дает спектрограмму звуков, т. е. график того типа, который приведен на схеме № 2. Кроме спектра частот, этот аппарат также указывает их интенсивность, давая тем более густые штрихи, чем она больше.
Аппарат синтетической речи, или синтезатор, сравнительно недавнее изобретение, основанное на достижениях электроники. Синтезатор позволяет искусственно производить гласные и до известной степени согласные, а также связные куски звучания, полностью подобные человеческой речи. Программой для работы синтезатора служат графики «видимой речи» или рисованные графики, полученные самыми различными путями. Электронное устройство считывает их и преобразует в звук.
Лучшие типы синтезаторов могут воспроизводить одновременно несколько переменных характеристик (параметров) речи:
1. основную частоту гортани – «тон»;
2. интенсивность этого тона – «громкость»;
3. интенсивность шипения – «фрикативный шум» (для согласных);
4. частоту первой форманты – F1;
5. частоту второй форманты – F2;
6. частоту третьей форманты – F3 —
и, кроме того, получать одновременные сдвиги основных параметров, дающие «детский тон», «женский тон» и т. п., в наборе из 8 черт.[1] Синтезаторы позволяют производить весьма важные и доказательные эксперименты (см. § 78).
По—видимому, не часто бывает так, чтобы понятия, увлекающие человека, заинтересованного не столько гармонией, сколько звуками, связали его с наукой. Понятие «сферических гармоник», как мы только что видели (Изотема 5), использовал в сравнительно недавнее время А. Тьюринг.
Представления о естественной речи человека – импульсе звука и о его естественном механическом инструменте – струне издревле пронизывают все зачастую весьма сложные математические понятия. Задача о колебаниях струны в XVIII веке – веке Амати и Страдивари – увлекла многих великих математиков. Струна при ее делении на 2, 3, 4… и т. д. равные части дает звуки, гармонирующие с основным тоном. Л. Эйлер (1707–1783) в одной из своих 15 статей, посвященных этой задаче о колебании струны, дал решение одного из частных случаев. Д. Бернулли через пять лет предложил общее решение, исходя из физического соображения, что звук, издаваемый колеблющейся струной, слагается из основного тона и бесконечного множества обертонов. Именно:
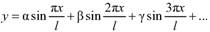
(l – длина струны, а = a(t), β = β(t), γ = γ(t)…) – (по работе: К. А. Рыбников. История математики. М., 1974. С. 207).
Более точным математическим анализом может служить понятие «гармонического ряда». Название связано с тем, что струна при делении ее на 2, 3, 4, равные части дает звуки, гармонирующие с основным тоном («Справочник по высшей математике» [Выгодский 1995: 536]).
(Культурологу здесь может быть необходимо, как нам думается, целое математическое п р и м е ч а н и е, для которого просто указываем соответствующую страницу названной книги М. Я. Выгодского (с. 532–533).)
Мы продолжаем историческое изложение К. А. Рыбникова. «Однако Эйлер выступил против такой трактовки общего решения, так как, по его мнению, функция, предложенная Д. Бернулли, являлась недостаточно общей. В самом деле, она непрерывная, нечетная, периодическая. Поэтому, по Эйлеру, она могла выражать лишь частное решение, в крайнем случае – класс частных решений. Возникший спор привел к задаче: выяснить объем класса функций, представи—мых тригонометрическими рядами.
В 1807 г. (опубликовано в 1822) Фурье в работах по аналитической теории тепла показал, что [.] все эйлеровские связанные кривые, начерченные свободным движением руки, оказались охваченными аналитическим аппаратом тригонометрических рядов» [Рыбников 1974: 207].
Мы продолжаем изложение К. А. Рыбникова (с. 209, 354). В 1822 г. Фурье опубликовал «аналитическую теорию тепла», оказавшую огромное влияние на развитие математики, в дальнейшем математические методы, ведущие свое начало от Фурье, в соединении с соображениями о законах сохранения энергии (С. Карно, 1824; Р. Майер; Г. Гельмгольц; Дж. Джоуль – 1840–е; Р. Клаузиус, 1850; У. Томсон—Кельвин, 1851) привели к формулировке второго начала термодинамики и установлению понятия энтропии.
Однако сейчас для развития нашей темы нам важны не столько общие принципы вроде начал термодинамики, энтропии и т. п., сколько более конкретные исследовательские понятия, в частности, понятие функции. Это понятие очень популярно у современных исследователей разных областей науки. Математик и культуролог А. Н. П а р ш и н исследовал «числа как функции» [Паршин 2002: 7 и сл. ] (культурологам, в частности, будет интересно «рисунчатое, движением руки, изображение» кривой и знака функции).
Необходимые К. А. Рыбникову для его «Истории математики» (с. 354) ссылки на Л. Больцмана и, самое главное, на развитие понятия функции (с. 200, 206 и сл.) оказываются параллельными (как «изотемы») ссылкам автора данной книги для его истории культуры (например, в работе «Язык и метод. К современной философии языка» [Степанов 1998: 332, 495]; в работе «Функции и глубинное» [Степанов 2002] и др.). По этой причине последнюю изотему мы подчеркнем отдельно – в следующем разделе.
9. Изотема 9
Функции и глубинное. Логико—математическое понятие функции & Пропозициональная функция в лингвистике &
Бинарная функция в математике и сложное слово в лингвистике
Логико—математическое понятие функции является в настоящее время, несомненно, центральным по положению в нашей системе рассуждения и содержательно важнейшим для нашей цели. Им вводится целый класс математико—лингвистических аналогий, параллелей и исследовательских ситуаций. Ниже нумеруем их – в порядке возникновения в нашем рассуждении – цифрами от 1 и далее; но эта нумерация все же связана до некоторой степени с иерархией понятий в системе.
Теперь рассмотрим более конкретно группу лингвистических явлений, составляющих параллели, аналоги, аналогии (все эти термины для нас равнозначны) к логико—математическим понятиям, покрываемым общим понятием «Функция» или находящимся в какой—либо существенной связи с ним. Для этого «слева» указываем то или иное необходимое частное понятие функции в математическом смысле или контексте, а «справа» его лингвистический аналог.
Таким образом, нижеследующий текст представляет собой своего рода двуязычный словарь, хотя в типографском отношении входной «левый» термин и «переводной» «правый» могут быть разъединены несколькими строками или даже абзацами.
Лейтмотивом в классе «Функция» является для нас (для лингвиста) идея процесса (вычисления или построения), но, как мы увидим уже в разделе 1, со стороны математики именно ее важность иногда отрицается.
1. Рекурсивные функции и предикаты: процесс и рекурсия. Дж. Литлвуд, рассматривая (резко критически) книгу А. Р. Форсайта «Теория функций комплексного переменного», изданную в 1893 г., но все еще читаемую, цитирует из нее: «Возникновение идеи функциональности вначале было связано с функциями вещественных переменных, и тогда эта идея была равнозначна идее зависимости. Так, если X зависит от значения x и не зависит ни от какой другой изменяющейся величины, то принято X рассматривать как функцию от х; при этом обычно еще
Теперь рассмотрим более конкретно группу лингвистических явлений, составляющих параллели, аналоги, аналогии (все эти термины для нас равнозначны) к логико—математическим понятиям, покрываемым общим понятием «Функция» или находящимся в какой—либо существенной связи с ним. Для этого «слева» указываем то или иное необходимое частное понятие функции в математическом смысле или контексте, а «справа» его лингвистический аналог.
Таким образом, нижеследующий текст представляет собой своего рода двуязычный словарь, хотя в типографском отношении входной «левый» термин и «переводной» «правый» могут быть разъединены несколькими строками или даже абзацами.
Лейтмотивом в классе «Функция» является для нас (для лингвиста) идея процесса (вычисления или построения), но, как мы увидим уже в разделе 1, со стороны математики именно ее важность иногда отрицается.
1. Рекурсивные функции и предикаты: процесс и рекурсия. Дж. Литлвуд, рассматривая (резко критически) книгу А. Р. Форсайта «Теория функций комплексного переменного», изданную в 1893 г., но все еще читаемую, цитирует из нее: «Возникновение идеи функциональности вначале было связано с функциями вещественных переменных, и тогда эта идея была равнозначна идее зависимости. Так, если X зависит от значения x и не зависит ни от какой другой изменяющейся величины, то принято X рассматривать как функцию от х; при этом обычно еще
