Страница:
Впрочем, мы нашли, что результаты, полученные при пользовании обоими приемами, вполне равноценны. Итак, при смешанном употреблении их обоих получается своего рода контроль, что и надо принять в расчет при последующих исследованиях.
Когда опыт проведен, детей меняют ролями; высылают из комнаты объяснителя, который становится во время этого второго опыта воспроизводителем, рассказывают новый рассказ бывшему воспроизводителю, который становится объявителем, и дальше поступают таким же образом, как и раньше.
После этого обмена рассказами мы устраиваем обмен объяснениями, относящимися к механическим предметам. Объяснителю показывают рисунок крана или шприца (иногда мы пользовались рисунком велосипеда), давая ребенку в определенном порядке пояснение относительно функционирования частей. Мы сделали такой странный выбор не случайно, а сообразуясь с интересом мальчиков 6–8 лет. Часто они были даже слишком хорошо знакомы с предметами, чтобы опыт мог быть показательным.
При пояснениях мы действовали следующим образом. Объяснитель, выслушав комментарий к рисунку и имея изображение перед собой, объясняет его воспроизводителю. Тот, в свою очередь, сам дает объяснение, все время имея рисунок перед глазами.
Мы устроили при помощи этих технических приемов сотню опытов с 30 детьми 7–8 лет, взятыми по двое (следовательно, 15 пар, по 4 опыта на пару – по 2 объяснения и по 2 рассказа), и с 20 детьми 6–7 лет (10 пар, по 4 опыта на пару).
Вот рассказы, которыми мы пользовались.
(1) Ты видишь эти два рисунка [I и II], это кран.
(2) Ты видишь это [а]: это ручки крана.
(3) Для того чтобы их повернуть, ты видишь, делают так пальцами [жест пальцем на рисунок I. Показать результат на рисунке II]. Теперь получается так [рисунок II].
(4) Ты видишь здесь [рисунок I], когда ручка открыта вот так [сделать жест по горизонтали, показывая а], канал, ты видишь [показать в. Назвать его также маленькой дырочкой или дверцей], открыт.
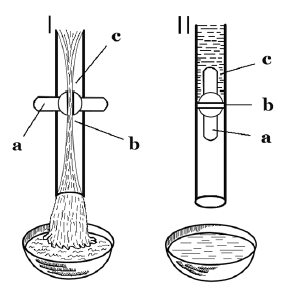
(5) Тогда течет вода, видишь [рисунок I, показать в]?
(6) Она течет потому, что канал открыт.
(7) Видишь, там [рисунок II], когда ручка повернута [показать а, сделать вертикальный жест], канал [показать в. Назвать его тоже дырочкой или дверцей] также закрыт.
(8) Вода не может пройти, видишь [показать с]. Она остановилась.
(9) Она не может течь, потому что канал [показать в] закрыт.
Надо заметить, что каждый из этих пунктов необходимо сообщить ребенку Действительно, часто случается, что испытуемый понимает, например, пункт 5 (вода течет) и думает, что вода течет просто оттого, что повернули ручку крана, не учитывая, что ручка открыла канал и что лишь это обстоятельство дает возможность воде протекать.
Вот второй из опытов.
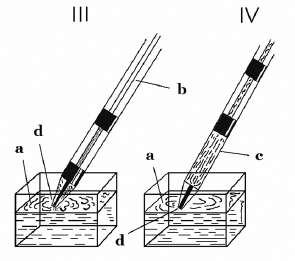
(1) Ты видишь это [рисунки III и IV], а знаешь, что это такое? Это шприц.
(2) Знаешь, что такое шприц? Это для того, чтобы прыскать водой.
(3) Видишь, как это делается. Видишь, его опускают в воду: там [а] есть вода.
(4) Видишь – здесь [в] поршень. Когда хотят, чтобы вода поднялась, тянут поршень.
(5) Тогда вода поднимается, видишь [показать на рисунке IV воду – с].
(6) Она поднялась через дырочку, видишь [d].
(7) Она поднялась потому, что, когда потянули поршень, получилось свободное место [показать с]. Тогда вода заполняет место.
(8) Для того чтобы выпрыснуть воду, нажимают на поршень [d].
(9) Тогда вода выходит [показать d].
Итак, техника очень проста. Объяснителю читают одну из историй или одно из объяснений, говоря при этом по возможности естественно. Затем объяснитель рассказывает воспроизводителю и тот передает его слова нам.
Но это не всё. По получении рассказа воспроизводителя, который записывается целиком, на время устраняют объяснителя и задают воспроизводителю несколько вопросов по пропущенным им пунктам, для того чтобы увидеть, действительно ли он их не понял. Ведь он может или забыть их, или же не уметь их выразить.
Для того чтобы судить о понимании ребенка, надо во что бы то ни стало исключить эти факторы и производить исследование весьма тщательно. Если, например, в истории о Ниобее забыт конец, спрашивают ребенка, не говорится ли там о ручье. Посредством вопросов, сначала в общей форме, а затем все более и более точных, помогая себе делением рассказа на пункты (которые мы только что привели, говоря об объяснениях, и которые мы дадим в следующем параграфе и для рассказов), контролируют понимание воспроизводителя. Когда это сделано, таким же образом спрашивают объяснителя по пунктам, которые кажутся сомнительными, чтобы видеть, хорошо ли он нас понял.
Мы разделим каждый из наших текстов на определенное количество пунктов, как это делается при разборе экспериментов со свидетельскими показаниями, для того чтобы видеть, какие из этих пунктов были воспроизведены и какие упущены испытуемыми. Но вместо того, чтобы выбирать эти пункты в большом количестве и относить их к вопросам о подробностях, мы попробовали ограничиться небольшим числом рубрик, относящихся только к пониманию рассказа. Кроме того, при оценке правильности или неправильности каждого из пунктов во время разбора материалов мы нисколько не принимали в расчет память и другие не существенные для понимания рассказа факторы. Так, в истории о Ниобее имя Ниобеи не играет никакой роли: достаточно, чтобы была упомянута женщина или даже фея, «12 сыновей и 12 дочерей» также могут быть заменены «многими детьми» или «тремя детьми» и т. д., лишь была бы сохранена разница в количестве детей женщины и «феи».
Вот, между прочим, перечень пунктов, принятых в соображение:
I. Ниобея. (1) Жила-была женщина (или фея и т. д.). (2) У нее были дети (лишь бы количество их было более количества детей феи). (3) Она встретила фею (или девушку и т. д.). (4) У этой феи было мало детей (или совсем не было – лишь бы число их было меньше предыдущего). (5) Женщина стала смеяться над феей. (6) Потому что у феи было мало детей. (7) Фея рассердилась. (8) Фея привязала женщину (к скале, дереву, берегу и т. д.). (9) Женщина плакала. (10) Она превратилась в скалу (11) Из слез образовался ручей. (12) Который течет еще и теперь.
Несомненно, за исключением пункта (7), который легко может быть подразумеваем, и пунктов от (9) до (12), которые являются дополнением к основному стержню истории, каждый из представленных пунктов необходим для понимания хода событий. Во всем прочем читатель видит, что мы очень свободны в оценке, поскольку допускаем различные искажения деталей.
Разбор рассказа об Эпаминонде и рассказа о четырех лебедях производился согласно этим же самым принципам[22]. Что же касается пунктов, которыми мы пользовались при разборе механических объяснений, то они уже были указаны в предыдущем параграфе. Оценка правильности и неправильности была там также очень свободной.
Теперь скажем, как мы оценивали понимание детей. Прежде всего мы пробовали свести наши результаты к цифрам и коэффициентам понимания. Нам, конечно, небезызвестны различного рода возражения по поводу измерений в психологии. Нам известны и неточность, и произвольность оценок, и особенно опасное ослепление, которое заставляет статистиков забывать, что именно представляют собой конкретные числа. Но все же не надо думать, что психологи более наивны, чем на самом деле. Очень часто читатель понимает числа буквально, между тем как психолог не спешит делать из них выводы. Из наших цифр мы извлечем значительно меньше того, что они, по-видимому, в себе заключают. Мы будем искать в них в этом труде не столько точное цифровое выражение – что нам кажется преждевременным, – сколько вспомогательное средство, содействующее изучению и уточнению проблем. Что же касается решения этих проблем, то, чтобы дать его, мы будем больше полагаться на методы чистого наблюдения и клинического исследования, чем на сырой цифровой результат. Короче, числа нам будут служить самое большее для того, чтобы заострить нашу критическую оценку. В таком виде нельзя будет оспаривать ее законности. Итак, пусть критики не торопятся поднимать шум, а, напротив, подождут наших выводов. До сих пор мы пытались сделать лишь одно – найти схемы объективных оценок, таких, которые хотя и основаны на чистых условностях, но могут, однако, с успехом быть использованы каждым исследователем.
Мы различаем сначала общее понимание, то есть то, как воспроизводитель понял весь рассказ объяснителя, и понимание вербальное, касающееся причинных или логических связей. Это последнее относится к некоторым пунктам рассказов. Мы им займемся позднее.
Что же касается общего понимания, то мы будем различать в нем, с одной стороны, понимание имплицитное (то, что ребенок понял, причем вовсе не обязательно, чтобы он был в состоянии выразить понятое) и понимание эксплицитное (то, что ребенок спонтанно воспроизводит), с другой – понимание объяснителя по отношению к взрослому и понимание воспроизводителя по отношению к объяснителю. Это деление приводит нас к установлению четырех различных коэффициентов понимания:
α = что воспроизводитель понял по отношению к понятому объяснителем.
β = что воспроизводитель понял по отношению к высказанному объяснителем.
γ = что объяснитель понял из сказанного взрослым.
δ = что объяснитель выразил из того, что он понял.
В самом деле, когда объясняют что-либо объяснителю, то возможны три случая. Либо он не понимает и поэтому не может повторить, либо он понимает, но не может или не хочет повторить (из-за недостатка средств выражения или потому, что он считает ту или другую вещь саму по себе понятной, известной собеседнику и т. д.), либо он понимает и повторяет правильно. Поэтому важно рассмотреть эти три случая в отдельности. Одна из существенных причин непонимания между детьми может лежать в объясняющем. Важно этот фактор учитывать. Вот пример:
Девять пунктов объяснения, которые Шла должен дать, им поняты. Если он не сумел все выразить Риву в ясных и понятных словах, то лично он все понял и может спонтанно дать нам доказательства этого (не будь этого, мы могли бы впоследствии произвести проверку посредством вопросов, о которых мы говорили в предыдущем параграфе). Если мы вычислим коэффициент γ, то получим:
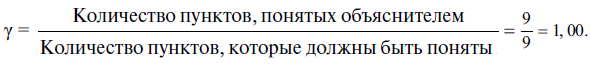
Пункты, не переданные воспроизводителю (Риву), следовательно, не входят в этот коэффициент. Напротив, они входят в расчет коэффициента δ.
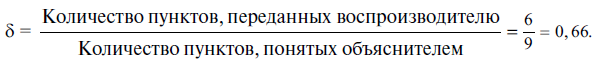
Здесь видно значение коэффициентов γ и δ. Первый – степень понимания объяснителя по отношению к взрослому, производящему опыт. Второй – оценка объяснения, данного объяснителем воспроизводителю.
Посмотрим теперь, что понял Рив из объяснения Шла. Вот текстуально слова Рива:
Можно попытаться указать на два обстоятельства по поводу понимания Рива. Это, с одной стороны, его отношение к пониманию Шла, то есть не только к тому, что Шла передал, но также к тому, что Шла понял, не передавая (α). С другой стороны – это его отношение к тому, что Шла ясно выразил (β). В этом смысле пункты (4) и (7), которые Шла передал («Там закрыто, он не находит больше трубочки, которая течет» и т. д.), не поняты Ривом. Однако Рив, даже не зная, что а – ручки крана, мог бы додуматься, что для того, чтобы закрыть или расположить горизонтально канал в, надо повернуть или «закрыть» что-то. Эта связь совершенно ускользнула от него, хотя Шла и указал на нее, подчеркнув свои слова жестом. Можно, конечно, признать, что Шла не выражает этой мысли достаточно ясно, но он ее выражает именно в детском стиле «соположения» (см. § 6). Вместо того чтобы сказать: «Он не находит больше трубочки, потому что закрыто», Шла говорит: «Закрыто, он больше не находит трубочки». Таков стиль его мысли. Почему же Рив не понимает его, если и он, вероятно, думает таким же образом?
Итак, Рив понял 4 пункта из 6, которые передал Шла, и из 9, которые Шла понял. Отсюда можно вывести два коэффициента – α и β:
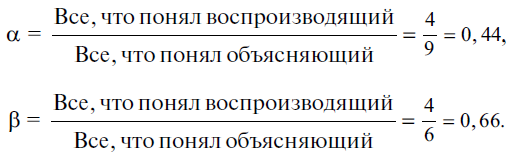
Так как два пункта (4) и (7) переданы Шла в стиле соположения, можно их было бы считать непереданными, что изменило бы коэффициент β в 4/4 = 1,00. Мы условимся рассматривать соположение в качестве манеры выражаться, но с тем, чтобы впоследствии рассмотреть его отдельно (§ 6).
Значения же коэффициентов α и β ясны. Коэффициент α показывает то, что объяснитель сумел сделать понятным для воспроизводителя. Разновидность этого коэффициента зависит от двух весьма различных факторов, но здесь смешанных в одно целое: 1) от того, что объяснитель не умеет или не хочет выражаться ясно; 2) от того, что воспроизводитель не всегда понимает то, что ему говорит объяснитель, даже если этот последний выражается ясно. Эти два фактора – качество выражения объяснителя и качество понимания воспроизводителя – выражены соответственно коэффициентами δ и β. Коэффициент α, потенциально содержащий их оба, представляет (постольку, поскольку опыты не искусственны и отбор не произволен) меру словесного понимания ребенком ребенка, потому что он одновременно измеряет способ, посредством которого один из собеседников заставляет себя понять, а другой понимает. Кроме того, этот коэффициент α есть действительно мерило понимания ребенком ребенка, ибо он исчислен по отношению к тому, что объяснитель запомнил и понял из текста в оригинале, а не по отношению к тому, что он должен был понять. Если бы Шла понял 4 пункта вместо 9, то α была бы 4/4 и γ была бы 0,44.
Понимание ребенком ребенка (α) было бы совершенным, даже если бы понимание ребенком взрослого (γ) было бы плохим.
Коэффициент β – это мера понимания ребенка ребенком в узком смысле, то есть понимания воспроизводителя по отношению к тому, что объяснитель сумел выразить. Не следует поэтому смешивать значение коэффициентов α и β, из которых каждый по-своему интересен.
Чтобы сразу же показать, что мы можем извлечь из наших коэффициентов, скажем, что из рассмотренного случая со Шла и Ривом ясно: один из детей понял другого менее хорошо, чем этот последний нас самих, ибо Рив понял Шла в отношении 0,44 (α = 4/9), a Шла понял нас в отношении 1,00 (γ = 9/9). От чего зависит это непонимание Шла Ривом – от дурного ли понимания Рива или от дурного изложения Шла? Понимание Рива по отношению к тому, что Шла сумел выразить, – 0,66 (β = 4/6). Оценка выраженного Шла по отношению к тому, что он сам понял, тоже 0,66 (δ = 6/9). Отсюда можно вывести, что непонимание между Шла и Ривом столько же зависит от недостатков изложения Шла, сколько и от недостаточности понимания Рива.
Разбор историй производится точно так же, при помощи той же самой техники. Что же касается специального понимания (причинного и т. д.), то мы его рассмотрим позднее.
Мы снова настаиваем на том, что цифры не являются в наших глазах решением проблемы, которую мы себе поставили.
Действительно, мы недостаточно доверяем ценности нашей классификации наблюдавшихся фактов и особенно общей ценности наших опытов, чтобы так поспешно делать выводы. Наши опыты являются просто «опытами-прикидками», предназначенными для того, чтобы ориентироваться в дальнейших изысканиях.
Цифры, которые позже будут приведены, составляют только введение в наблюдение и клиническое исследование. Правда, они содержат статистическое решение, но мы примем это решение только в качестве рабочей гипотезы, для того чтобы увидеть в последующих параграфах, действительно ли эта гипотеза соответствует клиническим фактам и соответствуют ли эти последние, в свою очередь, фактам, обнаруживаемым обычными наблюдениями.
Перейдем теперь к цифрам. Что касается рассказов, то понимание между детьми, отмеченное коэффициентом а, оказалось равным лишь 0,58. Объяснитель нас понял в среднем хорошо, потому коэффициент γ доходит до 0,82. Способность объяснителя к изложению также оказалась относительно хорошей: коэффициент δ равен 0,95. Значит, прежде всего слабо понимание воспроизводителя β = 0,64.
Надо отметить, что недочет, зависящий от объяснителя (1,00–0,95 = 0,05), за минусом того, что зависит от воспроизводителя (0,64–0,05 = 0,59), равен всему недочету (0,58); для нас это будет иметь значение в дальнейшем.
Что же касается объяснений, то понимание между детьми также значительно слабее понимания между объяснителем и взрослым: так, коэффициент α = 0,68, a γ = 0,93. В среднем объяснения были лучше поняты, чем рассказы, как при передаче их детям детьми, так и при рассказывании их взрослым ребенку Может быть, тут несчастная случайность, зависящая от классификации (9 пунктов объяснений, возможно, легче запоминаются, потому что они не столь детальны). Но это неважно. Интересна не оценка в 0,68, взятая абсолютно, а отношения, которые за ней скрываются. Участие воспроизводителя и объяснителя в этом коэффициенте, действительно, совершенно иное, чем в случае с историями. Объяснитель передает здесь значительно хуже: δ = лишь 0,76 вместо 0,95. Что же касается понимания воспроизводителя по отношению к тому, что передал объяснитель, то оно равно 0,79 (β) вместо 0,64 в случае с историями. Ситуация с объяснениями кажется значительно более близкой к тому, что происходит на практике, чем ситуация с историями. Кроме того (что также подтверждает это впечатление), часть, относящаяся к объяснителю и отмеченная коэффициентом β, и часть, относящаяся к воспроизводителю (β), если их сложить, не образуют результата, равного общей величине, а дают результат меньший:
Величина коэффициента а, следовательно, не обязательно указывает на хорошее абсолютное понимание. Она не означает, что объяснитель способен дать понять воспроизводителю что-либо новое для этого последнего и неизвестное до тех пор. Напротив, сложение недочетов дает 0,56, тогда как оно равно 0,59 для историй. Общее же понимание объяснений хуже понимания историй, что вполне естественно. Если α выше в случае объяснений, то это значит, что воспроизводитель прибавил кое-что от себя к тому, что он воспроизводил благодаря рисунку или своим предшествующим интересам. Здесь понимание – не больше, чем взаимное возбуждение к индивидуальному размышлению. Впрочем, надо сказать, что с этого начинается всякое понимание, даже у взрослого.
Когда опыт проведен, детей меняют ролями; высылают из комнаты объяснителя, который становится во время этого второго опыта воспроизводителем, рассказывают новый рассказ бывшему воспроизводителю, который становится объявителем, и дальше поступают таким же образом, как и раньше.
После этого обмена рассказами мы устраиваем обмен объяснениями, относящимися к механическим предметам. Объяснителю показывают рисунок крана или шприца (иногда мы пользовались рисунком велосипеда), давая ребенку в определенном порядке пояснение относительно функционирования частей. Мы сделали такой странный выбор не случайно, а сообразуясь с интересом мальчиков 6–8 лет. Часто они были даже слишком хорошо знакомы с предметами, чтобы опыт мог быть показательным.
При пояснениях мы действовали следующим образом. Объяснитель, выслушав комментарий к рисунку и имея изображение перед собой, объясняет его воспроизводителю. Тот, в свою очередь, сам дает объяснение, все время имея рисунок перед глазами.
Мы устроили при помощи этих технических приемов сотню опытов с 30 детьми 7–8 лет, взятыми по двое (следовательно, 15 пар, по 4 опыта на пару – по 2 объяснения и по 2 рассказа), и с 20 детьми 6–7 лет (10 пар, по 4 опыта на пару).
Вот рассказы, которыми мы пользовались.
I. Эпаминонд – маленький негр, живет в стране, где очень жарко. Его мама говорит ему: «Отнеси эту лепешку бабушке, да не сломай ее». Эпаминонд берет лепешку под мышку, и, когда приходит к бабушке, оказывается, что вся лепешка искрошена. Бабушка дает ему кусок масла, чтобы отнести маме. Эпаминонд думает: «Теперь я буду осторожен». Он кладет кусок масла на голову. Солнце сильно печет, и когда он приходит домой, то оказывается, что все масло растаяло. «Ты дурачок, – говорит ему мама, – ты должен был завернуть масло в листок, и тогда ты принес бы его целым».
II. Жила-была одна женщина по имени Ниобея; у нее было 12 сыновей и 12 дочерей. Она встретилась с феей, у которой был лишь один сын и вовсе не было дочерей. Ниобея стала смеяться над феей, потому что у феи был только один мальчик. Фея рассердилась и привязала женщину к скале. Женщина плакала в течение десяти лет. В конце концов она превратилась в скалу, а из ее слез образовался ручеек, который течет и поныне.
III. Однажды в одном замке жили-были король и королева; у них было трое сыновей и одна дочка. Возле замка жила злая фея, которая не любила детей. Она увела детей короля и королевы на берег моря и превратила их в четырех прекрасных белых лебедей. Так как дети долго не возвращались, король и королева стали искать их всюду до самого берега моря. Там они увидели четырех прекрасных лебедей, которые им сказали, что они – их дети. Лебеди долго оставались на море, а потом улетели в очень холодную страну. Через много лет они вернулись туда, где был их замок. Замка больше не было, родители их умерли. Лебеди вошли в церковь и превратились в трех старичков и старушку.Во всех этих трех рассказах имеется большое разнообразие связей между фактами – от связей самых простых и естественных до самых фантастических. Приведем теперь два механических объяснения, которыми мы больше всего пользовались. Между причинными связями, которые они заключают в себе, и связями, содержащимися в предыдущих рассказах, мы найдем материал для изучения способа, посредством которого дети выражают и понимают всю гамму возможных отношений.
(1) Ты видишь эти два рисунка [I и II], это кран.
(2) Ты видишь это [а]: это ручки крана.
(3) Для того чтобы их повернуть, ты видишь, делают так пальцами [жест пальцем на рисунок I. Показать результат на рисунке II]. Теперь получается так [рисунок II].
(4) Ты видишь здесь [рисунок I], когда ручка открыта вот так [сделать жест по горизонтали, показывая а], канал, ты видишь [показать в. Назвать его также маленькой дырочкой или дверцей], открыт.

(5) Тогда течет вода, видишь [рисунок I, показать в]?
(6) Она течет потому, что канал открыт.
(7) Видишь, там [рисунок II], когда ручка повернута [показать а, сделать вертикальный жест], канал [показать в. Назвать его тоже дырочкой или дверцей] также закрыт.
(8) Вода не может пройти, видишь [показать с]. Она остановилась.
(9) Она не может течь, потому что канал [показать в] закрыт.
Надо заметить, что каждый из этих пунктов необходимо сообщить ребенку Действительно, часто случается, что испытуемый понимает, например, пункт 5 (вода течет) и думает, что вода течет просто оттого, что повернули ручку крана, не учитывая, что ручка открыла канал и что лишь это обстоятельство дает возможность воде протекать.
Вот второй из опытов.
(1) Ты видишь это [рисунки III и IV], а знаешь, что это такое? Это шприц.
(2) Знаешь, что такое шприц? Это для того, чтобы прыскать водой.
(3) Видишь, как это делается. Видишь, его опускают в воду: там [а] есть вода.
(4) Видишь – здесь [в] поршень. Когда хотят, чтобы вода поднялась, тянут поршень.
(5) Тогда вода поднимается, видишь [показать на рисунке IV воду – с].
(6) Она поднялась через дырочку, видишь [d].
(7) Она поднялась потому, что, когда потянули поршень, получилось свободное место [показать с]. Тогда вода заполняет место.
(8) Для того чтобы выпрыснуть воду, нажимают на поршень [d].
(9) Тогда вода выходит [показать d].

Итак, техника очень проста. Объяснителю читают одну из историй или одно из объяснений, говоря при этом по возможности естественно. Затем объяснитель рассказывает воспроизводителю и тот передает его слова нам.
Но это не всё. По получении рассказа воспроизводителя, который записывается целиком, на время устраняют объяснителя и задают воспроизводителю несколько вопросов по пропущенным им пунктам, для того чтобы увидеть, действительно ли он их не понял. Ведь он может или забыть их, или же не уметь их выразить.
Для того чтобы судить о понимании ребенка, надо во что бы то ни стало исключить эти факторы и производить исследование весьма тщательно. Если, например, в истории о Ниобее забыт конец, спрашивают ребенка, не говорится ли там о ручье. Посредством вопросов, сначала в общей форме, а затем все более и более точных, помогая себе делением рассказа на пункты (которые мы только что привели, говоря об объяснениях, и которые мы дадим в следующем параграфе и для рассказов), контролируют понимание воспроизводителя. Когда это сделано, таким же образом спрашивают объяснителя по пунктам, которые кажутся сомнительными, чтобы видеть, хорошо ли он нас понял.
§ 2. Разбор материалов
Как видно, такие опыты во многом походят на опыты Клапареда и Борста, Штерна и др., имеющие предметом свидетельские показания. В самом деле, в манере объяснителя и в особенности воспроизводителя искажать услышанный рассказ видно действие различных факторов, таких, как запоминание фактов, логическая память и т. д., которые мы называем факторами свидетельства (témoignage). А устранить эти факторы очень важно для того, чтобы изучить факты понимания или непонимания как таковых, независимо от искажений, зависящих от других причин. Тогда каким же образом избежать факторов свидетельства, которые нас здесь не интересуют? Путем соответствующей классификации.Мы разделим каждый из наших текстов на определенное количество пунктов, как это делается при разборе экспериментов со свидетельскими показаниями, для того чтобы видеть, какие из этих пунктов были воспроизведены и какие упущены испытуемыми. Но вместо того, чтобы выбирать эти пункты в большом количестве и относить их к вопросам о подробностях, мы попробовали ограничиться небольшим числом рубрик, относящихся только к пониманию рассказа. Кроме того, при оценке правильности или неправильности каждого из пунктов во время разбора материалов мы нисколько не принимали в расчет память и другие не существенные для понимания рассказа факторы. Так, в истории о Ниобее имя Ниобеи не играет никакой роли: достаточно, чтобы была упомянута женщина или даже фея, «12 сыновей и 12 дочерей» также могут быть заменены «многими детьми» или «тремя детьми» и т. д., лишь была бы сохранена разница в количестве детей женщины и «феи».
Вот, между прочим, перечень пунктов, принятых в соображение:
I. Ниобея. (1) Жила-была женщина (или фея и т. д.). (2) У нее были дети (лишь бы количество их было более количества детей феи). (3) Она встретила фею (или девушку и т. д.). (4) У этой феи было мало детей (или совсем не было – лишь бы число их было меньше предыдущего). (5) Женщина стала смеяться над феей. (6) Потому что у феи было мало детей. (7) Фея рассердилась. (8) Фея привязала женщину (к скале, дереву, берегу и т. д.). (9) Женщина плакала. (10) Она превратилась в скалу (11) Из слез образовался ручей. (12) Который течет еще и теперь.
Несомненно, за исключением пункта (7), который легко может быть подразумеваем, и пунктов от (9) до (12), которые являются дополнением к основному стержню истории, каждый из представленных пунктов необходим для понимания хода событий. Во всем прочем читатель видит, что мы очень свободны в оценке, поскольку допускаем различные искажения деталей.
Разбор рассказа об Эпаминонде и рассказа о четырех лебедях производился согласно этим же самым принципам[22]. Что же касается пунктов, которыми мы пользовались при разборе механических объяснений, то они уже были указаны в предыдущем параграфе. Оценка правильности и неправильности была там также очень свободной.
Теперь скажем, как мы оценивали понимание детей. Прежде всего мы пробовали свести наши результаты к цифрам и коэффициентам понимания. Нам, конечно, небезызвестны различного рода возражения по поводу измерений в психологии. Нам известны и неточность, и произвольность оценок, и особенно опасное ослепление, которое заставляет статистиков забывать, что именно представляют собой конкретные числа. Но все же не надо думать, что психологи более наивны, чем на самом деле. Очень часто читатель понимает числа буквально, между тем как психолог не спешит делать из них выводы. Из наших цифр мы извлечем значительно меньше того, что они, по-видимому, в себе заключают. Мы будем искать в них в этом труде не столько точное цифровое выражение – что нам кажется преждевременным, – сколько вспомогательное средство, содействующее изучению и уточнению проблем. Что же касается решения этих проблем, то, чтобы дать его, мы будем больше полагаться на методы чистого наблюдения и клинического исследования, чем на сырой цифровой результат. Короче, числа нам будут служить самое большее для того, чтобы заострить нашу критическую оценку. В таком виде нельзя будет оспаривать ее законности. Итак, пусть критики не торопятся поднимать шум, а, напротив, подождут наших выводов. До сих пор мы пытались сделать лишь одно – найти схемы объективных оценок, таких, которые хотя и основаны на чистых условностях, но могут, однако, с успехом быть использованы каждым исследователем.
Мы различаем сначала общее понимание, то есть то, как воспроизводитель понял весь рассказ объяснителя, и понимание вербальное, касающееся причинных или логических связей. Это последнее относится к некоторым пунктам рассказов. Мы им займемся позднее.
Что же касается общего понимания, то мы будем различать в нем, с одной стороны, понимание имплицитное (то, что ребенок понял, причем вовсе не обязательно, чтобы он был в состоянии выразить понятое) и понимание эксплицитное (то, что ребенок спонтанно воспроизводит), с другой – понимание объяснителя по отношению к взрослому и понимание воспроизводителя по отношению к объяснителю. Это деление приводит нас к установлению четырех различных коэффициентов понимания:
α = что воспроизводитель понял по отношению к понятому объяснителем.
β = что воспроизводитель понял по отношению к высказанному объяснителем.
γ = что объяснитель понял из сказанного взрослым.
δ = что объяснитель выразил из того, что он понял.
В самом деле, когда объясняют что-либо объяснителю, то возможны три случая. Либо он не понимает и поэтому не может повторить, либо он понимает, но не может или не хочет повторить (из-за недостатка средств выражения или потому, что он считает ту или другую вещь саму по себе понятной, известной собеседнику и т. д.), либо он понимает и повторяет правильно. Поэтому важно рассмотреть эти три случая в отдельности. Одна из существенных причин непонимания между детьми может лежать в объясняющем. Важно этот фактор учитывать. Вот пример:
Шла (6 л. 6 м.) дает объяснения Риву (6 л. 6 м.). Объяснение рисунка крана: «Видишь, это так [рисунок I], это открыто, маленькая трубка, которая проходит [с], находит маленькую трубку [b], так течет вода. Там [рисунок II] закрыто, она не находит больше трубочки, которая течет. Вода – она идет так [рисунок I, с], она идет в маленькую трубку. Это открыто, а потом там [рисунок II] закрыто. Видишь [рисунок II], больше не заметно трубочки, она лежит, потом вода идет так [с], она ее не нашла больше».Если обратиться к представленным в предыдущем параграфе пунктам, то найдем следующее. Пункт (1) понял Шла: он нам сказал, как раз перед тем, как говорить Риву, что дело идет о кране. Но он забывает напомнить об этом Риву, вероятно, потому, что это для него ясно само собой. Пункт (2), то есть значение ручек, тоже понят. Шла нам сказал: «Там есть две палочки [а], когда поворачивают, то течет, так как они поворачивают трубку». Объяснение хорошее. В изложении Риву, наоборот, упоминание о ручках крана совершенно выпадает. Шла довольствуется тем, что говорит: «Открыто» или «Закрыто», этого ему кажется достаточно для того, чтобы напомнить жест, посредством которого поворачивают ручки крана. Что здесь – небрежность или забывчивость или Шла думает, что Рив достаточно хорошо понимает? Мы не будем обсуждать этих факторов в настоящий момент. Достаточно того, что мы увидели их важность в механизме детской речи. Пункт (3) тоже понят («Когда поворачивают»). Шла знает и говорит нам, что ручки крана нужно поворачивать пальцами. Этого он также не говорит Риву, потому что это само собой понятно или по какой-либо другой причине. Что же касается других пунктов, то видно, что они все поняты и правильно переданы Риву Связь между тем фактом, что «это – открыто», и тем, что вода проходит по каналу в, хорошо отмечена, движение воды также. Обратная связь (между закрытием канала, движением ручек и остановкой воды) также указана.
Девять пунктов объяснения, которые Шла должен дать, им поняты. Если он не сумел все выразить Риву в ясных и понятных словах, то лично он все понял и может спонтанно дать нам доказательства этого (не будь этого, мы могли бы впоследствии произвести проверку посредством вопросов, о которых мы говорили в предыдущем параграфе). Если мы вычислим коэффициент γ, то получим:
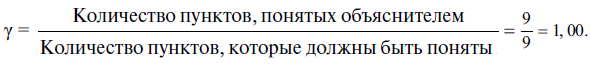
Пункты, не переданные воспроизводителю (Риву), следовательно, не входят в этот коэффициент. Напротив, они входят в расчет коэффициента δ.
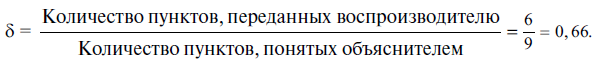
Здесь видно значение коэффициентов γ и δ. Первый – степень понимания объяснителя по отношению к взрослому, производящему опыт. Второй – оценка объяснения, данного объяснителем воспроизводителю.
Посмотрим теперь, что понял Рив из объяснения Шла. Вот текстуально слова Рива:
Рив (6 л. 6 м.). «Там [рисунок I, с] трубочка, потом она открыта, потом – вода, которая течет в миску, потом там [II, с] она закрыта, тогда больше нет воды, которая течет, потом есть маленькая трубочка [II, в], она лежит, потом есть миска, которая полная. Вода больше не может течь, потому что трубочка, которая лежит, она мешает».Пункт (1) (название «кран») пропущен. Но понял ли Рив его? Мы его спрашиваем: «Что все это такое?» – «Трубка». – «Это кран?» – «Нет». Итак, он не понял, что неудивительно, так как Шла не сказал ему этого. Пункт (2) также пропущен. Мы показываем Риву ручки (а) и спрашиваем, что это такое. Он ничего о них не знает. Он также не понял, как поступают, чтобы повернуть трубочку (в), о чем он мог бы догадаться, слушая, как Шла говорит: «Открыто» и т. д., даже не понимая, что а – ручки. Пункты (3), (4) и (7), следовательно, тоже ему не удались. Мы контролируем это истолкование посредством различных вопросов: «Как нужно делать, чтобы положить трубочку?» и т. д. Все же остальное понятно.
Можно попытаться указать на два обстоятельства по поводу понимания Рива. Это, с одной стороны, его отношение к пониманию Шла, то есть не только к тому, что Шла передал, но также к тому, что Шла понял, не передавая (α). С другой стороны – это его отношение к тому, что Шла ясно выразил (β). В этом смысле пункты (4) и (7), которые Шла передал («Там закрыто, он не находит больше трубочки, которая течет» и т. д.), не поняты Ривом. Однако Рив, даже не зная, что а – ручки крана, мог бы додуматься, что для того, чтобы закрыть или расположить горизонтально канал в, надо повернуть или «закрыть» что-то. Эта связь совершенно ускользнула от него, хотя Шла и указал на нее, подчеркнув свои слова жестом. Можно, конечно, признать, что Шла не выражает этой мысли достаточно ясно, но он ее выражает именно в детском стиле «соположения» (см. § 6). Вместо того чтобы сказать: «Он не находит больше трубочки, потому что закрыто», Шла говорит: «Закрыто, он больше не находит трубочки». Таков стиль его мысли. Почему же Рив не понимает его, если и он, вероятно, думает таким же образом?
Итак, Рив понял 4 пункта из 6, которые передал Шла, и из 9, которые Шла понял. Отсюда можно вывести два коэффициента – α и β:
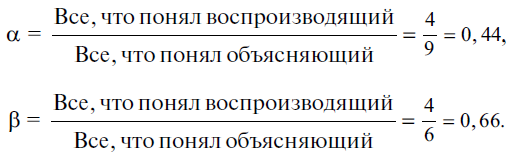
Так как два пункта (4) и (7) переданы Шла в стиле соположения, можно их было бы считать непереданными, что изменило бы коэффициент β в 4/4 = 1,00. Мы условимся рассматривать соположение в качестве манеры выражаться, но с тем, чтобы впоследствии рассмотреть его отдельно (§ 6).
Значения же коэффициентов α и β ясны. Коэффициент α показывает то, что объяснитель сумел сделать понятным для воспроизводителя. Разновидность этого коэффициента зависит от двух весьма различных факторов, но здесь смешанных в одно целое: 1) от того, что объяснитель не умеет или не хочет выражаться ясно; 2) от того, что воспроизводитель не всегда понимает то, что ему говорит объяснитель, даже если этот последний выражается ясно. Эти два фактора – качество выражения объяснителя и качество понимания воспроизводителя – выражены соответственно коэффициентами δ и β. Коэффициент α, потенциально содержащий их оба, представляет (постольку, поскольку опыты не искусственны и отбор не произволен) меру словесного понимания ребенком ребенка, потому что он одновременно измеряет способ, посредством которого один из собеседников заставляет себя понять, а другой понимает. Кроме того, этот коэффициент α есть действительно мерило понимания ребенком ребенка, ибо он исчислен по отношению к тому, что объяснитель запомнил и понял из текста в оригинале, а не по отношению к тому, что он должен был понять. Если бы Шла понял 4 пункта вместо 9, то α была бы 4/4 и γ была бы 0,44.
Понимание ребенком ребенка (α) было бы совершенным, даже если бы понимание ребенком взрослого (γ) было бы плохим.
Коэффициент β – это мера понимания ребенка ребенком в узком смысле, то есть понимания воспроизводителя по отношению к тому, что объяснитель сумел выразить. Не следует поэтому смешивать значение коэффициентов α и β, из которых каждый по-своему интересен.
Чтобы сразу же показать, что мы можем извлечь из наших коэффициентов, скажем, что из рассмотренного случая со Шла и Ривом ясно: один из детей понял другого менее хорошо, чем этот последний нас самих, ибо Рив понял Шла в отношении 0,44 (α = 4/9), a Шла понял нас в отношении 1,00 (γ = 9/9). От чего зависит это непонимание Шла Ривом – от дурного ли понимания Рива или от дурного изложения Шла? Понимание Рива по отношению к тому, что Шла сумел выразить, – 0,66 (β = 4/6). Оценка выраженного Шла по отношению к тому, что он сам понял, тоже 0,66 (δ = 6/9). Отсюда можно вывести, что непонимание между Шла и Ривом столько же зависит от недостатков изложения Шла, сколько и от недостаточности понимания Рива.
Разбор историй производится точно так же, при помощи той же самой техники. Что же касается специального понимания (причинного и т. д.), то мы его рассмотрим позднее.
§ 3. Цифровые результаты
Разбирая таким способом 60 опытов, произведенных над нашими 30 детьми 7–8 лет (все мальчики), мы пришли к следующим результатам.Мы снова настаиваем на том, что цифры не являются в наших глазах решением проблемы, которую мы себе поставили.
Действительно, мы недостаточно доверяем ценности нашей классификации наблюдавшихся фактов и особенно общей ценности наших опытов, чтобы так поспешно делать выводы. Наши опыты являются просто «опытами-прикидками», предназначенными для того, чтобы ориентироваться в дальнейших изысканиях.
Цифры, которые позже будут приведены, составляют только введение в наблюдение и клиническое исследование. Правда, они содержат статистическое решение, но мы примем это решение только в качестве рабочей гипотезы, для того чтобы увидеть в последующих параграфах, действительно ли эта гипотеза соответствует клиническим фактам и соответствуют ли эти последние, в свою очередь, фактам, обнаруживаемым обычными наблюдениями.
Перейдем теперь к цифрам. Что касается рассказов, то понимание между детьми, отмеченное коэффициентом а, оказалось равным лишь 0,58. Объяснитель нас понял в среднем хорошо, потому коэффициент γ доходит до 0,82. Способность объяснителя к изложению также оказалась относительно хорошей: коэффициент δ равен 0,95. Значит, прежде всего слабо понимание воспроизводителя β = 0,64.
Надо отметить, что недочет, зависящий от объяснителя (1,00–0,95 = 0,05), за минусом того, что зависит от воспроизводителя (0,64–0,05 = 0,59), равен всему недочету (0,58); для нас это будет иметь значение в дальнейшем.
Что же касается объяснений, то понимание между детьми также значительно слабее понимания между объяснителем и взрослым: так, коэффициент α = 0,68, a γ = 0,93. В среднем объяснения были лучше поняты, чем рассказы, как при передаче их детям детьми, так и при рассказывании их взрослым ребенку Может быть, тут несчастная случайность, зависящая от классификации (9 пунктов объяснений, возможно, легче запоминаются, потому что они не столь детальны). Но это неважно. Интересна не оценка в 0,68, взятая абсолютно, а отношения, которые за ней скрываются. Участие воспроизводителя и объяснителя в этом коэффициенте, действительно, совершенно иное, чем в случае с историями. Объяснитель передает здесь значительно хуже: δ = лишь 0,76 вместо 0,95. Что же касается понимания воспроизводителя по отношению к тому, что передал объяснитель, то оно равно 0,79 (β) вместо 0,64 в случае с историями. Ситуация с объяснениями кажется значительно более близкой к тому, что происходит на практике, чем ситуация с историями. Кроме того (что также подтверждает это впечатление), часть, относящаяся к объяснителю и отмеченная коэффициентом β, и часть, относящаяся к воспроизводителю (β), если их сложить, не образуют результата, равного общей величине, а дают результат меньший:
1,00–0,76=0,24 и 0,79–0,24=0,55<0,68.Этот факт легко объяснить. В случае с историями, когда объяснитель выражается плохо, воспроизводитель не может пополнить неясное или забытое в полученном объяснении. Более того, со своей стороны, он привносит стремление искажать то, что ему передается правильно. К тому же у него есть тенденция не слушать своего собеседника, как это нам часто подтверждало обычное наблюдение над спонтанными разговорами детей (коллективный монолог. Мы напоминаем пример, приведенный на с. 14, когда некто говорит Беа: «Я делаю лестницу, посмотри». Беа отвечает: «Я не могу прийти сегодня после обеда, у меня урок ритмики»). В случае механических объяснений, наоборот, воспроизводитель сам интересовался действием кранов и шприцев. Кроме того, у него перед глазами рисунки, и в то время, когда объяснитель говорит, он размышляет о значении этих рисунков. Поэтому, даже если он и не слушает объяснителя или тот неясен и краток, воспроизводитель сам восстанавливает объяснение, которое ему должны дать. Отсюда и происходит тот факт, что общее понимание (α) лучше, чем это должно было бы быть при сложении величин, отмеченных коэффициентами δ и β. Существование этих отношений представляется не зависящим от нашего способа анализа результатов.
Величина коэффициента а, следовательно, не обязательно указывает на хорошее абсолютное понимание. Она не означает, что объяснитель способен дать понять воспроизводителю что-либо новое для этого последнего и неизвестное до тех пор. Напротив, сложение недочетов дает 0,56, тогда как оно равно 0,59 для историй. Общее же понимание объяснений хуже понимания историй, что вполне естественно. Если α выше в случае объяснений, то это значит, что воспроизводитель прибавил кое-что от себя к тому, что он воспроизводил благодаря рисунку или своим предшествующим интересам. Здесь понимание – не больше, чем взаимное возбуждение к индивидуальному размышлению. Впрочем, надо сказать, что с этого начинается всякое понимание, даже у взрослого.
