Большая Советская Энциклопедия (УР)
эль-обейдской культуры.В 4-м тыс., в период Урука, произошло становление У. как города. В 25 в. до н. э., в период 1 династии Ура (правители Месанспада, Аанепада и др.), представлял собой сильное государство. В течение 24–22 вв. (с небольшими перерывами) был подчинён соседним городам-государствам
Лагашу,
Умме,
Уруку,затем царству
Аккада,кутиям. Около 21 в. стал столицей «царства Шумера и Аккада» (III династия Ура). При царе Ур-Намму (21 в.) были созданы, возможно, самые древние в Двуречье писаные законы. Для этого периода истории У. характерно наличие больших царских хозяйств с фактически рабовладельческой эксплуатацией подневольных работников. Создавались идеологические основы деспотической царской власти (единая система пантеона, учение о вечности «царственности» и т.д.). Четыре следующих царя III династии Ура (Шульги, Амар-Суэн, Шу-Суэн, Ибби-Суэн) были обожествлены при жизни. Государство III династии Ура пало около 2000 до н. э. в ходе войны с аморитами и Эламом. У. оставался важным торгово-ремесленным центром, находясь под властью вавилонского (с 18 по 6 вв.) и ахеменидского (с 6 в.) царств. К концу 4 в. до н. э. У. пришёл в упадок.
У. раскапывался англ. учёными Д. Тейлором в 1854, Р. Кэмпбелл-Томпсоном в 1918, Г. Р. Холлом в 1919–22 и особенно широко – англо-амер. экспедицией под руководством Ч. Л.
Вулли
в 1922–34. Наиболее многочисленные и интересные памятники, вскрытые раскопками, датируются временем правления в У. I и III династий. Ко времени правления 1 династии (25 в. до н. э.) относятся 16 царских (?) гробниц, в которых были найдены многочисленные образцы роскошной утвари (из золота, серебра, алебастра, ляпис-лазури, обсидиана и др. материалов, иногда – с применением мозаичной техники). У. времени III династии (21 в. до н. э.) представлял собой в плане неправильный овал, окруженный кирпичной стеной. Среди сохранившихся фрагментарно кирпичных зданий этого времени – остатки дворца, храмового комплекса, в центре которого находился четырёхъярусный зиккурат, и др. сооружений. О художественной культуре У. см. также в ст.
Вавилоно-ассирийская культура.
Лит.:Тюменев А. И., Государственное хозяйство древнего Шумера, М. – Л., 1956; Вулли Л., Ур халдеев, пер. с англ., М., 1961; Gadd C. J., The history and monuments of Ur, L., 1929; Ur excavations, v. 1–5, 8–10, Oxf. – L., 1927–62; Ur excavations texts, fv. 1–6, L., 1928–63.
И. М. Дьяконов.
Ур. Голова быка с арфы из «царской гробницы». Золото, лазурит. 25 в. до н. э. Университет. Филадельфия.
Токио.324 тыс. жителей (1974). Металлообработка и машиностроение; химическая, текстильная промышленность. Университет.
Равносильные уравнения
)
.Например, У.
х– 4 = 0 и 2
x– 8 = 0 равносильны, т.к. решением обоих У. является лишь
х =4. Всякая система У. равносильна системе вида
f
k(
x
1
, x
2
,..., х
п)
= 0, где
k =1, 2,...
Процесс разыскания решений У. заключается обычно в замене У. равносильным. В некоторых случаях приходится заменять данное У. другим, для которого совокупность решений шире, чем у данного У. Решения нового У., не являющиеся решениями данного У., называются посторонними решениями (см.
Посторонний корень
)
.
Например, возводя в квадрат У.
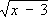 , получают У.
x- 3 = 4, решение которого
х= 7 является посторонним для исходного У. Поэтому, если при решении У. делались действия, могущие привести к появлению посторонних решений (например, возведение У. в квадрат), то все полученные решения преобразованного У. проверяют подстановкой в исходное У.
, получают У.
x- 3 = 4, решение которого
х= 7 является посторонним для исходного У. Поэтому, если при решении У. делались действия, могущие привести к появлению посторонних решений (например, возведение У. в квадрат), то все полученные решения преобразованного У. проверяют подстановкой в исходное У.
Наиболее изучены У., для которых функции
f
kявляются многочленами от переменных
x
1
, x
2
,..., х
п
, –алгебраические У. Например, алгебраическое У. с одним неизвестным имеет вид:
a
0
x
n
+ a
1
x
n-1
+... + a
n= 0
(
a
0¹ 0); (*)
число
nназывается степенью У. Решение алгебраич. У. было одной из важнейших задач алгебры в 16–17 вв., когда были получены формулы и методы решения алгебраических У. 3-й и 4-й степеней (см.
Алгебра,
Кардано формула) (правила решения алгебраических У. 1-й и 2-й степеней были известны ещё в глубокой древности). Для корней У. 5-й и высших степеней общей формулы не существует, поскольку эти У., вообще говоря, не могут быть решены в радикалах (Н.
Абель,1824). Вопрос о разрешимости алгебраических У. в радикалах привёл (около 1830) Э.
Галуа
к общей теории алгебраических У. (см.
Галуа теория
)
.
Каждое алгебраическое У. всегда имеет хотя бы одно решение, действительное или комплексное. Это составляет содержание т. н. основной теоремы алгебры, строгое доказательство которой впервые было дано К.
Гауссом
в 1799. Если a – решение У. (*), то многочлен
a
0
x
n
+ a
1
x
n-1
+... + a
n
делится на
х –a
.Если он делится на (
х –a)
k
,но не делится на (
х –a)
k+1, то решение a имеет кратность
k.Число всех решений У. (*), если каждое считать столько раз, какова его кратность, равно
n.
Если
f(
x)
–
трансцендентная функция,то У.
f(
x)
=0 называются трансцендентным (см., например,
Кеплера уравнение
)
,причём в зависимости от вида
f(
x) оно называется тригонометрическим У., логарифмическим У., показательным У. Рассматриваются также иррациональные У., то есть У., содержащие неизвестное под знаком радикала. При практическом решении У. обычно применяются различные приближённые методы решения У.
Среди систем У. простейшими являются системы линейных У., то есть У., в которых
f
kсуть многочлены первых степеней относительно
x
1
, x
2
,..., х
п(см.
Линейное уравнение
)
.
Решение системы У. (не обязательно линейных) сводится, вообще говоря, к решению одного У. при помощи т. н. исключения неизвестных (см. также
Результант
)
.
В аналитической геометрии одно У. с двумя неизвестными интерпретируется при помощи кривой на плоскости, координаты всех точек которой удовлетворяют данному У. Одно У. с тремя неизвестными интерпретируется при помощи поверхности в трёхмерном пространстве. При этой интерпретации решение системы У. совпадает с задачей о разыскании точек пересечения линий, поверхностей и т.д. У. с большим числом неизвестных интерпретируются при помощи многообразий в
n-мерных пространствах.
В теории чисел рассматриваются неопределенные У., то есть У. с несколькими неизвестными, для которых ищутся целые или же рациональные решения (см.
Диофантовы уравнения
)
.Например, целые решения У.
x
2
+ y
2
= z
2
вид
х = m
2
-n
2
, у =2
mn, z = m
2
+ n
2
где
mи
n –целые числа.
С наиболее общей точки зрения, У. является записью задачи о разыскании таких элементов некоторого множества
А,что
F(
a)
= Ф(
а), где
Fи Ф – заданные
отображения
множества
Ав множество
В.Если множества
Аи
Вявляются множествами чисел, то возникают У. рассмотренного выше вида. Если
Аи
В– множества точек в многомерных пространствах, то получаются системы У., если же
Aи
В– множества функций, то в зависимости от характера отображения могут получаться также
дифференциальные уравнения,
интегральные уравненияи др. виды У. Наряду с вопросами нахождения решения У. в общей теории У. различного вида изучаются вопросы существования и единственности решения, непрерывной зависимости его от тех или иных данных и т.д.
Термин «У.» употребляется (в отличном от указанного выше смысле) и в др. естественных науках, см., например,
Уравнение времени
(в астрономии),
Уравнение состояния
(в физике),
Уравнения химические,
Максвелла уравненияв электродинамике,
Кинетическое уравнение Больцмана
в теории газов.
Время.
График уравнения времени: 1 — составляющая уравнения времени, определяемая неравномерностью движения Земли по орбите; 2 — составляющая уравнения времени, определяемая наклоном эклиптики к экватору; 3 — уравнение времени.
равновесия термодинамического: f(
p, V, Т)
=0. Это уравнение называется термическим У. с., в отличие от калорического У. с., определяющего
внутреннюю энергию
системы
Uкак функцию какого-либо двух из трёх параметров
р, V, Т.Термическое У. с. позволяет выразить давление через объём и температуру
р = p(
V, Т) и определить элементарную работу d
A= =
pd
Vпри бесконечно малом расширении системы d
V. У. с. является необходимым дополнением к термодинамическим законам, которое делает возможным их применение к реальным веществам. Оно не может быть выведено с помощью одних только законов
термодинамики,а определяется или рассчитывается теоретически на основе представлений о строении вещества методами
статистической физики.Из
первого начала термодинамики
следует лишь существование калорического У. с., а из
второго начала термодинамики
– связь между термическим и калорическим У. с.
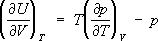 ,откуда вытекает, что для
идеального газа
внутренняя энергия не зависит от объёма
,откуда вытекает, что для
идеального газа
внутренняя энергия не зависит от объёма
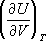 = 0. Термодинамика показывает, что для вычисления как термического, так и калорического У. с., достаточно знать любой из
потенциалов термодинамических
ввиде функции своих параметров. Например, если известна
Гельмгольцева энергияFкак функция
Ти
V,то У. с. находят дифференцированием:
= 0. Термодинамика показывает, что для вычисления как термического, так и калорического У. с., достаточно знать любой из
потенциалов термодинамических
ввиде функции своих параметров. Например, если известна
Гельмгольцева энергияFкак функция
Ти
V,то У. с. находят дифференцированием:
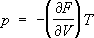 ,
,
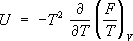 .
.
Примерами У. с. для газов может служить
Клапейрона уравнение
для идеального газа
pu
= RT,где
R –
газовая постоянная,u
–объём 1
молягаза;
Ван-дер-Ваальса уравнение
,где
аи
b– постоянные, зависящие от природы газа и учитывающие влияние сил притяжения между молекулами и конечность из объёма, вириальное У. с. для неидеального pu / RT = 1 + B (
T)
/u
+С (
Т)/ u
2
+.., где
В(
Т)
, С(
Т)
... –2-й, 3-й и т.д. вириальные коэффициенты, зависящие от сил взаимодействия между молекулами (см.
Газы
)
.Это уравнение является наиболее надёжным и теоретически обоснованным У. с. для газов и позволяет объяснить многочисленные экспериментальные результаты на основании простых моделей
межмолекулярного взаимодействия.Были предложены также различные эмпирические У. с., основанные на экспериментальных данных о теплоёмкости и сжимаемости. У. с. неидеальных газов указывает на существование критической точки (с параметрами
p
k
, V
k
, T
k)
,в которой газообразная и жидкая фазы становятся идентичными (см.
Критическое состояние
)
.Если У. с. представить в виде приведенного У. с., т. е. в безразмерных переменных
p/p
k
, V/V
k
, T/T
k
,то при не слишком низких температурах это уравнение мало меняется для различных веществ (закон
соответственных состояний
)
.
Для равновесного излучения, или фотонного газа, У. с. определяется
Планка законом излучения
для средней плотности энергии.
Для жидкостей из-за сложности учёта всех особенностей взаимодействия молекул пока не удалось теоретически получить общее У. с. Уравнение Ван-дер-Ваальса хотя и применяют для качественной оценки поведения жидкостей, но оно по существу неприменимо ниже критической точки, когда возможно сосуществование жидкой и газообразной фаз. У. с., хорошо описывающее свойства ряда простых жидкостей, можно получить из приближённых теорий жидкого состояния типа теории свободного объёма или дырочной теории (см.
Жидкость
)
.Знание распределения вероятности взаимного расположения молекул (парной корреляционной функции) принципиально позволяет вычислить У. с. жидкости, но эта задача очень сложна и полностью ещё не решена даже с помощью вычислительных машин.
Для твёрдых тел термическое У. с. определяет зависимость
модулей упругости
от температуры и давления. Оно может быть получено на основании теории теплового движения в кристаллах, рассматривающей
фононы
и их взаимодействие, но пока общего У. с. для твёрдых тел не найдено.
Для магнитных сред элементарная работа при намагничивании равна d
A= -
Нd
М,где
М– магнитный момент,
Н –напряжённость магнитного поля. Следовательно, зависимость
М = М(
Н, Т) представляет собой магнитное У. с.
Для электрически поляризуемых сред элементарная работа при поляризации равна d
A= -
Еd
Ргде
Р -поляризация,
Е -напряжённость электрического поля, следовательно, У. с. имеет вид
Р= (
Е, Т)
.
Лит.:Хилл Т., Статистическая механика, пер. с англ., М., 1960; Вукалович М. П., Новиков И. И., Уравнение состояния реальных газов, М. – Л., 1948; Мейсон Э., Сперлинг Т., Вириальное уравнение состояния, пер. с англ., М., 1972; Лейбфрид Г., Людвиг В., Теория ангармонических эффектов в кристаллах, пер. с англ., М., 1963. См. также лит. при статьях
Статистическая физика
и
Термодинамика
.
Д. Н. Зубарев.
Математическая физика
).
Классификация уравнений математической физики.Значительная часть У. м. ф. составляют линейные уравнения с частными производными 2-го порядка общего вида:
 , (1)
, (1)
где все коэффициенты
a
ij(
a
ij
= a
ij)
, b
i
, си правая часть
fпредставляют собой заданные функции независимых переменных
x
1
, x
2
,..., х
п(
n³ 2)
,а
u –искомая функция тех же аргументов. Свойства решений уравнения (1) существенно зависят от знаков корней (алгебраического относительно l) уравнения
 = 0, (2)
= 0, (2)
и поэтому классификация уравнений (1) проводится в соответствии с этими знаками. Если все
nкорней уравнения (2) имеют одинаковый знак, то говорят, что уравнение (1) принадлежит к эллиптическому типу; если один из корней имеет знак, противоположный знаку остальных
n –1 корней, – к гиперболическому типу; наконец, если уравнение (2) имеет один нулевой корень, а прочие корни одинакового знака, – к параболическому типу. Если коэффициенты
a
ijпостоянны, то уравнение (1) принадлежит к определенному типу независимо от значений аргументов; если же эти коэффициенты зависят от
x
1
,..., х
п
,то и корни уравнения (2) зависят от
x
1
,..., х
п
,а потому уравнение (1) может принадлежать к разным типам при различных значениях аргументов. В последнем случае (уравнение смешанного типа) изучаемая область изменения аргументов состоит из зон, в которых тип уравнения (1) сохраняется. Если корень уравнения (2), переходя от положительных значений к отрицательным, обращается в нуль, то между зонами эллиптичности и гиперболичности расположены зоны параболичности (надо отметить, что и в ряде др. отношений параболического уравнения занимают промежуточное положение между эллиптическими и гиперболическими).
Для линейных уравнений с частными производными выше 2-го порядка и для систем уравнений с несколькими искомыми функциями классификация более сложна.
 Ур. Голова быка с арфы из «царской гробницы». Золото, лазурит. 25 в. до н. э. Университет. Филадельфия.
Ур. Голова быка с арфы из «царской гробницы». Золото, лазурит. 25 в. до н. э. Университет. Филадельфия.

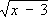 , получают У.
x- 3 = 4, решение которого
х= 7 является посторонним для исходного У. Поэтому, если при решении У. делались действия, могущие привести к появлению посторонних решений (например, возведение У. в квадрат), то все полученные решения преобразованного У. проверяют подстановкой в исходное У.
, получают У.
x- 3 = 4, решение которого
х= 7 является посторонним для исходного У. Поэтому, если при решении У. делались действия, могущие привести к появлению посторонних решений (например, возведение У. в квадрат), то все полученные решения преобразованного У. проверяют подстановкой в исходное У.
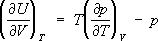 ,откуда вытекает, что для
идеального газа
внутренняя энергия не зависит от объёма
,откуда вытекает, что для
идеального газа
внутренняя энергия не зависит от объёма
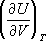 = 0. Термодинамика показывает, что для вычисления как термического, так и калорического У. с., достаточно знать любой из
потенциалов термодинамических
ввиде функции своих параметров. Например, если известна
Гельмгольцева энергияFкак функция
Ти
V,то У. с. находят дифференцированием:
= 0. Термодинамика показывает, что для вычисления как термического, так и калорического У. с., достаточно знать любой из
потенциалов термодинамических
ввиде функции своих параметров. Например, если известна
Гельмгольцева энергияFкак функция
Ти
V,то У. с. находят дифференцированием: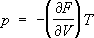 ,
,
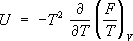 .
.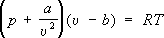
 , (1)
, (1) = 0, (2)
= 0, (2)