Страница:
Термин «синергетика» подчеркивает основную роль коллективных, корреляционно-кооперативных взаимодействий в возникновении и функционировании явлений самоорганизации в различных открытых системах, в нашем случае – организма и его подсистем при рассмотрении человека в качестве части геокосмического пространства.
Цели изучения системы заключаются в исследовании ее функционирования в целом и управления ею внешними и внутренними факторами. Подобными задачами занимается системный анализ. Наиболее близки к системному подходу такие области, как исследования методами многомерной статистики и оптимизация. В нашей работе за определение системы принято следующее: система – множество элементов, характеризующихся связями друг с другом и дополнительным свойством – функцией, не совпадающей или не характеризующейся ни одним из свойств отдельного ее элемента (Губанов В. А., 1988).
3.2. Оптимизация параметров биосистем
3.3. Функциональное состояние и системный подход в физиологии
3.4. Критериальные функции и функционалы биосистем. Множественные корреляции
3.5. Системный подход к изучению биосферы
Глава 4
4.1. Некоторые механизмы влияния космогеофизических факторов на биофизические и биохимические системы
Цели изучения системы заключаются в исследовании ее функционирования в целом и управления ею внешними и внутренними факторами. Подобными задачами занимается системный анализ. Наиболее близки к системному подходу такие области, как исследования методами многомерной статистики и оптимизация. В нашей работе за определение системы принято следующее: система – множество элементов, характеризующихся связями друг с другом и дополнительным свойством – функцией, не совпадающей или не характеризующейся ни одним из свойств отдельного ее элемента (Губанов В. А., 1988).
3.2. Оптимизация параметров биосистем
Понятие гармонии и оптимизации включает в себя проблему пропорционального деления отрезка – вопрос «золотого сечения». Принципам «золотого сечения» подчиняются параметры гемодинамики, выделительная функция почек, организация генотипа, фенотипические способности к реагированию и суточному ритму, модификационная изменчивость стереотипа биоритмов и реактивности, что связано с ГМП, гравитацией, многообразными связями с окружающей средой (Суббота А. Г., 1994).
Направление развития науки от многочисленных фактов и законов имеет тенденцию к централизации и сведению к нескольким или одному закону. Для естественных наук в центре стоит принцип оптимальности (экстремальности) – утверждение о минимуме (или максимуме) некоторой величины (функционала или целевой функции). Это обстоятельство не случайно, у вариационного принципа экстремума нет соперников (Голицин Г. А., Петров В. М., 1990).
Основные проблемы оптимальности организации биологических систем изложены в ряде работ (Розен Р., 1976; Розен В. В., 1982). Проблема сводится к поиску функционала системы, экстремум которого соответствует поставленной задаче. А задача заключается в соответствии теории и данных физиологических исследований при различных функциональных состояниях, когда оптимальные параметры биосистемы доставляют экстремум определенного функционала (Образцов И. Ф., Ханин М. А., 1989; Лушнов М. С., 1995б; 1997б).
В работах, посвященных биооптимальности, применяются самые различные критерии, например минимума гемодинамических параметров (Cohn D., 1954; 1955), минимума потребления энергии физиологическими системами (Ханин М. А. с соавт., 1978), а также более сложные критерии (Fisher R. A., 1930; Yamashiro S. M., Grodins F. S., 1971). Можно утверждать, что многие законы науки имеют экстремальную форму (Полак Л. С., 1960).
Идея оптимальности, экономии соответствует давнему представлению о совершенстве и целесообразности живой природы (Рашевски Н., 1968). Развивая эти положения, Р. Розен (1976) сумел вывести из этого принципа такие физиологические константы, как оптимальные радиусы и углы ветвления артерий, размеры и форма эритроцитов. Выведен ряд закономерностей: параметры систем дыхания и кровообращения, реакции систем в условиях нормы и патологии, концентрация эритроцитов в крови также оптимальны (Ханин М. А. с соавт., 1978). Из этих принципов выводится целостность работы мозга, объясняющая целый ряд качественных результатов: передачу нервных импульсов, память, восприятие, подсознание, эмоции и интеллект, поведенческие функции организма (Емельянов-Ярославский Л. Б., 1974). При этом принцип экономии энергии совсем не является универсальным, а почти всегда сопровождается дополнительными условиями нормального функционирования физиологических систем (Бать О. Г., Ханин М. А., 1984) или нужд выживания (Розен Р., 1976).
В термине «адаптация» различают два разных смысла: приспособление живого существа к условиям окружающей среды, а при исследовании адаптации рецепторов имеется в виду просто привыкание рецепторов к раздражителю. Полная адаптация вида к условиям среды является равновесным состоянием. Если на организм воздействуют два разных стимула с переключением с одного на другой, то сам он будет поддерживать «автоколебания» с оптимальной частотой. Одним из наиболее интересных следствий автоколебательного характера поведения является «эффект границы», так как граница наиболее информативна (Голицин Г. А., Петров В. М., 1990).
Подавляющее большинство процессов протекают симметрично в правом и левом полушариях. Однако левое полушарие – средоточие рефлексивной и речевой функций, правое – интуитивно-чувственных функций, образного освоения мира, эмоций. Эти последствия специализации для межчеловеческих отношений очень важны (Иванов В. В., 1978). Одно из таких важных последствий для социально-психологической жизни общества заключается в том, что наблюдаются периодические колебательные процессы между господством настроений, типичных для доминирования то левого полушария (20–25 лет), то правого (тоже 20–25 лет) (Маслов С. Ю., 1979; 1983). Такие циклы прослежены строго количественно на материале социально-психологического «климата» общества, а также на материале тех сфер, которые подвержены сильному влиянию этого «климата»: архитектуры, стиля музыки. Причем эти циклы приблизительно совпадают по длительности с одним из основых периодов солнечной активности (22 года).
Направление развития науки от многочисленных фактов и законов имеет тенденцию к централизации и сведению к нескольким или одному закону. Для естественных наук в центре стоит принцип оптимальности (экстремальности) – утверждение о минимуме (или максимуме) некоторой величины (функционала или целевой функции). Это обстоятельство не случайно, у вариационного принципа экстремума нет соперников (Голицин Г. А., Петров В. М., 1990).
Основные проблемы оптимальности организации биологических систем изложены в ряде работ (Розен Р., 1976; Розен В. В., 1982). Проблема сводится к поиску функционала системы, экстремум которого соответствует поставленной задаче. А задача заключается в соответствии теории и данных физиологических исследований при различных функциональных состояниях, когда оптимальные параметры биосистемы доставляют экстремум определенного функционала (Образцов И. Ф., Ханин М. А., 1989; Лушнов М. С., 1995б; 1997б).
В работах, посвященных биооптимальности, применяются самые различные критерии, например минимума гемодинамических параметров (Cohn D., 1954; 1955), минимума потребления энергии физиологическими системами (Ханин М. А. с соавт., 1978), а также более сложные критерии (Fisher R. A., 1930; Yamashiro S. M., Grodins F. S., 1971). Можно утверждать, что многие законы науки имеют экстремальную форму (Полак Л. С., 1960).
Идея оптимальности, экономии соответствует давнему представлению о совершенстве и целесообразности живой природы (Рашевски Н., 1968). Развивая эти положения, Р. Розен (1976) сумел вывести из этого принципа такие физиологические константы, как оптимальные радиусы и углы ветвления артерий, размеры и форма эритроцитов. Выведен ряд закономерностей: параметры систем дыхания и кровообращения, реакции систем в условиях нормы и патологии, концентрация эритроцитов в крови также оптимальны (Ханин М. А. с соавт., 1978). Из этих принципов выводится целостность работы мозга, объясняющая целый ряд качественных результатов: передачу нервных импульсов, память, восприятие, подсознание, эмоции и интеллект, поведенческие функции организма (Емельянов-Ярославский Л. Б., 1974). При этом принцип экономии энергии совсем не является универсальным, а почти всегда сопровождается дополнительными условиями нормального функционирования физиологических систем (Бать О. Г., Ханин М. А., 1984) или нужд выживания (Розен Р., 1976).
В термине «адаптация» различают два разных смысла: приспособление живого существа к условиям окружающей среды, а при исследовании адаптации рецепторов имеется в виду просто привыкание рецепторов к раздражителю. Полная адаптация вида к условиям среды является равновесным состоянием. Если на организм воздействуют два разных стимула с переключением с одного на другой, то сам он будет поддерживать «автоколебания» с оптимальной частотой. Одним из наиболее интересных следствий автоколебательного характера поведения является «эффект границы», так как граница наиболее информативна (Голицин Г. А., Петров В. М., 1990).
Подавляющее большинство процессов протекают симметрично в правом и левом полушариях. Однако левое полушарие – средоточие рефлексивной и речевой функций, правое – интуитивно-чувственных функций, образного освоения мира, эмоций. Эти последствия специализации для межчеловеческих отношений очень важны (Иванов В. В., 1978). Одно из таких важных последствий для социально-психологической жизни общества заключается в том, что наблюдаются периодические колебательные процессы между господством настроений, типичных для доминирования то левого полушария (20–25 лет), то правого (тоже 20–25 лет) (Маслов С. Ю., 1979; 1983). Такие циклы прослежены строго количественно на материале социально-психологического «климата» общества, а также на материале тех сфер, которые подвержены сильному влиянию этого «климата»: архитектуры, стиля музыки. Причем эти циклы приблизительно совпадают по длительности с одним из основых периодов солнечной активности (22 года).
3.3. Функциональное состояние и системный подход в физиологии
М. В. Фролов (1987) определяет функциональное состояние (ФС) как результат взаимодействия внешней среды и исходных свойств субъекта. Иначе, ФС – совокупность признаков, свойств, функций и качеств субъекта, которые прямо или косвенно характеризуют ту или иную деятельность.
При наличии информации о закономерностях формирования ФС можно использовать свойства состояний с целью их корректировки в нужном направлении. Проблема определения ФС остается актуальной и по настоящее время. Однако до сих пор в дефинициях ФС существуют разночтения. Недостаточно разработаны единые теоретические позиции исследования ФС. На наш взгляд продуктивным могут оказаться системный подход и синергетика. С иерархических позиций рассматриваются комплексы механизмов гомеостаза, функционирующие в оптимальных пределах для различных условий жизнедеятельности. С позиций системного подхода реализация действий (управления) осуществляется функциональной системой на основе системообразующих факторов. Для биологической системы такой основой является конкретный результат ее деятельности (Ухтомский А. А., 1923; 1950; Анохин П. К., 1973; Фролов Б. С., 1987).
Один из механизмов, обусловливающих измерение психических и физиологических функций организма, известен как стресс-реакция или стресс-синдром (Кокс Т., 1981; Бестужев-Лада И. В., 1982; Каспин В. И. с соавт., 1982). Изменение функций организма в соответствии с механизмом стресс-реакции происходит в ответ на действие достаточного по силе стимула (Селье Г., 1960). «Cтресс есть неспецифический ответ организма на любое предъявленное ему требование» в определенной последовательности (Фресс Н., Пиаже Ж., 1970).
Синергетика позволяет выявлять общность закономерностей развития объектов различной природы и уровней организации. Обнаруженное синергетикой сходство закономерностей, описывающих процессы в самых различных областях знаний, позволяет говорить о структурном изоморфизме процессов самоорганизации любых систем (Герд А. С., Коротков В. И., 1996). Сложность и неоднозначность биосферно-космических явлений требует обращения к новому системно-методологическому подходу. Системный подход базируется на средствах, сложившихся в междисциплинарных направлениях анализа данных и распознавания образов, включая секвентивный, кластерный, дискриминантный, бифуркационный методы (Ковалевский И. В., Ковалевская Е. И., 1996).
Серьезное исследование указанных проблем, на наш взгляд, в настоящее время представляется невозможным без комплексного информационно-статистического подхода, включающего непрерывный динамический мониторинг всего комплекса факторов окружающей cреды с хранением и архивированием в компьютерных базах данных физиологических и психологических параметров с целью оценки динамики ФС организма (Лушнов М. С., 1997а; 1997б).
При оценке функционального состояния необходимо учитывать ряд научно-практических положений, важных при исследовании здорового и особенно больного человека: 1) человек рассматривается в качестве биологической системы в положении устойчивого или неустойчивого равновесия в зависимости от его функционального состояния (Чижевский А. Л., 1976); 2) отдельные свойства функций человека оцениваются посредством оптимизационных приемов, основанных на физиологических представлениях оптимальности и лабильности течения процессов организма (Ухтомский А. А., 1950; Шанин Ю. Н. с соавт., 1978); 3) функциональное состояние дифференцируется качественно и/или количественно по нескольким шкалам одновременно (Генкин А. А., Медведев В. И., 1973); 4) оцениваются свойства целевой функции, обусловливающей функциональное состояние прямо или косвенно (Медведев В. И., 1970); 5) учитывается иерархическая совокупность результатов адаптации и гомеостаза в случае взаимодействия между собой физиологических подсистем (Симонов П. В., 1981); 6) при моделировании ФС учитывается учение о стресс-реакции и стресс-синдроме (Селье Г., 1960).
Получение интегральных критериев, описывающих системные реакции человека при адаптации к внешним условиям, является одним из важнейших условий изучения ФС организма.
При наличии информации о закономерностях формирования ФС можно использовать свойства состояний с целью их корректировки в нужном направлении. Проблема определения ФС остается актуальной и по настоящее время. Однако до сих пор в дефинициях ФС существуют разночтения. Недостаточно разработаны единые теоретические позиции исследования ФС. На наш взгляд продуктивным могут оказаться системный подход и синергетика. С иерархических позиций рассматриваются комплексы механизмов гомеостаза, функционирующие в оптимальных пределах для различных условий жизнедеятельности. С позиций системного подхода реализация действий (управления) осуществляется функциональной системой на основе системообразующих факторов. Для биологической системы такой основой является конкретный результат ее деятельности (Ухтомский А. А., 1923; 1950; Анохин П. К., 1973; Фролов Б. С., 1987).
Один из механизмов, обусловливающих измерение психических и физиологических функций организма, известен как стресс-реакция или стресс-синдром (Кокс Т., 1981; Бестужев-Лада И. В., 1982; Каспин В. И. с соавт., 1982). Изменение функций организма в соответствии с механизмом стресс-реакции происходит в ответ на действие достаточного по силе стимула (Селье Г., 1960). «Cтресс есть неспецифический ответ организма на любое предъявленное ему требование» в определенной последовательности (Фресс Н., Пиаже Ж., 1970).
Синергетика позволяет выявлять общность закономерностей развития объектов различной природы и уровней организации. Обнаруженное синергетикой сходство закономерностей, описывающих процессы в самых различных областях знаний, позволяет говорить о структурном изоморфизме процессов самоорганизации любых систем (Герд А. С., Коротков В. И., 1996). Сложность и неоднозначность биосферно-космических явлений требует обращения к новому системно-методологическому подходу. Системный подход базируется на средствах, сложившихся в междисциплинарных направлениях анализа данных и распознавания образов, включая секвентивный, кластерный, дискриминантный, бифуркационный методы (Ковалевский И. В., Ковалевская Е. И., 1996).
Серьезное исследование указанных проблем, на наш взгляд, в настоящее время представляется невозможным без комплексного информационно-статистического подхода, включающего непрерывный динамический мониторинг всего комплекса факторов окружающей cреды с хранением и архивированием в компьютерных базах данных физиологических и психологических параметров с целью оценки динамики ФС организма (Лушнов М. С., 1997а; 1997б).
При оценке функционального состояния необходимо учитывать ряд научно-практических положений, важных при исследовании здорового и особенно больного человека: 1) человек рассматривается в качестве биологической системы в положении устойчивого или неустойчивого равновесия в зависимости от его функционального состояния (Чижевский А. Л., 1976); 2) отдельные свойства функций человека оцениваются посредством оптимизационных приемов, основанных на физиологических представлениях оптимальности и лабильности течения процессов организма (Ухтомский А. А., 1950; Шанин Ю. Н. с соавт., 1978); 3) функциональное состояние дифференцируется качественно и/или количественно по нескольким шкалам одновременно (Генкин А. А., Медведев В. И., 1973); 4) оцениваются свойства целевой функции, обусловливающей функциональное состояние прямо или косвенно (Медведев В. И., 1970); 5) учитывается иерархическая совокупность результатов адаптации и гомеостаза в случае взаимодействия между собой физиологических подсистем (Симонов П. В., 1981); 6) при моделировании ФС учитывается учение о стресс-реакции и стресс-синдроме (Селье Г., 1960).
Получение интегральных критериев, описывающих системные реакции человека при адаптации к внешним условиям, является одним из важнейших условий изучения ФС организма.
3.4. Критериальные функции и функционалы биосистем. Множественные корреляции
Среди множества оптимизационных методов встречается довольно ограниченное число методик, способных давать индивидуальные статистические функциональные оценки системы (функционального множества биологических системных параметров). Одна из методик, примененная нами, позволила получить корреляционные системные оценки. Биологический смысл таких моделей основан на представлениях, сформулированных Ю. Н. Шаниным с соавторами (1978) о максимуме корреляционных связей в норме и различной степени их разбалансировки в патологии.
Для всей выборки биосистемы строится корреляционная матрица, которая подвергается специальному преобразованию с использованием процедуры ветвей и границ с выбором оптимального подмножества признаков и оценкой для каждого пациента критериальной функции (КФ) (Narenda P. M., Fukunaga K., 1977). Метод основан на оценке некоторой монотонной функции – КФ от какого-либо биологического множества (A), такой, что если существуют два подмножества Ai и Aj, причем Ai содержится в Aj, тогда: C(Ai) < C(Aj) или C(Ai) = C(Aj) – что и означает свойство монотонности. Алгоритм построен на вычислении максимальной КФ на основе определенной квадратической формы и на поиске наибольшего набора из n переменных, максимизирующего КФ для всего подмножества, содержащего m признаков. КФ вычисляется через квадратическую форму: C(Am) = (XmT)Sm–1(Xm), где Am – набор m переменных, Xm – вектор переменных (набор биопараметров – функциональная система конкретного индивида) и Sm – симметричная положительно определенная корреляционная матрица размера mxm; символ XmT означает операцию транспонирования вектора, Sm–1 – операцию вычисления обратной матрицы. Такой класс КФ называют расстояниями Махаланобиса и критериями Фишера.
Эти статистические оценки полностью покрывают (характеризуют) всю исследуемую функциональную систему по определению M. S. Ridout (1988) и являются индивидуальными системными показателями. Они отражают системную организацию и указывают на различную степень закоррелированности (управляемости), гибкости ее реагирования и адаптивности. Таким образом, можно оценить место в динамике системы каждого пациента в течение многолетнего периода исследований. Такие показатели также можно включать в набор зависимых параметров при вычислениях множественных корреляций (МК) в качестве самостоятельных параметров. Динамика функционала биопараметров, описываемого ниже, или КФ, вычисленные на основе «внутренних» корреляций элементов биосистемы, может обнаружить определенную синхронность смещения всей системы регуляции с воздействующими факторами, переход ее на новый уровень функционирования. Это указывает на возможность существенных межсистемных регуляторных сдвигов, что может привести к системному дисбалансу ФС организма от воздействия ионосферы, ГМП, КЛ, СА, приливообразующего потенциала.
Другим системным статистическим методом описания ФС биосистем может служить определенная суммарная оценка – функционал. Он способен описать совокупность признаков нескольких биологических объектов (определенной статистической выборки) в некоторый момент времени. Алгоритм его вычисления изложен ниже.
Кратко суть его заключается в следующем. Производится поиск разбиения множества объектов (лейкограммы, биохимических параметров, системы ферментов, ионов сыворотки крови) на непересекающиеся классы – наборы функциональной подсистемы биологических параметров (например, лейкограммы: лейкоцитов, базофилов, моноцитов и так далее), дающего локальный максимум функционалу – сумме «внутренних» корреляционных связей за вычетом некоторого порогового значения (Миркин Б. Г., 1974; Куперштох В. Л. с соавт., 1976).
Производится поиск разбиения R = (R1, R2, …, RM) множества объектов (лейкограммы, биохимических параметров, системы ферментов, ионов сыворотки крови) на непересекающиеся классы – наборы функциональной подсистемы биологических параметров (например, лейкограммы: лейкоцитов, базофилов, моноцитов и так далее) R1, R2, …, RM (M = 1 или M > 1), дающего локальный максимум функционалу F – сумме «внутренних» корреляционных связей за вычетом некоторого порогового значения корреляций, характеризующего их существенность:
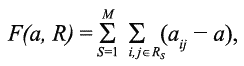
где a – порог существенности связей (при aij > a связь существенна между объектами i и j, при aij < a – связь несущественна), aij – показатель связи между i-м и j-м объектами (aij = aji, aii – не исследуются и не рассматриваются), выражение i, j ∈ RS означает принадлежность элемента aij к множеству RS (Миркин Б. Г., 1974; Куперштох В. Л. с соавт., 1976).
Таким образом, два приведенных здесь способа моделирования способны адекватно описать биологические системы, поскольку содержат основные ее признаки: множество элементов, характеризующихся в данном случае корреляционными связями друг с другом и дополнительным свойством – функцией или функционалом, не совпадающими или не характеризующимися ни одним из свойств отдельного элемента системы (Губанов В. А. с соавт., 1988). Поэтому они являются системными. Кроме того, они способны одновременно быть индикаторами функционального состояния биосистемы, так как КФ и функционал способны описать результат взаимодействия внешней среды и исходных корреляционных свойств субъектов через совокупность признаков, динамику их функций и качеств, которые прямо или косвенно характеризуют исследуемую деятельность – адаптацию (Фролов М. В., 1987).
Кроме двух вышеприведенных статистических методов исследования широко применяюся физиологически обоснованные следующие системные и межсистемные методы: множественные корреляции (BMDP-77. …, 1977; BMDP User's …, 1987), спектральные, авторегрессионные оценки (Дженкинс Г., Ваттс Д., 1971; 1972; Бокс Дж., Дженкинс Г., 1974; Buchman J., Schulten K., 1986), таксономии и классификации (Жирмунская Е. А., Лосев В. С., 1984), раскраски графа динамических процессов (Зыков А. А., 1969; Гладких Б. А. с соавт., 1971; Хаткевич Л. А., 1981), а также построения логических статистических решающих правил (Загоруйко Н. Г. с соавт., 1985). Основным методом изучения статистических связей c КЛ, СА, ИП был метод множественных корреляций (МК) (Aфифи А., Эйзен С., 1982; Боровиков В. П., Боровиков И. П., 1997).
Множественные корреляции (МК) вычисляются для моделей множественной линейной регрессии, что позволяет строить прогнозы при наличии достаточных уровней их значимости одного набора данных (например, совокупности медицинских параметров: лейкограммы, биохимических, ионов крови) по другому набору – геофизических. Если Y – один из медицинских системных параметров (например, количество эозинофилов лейкограммы), тогда X1, X2, …, Xn – набор системы ионосферных (независимых) показателей (например, частоты ионосфeрных слоев f0ES, f0F2 и другие). Квадрат МК – доля дисперсии признака Y, «объясненной» регрессионной зависимостью на наборе признаков (x1, x2, …, xp). МК положительны по определению. При МК = 1 признак описывается линейной комбинацией независимых признаков (Aфифи А., Эйзен С., 1982). МК являются максимумом значения простого коэффициента корреляции между исследуемым множеством и переменной, то есть являются в этом смысле оптимизационной оценкой.
Для всей выборки биосистемы строится корреляционная матрица, которая подвергается специальному преобразованию с использованием процедуры ветвей и границ с выбором оптимального подмножества признаков и оценкой для каждого пациента критериальной функции (КФ) (Narenda P. M., Fukunaga K., 1977). Метод основан на оценке некоторой монотонной функции – КФ от какого-либо биологического множества (A), такой, что если существуют два подмножества Ai и Aj, причем Ai содержится в Aj, тогда: C(Ai) < C(Aj) или C(Ai) = C(Aj) – что и означает свойство монотонности. Алгоритм построен на вычислении максимальной КФ на основе определенной квадратической формы и на поиске наибольшего набора из n переменных, максимизирующего КФ для всего подмножества, содержащего m признаков. КФ вычисляется через квадратическую форму: C(Am) = (XmT)Sm–1(Xm), где Am – набор m переменных, Xm – вектор переменных (набор биопараметров – функциональная система конкретного индивида) и Sm – симметричная положительно определенная корреляционная матрица размера mxm; символ XmT означает операцию транспонирования вектора, Sm–1 – операцию вычисления обратной матрицы. Такой класс КФ называют расстояниями Махаланобиса и критериями Фишера.
Эти статистические оценки полностью покрывают (характеризуют) всю исследуемую функциональную систему по определению M. S. Ridout (1988) и являются индивидуальными системными показателями. Они отражают системную организацию и указывают на различную степень закоррелированности (управляемости), гибкости ее реагирования и адаптивности. Таким образом, можно оценить место в динамике системы каждого пациента в течение многолетнего периода исследований. Такие показатели также можно включать в набор зависимых параметров при вычислениях множественных корреляций (МК) в качестве самостоятельных параметров. Динамика функционала биопараметров, описываемого ниже, или КФ, вычисленные на основе «внутренних» корреляций элементов биосистемы, может обнаружить определенную синхронность смещения всей системы регуляции с воздействующими факторами, переход ее на новый уровень функционирования. Это указывает на возможность существенных межсистемных регуляторных сдвигов, что может привести к системному дисбалансу ФС организма от воздействия ионосферы, ГМП, КЛ, СА, приливообразующего потенциала.
Другим системным статистическим методом описания ФС биосистем может служить определенная суммарная оценка – функционал. Он способен описать совокупность признаков нескольких биологических объектов (определенной статистической выборки) в некоторый момент времени. Алгоритм его вычисления изложен ниже.
Кратко суть его заключается в следующем. Производится поиск разбиения множества объектов (лейкограммы, биохимических параметров, системы ферментов, ионов сыворотки крови) на непересекающиеся классы – наборы функциональной подсистемы биологических параметров (например, лейкограммы: лейкоцитов, базофилов, моноцитов и так далее), дающего локальный максимум функционалу – сумме «внутренних» корреляционных связей за вычетом некоторого порогового значения (Миркин Б. Г., 1974; Куперштох В. Л. с соавт., 1976).
Производится поиск разбиения R = (R1, R2, …, RM) множества объектов (лейкограммы, биохимических параметров, системы ферментов, ионов сыворотки крови) на непересекающиеся классы – наборы функциональной подсистемы биологических параметров (например, лейкограммы: лейкоцитов, базофилов, моноцитов и так далее) R1, R2, …, RM (M = 1 или M > 1), дающего локальный максимум функционалу F – сумме «внутренних» корреляционных связей за вычетом некоторого порогового значения корреляций, характеризующего их существенность:
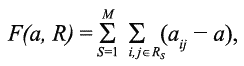
где a – порог существенности связей (при aij > a связь существенна между объектами i и j, при aij < a – связь несущественна), aij – показатель связи между i-м и j-м объектами (aij = aji, aii – не исследуются и не рассматриваются), выражение i, j ∈ RS означает принадлежность элемента aij к множеству RS (Миркин Б. Г., 1974; Куперштох В. Л. с соавт., 1976).
Таким образом, два приведенных здесь способа моделирования способны адекватно описать биологические системы, поскольку содержат основные ее признаки: множество элементов, характеризующихся в данном случае корреляционными связями друг с другом и дополнительным свойством – функцией или функционалом, не совпадающими или не характеризующимися ни одним из свойств отдельного элемента системы (Губанов В. А. с соавт., 1988). Поэтому они являются системными. Кроме того, они способны одновременно быть индикаторами функционального состояния биосистемы, так как КФ и функционал способны описать результат взаимодействия внешней среды и исходных корреляционных свойств субъектов через совокупность признаков, динамику их функций и качеств, которые прямо или косвенно характеризуют исследуемую деятельность – адаптацию (Фролов М. В., 1987).
Кроме двух вышеприведенных статистических методов исследования широко применяюся физиологически обоснованные следующие системные и межсистемные методы: множественные корреляции (BMDP-77. …, 1977; BMDP User's …, 1987), спектральные, авторегрессионные оценки (Дженкинс Г., Ваттс Д., 1971; 1972; Бокс Дж., Дженкинс Г., 1974; Buchman J., Schulten K., 1986), таксономии и классификации (Жирмунская Е. А., Лосев В. С., 1984), раскраски графа динамических процессов (Зыков А. А., 1969; Гладких Б. А. с соавт., 1971; Хаткевич Л. А., 1981), а также построения логических статистических решающих правил (Загоруйко Н. Г. с соавт., 1985). Основным методом изучения статистических связей c КЛ, СА, ИП был метод множественных корреляций (МК) (Aфифи А., Эйзен С., 1982; Боровиков В. П., Боровиков И. П., 1997).
Множественные корреляции (МК) вычисляются для моделей множественной линейной регрессии, что позволяет строить прогнозы при наличии достаточных уровней их значимости одного набора данных (например, совокупности медицинских параметров: лейкограммы, биохимических, ионов крови) по другому набору – геофизических. Если Y – один из медицинских системных параметров (например, количество эозинофилов лейкограммы), тогда X1, X2, …, Xn – набор системы ионосферных (независимых) показателей (например, частоты ионосфeрных слоев f0ES, f0F2 и другие). Квадрат МК – доля дисперсии признака Y, «объясненной» регрессионной зависимостью на наборе признаков (x1, x2, …, xp). МК положительны по определению. При МК = 1 признак описывается линейной комбинацией независимых признаков (Aфифи А., Эйзен С., 1982). МК являются максимумом значения простого коэффициента корреляции между исследуемым множеством и переменной, то есть являются в этом смысле оптимизационной оценкой.
3.5. Системный подход к изучению биосферы
В последние годы специалистов, занимающихся изучением географической оболочки Земли, стали все больше привлекать такие хорошо известные свойства, как дискретность внутреннего устройства, иерархический характер масштабов структурных единиц и связей между ними, а также синергетический колебательный характер переработки энергии в географических и биосистемах (Лушнов М. С. с соавт., 1995). Направление исследований этих свойств можно характеризовать как системную ориентацию (Арманд А. Д., 1988; Басин М. А., 1996).
Одна из важнейших проблем современной науки – выявление законов самоорганизации и эволюции (саморегуляции) сложных динамических систем различной природы (неживой, биологической и социальной) (Дегтярев Г. М. с соавт., 1991). Обнаружены неизвестные ранее закономерности проявления симметрии. Эта закономерность опирается на такие общие свойства открытых динамических систем, как иерархичность, автомодельность и колебательный характер переработки энергий. Она заключается в инвариантности системных связей пространственных и временных масштабов процессов самоорганизации и саморегуляции, проявляющейся в виде сопряженных самоорганизованных структур и бинарных сигналов саморегуляции.
Под саморегуляцией понимается функционирование определенной структуры (системы), при котором идет переработка потоков энергии, массы и информации путем возбуждения сопряженных колебательных и волновых процессов (Дегтярев Г. М. с соавт., 1990). Под понятием гомологичной саморегуляции имеется в виду адаптация, подстройка, эволюционирование, гомеостаз, жизнь.
Базовым свойством биосферы как системы взаимодействия организмов с неживой природой является организованность – совокупность иерархически, ассоциативно и субординационно соотнесенных между собой уровней самоорганизации (организменного, популяционно-видового, биосферного), каждый из которых обладает собственными целостными элементарными единицами функционирования – самоорганизации (циклы, пространственно-временные ряды) (Задде И. Н., 1996). Гомеостаз человека основан на циклическом взаимодействии иерархической многоуровневой регуляторной системы жизнеобеспечения от клеточного уровня до целостного организма и синхронизирован с внешними циклами – временами года, фазами Луны, суточными фазами (Алдонин Г. М., 1996; Бинги В. Н., 1996; Мартынюк В. С., 1996). Обнаружены общие закономерности в частотных характеристиках колебательных систем (Фролов К. В., 1987), в распределениях размеров различных представителей органического мира (Численко Л. Л., 1981).
Синергетика представляет собой подход к изучению кризисов, нестабильности, к созданию средств управления ими. Она ориентирована на поиски принципов самоорганизации сложных природных и социальных систем, представляет собой трансдисциплинарное научное направление с развитием горизонтальных кросс-профессиональных коммуникаций. Синергетическая парадигма по И. Пригожину предоставляет большие возможности для развития социосинергетики и гомосинергетики (Соколов В. Е., Шилов И. А., 1989; Аршинов В. И., Князева Е. Н., 1996). Синергетические методики позволили сформулировать гипотезу о существовании нового типа резонансного взаимодействия сложных структур и систем с окружающими их полями (Баранец А. Н. с соавт., 1989). Важная роль в разработке таких проблем принадлежит статистике, системным и комплексным подходам к прикладным задачам всюду, где требуются сбор и интерпретация данных (Marquardt D. W., 1963; Милюкас В. Ю., 1969).
Одна из важнейших проблем современной науки – выявление законов самоорганизации и эволюции (саморегуляции) сложных динамических систем различной природы (неживой, биологической и социальной) (Дегтярев Г. М. с соавт., 1991). Обнаружены неизвестные ранее закономерности проявления симметрии. Эта закономерность опирается на такие общие свойства открытых динамических систем, как иерархичность, автомодельность и колебательный характер переработки энергий. Она заключается в инвариантности системных связей пространственных и временных масштабов процессов самоорганизации и саморегуляции, проявляющейся в виде сопряженных самоорганизованных структур и бинарных сигналов саморегуляции.
Под саморегуляцией понимается функционирование определенной структуры (системы), при котором идет переработка потоков энергии, массы и информации путем возбуждения сопряженных колебательных и волновых процессов (Дегтярев Г. М. с соавт., 1990). Под понятием гомологичной саморегуляции имеется в виду адаптация, подстройка, эволюционирование, гомеостаз, жизнь.
Базовым свойством биосферы как системы взаимодействия организмов с неживой природой является организованность – совокупность иерархически, ассоциативно и субординационно соотнесенных между собой уровней самоорганизации (организменного, популяционно-видового, биосферного), каждый из которых обладает собственными целостными элементарными единицами функционирования – самоорганизации (циклы, пространственно-временные ряды) (Задде И. Н., 1996). Гомеостаз человека основан на циклическом взаимодействии иерархической многоуровневой регуляторной системы жизнеобеспечения от клеточного уровня до целостного организма и синхронизирован с внешними циклами – временами года, фазами Луны, суточными фазами (Алдонин Г. М., 1996; Бинги В. Н., 1996; Мартынюк В. С., 1996). Обнаружены общие закономерности в частотных характеристиках колебательных систем (Фролов К. В., 1987), в распределениях размеров различных представителей органического мира (Численко Л. Л., 1981).
Синергетика представляет собой подход к изучению кризисов, нестабильности, к созданию средств управления ими. Она ориентирована на поиски принципов самоорганизации сложных природных и социальных систем, представляет собой трансдисциплинарное научное направление с развитием горизонтальных кросс-профессиональных коммуникаций. Синергетическая парадигма по И. Пригожину предоставляет большие возможности для развития социосинергетики и гомосинергетики (Соколов В. Е., Шилов И. А., 1989; Аршинов В. И., Князева Е. Н., 1996). Синергетические методики позволили сформулировать гипотезу о существовании нового типа резонансного взаимодействия сложных структур и систем с окружающими их полями (Баранец А. Н. с соавт., 1989). Важная роль в разработке таких проблем принадлежит статистике, системным и комплексным подходам к прикладным задачам всюду, где требуются сбор и интерпретация данных (Marquardt D. W., 1963; Милюкас В. Ю., 1969).
Глава 4
Механизмы воздействия космогелиогеофизических факторов на системы организма
4.1. Некоторые механизмы влияния космогеофизических факторов на биофизические и биохимические системы
Необходимо отметить, что флуктуациям подвержены элементы неживой и живой природы. Так, Дж. Пиккарди (1967) на основе многолетних наблюдений за периодическими химическими реакциями гидролиза хлористого висмута пришел к выводу о связи с периодичностью СА. Он провел исследования по влиянию ГМП на реакцию хлористого висмута, изучал 11-летние циклы, годовой ход, 27-суточную периодику, суточные вариации, широтную зависимость (Tromp S. W., 1975), синхронность и влияние высоты местности над уровнем моря, атмосферного давления, температуры окружающей среды, солнечных вспышек, ЭМП различных параметров, ультрафиолетовых излучений, рентгеновских лучей, видимого света (Becker R. O., 1963).
В водных средах благодаря кооперативности постоянно возникают и разрушаются системы водородных связей. Наиболее приемлемая и допустимая гипотеза (Кисловский Л. Д., 1971; 1982) гласит о «чувствительности» водных систем к энергетически слабым воздействиям, которое обеспечивается кооперативностью, возможностью существования в воде метастабильных неравновесных, но сравнительно долго живущих структур. В биосистемах каждый составной элемент пребывает в постоянном и неразрывном взаимодействии друг с другом, определяющем динамику поведения целостной системы, механизмы саморегуляции и управления. Биологическая кинетика характеризуется определенными особенностями: переменными выступают концентрации, изменяемые во времени и пространстве, наличие специальных механизмов обратной связи, возможность участия других признаков и свойств в биорегуляции. Управление может осуществляться по принципу триггера, заключающемуся в способности переключаться из одного режима в другой, при наличии устойчивых стационарных состояний и переходов между ними (Рубин А. Б., 1994).
Существенно влияют на биологические процессы электромагнитные свойства биомолекул, свободных радикалов (включая неорганические), белков и ферментов и вообще взаимодействие их с ионизирующими и неионизирующими излучениями, в число которых входят и космические лучи, и солнечные излучения, и факторы ионосферы. Электромагнитные излучения представляют собой диапазон длин волн от км-радиоволн до 10–12 м и менее (жесткое γ-излучение) (рис. 4.1).
 Рис. 4.1. Электромагнитные излучения, наблюдаемые в природе
Рис. 4.1. Электромагнитные излучения, наблюдаемые в природе
Тканевое дыхание сопряжено с окислительным фосфорилированием внутри митохондриальной мембраны, благодаря которой возникает движущая сила – протонный градиент. Таким образом, воздействие квантов энергии ЭМП извне, реагирующих с электронами или протонами через изменение состояния аденозинтрифосфата или других переносчиков заряженных частиц или ферментных белков, что сопровождается регулирующими биологическими воздействиями, изменениями скорости метаболизма (Бышевский А. Ш., Терсенов О. А., 1994). Для различных ферментных реакций с участием переноса электронов существуют области значений параметров, в которых происходят незатухающие колебания переменных – квазистационарные концентрации (Сельков Е. Е., 1977). В механизме же развития лучевого поражения центральное место принадлежит повреждению структур ДНК. Однако повреждение гамма-квантом или вторичным окисляющим радикалом не исключает вероятности успешной репарации структуры ДНК за счет комплементарной цепи, что может сопровождаться активацией соответствующих ферментативных систем (Иванов И. И. с соавт., 1969).
Динамика взаимодействия квантовых полей и частиц определяется основным законом физики – принципом наименьшего действия, величина действия экстремальна. Все превращения в КЛ, веществе протекают по этим принципам. В ЭМП электроны изменяются по-разному в зависимости от спина: от аннигиляции до испускания γ-квантов. Имеет место взаимопревращения нуклонов (протонов и нейтронов) с рождением кванта-бозона или π-мезонов, которые имеют резонансный характер в критическом состоянии с нулевой энергией перехода (Мигдал А. Б., 1977; Леонов А. И., 1995).
В водных средах благодаря кооперативности постоянно возникают и разрушаются системы водородных связей. Наиболее приемлемая и допустимая гипотеза (Кисловский Л. Д., 1971; 1982) гласит о «чувствительности» водных систем к энергетически слабым воздействиям, которое обеспечивается кооперативностью, возможностью существования в воде метастабильных неравновесных, но сравнительно долго живущих структур. В биосистемах каждый составной элемент пребывает в постоянном и неразрывном взаимодействии друг с другом, определяющем динамику поведения целостной системы, механизмы саморегуляции и управления. Биологическая кинетика характеризуется определенными особенностями: переменными выступают концентрации, изменяемые во времени и пространстве, наличие специальных механизмов обратной связи, возможность участия других признаков и свойств в биорегуляции. Управление может осуществляться по принципу триггера, заключающемуся в способности переключаться из одного режима в другой, при наличии устойчивых стационарных состояний и переходов между ними (Рубин А. Б., 1994).
Существенно влияют на биологические процессы электромагнитные свойства биомолекул, свободных радикалов (включая неорганические), белков и ферментов и вообще взаимодействие их с ионизирующими и неионизирующими излучениями, в число которых входят и космические лучи, и солнечные излучения, и факторы ионосферы. Электромагнитные излучения представляют собой диапазон длин волн от км-радиоволн до 10–12 м и менее (жесткое γ-излучение) (рис. 4.1).

Тканевое дыхание сопряжено с окислительным фосфорилированием внутри митохондриальной мембраны, благодаря которой возникает движущая сила – протонный градиент. Таким образом, воздействие квантов энергии ЭМП извне, реагирующих с электронами или протонами через изменение состояния аденозинтрифосфата или других переносчиков заряженных частиц или ферментных белков, что сопровождается регулирующими биологическими воздействиями, изменениями скорости метаболизма (Бышевский А. Ш., Терсенов О. А., 1994). Для различных ферментных реакций с участием переноса электронов существуют области значений параметров, в которых происходят незатухающие колебания переменных – квазистационарные концентрации (Сельков Е. Е., 1977). В механизме же развития лучевого поражения центральное место принадлежит повреждению структур ДНК. Однако повреждение гамма-квантом или вторичным окисляющим радикалом не исключает вероятности успешной репарации структуры ДНК за счет комплементарной цепи, что может сопровождаться активацией соответствующих ферментативных систем (Иванов И. И. с соавт., 1969).
Динамика взаимодействия квантовых полей и частиц определяется основным законом физики – принципом наименьшего действия, величина действия экстремальна. Все превращения в КЛ, веществе протекают по этим принципам. В ЭМП электроны изменяются по-разному в зависимости от спина: от аннигиляции до испускания γ-квантов. Имеет место взаимопревращения нуклонов (протонов и нейтронов) с рождением кванта-бозона или π-мезонов, которые имеют резонансный характер в критическом состоянии с нулевой энергией перехода (Мигдал А. Б., 1977; Леонов А. И., 1995).
