Ответить на этот вопрос нетрудно: чтобы поле через второе вещество воздействовало на первое вещество или, наоборот, чтобы первое вещество через второе давало на выходе поле, несущее информацию.
В самом деле, очевидно, что нет поля, которое умело бы обнаруживать маленькие капельки фреона или масла. Но есть ультрафиолетовое излучение, которое легко обнаруживает даже ничтожные количества люминофоров, и вот мы вводим эту пару - поле и второе вещество, связывающее поле с первым (исходным) веществом.
Обозначим поле буквой П, первое вещество В1, второе вещество - В2. Связи будем обозначать стрелками. Тогда для задачи 9 можно написать схему решения (двойная стрелка направлена от «дано» к «получено»):
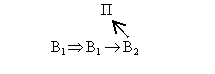
У задачи 10 такая же схема решения, но вещество В2 само создает поле, зависящее от состояния В2, которое, в свою очередь, зависит от состояния В1. Соответственно схемы решения задач 11 и 12 запишем так:

В решениях взятых нами задач присутствуют три «действующих лица»: вещество В1, которое надо менять, обрабатывать, перемешать, обнаруживать, контролировать и т. д.; вещество В2 - «инструмент», осуществляющий необходимое действие; поле П, которое дает энергию, силу, т. е. обеспечивает воздействие В2 на В1 (или их взаимодействие). Нетрудно заметить, что эти три «действующих лица» необходимы и достаточны для получения требуемого в задаче результата. Само по себе поле или сами по себе вещества никакого действия не производят. Чтобы сделать что-то с веществом В1, нужны инструмент (вещество В2) и энергия (поле П).
Можно сказать иначе. В любой изобретательской задаче есть объект: в задаче 9 - капельки жидкости, в задаче 10 - полимер и т. д. Этот объект не может осуществлять требуемого действия сам по себе, он должен взаимодействовать с внешней средой (или с другим объектом). При этом любое изменение сопровождается выделением, поглощением или преобразованием энергии.
Два вещества и поле могут быть самыми различными, но они необходимы и достаточны для образования минимальной технической системы, получившей название веполь (от слов «вещество» и «поле»).
Вводя понятие о веполе, мы используем три термина: вещество, поле, взаимодействие (воздействие, действие, связь). Под термином «вещество» понимаются любые объекты независимо от степени их сложности. Лед и ледокол, винт и гайка, трос и груз - все это «вещества». Взаимодействие - всеобщая форма связи тел или явлений, осуществляющаяся в их взаимном изменении. Четкую характеристику взаимодействия дал Ф. Энгельс: «Взаимодействие - вот первое, что выступает перед нами, когда мы рассматриваем движущуюся материю в целом с точки зрения теперешнего естествознания. Мы наблюдаем ряд форм движения: механическое движение, теплоту, свет, электричество, магнетизм, химическое соединение и разложение, переходы агрегатных состояний, органическую жизнь, которые все - если исключить пока органическую жизнь - переходят друг в друга, обусловливают взаимно друг друга, являясь здесь причиной, там действием...» (К. Маркс, Ф. Энгельс. Соч., т. 20, с. 544).
Сложнее обстоит дело с определением понятия поля. В физике полем называют форму материи, осуществляющую взаимодействие между частицами вещества. Различают четыре вида полей: электромагнитное, гравитационное, поле сильных и слабых взаимодействий. В технике термин «поле» используют шире: это пространство, каждой точке которого поставлена в соответствие некоторая векторная или скалярная величина. Подобные поля часто связаны с веществами - носителями векторных или скалярных величин. Например, поле температур (тепловое поле), поле центробежных сил. Мы будем применять термин «поле» очень широко, рассматривая наряду с «законными» физическими полями и все- возможные «технические» поля - тепловое, механическое, акустическое и т. д.
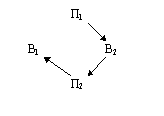
В решении задачи 12 тепловое поле действует на В2, меняя механическое взаимодействие между В2 и В1:
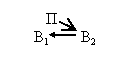
Может возникнуть вопрос: почему тепловое поле показано в формуле веполя, а механического поля взаимодействия между В2 и В1 в формуле нет? Разумеется, можно было бы записать и так:
где П1 - тепловое поле, а П2 - механическое поле.
В вепольных формулах обычно записывают только поля на входе и на выходе, т. е. поля, которыми по условиям данной задачи можно непосредственно управлять - вводить, обнаруживать, изменять, измерять. Взаимодействие между веществами указывают без детализации вида взаимодействия (тепловое, механическое и т. д.).
Принятые обозначения:
- веполь (в общем виде);
- действие или взаимодействие (в общем виде, без конкретизации);
- действие;
- взаимодействие;
- действие (или взаимодействие), которое надо ввести по условиям задачи;
~ - неудовлетворительное действие (или взаимодействие), которое по условиям задачи должно быть изменено;
П - поле на входе: «поле действует»;
П - поле на выходе: «поле хорошо поддается действию (изменению, обнаружению, измерению)»;
П' - состояние поля на входе;
П'' - состояние того же поля на выходе (меняются параметры, но не природа поля);
В' - состояние вещества на входе;
В'' - состояние вещества на выходе;
В' - В'' - «переменное» вещество, находящееся то в состоянии В', то в состоянии В'' (например, под действием переменного поля);
- переменное поле.
В вепольных формулах вещества надо записывать в строчку, а поля сверху и снизу; это позволяет нагляднее отразить действие нескольких полей на одно и то же вещество.
На первых порах представление технических систем в виде веполей наталкивается на чисто психологические трудности. Нечто подобное наблюдается при освоении ребенком понятия «треугольник». Почему три яблока, лежащие в сумке, это не треугольник, а те же три яблока, расположенные на столе, образуют треугольник? Почему три точки дают треугольник и три дома тоже дают треугольник, хотя точки очень маленькие, а дома очень большие?.. Эти затруднения довольно быстро преодолеваются,
Кстати, об аналогии с геометрией. Треугольник - минимальная геометрическая фигура. Любую более сложную фигуру (квадрат, ромб, четырехугольник и т. д.) можно свести к сумме треугольников. Именно поэтому изучение свойств треугольника выделено в особую науку-тригонометрию. - система из трех элементов В1, В2 и П - играет в технике такую же фундаментальную роль, какую треугольник играет в геометрии. Зная несколько основных правил и имея таблицы тригонометрических функций, можно легко решать задачи, которые без этого потребовали бы кропотливых измерений и вычислений. Точно так же, зная правила построения и преобразования веполей, можно легко решать многие трудные изобретательские задачи.
Первое правило, с которым мы уже познакомились, состоит в том, что невепольные системы (один элемент - вещество или поле) и неполные вепольные системы (два элемента - поле и вещество, два вещества) необходимо - для повышения эффективности и управляемости - достраивать до полного веполя (три элемента - два вещества и поле).
Выше была приведена задача 3 о разделении щепы древесины и коры. В ней даны два вещества, и, следовательно, для достройки веполя необходимо ввести поле. Огромное поисковое пространство резко сужается; нужно рассмотреть всего несколько вариантов. В сущности, если отбросить поля сильных и слабых взаимодействий (в данной задаче они явно ведут к слишком сложным решениям), остаются два «законных» поля: электромагнитное и гравитационное. Учитывая ничтожную разницу в удельном весе щепок, следует сразу отбросить и гравитационное поле. Остается одно поле - электромагнитное. Поскольку магнитное поле не действует на кору и древесину, можно сразу ставить решающий эксперимент: как ведут себя щепки в электрическом поле? Оказывается, в электрическом поле частицы коры заряжаются отрицательно, а частицы древесины - положительно. Это позволяет построить сепаратор, обеспечивающий надежное разделение щепок.
Ну, а если бы щепки не электризовались? И в этом случае правило о постройке веполя сохраняет силу. Задача состоит в том, чтобы удалить один вид щепок. Следовательно, мы имеем право считать, что дано одно вещество, которое надо перемещать. Достроим веполь: добавим к этому веществу пару «вещество и поле». Например, до раздробления ствола и ветвей нанесем на кору ферромагнитные частицы, а затем - после дробления - используем для сепарации магнитное поле. Тут уже не требуются эксперименты: магнитное поле заведомо способно перемещать «омагниченную» кору.
Это решение можно изобразить так:

Дана смесь двух веществ, эти вещества сами не хотят разделяться. Решение состоит в достройке веполя, причем вместо В2 надо взять комплекс (В2 В3).
Возможность строить «комплексные» веполи намного расширяет область применения правила о достройке веполя.
Решение задачи 9 тоже можно рассматривать как построение комплексного веполя (в жидкость добавлен люминофор):
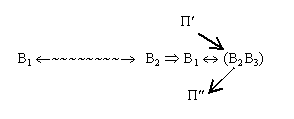
Здесь В1- холодильный агрегат; В2 - холодильная жидкость; В3 - люминофор; П- поле на входе (невидимое ультрафиолетовое излучение); П - поле на выходе (видимое излучение люминофора).
Правило достройки веполянепосредственно вытекает из самого определения понятия «веполь»: минимально полная техническая система заведомо эффективнее неполной системы, поэтому данные в задачах невепольные и неполные вепольные системы надо достраивать до полных веполей. Существуют и другие правила, относящиеся к построению и преобразованию вепольных систем. Использование этих правил лежит в основе вепольного анализа, составляющего один из важнейших разделов теории решения изобретательских задач. Приведем задачу.
Задача 13
Для очистки горячих газов от немагнитной пыли применяют фильтры, представляющие собой пакет, образованный многими слоями металлической ткани. Эти фильтры удовлетворительно задерживают пыль, но именно поэтому их потом трудно очищать. Приходится часто отключать фильтр и подолгу продувать его в обратном направлении, чтобы выбить пыль. Как быть?
Задача была решена так: в качестве фильтра стали использовать ферромагнитный порошок, помещенный между полюсами магнита и образующий пористую структуру. Отключая и включая магнитное поле, можно эффективно управлять фильтром. Поры фильтра могут быть маленькими (когда ловят пыль) и большими (когда идет очистка фильтра).
В условиях этой задачи уже описана вепольная система: есть В1 (пыль), есть В2 (пакет ткани), есть П (механическое поле сил, создаваемых потоком воздуха). Решение состоит в том, что:
- В2 раздробили в ферромагнитный порошок Вф;
- действие поля П направили не на В1 (изделие), а на Вф (инструмент);
- само поле стало не механическим (Пмех.) а магнитным (Пм).
Это можно записать так:
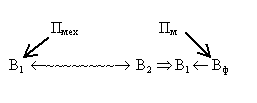
Сильное решение получено благодаря тому, что реализовано правило развития веполей:с увеличением степени дисперсности В2 (инструмента) эффективность веполя повышается; действие поля на В2 (инструмент) эффективнее действия на В1 (изделие); электрические (электромагнитные, магнитные) поля в веполях эффективнее неэлектрических (механических, тепловых и т. д.). Действительно, едва ли надо доказывать, что чем меньше частицы В2, тем более гибким может быть управление инструментом. Очевидно также, что выгоднее менять инструмент (это зависит от нас), а не изделие (зачастую являющееся природным объектом). Порознь целесообразность этих преобразований очевидна, но сила правила заключается в использовании системы преобразований.
Задача 13 на протяжении ряда лет применялась в качестве учебной на занятиях в общественных школах изобретательского творчества. Решая ее в начале учебы, слушатели ни разу не давали верного ответа. После изучения вепольного анализа задача без затруднений решалась практически всеми - научными работниками, инженерами, студентами, школьниками.
Вернемся теперь к задаче 6, которая также широко использовалась при обучении ТРИЗ. Вот запись, сделанная опытным конструктором в первый день занятий:
«1-й путь - построить необходимое количество площадок. Кажущаяся простота и получаемая исчерпываемость результатов, Однако на самом деле - дороговизна осуществления (строительство), сложность эксплуатации. Таким образом, этот путь нецелесообразен.
2-й путь - имитация только экстремальных условий: наиболее благоприятных для эксплуатации тракторов и наименее благоприятных, т. е. создание на уже имеющейся площадке двух участков с соответствующими качествами грунтов.
Принимаю 2-й путь и как вариант - площадку с тремя участками: наилучшие условия, наихудшие и средние».
Ход решения и полученный ответ весьма характерны для обычного конструкторского мышления. Сначала рассмотрен прямой путь - построим необходимое количество площадок. Здесь очевидное техническое противоречие: выигрыш в качестве испытаний и проигрыш в сложности и дороговизне строительства. Конструктор ищет компромисс, нет стремления преодолеть противоречие. Выдвигается 2-й вариант: ограничимся двумя-тремя площадками. Но и здесь имеется техническое противоречие: проигрыш в качестве испытаний (2 площадки вместо 200!) и выигрыш в простоте и дешевизне. И снова нет попытки преодолеть противоречие. Второй вариант представляется более приемлемым (дешевизна!) - и выбор сделан...
Ни один из решавших эту задачу конструкторов (в их числе были и весьма опытные изобретатели, имевшие по 30-50 авторских свидетельств) не смог дать удовлетворительного решения. После освоения ТРИЗ слушатели общественных школ (включая студентов и школьников) без затруднений решали эту задачу.
Типичная запись решения: «Много общего с задачей о магнитном фильтре. В1 - почва. Введем В2 в виде ферромагнитного порошка. Используем для достройки веполя магнитное поле Пм. Действуя полем, можно менять характеристики смеси В2 и В1.
Интересно сопоставить записи вепольных преобразований с записями химических реакций. Записывая химическую формулу вещества, мы отбрасываем множество свойств, присущих этому веществу. Химические формулы ничего не говорят, например, о магнитных и оптических свойствах вещества, его плотности и т. д. Отражены лишь свойства, принципиально важные для химии: состав и структура молекул. Точно так же, записывая вепольную формулу технической системы, мы отбрасываем все свойства этой системы, кроме тех, которые принципиально важны для ее развития: вепольная формула отражает вещественно-полевой состав и структуру системы.
Появление языка химических формул стало возможным только тогда, когда в химию прочно вошли такие фундаментальные понятия, как атом, молекула, молекулярный вес, и столь же фундаментальные законы взаимодействия и преобразования веществ. Так, уравнивая коэффициенты в записи химической реакции, мы пользуемся законом сохранения вещества, хотя не каждый раз об этом вспоминаем. В отличие от математических формул химические не позволяют открывать новые явления исходя только из самих формул и некоторых начальных постулатов. Химическая символика отражает лишь те знания, которые уже есть. В этом смысле вепольный анализ скорее похож на химический язык, чем на математический.
В некоторых изобретательских задачах требуется устранить вредное взаимодействие двух объектов. В таких случаях надо использовать правило разрушения веполей.Запишем формулу веполя в общем виде:
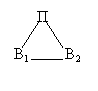
Разломать этот «треугольник» можно различными путями: удалить один из элементов, «оборвать» связи, заменить поле третьим веществом и т. д. Анализ большого числа задач на разрушение веполя показал, что самым эффективным решением оказывается введение третьего вещества, являющегося видоизменением одного из двух имеющихся.
Задача 14
В светокопировальной машине по стеклу протягивается калька с чертежом. К кальке прилегает светочувствительная бумага. Стекло (сложной формы) сломалось. Изготовление нового стекла требует значительного времени. Поэтому решили поставить оргстекло. Однако оказалось, что калька при движении электризуется и прилипает к стеклу. Как быть?
Инженеры, не знающие правила о разрушении веполя, обычно начинают перебирать варианты, связанные с удалением электрических зарядов. Но отводить заряды, не загораживая свет и не усложняя аппаратуру, очень трудно. С позиций вепольного анализа задача решается иначе. Между калькой и стеклом нужно ввести третье вещество, являющееся видоизмененной калькой или видоизмененным стеклом. Проще взять кальку - она дешевле. Поскольку эта калька должна находиться между стеклом и калькой с чертежом, нужно, чтобы вводимая калька была прозрачной и не задерживала свет. Значит, надо взять чистую кальку. Задача решена. Если протянуть чистую кальку по стеклу, она прилипнет. Калька с чертежом теперь пойдет не по стеклу, а по этой прилипшей кальке.
На этом примере хорошо видно, почему в правиле говорится, что вводимое третье вещество должно быть видоизменением одного из двух имеющихся. Если просто ввести какое-то третье вещество, могут возникнуть осложнения: «чужое» вещество будет плохо чувствовать себя в «посторонней» ему технической системе. Нужно, чтобы третье вещество было и чтобы его не было; тогда оно не сломается, не удорожит систему, не нарушит ее работу - словом, не привнесет никаких осложнений. Правило разрушения веполя, указывая на необходимость использования одного из имеющихся веществ (видоизменив его), подсказывает, как преодолеть противоречие «третье вещество есть и третьего вещества нет».
Правило достройки веполя тоже включает указания на преодоление противоречия. Поле должно действовать на вещество В1 , и поле не должно (не умеет) действовать на это вещество. Вводя вещество В2 и действуя через него на В1 , мы тем самым преодолеваем противоречие.
Таким образом, вепольный анализ, как и анализ по АРИЗ, построен на решении задач выявлением и устранением противоречий.
Часто приходится решать задачи, в которых противоречие возникает из-за того, что нужно сохранить имеющийся веполь и в то же время ввести новое взаимодействие. Такова, например, задача 8. По ее условиям уже дан веполь, причем «хороший», нужный: механическое поле Пмех через В2 (круг) действует на В1 (цилиндр). Невыгодно перестраивать этот веполь или ломать его, поскольку условия задачи не содержат никаких претензий к самому процессу шлифовки. Такие задачи решаются по правилу построения цепных веполей:
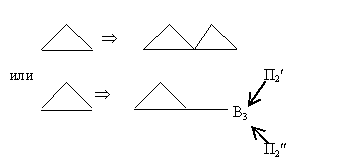
Как видно из формул, суть решения состоит в том, что В2 (инструмент) разворачивается в веполь, присоединенный к имеющемуся веполю. Иногда В3 в свою очередь разворачивается в веполь, продолжающий цепь.
В задачах на измерение и обнаружение веполь должен иметь на выходе поле, которое легко измерить и обнаружить. Поэтому при решении этих задач конечное звено цепи В1 - В2 - . . . обычно имеет такой вид:

Например, в задаче 9 люминофор преобразует параметры оптического поля (невидимое ультрафиолетовое излучение превращается в излучение видимое): П П. Не менее часто встречается преобразование одного поля в другое: П1 П2. Реже используется излучение, генерируемое самим веществом, входящим в веполь.
Если вещество должно превращать одно поле в другое (или менять параметры поля), можно сразу определить необходимый физический эффект, используя простое правило: название эффекта образуется соединением названий двух полей.Например:
(оптико-акустический эффект)
Задача 15
Из-за сдвига горных пород буровую колонну иногда намертво «прихватывает» в скважине. Чтобы ликвидировать прихват, внутрь буровой колонны на глубину прихвата опускают вибратор. Но как узнать, на какой глубине возник прихват?
Зона прихвата невелика - несколько десятков метров, а длина колонны - километры. Задача не решается непосредственным зондированием; не годится и предложение измерять деформацию трубы при определенном усилии (буровую колонну нельзя рассматривать как жесткий стержень, к тому же колонна испытывает неучитываемое трение о стенки скважины).
Вепольная схема решения задачи несложна:

где П1 - механическое поле на входе; П2 - поле на выходе; В1 - грунт; В2 - труба.
Обычно при решении таких задач целесообразно иметь на выходе легко поддающееся обнаружению и измерению электромагнитное поле. Веществом-преобразователем целесообразно взять стальную трубу, а не грунт, поскольку мы не знаем, какой именно грунт окажется в месте прихвата. свойства же стали нам известны. Сталь - ферромагнетик; логично прежде всего использовать именно магнитные свойства стали: эти свойства уже есть, их не надо придавать извне. Таким образом, определилось название нужного физического эффекта: механомагнитный ( в физике он называется магнитоупругим эффектом); магнитное поле ферромагнетика меняется в зависимости от напряжения, испытываемого ферромагнетиком.
Внутрь опускают прибор, ставящий через каждый метр магнитные метки. Затем лебедкой дергают трубу вверх. От ударной нагрузки все глотки выше места прихвата размагничиваются. Метки, расположенные ниже места прихвата, остаются без изменений. Это легко обнаруживается магнитометром.
Попробуйте решить несколько учебных задач. Это несложные задачи, для их решения достаточно знать изложенные выше простейшие правила вепольного анализа.
Решить учебную задачу означает: указать правило, на основе которого решается данная задача; дать конкретный ответ, основанный на этом правиле. Распространенная ошибка состоит в том, что пытаются угадать ответ, используя привычный метод проб и ошибок. Это все равно, что подойти к спортивному снаряду... и обойти его, став на то место, куда надо спрыгнуть со снаряда. Нетрудно обойти, скажем, турник, но и пользы от этого не будет. Весь смысл решения учебных задач в том, чтобы выработать навыки анализа, приобрести опыт, который потом пригодится при решении более трудных задач.
Задача 16
В формуле изобретения по а. с. № 527 280 сказано: «Манипулятор для сварочных работ, содержащий поворотный стол и узел поворота стола, выполненный в виде поплавкового механизма, шарнирно соединенного) через кронштейн со столом и помещенного в емкость с жидкостью, отличающийся тем, что с целью увеличения скорости перемещения стола в жидкость введена ферромагнитная взвесь, а емкость с жидкостью помещена в электромагнитную обмотку.» В чем суть этого изобретения с позиций вепольного анализа?
Задача 17
По трубопроводу, имеющему сложную форму (повороты), транспортируют пневмопотоком мелкие стальные шарики. В местах «поворота трубопровод сильно изнашивается изнутри из-за ударов транспортируемых шариков о стенки трубы. Пытались вводить защитные прокладки, но они быстро изнашивались.
Какое правило вепольного анализа следует применить при решении этой задачи? Каков ответ, основанный на этом правиле? Как быть, если по трубопроводу транспортируются не стальные, а, например, медные шарики?
Задача 18
Притирку одной поверхности к другой проверяют, нанося на одну поверхность тонкий слой краски и проверяя равномерность отпечатка на другой поверхности. Для поверхностей высших классов частоты необходимо применять очень тонкий слой краски (десятые доли микрона). Такой слой дает отпечатки, которые трудно различать. Ваше предложение? На каком правиле оно основано?
Задача 19
В а. с. № 253 753 описано следующее изобретение: «Электромагнитное перемешивающее устройство, включающее цилиндрический сосуд, статор, создающий электромагнитное поле, и ротор, о т л и ч а ю щ е е с я тем, что с целью интенсификации перемешивания ротор выполнен в виде эластичного перфорированного кольца. свободно размещенного в сосуде.» Итак, вместо жесткой лопастной мешалки использована эластичная «дырчатая» лента, приводимая во вращение электромагнитным полем. Спрогнозируйте следующее изобретение, развивающее то, что описано в а. с. 253 753. На каком правиле вепольного анализа основан ваш прогноз?
Задача 20
При изготовлении шлифовального инструмента мало уложить маленькие алмазные зерна, имеющие форму пирамидок, не как попало, а в определенном положении - острым углом вверх. Как это сделать?
Задача 21
На скоростных судах подводные крылья быстро разрушаются из-за кавитационного воздействия потока воды.
Каково ваше решение? На каком правиле вепольного анализа оно основано?
Задача 22
После изготовления некоторых железобетонных изделий с предварительно напряженной (растянутой) арматурой (стальными стержнями) возникает необходимость измерять напряжение (или фактическую величину удлинения) арматуры в готовом изделии. Трудность заключается в том, что арматура находится внутри готового и установленного изделия. Делать дырки или выводить концы арматуры наружу нельзя. Применить просвечивание с помощью ультразвука или рентгеновских лучей слишком сложно. Как быть?
СИТУАЦИЯ - ЗАДАЧА - МОДЕЛЬ ЗАДАЧИ
ОСНОВНЫЕ МЕХАНИЗМЫ УСТРАНЕНИЯ ПРОТИВОРЕЧИЙ
ПРОГРАММА + ИНФОРМАЦИЯ + УПРАВЛЕНИЕ ПСИХОЛОГИЧЕСКИМИ ФАКТОРАМИ
В самом деле, очевидно, что нет поля, которое умело бы обнаруживать маленькие капельки фреона или масла. Но есть ультрафиолетовое излучение, которое легко обнаруживает даже ничтожные количества люминофоров, и вот мы вводим эту пару - поле и второе вещество, связывающее поле с первым (исходным) веществом.
Обозначим поле буквой П, первое вещество В1, второе вещество - В2. Связи будем обозначать стрелками. Тогда для задачи 9 можно написать схему решения (двойная стрелка направлена от «дано» к «получено»):
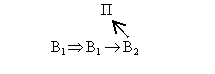
У задачи 10 такая же схема решения, но вещество В2 само создает поле, зависящее от состояния В2, которое, в свою очередь, зависит от состояния В1. Соответственно схемы решения задач 11 и 12 запишем так:

В решениях взятых нами задач присутствуют три «действующих лица»: вещество В1, которое надо менять, обрабатывать, перемешать, обнаруживать, контролировать и т. д.; вещество В2 - «инструмент», осуществляющий необходимое действие; поле П, которое дает энергию, силу, т. е. обеспечивает воздействие В2 на В1 (или их взаимодействие). Нетрудно заметить, что эти три «действующих лица» необходимы и достаточны для получения требуемого в задаче результата. Само по себе поле или сами по себе вещества никакого действия не производят. Чтобы сделать что-то с веществом В1, нужны инструмент (вещество В2) и энергия (поле П).
Можно сказать иначе. В любой изобретательской задаче есть объект: в задаче 9 - капельки жидкости, в задаче 10 - полимер и т. д. Этот объект не может осуществлять требуемого действия сам по себе, он должен взаимодействовать с внешней средой (или с другим объектом). При этом любое изменение сопровождается выделением, поглощением или преобразованием энергии.
Два вещества и поле могут быть самыми различными, но они необходимы и достаточны для образования минимальной технической системы, получившей название веполь (от слов «вещество» и «поле»).
Вводя понятие о веполе, мы используем три термина: вещество, поле, взаимодействие (воздействие, действие, связь). Под термином «вещество» понимаются любые объекты независимо от степени их сложности. Лед и ледокол, винт и гайка, трос и груз - все это «вещества». Взаимодействие - всеобщая форма связи тел или явлений, осуществляющаяся в их взаимном изменении. Четкую характеристику взаимодействия дал Ф. Энгельс: «Взаимодействие - вот первое, что выступает перед нами, когда мы рассматриваем движущуюся материю в целом с точки зрения теперешнего естествознания. Мы наблюдаем ряд форм движения: механическое движение, теплоту, свет, электричество, магнетизм, химическое соединение и разложение, переходы агрегатных состояний, органическую жизнь, которые все - если исключить пока органическую жизнь - переходят друг в друга, обусловливают взаимно друг друга, являясь здесь причиной, там действием...» (К. Маркс, Ф. Энгельс. Соч., т. 20, с. 544).
Сложнее обстоит дело с определением понятия поля. В физике полем называют форму материи, осуществляющую взаимодействие между частицами вещества. Различают четыре вида полей: электромагнитное, гравитационное, поле сильных и слабых взаимодействий. В технике термин «поле» используют шире: это пространство, каждой точке которого поставлена в соответствие некоторая векторная или скалярная величина. Подобные поля часто связаны с веществами - носителями векторных или скалярных величин. Например, поле температур (тепловое поле), поле центробежных сил. Мы будем применять термин «поле» очень широко, рассматривая наряду с «законными» физическими полями и все- возможные «технические» поля - тепловое, механическое, акустическое и т. д.
В решении задачи 12 тепловое поле действует на В2, меняя механическое взаимодействие между В2 и В1:
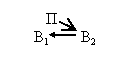
Может возникнуть вопрос: почему тепловое поле показано в формуле веполя, а механического поля взаимодействия между В2 и В1 в формуле нет? Разумеется, можно было бы записать и так:

где П1 - тепловое поле, а П2 - механическое поле.
В вепольных формулах обычно записывают только поля на входе и на выходе, т. е. поля, которыми по условиям данной задачи можно непосредственно управлять - вводить, обнаруживать, изменять, измерять. Взаимодействие между веществами указывают без детализации вида взаимодействия (тепловое, механическое и т. д.).
Принятые обозначения:
- веполь (в общем виде);
- действие или взаимодействие (в общем виде, без конкретизации);
- действие;
- взаимодействие;
- действие (или взаимодействие), которое надо ввести по условиям задачи;
~ - неудовлетворительное действие (или взаимодействие), которое по условиям задачи должно быть изменено;
П - поле на входе: «поле действует»;
П - поле на выходе: «поле хорошо поддается действию (изменению, обнаружению, измерению)»;
П' - состояние поля на входе;
П'' - состояние того же поля на выходе (меняются параметры, но не природа поля);
В' - состояние вещества на входе;
В'' - состояние вещества на выходе;
В' - В'' - «переменное» вещество, находящееся то в состоянии В', то в состоянии В'' (например, под действием переменного поля);
- переменное поле.
В вепольных формулах вещества надо записывать в строчку, а поля сверху и снизу; это позволяет нагляднее отразить действие нескольких полей на одно и то же вещество.
На первых порах представление технических систем в виде веполей наталкивается на чисто психологические трудности. Нечто подобное наблюдается при освоении ребенком понятия «треугольник». Почему три яблока, лежащие в сумке, это не треугольник, а те же три яблока, расположенные на столе, образуют треугольник? Почему три точки дают треугольник и три дома тоже дают треугольник, хотя точки очень маленькие, а дома очень большие?.. Эти затруднения довольно быстро преодолеваются,
Кстати, об аналогии с геометрией. Треугольник - минимальная геометрическая фигура. Любую более сложную фигуру (квадрат, ромб, четырехугольник и т. д.) можно свести к сумме треугольников. Именно поэтому изучение свойств треугольника выделено в особую науку-тригонометрию. - система из трех элементов В1, В2 и П - играет в технике такую же фундаментальную роль, какую треугольник играет в геометрии. Зная несколько основных правил и имея таблицы тригонометрических функций, можно легко решать задачи, которые без этого потребовали бы кропотливых измерений и вычислений. Точно так же, зная правила построения и преобразования веполей, можно легко решать многие трудные изобретательские задачи.
Первое правило, с которым мы уже познакомились, состоит в том, что невепольные системы (один элемент - вещество или поле) и неполные вепольные системы (два элемента - поле и вещество, два вещества) необходимо - для повышения эффективности и управляемости - достраивать до полного веполя (три элемента - два вещества и поле).
Выше была приведена задача 3 о разделении щепы древесины и коры. В ней даны два вещества, и, следовательно, для достройки веполя необходимо ввести поле. Огромное поисковое пространство резко сужается; нужно рассмотреть всего несколько вариантов. В сущности, если отбросить поля сильных и слабых взаимодействий (в данной задаче они явно ведут к слишком сложным решениям), остаются два «законных» поля: электромагнитное и гравитационное. Учитывая ничтожную разницу в удельном весе щепок, следует сразу отбросить и гравитационное поле. Остается одно поле - электромагнитное. Поскольку магнитное поле не действует на кору и древесину, можно сразу ставить решающий эксперимент: как ведут себя щепки в электрическом поле? Оказывается, в электрическом поле частицы коры заряжаются отрицательно, а частицы древесины - положительно. Это позволяет построить сепаратор, обеспечивающий надежное разделение щепок.
Ну, а если бы щепки не электризовались? И в этом случае правило о постройке веполя сохраняет силу. Задача состоит в том, чтобы удалить один вид щепок. Следовательно, мы имеем право считать, что дано одно вещество, которое надо перемещать. Достроим веполь: добавим к этому веществу пару «вещество и поле». Например, до раздробления ствола и ветвей нанесем на кору ферромагнитные частицы, а затем - после дробления - используем для сепарации магнитное поле. Тут уже не требуются эксперименты: магнитное поле заведомо способно перемещать «омагниченную» кору.
Это решение можно изобразить так:

Дана смесь двух веществ, эти вещества сами не хотят разделяться. Решение состоит в достройке веполя, причем вместо В2 надо взять комплекс (В2 В3).
Возможность строить «комплексные» веполи намного расширяет область применения правила о достройке веполя.
Решение задачи 9 тоже можно рассматривать как построение комплексного веполя (в жидкость добавлен люминофор):
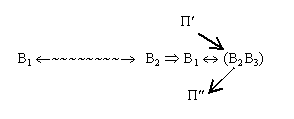
Здесь В1- холодильный агрегат; В2 - холодильная жидкость; В3 - люминофор; П- поле на входе (невидимое ультрафиолетовое излучение); П - поле на выходе (видимое излучение люминофора).
Правило достройки веполянепосредственно вытекает из самого определения понятия «веполь»: минимально полная техническая система заведомо эффективнее неполной системы, поэтому данные в задачах невепольные и неполные вепольные системы надо достраивать до полных веполей. Существуют и другие правила, относящиеся к построению и преобразованию вепольных систем. Использование этих правил лежит в основе вепольного анализа, составляющего один из важнейших разделов теории решения изобретательских задач. Приведем задачу.
Задача 13
Для очистки горячих газов от немагнитной пыли применяют фильтры, представляющие собой пакет, образованный многими слоями металлической ткани. Эти фильтры удовлетворительно задерживают пыль, но именно поэтому их потом трудно очищать. Приходится часто отключать фильтр и подолгу продувать его в обратном направлении, чтобы выбить пыль. Как быть?
Задача была решена так: в качестве фильтра стали использовать ферромагнитный порошок, помещенный между полюсами магнита и образующий пористую структуру. Отключая и включая магнитное поле, можно эффективно управлять фильтром. Поры фильтра могут быть маленькими (когда ловят пыль) и большими (когда идет очистка фильтра).
В условиях этой задачи уже описана вепольная система: есть В1 (пыль), есть В2 (пакет ткани), есть П (механическое поле сил, создаваемых потоком воздуха). Решение состоит в том, что:
- В2 раздробили в ферромагнитный порошок Вф;
- действие поля П направили не на В1 (изделие), а на Вф (инструмент);
- само поле стало не механическим (Пмех.) а магнитным (Пм).
Это можно записать так:
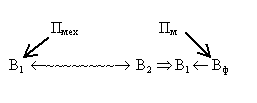
Сильное решение получено благодаря тому, что реализовано правило развития веполей:с увеличением степени дисперсности В2 (инструмента) эффективность веполя повышается; действие поля на В2 (инструмент) эффективнее действия на В1 (изделие); электрические (электромагнитные, магнитные) поля в веполях эффективнее неэлектрических (механических, тепловых и т. д.). Действительно, едва ли надо доказывать, что чем меньше частицы В2, тем более гибким может быть управление инструментом. Очевидно также, что выгоднее менять инструмент (это зависит от нас), а не изделие (зачастую являющееся природным объектом). Порознь целесообразность этих преобразований очевидна, но сила правила заключается в использовании системы преобразований.
Задача 13 на протяжении ряда лет применялась в качестве учебной на занятиях в общественных школах изобретательского творчества. Решая ее в начале учебы, слушатели ни разу не давали верного ответа. После изучения вепольного анализа задача без затруднений решалась практически всеми - научными работниками, инженерами, студентами, школьниками.
Вернемся теперь к задаче 6, которая также широко использовалась при обучении ТРИЗ. Вот запись, сделанная опытным конструктором в первый день занятий:
«1-й путь - построить необходимое количество площадок. Кажущаяся простота и получаемая исчерпываемость результатов, Однако на самом деле - дороговизна осуществления (строительство), сложность эксплуатации. Таким образом, этот путь нецелесообразен.
2-й путь - имитация только экстремальных условий: наиболее благоприятных для эксплуатации тракторов и наименее благоприятных, т. е. создание на уже имеющейся площадке двух участков с соответствующими качествами грунтов.
Принимаю 2-й путь и как вариант - площадку с тремя участками: наилучшие условия, наихудшие и средние».
Ход решения и полученный ответ весьма характерны для обычного конструкторского мышления. Сначала рассмотрен прямой путь - построим необходимое количество площадок. Здесь очевидное техническое противоречие: выигрыш в качестве испытаний и проигрыш в сложности и дороговизне строительства. Конструктор ищет компромисс, нет стремления преодолеть противоречие. Выдвигается 2-й вариант: ограничимся двумя-тремя площадками. Но и здесь имеется техническое противоречие: проигрыш в качестве испытаний (2 площадки вместо 200!) и выигрыш в простоте и дешевизне. И снова нет попытки преодолеть противоречие. Второй вариант представляется более приемлемым (дешевизна!) - и выбор сделан...
Ни один из решавших эту задачу конструкторов (в их числе были и весьма опытные изобретатели, имевшие по 30-50 авторских свидетельств) не смог дать удовлетворительного решения. После освоения ТРИЗ слушатели общественных школ (включая студентов и школьников) без затруднений решали эту задачу.
Типичная запись решения: «Много общего с задачей о магнитном фильтре. В1 - почва. Введем В2 в виде ферромагнитного порошка. Используем для достройки веполя магнитное поле Пм. Действуя полем, можно менять характеристики смеси В2 и В1.
Интересно сопоставить записи вепольных преобразований с записями химических реакций. Записывая химическую формулу вещества, мы отбрасываем множество свойств, присущих этому веществу. Химические формулы ничего не говорят, например, о магнитных и оптических свойствах вещества, его плотности и т. д. Отражены лишь свойства, принципиально важные для химии: состав и структура молекул. Точно так же, записывая вепольную формулу технической системы, мы отбрасываем все свойства этой системы, кроме тех, которые принципиально важны для ее развития: вепольная формула отражает вещественно-полевой состав и структуру системы.
Появление языка химических формул стало возможным только тогда, когда в химию прочно вошли такие фундаментальные понятия, как атом, молекула, молекулярный вес, и столь же фундаментальные законы взаимодействия и преобразования веществ. Так, уравнивая коэффициенты в записи химической реакции, мы пользуемся законом сохранения вещества, хотя не каждый раз об этом вспоминаем. В отличие от математических формул химические не позволяют открывать новые явления исходя только из самих формул и некоторых начальных постулатов. Химическая символика отражает лишь те знания, которые уже есть. В этом смысле вепольный анализ скорее похож на химический язык, чем на математический.
В некоторых изобретательских задачах требуется устранить вредное взаимодействие двух объектов. В таких случаях надо использовать правило разрушения веполей.Запишем формулу веполя в общем виде:
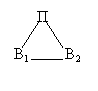
Разломать этот «треугольник» можно различными путями: удалить один из элементов, «оборвать» связи, заменить поле третьим веществом и т. д. Анализ большого числа задач на разрушение веполя показал, что самым эффективным решением оказывается введение третьего вещества, являющегося видоизменением одного из двух имеющихся.
Задача 14
В светокопировальной машине по стеклу протягивается калька с чертежом. К кальке прилегает светочувствительная бумага. Стекло (сложной формы) сломалось. Изготовление нового стекла требует значительного времени. Поэтому решили поставить оргстекло. Однако оказалось, что калька при движении электризуется и прилипает к стеклу. Как быть?
Инженеры, не знающие правила о разрушении веполя, обычно начинают перебирать варианты, связанные с удалением электрических зарядов. Но отводить заряды, не загораживая свет и не усложняя аппаратуру, очень трудно. С позиций вепольного анализа задача решается иначе. Между калькой и стеклом нужно ввести третье вещество, являющееся видоизмененной калькой или видоизмененным стеклом. Проще взять кальку - она дешевле. Поскольку эта калька должна находиться между стеклом и калькой с чертежом, нужно, чтобы вводимая калька была прозрачной и не задерживала свет. Значит, надо взять чистую кальку. Задача решена. Если протянуть чистую кальку по стеклу, она прилипнет. Калька с чертежом теперь пойдет не по стеклу, а по этой прилипшей кальке.
На этом примере хорошо видно, почему в правиле говорится, что вводимое третье вещество должно быть видоизменением одного из двух имеющихся. Если просто ввести какое-то третье вещество, могут возникнуть осложнения: «чужое» вещество будет плохо чувствовать себя в «посторонней» ему технической системе. Нужно, чтобы третье вещество было и чтобы его не было; тогда оно не сломается, не удорожит систему, не нарушит ее работу - словом, не привнесет никаких осложнений. Правило разрушения веполя, указывая на необходимость использования одного из имеющихся веществ (видоизменив его), подсказывает, как преодолеть противоречие «третье вещество есть и третьего вещества нет».
Правило достройки веполя тоже включает указания на преодоление противоречия. Поле должно действовать на вещество В1 , и поле не должно (не умеет) действовать на это вещество. Вводя вещество В2 и действуя через него на В1 , мы тем самым преодолеваем противоречие.
Таким образом, вепольный анализ, как и анализ по АРИЗ, построен на решении задач выявлением и устранением противоречий.
Часто приходится решать задачи, в которых противоречие возникает из-за того, что нужно сохранить имеющийся веполь и в то же время ввести новое взаимодействие. Такова, например, задача 8. По ее условиям уже дан веполь, причем «хороший», нужный: механическое поле Пмех через В2 (круг) действует на В1 (цилиндр). Невыгодно перестраивать этот веполь или ломать его, поскольку условия задачи не содержат никаких претензий к самому процессу шлифовки. Такие задачи решаются по правилу построения цепных веполей:
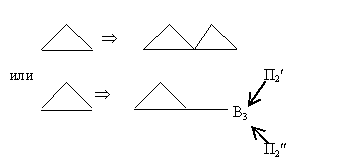
Как видно из формул, суть решения состоит в том, что В2 (инструмент) разворачивается в веполь, присоединенный к имеющемуся веполю. Иногда В3 в свою очередь разворачивается в веполь, продолжающий цепь.
В задачах на измерение и обнаружение веполь должен иметь на выходе поле, которое легко измерить и обнаружить. Поэтому при решении этих задач конечное звено цепи В1 - В2 - . . . обычно имеет такой вид:

Например, в задаче 9 люминофор преобразует параметры оптического поля (невидимое ультрафиолетовое излучение превращается в излучение видимое): П П. Не менее часто встречается преобразование одного поля в другое: П1 П2. Реже используется излучение, генерируемое самим веществом, входящим в веполь.
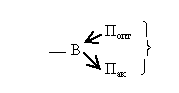
Если вещество должно превращать одно поле в другое (или менять параметры поля), можно сразу определить необходимый физический эффект, используя простое правило: название эффекта образуется соединением названий двух полей.Например:

(оптико-акустический эффект)
Задача 15
Из-за сдвига горных пород буровую колонну иногда намертво «прихватывает» в скважине. Чтобы ликвидировать прихват, внутрь буровой колонны на глубину прихвата опускают вибратор. Но как узнать, на какой глубине возник прихват?
Зона прихвата невелика - несколько десятков метров, а длина колонны - километры. Задача не решается непосредственным зондированием; не годится и предложение измерять деформацию трубы при определенном усилии (буровую колонну нельзя рассматривать как жесткий стержень, к тому же колонна испытывает неучитываемое трение о стенки скважины).
Вепольная схема решения задачи несложна:

где П1 - механическое поле на входе; П2 - поле на выходе; В1 - грунт; В2 - труба.
Обычно при решении таких задач целесообразно иметь на выходе легко поддающееся обнаружению и измерению электромагнитное поле. Веществом-преобразователем целесообразно взять стальную трубу, а не грунт, поскольку мы не знаем, какой именно грунт окажется в месте прихвата. свойства же стали нам известны. Сталь - ферромагнетик; логично прежде всего использовать именно магнитные свойства стали: эти свойства уже есть, их не надо придавать извне. Таким образом, определилось название нужного физического эффекта: механомагнитный ( в физике он называется магнитоупругим эффектом); магнитное поле ферромагнетика меняется в зависимости от напряжения, испытываемого ферромагнетиком.
Внутрь опускают прибор, ставящий через каждый метр магнитные метки. Затем лебедкой дергают трубу вверх. От ударной нагрузки все глотки выше места прихвата размагничиваются. Метки, расположенные ниже места прихвата, остаются без изменений. Это легко обнаруживается магнитометром.
Попробуйте решить несколько учебных задач. Это несложные задачи, для их решения достаточно знать изложенные выше простейшие правила вепольного анализа.
Решить учебную задачу означает: указать правило, на основе которого решается данная задача; дать конкретный ответ, основанный на этом правиле. Распространенная ошибка состоит в том, что пытаются угадать ответ, используя привычный метод проб и ошибок. Это все равно, что подойти к спортивному снаряду... и обойти его, став на то место, куда надо спрыгнуть со снаряда. Нетрудно обойти, скажем, турник, но и пользы от этого не будет. Весь смысл решения учебных задач в том, чтобы выработать навыки анализа, приобрести опыт, который потом пригодится при решении более трудных задач.
Задача 16
В формуле изобретения по а. с. № 527 280 сказано: «Манипулятор для сварочных работ, содержащий поворотный стол и узел поворота стола, выполненный в виде поплавкового механизма, шарнирно соединенного) через кронштейн со столом и помещенного в емкость с жидкостью, отличающийся тем, что с целью увеличения скорости перемещения стола в жидкость введена ферромагнитная взвесь, а емкость с жидкостью помещена в электромагнитную обмотку.» В чем суть этого изобретения с позиций вепольного анализа?
Задача 17
По трубопроводу, имеющему сложную форму (повороты), транспортируют пневмопотоком мелкие стальные шарики. В местах «поворота трубопровод сильно изнашивается изнутри из-за ударов транспортируемых шариков о стенки трубы. Пытались вводить защитные прокладки, но они быстро изнашивались.
Какое правило вепольного анализа следует применить при решении этой задачи? Каков ответ, основанный на этом правиле? Как быть, если по трубопроводу транспортируются не стальные, а, например, медные шарики?
Задача 18
Притирку одной поверхности к другой проверяют, нанося на одну поверхность тонкий слой краски и проверяя равномерность отпечатка на другой поверхности. Для поверхностей высших классов частоты необходимо применять очень тонкий слой краски (десятые доли микрона). Такой слой дает отпечатки, которые трудно различать. Ваше предложение? На каком правиле оно основано?
Задача 19
В а. с. № 253 753 описано следующее изобретение: «Электромагнитное перемешивающее устройство, включающее цилиндрический сосуд, статор, создающий электромагнитное поле, и ротор, о т л и ч а ю щ е е с я тем, что с целью интенсификации перемешивания ротор выполнен в виде эластичного перфорированного кольца. свободно размещенного в сосуде.» Итак, вместо жесткой лопастной мешалки использована эластичная «дырчатая» лента, приводимая во вращение электромагнитным полем. Спрогнозируйте следующее изобретение, развивающее то, что описано в а. с. 253 753. На каком правиле вепольного анализа основан ваш прогноз?
Задача 20
При изготовлении шлифовального инструмента мало уложить маленькие алмазные зерна, имеющие форму пирамидок, не как попало, а в определенном положении - острым углом вверх. Как это сделать?
Задача 21
На скоростных судах подводные крылья быстро разрушаются из-за кавитационного воздействия потока воды.
Каково ваше решение? На каком правиле вепольного анализа оно основано?
Задача 22
После изготовления некоторых железобетонных изделий с предварительно напряженной (растянутой) арматурой (стальными стержнями) возникает необходимость измерять напряжение (или фактическую величину удлинения) арматуры в готовом изделии. Трудность заключается в том, что арматура находится внутри готового и установленного изделия. Делать дырки или выводить концы арматуры наружу нельзя. Применить просвечивание с помощью ультразвука или рентгеновских лучей слишком сложно. Как быть?
