Страница:
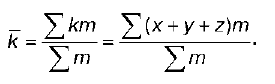
4) если все варианты (х) увеличить или уменьшить на какое-либо постоянное число (а), средняя (x) увеличится или уменьшится на то же самое число (y):
(х – а) = у;
x – a = y;
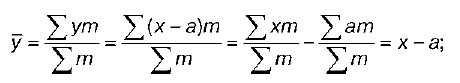
если
, 
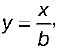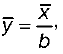то,
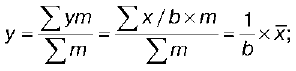
8. Средняя гармоническая, геометрическая, квадратическая, степенная
При решении задач расчет средней величины начинается с составления исходного отношения – логической словесной формулы средней. Она составляется на основе теоретического и логического анализа. Иногда среднюю арифметическую нельзя использовать. В этом случае в зависимости от ситуации применяется одна из трех форм средней.
Средняя гармоническая простая строится по формуле:
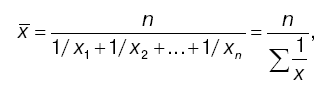где n — число единиц совокупности или число вариантов;
х — значения варьирующегося признака.
Средняя гармоническая простая используется для несгруппированных данных.
Средняя гармоническая взвешенная строится по формуле:
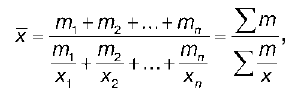где х — значения варьирующего признака;
m — веса;
n — число единиц совокупности. Среднюю гармоническую взвешенную используют для сгруппированных данных, т. е. когда каждое значение х повторяется различное число раз.
Средняя квадратическая простая строится по формуле:
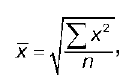где n — число единиц совокупности или число вариантов; х — значения варьирующегося признака.
Средняя квадратическая простая используется для несгруппированных данных.
Средняя квадратическая взвешенная строится по формуле:
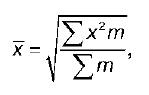где m – веса;
х – значения варьирующего признака.
Среднюю квадратическую взвешенную используют для сгруппированных данных.
Данные формулы используются редко, в специальных расчетах.
Средняя геометрическая простая строится по формуле:
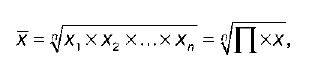где n – число единиц совокупности или число вариантов;
х – значения варьирующегося признака. Средняя геометрическая простая используется для несгруппированных данных.
Средняя геометрическая взвешенная строится по формуле:
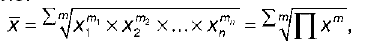где х – значения варьирующего признака;
m – веса;
n – число единиц совокупности или число вариантов. Различные формулы средних величин можно объединить в одной формуле – формуле степенной средней:
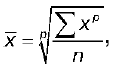где р – порядок средней.
Средняя гармоническая простая строится по формуле:
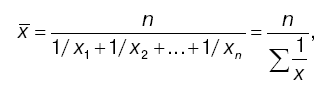
х — значения варьирующегося признака.
Средняя гармоническая простая используется для несгруппированных данных.
Средняя гармоническая взвешенная строится по формуле:
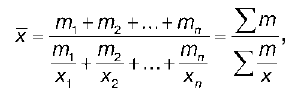
m — веса;
n — число единиц совокупности. Среднюю гармоническую взвешенную используют для сгруппированных данных, т. е. когда каждое значение х повторяется различное число раз.
Средняя квадратическая простая строится по формуле:
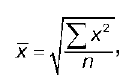
Средняя квадратическая простая используется для несгруппированных данных.
Средняя квадратическая взвешенная строится по формуле:
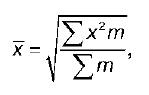
х – значения варьирующего признака.
Среднюю квадратическую взвешенную используют для сгруппированных данных.
Данные формулы используются редко, в специальных расчетах.
Средняя геометрическая простая строится по формуле:
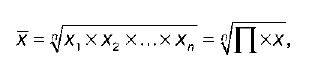
х – значения варьирующегося признака. Средняя геометрическая простая используется для несгруппированных данных.
Средняя геометрическая взвешенная строится по формуле:
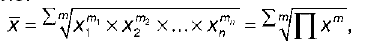
m – веса;
n – число единиц совокупности или число вариантов. Различные формулы средних величин можно объединить в одной формуле – формуле степенной средней:
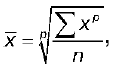
9. Медиана и мода. Асимметрия распределения
Медианой Ме называется варианта, которая делит ранжированный вариационный ряд на две равные части, из которых значение одной половины меньше медианы, а значения другой – больше медианы.
Медиана для несгруппированных данных при нечетном числе вариантов (n = 2k+ 1), определяется как Me = xk + 1, а при четном числе вариантов (n = 2k), медиана определяется по формуле:
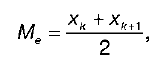Медиана для сгруппированных данных рассчитывается по формуле:
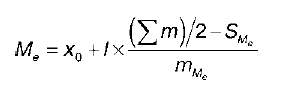где х0 – это нижняя граница медианного интервала;
/– величина медианного интервала;
em / 2 – полусумма всех частот;
SMe – накопленная частота, предшествующая медианному интервалу;
mМе – частота медианного интервала.
Медиана рассчитывают наряду со средней величиной или вместо нее, когда в ряду данных присутствуют открытые или неравные интервалы. Это не влияет на точность медианы, однако, влияет на точность величины.
Модой М0 называется варианта, которая имеет наибольшую частоту по сравнению с другими частотами. В дискретно-вариационном ряду мода – это та варианта, которой соответствует наибольшая частота.
В интервальном вариационном ряду с равными интервалами моду определяют по формуле:
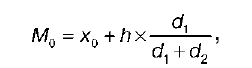где х0 – это нижняя граница модального интервала;
h – величина модального интервала;
d1 – разность между частотами модального и предмодального интервалов;
d2 – разность между частотами модального и послемодального интервалов.
Мода рассчитывается в тех случаях, когда невозможно или нецелесообразно рассчитывать среднюю величину по обычным формулам.
Асимметрией распределения называется несоразмерность, т. е. нарушение соответствия в расположении частей одного целого относительно средней линии или центра. На графике асимметрия распределения определяется как вытянутость одной из ветвей распределения. Асимметрия распределения возникает в связи с различной частотой появления вариант больших или меньших моды (т. к. мода соответствует вершине распределения) под влиянием преобладающего действия определенных факторов. Таким образом, наличие асимметрии говорит о неустойчивости распределения совокупности в связи с преобладающим воздействием какой-либо группы факторов.
Асимметрия распределения легко обнаруживается и измеряется на основе разницы между средней величиной и модой. В умеренно асимметричных распределениях мода и средняя образуют интервал, в пределах которого находится медиана. Если разделить этот интервал на 3, то медиана отстоит от моды на 2/3, а от средней – на 1/3.
Для измерения асимметрии рядов распределения применяется эмпирический коэффициент асимметрии:
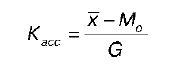где x— – простая средняя;
Мо– мода;
G – среднеквадратическое отклонение.
Медиана для несгруппированных данных при нечетном числе вариантов (n = 2k+ 1), определяется как Me = xk + 1, а при четном числе вариантов (n = 2k), медиана определяется по формуле:
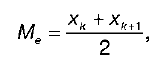
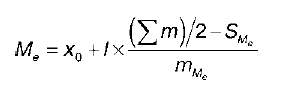
/– величина медианного интервала;
em / 2 – полусумма всех частот;
SMe – накопленная частота, предшествующая медианному интервалу;
mМе – частота медианного интервала.
Медиана рассчитывают наряду со средней величиной или вместо нее, когда в ряду данных присутствуют открытые или неравные интервалы. Это не влияет на точность медианы, однако, влияет на точность величины.
Модой М0 называется варианта, которая имеет наибольшую частоту по сравнению с другими частотами. В дискретно-вариационном ряду мода – это та варианта, которой соответствует наибольшая частота.
В интервальном вариационном ряду с равными интервалами моду определяют по формуле:
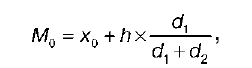
h – величина модального интервала;
d1 – разность между частотами модального и предмодального интервалов;
d2 – разность между частотами модального и послемодального интервалов.
Мода рассчитывается в тех случаях, когда невозможно или нецелесообразно рассчитывать среднюю величину по обычным формулам.
Асимметрией распределения называется несоразмерность, т. е. нарушение соответствия в расположении частей одного целого относительно средней линии или центра. На графике асимметрия распределения определяется как вытянутость одной из ветвей распределения. Асимметрия распределения возникает в связи с различной частотой появления вариант больших или меньших моды (т. к. мода соответствует вершине распределения) под влиянием преобладающего действия определенных факторов. Таким образом, наличие асимметрии говорит о неустойчивости распределения совокупности в связи с преобладающим воздействием какой-либо группы факторов.
Асимметрия распределения легко обнаруживается и измеряется на основе разницы между средней величиной и модой. В умеренно асимметричных распределениях мода и средняя образуют интервал, в пределах которого находится медиана. Если разделить этот интервал на 3, то медиана отстоит от моды на 2/3, а от средней – на 1/3.
Для измерения асимметрии рядов распределения применяется эмпирический коэффициент асимметрии:
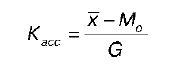
Мо– мода;
G – среднеквадратическое отклонение.
10. Абсолютные показатели вариации
К абсолютным показателям вариации относятся:
1) вариационный размах (R);
2) среднее абсолютное (линейное) отклонение (в);
3) дисперсия (G2);
4) среднеквадратическое отклонение (G).
Вариационный размах R — это разность между
наибольшей и наименьшей вариантами вариационного ряда:
R =хmax – хmin
Вариационный размах является наиболее простой характеристикой рассеяния вариационного ряда. Недостатки данного показателя:
1) неточно характеризует колеблемость, потому что зависит только от двух значений признака;
2) зависит от объема совокупности, т. е. с увеличением объема совокупности увеличивается вероятность размера вариационного размаха.
Среднее абсолютное отклонение в — это вели чина, которая рассчитывается как среднее арифметическое абсолютных отклонений в данной совокупности.
Различают простое и взвешенное среднее абсолютное отклонение.
Среднее абсолютное простое отклонение рассчитывается по формуле:
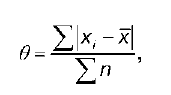где – n– объем совокупности;
x – выборочное среднее.
Среднее абсолютное взвешенное отклонение рассчитывается по формуле:
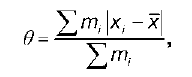где x – выборочное среднее;
m – веса.
Недостатки данного показателя:
1) оторванность от других показателей. Это объясняется тем, что при построении показателя используется искусственный подход, т. е. отклонение берется по модулю (положительное);
2) недостаточная реакция на слабые различия в степени вариации.
Дисперсия – это среднее арифметическое квадратов отклонения наблюдаемых значений признака от – их среднего значения x.
Если значения признака, полученные в результате выборочного наблюдения, не группировать и не представлять в виде вариационного ряда, то для вычисления дисперсии используют формулу:
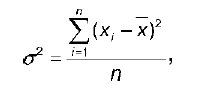где n – объем выборки.
Среднеквадратическое отклонение – это квадратный корень из среднего арифметического квадратов отклонения наблюдаемых значений признака от – их среднего значения x, или квадратный корень из дисперсии.
Среднеквадратическое отклонение для несгруппированных данных рассчитывается по формуле:
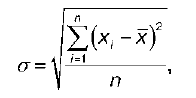
1) вариационный размах (R);
2) среднее абсолютное (линейное) отклонение (в);
3) дисперсия (G2);
4) среднеквадратическое отклонение (G).
Вариационный размах R — это разность между
наибольшей и наименьшей вариантами вариационного ряда:
R =хmax – хmin
Вариационный размах является наиболее простой характеристикой рассеяния вариационного ряда. Недостатки данного показателя:
1) неточно характеризует колеблемость, потому что зависит только от двух значений признака;
2) зависит от объема совокупности, т. е. с увеличением объема совокупности увеличивается вероятность размера вариационного размаха.
Среднее абсолютное отклонение в — это вели чина, которая рассчитывается как среднее арифметическое абсолютных отклонений в данной совокупности.
Различают простое и взвешенное среднее абсолютное отклонение.
Среднее абсолютное простое отклонение рассчитывается по формуле:
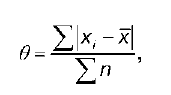
x – выборочное среднее.
Среднее абсолютное взвешенное отклонение рассчитывается по формуле:
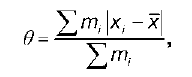
m – веса.
Недостатки данного показателя:
1) оторванность от других показателей. Это объясняется тем, что при построении показателя используется искусственный подход, т. е. отклонение берется по модулю (положительное);
2) недостаточная реакция на слабые различия в степени вариации.
Дисперсия – это среднее арифметическое квадратов отклонения наблюдаемых значений признака от – их среднего значения x.
Если значения признака, полученные в результате выборочного наблюдения, не группировать и не представлять в виде вариационного ряда, то для вычисления дисперсии используют формулу:
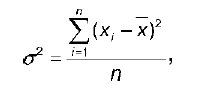
Среднеквадратическое отклонение – это квадратный корень из среднего арифметического квадратов отклонения наблюдаемых значений признака от – их среднего значения x, или квадратный корень из дисперсии.
Среднеквадратическое отклонение для несгруппированных данных рассчитывается по формуле:
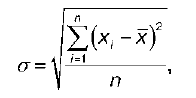
11. Относительные показатели вариации. Правило сложения дисперсий
Основной недостаток абсолютных показателей заключается в том, что они не позволяют сопоставлять между собой средние отклонения различных показателей. Для сопоставления необходимы относительные показатели, характеризующие относительную колеблемость. К ним относятся:
1) коэффициент вариации. Рассчитывается как процентное отношение среднего квадратического отклонения к средней арифметической величине:
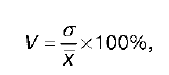2) коэффициент колеблемости. Рассчитывается как процентное отношение среднего абсолютного (линейного) отклонения к средней арифметической величине:
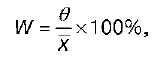3) коэффициент асциляции. Рассчитывается как отношение вариационного размаха к средней арифметической величине:
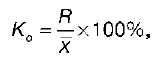С помощью относительных показателей вариации решаются следующие задачи:
1) сравнение степени вариации в процентах различных признаков в одной и той же совокупности;
2) сравнение степени вариации одного и того же признака в различных совокупностях.
Правило или теорему сложения дисперсий сформулировал и доказал В. Лексис. В связи с тем что некоторые совокупности делятся на группы, помимо общей дисперсии, могут быть рассчитаны также дисперсии для каждой отдельной группы. Кроме этого, можно рассчитать среднюю из групповых дисперсий и межгрупповую дисперсию. В. Лексис доказал, что между данными показателями существует связь.
Теорема. Если совокупность состоит из нескольких групп, то общая дисперсия равна сумме внутри-групповой и межгрупповой дисперсий:
где σобщ – общая дисперсия:
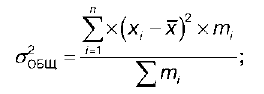σвнгр – внутригрупповая дисперсия:
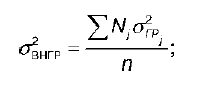σгр – групповая дисперсия:
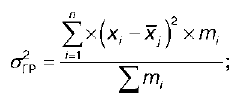σмегр – межгрупповая дисперсия:
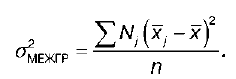Если межгрупповая дисперсия равна нулю, то общая дисперсия равна средней из групповых дисперсий.
С помощью теоремы сложения дисперсий решаются следующие задачи:
1) исследование зависимостей между признаками;
2) оценка тесноты связи между признаками;
3) оценка точности типичной выборки.
1) коэффициент вариации. Рассчитывается как процентное отношение среднего квадратического отклонения к средней арифметической величине:
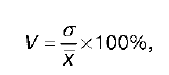
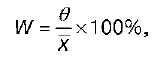
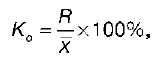
1) сравнение степени вариации в процентах различных признаков в одной и той же совокупности;
2) сравнение степени вариации одного и того же признака в различных совокупностях.
Правило или теорему сложения дисперсий сформулировал и доказал В. Лексис. В связи с тем что некоторые совокупности делятся на группы, помимо общей дисперсии, могут быть рассчитаны также дисперсии для каждой отдельной группы. Кроме этого, можно рассчитать среднюю из групповых дисперсий и межгрупповую дисперсию. В. Лексис доказал, что между данными показателями существует связь.
Теорема. Если совокупность состоит из нескольких групп, то общая дисперсия равна сумме внутри-групповой и межгрупповой дисперсий:
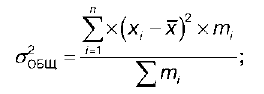
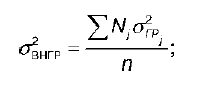
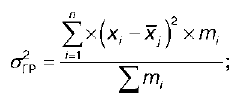
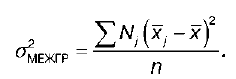
С помощью теоремы сложения дисперсий решаются следующие задачи:
1) исследование зависимостей между признаками;
2) оценка тесноты связи между признаками;
3) оценка точности типичной выборки.
12. Понятие индексов. Классификация индексов
Индексный метод является одним из важнейших методов в статистике. Индексы относятся к числу обобщающих показателей. Следует различать понятие индекса в широком и узком смысле.
В широком смысле индекс – это относительная величина, характеризующая изменения явлений во времени (динамику). Но подобные относительные величины могут быть рассчитаны лишь для простых явлений или однородных совокупностей, единицы которых могут быть суммированы. Такие совокупности называются соизмеримыми.
Индекс в узком смысле слова – это обобщающий показатель сравнения двух совокупностей, состоящий из элементов, непосредственно не поддающихся суммированию.
С помощью индексов решаются две основные задачи:
1) синтетическая задача – обобщение, синтез дина мики отдельных элементов в сложные явления в од ном обобщающем показателе (сводном индексе);
2) аналитическая задача – анализ влияния изменения отдельных факторов на изменение сложного явления.
Классификация индексов по различным при знакам:
1) по степени охвата совокупности выделяют индивидуальные индексы (элементарные) и общие индексы (сводные или сложные);
2) по форме построения выделяют агрегатные, средневзвешенные (арифметические, гармонические) индексы;
3) по применяемым весам выделяют индивидуальные индексы с постоянными и переменными весами;
4) по состоянию явления выделяют индексы переменного состава, постоянного состава, структурных сдвигов;
5) по содержанию индексируемых величин выделяют индексы цен, физического объема товарооборота, себестоимости, трудоемкости и т. д.;
6) по базе сравнения выделяют динамические (базисные, цепные) индексы, индексы выполнения плана, планового задания, территориального сравнения.
Классификация показателей при построении индексов:
1) количественные показатели, характеризующие объем того или иного явления.
К ним относятся:
а) q – физический объем товарооборота (количество проданной продукции в натуральном выражении);
б) q – физический объем продукции (количество произведенной продукции на предприятии);
в) t – число рабочих;
г) h – посевная площадь и др. Количественные показатели получают путем подсчета;
2) качественные показатели характеризуют уровень явления в расчете на ту или иную единицу совокупности.
К ним относятся:
а) р – цена единицы товара (себестоимость);
б) z – себестоимость единицы продукции (затраты на производство единицы продукции);
в) t – трудоемкость единицы продукции (затраты рабочего времени на производство единицы продукции);
г) w – производительность труда (выработка продукции в единицу времени);
д) у – урожайность;
3) суммарные (итоговые, количественно-качественные) показатели, характеризующие суммарные, общие размеры исследуемого явления.
К ним относятся:
а) S – товарооборот:
S = p × q;
б) Т – затраты рабочего времени (труда) на производство всей продукции:
Т = t × q;
в) С – затраты на производство продукции:
С = z × q;
г) V – валовой сбор с/х культур по видам:
V = y × n.
В широком смысле индекс – это относительная величина, характеризующая изменения явлений во времени (динамику). Но подобные относительные величины могут быть рассчитаны лишь для простых явлений или однородных совокупностей, единицы которых могут быть суммированы. Такие совокупности называются соизмеримыми.
Индекс в узком смысле слова – это обобщающий показатель сравнения двух совокупностей, состоящий из элементов, непосредственно не поддающихся суммированию.
С помощью индексов решаются две основные задачи:
1) синтетическая задача – обобщение, синтез дина мики отдельных элементов в сложные явления в од ном обобщающем показателе (сводном индексе);
2) аналитическая задача – анализ влияния изменения отдельных факторов на изменение сложного явления.
Классификация индексов по различным при знакам:
1) по степени охвата совокупности выделяют индивидуальные индексы (элементарные) и общие индексы (сводные или сложные);
2) по форме построения выделяют агрегатные, средневзвешенные (арифметические, гармонические) индексы;
3) по применяемым весам выделяют индивидуальные индексы с постоянными и переменными весами;
4) по состоянию явления выделяют индексы переменного состава, постоянного состава, структурных сдвигов;
5) по содержанию индексируемых величин выделяют индексы цен, физического объема товарооборота, себестоимости, трудоемкости и т. д.;
6) по базе сравнения выделяют динамические (базисные, цепные) индексы, индексы выполнения плана, планового задания, территориального сравнения.
Классификация показателей при построении индексов:
1) количественные показатели, характеризующие объем того или иного явления.
К ним относятся:
а) q – физический объем товарооборота (количество проданной продукции в натуральном выражении);
б) q – физический объем продукции (количество произведенной продукции на предприятии);
в) t – число рабочих;
г) h – посевная площадь и др. Количественные показатели получают путем подсчета;
2) качественные показатели характеризуют уровень явления в расчете на ту или иную единицу совокупности.
К ним относятся:
а) р – цена единицы товара (себестоимость);
б) z – себестоимость единицы продукции (затраты на производство единицы продукции);
в) t – трудоемкость единицы продукции (затраты рабочего времени на производство единицы продукции);
г) w – производительность труда (выработка продукции в единицу времени);
д) у – урожайность;
3) суммарные (итоговые, количественно-качественные) показатели, характеризующие суммарные, общие размеры исследуемого явления.
К ним относятся:
а) S – товарооборот:
S = p × q;
б) Т – затраты рабочего времени (труда) на производство всей продукции:
Т = t × q;
в) С – затраты на производство продукции:
С = z × q;
г) V – валовой сбор с/х культур по видам:
V = y × n.
13. Индивидуальные индексы
Индивидуальный индекс – это отношение величины показателя в отчетном или текущем периоде к величине того же показателя в базисном периоде:
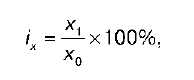где i – индивидуальный индекс;
х — любой индексируемый показатель (качественный, количественный, качественно-количественный);
1 – отчетный или текущий период;
х1 – сравниваемый уровень;
0 – базисный период;
х0 – базисный уровень.
Индивидуальные индексы строятся для соизмеримых однородных совокупностей и чаще всего выражаются в процентах.
Индивидуальный индекс характеризует изменение объема или уровня исследуемого показателя в отчетном периоде по сравнению с базисным. Если ix < 100 %, то уровень индексируемого показателя снизился по сравнению с базисным периодом. Если ix > 100 %, то уровень индексируемого показателя увеличился по сравнению с базисным периодом. Если ix = 100 %, то уровень индексируемого показателя остался прежним.
Примеры индивидуальных индексов:
1) индивидуальный индекс цен:
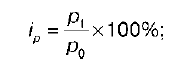2) индивидуальный индекс физического объема товарооборота:
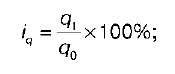3) индивидуальный индекс товарооборота:
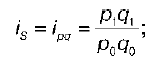В связи с тем, что индивидуальные индексы используются для изучения динамики индексируемого показателя за короткие и более продолжительные периоды, возникает необходимость исчисления системы последовательных индексов. Различают два метода последовательного индексирования.
1. Метод постоянной (фиксированной) базы.
Согласно данному методу один из периодов, находящихся в знаменателе, принимается в качестве базисного, а остальные, находящиеся в числителе, последовательно меняются.
Предположим, что имеются данные р0, р1, …, рn-1, pn. Тогда система индивидуальных индексов с постоянной базой может быть записана следующим образом:
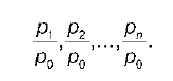Это система базисных индексов. Индексы этой системы называются базисными и показывают, как изменяется цена по мере увеличения длительности рассматриваемого периода по отношению к одной базе.
2. Метод меняющейся (переменной) базы.
Согласно данному методу каждая индексная система исчисляется на основе своей базы по определенному порядку: в качестве базы индекса принимается предшествующий i-ый период.
Система индексов меняющейся базы может быть записана следующим образом:
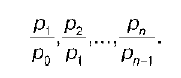Эта система цепных индексов. Индексы этой системы называются цепными, они характеризуют цену от одного периода к другому.
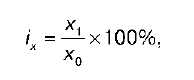
х — любой индексируемый показатель (качественный, количественный, качественно-количественный);
1 – отчетный или текущий период;
х1 – сравниваемый уровень;
0 – базисный период;
х0 – базисный уровень.
Индивидуальные индексы строятся для соизмеримых однородных совокупностей и чаще всего выражаются в процентах.
Индивидуальный индекс характеризует изменение объема или уровня исследуемого показателя в отчетном периоде по сравнению с базисным. Если ix < 100 %, то уровень индексируемого показателя снизился по сравнению с базисным периодом. Если ix > 100 %, то уровень индексируемого показателя увеличился по сравнению с базисным периодом. Если ix = 100 %, то уровень индексируемого показателя остался прежним.
Примеры индивидуальных индексов:
1) индивидуальный индекс цен:
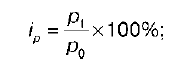
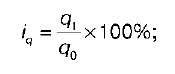
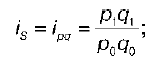
1. Метод постоянной (фиксированной) базы.
Согласно данному методу один из периодов, находящихся в знаменателе, принимается в качестве базисного, а остальные, находящиеся в числителе, последовательно меняются.
Предположим, что имеются данные р0, р1, …, рn-1, pn. Тогда система индивидуальных индексов с постоянной базой может быть записана следующим образом:
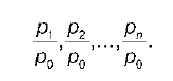
2. Метод меняющейся (переменной) базы.
Согласно данному методу каждая индексная система исчисляется на основе своей базы по определенному порядку: в качестве базы индекса принимается предшествующий i-ый период.
Система индексов меняющейся базы может быть записана следующим образом:
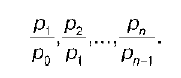
14. Агрегатная форма общего индекса. Правила взвешивания общих индексов
В связи с тем что статистика часто имеет дело с несоизмеримыми совокупностями, для изучения динамики таких совокупностей используют общие индексы или собственно индексы. Они строятся в агрегатной форме и в средней форме.
Агрегатная форма общего индекса качественных показателей.
Рассмотрим агрегатную форму общего индекса цены. Первоначально эти индексы строились по формулам, предложенным учеными Г. Дюто и П. Карли. Однако эти формулы обладали рядом недостатков, поэтому позднее были предложены другие формулы, например формула Ласпейраса:
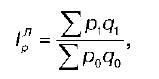где р — индексируемая величина (цена);
q — количество проданных товаров в натуральном выражении (веса).
В настоящее время именно эта формула используется при изучении динамики цен. Этот индекс характеризует изменение цен в среднем по совокупности товаров в отчетном периоде по сравнению с базисным.
Общий индекс цены можно также определить по формуле Пааше:
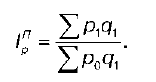Эта формула длительное время использовалась в СССР при изучении динамики цен. Но с переходом к рыночной экономике стала существенно изменяться структура потребительских расходов населения, т. е. на динамику цен существенное влияние стало оказывать изменение параметра q.
Правило взвешивания общих индексов качественных показателей.
Общий индекс качественных показателей в агрегатной форме взвешивается по весам отчетного периода. Например, общий индекс себестоимости в агрегатной форме:
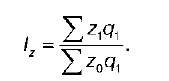Общий индекс урожайности в агрегатной форме:
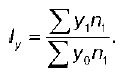Агрегатная форма общих индексов количественных показателей. Рассмотрим агрегатную форму общего индекса физического объема товарооборота (q). Iq может быть построен по формуле Ласпейраса, которая является основной:
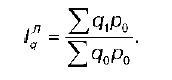Данный индекс характеризует изменение физического объема товарооборота в среднем по совокупности товаров. Возможно также построение Iq по формуле Пааше:
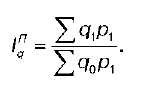Правило взвешивания общего индекса количественных показателей. Данные индексы взвешиваются по весам базисного периода.
Например, общий индекс посевной площади в агрегатной форме:
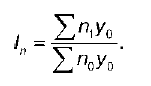
Агрегатная форма общего индекса качественных показателей.
Рассмотрим агрегатную форму общего индекса цены. Первоначально эти индексы строились по формулам, предложенным учеными Г. Дюто и П. Карли. Однако эти формулы обладали рядом недостатков, поэтому позднее были предложены другие формулы, например формула Ласпейраса:
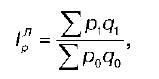
q — количество проданных товаров в натуральном выражении (веса).
В настоящее время именно эта формула используется при изучении динамики цен. Этот индекс характеризует изменение цен в среднем по совокупности товаров в отчетном периоде по сравнению с базисным.
Общий индекс цены можно также определить по формуле Пааше:
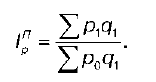
Правило взвешивания общих индексов качественных показателей.
Общий индекс качественных показателей в агрегатной форме взвешивается по весам отчетного периода. Например, общий индекс себестоимости в агрегатной форме:
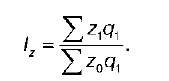
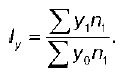
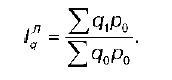
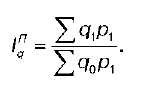
Например, общий индекс посевной площади в агрегатной форме:
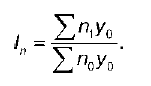
15. Средняя арифметическая форма общего индекса. Средняя гармоническая форма общего индекса
Средняя арифметическая форма общего индекса является преобразованием от агрегатной формы.
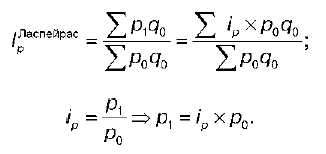Средняя арифметическая форма общего индекса качественных показателей (на примере показателя цены) по схеме Ласпейраса:
Данную формулу удобнее использовать при расчетах, потому что для расчета можно использовать индивидуальный индекс цены ip и произведение p0q0.
Средняя арифметическая форма общего индекса качественных показателей (цены) по схеме Пааше:
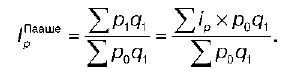Средняя арифметическая форма общего индекса количественных показателей (на примере физического объема товарооборота):
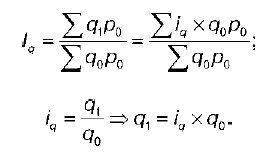Средняя гармоническая форма общих индексов также является преобразованием агрегатной формы.
Средняя гармоническая форма общего индекса качественных показателей (на примере показателя цены) по схеме Ласпейраса:
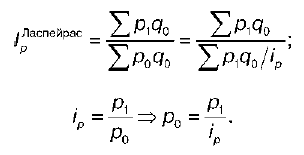Однако эта формула неудобна на практике. Поэтому при расчетах используется средняя гармоническая форма общего индекса качественных показателей (цены) по схеме Пааше:
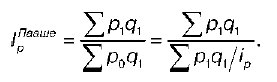Средняя гармоническая форма общего индекса количественных показателей:
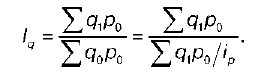Индексы количественно-качественных показателей используют в агрегатной форме, но они могут быть преобразованы в средние формы, называемые неявными.
Например, средняя арифметическая форма индекса товарооборота:
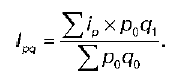Средняя геометрическая форма индекса товарооборота:
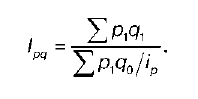
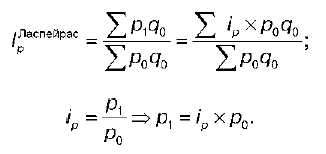
Данную формулу удобнее использовать при расчетах, потому что для расчета можно использовать индивидуальный индекс цены ip и произведение p0q0.
Средняя арифметическая форма общего индекса качественных показателей (цены) по схеме Пааше:
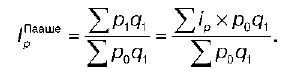
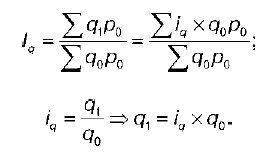
Средняя гармоническая форма общего индекса качественных показателей (на примере показателя цены) по схеме Ласпейраса:
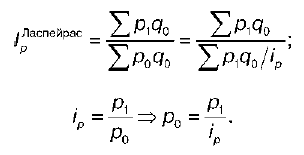
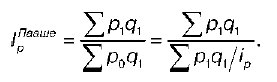
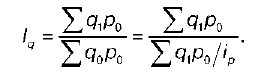
Например, средняя арифметическая форма индекса товарооборота:
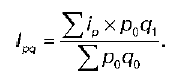
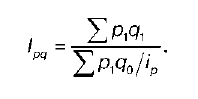
16. Индексный метод анализа динамики среднего уровня
Индексы качественных показателей – индексы средней арифметической величины, поэтому изменение среднего уровня качественного показателя зависит от изменения:
1) отдельных уровней показателей;
2) частей совокупности или структуры совокупности. Для определения того, в какой мере происходит изменение среднего уровня и каково влияние каждого фактора, используют систему взаимосвязанных индексов.
Индекс переменного состава – это отношение среднего уровня какого-либо показателя в отчетном периоде к среднему уровню его в базисном периоде:
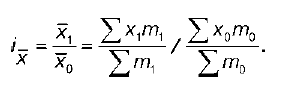Эту формулу используют, если веса (часть совокупности) – абсолютные показатели. Если же веса – относительные показатели (доля, удельный вес), то формула индекса переменного состава такова:
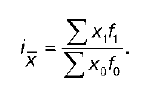Он показывает, в какой мере произошло изменение среднего уровня показателя за счет влияния:
1) изменения индексируемого показателя (х);
2) изменения частей совокупности (m) или доли (удельного веса – f).
Индекс постоянного состава позволяет устранить влияние одного из факторов и оценить степень влияния другого фактора.
Общий вид формулы индекса постоянного состава:
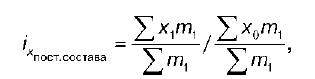или если веса – относительные показатели, то;
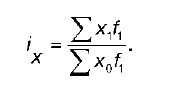Индекс постоянного состава показывает изменение в среднем уровня какого-либо показателя х за счет изменения усредняемых уровней показателя. Таким способом устраняется влияние второго фактора и показывается, в какой степени изменение х влияет на изменение x.
Индекс структурных сдвигов позволяет оценить степень влияния m или f, при условии элиминирования влияния другого фактора, т. е.
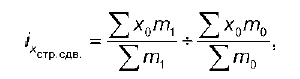или, если веса – относительные показатели, то:
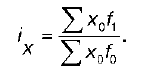Индекс структурных сдвигов показывает, в какой мере влияет изменение состава или структуры совокупности на изменение среднего уровня, тем самым отвечая на вопрос, как изменяется средний уровень за счет m (или f).
Формула индекса переменного состава может быть конкретизирована к той или иной задаче. Например, индекс цен структурных сдвигов:
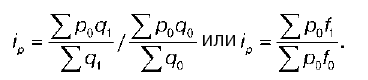Между рассмотренными индексами существует взаимосвязь: индекс переменного состава равен произведению индексов постоянного состава и структурных сдвигов.
1) отдельных уровней показателей;
2) частей совокупности или структуры совокупности. Для определения того, в какой мере происходит изменение среднего уровня и каково влияние каждого фактора, используют систему взаимосвязанных индексов.
Индекс переменного состава – это отношение среднего уровня какого-либо показателя в отчетном периоде к среднему уровню его в базисном периоде:
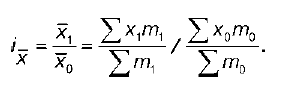
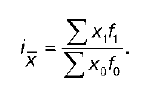
1) изменения индексируемого показателя (х);
2) изменения частей совокупности (m) или доли (удельного веса – f).
Индекс постоянного состава позволяет устранить влияние одного из факторов и оценить степень влияния другого фактора.
Общий вид формулы индекса постоянного состава:
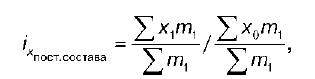
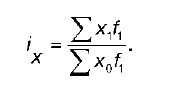
Индекс структурных сдвигов позволяет оценить степень влияния m или f, при условии элиминирования влияния другого фактора, т. е.
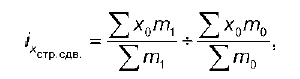
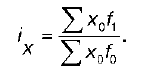
Формула индекса переменного состава может быть конкретизирована к той или иной задаче. Например, индекс цен структурных сдвигов:
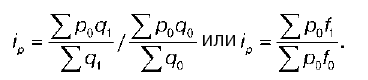
17. Динамические ряды. виды, элементы и компоненты динамических рядов. Средняя хронологическая
Динамический ряд – это ряд чисел, характеризующих изменение явления во времени.
Элементы динамического ряда:
1) время (период времени) – интервал или момент (хронологическая дата);
2) уровень ряда, т. е. показатель количества значе ний за периоды времени или какой-либо даты. Уровни ряда обозначаются как у0, у1, …, уn. Разли чают крайние уровни ряда (первый и последний) и промежуточные уровни.
Динамические ряды классифицируются по различным признакам в зависимости от способов получения.
Первичные динамические ряды – это ряды, в которых уровни представлены исходными цифровыми данными, полученными в результате статистического наблюдения. Первичные ряды всегда являются количественными (объем продукции за каждый год).
Вторичные (производные) динамические ряды – это ряды, в которых уровни представлены в виде производных величин (средних или относительных показателей), например динамический ряд показателя средней урожайности.
В зависимости от признака времени выделяют интервальные и моментные динамические ряды.
Моментный динамический ряд – это ряд, уровни которого фиксируют значение изучаемого показателя на определенный момент времени.
Интервальный динамический ряд – это ряд, уровни которого характеризуют значение показателя за определенный период времени.
Методы вычисления среднего уровня динамического ряда (средней хронологической).
С течением времени уровни динамического ряда изменяются, и возникает необходимость обобщающей характеристики развития явления во времени. Эта задача решается с помощью средней величины – среднего уровня ряда, который называется для динамических рядов средней хронологической. Ее рассчитывают для интервальных и моментных рядов.
Элементы динамического ряда:
1) время (период времени) – интервал или момент (хронологическая дата);
2) уровень ряда, т. е. показатель количества значе ний за периоды времени или какой-либо даты. Уровни ряда обозначаются как у0, у1, …, уn. Разли чают крайние уровни ряда (первый и последний) и промежуточные уровни.
Динамические ряды классифицируются по различным признакам в зависимости от способов получения.
Первичные динамические ряды – это ряды, в которых уровни представлены исходными цифровыми данными, полученными в результате статистического наблюдения. Первичные ряды всегда являются количественными (объем продукции за каждый год).
Вторичные (производные) динамические ряды – это ряды, в которых уровни представлены в виде производных величин (средних или относительных показателей), например динамический ряд показателя средней урожайности.
В зависимости от признака времени выделяют интервальные и моментные динамические ряды.
Моментный динамический ряд – это ряд, уровни которого фиксируют значение изучаемого показателя на определенный момент времени.
Интервальный динамический ряд – это ряд, уровни которого характеризуют значение показателя за определенный период времени.
Методы вычисления среднего уровня динамического ряда (средней хронологической).
С течением времени уровни динамического ряда изменяются, и возникает необходимость обобщающей характеристики развития явления во времени. Эта задача решается с помощью средней величины – среднего уровня ряда, который называется для динамических рядов средней хронологической. Ее рассчитывают для интервальных и моментных рядов.