Страница:
Для интервального ряда средняя хронологическая рассчитывается по формуле:
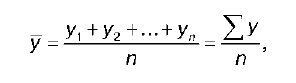где n – число уровней динамического ряда.
Для моментного ряда средняя хронологическая рассчитывается по формуле:
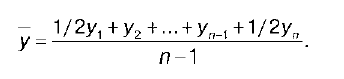При изучении динамических рядов выделяют две основные задачи:
1) характеристика структуры ряда;
2) прогнозирование будущих уровней временного ряда на основании прошлых и настоящих уровней.
Данные, представленные в виде динамических рядов, могут содержать два вида компонентов:
1) систематическая составляющая;
2) случайная составляющая.
Систематическая составляющая – это результат воздействия постоянно действующих факторов.
Выделяют три основных систематических компоненты динамического ряда:
1) тренд (тенденция) – это систематическая линейная или нелинейная компонента, изменяющаяся во времени;
2) сезонность – это периодические колебания уровней временного ряда внутри года;
3) цикличность – это периодические колебания, вы ходящие за рамки одного года. Промежуток времени между двумя соседними вершинами или впадинами в масштабах года считается длиной цикла. Все три систематические составляющие могут одновременно присутствовать в динамическом ряду.
18. Сопоставимость уровней динамического ряда. Абсолютные показатели динамики
19. Относительные показатели динамики. Абсолютное значение однопроцентного прироста
20. Методы выявления основных тенденций динамического ряда
21. Выборочное наблюдение. Ошибки выборки
22. Способы отбора данных. Способы распространения данных выборки на всю генеральную совокупность
23. Функциональная, статистическая и корреляционная зависимости. Определение регрессии
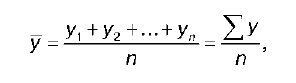
Для моментного ряда средняя хронологическая рассчитывается по формуле:
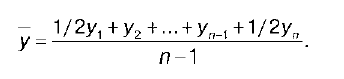
1) характеристика структуры ряда;
2) прогнозирование будущих уровней временного ряда на основании прошлых и настоящих уровней.
Данные, представленные в виде динамических рядов, могут содержать два вида компонентов:
1) систематическая составляющая;
2) случайная составляющая.
Систематическая составляющая – это результат воздействия постоянно действующих факторов.
Выделяют три основных систематических компоненты динамического ряда:
1) тренд (тенденция) – это систематическая линейная или нелинейная компонента, изменяющаяся во времени;
2) сезонность – это периодические колебания уровней временного ряда внутри года;
3) цикличность – это периодические колебания, вы ходящие за рамки одного года. Промежуток времени между двумя соседними вершинами или впадинами в масштабах года считается длиной цикла. Все три систематические составляющие могут одновременно присутствовать в динамическом ряду.
18. Сопоставимость уровней динамического ряда. Абсолютные показатели динамики
Сопоставимость – это сравнимость показателей во времени. Несопоставимость данных во времени может быть вызвана следующими причинами:
1) территориальными изменениями;
2) изменением единиц счета;
3) изменением методологии расчетов;
4) изменением круга охвата объектов.
В связи с тем что экономические явления изменяются во времени, для характеристики скорости и интенсивности изменения этих явлений используются абсолютные и относительные показатели динамики.
К абсолютным показателям динамики относятся:
1) абсолютный прирост;
2) средний абсолютный прирост.
Эти показатели рассчитываются за месяц, квартал, год. Они характеризуют скорость изменения уровней динамического ряда в единицу времени. Единицы измерения абсолютных показателей динамики совпадают с единицами измерения уровней динамического ряда. Абсолютные показатели динамики отвечают на вопрос, насколько в абсолютном выражении изменился уровень динамического ряда за прошедший период.
Абсолютный прирост – это разность между последующим и предшествующим уровнями динамического ряда. В тех случаях, когда разность получается со знаком минус, показатель называется абсолютным снижением.
Различают базисные и цепные абсолютные приросты. Предположим, что данолуровней динамического ряда: у у …, уn-1, уn.
Рассчитаем базисные абсолютные приросты для данного динамического ряда:
Δ1 = у1 – у0; Δ2 = у2 – у0; … Δn = уn – у0.
где уn – называется сравниваемым уровнем, у0 – базисным уровнем динамического ряда. Базисные абсолютные приросты показывают увеличение или снижение в каждом последующем периоде уровня исследуемого показателя по сравнению с базой.
Рассчитаем цепные абсолютные приросты для данного динамического ряда:
δ1 = у1 – у0; δ2 = у2 – у1; … δn = уn – уn-1.
Базисные абсолютные приросты показывают увеличение или снижение уровня исследуемого показателя по сравнению с предыдущим периодом.
Между базисными и цепными абсолютными приростами существует зависимость:
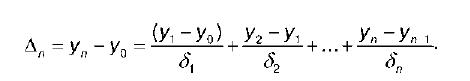Таким образом, базисный абсолютный прирост равен сумме последовательных цепных приростов. Это связь позволяет определить базисные абсолютные приросты другим путем.
Рассчитаем показатель среднего абсолютного прироста для заданного динамического ряда. Данный показатель получают на основе зависимости между базисными и цепными абсолютными приростами:
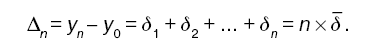Следовательно:
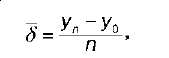где n – период времени,
или:
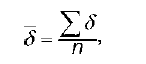где n – период времени, соответствующий количеству приростов. Показатель среднего абсолютного прироста показывает, на сколько единиц (например ежегодно за изучаемый период), изменяется в среднем уровень динамического ряда.
1) территориальными изменениями;
2) изменением единиц счета;
3) изменением методологии расчетов;
4) изменением круга охвата объектов.
В связи с тем что экономические явления изменяются во времени, для характеристики скорости и интенсивности изменения этих явлений используются абсолютные и относительные показатели динамики.
К абсолютным показателям динамики относятся:
1) абсолютный прирост;
2) средний абсолютный прирост.
Эти показатели рассчитываются за месяц, квартал, год. Они характеризуют скорость изменения уровней динамического ряда в единицу времени. Единицы измерения абсолютных показателей динамики совпадают с единицами измерения уровней динамического ряда. Абсолютные показатели динамики отвечают на вопрос, насколько в абсолютном выражении изменился уровень динамического ряда за прошедший период.
Абсолютный прирост – это разность между последующим и предшествующим уровнями динамического ряда. В тех случаях, когда разность получается со знаком минус, показатель называется абсолютным снижением.
Различают базисные и цепные абсолютные приросты. Предположим, что данолуровней динамического ряда: у у …, уn-1, уn.
Рассчитаем базисные абсолютные приросты для данного динамического ряда:
Δ1 = у1 – у0; Δ2 = у2 – у0; … Δn = уn – у0.
где уn – называется сравниваемым уровнем, у0 – базисным уровнем динамического ряда. Базисные абсолютные приросты показывают увеличение или снижение в каждом последующем периоде уровня исследуемого показателя по сравнению с базой.
Рассчитаем цепные абсолютные приросты для данного динамического ряда:
δ1 = у1 – у0; δ2 = у2 – у1; … δn = уn – уn-1.
Базисные абсолютные приросты показывают увеличение или снижение уровня исследуемого показателя по сравнению с предыдущим периодом.
Между базисными и цепными абсолютными приростами существует зависимость:
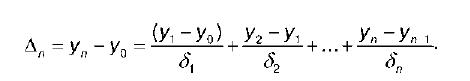
Рассчитаем показатель среднего абсолютного прироста для заданного динамического ряда. Данный показатель получают на основе зависимости между базисными и цепными абсолютными приростами:
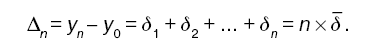
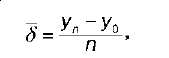
или:
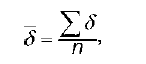
19. Относительные показатели динамики. Абсолютное значение однопроцентного прироста
К относительным показателям динамики относятся:
1) темп роста;
2) темп прироста;
3) средний темп роста;
4) средний темп прироста.
Данные показатели характеризуют интенсивность изменения уровня динамического ряда за период и выражаются в форме коэффициента или в процентах.
Предположим, что дано n уровней динамического ряда: у0, у1, …, уn-1, уn.
Рассчитаем показатель темпа роста для заданного динамического ряда.
Темп роста – это отношение последующего уровня динамического ряда к предыдущему уровню. Если числитель меньше знаменателя, то говорят о темпах снижения.
Различают базисные и цепные темпы роста.
Базисные темпы роста:
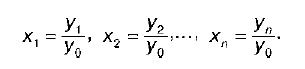Эти показатели показывают, во сколько раз последующий уровень динамического ряда больше или меньше его базисного уровня у0.
Цепные темпы роста:
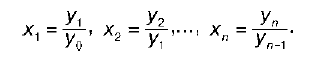Эти показатели показывают, во сколько раз последующий уровень динамического ряда больше или меньше его предыдущего уровня.
Базисный темп роста всего динамического ряда равен произведению последовательных цепных темпов роста. Данная взаимосвязь позволяет определить базисные темпы роста на основе цепных темпов роста.
Рассчитаем показатель темпа прироста для заданного динамического ряда.
Темп прироста – это отношение абсолютного прироста к базисному уровню ряда:
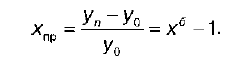Темп прироста – это темп роста, уменьшенный на одну единицу, или на 100 %. Различают базисные и цепные темпы прироста. Они показывают, на сколько процентов изменился уровень.
Рассчитаем показатель среднего (годового) темпа роста для заданного динамического ряда. В основу его расчета положена взаимосвязь базисного и цепных темпов роста.
Доказано, что xб = xц1 × xц2 ×… × xцn. Заменим каждое x на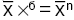
. Отсюда получим три формулы среднего темпа роста:
1)
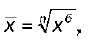
где n – это показатель времени, за который рассчитывается средний темп роста;
2)
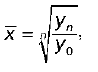
где у – уровень ряда (абсолютный показатель);
3)
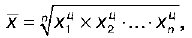
где х – цепные темпы роста;
n – период времени, который соответствует числу сомножителей. Средний темп роста показывает, во сколько раз ежегодно изменяется уровень исследуемого динамического ряда за изучаемый период в среднем.
Рассчитаем показатель среднего годового темпа прироста для заданного динамического ряда:
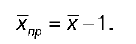
1) темп роста;
2) темп прироста;
3) средний темп роста;
4) средний темп прироста.
Данные показатели характеризуют интенсивность изменения уровня динамического ряда за период и выражаются в форме коэффициента или в процентах.
Предположим, что дано n уровней динамического ряда: у0, у1, …, уn-1, уn.
Рассчитаем показатель темпа роста для заданного динамического ряда.
Темп роста – это отношение последующего уровня динамического ряда к предыдущему уровню. Если числитель меньше знаменателя, то говорят о темпах снижения.
Различают базисные и цепные темпы роста.
Базисные темпы роста:
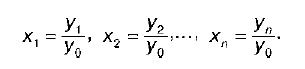
Цепные темпы роста:
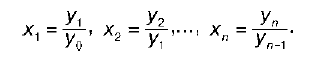
Базисный темп роста всего динамического ряда равен произведению последовательных цепных темпов роста. Данная взаимосвязь позволяет определить базисные темпы роста на основе цепных темпов роста.
Рассчитаем показатель темпа прироста для заданного динамического ряда.
Темп прироста – это отношение абсолютного прироста к базисному уровню ряда:
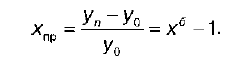
Рассчитаем показатель среднего (годового) темпа роста для заданного динамического ряда. В основу его расчета положена взаимосвязь базисного и цепных темпов роста.
Доказано, что xб = xц1 × xц2 ×… × xцn. Заменим каждое x на
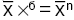. Отсюда получим три формулы среднего темпа роста:1)
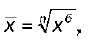
где n – это показатель времени, за который рассчитывается средний темп роста;
2)
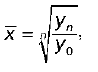
где у – уровень ряда (абсолютный показатель);
3)
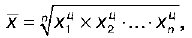
где х – цепные темпы роста;
n – период времени, который соответствует числу сомножителей. Средний темп роста показывает, во сколько раз ежегодно изменяется уровень исследуемого динамического ряда за изучаемый период в среднем.
Рассчитаем показатель среднего годового темпа прироста для заданного динамического ряда:
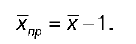
20. Методы выявления основных тенденций динамического ряда
Уровни динамического ряда изменяются под влиянием двух групп факторов: систематических (детерминированных) и случайных. Задача исследователя состоит в устранении в какой-то мере случайных факторов и выявлении основной тенденции развития уровней динамического ряда.
Эта задача может быть решена двумя способами:
1) сглаживанием по методу скользящих средних;
2) аналитическим выравниванием по методу наименьших квадратов.
Суть сглаживания уровней динамического ряда по методу скользящей средней заключается в следующем. Данный метод основан на идее перехода от менее крупных интервалов времени к более крупным. Такие средние величины называются скользящими. Они образуют сглаженный динамический ряд, по которому судят об основных тенденциях ряда. В сглаживании постепенно участвуют все уровни ряда путем передвижки на один уровень вперед.
Например, первое значение х1 сглаженного динамического ряда рассчитывается по формуле:
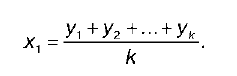Второе значение х2 сглаженного динамического ряда рассчитывается по формуле:
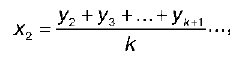где к — период сглаживания.
Таким образом, полученные средние величины х1, х2 … образуют сглаженный ряд динамики.
Сглаживание можно производить и для четного периода, например для четырех лет. Вспомогательный ряд скользящих средних рассчитывается так же, как и при нечетном периоде, а основной рассчитывается постепенно на основе двух соседних средних вспомогательного ряда по формуле простой средней.
Аналитическое выравнивание – это более сложный прием выявления основных тенденций динамического ряда. Данный процесс включает два этапа:
1) выбор вида кривой (функции), форма которой соответствует характеру изменения динамического ряда;
2) определение параметров и выравненных значений уровней динамического ряда.
На первом этапе на линейном графике по фактическим данным строят ломаную кривую. При этом по оси абсцисс откладывают время, а по оси ординат – значения динамического ряда. Затем глазомерно оценивают ее и выбирают наиболее подходящую кривую. Это может быть прямая или парабола, показательная функция и т. д. Во всех случаях выбранная кривая должна удовлетворять методу наименьших квадратов. Его суть:
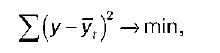где у – фактические уровни динамического ряда;
yt – выровненные или теоретические уровни для каждого периода t.
На втором этапе аналитического выравнивания параметры функции, например прямой yt = a0 + a1t, определяются с помощью системы нормальных уравнений, например:
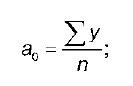
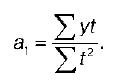Определив а0 и а1, подставляют их значения в уравнение прямой, где t – время.
Параметр а0 интерпретируется как вычисленный теоретический уровень срединного члена ряда. Параметр а1 трактуется как средняя скорость изменения уровня ряда (средний абсолютный прирост).
Эта задача может быть решена двумя способами:
1) сглаживанием по методу скользящих средних;
2) аналитическим выравниванием по методу наименьших квадратов.
Суть сглаживания уровней динамического ряда по методу скользящей средней заключается в следующем. Данный метод основан на идее перехода от менее крупных интервалов времени к более крупным. Такие средние величины называются скользящими. Они образуют сглаженный динамический ряд, по которому судят об основных тенденциях ряда. В сглаживании постепенно участвуют все уровни ряда путем передвижки на один уровень вперед.
Например, первое значение х1 сглаженного динамического ряда рассчитывается по формуле:
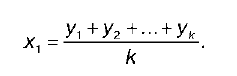
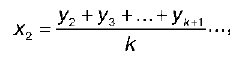
Таким образом, полученные средние величины х1, х2 … образуют сглаженный ряд динамики.
Сглаживание можно производить и для четного периода, например для четырех лет. Вспомогательный ряд скользящих средних рассчитывается так же, как и при нечетном периоде, а основной рассчитывается постепенно на основе двух соседних средних вспомогательного ряда по формуле простой средней.
Аналитическое выравнивание – это более сложный прием выявления основных тенденций динамического ряда. Данный процесс включает два этапа:
1) выбор вида кривой (функции), форма которой соответствует характеру изменения динамического ряда;
2) определение параметров и выравненных значений уровней динамического ряда.
На первом этапе на линейном графике по фактическим данным строят ломаную кривую. При этом по оси абсцисс откладывают время, а по оси ординат – значения динамического ряда. Затем глазомерно оценивают ее и выбирают наиболее подходящую кривую. Это может быть прямая или парабола, показательная функция и т. д. Во всех случаях выбранная кривая должна удовлетворять методу наименьших квадратов. Его суть:
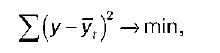
yt – выровненные или теоретические уровни для каждого периода t.
На втором этапе аналитического выравнивания параметры функции, например прямой yt = a0 + a1t, определяются с помощью системы нормальных уравнений, например:
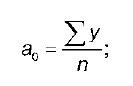
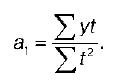
Параметр а0 интерпретируется как вычисленный теоретический уровень срединного члена ряда. Параметр а1 трактуется как средняя скорость изменения уровня ряда (средний абсолютный прирост).
21. Выборочное наблюдение. Ошибки выборки
Одной из задач статистического исследования зачастую является задача исследования группы однородных объектов, явлений или процессов относительно некоторого качественного или количественного признака, характеризующего эти объекты.
При решении данной задачи можно провести сплошное обследование, т. е. обследовать каждый из объектов данной совокупности относительно изучаемого признака.
Выборочное наблюдение – это такой тип несплошного наблюдения, при котором обследованию подвергаются не все единицы изучаемой совокупности, а лишь отобранные в определенном порядке.
Применение выборочного наблюдения способствует:
1) экономии времени и средств в результате сокращения объема работ;
2) минимизации порчи или уничтожения исследуемых объектов;
3) возможности детального исследования каждой единицы наблюдения при неосуществимости охвата всех единиц;
4) достижению большей точности результатов обследования.
Основные понятия выборочного наблюдения.
Генеральная совокупность (N) – это совокупность объектов, явлений или процессов, из которых производится выборка.
Выборочная совокупность (выборка) (п) – это совокупность случайно отобранных объектов из генеральной совокупности.
Генеральная средняя (x) – средняя величина признака для генеральной совокупности.
Выборочная средняя (x) – средняя величина признака для выборочной совокупности.
Генеральная доля (p) – отношение числа единиц генеральной совокупности, обладающих изучаемым признаком, ко всей генеральной совокупности.
Выборочная доля (w) – отношение числа единиц выборочной совокупности, обладающих изучаемым признаком (m), к объему выборочной совокупности:
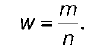Одним из основных требований к формированию выборочных совокупностей является требование репрезентативности выборки, т. е. для характеристики по данным выборочной совокупности интересующего исследователей признака генеральной совокупности необходимо, чтобы единицы выборки в достаточной степени обладали этим признаком.
Ошибки выборки.
В процессе всякого наблюдения возникают ошибки регистрации. При выборочном наблюдении возникают специфические ошибки – ошибки репрезентативности (или представительности) выборки.
Ошибка репрезентативности – это разность между обобщающими выборочными показателями и соответствующими показателями генеральной совокупности. Например, для показателя средней ошибка репрезентативности равна модулю разности между выборочной средней и генеральной средней:
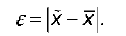Для показателя доли ошибка репрезентативности равна модулю разности между выборочной долей и генеральной долей:
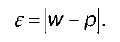Ошибки репрезентативности выборки делятся на случайные и систематические.
Систематические ошибки выборки направлены в одну определенную сторону (либо в сторону увеличения, либо в сторону уменьшения). Они могут быть преднамеренными и непреднамеренными.
Задача статистики состоит в избежании ошибок репрезентативности, в устранении причин их появления. Также статистика определяет величину случайных ошибок репрезентативности и устанавливает их возможные пределы.
При решении данной задачи можно провести сплошное обследование, т. е. обследовать каждый из объектов данной совокупности относительно изучаемого признака.
Выборочное наблюдение – это такой тип несплошного наблюдения, при котором обследованию подвергаются не все единицы изучаемой совокупности, а лишь отобранные в определенном порядке.
Применение выборочного наблюдения способствует:
1) экономии времени и средств в результате сокращения объема работ;
2) минимизации порчи или уничтожения исследуемых объектов;
3) возможности детального исследования каждой единицы наблюдения при неосуществимости охвата всех единиц;
4) достижению большей точности результатов обследования.
Основные понятия выборочного наблюдения.
Генеральная совокупность (N) – это совокупность объектов, явлений или процессов, из которых производится выборка.
Выборочная совокупность (выборка) (п) – это совокупность случайно отобранных объектов из генеральной совокупности.
Генеральная средняя (x) – средняя величина признака для генеральной совокупности.
Выборочная средняя (x) – средняя величина признака для выборочной совокупности.
Генеральная доля (p) – отношение числа единиц генеральной совокупности, обладающих изучаемым признаком, ко всей генеральной совокупности.
Выборочная доля (w) – отношение числа единиц выборочной совокупности, обладающих изучаемым признаком (m), к объему выборочной совокупности:
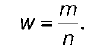
Ошибки выборки.
В процессе всякого наблюдения возникают ошибки регистрации. При выборочном наблюдении возникают специфические ошибки – ошибки репрезентативности (или представительности) выборки.
Ошибка репрезентативности – это разность между обобщающими выборочными показателями и соответствующими показателями генеральной совокупности. Например, для показателя средней ошибка репрезентативности равна модулю разности между выборочной средней и генеральной средней:
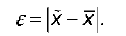
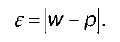
Систематические ошибки выборки направлены в одну определенную сторону (либо в сторону увеличения, либо в сторону уменьшения). Они могут быть преднамеренными и непреднамеренными.
Задача статистики состоит в избежании ошибок репрезентативности, в устранении причин их появления. Также статистика определяет величину случайных ошибок репрезентативности и устанавливает их возможные пределы.
22. Способы отбора данных. Способы распространения данных выборки на всю генеральную совокупность
Для формирования выборочной совокупности применяются различные способы отбора.
1. Отбор, при котором генеральная совокупность не разбивается на части:
1) простой случайный повторный отбор. Он характеризуется следующими чертами:
а) отбор единиц выборочной совокупности производится из всей генеральной совокупности;
б) отбор носит случайный характер;
в) единицы генеральной совокупности, попавшие в выборочную совокупность, вновь возвращаются в генеральную совокупность после изучения;
2) простой случайный бесповторный отбор. Он характеризуется следующими чертами:
а) отбор единиц выборочной совокупности производится из всей генеральной совокупности;
б) отбор носит случайный характер;
в) единицы генеральной совокупности после об следования не возвращаются в генеральную совокупность.
В случае применения простого случайного отбора все единицы генеральной совокупности имеют одинаковую вероятность попасть в выборочную совокупность.
2. Отбор, при котором генеральная совокупность разбивается на части:
1) типический отбор, характеризующийся следующими чертами:
а) вся генеральная совокупность разбивается на типически однородные группы или части;
б) отбор единиц производится не из всей генеральной совокупности, а из отдельных типичных групп либо механически, либо случайно.
При типическом способе отбора в выборочную совокупность попадают все представители типических групп, что обеспечивает большую репрезентативность и точность полученных результатов. Одной из предпосылок применения типического отбора являются большое разнообразие генеральной совокупности и ее элементов и значительная неоднородность изучаемых при этом признаков. Его применение связано со сложными социально-экономическими явлениями. Типический отбор является достаточно дорогим, но самым точным способом отбора;
2) серийный отбор, характеризующийся следующими чертами:
а) вся генеральная совокупность разбивается на части (серии или гнезда);
б) отбор единиц генеральной совокупности производится целыми сериями;
в) наблюдению подвергаются все без исключения единицы отобранной серии;
г) отбор носит случайный характер; Серийный отбор является менее точным способом отбора, однако его легче организовать;
3) механический отбор, который характеризует ся следующими чертами:
а) отбор осуществляется из всей генеральной совокупности;
б) отбор производится по механическому принципу (по списку, в шахматном порядке, по географическому признаку, в порядке убывания или возрастания).
Механический отбор является более точным, чем случайный, однако уступает типическому отбору.
На практике также часто применяется комбинированный отбор, при котором сочетаются указанные выше способы отбора.
Существуют два способа распространения данных выборочной совокупности на всю генеральную совокупность:
1) прямой, или способ прямого счета;
2) косвенный, или способ поправочных коэффициентов. При первом способе показатели, найденные посредством выборки (выборочная средняя или выборочная доля) умножаются на число единиц генеральной совокупности.
Второй способ применяется в целях проверки и уточнения данных сплошного наблюдения. В этом случае сопоставляют по соответствующим объектам данные выборочного наблюдения со сплошным, исчисляют поправочный коэффициент, которым и пользуются для внесения поправок в материалы сплошного наблюдения.
1. Отбор, при котором генеральная совокупность не разбивается на части:
1) простой случайный повторный отбор. Он характеризуется следующими чертами:
а) отбор единиц выборочной совокупности производится из всей генеральной совокупности;
б) отбор носит случайный характер;
в) единицы генеральной совокупности, попавшие в выборочную совокупность, вновь возвращаются в генеральную совокупность после изучения;
2) простой случайный бесповторный отбор. Он характеризуется следующими чертами:
а) отбор единиц выборочной совокупности производится из всей генеральной совокупности;
б) отбор носит случайный характер;
в) единицы генеральной совокупности после об следования не возвращаются в генеральную совокупность.
В случае применения простого случайного отбора все единицы генеральной совокупности имеют одинаковую вероятность попасть в выборочную совокупность.
2. Отбор, при котором генеральная совокупность разбивается на части:
1) типический отбор, характеризующийся следующими чертами:
а) вся генеральная совокупность разбивается на типически однородные группы или части;
б) отбор единиц производится не из всей генеральной совокупности, а из отдельных типичных групп либо механически, либо случайно.
При типическом способе отбора в выборочную совокупность попадают все представители типических групп, что обеспечивает большую репрезентативность и точность полученных результатов. Одной из предпосылок применения типического отбора являются большое разнообразие генеральной совокупности и ее элементов и значительная неоднородность изучаемых при этом признаков. Его применение связано со сложными социально-экономическими явлениями. Типический отбор является достаточно дорогим, но самым точным способом отбора;
2) серийный отбор, характеризующийся следующими чертами:
а) вся генеральная совокупность разбивается на части (серии или гнезда);
б) отбор единиц генеральной совокупности производится целыми сериями;
в) наблюдению подвергаются все без исключения единицы отобранной серии;
г) отбор носит случайный характер; Серийный отбор является менее точным способом отбора, однако его легче организовать;
3) механический отбор, который характеризует ся следующими чертами:
а) отбор осуществляется из всей генеральной совокупности;
б) отбор производится по механическому принципу (по списку, в шахматном порядке, по географическому признаку, в порядке убывания или возрастания).
Механический отбор является более точным, чем случайный, однако уступает типическому отбору.
На практике также часто применяется комбинированный отбор, при котором сочетаются указанные выше способы отбора.
Существуют два способа распространения данных выборочной совокупности на всю генеральную совокупность:
1) прямой, или способ прямого счета;
2) косвенный, или способ поправочных коэффициентов. При первом способе показатели, найденные посредством выборки (выборочная средняя или выборочная доля) умножаются на число единиц генеральной совокупности.
Второй способ применяется в целях проверки и уточнения данных сплошного наблюдения. В этом случае сопоставляют по соответствующим объектам данные выборочного наблюдения со сплошным, исчисляют поправочный коэффициент, которым и пользуются для внесения поправок в материалы сплошного наблюдения.
23. Функциональная, статистическая и корреляционная зависимости. Определение регрессии
Большинство социально-экономических явлений и процессов, исследуемых статистикой, взаимосвязаны между собой. Поэтому одна из основных задач статистики состоит в установлении и измерении причинно-следственных связей между изучаемой случайной величиной Y и одной или несколькими случайными (или неслучайными) величинами Х1, Х2, …, Хn.
При изучении причинно-следственных связей выделяют факторные и результативные признаки. Результативные признаки Y выступают в роли функции, т. к. они изменяются под воздействием факторных признаков. Факторные признаки Х1, Х2, …, Хn выступают в роли аргументов функции, т. к. они влияют на изменение результативных признаков.
Различают два вида связей между случайными величинами – функциональную и корреляционную.
Функциональная зависимость характеризуется полным соответствием между зависимой (результативной) переменной Y и факторной переменной Х. Но в связи с тем что факторные и результативные переменные подвержены воздействию случайных факторов, как общих для обоих переменных, так и индивидуальных, то строгая функциональная зависимость на практике встречается редко.
Предположим, что результативная переменная /зависит от случайных факторов Т1, Т2, М1, М2, а факторная переменная Х зависит от случайных факторов Т1, Т2, К1, то Y и Х связаны статистической зависимостью, т. к. среди случайных факторов есть общие – Т1 и Т2.
При изучении причинно-следственных связей выделяют факторные и результативные признаки. Результативные признаки Y выступают в роли функции, т. к. они изменяются под воздействием факторных признаков. Факторные признаки Х1, Х2, …, Хn выступают в роли аргументов функции, т. к. они влияют на изменение результативных признаков.
Различают два вида связей между случайными величинами – функциональную и корреляционную.
Функциональная зависимость характеризуется полным соответствием между зависимой (результативной) переменной Y и факторной переменной Х. Но в связи с тем что факторные и результативные переменные подвержены воздействию случайных факторов, как общих для обоих переменных, так и индивидуальных, то строгая функциональная зависимость на практике встречается редко.
Предположим, что результативная переменная /зависит от случайных факторов Т1, Т2, М1, М2, а факторная переменная Х зависит от случайных факторов Т1, Т2, К1, то Y и Х связаны статистической зависимостью, т. к. среди случайных факторов есть общие – Т1 и Т2.
Конец бесплатного ознакомительного фрагмента