И вряд ли можно считать неожиданным, что программист-практик Макконнел выдвигает и разрабатывает экстравагантную на первый взгляд идею, согласно которой наилучшим языком общения между инопланетными цивилизациями являются компьютерные программы. Как убеждает читателей автор, передача компьютерных программ, моделирующих постигнутые феномены или решенные задачи, предоставляет возможности для наиболее емкого донесения информации относительно уровня знаний и технологических возможностей отправителя.
У читателя, в свою очередь, тут же возникает вполне естественный вопрос: «Но ведь даже программы перевода с одного человеческого языка на другой, несмотря на усилия разработчиков, продолжают оставаться предельно убогими. Так как же, опираясь на столь несовершенные компьютерные алгоритмы, мы сможем общаться с инопланетной цивилизацией?»
Ответ компьютерных ученых (и Макконнела) на данный вопрос звучит следующим образом. Программы машинного перевода столь убоги по той причине, что подаваемые им на вход документы имеют нестандартизованный формат. Множество значений одного и того же слова либо сразу приводит к ошибкам перевода, либо занимает неоправданно много времени на анализ групп слов и фраз целиком (а в итоге тоже приводит к ошибкам, хотя и не столь грубым).
Но проблему можно снять, если предварительно кодировать исходное сообщение таким образом, чтобы его разметка сама вела получателя к правильному декодированию послания. Один из способов, которым это можно сделать, заключается в создании некоего «числового языка», в котором каждой идее присвоен уникальный цифровой адрес. Тогда исчезает вся путаница вокруг множества смыслов и особенностей контекста, окружающего каждое конкретное слово или символ в выражении. Конечно, подобный подход несоизмеримо увеличивает трудозатраты автора исходного текста, поскольку процесс подготовки сводится к весьма утомительному кодированию, однако на приемном конце задача восстановления смысла послания чрезвычайно упрощается.
Эта общая методика изготовления посланий, имеющих встроенные в свое тело ключи к тому, как их декодировать, уже имеет и собственное название – антикриптография. Данной дисциплине, пока что не имеющей широкой известности, Брайен Макконнел посвятил специальную статью под бравым заглавием «Антикриптография – очередной рубеж в компьютерной науке»[24]. В статье подробно разбирается, каким образом можно наиболее эффективно компрессировать информацию, чтобы она (а) обладала наименьшей избыточностью, т. е. несла максимум полезных данных; (б) одновременно содержала исчерпывающие подсказки о том, как послание декодировать получателю, изначально не имеющему ни малейшего представления о содержимом.
Понятно, что данное направление исследований имеет самое непосредственное отношение к экзотической задаче контактов с инопланетным разумом. Однако уже сейчас исследователям видятся для антикриптографии и вполне конкретные земные области применения.
В сущности, достаточно просто осмыслить, что идея конструирования и рассылки файлов, которые сами себя описывают (хотя бы отчасти), является весьма и весьма практичной. Один из наиболее часто приводимых в этой связи примеров – программное обеспечение для распространения в Интернете графических изображений и видеороликов. При опоре на принципы антикриптографии становится возможным создать систему, которая снимает достаточно обременительную необходимость в загрузке специальных программ для просмотра компрессированных изображений.
Трюк заключается в том, чтобы перемежать данные, описывающие картинку, с алгоритмом (или командами) для преобразования данных в визуально воспринимаемый образ. При подобном сценарии компьютер пользователя автоматически обучается тому, как обрабатывать и выводить на дисплей любой новый тип кодирования графики. Ясно, что такой принцип был бы существенным шагом вперед по сравнению с нынешней ситуацией, когда для одних роликов надо загружать программу QuickTime, для других RealPlayer, для третьих – что-то еще столь же «фирменное».
Таким образом, подводит итог Макконнел, даже если SETI вообще не удастся ничего найти в безбрежных космических просторах, все равно «поиск внеземного разума» – это весьма полезная метафора для решения тех задач, с которыми постоянно сталкиваются разработчики программного обеспечения и телекоммуникационных систем. Научившись создавать такие конструкции, которые эффективно сами себя описывают, программисты смогут создавать значительно лучшие программы и сетевые услуги, на этих программах основанные.
3.2. Звездный код
Практически все усилия SETI, как известно, направлены на выявление и анализ возможной «искусственности» в радиоастрономических данных из дальнего космоса. Однако часть исследователей занимается изучением радиосигналов, уже давно известных своей аномальностью и полученных, что называется, прямо под боком. Речь идет об «эхе длительной задержки» или LDE (long delayed echoes) – феномене, неоднократно отмечавшемся с самого начала эры радиосвязи и по сию пору не получившем объяснения в физике. Основная особенность LDE, также известного под названием «парадокс Штёрмера», – это различной длительности задержки радиосигналов, приходящих с запаздыванием на секунды, десятки секунд, а иногда даже минуты.
Самыми знаменитыми сериями LDE, по всей видимости, являются 5 последовательностей, зарегистрированных 11 октября 1928 года в ходе экспериментов астрофизика Карла Штёрмера, инженера Йоргена Халса и физика Валтасара ван дер Пола:
15, 9, 4, 8, 13, 8, 12, 10, 9, 5, 8, 7, 6
12,14,14,12,8
12,5,8
12,8,5,14,14,15,12,7,5,5,13,8,8,8,13, 9,10,7,14, 6, 9,5, 9
8,11,15,8,13,3,8,8,8,12,15,13,8,8
В 1967 году эксперименты с LDE проводились в Стэнфордском университете. Феномен вновь удалось подтвердить, однако столь длинных серий, какие наблюдались в 1920-30-х годах, зарегистрировать уже не получилось. И вообще отмечено, что в любом новом диапазоне радиоволн, который лишь начинает использоваться, феномен проявляется четко и серийно, так же как и в 20-х годах, но впоследствии, по прошествии нескольких лет эхо как бы расплывается и серии исчезают.
Английский астроном Данкан Лунен обратил внимание на то, что сигналы радиоэха, наблюдавшиеся в 20-х годах, были совершенно «ненатуральными» с физической точки зрения: не было временного сжатия, не было доплеровского сдвига частот, а интенсивность сигналов в штёрмеровских сериях оставалась постоянной независимо от времени запаздывания. Все эти вещи в совокупности практически невозможно объяснить в рамках предположений о естественности сигнала, потому что естественное радиоэхо с задержкой 3 секунды и 3 минуты в принципе не может иметь одну и ту же интенсивность.
Данкан Лунен первым, видимо, выдвинул гипотезу о том, что серии Штёрмера представляют собой сигналы инопланетного происхождения. Например, их может генерировать некий межзвездный зонд, а изменение времени запаздывания представляет собой закодированную попытку передачи нам какой-то информации от инопланетного разума. Предложил Лунен и собственную интерпретацию этих задержек, полагая, что в них зашифрованы звезда и созвездие цивилизации, приславшей зонд. У Лунена получалось, что отправитель – эпсилон Волопаса, но вскоре появилось и множество других интерпретаций, привязывающих сигналы к самым разным точкам небесной сферы – к дзете Льва, к тау Кита и т. д. В целом же было продемонстрировано, что подобные умозаключения являются не только крайне произвольными, бездоказательными и искусственными, но и подозрительно напоминающими арифметические экзерсисы «пирамидологов-нумерологов», легко выводящих из параметров Великой пирамиды в Гизе и всю хронологию истории человечества, и основные константы мироздания.
Но вот несколько лет назад собственную интерпретацию серий Штёрмера предложил российский ученый Рашид Тагирович Файзуллин, профессор-математик из Омского университета. Полученные Файзуллиным результаты чрезвычайно интересны не только тем, что привели к открытию новых закономерностей в фундаментальной науке, но и в буквальном смысле очень красивы с эстетической точки зрения. Подробное описание этих результатов можно найти в авторской публикации[25] в Интернете, здесь же изложим суть сделанных ученым открытий.
В качестве базиса для начала декодирования сигналов Файзуллин выбрал следующие соображения. Как и во всех предыдущих попытках разумно полагать, что сообщение космического послания так или иначе связано со звездами. Но созвездия – вещь слишком «человеческая», условная и привязанная как к определенным культурам, так и к узким временным интервалам. Потому более естественно попытаться интерпретировать интервалы задержек сигнала как номера звезд в некотором объективном упорядочении, например, по светимости (визуальной яркости).
Подобный выбор предпочтителен и по той причине, что звездная величина является «автомодельным» параметром, одновременно характеризующим и массу объекта, и расстояние до него. Далее было сделано предположение, что расположение звезд в сериях должно доносить какую-то осмысленную идею (возможно, геометрическую), причем подтверждением правильности предположения было бы повторение этой идеи в нескольких сериях радиозадержек, полученных в разное время и разными исследователями.
Но каким образом искать эти геометрические соотношения? Файзуллин решил использовать сферическую систему координат, когда для наблюдателя в центре сферы всякая точка пространства задается парой угловых координат, одна из которых изменяется от 0 до 360 градусов, а вторая – от -90 до +90 градусов. В математике сферическая система координат позволяет изображать всю звездную сферу на ограниченном куске плоскости – прямоугольнике размером (0,360)x(-90,90) – и является для небесной механики наиболее естественной: в силу локальной сферической симметрии, в силу изотропности пространства и в силу естественного выбора координатной секущей плоскости в соответствии с моментом вращения системы.
И вот, выбрав наиболее естественную «галактическую» систему координат, где плоскость сечения звездной сферы совпадает с плоскостью Галактики, а вторая координатная ось отвечает направлению на центр Галактики, Файзуллин получил для звезд первой серии Штёрмера весьма необычную фигуру, обладающую целым букетом особенностей примечательного свойства.
При соединении точек в порядке поступления сигналов, получаются 8 отрезков прямых, из которых можно образовать две тройки параллельных прямых (15—19, 8-12, 10-9) (9-4, 8-13, 12—10) плюс еще одну пару взаимно параллельных отрезков (9-5, 7-6). Более того, иллюстрацией свойства параллельности оказывается и другая, самая длинная четвертая серия Штёрмера.
Поскольку для столь небольшого числа точек вероятность случайного выхода на такое множество параллельных прямых чрезвычайно мала, то разумно допустить, что предположенный ключ к декодированию послания оказался верен. Тем более, что вполне содержательными оказываются и другие серии. Третьей, самой короткой серии (12, 5, 8) соответствуют звезды Альтаир, альфа Центавра и Процион. В прямоугольнике сферических координат эти три звезды оказываются лежащими на одной прямой линии, причем точка 5 лежит на «перекрестье» двух линий, если прямоугольник свернут в цилиндр, совмещающий 0 и 360 градусов.
Еще более примечательно, что симметрии такого рода, располагающие последовательные группы точек на прямых, выявлены не только в остальных сериях Штёрмера, но и в независимых от них результатах аналогичных экспериментов Эпплтона 1934 года. Проведенные численные эксперименты показывают, что «случайно» получить подобные симметрии практически невозможно.
Далее, опираясь на полученные результаты, Файзуллин обнаружил, что задаваемые сериями радиоэхо точки позволяют из полусотни самых ярких звезд построить конфигурацию, сохраняющую инвариантным (т. е. неизменным) свойство точек «лежать на одной прямой» как при изменении координатных плоскостей, так и при переносе центра сферы по пространству. Т. е. тройки звезд «сетки» все так же продолжают оставаться на одной прямой, если начало координат помещено куда-нибудь в альфу Центавра или на Процион. Более того, выявленные закономерности в симметрии расположения звезд позволили Файзуллину обнаружить аналогичные структуры и в пространственном расположении ближайших к нам наиболее ярких галактик.
Что же означают с точки зрения математики и математической физики открытые столь экзотическим способом природные геометрические соотношения? В математике изучаются объекты, весьма напоминающие открытые Файзуллиным сетки, которые именуются «конфигурациями» и являются базовыми для проективной геометрии. Близким по смыслу объектом является, например, так называемая конфигурация Брианшо-на-Паскаля, где любая из 9 точек является пересечением трех прямых, а на каждой из прямых лежит по три точки.
Полагая, что выявленные интересные конфигурационные свойства расположения небесных объектов являются следствием энергетически устоявшегося (экстремального) состояния системы, Рашид Файзуллин вышел на известную математическую проблему под названием «задача Штейнера». Суть ее в следующем: имеется N точек на плоскости или в пространстве, которые необходимо соединить отрезками прямых так, чтобы сумма длин этих отрезков была минимальна. Когда минимум длины интерпретируется как некий экстремальный энергетический принцип для механической системы, задача приобретает важнейшее прикладное значение.
Другими словами, пользуясь аналогией со звездами, которые для энергетически оптимального состояния располагаются по прямым «конфигурации», омский ученый создал несколько оригинальных алгоритмов оптимизации, примененных в разнообразных областях от физики высоких энергий до проектирования гидравлических устройств, а также построил новый алгоритм приближенного решения задачи Штейнера для пространства произвольной размерности.
В заключение необходимо подчеркнуть, что все результаты Файзуллина, полученные в ходе данной работы – от открытия неизвестных прежде симметрии во Вселенной до новых методов решения общеизвестных математических проблем, – обладают «самодостаточной» ценностью и уже прошли верификацию в научном сообществе через публикации и доклады на солидных математических конференциях. Но нельзя забывать, что первоисточником-то всего явилась удачная гипотеза о «ключе» к звездному коду – соотнести длительности задержек радиоэха с номерами звезд в естественном упорядочении по звездной величине.
Обратил ли хоть кто-нибудь из светил научного мира внимание на столь поразительный по красоте, необычности и глубине результат? Увы, наука предпочитает такие результаты игнорировать. Как невероятные.
3.3. Плоды невнимательности
События последнего времени определенно свидетельствуют, что организация «Поиск внеземного разума» (SETI), много лет существовавшая благодаря лишь частным пожертвованиям и усилиям энтузиастов, вновь начинает входить в фавор у американских политиков и руководящих наукой чиновников. Если в 1994 году конгресс США решительно отверг всякое государственное финансирование исследований SETI, презрительно заклеймив такого рода занятия возней «по розыску зеленых человечков», то теперь в парламентском подкомитете по космосу вполне серьезно обсуждают размеры бюджетных фондов, которые следует выделить на поиски жизни среди звездных просторов.
По свидетельству же Кристофера Чибы, одного из руководителей калифорнийского «Института SETI», свои многолетние ограничения на финансирование исследований подобной направленности уже снял и Национальный научный фонд США. Другой же лидер этого Института, Фрэнк Дрейк, сообщил, что теперь в дополнение к обширным радиосканированиям глубокого космоса добавляется и масштабный проект «оптического SETI» по поиску осмысленных сигналов от дальних звезд в световом диапазоне…
Обо всех этих новостях достаточно громко протрубили центральные средства массовой информации, но особо интересно, что при этом никто не обронил хотя бы пары слов о другой аналогичной инициативе под названием FACETS, которая вместо поиска гипотетических искусственных сигналов из галактических глубин настойчиво предлагает NASA обратиться к изучению вполне конкретных объектов, давным-давно лежащих у нас, что называется, «прямо под носом».
За кулисами недавней истории с весьма шумной публикацией NASA новой фотографии так называемого «лица Марса»[26] параллельно происходило (да и сейчас происходит) значительно менее заметное разбирательство с еще одной интереснейшей структурой в области Сидония – так называемой «пирамидой Ди Пьетро и Моленаара».
Эту пирамиду (получившую краткое название D amp;M), наряду с рядом других любопытных объектов и заново переоткрытым «лицом», обнаружили на фотоснимках Марса в 1979 году компьютерщики Винсент Ди Пьетро и Грегори Моленаар, работавшие в то время в Центре космических полетов им. Годдарда. Пирамида расположена примерно в 15 километрах от «лица» и имеет пять правильных, достаточно отчетливых граней. Структура имеет весьма солидные размеры – 2,6 километра в максимальном поперечнике и около 800 метров в высоту. У основания каждого из пяти ее углов можно разглядеть не очень ясные «подпорки», что лишь усиливает впечатление об искусственном происхождении объекта.
Главные же открытия необычных свойств пирамиды были сделаны в 1988—1989 годах системным аналитиком Картографического управления Министерства обороны США Эролом Торуном. Как профессионал-картограф, Торун хорошо знает геоморфологию и не сумел найти естественных объяснений для образования на поверхности планеты структуры подобной формы. Аккуратно восстановив по фотографии геометрию пирамиды D amp;M, Торун показал, что объект имеет по две пары конгруэнтных углов и осевую двустороннюю симметрию (эта ось направлена на «лицо»).
Итак, анализ показал, что на Марсе имеется чрезвычайно богатая с математической точки зрения фигура, геометрия которой включает математические основы шести– и пятиугольника, а также классические геометрические пропорции «золотого сечения». Двадцать внутренних углов модели, угловые соотношения и тригонометрические функции избыточно выражают три величины квадратных корней из 2, 3, 5 и две математические константы: число «пи» и число «е» (основание натуральных логарифмов). Причем константы появляются не одни, а в семи разных математических комбинациях.
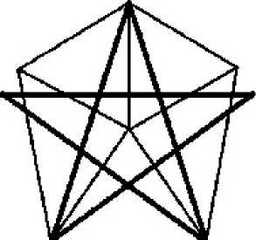
Естественно, ошеломительные результаты Торуна поначалу вызвали у большинства ученых скепсис. Как выразился Хорас Крейтер, специалист в физике частиц и известный эксперт по преобразованию экспериментальных данных в математические структуры, сначала он «подозревал, что пропорции с подобной избыточностью могли бы случиться с разумной вероятностью в любой полусимметричной пятигранной фигуре». Многие из изученных Крейтером различных пятисторонних фигур обнаруживали пропорции, подобные соотношениям D amp;M. Увеличив точность расчетов, Крейтер к своему удивлению получил странный результат. На более высоких уровнях точности лишь модель Торуна смогла продемонстрировать столь значимый уровень избыточности.
Компьютерщик Кит Морган из Говардского университета (Вашингтон) написал специальную программу, чтобы установить перебором, какие еще пятиугольные фигуры подобного вида способны порождать такое количество математических констант. Зафиксировав два передних угла по 60 градусов, Морган прогнал ребра противоположной стороны через разные углы, получив в общей сложности 680 вариантов основания пирамидальной формы. Как показали результаты обсчета, модель Торуна является единственной пятиугольной формой с двумя углами по 60 градусов, которая выдает все эти константы, причем в таком разнообразии соотношений.
В известном исследовании «Отчет Макдэниела»[27] напрямую ставится вопрос о том, что случилось бы, натолкнись человечество Земли на ту же самую информацию не у себя, что называется, под боком, а в радиочастотных сигналах из звездных далей:
Представим себе, что с помощью радиотелескопа, работающего по программе SETI, получены цифровые радиосигналы из глубокого космоса. После их компьютерного перевода в образы первым получается изображение гуманоидного лица, а вторым – пятиугольная диаграмма (вроде пирамиды D amp;M) с уникальными пропорциями и множеством математических констант… Припрячет ли NASA и эти изображения, заявив, что они являются лишь «игрой излучения и помех»? Если же часть сигнала окажется искаженной межзвездными помехами, перестанет ли NASA прислушиваться к этой частоте, заявив, что послание было недостаточно полным?
Подводя итог, нельзя не отметить, что NASA вполне определенно интересуется областью Сидония и ее необычными объектами. Только вот отражается этот интерес весьма своеобразно. Качественный снимок высокого разрешения (SP1-22003)[28], сделанный орбитальным кораблем MGS и накрывающий окрестность D amp;M, с хирургической точностью выхватывает всего лишь одну, самую нечеткую грань пирамиды, так что нам, любопытствующим обывателям, остается лишь поражаться столь неприятной случайности.
У читателя, в свою очередь, тут же возникает вполне естественный вопрос: «Но ведь даже программы перевода с одного человеческого языка на другой, несмотря на усилия разработчиков, продолжают оставаться предельно убогими. Так как же, опираясь на столь несовершенные компьютерные алгоритмы, мы сможем общаться с инопланетной цивилизацией?»
Ответ компьютерных ученых (и Макконнела) на данный вопрос звучит следующим образом. Программы машинного перевода столь убоги по той причине, что подаваемые им на вход документы имеют нестандартизованный формат. Множество значений одного и того же слова либо сразу приводит к ошибкам перевода, либо занимает неоправданно много времени на анализ групп слов и фраз целиком (а в итоге тоже приводит к ошибкам, хотя и не столь грубым).
Но проблему можно снять, если предварительно кодировать исходное сообщение таким образом, чтобы его разметка сама вела получателя к правильному декодированию послания. Один из способов, которым это можно сделать, заключается в создании некоего «числового языка», в котором каждой идее присвоен уникальный цифровой адрес. Тогда исчезает вся путаница вокруг множества смыслов и особенностей контекста, окружающего каждое конкретное слово или символ в выражении. Конечно, подобный подход несоизмеримо увеличивает трудозатраты автора исходного текста, поскольку процесс подготовки сводится к весьма утомительному кодированию, однако на приемном конце задача восстановления смысла послания чрезвычайно упрощается.
Эта общая методика изготовления посланий, имеющих встроенные в свое тело ключи к тому, как их декодировать, уже имеет и собственное название – антикриптография. Данной дисциплине, пока что не имеющей широкой известности, Брайен Макконнел посвятил специальную статью под бравым заглавием «Антикриптография – очередной рубеж в компьютерной науке»[24]. В статье подробно разбирается, каким образом можно наиболее эффективно компрессировать информацию, чтобы она (а) обладала наименьшей избыточностью, т. е. несла максимум полезных данных; (б) одновременно содержала исчерпывающие подсказки о том, как послание декодировать получателю, изначально не имеющему ни малейшего представления о содержимом.
Понятно, что данное направление исследований имеет самое непосредственное отношение к экзотической задаче контактов с инопланетным разумом. Однако уже сейчас исследователям видятся для антикриптографии и вполне конкретные земные области применения.
В сущности, достаточно просто осмыслить, что идея конструирования и рассылки файлов, которые сами себя описывают (хотя бы отчасти), является весьма и весьма практичной. Один из наиболее часто приводимых в этой связи примеров – программное обеспечение для распространения в Интернете графических изображений и видеороликов. При опоре на принципы антикриптографии становится возможным создать систему, которая снимает достаточно обременительную необходимость в загрузке специальных программ для просмотра компрессированных изображений.
Трюк заключается в том, чтобы перемежать данные, описывающие картинку, с алгоритмом (или командами) для преобразования данных в визуально воспринимаемый образ. При подобном сценарии компьютер пользователя автоматически обучается тому, как обрабатывать и выводить на дисплей любой новый тип кодирования графики. Ясно, что такой принцип был бы существенным шагом вперед по сравнению с нынешней ситуацией, когда для одних роликов надо загружать программу QuickTime, для других RealPlayer, для третьих – что-то еще столь же «фирменное».
Таким образом, подводит итог Макконнел, даже если SETI вообще не удастся ничего найти в безбрежных космических просторах, все равно «поиск внеземного разума» – это весьма полезная метафора для решения тех задач, с которыми постоянно сталкиваются разработчики программного обеспечения и телекоммуникационных систем. Научившись создавать такие конструкции, которые эффективно сами себя описывают, программисты смогут создавать значительно лучшие программы и сетевые услуги, на этих программах основанные.
3.2. Звездный код
Я не вижу логики в том, чтобы отвергать данные лишь по той причине, что они выглядят невероятными.
Фред Хойл.
Практически все усилия SETI, как известно, направлены на выявление и анализ возможной «искусственности» в радиоастрономических данных из дальнего космоса. Однако часть исследователей занимается изучением радиосигналов, уже давно известных своей аномальностью и полученных, что называется, прямо под боком. Речь идет об «эхе длительной задержки» или LDE (long delayed echoes) – феномене, неоднократно отмечавшемся с самого начала эры радиосвязи и по сию пору не получившем объяснения в физике. Основная особенность LDE, также известного под названием «парадокс Штёрмера», – это различной длительности задержки радиосигналов, приходящих с запаздыванием на секунды, десятки секунд, а иногда даже минуты.
Самыми знаменитыми сериями LDE, по всей видимости, являются 5 последовательностей, зарегистрированных 11 октября 1928 года в ходе экспериментов астрофизика Карла Штёрмера, инженера Йоргена Халса и физика Валтасара ван дер Пола:
15, 9, 4, 8, 13, 8, 12, 10, 9, 5, 8, 7, 6
12,14,14,12,8
12,5,8
12,8,5,14,14,15,12,7,5,5,13,8,8,8,13, 9,10,7,14, 6, 9,5, 9
8,11,15,8,13,3,8,8,8,12,15,13,8,8
В 1967 году эксперименты с LDE проводились в Стэнфордском университете. Феномен вновь удалось подтвердить, однако столь длинных серий, какие наблюдались в 1920-30-х годах, зарегистрировать уже не получилось. И вообще отмечено, что в любом новом диапазоне радиоволн, который лишь начинает использоваться, феномен проявляется четко и серийно, так же как и в 20-х годах, но впоследствии, по прошествии нескольких лет эхо как бы расплывается и серии исчезают.
Английский астроном Данкан Лунен обратил внимание на то, что сигналы радиоэха, наблюдавшиеся в 20-х годах, были совершенно «ненатуральными» с физической точки зрения: не было временного сжатия, не было доплеровского сдвига частот, а интенсивность сигналов в штёрмеровских сериях оставалась постоянной независимо от времени запаздывания. Все эти вещи в совокупности практически невозможно объяснить в рамках предположений о естественности сигнала, потому что естественное радиоэхо с задержкой 3 секунды и 3 минуты в принципе не может иметь одну и ту же интенсивность.
Данкан Лунен первым, видимо, выдвинул гипотезу о том, что серии Штёрмера представляют собой сигналы инопланетного происхождения. Например, их может генерировать некий межзвездный зонд, а изменение времени запаздывания представляет собой закодированную попытку передачи нам какой-то информации от инопланетного разума. Предложил Лунен и собственную интерпретацию этих задержек, полагая, что в них зашифрованы звезда и созвездие цивилизации, приславшей зонд. У Лунена получалось, что отправитель – эпсилон Волопаса, но вскоре появилось и множество других интерпретаций, привязывающих сигналы к самым разным точкам небесной сферы – к дзете Льва, к тау Кита и т. д. В целом же было продемонстрировано, что подобные умозаключения являются не только крайне произвольными, бездоказательными и искусственными, но и подозрительно напоминающими арифметические экзерсисы «пирамидологов-нумерологов», легко выводящих из параметров Великой пирамиды в Гизе и всю хронологию истории человечества, и основные константы мироздания.
Но вот несколько лет назад собственную интерпретацию серий Штёрмера предложил российский ученый Рашид Тагирович Файзуллин, профессор-математик из Омского университета. Полученные Файзуллиным результаты чрезвычайно интересны не только тем, что привели к открытию новых закономерностей в фундаментальной науке, но и в буквальном смысле очень красивы с эстетической точки зрения. Подробное описание этих результатов можно найти в авторской публикации[25] в Интернете, здесь же изложим суть сделанных ученым открытий.
В качестве базиса для начала декодирования сигналов Файзуллин выбрал следующие соображения. Как и во всех предыдущих попытках разумно полагать, что сообщение космического послания так или иначе связано со звездами. Но созвездия – вещь слишком «человеческая», условная и привязанная как к определенным культурам, так и к узким временным интервалам. Потому более естественно попытаться интерпретировать интервалы задержек сигнала как номера звезд в некотором объективном упорядочении, например, по светимости (визуальной яркости).
Но каким образом искать эти геометрические соотношения? Файзуллин решил использовать сферическую систему координат, когда для наблюдателя в центре сферы всякая точка пространства задается парой угловых координат, одна из которых изменяется от 0 до 360 градусов, а вторая – от -90 до +90 градусов. В математике сферическая система координат позволяет изображать всю звездную сферу на ограниченном куске плоскости – прямоугольнике размером (0,360)x(-90,90) – и является для небесной механики наиболее естественной: в силу локальной сферической симметрии, в силу изотропности пространства и в силу естественного выбора координатной секущей плоскости в соответствии с моментом вращения системы.
И вот, выбрав наиболее естественную «галактическую» систему координат, где плоскость сечения звездной сферы совпадает с плоскостью Галактики, а вторая координатная ось отвечает направлению на центр Галактики, Файзуллин получил для звезд первой серии Штёрмера весьма необычную фигуру, обладающую целым букетом особенностей примечательного свойства.
При соединении точек в порядке поступления сигналов, получаются 8 отрезков прямых, из которых можно образовать две тройки параллельных прямых (15—19, 8-12, 10-9) (9-4, 8-13, 12—10) плюс еще одну пару взаимно параллельных отрезков (9-5, 7-6). Более того, иллюстрацией свойства параллельности оказывается и другая, самая длинная четвертая серия Штёрмера.
Поскольку для столь небольшого числа точек вероятность случайного выхода на такое множество параллельных прямых чрезвычайно мала, то разумно допустить, что предположенный ключ к декодированию послания оказался верен. Тем более, что вполне содержательными оказываются и другие серии. Третьей, самой короткой серии (12, 5, 8) соответствуют звезды Альтаир, альфа Центавра и Процион. В прямоугольнике сферических координат эти три звезды оказываются лежащими на одной прямой линии, причем точка 5 лежит на «перекрестье» двух линий, если прямоугольник свернут в цилиндр, совмещающий 0 и 360 градусов.
Далее, опираясь на полученные результаты, Файзуллин обнаружил, что задаваемые сериями радиоэхо точки позволяют из полусотни самых ярких звезд построить конфигурацию, сохраняющую инвариантным (т. е. неизменным) свойство точек «лежать на одной прямой» как при изменении координатных плоскостей, так и при переносе центра сферы по пространству. Т. е. тройки звезд «сетки» все так же продолжают оставаться на одной прямой, если начало координат помещено куда-нибудь в альфу Центавра или на Процион. Более того, выявленные закономерности в симметрии расположения звезд позволили Файзуллину обнаружить аналогичные структуры и в пространственном расположении ближайших к нам наиболее ярких галактик.
Что же означают с точки зрения математики и математической физики открытые столь экзотическим способом природные геометрические соотношения? В математике изучаются объекты, весьма напоминающие открытые Файзуллиным сетки, которые именуются «конфигурациями» и являются базовыми для проективной геометрии. Близким по смыслу объектом является, например, так называемая конфигурация Брианшо-на-Паскаля, где любая из 9 точек является пересечением трех прямых, а на каждой из прямых лежит по три точки.
Полагая, что выявленные интересные конфигурационные свойства расположения небесных объектов являются следствием энергетически устоявшегося (экстремального) состояния системы, Рашид Файзуллин вышел на известную математическую проблему под названием «задача Штейнера». Суть ее в следующем: имеется N точек на плоскости или в пространстве, которые необходимо соединить отрезками прямых так, чтобы сумма длин этих отрезков была минимальна. Когда минимум длины интерпретируется как некий экстремальный энергетический принцип для механической системы, задача приобретает важнейшее прикладное значение.
Другими словами, пользуясь аналогией со звездами, которые для энергетически оптимального состояния располагаются по прямым «конфигурации», омский ученый создал несколько оригинальных алгоритмов оптимизации, примененных в разнообразных областях от физики высоких энергий до проектирования гидравлических устройств, а также построил новый алгоритм приближенного решения задачи Штейнера для пространства произвольной размерности.
В заключение необходимо подчеркнуть, что все результаты Файзуллина, полученные в ходе данной работы – от открытия неизвестных прежде симметрии во Вселенной до новых методов решения общеизвестных математических проблем, – обладают «самодостаточной» ценностью и уже прошли верификацию в научном сообществе через публикации и доклады на солидных математических конференциях. Но нельзя забывать, что первоисточником-то всего явилась удачная гипотеза о «ключе» к звездному коду – соотнести длительности задержек радиоэха с номерами звезд в естественном упорядочении по звездной величине.
Обратил ли хоть кто-нибудь из светил научного мира внимание на столь поразительный по красоте, необычности и глубине результат? Увы, наука предпочитает такие результаты игнорировать. Как невероятные.
3.3. Плоды невнимательности
Жил некогда король, пожелавший набраться суфийской мудрости. Однако знакомый учитель, к которому обратился монарх, вежливо тому отказал, подчеркнув, что для вступления на суфийский путь прежде необходимо преодолеть свойственную людям невнимательность. Суфии имеют дело со знанием, а не с аргументами, и если король согласится подвергнуться нехитрому испытанию, то ему будет предоставлена демонстрация его невнимательности… Короля не особо убедили доводы суфия и он согласился (про себя полагая, что вполне готов к вступлению на путь), поэтому учитель попросил его отвечать «Я верю» на все, что будет сказано в течение нескольких следующих минут.
Суфий начал испытание и сказал: «Я человек из-за небес».
– Я верю.
– Обычные люди стараются получить знание, суфии же имеют его так много, что стараются не использовать.
– Я верю.
– Я лжец.
– Я верю.
– Я присутствовал при вашем рождении.
– Я верю.
– И ваш отец был крестьянином.
– Это ложь! – возмутился король.
Суфий посмотрел на него с сожалением и сказал: «Вы настолько невнимательны, что не можете и в течение одной минуты сосредоточиться на единственной фразе без проявления предрассудков. Поэтому ни один суфий не в состоянии вас ничему научить»…
Из притч потаенного наставника суфиев Шаха Фироза, XVII век.
События последнего времени определенно свидетельствуют, что организация «Поиск внеземного разума» (SETI), много лет существовавшая благодаря лишь частным пожертвованиям и усилиям энтузиастов, вновь начинает входить в фавор у американских политиков и руководящих наукой чиновников. Если в 1994 году конгресс США решительно отверг всякое государственное финансирование исследований SETI, презрительно заклеймив такого рода занятия возней «по розыску зеленых человечков», то теперь в парламентском подкомитете по космосу вполне серьезно обсуждают размеры бюджетных фондов, которые следует выделить на поиски жизни среди звездных просторов.
По свидетельству же Кристофера Чибы, одного из руководителей калифорнийского «Института SETI», свои многолетние ограничения на финансирование исследований подобной направленности уже снял и Национальный научный фонд США. Другой же лидер этого Института, Фрэнк Дрейк, сообщил, что теперь в дополнение к обширным радиосканированиям глубокого космоса добавляется и масштабный проект «оптического SETI» по поиску осмысленных сигналов от дальних звезд в световом диапазоне…
Обо всех этих новостях достаточно громко протрубили центральные средства массовой информации, но особо интересно, что при этом никто не обронил хотя бы пары слов о другой аналогичной инициативе под названием FACETS, которая вместо поиска гипотетических искусственных сигналов из галактических глубин настойчиво предлагает NASA обратиться к изучению вполне конкретных объектов, давным-давно лежащих у нас, что называется, «прямо под носом».
За кулисами недавней истории с весьма шумной публикацией NASA новой фотографии так называемого «лица Марса»[26] параллельно происходило (да и сейчас происходит) значительно менее заметное разбирательство с еще одной интереснейшей структурой в области Сидония – так называемой «пирамидой Ди Пьетро и Моленаара».
Эту пирамиду (получившую краткое название D amp;M), наряду с рядом других любопытных объектов и заново переоткрытым «лицом», обнаружили на фотоснимках Марса в 1979 году компьютерщики Винсент Ди Пьетро и Грегори Моленаар, работавшие в то время в Центре космических полетов им. Годдарда. Пирамида расположена примерно в 15 километрах от «лица» и имеет пять правильных, достаточно отчетливых граней. Структура имеет весьма солидные размеры – 2,6 километра в максимальном поперечнике и около 800 метров в высоту. У основания каждого из пяти ее углов можно разглядеть не очень ясные «подпорки», что лишь усиливает впечатление об искусственном происхождении объекта.
Главные же открытия необычных свойств пирамиды были сделаны в 1988—1989 годах системным аналитиком Картографического управления Министерства обороны США Эролом Торуном. Как профессионал-картограф, Торун хорошо знает геоморфологию и не сумел найти естественных объяснений для образования на поверхности планеты структуры подобной формы. Аккуратно восстановив по фотографии геометрию пирамиды D amp;M, Торун показал, что объект имеет по две пары конгруэнтных углов и осевую двустороннюю симметрию (эта ось направлена на «лицо»).
Структура пирамиды D amp;M имеет весьма солидные размеры – 2,6 километра в максимальном поперечнике и около 800 метров в высоту.
Собственно говоря, осевая симметрия и ориентация пирамиды были установлены несколькими годами ранее, в 1984 году Ричардом Хоуглендом, однако Торун продемонстрировал, что в D amp;M причудливым образом сочетаются пятикратная и шестикратная симметрии. Обе эти симметрии присутствуют одновременно, поскольку углы «фасада», обращенного к «лицу», обладают признаками 6-кратной симметричности, в то время как углы «основания» отсылают к симметрии правильной 5-конечной звезды. Но самое интересное, что в соотношении углов пирамиды D amp;M Эрол Торун обнаружил просто-таки кучу всякого рода примечательных пропорций. Поскольку пропорции носят геометрический характер, они «безразмерны» и никак не связаны с различными единицами измерения углов или сторон.Итак, анализ показал, что на Марсе имеется чрезвычайно богатая с математической точки зрения фигура, геометрия которой включает математические основы шести– и пятиугольника, а также классические геометрические пропорции «золотого сечения». Двадцать внутренних углов модели, угловые соотношения и тригонометрические функции избыточно выражают три величины квадратных корней из 2, 3, 5 и две математические константы: число «пи» и число «е» (основание натуральных логарифмов). Причем константы появляются не одни, а в семи разных математических комбинациях.
В известном исследовании «Отчет Макдэниела»[27] напрямую ставится вопрос о том, что случилось бы, натолкнись человечество Земли на ту же самую информацию не у себя, что называется, под боком, а в радиочастотных сигналах из звездных далей:
Представим себе, что с помощью радиотелескопа, работающего по программе SETI, получены цифровые радиосигналы из глубокого космоса. После их компьютерного перевода в образы первым получается изображение гуманоидного лица, а вторым – пятиугольная диаграмма (вроде пирамиды D amp;M) с уникальными пропорциями и множеством математических констант… Припрячет ли NASA и эти изображения, заявив, что они являются лишь «игрой излучения и помех»? Если же часть сигнала окажется искаженной межзвездными помехами, перестанет ли NASA прислушиваться к этой частоте, заявив, что послание было недостаточно полным?
Подводя итог, нельзя не отметить, что NASA вполне определенно интересуется областью Сидония и ее необычными объектами. Только вот отражается этот интерес весьма своеобразно. Качественный снимок высокого разрешения (SP1-22003)[28], сделанный орбитальным кораблем MGS и накрывающий окрестность D amp;M, с хирургической точностью выхватывает всего лишь одну, самую нечеткую грань пирамиды, так что нам, любопытствующим обывателям, остается лишь поражаться столь неприятной случайности.