Достаточно быстро Шенноном был сделан вывод, что наилучшим решением проблемы стало бы более эффективное кодирование или «упаковка» информации. Однако для начала требовалось строго определить, что это собственно такое – «информация» – и чем измерять ее количество. Имея за плечами аппарат двоичной логики, за единицу информации Шеннон принял то, что впоследствии окрестили бинарной цифрой или просто «битом», другими словами, выбор одного из двух равновероятных вариантов.
Что же касается количества информации, то ее Шеннон определил через энтропию – математическую меру, в термодинамике и статистической физике применяемую для характеристики степени хаотичности (разупорядоченности) систем. Как гласит предание, пошедшее из уст самого автора, использовать энтропию ему посоветовал знаменитый математик Джон фон Нейман. Со своеобразным чувством юмора, свойственным этим людям, фон Нейман обосновал свой совет тем, что в среде математиков и инженеров мало кто знает об энтропии, а посему Шеннон получит огромное преимущество в неизбежных грядущих спорах вокруг новой теории. Однако вопреки ожиданиям, новаторской теории Шеннона был сужден мгновенный и широчайший успех среди инженеров, занимающихся системами связи. Она породила огромное количество исследовательских работ и стала мощным стимулом к развитию всех тех технологий, что в конечном счете привели к сегодняшнему «веку информации».
Другая эпохальная работа Клода Шеннона, вышедшая практически одновременно с «теорией информации», по ряду причин не получила такого же широкого резонанса, поскольку явно опережала свое время сразу на несколько десятилетий. Речь идет, конечно же, об опубликованной в 1949 году статье «Теория связи в системах засекречивания» [38](Communication Theory of Secrecy Systems). На самом деле данная статья представляла собой несколько переработанный отчет, подготовленный Шенноном еще в 1945 году. То, что эта работа была рассекречена и опубликована в открытой печати – уже само по себе маленькое чудо, рационально объяснить которое можно лишь тем, что уровень абстрагирования явно показался принимающим решения инстанциям чересчур далеким от практики. Ну а то, что значит этот труд для современной криптологии, можно проиллюстрировать лишь одним примером. Всю историю криптографии от античности до наших дней принято делить на два периода: до 1949 года, когда «тайнопись» считали шаманством, оккультизмом и родом искусства; и после 1949 года, когда криптология стала полноценной прикладной наукой со строгой математической теорией в фундаменте.
За Клодом Шенноном всегда ходила слава весьма разнообразно одаренного человека. Во многом он напоминал «универсальных людей» эпохи Возрождения, причем порою отличался весьма эксцентричным поведением. Одной из наиболее примечательных деталей его жизни непременно упоминают следующую – временами Шеннон любил разъезжать по коридорам Bell Labs на одноколесном велосипеде, да еще жонглируя при этом мячами.

В 50-е годы ученым был предпринят целый ряд интереснейших работ, связанных с системами искусственного интеллекта. Одним из первых Шеннон высказал мысль о том, что машины могут играть в игры и самообучаться. Эти идеи сразу стали находить практическое воплощение. Для решения задач поиска выхода из лабиринта Шеннон построил «умную электромеханическую мышку», получившую имя античного героя Тесея. Это устройство стало одной из самых ранних попыток «научить» машину самостоятельно обучаться и находить выход из запутанных коридоров. В честь шенноновского Тесея институтом IEEE впоследствии был учрежден международный конкурс изобретений «микромышь», в котором и поныне тысячами участвуют студенты технических вузов из разных стран мира.
В 1950 году, фактически на самой заре компьютерной эпохи, Клод Шеннон написал статью «Программирование компьютера для игры в шахматы», где сформулировал два типа стратегий, в конечном счете приводящих к машинам, играющим в шахматы на весьма приличном уровне. Для той поры подобная статья выглядела как чудачество ученого-фантазера, однако взгляд Шеннона был устремлен не на современных ему громоздких и неудобных в программировании монстров, а значительно дальше в будущее. Обосновывая важность создания компьютерного шахматиста, Шеннон писал так: «Проблема игры в шахматы жестко очерчена, как в терминах допустимых операций, так и в своей конечной цели. Она не настолько проста, чтобы быть тривиальной, но и не слишком сложна для отыскания удовлетворительных решений».
Для наглядного пояснения этих мыслей можно сказать, что постоянно изменяющаяся сложность шахматной доски – это, к примеру, проблема работы авиадиспетчера в миниатюре. Поэтому на протяжении последнего полувека шахматы для компьютерных ученых являются как бы лабораторным полигоном, на котором обкатываются самые разнообразные технологии систем искусственного интеллекта. И ныне, когда общедоступные шахматные программы вроде Fritz или Junior, работающие на обычном персональном компьютере, уже вполне способны наносить в турнирах поражение чемпионам мира, особо важно подчеркнуть, что в основе всех современных шахматных программ по-прежнему лежат шенноновские стратегии «типа A и B».
В те же 50-е годы Шеннон создал любопытную «машину, способную читать мысли». Говоря точнее, коллега Шеннона Дэйв Хэйглбергер построил аппарат, который в опытах с подбрасыванием монеты предсказывал, что будет выбирать человек – «орла» или «решку». Эта машина явно предсказывала выбор с вероятностью, большей 50%. Так, в эксперименте с 9795 бросками машина 5218 раз сделала правильное предсказание выбора человека. Идея «чтения мыслей» состояла в том, что человек не способен генерировать «чисто случайные» последовательности, невольно подстраиваясь под результаты предыдущих испытаний. Логика обычно примерно такова: «вот выпало три подряд „решки“, значит, теперь-то уж точно выпадет „орел“». Основываясь на этой логике Хэйглбергер и разработал ряд несложных алгоритмов предсказания. Шеннона эта задача тоже заинтересовала и он построил собственную машину для чтения мыслей, выставив ее на соревнование с хэйглбергеровской. В конечном итоге машина Шеннона выиграла, правда, с минимальным преимуществом.
А в 1956 году Шеннону исполнилось 40 лет, и, как стало очевидным несколько позже, рубеж этот стал в его жизни переломным. По каким-то труднообъяснимым причинам ученому, находившемуся, казалось бы, в зените карьеры и творческих сил, наскучила исследовательская работа в Bell Labs, и он решает заняться преподаванием. С 56-го года Шеннон начинает работать в МТИ в качестве приглашенного профессора, а в 1958-м становится там постоянным преподавателем. Последующие 20 лет в МТИ показали, что Шеннону явно стало «неинтересно» заниматься областями, где он достиг столь впечатляющих высот. Зато в эти годы и особенно после ухода в 1978 году на пенсию ученый полностью отдался своей давней страсти – жонглированию. Шенноном было построено несколько жонглирующих машин и даже была создана «общая теория жонглирования». Его постоянно и бесконечно притягивала эта завораживающая игра из непрекращающейся ловли и подбрасывания падающих предметов, формирующих в воздухе причудливые динамические фигуры.
И кто знает, быть может суть этого увлечения и истинный смысл «теории жонглирования» Шеннона человечеству еще только предстоит постичь в будущем. Ведь и очень многие прежние его работы расценивались современниками как блажь и эксцентричное чудачество. Причем и от самого Шеннона неоднократно можно было услышать, что мотивацией его деятельности в значительно большей степени всегда руководило любопытство, нежели «практическая полезность»: «Я всегда следовал своим интересам, не думая ни о том, во что они для меня выльются, ни об их ценности для мира. Я потратил уйму времени на совершенно бесполезные вещи… Мне просто было интересно, как эти вещи устроены».
В сущности, можно говорить, что научную работу Шеннон обращал в забаву. Но в результате этих забав рождались воистину гениальные открытия.
Глава 6. Реальность как эволюция сознания
Что же касается количества информации, то ее Шеннон определил через энтропию – математическую меру, в термодинамике и статистической физике применяемую для характеристики степени хаотичности (разупорядоченности) систем. Как гласит предание, пошедшее из уст самого автора, использовать энтропию ему посоветовал знаменитый математик Джон фон Нейман. Со своеобразным чувством юмора, свойственным этим людям, фон Нейман обосновал свой совет тем, что в среде математиков и инженеров мало кто знает об энтропии, а посему Шеннон получит огромное преимущество в неизбежных грядущих спорах вокруг новой теории. Однако вопреки ожиданиям, новаторской теории Шеннона был сужден мгновенный и широчайший успех среди инженеров, занимающихся системами связи. Она породила огромное количество исследовательских работ и стала мощным стимулом к развитию всех тех технологий, что в конечном счете привели к сегодняшнему «веку информации».
Другая эпохальная работа Клода Шеннона, вышедшая практически одновременно с «теорией информации», по ряду причин не получила такого же широкого резонанса, поскольку явно опережала свое время сразу на несколько десятилетий. Речь идет, конечно же, об опубликованной в 1949 году статье «Теория связи в системах засекречивания» [38](Communication Theory of Secrecy Systems). На самом деле данная статья представляла собой несколько переработанный отчет, подготовленный Шенноном еще в 1945 году. То, что эта работа была рассекречена и опубликована в открытой печати – уже само по себе маленькое чудо, рационально объяснить которое можно лишь тем, что уровень абстрагирования явно показался принимающим решения инстанциям чересчур далеким от практики. Ну а то, что значит этот труд для современной криптологии, можно проиллюстрировать лишь одним примером. Всю историю криптографии от античности до наших дней принято делить на два периода: до 1949 года, когда «тайнопись» считали шаманством, оккультизмом и родом искусства; и после 1949 года, когда криптология стала полноценной прикладной наукой со строгой математической теорией в фундаменте.
За Клодом Шенноном всегда ходила слава весьма разнообразно одаренного человека. Во многом он напоминал «универсальных людей» эпохи Возрождения, причем порою отличался весьма эксцентричным поведением. Одной из наиболее примечательных деталей его жизни непременно упоминают следующую – временами Шеннон любил разъезжать по коридорам Bell Labs на одноколесном велосипеде, да еще жонглируя при этом мячами.

Одним из первых Шеннон высказал мысль о том, что машины могут играть в игры и самообучаться.
В 50-е годы ученым был предпринят целый ряд интереснейших работ, связанных с системами искусственного интеллекта. Одним из первых Шеннон высказал мысль о том, что машины могут играть в игры и самообучаться. Эти идеи сразу стали находить практическое воплощение. Для решения задач поиска выхода из лабиринта Шеннон построил «умную электромеханическую мышку», получившую имя античного героя Тесея. Это устройство стало одной из самых ранних попыток «научить» машину самостоятельно обучаться и находить выход из запутанных коридоров. В честь шенноновского Тесея институтом IEEE впоследствии был учрежден международный конкурс изобретений «микромышь», в котором и поныне тысячами участвуют студенты технических вузов из разных стран мира.
В 1950 году, фактически на самой заре компьютерной эпохи, Клод Шеннон написал статью «Программирование компьютера для игры в шахматы», где сформулировал два типа стратегий, в конечном счете приводящих к машинам, играющим в шахматы на весьма приличном уровне. Для той поры подобная статья выглядела как чудачество ученого-фантазера, однако взгляд Шеннона был устремлен не на современных ему громоздких и неудобных в программировании монстров, а значительно дальше в будущее. Обосновывая важность создания компьютерного шахматиста, Шеннон писал так: «Проблема игры в шахматы жестко очерчена, как в терминах допустимых операций, так и в своей конечной цели. Она не настолько проста, чтобы быть тривиальной, но и не слишком сложна для отыскания удовлетворительных решений».
Для наглядного пояснения этих мыслей можно сказать, что постоянно изменяющаяся сложность шахматной доски – это, к примеру, проблема работы авиадиспетчера в миниатюре. Поэтому на протяжении последнего полувека шахматы для компьютерных ученых являются как бы лабораторным полигоном, на котором обкатываются самые разнообразные технологии систем искусственного интеллекта. И ныне, когда общедоступные шахматные программы вроде Fritz или Junior, работающие на обычном персональном компьютере, уже вполне способны наносить в турнирах поражение чемпионам мира, особо важно подчеркнуть, что в основе всех современных шахматных программ по-прежнему лежат шенноновские стратегии «типа A и B».
В те же 50-е годы Шеннон создал любопытную «машину, способную читать мысли». Говоря точнее, коллега Шеннона Дэйв Хэйглбергер построил аппарат, который в опытах с подбрасыванием монеты предсказывал, что будет выбирать человек – «орла» или «решку». Эта машина явно предсказывала выбор с вероятностью, большей 50%. Так, в эксперименте с 9795 бросками машина 5218 раз сделала правильное предсказание выбора человека. Идея «чтения мыслей» состояла в том, что человек не способен генерировать «чисто случайные» последовательности, невольно подстраиваясь под результаты предыдущих испытаний. Логика обычно примерно такова: «вот выпало три подряд „решки“, значит, теперь-то уж точно выпадет „орел“». Основываясь на этой логике Хэйглбергер и разработал ряд несложных алгоритмов предсказания. Шеннона эта задача тоже заинтересовала и он построил собственную машину для чтения мыслей, выставив ее на соревнование с хэйглбергеровской. В конечном итоге машина Шеннона выиграла, правда, с минимальным преимуществом.
А в 1956 году Шеннону исполнилось 40 лет, и, как стало очевидным несколько позже, рубеж этот стал в его жизни переломным. По каким-то труднообъяснимым причинам ученому, находившемуся, казалось бы, в зените карьеры и творческих сил, наскучила исследовательская работа в Bell Labs, и он решает заняться преподаванием. С 56-го года Шеннон начинает работать в МТИ в качестве приглашенного профессора, а в 1958-м становится там постоянным преподавателем. Последующие 20 лет в МТИ показали, что Шеннону явно стало «неинтересно» заниматься областями, где он достиг столь впечатляющих высот. Зато в эти годы и особенно после ухода в 1978 году на пенсию ученый полностью отдался своей давней страсти – жонглированию. Шенноном было построено несколько жонглирующих машин и даже была создана «общая теория жонглирования». Его постоянно и бесконечно притягивала эта завораживающая игра из непрекращающейся ловли и подбрасывания падающих предметов, формирующих в воздухе причудливые динамические фигуры.
И кто знает, быть может суть этого увлечения и истинный смысл «теории жонглирования» Шеннона человечеству еще только предстоит постичь в будущем. Ведь и очень многие прежние его работы расценивались современниками как блажь и эксцентричное чудачество. Причем и от самого Шеннона неоднократно можно было услышать, что мотивацией его деятельности в значительно большей степени всегда руководило любопытство, нежели «практическая полезность»: «Я всегда следовал своим интересам, не думая ни о том, во что они для меня выльются, ни об их ценности для мира. Я потратил уйму времени на совершенно бесполезные вещи… Мне просто было интересно, как эти вещи устроены».
В сущности, можно говорить, что научную работу Шеннон обращал в забаву. Но в результате этих забав рождались воистину гениальные открытия.
Глава 6. Реальность как эволюция сознания
6.1. Игры, в которые играет Пенроуз
Не так давно, когда газета «Нью-Йорк тайме» брала у знаменитого ученого Роджера Пенроуза интервью в его рабочем кабинете в Оксфорде, журналистка не могла не обратить внимание на игрушки, тут и там рассованные по комнате. «Зачем это вам здесь?» – последовал вопрос. В ответ на него Пенроуз рассмеялся и обронил: «Наука и забава – вещи неразделимые»…
Интересно, что смысл этого диалога практически точно был вновь воспроизведен спустя несколько месяцев опять же в оксфордских декорациях, но совсем другими людьми – Дэвидом Дойчем, создателем теории квантовых вычислений, и бравшим у него интервью редактором «Компьютерры» Леонидом Левковичем-Маслюком. Дойч сказал, что работает почти исключительно дома. И тут же уточнил, что «работает» – это не очень удачное слово для его занятий. Он скорее просто «делает то, что хочется». Решает задачи, смотрит телевизор, программирует, снимает анимационные фильмы, играет в компьютерные игры. Все эти занятия являются для него одним и тем же… Когда слышишь такие признания ученых, невольно всплывает слово «лила». В индуистской философии этим термином обозначают разворачивающийся процесс познания Абсолютом самого себя. «Лила» с санскрита переводится как «забава» или «игра».

Видимо, неслучайно эту же «божественную игру» постижения себя и природы столь естественным образом осваивают наиболее яркие мыслители человечества. Один из них, безусловно, и «рыцарь науки» сэр Роджер Пенроуз – математик и физик, автор книг и преподаватель. Ученый, отметивший в 2001-м году свой 70-летний юбилей и являющийся, возможно, одним из величайших ныне живущих последователей Альберта Эйнштейна.
В 1960-е годы Пенроузом в совместных со Стивеном Хокингом работах были заложены основы современной теории «черных дыр». На рубеже 60-70-х им начата огромная, продолжающаяся и поныне работа по созданию «теории твисторов», в конечном счете призванная свести в единую стройную систему гравитацию и квантовую механику. В 70-е ученый сделал удивительное открытие совсем в иной области, подарив миру «мозаику Пенроуза» (как стала она в итоге называться), позволяющую с помощью пары плиток весьма простой формы мостить бесконечную плоскость никогда не повторяющимся узором. В 80-90-е годы Пенроуз всерьез взялся за проблемы человеческого сознания и искусственного интеллекта, написав две весьма необычные книги – «Новый разум императора» и «Тени разума», – без преувеличения «зацепившие» не только научное сообщество, но и широкую публику. Однако все это, в конечном счете, проявления одной и той же забавы ученого под общим названием «А тут прихожу я и говорю…»
Занимательная математика всегда была страстью Роджера Пенроуза. Активный интерес ученого к этой области, можно сказать, семейная черта, унаследованная им от отца, генетика Л. С. Пенроуза, также увлекавшегося математическими головоломками. В 1950-е годы отец и сын Пенроузы, находясь под сильным впечатлением от знакомства с творчеством голландского художника Морица Эшера, придумали пару собственных «невозможных фигур» в эшеровском духе: широко известные ныне «бесконечную лестницу Пенроузов» и треугольник-«трибар».
Впоследствии Эшер использовал идеи Пенроузов в таких своих литографиях, как «Водопад» и «Восхождение и спуск».

Хотя основная работа Пенроуза сосредоточена на теории относительности и квантовой физике, свою докторскую диссертацию в Кембридже он защищал в области алгебраической геометрии. К этому разделу математики весьма тесно примыкают легкомысленные на первый взгляд задачи геометрических головоломок, связанных с проблемой «замощения», т. е. разбиения плоскости фигурами определенной формы.
Задачи разбиения плоскости тривиально решаются с помощью периодически повторяющихся комбинаций из таких фигур как равнобедренные треугольники, прямоугольники, шестиугольники, и т. п. Пенроуза же интересовала проблема отыскания такой формы фигур, которая приводила бы к замощению плоскости без порождения повторяющихся узоров. В действительности эта задача чрезвычайно важна, поскольку связана с проблемой разрешимости в математической логике. На протяжении многих лет считалось, что не может быть таких плиток, из которых строились бы только непериодические мозаики. Затем, в 1960-е годы решение нашли, но для плиток тривиальной квадратной формы, снабженных несколькими пазами и выступами.
Пенроузу удалось найти решение для неквадратных плиток, однако поначалу для этого требовалось несколько тысяч фигур различной формы. Еще несколько лет понадобилось на то, чтобы к 1973 г. сократить это число до шести. В конце же концов оказалось, что таких плиток нужно всего две, причем форма их предельно проста и замыкается на одну из величайших тайн природы – знаменитое «золотое сечение», лежащее в основе всех гармоничных соотношений. Получаются фигуры из ромба с углами 72 и 108 градусов, большая диагональ которого поделена в отношении, равном «золотому сечению». Эти фигуры получили название Kite и Dart («воздушный змей» и «дротик»).

Чуть позже выяснилось, что и две фигуры можно свести до совсем простых форм – просто ромбов, составленных на основе «золотого треугольника» (с углами 36 и 144 градуса).
Мозаики Пенроуза стали предметом пристального изучения, поскольку демонстрируют множество примечательных свойств и поистине неисчерпаемую глубину, скрытую за «золотым сечением»: количество укладываемых плиток постоянно пребывает в соотношении, близком к золотой пропорции; получающиеся узоры «квазисимметричны» и имеют ось симметрии пятого порядка; структура рисунков мозаики тесно связана с последовательностью Фибоначчи…
Пенроуз вполне понимал, что найденные им фигуры можно заложить в основу коммерческих игр-головоломок. Поэтому он несколько лет предусмотрительно воздерживался от публикации своего открытия до тех пор, пока не оформил на него патенты в Британии, США и Японии. Правда, в результате судьба чуть было не сыграла с излишне, быть может, расчетливым ученым злую шутку, поскольку в 1976 году по сути дела то же самое открытие независимо сделал молодой американский математик Роберт Амман.
И случись так, что обратил бы свое внимание великий популяризатор науки Мартин Гарднер на открытие Аммана, а не Пенроуза, то и вошли бы знаменитые мозаики в историю совсем под другим именем… но что сделано, то сделано, и патент на свое изобретение Пенроуз передал компании Pentaplex, которая делает на этой основе забавные, но не такие уж простые в решении мозаики-головоломки из «петушков» и «курочек».

В 1995 году ученый-математик по имени Роджер Шлафли оформил патент на два очень больших простых числа, им найденных, а посему, в некотором смысле, изобретенных. По поводу подобного «изобретения» в научном сообществе поднялась целая буря протестов, поскольку еще никому в голову не приходило объявлять права интеллектуальной собственности на числа. Среди громко осудивших Шлафли, как это ни странно, был и сэр Роджер Пенроуз, с возрастом, похоже, несколько изменивший свои воззрения на этическую проблему патентования математических решений. «Это абсурд, – сказал он,– математика существует для всех».
Но судьба тут же приготовила Пенроузу ироничный урок. В 1997 году его жена принесла из магазина пачку рулонов туалетной бумаги, на которой ученый мгновенно узнал характерный рисунок своего знаменитого детища – мозаику Пенроуза! Последовавшее негодование ученого по-человечески вполне можно понять. Он столько лет занимался поиском решения сложнейшей задачи, а тут некая бесстыжая фирма использует его открытие для подтирания… ну, понятно чего. Математика – это, конечно, для всех, но не до такой же степени. И оскорбленный Пенроуз подал на компанию в суд (хотя какой-нибудь рассудительный индус, наверное, на подобную коллизию прореагировал бы спокойнее – «это карма»).
Ныне мозаики Пенроуза – это не только куча доказанных абстрактных теорем, головоломки Pentaplex и комичная история с сортиром. В 1984 году сотрудники НИСТ США сделали сенсационное открытие, обнаружив непериодическую структуру на электронограмме быстро охлажденного сплава марганца и алюминия. Расположение рефлексов – светлых пятен – на снимке обладало осью симметрии 5-го порядка, что с математической точки зрения убедительно свидетельствовало о существовании непериодического пространственного расположения атомов, аналогичного мозаике Пенроуза.

Это открытие было чрезвычайно сильным ударом по фундаментальным догмам кристаллографии, где долгое время господствовало утверждение, что кристаллы могут обладать лишь осями симметрии 2-го, 3-го, 4-го и 6-го порядка, но никак не 5-го. Согласно другой догме, твердое вещество могло существовать только в двух формах: либо с регулярной периодической решеткой атомов в кристалле, либо в хаотическом беспорядке атомов аморфных тел, как в стекле, к примеру. Открытие кристаллов с непериодической «квазисимметричной» структурой означает, что между аморфными телами и периодическими кристаллами имеется не четкое разграничение, как казалось долгое время, а плавный переход.
Но означает это и нечто значительно большее. В частности, для понимания природы человеческого сознания, способного предсказывать вещи, противоречащие повседневному опыту и не вычисляемые с помощью компьютера.
Проблема непериодического покрытия плоскости, решаемая мозаикой Пенроуза, как было доказано значительно позже, принадлежит к классу задач, не вычислимых алгоритмически на компьютере. И это далеко не единственная задача из тех, что успешно решены человеком, но не укладываются в логику вычислительных машин. Более того, если учитывать богатый опыт кристаллографии, то решение найдено Пенроузом и вопреки опыту, в некотором смысле. Тем не менее ответ на задачу искался математиком с завидным упорством по той, в сущности, причине, что Пенроуз чувствовал – решение есть.
Ученым, делающим открытия, очень хорошо известно, что решения задач нередко рождаются как бы уже в готовом виде. И лишь затем, для обоснования найденного ответа и внятного его пояснения коллегам, выстраиваются цепочки формул или логических аргументов. Правда, удается это не всегда, и в физике, к примеру, имеется достаточное количество формул, которые ниоткуда не выводятся, а существуют сами по себе. Как проявления пытливого ума человеческого.
Пенроуза крайне занимала эта особенность мыслительных процессов. Но чем больше он над этим размышлял, тем больше понимал, что сознание – это такая область науки, где по сию пору вопросов существует намного больше чем ответов. В итоге он, будучи сам математиком и физиком, пришел к выводу, что ухватить суть разума в строгих научных и логических терминах человеку мешает непонимание фундаментальных законов физики.
В 1989 году Пенроуз выпускает книгу «Новый разум императора. О компьютерах, сознании и законах физики» (The Emperor's New Mind: Concerning Computers, Minds, and the Laws of Physics). Книга стала заметнейшей вехой в дискуссиях, ведущихся вокруг феномена сознания и проблем построения мощных систем искусственного интеллекта (ИИ).
Главный тезис Пенроуза: «Сознание не поддается расчету и функционирует не алгоритмически… Мозг – это не компьютер». С помощью логических аргументов, привлекая известные факты физики и математики, Пенроуз показывает, какие вещи о сознании можно установить, а какие нет. Демонстрирует, что в человеческом мышлении есть такие аспекты, которые никогда не удастся повторить с помощью машины. Что имеется некая внутренняя, непостижимая пока связь между квантовыми эффектами взаимодействия субатомных частиц в живом организме и нашим мышлением («квантовое сознание»). В конечном же счете из этого выводится твердое заключение, что «искусственный интеллект» невозможен, поскольку значительная часть сознания, а может и все оно целиком, не является по природе своей алгоритмическим. Так что прежде, чем поднимать вопрос об искусственном интеллекте, необходимо разобраться с физическими процессами, сознание образующими.
Вскоре после выхода книги, вызвавшей бурю дискуссий и опровержений из лагеря сторонников ИИ, внимание Пенроуза привлекла работа американского врача и биолога Стюарта Хамерофа, посвященная так называемым микротрубкам цитоскелета. Эти весьма специфические цилиндрические молекулы диаметром около 25 нанометров, имеющиеся почти во всех клетках, были обнаружены наукой относительно поздно и фактически «по недоразумению».
При подготовке проб для электронного микроскопа всегда использовали жидкость, которая растворяла те белки, из которых состоят микротрубки. И лишь когда перешли на другой растворитель, случайно выявили в клетках новые структуры, выполняющие, как поначалу решили, функции «скелета». Однако при более глубоком анализе было установлено, что образующие микротрубки элементы – тубулины – имеют два возможных состояния, переключение между которыми происходит небывало для биологии быстро, за наносекунды.
По сути дела, был открыт «клеточный автомат», изготовленный самой природой. Хамероф предположил, что микротрубки в нейронах мозга и являются местом воплощения «квантового сознания».
Роджер Пенроуз счел эти идеи квантового разума вполне «безумными, чтобы быть верными» и взялся за их разработку в следующей своей книге «Тени разума. В поисках недостающей науки сознания» (Shadows of the Mind: A Search for the Missing Science of Consciousness). В самом обобщенном виде созданная Хамерофом-Пенроузом модель «физики сознания» выглядит так. На основе косвенных экспериментальных данных и ряда физических соображений-аргументов делается предположение, что тубулины в микротрубках способны образовывать большие когерентные квантовые системы. Говоря иначе, большая совокупность тубулинов может некоторое время жить «квантовой жизнью», а потом переходить в классическое состояние с помощью невычислимой процедуры OR («операционной редукции»). Именно этот переход и есть «момент сознания» или «элементарный фактор чувственного опыта», если пользоваться терминологией философа Уайтхеда. Поток таких событий и образует субъективно ощущаемый человеком «поток сознания». Так что все происходящее с нейронами мозга – это как бы «тень» истинно важных квантовых процессов, или «операционной редукции» в микротрубках.
Хотя в обоснование всей этой модели выстроен фундамент логических аргументов, строго говоря, она остается чисто умозрительным построением ученых. Уровень сегодняшней экспериментальной физики, занимающейся масштабно организованными событиями на квантовом уровне, вынуждает строить исследования при тщательном исключении температурных и других хаотических эффектов, что никак не сопоставимо с теплой и влажной субстанцией мозга. Да и сам механизм, который позволял бы огромной массе микротрубок взаимодействовать друг с другом через стенки клеток, остается пока под очень большим вопросом.
Короче говоря, на нынешнем этапе по-прежнему совершенно не ясно, что именно происходит в сознании и как, и вообще, есть ли в теории Хамерофа-Пенроуза более глубокий смысл, чем в удачной шутке философа Дэвида Чалмерса: «Сознание – тайна, квантовая механика – тоже тайна. Две тайны – все равно, что одна. Так может быть, это и есть одно и тоже?»…
Еще один важнейший тезис в позиции Пенроуза, глубоко развиваемый им в обеих посвященных тайнам сознания книгах, состоит в том, что современная наука вообще и физика в частности в принципе неадекватны для решения проблем мышления. И неадекватна она будет всегда, когда дело доходит до описания природы человеческого интеллекта, познавательных способностей и сознания вообще. Этот тезис весьма близок теореме Курта Геделя о неполноте, говорящей что для любой конечной системы аксиом всегда существуют утверждения, истинность или ложность которых в рамках этой системы доказать невозможно. Говоря иначе, Пенроуз полагает, что имеются элементарные ограничения внутри самой науки, сужающие наше понимание собственных мысленных процессов, что естественным образом ограничивает и возможности к созданию искусственного интеллекта.
Когда Пенроузу случается встречаться с журналистами, то неизменно возникают вопросы о том, почему сторонники искусственного интеллекта столь яростно защищают идею о машинах, способных разумом превзойти человеческое существо.
Интересно, что смысл этого диалога практически точно был вновь воспроизведен спустя несколько месяцев опять же в оксфордских декорациях, но совсем другими людьми – Дэвидом Дойчем, создателем теории квантовых вычислений, и бравшим у него интервью редактором «Компьютерры» Леонидом Левковичем-Маслюком. Дойч сказал, что работает почти исключительно дома. И тут же уточнил, что «работает» – это не очень удачное слово для его занятий. Он скорее просто «делает то, что хочется». Решает задачи, смотрит телевизор, программирует, снимает анимационные фильмы, играет в компьютерные игры. Все эти занятия являются для него одним и тем же… Когда слышишь такие признания ученых, невольно всплывает слово «лила». В индуистской философии этим термином обозначают разворачивающийся процесс познания Абсолютом самого себя. «Лила» с санскрита переводится как «забава» или «игра».

Роджер Пенроуз.
Видимо, неслучайно эту же «божественную игру» постижения себя и природы столь естественным образом осваивают наиболее яркие мыслители человечества. Один из них, безусловно, и «рыцарь науки» сэр Роджер Пенроуз – математик и физик, автор книг и преподаватель. Ученый, отметивший в 2001-м году свой 70-летний юбилей и являющийся, возможно, одним из величайших ныне живущих последователей Альберта Эйнштейна.
В 1960-е годы Пенроузом в совместных со Стивеном Хокингом работах были заложены основы современной теории «черных дыр». На рубеже 60-70-х им начата огромная, продолжающаяся и поныне работа по созданию «теории твисторов», в конечном счете призванная свести в единую стройную систему гравитацию и квантовую механику. В 70-е ученый сделал удивительное открытие совсем в иной области, подарив миру «мозаику Пенроуза» (как стала она в итоге называться), позволяющую с помощью пары плиток весьма простой формы мостить бесконечную плоскость никогда не повторяющимся узором. В 80-90-е годы Пенроуз всерьез взялся за проблемы человеческого сознания и искусственного интеллекта, написав две весьма необычные книги – «Новый разум императора» и «Тени разума», – без преувеличения «зацепившие» не только научное сообщество, но и широкую публику. Однако все это, в конечном счете, проявления одной и той же забавы ученого под общим названием «А тут прихожу я и говорю…»
Узоры золотого сечения
Занимательная математика всегда была страстью Роджера Пенроуза. Активный интерес ученого к этой области, можно сказать, семейная черта, унаследованная им от отца, генетика Л. С. Пенроуза, также увлекавшегося математическими головоломками. В 1950-е годы отец и сын Пенроузы, находясь под сильным впечатлением от знакомства с творчеством голландского художника Морица Эшера, придумали пару собственных «невозможных фигур» в эшеровском духе: широко известные ныне «бесконечную лестницу Пенроузов» и треугольник-«трибар».
Впоследствии Эшер использовал идеи Пенроузов в таких своих литографиях, как «Водопад» и «Восхождение и спуск».

«Бесконечная лестница» и треугольник-«трибар».
Хотя основная работа Пенроуза сосредоточена на теории относительности и квантовой физике, свою докторскую диссертацию в Кембридже он защищал в области алгебраической геометрии. К этому разделу математики весьма тесно примыкают легкомысленные на первый взгляд задачи геометрических головоломок, связанных с проблемой «замощения», т. е. разбиения плоскости фигурами определенной формы.
Задачи разбиения плоскости тривиально решаются с помощью периодически повторяющихся комбинаций из таких фигур как равнобедренные треугольники, прямоугольники, шестиугольники, и т. п. Пенроуза же интересовала проблема отыскания такой формы фигур, которая приводила бы к замощению плоскости без порождения повторяющихся узоров. В действительности эта задача чрезвычайно важна, поскольку связана с проблемой разрешимости в математической логике. На протяжении многих лет считалось, что не может быть таких плиток, из которых строились бы только непериодические мозаики. Затем, в 1960-е годы решение нашли, но для плиток тривиальной квадратной формы, снабженных несколькими пазами и выступами.
Пенроузу удалось найти решение для неквадратных плиток, однако поначалу для этого требовалось несколько тысяч фигур различной формы. Еще несколько лет понадобилось на то, чтобы к 1973 г. сократить это число до шести. В конце же концов оказалось, что таких плиток нужно всего две, причем форма их предельно проста и замыкается на одну из величайших тайн природы – знаменитое «золотое сечение», лежащее в основе всех гармоничных соотношений. Получаются фигуры из ромба с углами 72 и 108 градусов, большая диагональ которого поделена в отношении, равном «золотому сечению». Эти фигуры получили название Kite и Dart («воздушный змей» и «дротик»).

Плитки мозаики Пенроуза.
Чуть позже выяснилось, что и две фигуры можно свести до совсем простых форм – просто ромбов, составленных на основе «золотого треугольника» (с углами 36 и 144 градуса).
Мозаики Пенроуза стали предметом пристального изучения, поскольку демонстрируют множество примечательных свойств и поистине неисчерпаемую глубину, скрытую за «золотым сечением»: количество укладываемых плиток постоянно пребывает в соотношении, близком к золотой пропорции; получающиеся узоры «квазисимметричны» и имеют ось симметрии пятого порядка; структура рисунков мозаики тесно связана с последовательностью Фибоначчи…
Пенроуз вполне понимал, что найденные им фигуры можно заложить в основу коммерческих игр-головоломок. Поэтому он несколько лет предусмотрительно воздерживался от публикации своего открытия до тех пор, пока не оформил на него патенты в Британии, США и Японии. Правда, в результате судьба чуть было не сыграла с излишне, быть может, расчетливым ученым злую шутку, поскольку в 1976 году по сути дела то же самое открытие независимо сделал молодой американский математик Роберт Амман.
И случись так, что обратил бы свое внимание великий популяризатор науки Мартин Гарднер на открытие Аммана, а не Пенроуза, то и вошли бы знаменитые мозаики в историю совсем под другим именем… но что сделано, то сделано, и патент на свое изобретение Пенроуз передал компании Pentaplex, которая делает на этой основе забавные, но не такие уж простые в решении мозаики-головоломки из «петушков» и «курочек».

Мозаики Пенроуза стали предметом пристального изучения, поскольку демонстрируют множество примечательных свойств и поистине неисчерпаемую глубину.
В 1995 году ученый-математик по имени Роджер Шлафли оформил патент на два очень больших простых числа, им найденных, а посему, в некотором смысле, изобретенных. По поводу подобного «изобретения» в научном сообществе поднялась целая буря протестов, поскольку еще никому в голову не приходило объявлять права интеллектуальной собственности на числа. Среди громко осудивших Шлафли, как это ни странно, был и сэр Роджер Пенроуз, с возрастом, похоже, несколько изменивший свои воззрения на этическую проблему патентования математических решений. «Это абсурд, – сказал он,– математика существует для всех».
Но судьба тут же приготовила Пенроузу ироничный урок. В 1997 году его жена принесла из магазина пачку рулонов туалетной бумаги, на которой ученый мгновенно узнал характерный рисунок своего знаменитого детища – мозаику Пенроуза! Последовавшее негодование ученого по-человечески вполне можно понять. Он столько лет занимался поиском решения сложнейшей задачи, а тут некая бесстыжая фирма использует его открытие для подтирания… ну, понятно чего. Математика – это, конечно, для всех, но не до такой же степени. И оскорбленный Пенроуз подал на компанию в суд (хотя какой-нибудь рассудительный индус, наверное, на подобную коллизию прореагировал бы спокойнее – «это карма»).
Ныне мозаики Пенроуза – это не только куча доказанных абстрактных теорем, головоломки Pentaplex и комичная история с сортиром. В 1984 году сотрудники НИСТ США сделали сенсационное открытие, обнаружив непериодическую структуру на электронограмме быстро охлажденного сплава марганца и алюминия. Расположение рефлексов – светлых пятен – на снимке обладало осью симметрии 5-го порядка, что с математической точки зрения убедительно свидетельствовало о существовании непериодического пространственного расположения атомов, аналогичного мозаике Пенроуза.

Электронограмма непериодического кристалла с осью симметрии пятого порядка.
Это открытие было чрезвычайно сильным ударом по фундаментальным догмам кристаллографии, где долгое время господствовало утверждение, что кристаллы могут обладать лишь осями симметрии 2-го, 3-го, 4-го и 6-го порядка, но никак не 5-го. Согласно другой догме, твердое вещество могло существовать только в двух формах: либо с регулярной периодической решеткой атомов в кристалле, либо в хаотическом беспорядке атомов аморфных тел, как в стекле, к примеру. Открытие кристаллов с непериодической «квазисимметричной» структурой означает, что между аморфными телами и периодическими кристаллами имеется не четкое разграничение, как казалось долгое время, а плавный переход.
Но означает это и нечто значительно большее. В частности, для понимания природы человеческого сознания, способного предсказывать вещи, противоречащие повседневному опыту и не вычисляемые с помощью компьютера.
Тени сознания императора
Проблема непериодического покрытия плоскости, решаемая мозаикой Пенроуза, как было доказано значительно позже, принадлежит к классу задач, не вычислимых алгоритмически на компьютере. И это далеко не единственная задача из тех, что успешно решены человеком, но не укладываются в логику вычислительных машин. Более того, если учитывать богатый опыт кристаллографии, то решение найдено Пенроузом и вопреки опыту, в некотором смысле. Тем не менее ответ на задачу искался математиком с завидным упорством по той, в сущности, причине, что Пенроуз чувствовал – решение есть.
Ученым, делающим открытия, очень хорошо известно, что решения задач нередко рождаются как бы уже в готовом виде. И лишь затем, для обоснования найденного ответа и внятного его пояснения коллегам, выстраиваются цепочки формул или логических аргументов. Правда, удается это не всегда, и в физике, к примеру, имеется достаточное количество формул, которые ниоткуда не выводятся, а существуют сами по себе. Как проявления пытливого ума человеческого.
Пенроуза крайне занимала эта особенность мыслительных процессов. Но чем больше он над этим размышлял, тем больше понимал, что сознание – это такая область науки, где по сию пору вопросов существует намного больше чем ответов. В итоге он, будучи сам математиком и физиком, пришел к выводу, что ухватить суть разума в строгих научных и логических терминах человеку мешает непонимание фундаментальных законов физики.
В 1989 году Пенроуз выпускает книгу «Новый разум императора. О компьютерах, сознании и законах физики» (The Emperor's New Mind: Concerning Computers, Minds, and the Laws of Physics). Книга стала заметнейшей вехой в дискуссиях, ведущихся вокруг феномена сознания и проблем построения мощных систем искусственного интеллекта (ИИ).
Главный тезис Пенроуза: «Сознание не поддается расчету и функционирует не алгоритмически… Мозг – это не компьютер». С помощью логических аргументов, привлекая известные факты физики и математики, Пенроуз показывает, какие вещи о сознании можно установить, а какие нет. Демонстрирует, что в человеческом мышлении есть такие аспекты, которые никогда не удастся повторить с помощью машины. Что имеется некая внутренняя, непостижимая пока связь между квантовыми эффектами взаимодействия субатомных частиц в живом организме и нашим мышлением («квантовое сознание»). В конечном же счете из этого выводится твердое заключение, что «искусственный интеллект» невозможен, поскольку значительная часть сознания, а может и все оно целиком, не является по природе своей алгоритмическим. Так что прежде, чем поднимать вопрос об искусственном интеллекте, необходимо разобраться с физическими процессами, сознание образующими.

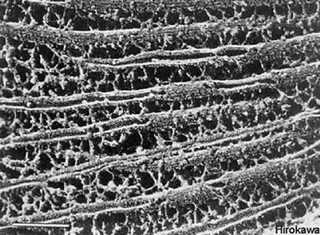
Микротрубки цитоскелета.
Вскоре после выхода книги, вызвавшей бурю дискуссий и опровержений из лагеря сторонников ИИ, внимание Пенроуза привлекла работа американского врача и биолога Стюарта Хамерофа, посвященная так называемым микротрубкам цитоскелета. Эти весьма специфические цилиндрические молекулы диаметром около 25 нанометров, имеющиеся почти во всех клетках, были обнаружены наукой относительно поздно и фактически «по недоразумению».
При подготовке проб для электронного микроскопа всегда использовали жидкость, которая растворяла те белки, из которых состоят микротрубки. И лишь когда перешли на другой растворитель, случайно выявили в клетках новые структуры, выполняющие, как поначалу решили, функции «скелета». Однако при более глубоком анализе было установлено, что образующие микротрубки элементы – тубулины – имеют два возможных состояния, переключение между которыми происходит небывало для биологии быстро, за наносекунды.
По сути дела, был открыт «клеточный автомат», изготовленный самой природой. Хамероф предположил, что микротрубки в нейронах мозга и являются местом воплощения «квантового сознания».
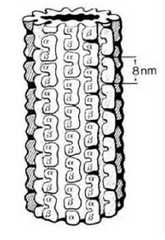
Роджер Пенроуз счел эти идеи квантового разума вполне «безумными, чтобы быть верными» и взялся за их разработку в следующей своей книге «Тени разума. В поисках недостающей науки сознания» (Shadows of the Mind: A Search for the Missing Science of Consciousness). В самом обобщенном виде созданная Хамерофом-Пенроузом модель «физики сознания» выглядит так. На основе косвенных экспериментальных данных и ряда физических соображений-аргументов делается предположение, что тубулины в микротрубках способны образовывать большие когерентные квантовые системы. Говоря иначе, большая совокупность тубулинов может некоторое время жить «квантовой жизнью», а потом переходить в классическое состояние с помощью невычислимой процедуры OR («операционной редукции»). Именно этот переход и есть «момент сознания» или «элементарный фактор чувственного опыта», если пользоваться терминологией философа Уайтхеда. Поток таких событий и образует субъективно ощущаемый человеком «поток сознания». Так что все происходящее с нейронами мозга – это как бы «тень» истинно важных квантовых процессов, или «операционной редукции» в микротрубках.

Тубулины.
Хотя в обоснование всей этой модели выстроен фундамент логических аргументов, строго говоря, она остается чисто умозрительным построением ученых. Уровень сегодняшней экспериментальной физики, занимающейся масштабно организованными событиями на квантовом уровне, вынуждает строить исследования при тщательном исключении температурных и других хаотических эффектов, что никак не сопоставимо с теплой и влажной субстанцией мозга. Да и сам механизм, который позволял бы огромной массе микротрубок взаимодействовать друг с другом через стенки клеток, остается пока под очень большим вопросом.
Короче говоря, на нынешнем этапе по-прежнему совершенно не ясно, что именно происходит в сознании и как, и вообще, есть ли в теории Хамерофа-Пенроуза более глубокий смысл, чем в удачной шутке философа Дэвида Чалмерса: «Сознание – тайна, квантовая механика – тоже тайна. Две тайны – все равно, что одна. Так может быть, это и есть одно и тоже?»…
Еще один важнейший тезис в позиции Пенроуза, глубоко развиваемый им в обеих посвященных тайнам сознания книгах, состоит в том, что современная наука вообще и физика в частности в принципе неадекватны для решения проблем мышления. И неадекватна она будет всегда, когда дело доходит до описания природы человеческого интеллекта, познавательных способностей и сознания вообще. Этот тезис весьма близок теореме Курта Геделя о неполноте, говорящей что для любой конечной системы аксиом всегда существуют утверждения, истинность или ложность которых в рамках этой системы доказать невозможно. Говоря иначе, Пенроуз полагает, что имеются элементарные ограничения внутри самой науки, сужающие наше понимание собственных мысленных процессов, что естественным образом ограничивает и возможности к созданию искусственного интеллекта.
Когда Пенроузу случается встречаться с журналистами, то неизменно возникают вопросы о том, почему сторонники искусственного интеллекта столь яростно защищают идею о машинах, способных разумом превзойти человеческое существо.
