TheLib.Ru » Энциклопедии » БСЭ » Большая Советская Энциклопедия (СР) » онлайн-чтение (стр. 9)

 

 

барабанной перепонкой ; от внутреннего уха оно отделено хрящевой или костной стенкой преддверия лабиринта. Слуховые косточку передают звуковые колебания с барабанной перепонки во внутреннее ухо. С. у. у большинства животных соединяется с глоткой посредством евстахиевой трубы . С. у. ряда наземных позвоночных и особенно млекопитающих включает многие дополнительные образования, выполняющие важные акустические функции (см. Барабаны слуховые ). У ряда вторичноводных и наземных земноводных, млекопитающих, а также у некоторых черепах и змеи наблюдается частичная или полная редукция С. у. О воспалении С. у. см. Отит .

Герцинской Европы . Длина с З. на В. около 600 км, ширина от 200 до 500 км, преобладают высоты 50—100 м(в отдельных моренных грядах свыше 300 м). Сложена главным образом известняками и песчаниками, перекрытыми ледниковыми отложениями (моренные гряды, зандровые поля и др.). Климат умеренный, переходный от морского к континентальному. Средняя температура января на З. от —1 до —3°С, на В. от —2 до —4°С; июля — повсеместно 17—19 °С. Сумма осадков уменьшается с З. на В. от 800 до 500 ммв год. Снежный покров на З. неустойчив, на В. — 1,5—2 мес. Густая сеть рек (бассейна Одры, Эльбы, Везера, Рейна и др.). Многочисленны ледниковые озёра. Преобладают бурые лесные и подзолистые почвы. Естественная растительность — дубово-буковые (на З.) и смешанные (на В.) леса — в значительной степени сведена или замещена насаждениями хвойных пород; на С. — верещатники, торфяники. По долинам рек — луга. Посевы зерновых, сахарной свёклы, животноводство. С. р. густо заселена. На С. р. — гг. Познань (Польша), Берлин (ГДР), Западный Берлин (особая политическая единица), Гамбург, Бремен, Ганновер (ФРГ), Амстердам, Роттердам (Нидерланды).
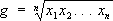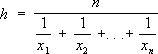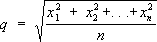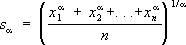
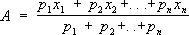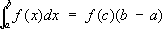      К. Г. Тарасов.

европеоидную расу . По пигментации занимает промежуточное положение между северными и южными европеоидами (ближе к первым). Характеризуется светлой кожей, русыми волосами, светлыми или смешанными глазами, средним или выше среднего ростом, брахикефалией . Распространена в Центральной и Восточной Европе среди южных немцев, австрийцев, венгров, чехов и словаков, северных украинцев, южных белорусов, русских средней полосы и соседних с ними народов.

Кухруд и Кухбенан). Высота до 4420 м(потухший вулкан Хезар), относительные превышения над прилегающими равнинами — 2000—2500 м. С. г. сложены осадочными и вулканическими породами, многочисленные осыпи. Осадков 100—300 ммв год. В межгорных долинах и нижних частях склонов — полынно-эфемеровые пустыни; в верхнем поясе гор — фриганоидная растительность. По долинам рек —заросли тополя, ивы, лоха, грецкого ореха. Кочевое животноводство.

Центральночернозёмный заповедник им. В. В. Алехина, заповедник Галичья гора .
     Лит.:Средняя полоса Европейской части СССР, М., 1967.
      В. К. Жучкова.

Сибирской платформы . Средняя высота плоскогорья 500—700 м. Большая часть территории плоскогорья, расположенная в бассейнах рр. Нижней Тунгуски и Подкаменной Тунгуски, Ангары и верховьев Вилюя, характеризуется сглаженным рельефом, здесь широко распространены плоские и широкие междуречья. Наиболее приподнятые участки располагаются на С.-З., где массивы плато Путорана достигают высоты 1500—1700 м. Вилюйское плато и плоские междуречья в верховьях р. Лены — 900—1100 м. Из полезных ископаемых наибольшее значение имеют никелевые и медные руды (район Норильска), железные руды (Ангаро-Илимский район и Ангаро-Питский бассейна), каменный уголь (Тунгусский, Черемховский, Канский бассейна), графит, каменная соль, природный газ.
     Реки относятся к бассейну Северного Ледовитого океана. Большинство рек многоводны, текут преимущественно в глубоких и узких долинах, имеют быстрое течение, изобилуют порогами. Крупнейшие реки: Нижняя Тунгуска, Подкаменная Тунгуска, Ангара, Лена с Вилюем, Хатанга, Анабар, Оленек.
     Климат резко континентальный, с холодной (средняя температура января от —20 °С на Ю.-З. до —44 °С на С.-В.) и продолжительной зимой и тёплым (средняя температура июля от 12 °С на С. до 20 °С на Ю.) летом. Осадков выпадает от 200—350 ммна В. до 400—500 ммна З. (на плато Путорана до 700—800 мм) в год. Широко распространены многолетнемёрзлые горные породы.
     Большая часть плоскогорья расположена в зоне светлохвойной тайги, среди которой преобладают лиственничные леса (даурская лиственница на В. и сибирская на З.) на слабоподзолистых и дерново-подзолистых почвах, а на С. — на глеевато-подзолистых. На Ю., в бассейна Ангары широко распространены сосновые и сосново-лиственничные боры на дерново-подзолистых почвах; к С. от Подкаменной Тунгуски — главным образом редкостойные и низкорослые заболоченные лиственничники. На Ю. среди тайги в Канской, Иркутско-Черемховской впадинах и в бассейна р. Куды — острова лесостепей (Красноярская лесостепь, Канская лесостепь, Балаганские степи). На С. плато Путорана, Сыверма и возвышенностях Анабарского массива обширные пространства заняты горной тундрой; на Лено-Ангарском плато и Енисейском кряже (на высоте более 1000 м) — острова горной тундры. Для животного мира тундры характерны лемминги, песец, заяц-беляк, сев. олень, для тайги — лось, кабарга, бурый медведь, росомаха. Из птиц — глухарь, рябчик. Реки богаты рыбой (сибирский осётр, сиг, таймень и др.). Промысловое значение имеют белка, соболь, ондатра.
     Лит.:Воскресенский С. С., Геоморфология Сибири, М., 1962; Средняя Сибирь, М., 1964 (Природные условия и естественные ресурсы СССР); Равнины и горы Сибири. (Геоморфология СССР), М., 1975.

фотографический аппарат с форматами кадров (согласно ГОСТу): 45 Х 60; 60 Х 60; 60 X 70 и 60 X 90 мм. Получаемые на фотоплёнке изображения имеют соответственно размеры: 41 Х 57; 57х57; 57 X 72 и 57 X 82,5 ммс допуском ± 1 мм.

Прага . Северная часть области преимущественно равнинная (Полабье), южная — более пересечённая, лесисто-холмистая территория (бассейн р. Влтава).
     С. о. — высокоразвитый индустриальный район с интенсивным сельское хозяйством. На область приходится 9% промышленной (вместе с Прагой — 18%) и 11% с.-х. продукции страны. Добыча каменного угля (Кладно, Раковник), железной руды, полиметаллов. ТЭС (в гг. Мельник, Прага), ГЭС на р. Влтава. Металлургия (Кладно), машиностроение (Прага с окружением, Млада-Болеслав, Колин, Кладно): выпуск различного промышленного оборудования, станков, электротехнических изделий, автомобилей и т.п. Химическая промышленность (минеральные удобрения, искусственное волокно, искусственные каучук) — в гг. Колин, Кралупи, Нератовице; производство стройматериалов (цемент), деревообработка, лёгкая и пищевая (особенно сахарная) промышленность. Высокоинтенсивное сельское хозяйство специализировано на производстве зерна (пшеница, ячмень) и сахарной свёклы в сочетании с развитым мясомолочным животноводством. Крупное овощеводство и садоводство; на З. области культивируют хмель ( 1/ 3продукции страны).
      Л. А. Авдеичев.

Гёта-канал . Низины обычно распаханы и густо заселены, на холмах и скальных останцах — леса из ели, сосны, местами с примесью дуба. На С. н. — гг. Стокгольм, Вестерос, Норчёпинг, Упсала, Эребру.

арифметическое среднее  
    ,
     геометрическое среднее
    ,
      гармоническое среднее
     ,
      квадратичное среднее
     .
     Если все числа x i( i= l,2,..., n) положительны, то можно для любого a ¹ 0 определить степенное С.
    
     частными случаями которого являются арифметическое, гармоническое и квадратичное С., именно: s (а равняется a, hи qсоответственно при a = 1, —1 и 2. При a ® 0 степенное С, s aстремится к геометрическому С., так что можно считать s 0= g. Важную роль играет неравенство s aЈ s b, если a Ј b, в частности
     hЈ gЈ aЈ q.
     Арифметическое и квадратичное С. находят многочисленные применения в теории вероятностей, математической статистике, при вычислении по методу наименьших квадратов и др. Указанные выше С. могут быть получены из формулы
     ,
     где f -1(h) — функция, обратная к f(x) (см. Обратная функция ), при соответствующем подборе функции f(x). Так, арифметическое С. получается, если f(x) = x, геометрическое С. — если f(x) = log x, гармоническое С. — если f(x) = 1/x, квадратичное С. — если f(x) =x 2.
     Наряду со степенными С. рассматривают взвешенные степенные С.
    
     в частности при a = 1,
     ,
     которые переходят в обыкновенные степенные С. при р 1= р 2=... = p n. Взвешенные С. особенно важны при математической обработке результатов наблюдений (см. Наблюдений обработка ), когда различные наблюдения производятся с разной точностью (с разным весом).
     2) Арифметико-геометрическое среднее. Для пары положительных чисел аи bсоставляются арифметическое С. a 1и геометрическое С. g 1. Затем для пары a 1, g 1снова находятся арифметическое С. a 2и геометрическое С. g 2и т.д. Общий предел последовательностей a nи g b, существование которого было доказано К. Гауссом , называется арифметико-геометрическим С. чисел аи b; он важен в теории эллиптических функций.
     3) Средним значением функции называется любое число, заключённое между наименьшим и наибольшим её значениями. В дифференциальном и интегральном исчислении имеется ряд «теорем о среднем», устанавливающих существование таких точек, в которых функция или её производная получает то или иное среднее значение. Наиболее важной теоремой о С. в дифференциальном исчислении является теорема Лагранжа (теорема о конечном приращении): если f( x) непрерывна на отрезке [ а, b] и дифференцируема в интервале (а, b), то существует точка с, принадлежащая интервалу (а, b), такая, что f( b) — f( a) =( b—a) f’(c). В интегральном исчислении наиболее важной теоремой о С. является следующая: если f( x) непрерывна на отрезке [ а, b], а j( x) сохраняет постоянный знак, то существует точка сиз интервала ( а, b) такая, что
     .
     В частности, если j( x) = 1, то
     .
     Вследствие этого под средним значением функции f( x) на отрезке [ а, b] обычно понимают величину
     .
     Аналогично определяют среднее значение функции нескольких переменных в некоторой области.

древнего мира и предшествующего новой истории . Понятие С. в. (лат. medium aevum, буквально — средний век) появилось в 15—16 вв. у итальянских историков-гуманистов (Ф. Бьондо и др.), утвердилось в науке с 18 в. Марксистская историческая наука рассматривает С. в. как эпоху зарождения, развития и разложения феодализма , рубежом между древностью и С. в. считает крушение рабовладельческой Римской империи (условная дата — 476), между С. в. и новой историей — Английскую буржуазную революцию 17 в. Термин «С. в.», возникший применительно к истории стран Западной Европы, употребляется и по отношению к др. регионам мира (хотя эпоха средневековья и время существования в них феодализма не всегда совпадают). Наука, изучающая историю С. в., — медиевистика.

Средние ). При малой колеблемости индивидуальных величин выбор формы средней не имеет существенного значения, при большой колеблемости он диктуется природой объекта. Например, при вычислении средней производительности труда необходимо учитывать её прямую пропорциональность количеству произведённой продукции и обратную пропорциональность затрате рабочего времени на её выработку. Поэтому при нахождении средней из данных о дневной выработке рабочих вычисляют среднюю арифметическую, а при определении средней по данным о затрачиваемом ими на единицу продукции времени — среднюю гармоническую. При вычислении среднегодового темпа роста продукции, населения и т.д. исходят из того, что отношение окончательно достигнутого уровня к начальному (в данном ряде) равно произведению величин вида 1 + t i, где t i— темп роста для отдельного ( i-го) года. Поэтому из этих величин определяют среднюю геометрическую и из неё вычитают 1 для получения среднего темпа.
     С. в. следует различать от огульных средних, неправомерно используемых для характеристики совокупности разнородных единиц. Впервые это различие показал В. И. Ленин в работе «Развитие капитализма в России» (1896—99). В противоположность построениям, опиравшимся на антинаучное использование средних, он доказал, что разнородная масса крестьянских хозяйств не может характеризоваться одной средней, поскольку она в этом случае вместо обобщённой типической характеристики всех хозяйств превращается в огульную среднюю (см. Статистические группировки ).
     Со С. в. тесно связан закон больших чисел (см. Больших чисел закон ). При наличии случайного элемента в индивидуальных значениях он оказывается в С. в. погашенным тем в большей мере, чем больше количество охватываемых средней индивидуальных величин.