Страница:
Среди методов статистического анализа, наиболее полезных трейдеру, можно назвать проверку по критерию Стьюдента, корреляционный анализ и некоторые виды непараметрического статистического анализа.
Проверка по критерию Стьюдента необходима в тех случаях, когда надо определить вероятность того, что среднее или сумма некоторого ряда независимых значений (полученных из выборки) больше или меньше некоторого числа или находится в некоторых пределах от него. Например, проверка по критерию Стьюдента может вскрыть вероятность того, что общая прибыль ряда сделок (каждая с индивидуальными показателями прибыли/убытка) может превысить некоторый порог в результате простой случайности. Эти критерии также полезны для выбора периодичности данных, например при вычислении дневного или месячного дохода за период в несколько лет. Кроме того, проверка по критерию Стьюдента помогает установить границы производительности системы в будущем (если предположить, что на рынке не ожидается структурных изменений), что позволит заявить, например, следующее: «вероятность того, что в будущем средняя прибыль составит от х до y, более 95 %».
Корреляционный анализ помогает определить степень взаимосвязи двух различных переменных. При использовании для принятия решений он также помогает определить, являются ли связи «статистически значимыми» или просто случайными. С помощью таких методов можно определить доверительные интервалы границ «реальной» корреляции, т. е. корреляции по выборке данных за некоторый период времени. Корреляционная статистика важна при поиске переменных, которые можно использовать как прогностические показатели, например, в нейронной сети или в системе уравнений регрессии.
Корреляционный анализ и непараметрические статистические методы (критерий наличия «чередующихся полос» в ряду данных) полезны при оценке зависимости значений ряда данных от предыдущих значений в ряду (серийной корреляции). Например, действительно ли выгодные сделки следуют в виде полос или групп, между которыми сплошные убытки? Критерии наличия «полос» позволяют определить, что же на самом деле происходит. Если в системе есть серийная корреляция, ее можно использовать для перенастройки системы. Например, если в системе выражены периоды прибылей и убытков, можно разработать метасистему, которая будет проводить сделку за сделкой, пока есть прибыли, и прекращать торговлю после первой убыточной сделки, уходя в «виртуальную торговлю» до наступления новой прибыльной полосы. Если полосы реально существуют, то подобная стратегия может значительно улучшить поведение системы.
Зачем нужен статистический анализ при оценке торговых систем?
Выборка
Оптимизация и подгонка под исторические данные
Размер выборки и репрезентативность
Статистическая оценка системы
Проверка по критерию Стьюдента необходима в тех случаях, когда надо определить вероятность того, что среднее или сумма некоторого ряда независимых значений (полученных из выборки) больше или меньше некоторого числа или находится в некоторых пределах от него. Например, проверка по критерию Стьюдента может вскрыть вероятность того, что общая прибыль ряда сделок (каждая с индивидуальными показателями прибыли/убытка) может превысить некоторый порог в результате простой случайности. Эти критерии также полезны для выбора периодичности данных, например при вычислении дневного или месячного дохода за период в несколько лет. Кроме того, проверка по критерию Стьюдента помогает установить границы производительности системы в будущем (если предположить, что на рынке не ожидается структурных изменений), что позволит заявить, например, следующее: «вероятность того, что в будущем средняя прибыль составит от х до y, более 95 %».
Корреляционный анализ помогает определить степень взаимосвязи двух различных переменных. При использовании для принятия решений он также помогает определить, являются ли связи «статистически значимыми» или просто случайными. С помощью таких методов можно определить доверительные интервалы границ «реальной» корреляции, т. е. корреляции по выборке данных за некоторый период времени. Корреляционная статистика важна при поиске переменных, которые можно использовать как прогностические показатели, например, в нейронной сети или в системе уравнений регрессии.
Корреляционный анализ и непараметрические статистические методы (критерий наличия «чередующихся полос» в ряду данных) полезны при оценке зависимости значений ряда данных от предыдущих значений в ряду (серийной корреляции). Например, действительно ли выгодные сделки следуют в виде полос или групп, между которыми сплошные убытки? Критерии наличия «полос» позволяют определить, что же на самом деле происходит. Если в системе есть серийная корреляция, ее можно использовать для перенастройки системы. Например, если в системе выражены периоды прибылей и убытков, можно разработать метасистему, которая будет проводить сделку за сделкой, пока есть прибыли, и прекращать торговлю после первой убыточной сделки, уходя в «виртуальную торговлю» до наступления новой прибыльной полосы. Если полосы реально существуют, то подобная стратегия может значительно улучшить поведение системы.
Зачем нужен статистический анализ при оценке торговых систем?
Очень важно определить, действительно ли наблюдаемые прибыли реальны (т. е. основаны не на артефактах тестирования) и какова вероятность, что система будет давать подобные прибыли в будущем при реальной торговле. Хотя тестирование на данных вне пределов выборки может до некоторой степени показать, выдержит ли система испытание более новыми данными, при помощи статистики можно получить дополнительную информацию. Статистика позволяет определить, случаен ли результат или он основан на реальных достоинствах системы. Статистические расчеты могут быть использованы для обнаружения подгонки под исторические данные, т. е. могут определить, является ли наблюдаемая эффективность модели реальной или же она – результат подгонки.
Следует отметить, что в статистике, как правило, делаются некоторые теоретические предположения относительно образцов данных и выборок, к которым можно адекватно применять статистические методы. При работе с торговыми системами эти правила частично приходится нарушать, причем некоторые нарушения правил не имеют никакой практической ценности, тогда как более важные правила часто удается обойти без компромисса. При использовании дополнительного анализа порой удается обойти или скомпенсировать даже весьма тяжелые несоответствия данных требованиям статистического анализа. В общем, мы полностью отдаем себе отчет в существовании такой проблемы и продолжим ее обсуждение после подробного рассмотрения основ обсуждаемого вопроса.
Следует отметить, что в статистике, как правило, делаются некоторые теоретические предположения относительно образцов данных и выборок, к которым можно адекватно применять статистические методы. При работе с торговыми системами эти правила частично приходится нарушать, причем некоторые нарушения правил не имеют никакой практической ценности, тогда как более важные правила часто удается обойти без компромисса. При использовании дополнительного анализа порой удается обойти или скомпенсировать даже весьма тяжелые несоответствия данных требованиям статистического анализа. В общем, мы полностью отдаем себе отчет в существовании такой проблемы и продолжим ее обсуждение после подробного рассмотрения основ обсуждаемого вопроса.
Выборка
Для статистики, а следовательно, и для нашего понимания, фундаментальным является понятие выборки – извлечения образца данных из некоей обширной, абстрактно определимой популяции. Основная идея статистического анализа состоит в том, чтобы использовать выборку для получения заключения о популяции данных. При работе с торговыми моделями под популяцией обычно понимается вся совокупность данных (прошлых, настоящих и будущих) для определенного рыночного инструмента (например, все 5-минутные штрихи на все фьючерсы S&P 500), все сделки (прошлые, настоящие и будущие), совершенные данной системой или по данному инструменту, а также все прибыли – годовые, месячные и даже дневные. Например, все квартальные прибыли IBM – пример популяции данных. Выборка может представлять собой специфические исторические данные, используемые при разработке или тестировании системы, данные о проведенных сделках или о месячной прибыли, принесенной этими сделками.
При создании торговой системы разработчик обычно определяет выборку данных из моделируемой популяции. Например, чтобы разработать систему для торговли S&P 500 на основе гипотезы: «Если вчерашняя цена закрытия выше, чем цена закрытия три дня назад, то завтра рынок будет подниматься», разработчик берет выборку цен на конец дня по S&P 500, простирающуюся назад, например, на 5 лет. Остается надеяться, что выборка репрезентативна, т. е. отражает реальное типичное поведение рынка, и в будущем (или на другом, неизвестном образце данных) система будет работать не хуже, чем на использованном при разработке образце. Чтобы подтвердить или опровергнуть результаты оптимизации, разработчики системы проводят тестирование на одном или нескольких периодах вне выборки, т. е. на образцах данных, не использовавшихся для разработки или оптимизации системы. Например, в нашем случае разработчик использует данные с 1991 по 1995 г. для разработки и настройки системы и резервирует данные за 1996 г. для тестирования вне пределов выборки. Очень рекомендуется заранее зарезервировать один или несколько периодов для подобного исследования.
Одна из проблем с выборкой образцов из популяций финансовых данных заключается в сложной и переменчивой природе объекта: завтрашний рынок может быть не похож на сегодняшний. Иногда эти изменения заметны, и их причины могут быть легко определены. Например, поведение индекса S&P резко изменилось в 1983 г. в результате введения фьючерсов и опционов на этот индекс. В таких случаях можно расценить изменение как событие, создавшее две отдельные популяции: S&P до и после 1983 г. Выборка, взятая из более раннего периода, не будет репрезентативна для более позднего, поскольку она взята из другой популяции! Конечно, это экстремальный случай. Гораздо чаще структурные изменения рынка возникают ввиду слабых влияний, которые порой невозможно определить, особенно заранее. В некоторых случаях рынок может остаться принципиально тем же, но фазы процессов, которые на нем проходят, могут быть различными; неосмотрительно взятая выборка может принадлежать к другой фазе и быть репрезентативна только для нее, но не для рынка в целом. Как же можно определить, действительно ли выборка, использованная для тестирования, относится к тому же периоду, что и данные, на которых будет идти торговля? Если не прыгать в машину времени и не тестировать будущее, то не существует достоверного способа определить, не случится ли завтра на рынке ломающая системы метаморфоза. Множественные тесты вне пределов выборки могут дать некоторую гарантию устойчивости системы, поскольку они подтвердят, что система, по крайней мере в нескольких периодах, работала более или менее стабильно. При наличии репрезентативной выборки можно сделать статистически достоверные выводы о той популяции, из которой выбраны образцы данных. Статистика не может определить будущие фундаментальные изменения рынка.
При создании торговой системы разработчик обычно определяет выборку данных из моделируемой популяции. Например, чтобы разработать систему для торговли S&P 500 на основе гипотезы: «Если вчерашняя цена закрытия выше, чем цена закрытия три дня назад, то завтра рынок будет подниматься», разработчик берет выборку цен на конец дня по S&P 500, простирающуюся назад, например, на 5 лет. Остается надеяться, что выборка репрезентативна, т. е. отражает реальное типичное поведение рынка, и в будущем (или на другом, неизвестном образце данных) система будет работать не хуже, чем на использованном при разработке образце. Чтобы подтвердить или опровергнуть результаты оптимизации, разработчики системы проводят тестирование на одном или нескольких периодах вне выборки, т. е. на образцах данных, не использовавшихся для разработки или оптимизации системы. Например, в нашем случае разработчик использует данные с 1991 по 1995 г. для разработки и настройки системы и резервирует данные за 1996 г. для тестирования вне пределов выборки. Очень рекомендуется заранее зарезервировать один или несколько периодов для подобного исследования.
Одна из проблем с выборкой образцов из популяций финансовых данных заключается в сложной и переменчивой природе объекта: завтрашний рынок может быть не похож на сегодняшний. Иногда эти изменения заметны, и их причины могут быть легко определены. Например, поведение индекса S&P резко изменилось в 1983 г. в результате введения фьючерсов и опционов на этот индекс. В таких случаях можно расценить изменение как событие, создавшее две отдельные популяции: S&P до и после 1983 г. Выборка, взятая из более раннего периода, не будет репрезентативна для более позднего, поскольку она взята из другой популяции! Конечно, это экстремальный случай. Гораздо чаще структурные изменения рынка возникают ввиду слабых влияний, которые порой невозможно определить, особенно заранее. В некоторых случаях рынок может остаться принципиально тем же, но фазы процессов, которые на нем проходят, могут быть различными; неосмотрительно взятая выборка может принадлежать к другой фазе и быть репрезентативна только для нее, но не для рынка в целом. Как же можно определить, действительно ли выборка, использованная для тестирования, относится к тому же периоду, что и данные, на которых будет идти торговля? Если не прыгать в машину времени и не тестировать будущее, то не существует достоверного способа определить, не случится ли завтра на рынке ломающая системы метаморфоза. Множественные тесты вне пределов выборки могут дать некоторую гарантию устойчивости системы, поскольку они подтвердят, что система, по крайней мере в нескольких периодах, работала более или менее стабильно. При наличии репрезентативной выборки можно сделать статистически достоверные выводы о той популяции, из которой выбраны образцы данных. Статистика не может определить будущие фундаментальные изменения рынка.
Оптимизация и подгонка под исторические данные
Еще один аспект разработки торговых систем состоит в оптимизации, т. е. улучшении эффективности систем при помощи подбора таких значений параметров, при которых система дает наилучший результат на выборке данных. Если система не работает при тестировании на данных вне пределов выборки или на реальном рынке, говорят, что при оптимизации имела место подгонка под исторические данные. Впрочем, подгонка бывает полезной и вредной. Полезная подгонка – это случай, когда модель подогнана под всю популяцию (т. е. под достаточно большую и представительную) и при этом отражает все достоверные характеристики реальной популяции в системе. Подгонка вредна, если система соответствует только некоторым случайным характеристикам, не обязательно отражающим свойства всей популяции.
Разработчики недаром боятся вредной подгонки, т. е. ситуации, когда параметры, оптимизированные на данной выборке, не работают на популяции в целом. Если выборка была небольшой или не представительной, вероятнее всего, система будет работать хорошо на данной выборке и из рук вон плохо на другой или, что еще опаснее, приведет к потере денег в реальной торговле. Чем больше выборка данных, тем меньше эта опасность: вероятность вредной подгонки снижается, а полезной – возрастает. Все рассматриваемые методы статистики отражают это явление, даже специально предназначенные для оптимизации. Достоверно известно, что чем больше параметров подвергается оптимизации, тем больше вероятность того, что высокие результаты системы будут достигнуты чисто случайным сочетанием. Если же результаты статистического анализа удовлетворительны и тест основывался на достаточно большой выборке данных, то вероятность случайного результата снижается, и даже полученный при оптимизации множества параметров результат вполне может быть реальным и значимым.
Некоторые возражают, что размер не имеет значения, т. е. размер выборки и количество проведенных сделок не имеют ничего общего с риском избыточной оптимизации, и что большая выборка не снимает угрозы вредной подгонки под исторические данные. Это неверно и математически, и интуитивно. Никто не стал бы больше доверять системе, которая провела 3–4 сделки за десятилетний период, чем системе, которая провела более тысячи достаточно прибыльных сделок. Представьте себе модель линейной регрессии, в которой прямую линию подгоняют к ряду точек. Если точек всего две, то вне зависимости от их положения линию всегда можно «подогнать» идеально. Если точек три, то дело усложняется. Если же точек действительно много, то проблема становится еще сложнее, если только расположение точек не содержит некоего реального линейного распределения.
Пример с линейной регрессией показывает, что вредная подгонка затрудняется с ростом объема данных. Cравните две торговые системы: одна провела 2 сделки с прибылью $100 в каждой и стандартным отклонением $100; другая – 1000 сделок с такими же средним и стандартным отклонениями. При статистической оценке система, проведшая 1000 сделок, будет гораздо «статистически значимее», чем система, проведшая 2 сделки.
В моделях множественной линейной регрессии при увеличении количества параметров регрессии (бета-весов) по отношению к размеру выборки увеличивается степень вредной подгонки и уменьшается достоверность результатов модели. Другими словами, чем выше степень подгонки под исторические данные, тем сложнее добиться статистической значимости. Исключением является случай, когда повышение результативности модели, вызванное подгонкой, компенсирует потерю значимости при добавлении параметров. Оценка степени ожидаемого снижения корреляции при использовании данных вне выборки может производиться напрямую, исходя из объема данных и количества параметров: корреляция снижается с увеличением числа параметров и увеличивается с ростом объема данных. В общем, существуют достоверные математические доказательства того, что вероятность вредной подгонки повышается, если количество оптимизируемых параметров велико по отношению к объему используемой выборки данных. Фактически, когда n (размер выборки) стремится к бесконечности, вероятность того, что подгонка параметров будет непредставительной для данной популяции, стремится к нулю. Чем больше параметров оптимизируется, тем большая требуется выборка данных. На языке статистики это звучит так: оптимизируемые параметры используют доступные степени свободы.
Все это ведет к заключению, что чем больше выборка, тем выше вероятность того, что найденные параметры системы будут представительным отражением характеристик рынка в целом. Маленькая выборка, скорее всего, будет непредставительной: ее кривые вряд ли будут соответствовать долговременным, устойчивым характеристикам рынка. Любая модель, построенная с использованием маленькой выборки, может быть эффективной только по чистой случайности. Будет ли подгонка «полезной» или «вредной», во многом зависит от отражения в ней случайных ценовых движений или реальных рыночных процессов, что, в свою очередь, зависит от представительности выборки. Статистика полезна, поскольку позволяет принять в расчет при оценке системы степень подгонки.
При работе с нейронными сетями опасения относительно излишнего обучения, или генерализации, соответствуют опасениям относительно излишней подгонки под исторические данные. Если выборка достаточно объемиста и представительна, повышается вероятность отражения в найденных оптимальных параметрах реальных характеристик рынка, что полезно для реальной работы системы. Если же выборка мала, модель практически гарантированно будет настроена на особенности выборки, но никак не на особенности рынка в целом. Для нейронных сетей успех генерализации означает то же, что для других систем, – устойчивость в будущем и так же сильно зависит от размеров выборки, использованной для обучения сети. Чем больше выборка или чем меньше количество весов связей (т. е. параметров), тем выше вероятность удачной генерализации. Это также можно доказать математически путем разбора несложных примеров.
Как и в случае с регрессией, при разработке нейронной сети можно произвести оценку коррекции коэффициента корреляции (т. е. показателя, обратного генерализации). Фактически нейронная сеть представляет собой систему уравнений множественной регрессии, хотя и нелинейных, и корреляция выходных значений сети может рассматриваться как множественный коэффициент корреляции. Множественная корреляция между выходными и целевыми значениями может быть скорректирована для прогнозирования поведения системы на данных вне выборки. Такая скорректированная множественная корреляция должна постоянно использоваться для определения того, является ли эффективность нейронной сети случайной или она вызвана обнаружением реальной закономерности в ценовом поведении рынка. Формула коррекции коэффициента множественной корреляции приведена ниже:
 Формула приведена в стиле языка FORTRAN. Здесь SQRT означает квадратный корень; N – количество точек данных или фактов в случае нейронной сети; P – количество коэффициентов регрессии или (в случае нейронной сети) весов связей; R – некорректированную множественную корреляцию; RC – скорректированную корреляцию. Хотя эта формула строго приложима только к линейной множественной регрессии (для которой, собственно, и разрабатывалась), она неплохо работает с нейронными сетями и может быть использована для того, чтобы оценить, какая часть эффективности системы обусловлена вредной подгонкой на данном образце. Эта формула описывает связь между размером выборки, количеством параметров и снижением эффективности результатов. Статистическая коррекция, рассчитываемая по данной формуле, будет использована в главе о входах систем на нейронных сетях.
Формула приведена в стиле языка FORTRAN. Здесь SQRT означает квадратный корень; N – количество точек данных или фактов в случае нейронной сети; P – количество коэффициентов регрессии или (в случае нейронной сети) весов связей; R – некорректированную множественную корреляцию; RC – скорректированную корреляцию. Хотя эта формула строго приложима только к линейной множественной регрессии (для которой, собственно, и разрабатывалась), она неплохо работает с нейронными сетями и может быть использована для того, чтобы оценить, какая часть эффективности системы обусловлена вредной подгонкой на данном образце. Эта формула описывает связь между размером выборки, количеством параметров и снижением эффективности результатов. Статистическая коррекция, рассчитываемая по данной формуле, будет использована в главе о входах систем на нейронных сетях.
Разработчики недаром боятся вредной подгонки, т. е. ситуации, когда параметры, оптимизированные на данной выборке, не работают на популяции в целом. Если выборка была небольшой или не представительной, вероятнее всего, система будет работать хорошо на данной выборке и из рук вон плохо на другой или, что еще опаснее, приведет к потере денег в реальной торговле. Чем больше выборка данных, тем меньше эта опасность: вероятность вредной подгонки снижается, а полезной – возрастает. Все рассматриваемые методы статистики отражают это явление, даже специально предназначенные для оптимизации. Достоверно известно, что чем больше параметров подвергается оптимизации, тем больше вероятность того, что высокие результаты системы будут достигнуты чисто случайным сочетанием. Если же результаты статистического анализа удовлетворительны и тест основывался на достаточно большой выборке данных, то вероятность случайного результата снижается, и даже полученный при оптимизации множества параметров результат вполне может быть реальным и значимым.
Некоторые возражают, что размер не имеет значения, т. е. размер выборки и количество проведенных сделок не имеют ничего общего с риском избыточной оптимизации, и что большая выборка не снимает угрозы вредной подгонки под исторические данные. Это неверно и математически, и интуитивно. Никто не стал бы больше доверять системе, которая провела 3–4 сделки за десятилетний период, чем системе, которая провела более тысячи достаточно прибыльных сделок. Представьте себе модель линейной регрессии, в которой прямую линию подгоняют к ряду точек. Если точек всего две, то вне зависимости от их положения линию всегда можно «подогнать» идеально. Если точек три, то дело усложняется. Если же точек действительно много, то проблема становится еще сложнее, если только расположение точек не содержит некоего реального линейного распределения.
Пример с линейной регрессией показывает, что вредная подгонка затрудняется с ростом объема данных. Cравните две торговые системы: одна провела 2 сделки с прибылью $100 в каждой и стандартным отклонением $100; другая – 1000 сделок с такими же средним и стандартным отклонениями. При статистической оценке система, проведшая 1000 сделок, будет гораздо «статистически значимее», чем система, проведшая 2 сделки.
В моделях множественной линейной регрессии при увеличении количества параметров регрессии (бета-весов) по отношению к размеру выборки увеличивается степень вредной подгонки и уменьшается достоверность результатов модели. Другими словами, чем выше степень подгонки под исторические данные, тем сложнее добиться статистической значимости. Исключением является случай, когда повышение результативности модели, вызванное подгонкой, компенсирует потерю значимости при добавлении параметров. Оценка степени ожидаемого снижения корреляции при использовании данных вне выборки может производиться напрямую, исходя из объема данных и количества параметров: корреляция снижается с увеличением числа параметров и увеличивается с ростом объема данных. В общем, существуют достоверные математические доказательства того, что вероятность вредной подгонки повышается, если количество оптимизируемых параметров велико по отношению к объему используемой выборки данных. Фактически, когда n (размер выборки) стремится к бесконечности, вероятность того, что подгонка параметров будет непредставительной для данной популяции, стремится к нулю. Чем больше параметров оптимизируется, тем большая требуется выборка данных. На языке статистики это звучит так: оптимизируемые параметры используют доступные степени свободы.
Все это ведет к заключению, что чем больше выборка, тем выше вероятность того, что найденные параметры системы будут представительным отражением характеристик рынка в целом. Маленькая выборка, скорее всего, будет непредставительной: ее кривые вряд ли будут соответствовать долговременным, устойчивым характеристикам рынка. Любая модель, построенная с использованием маленькой выборки, может быть эффективной только по чистой случайности. Будет ли подгонка «полезной» или «вредной», во многом зависит от отражения в ней случайных ценовых движений или реальных рыночных процессов, что, в свою очередь, зависит от представительности выборки. Статистика полезна, поскольку позволяет принять в расчет при оценке системы степень подгонки.
При работе с нейронными сетями опасения относительно излишнего обучения, или генерализации, соответствуют опасениям относительно излишней подгонки под исторические данные. Если выборка достаточно объемиста и представительна, повышается вероятность отражения в найденных оптимальных параметрах реальных характеристик рынка, что полезно для реальной работы системы. Если же выборка мала, модель практически гарантированно будет настроена на особенности выборки, но никак не на особенности рынка в целом. Для нейронных сетей успех генерализации означает то же, что для других систем, – устойчивость в будущем и так же сильно зависит от размеров выборки, использованной для обучения сети. Чем больше выборка или чем меньше количество весов связей (т. е. параметров), тем выше вероятность удачной генерализации. Это также можно доказать математически путем разбора несложных примеров.
Как и в случае с регрессией, при разработке нейронной сети можно произвести оценку коррекции коэффициента корреляции (т. е. показателя, обратного генерализации). Фактически нейронная сеть представляет собой систему уравнений множественной регрессии, хотя и нелинейных, и корреляция выходных значений сети может рассматриваться как множественный коэффициент корреляции. Множественная корреляция между выходными и целевыми значениями может быть скорректирована для прогнозирования поведения системы на данных вне выборки. Такая скорректированная множественная корреляция должна постоянно использоваться для определения того, является ли эффективность нейронной сети случайной или она вызвана обнаружением реальной закономерности в ценовом поведении рынка. Формула коррекции коэффициента множественной корреляции приведена ниже:

Размер выборки и репрезентативность
Хотя из статистических соображений разработчику следует искать самые большие из возможных выборки данных, при работе с финансовыми рынками между размером и представительностью образца существуют неоднозначные связи. Большие выборки означают, что данные уходят назад, в такие периоды времени, когда рынок был фундаментально иным – вспомните S&P 500 в 1983 г.! Это означает, что в некоторых случаях больший образец данных может быть менее представительным или включать смесь из нескольких различных популяций данных! Следовательно, нельзя забывать, что хотя цель – максимальный размер выборки, столь же важно, чтобы данные отображали тот рынок, который система должна прогнозировать.
Статистическая оценка системы
Разобравшись с некоторыми основными положениями, рассмотрим применение статистики при разработке и оценке торговых систем. Примеры, приведенные ниже, основаны на системе, которая была оптимизирована на некоторой выборке данных и затем тестировалась вне пределов выборки. Оценка на данных вне пределов выборки будет рассмотрена перед оценкой на основе выборки, поскольку ее статистический анализ проще (и аналогичен анализу неоптимизированной системы), в нем не требуются поправки на оптимизацию или множественные тесты. Система представляет собой модель торговли индексом S&P 500, основанную на лунном цикле, она была опубликована нами ранее (Katz, McCormick, июнь 1997). Код для системы в формате TradeStation приведен ниже:

Пример 1: Оценка теста вне пределов выборки
Оценка оптимизированной системы на данных, взятых вне пределов выборки и ни разу не использованных при оптимизации, аналогична оценке неоптимизированной системы. В обоих случаях проводится один тест без подстройки параметров. В табл. 4–1 показано применение статистики для оценки неоптимизированной системы. Там приведены результаты проверки на данных вне пределов выборки совместно с рядом статистических показателей. Помните, что в этом тесте использованы «свежие данные», которые не применялись как основа для настройки параметров системы.
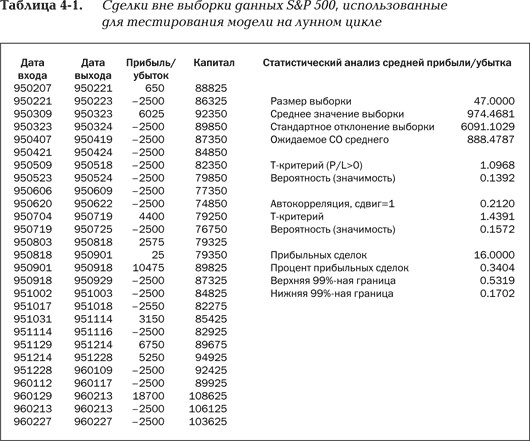 Параметры торговой модели уже были определены. Образец данных для оценки вне пределов выборки охватывает период с 1.01.1995 по 1.01.1997; модель тестировалась на этих данных и совершала смоделированные сделки. Было проведено 47 сделок. Этот набор сделок можно считать выборкой сделок, т. е. частью популяции смоделированных сделок, которые система совершила бы по данным правилам в прошлом или будущем. Здесь возникает вопрос по поводу оценки показателя средней прибыли в сделке – могло ли данное значение быть достигнуто за счет чистой случайности? Чтобы найти ответ, потребуется статистическая оценка системы.
Параметры торговой модели уже были определены. Образец данных для оценки вне пределов выборки охватывает период с 1.01.1995 по 1.01.1997; модель тестировалась на этих данных и совершала смоделированные сделки. Было проведено 47 сделок. Этот набор сделок можно считать выборкой сделок, т. е. частью популяции смоделированных сделок, которые система совершила бы по данным правилам в прошлом или будущем. Здесь возникает вопрос по поводу оценки показателя средней прибыли в сделке – могло ли данное значение быть достигнуто за счет чистой случайности? Чтобы найти ответ, потребуется статистическая оценка системы.
Чтобы начать оценку системы, для начала нужно рассчитать среднее в выборке для n сделок. Среднее здесь будет просто суммой прибылей/убытков, поделенной на n (в данном случае 47). Среднее составило $974,47 за сделку. Стандартное отклонение (изменчивость показателей прибылей/убытков) рассчитывается после этого вычитанием среднего из каждого результата, что дает 47 (n) отклонений. Каждое из значений отклонения возводится в квадрат, все квадраты складываются, сумма квадратов делится на n–1 (в данном случае 46), квадратный корень от результата и будет стандартным отклонением выборки. На основе стандартного отклонения выборки вычисляется ожидаемое стандартное отклонение прибыли в сделке: стандартное отклонение (в данном случае $6091,10) делится на квадратный корень из n. В нашем случае ожидаемое стандартное отклонение составляет $888,48.
 Чтобы определить вероятность случайного происхождения наблюдаемой прибыли, проводится простая проверка по критерию Стьюдента. Поскольку прибыльность выборки сравнивается с нулевой прибыльностью, из среднего, вычисленного выше, вычитается нуль, и результат делится на стандартное отклонение выборки для получения значения критерия t, в данном случае – 1,0968. В конце концов оценивается вероятность получения столь большого t по чистой случайности. Для этого рассчитывается функция распределения t для данных показателей с количеством степеней свободы, равным n–1 (или 46).
Чтобы определить вероятность случайного происхождения наблюдаемой прибыли, проводится простая проверка по критерию Стьюдента. Поскольку прибыльность выборки сравнивается с нулевой прибыльностью, из среднего, вычисленного выше, вычитается нуль, и результат делится на стандартное отклонение выборки для получения значения критерия t, в данном случае – 1,0968. В конце концов оценивается вероятность получения столь большого t по чистой случайности. Для этого рассчитывается функция распределения t для данных показателей с количеством степеней свободы, равным n–1 (или 46).
Программа работы с таблицами Microsoft Excel имеет функцию вычисления вероятностей на основе t-распределения. В сборнике Numerical Recipes in C приведены неполные бета-функции, при помощи которых очень легко рассчитывать вероятности, основанные на различных критериях распределения, включая критерий Стьюдента. Функция распределения Стьюдента дает показатели вероятности случайного происхождения результатов системы. Поскольку в данном случае этот показатель был мал, вряд ли причиной эффективности системы была подгонка под случайные характеристики выборки. Чем меньше этот показатель, тем меньше вероятность того, что эффективность системы обусловлена случаем. Здесь показатель был равен 0,1392, т. е. при испытании на независимых данных неэффективная система показала бы столь же высокую, как и в тесте, прибыль только в 14 % случаев.
Хотя проверка по критерию Стьюдента в этом случае рассчитывалась для прибылей/убытков, она могла быть с равным успехом применена, например, к выборке дневных прибылей. Дневные прибыли именно так использовались в тестах, описанных в последующих главах. Фактически соотношение риска/прибыли, выраженное в процентах годовых, упоминаемое во многих таблицах и примерах, представляет собой t-статистику дневных прибылей.
Кроме того, оценивался доверительный интервал вероятности выигрышной сделки. К примеру, из 47 сделок было 16 выигрышей, т. е. процент прибыльных сделок был равен 0,3404. При помощи особой обратной функции биноминального распределения мы рассчитали верхний и нижний 99 %-ные пределы. Вероятность того, что процент прибыльных сделок системы в целом составит от 0,1702 до 0,5319, – 99 %. В Excel для вычисления доверительных интервалов можно использовать функцию CRITBINOM.
Различные статистические показатели и вероятности, описанные выше, должны предоставить разработчику системы важную информацию о поведении торговой модели в случае, если соответствуют реальности предположения о нормальном распределении и независимости данных в выборке. Впрочем, чаще всего заключения, основанные на проверке по критерию Стьюдента и других статистических показателях, нарушаются; рыночные данные заметно отклоняются от нормального распределения, и сделки оказываются зависимыми друг от друга. Кроме того, выборка данных может быть непредставительной. Означает ли это, что все вышеописанное не имеет смысла? Рассмотрим примеры.
Что, если распределение не соответствует нормальному? При проведении проверки по критерию Стьюдента исходят из предположения, что данные соответствуют нормальному распределению. В реальности распределение показателей прибылей и убытков торговой системы таким не бывает, особенно при наличии защитных остановок и целевых прибылей, как показано на рис. 4–1. Дело в том, что прибыль выше, чем целевая, возникает редко. Фактически большинство прибыльных сделок будут иметь прибыль, близкую к целевой. С другой стороны, кое-какие сделки закроются с убытком, соответствующим уровню защитной остановки, а между ними будут разбросаны другие сделки, с прибылью, зависящей от методики выхода. Следовательно, это будет совсем непохоже на колоколообразную кривую, которая описывает нормальное распределение. Это составляет нарушение правил, лежащих в основе проверки по критерию Стьюдента. Впрочем, в этом случае спасает так называемая центральная предельная теорема: с ростом числа точек данных в выборке распределение стремится к нормальному. Если размер выборки составит 10, то ошибки будут небольшими; если же их будет 20–30, ошибки будут иметь исчезающе малое значение для статистических заключений. Следовательно, многие виды статистического анализа можно с уверенностью применять при адекватном размере выборки, например при n = 47 и выше, не опасаясь за достоверность заключений.
Что, если существует серийная зависимость? Более серьезным нарушением, способным сделать неправомочным вышеописанное применение проверки по критерию Стьюдента, является серийная зависимость – случай, когда данные в выборке не являются независимыми друг от друга. Сделки совершаются в виде временного ряда. Последовательность сделок, совершенных в течение некоторого периода времени, нельзя назвать случайной выборкой – подлинно случайная выборка состояла бы, например, из 100 сделок, выбранных случайным образом из всей популяции данных – от начала рынка (например, 1983 г. для S&P 500) до отдаленного будущего. Такая выборка не только была бы защищена от серийной зависимости, но и являлась бы более представительной для популяции. Однако при разработке торговых систем выборка сделок обычно производится на ограниченном временном отрезке; следовательно, может наблюдаться корреляция каждой сделки с соседними, что сделает данные зависимыми.

Пример 1: Оценка теста вне пределов выборки
Оценка оптимизированной системы на данных, взятых вне пределов выборки и ни разу не использованных при оптимизации, аналогична оценке неоптимизированной системы. В обоих случаях проводится один тест без подстройки параметров. В табл. 4–1 показано применение статистики для оценки неоптимизированной системы. Там приведены результаты проверки на данных вне пределов выборки совместно с рядом статистических показателей. Помните, что в этом тесте использованы «свежие данные», которые не применялись как основа для настройки параметров системы.

Чтобы начать оценку системы, для начала нужно рассчитать среднее в выборке для n сделок. Среднее здесь будет просто суммой прибылей/убытков, поделенной на n (в данном случае 47). Среднее составило $974,47 за сделку. Стандартное отклонение (изменчивость показателей прибылей/убытков) рассчитывается после этого вычитанием среднего из каждого результата, что дает 47 (n) отклонений. Каждое из значений отклонения возводится в квадрат, все квадраты складываются, сумма квадратов делится на n–1 (в данном случае 46), квадратный корень от результата и будет стандартным отклонением выборки. На основе стандартного отклонения выборки вычисляется ожидаемое стандартное отклонение прибыли в сделке: стандартное отклонение (в данном случае $6091,10) делится на квадратный корень из n. В нашем случае ожидаемое стандартное отклонение составляет $888,48.

Программа работы с таблицами Microsoft Excel имеет функцию вычисления вероятностей на основе t-распределения. В сборнике Numerical Recipes in C приведены неполные бета-функции, при помощи которых очень легко рассчитывать вероятности, основанные на различных критериях распределения, включая критерий Стьюдента. Функция распределения Стьюдента дает показатели вероятности случайного происхождения результатов системы. Поскольку в данном случае этот показатель был мал, вряд ли причиной эффективности системы была подгонка под случайные характеристики выборки. Чем меньше этот показатель, тем меньше вероятность того, что эффективность системы обусловлена случаем. Здесь показатель был равен 0,1392, т. е. при испытании на независимых данных неэффективная система показала бы столь же высокую, как и в тесте, прибыль только в 14 % случаев.
Хотя проверка по критерию Стьюдента в этом случае рассчитывалась для прибылей/убытков, она могла быть с равным успехом применена, например, к выборке дневных прибылей. Дневные прибыли именно так использовались в тестах, описанных в последующих главах. Фактически соотношение риска/прибыли, выраженное в процентах годовых, упоминаемое во многих таблицах и примерах, представляет собой t-статистику дневных прибылей.
Кроме того, оценивался доверительный интервал вероятности выигрышной сделки. К примеру, из 47 сделок было 16 выигрышей, т. е. процент прибыльных сделок был равен 0,3404. При помощи особой обратной функции биноминального распределения мы рассчитали верхний и нижний 99 %-ные пределы. Вероятность того, что процент прибыльных сделок системы в целом составит от 0,1702 до 0,5319, – 99 %. В Excel для вычисления доверительных интервалов можно использовать функцию CRITBINOM.
Различные статистические показатели и вероятности, описанные выше, должны предоставить разработчику системы важную информацию о поведении торговой модели в случае, если соответствуют реальности предположения о нормальном распределении и независимости данных в выборке. Впрочем, чаще всего заключения, основанные на проверке по критерию Стьюдента и других статистических показателях, нарушаются; рыночные данные заметно отклоняются от нормального распределения, и сделки оказываются зависимыми друг от друга. Кроме того, выборка данных может быть непредставительной. Означает ли это, что все вышеописанное не имеет смысла? Рассмотрим примеры.
Что, если распределение не соответствует нормальному? При проведении проверки по критерию Стьюдента исходят из предположения, что данные соответствуют нормальному распределению. В реальности распределение показателей прибылей и убытков торговой системы таким не бывает, особенно при наличии защитных остановок и целевых прибылей, как показано на рис. 4–1. Дело в том, что прибыль выше, чем целевая, возникает редко. Фактически большинство прибыльных сделок будут иметь прибыль, близкую к целевой. С другой стороны, кое-какие сделки закроются с убытком, соответствующим уровню защитной остановки, а между ними будут разбросаны другие сделки, с прибылью, зависящей от методики выхода. Следовательно, это будет совсем непохоже на колоколообразную кривую, которая описывает нормальное распределение. Это составляет нарушение правил, лежащих в основе проверки по критерию Стьюдента. Впрочем, в этом случае спасает так называемая центральная предельная теорема: с ростом числа точек данных в выборке распределение стремится к нормальному. Если размер выборки составит 10, то ошибки будут небольшими; если же их будет 20–30, ошибки будут иметь исчезающе малое значение для статистических заключений. Следовательно, многие виды статистического анализа можно с уверенностью применять при адекватном размере выборки, например при n = 47 и выше, не опасаясь за достоверность заключений.
Что, если существует серийная зависимость? Более серьезным нарушением, способным сделать неправомочным вышеописанное применение проверки по критерию Стьюдента, является серийная зависимость – случай, когда данные в выборке не являются независимыми друг от друга. Сделки совершаются в виде временного ряда. Последовательность сделок, совершенных в течение некоторого периода времени, нельзя назвать случайной выборкой – подлинно случайная выборка состояла бы, например, из 100 сделок, выбранных случайным образом из всей популяции данных – от начала рынка (например, 1983 г. для S&P 500) до отдаленного будущего. Такая выборка не только была бы защищена от серийной зависимости, но и являлась бы более представительной для популяции. Однако при разработке торговых систем выборка сделок обычно производится на ограниченном временном отрезке; следовательно, может наблюдаться корреляция каждой сделки с соседними, что сделает данные зависимыми.
