Практический эффект этого явления состоит в уменьшении размеров выборки. Если между данными существует серийная зависимость, то, делая статистические выводы, следует считать, что выборка в два или в четыре раза меньше реального количества точек данных. Вдобавок определить достоверным образом степень зависимости данных невозможно, можно только сделать грубую оценку – например, рассчитав серийную корреляцию точки данных с предшествующей и предыдущей точками. Рассчитывается корреляция прибыли/убытка сделки i и прибыли/убытка сделок i + 1 и i — 1. В данном случае серийная корреляция составила 0,2120. Это немного, но предпочтительным было бы меньшее значение. Можно также рассчитать связанный t-критерий для статистической значимости значения корреляции. В данном случае выясняется, что если бы в популяции действительно не было серьезной зависимости, то такой уровень корреляции наблюдался бы только в 16 % тестов.
Серийная зависимость – серьезная проблема. Если она высока, то для борьбы с ней надо считать выборку меньшей, чем она есть на самом деле. Другой вариант – выбрать случайным образом данные для тестирования из различных участков за длительный период времени. Это также повысит представительность выборки в отношении всей популяции.
Что, если изменится рынок? При разработке торговых систем возможно нарушение третьего положения t-критерия, и его невозможно предугадать или компенсировать. Причина этого нарушения в том, что популяция, из которой взят образец данных для тестирования или разработки, может отличаться от популяции, данные из которой будут использоваться в будущих сделках. Рынок может подвергаться структурным или иным изменениям. Как говорилось, популяция данных S&P 500 до 1983 г. принципиально отличается от последующих данных, когда началась торговля опционами и фьючерсами. Подобные события могут разрушить любой метод оценки системы. Как бы ни проводилось тестирование, при изменении рынка до начала реальной торговли окажется, что система разрабатывалась и тестировалась на одном рынке, а работать будет на другом. Естественно, модель разваливается на части. Даже самая лучшая модель будет уничтожена изменением рынка.
Тем не менее большинство рынков постоянно меняются. Несмотря на этот суровый факт, использование статистики в оценке системы остается принципиально важным, поскольку если рынок не изменится вскоре после начала работы системы или же изменения рынка недостаточны, чтобы оказать глубокое влияние, то статистически возможно произвести достаточно достоверную оценку ожидаемых вероятностей и прибылей системы.
Пример 2: Оценка тестов на данных в пределах выборки
Каким образом можно оценивать систему, которая подвергалась подгонке параметров (т. е. оптимизации) по некоторой выборке данных? Трейдеры часто оптимизируют системы для улучшения результатов. В данном аспекте применение статистики особенно важно, поскольку позволяет анализировать результаты, компенсируя этим большое количество тестовых прогонов во время оптимизации. В табл. 4–2 приведены показатели прибыли/убытка и различные статистические показатели для тестов в пределах выборки (т. е. на данных, использовавшихся для оптимизации системы). Система подвергалась оптимизации на данных за период с 1.01.1990 по 1.02.1995.
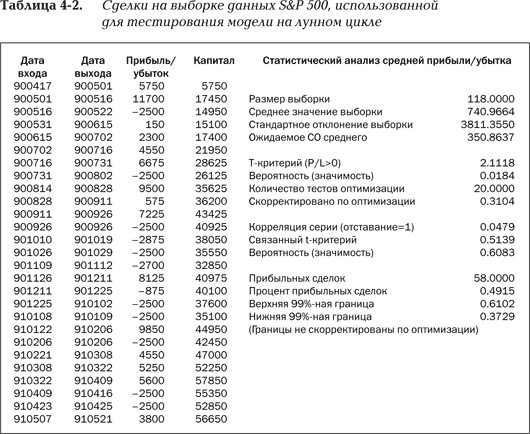 Большая часть статистики в табл. 4–2 идентична показателями табл. 4–1 из примера 1. Добавлены два дополнительных показателя – «Количество тестов оптимизации» и «Скорректировано по оптимизации». Первый показатель – просто количество различных комбинаций параметров, т. е. число испытаний системы по выборке данных с различными параметрами. Поскольку первый параметр системы на лунном цикле, L1, принимал значения от 1 до 20 с шагом в 1, было проведено 20 тестов и соответственно получено 20 значений t-критерия.
Большая часть статистики в табл. 4–2 идентична показателями табл. 4–1 из примера 1. Добавлены два дополнительных показателя – «Количество тестов оптимизации» и «Скорректировано по оптимизации». Первый показатель – просто количество различных комбинаций параметров, т. е. число испытаний системы по выборке данных с различными параметрами. Поскольку первый параметр системы на лунном цикле, L1, принимал значения от 1 до 20 с шагом в 1, было проведено 20 тестов и соответственно получено 20 значений t-критерия.
Количество тестов, использованных для коррекции вероятности (значимости) по лучшему показателю t-критерия, определяется следующим образом: от 1 отнимается статистическая значимость лучшего теста, результат возводится в степень m (где m – число прогонок тестов). Затем этот результат вычитается из единицы. Это показывает вероятность обнаружения в m тестах (в данном случае m = 20) по крайней мере одного значения t-критерия, как минимум не уступающего действительно обнаруженному в данном решении. Некорректированная вероятность случайного происхождения результатов составляет менее 2 % – весьма впечатляющий показатель. После коррекции по множественным тестам (оптимизации) картина в корне меняется. Результаты с такой прибыльностью системы могли быть достигнуты чисто случайно в 31 % случаев! Впрочем, все не так плохо. Настройка была крайне консервативной и исходила из полной независимости тестов друг от друга. На самом же деле между тестами будет идти значительная серийная корреляция, поскольку в большинстве традиционных систем небольшие изменения параметров вызывают небольшие изменения результатов. Это в точности напоминает серийную зависимость в выборках данных: эффективный размер снижается, если снижается эффективное количество проведенных тестов. Поскольку многие из тестов коррелируют друг с другом, 20 проведенных соответствуют 5–10 «реальным» независимым тестам. Учитывая серийную зависимость между тестами, вероятность с поправкой на оптимизацию составит около 0,15, а не 0,3104. Поскольку природа и точная величина серийной зависимости тестов неизвестны, менее консервативное заключение об оптимизации не может быть рассчитано напрямую, а только может быть примерно оценено.
В некоторых случаях, например в моделях множественной регрессии, существуют точные математические формулы для расчета статистических параметров с учетом процесса подгонки (оптимизации), что делает излишними поправки на оптимизацию.
Трактовка статистических показателей
В примере 1 представлен тест с проверкой системы, в примере 2 – оптимизация на данных из выборки. При обсуждении результатов мы возвращаемся к естественному порядку проведения тестов, т. е. сначала оптимизация, а потом проверка.
Результаты оптимизации. В табл. 4–2 показаны результаты анализа данных из выборки. За 5 лет периода оптимизации система провела 118 сделок (n = 118), средняя сделка дала прибыль в $740,97, и сделки были весьма различными: стандартное отклонение выборки составило около $3811. Таким образом, во многих сделках убытки составляли тысячи долларов, в других такого же масштаба достигали прибыли. Степень прибыльности легко оценить по столбцу «Прибыль/Убыток», в котором встречается немало убытков в $2500 (на этом уровне активировалась защитная остановка) и значительное количество прибылей, многие более $5000, а некоторые даже более $10 000. Ожидаемое стандартное отклонение средней прибыли в сделке показывает, что если бы такие расчеты многократно проводились на схожих выборках, то среднее колебалось бы в пределах десяти процентов, и многие выборки показывали бы среднюю прибыльность в размере $740 ± 350.
T-критерий для наилучшего решения составил 2,1118 при статистической значимости 0,0184. Это весьма впечатляющий результат. Если бы тест проводился только один раз (без оптимизации), то вероятность случайно достичь такого значения была бы около 2 %, что позволяет заключить, что система с большой вероятностью находит «скрытую неэффективность» рынка и имеет шанс на успех в реальной торговле. Впрочем, не забывайте: исследовались лучшие 20 наборов параметров. Если скорректировать статистическую значимость, то значение составит около 0,31, что вовсе не так хорошо – эффективность вполне может оказаться случайной. Следовательно, система имеет некоторые шансы на выживание в реальной торговле, однако в ее провале не будет ничего удивительного.
Серийная корреляция между сделками составляла всего 0,0479 при значимости 0,6083 – в данном контексте немного. Эти показатели говорят, что значительной серийной корреляции между сделками не наблюдалось, и вышеприведенный статистический анализ, скорее всего, справедлив.
За время проведения теста было 58 прибыльных сделок, т. е. доля прибыльных сделок составила около 49 %. Верхняя граница 99 %-ного доверительного интервала количества прибыльных сделок составила около 61 %, а нижняя – около 37 %. Это означает, что доля прибыльных сделок в популяции данных с вероятностью 99 % попала бы в интервал от 37 до 61 %. Фактически коррекция по оптимизации должна была бы расширить доверительный интервал; но мы этого не делали, поскольку не особенно интересовались показателем доли прибыльных сделок.
Результаты проверки. В табл. 4–1 содержатся данные и статистические заключения по тестированию модели на данных вне выборки. Поскольку все параметры уже определены при оптимизации и проводился всего один тест, мы не рассматривали ни оптимизацию, ни ее последствия. За период с 1.01.1995 по 1.01.1997 система провела 47 сделок, средняя сделка дала прибыль в $974, что выше, чем в выборке, использованной для оптимизации! Видимо, эффективность системы сохранилась.
Стандартное отклонение выборки составило более $6000, почти вдвое больше, чем в пределах выборки, по которой проводилась оптимизация. Следовательно, стандартное отклонение средней прибыли в сделке было около $890, что составляет немалую ошибку. С учетом небольшого размера выборки это приводит к снижению значения t-критерия по сравнению с полученным при оптимизации и к меньшей статистической значимости – около 14 %. Эти результаты не слишком плохи, но и не слишком хороши: вероятность нахождения «скрытой неэффективности» рынка составляет более 80 %. Но при этом серийная корреляция в тесте была значительно выше (ее вероятность составила 0,1572). Это означает, что такой серийной корреляции чисто случайно можно достичь лишь в 16 % случаев, даже если никакой реальной корреляции в данных нет. Следовательно, и t-критерий прибыли/убытка, скорее всего, переоценил статистическую значимость до некоторой степени (вероятно, на 20–30 %). Если размер выборки был бы меньше, то значение t составило бы около 0,18 вместо полученного 0,1392. Доверительный интервал для процента прибыльных сделок в популяции находился в пределах от 17 до приблизительно 53 %.
В общем, оценка показывает, что система, вероятно, сможет работать в будущем, но без особой уверенности в успехе. Учитывая, что в одном тесте вероятность случайности прибылей составила 31 %, в другом, независимом, – 14 % (с коррекцией на оптимизацию 18 %), шанс того, что средняя сделка будет выгодной и система в будущем сможет работать, остается неплохим.
Другие статистические методы и их использование
Серийная зависимость – серьезная проблема. Если она высока, то для борьбы с ней надо считать выборку меньшей, чем она есть на самом деле. Другой вариант – выбрать случайным образом данные для тестирования из различных участков за длительный период времени. Это также повысит представительность выборки в отношении всей популяции.
Что, если изменится рынок? При разработке торговых систем возможно нарушение третьего положения t-критерия, и его невозможно предугадать или компенсировать. Причина этого нарушения в том, что популяция, из которой взят образец данных для тестирования или разработки, может отличаться от популяции, данные из которой будут использоваться в будущих сделках. Рынок может подвергаться структурным или иным изменениям. Как говорилось, популяция данных S&P 500 до 1983 г. принципиально отличается от последующих данных, когда началась торговля опционами и фьючерсами. Подобные события могут разрушить любой метод оценки системы. Как бы ни проводилось тестирование, при изменении рынка до начала реальной торговли окажется, что система разрабатывалась и тестировалась на одном рынке, а работать будет на другом. Естественно, модель разваливается на части. Даже самая лучшая модель будет уничтожена изменением рынка.
Тем не менее большинство рынков постоянно меняются. Несмотря на этот суровый факт, использование статистики в оценке системы остается принципиально важным, поскольку если рынок не изменится вскоре после начала работы системы или же изменения рынка недостаточны, чтобы оказать глубокое влияние, то статистически возможно произвести достаточно достоверную оценку ожидаемых вероятностей и прибылей системы.
Пример 2: Оценка тестов на данных в пределах выборки
Каким образом можно оценивать систему, которая подвергалась подгонке параметров (т. е. оптимизации) по некоторой выборке данных? Трейдеры часто оптимизируют системы для улучшения результатов. В данном аспекте применение статистики особенно важно, поскольку позволяет анализировать результаты, компенсируя этим большое количество тестовых прогонов во время оптимизации. В табл. 4–2 приведены показатели прибыли/убытка и различные статистические показатели для тестов в пределах выборки (т. е. на данных, использовавшихся для оптимизации системы). Система подвергалась оптимизации на данных за период с 1.01.1990 по 1.02.1995.

Количество тестов, использованных для коррекции вероятности (значимости) по лучшему показателю t-критерия, определяется следующим образом: от 1 отнимается статистическая значимость лучшего теста, результат возводится в степень m (где m – число прогонок тестов). Затем этот результат вычитается из единицы. Это показывает вероятность обнаружения в m тестах (в данном случае m = 20) по крайней мере одного значения t-критерия, как минимум не уступающего действительно обнаруженному в данном решении. Некорректированная вероятность случайного происхождения результатов составляет менее 2 % – весьма впечатляющий показатель. После коррекции по множественным тестам (оптимизации) картина в корне меняется. Результаты с такой прибыльностью системы могли быть достигнуты чисто случайно в 31 % случаев! Впрочем, все не так плохо. Настройка была крайне консервативной и исходила из полной независимости тестов друг от друга. На самом же деле между тестами будет идти значительная серийная корреляция, поскольку в большинстве традиционных систем небольшие изменения параметров вызывают небольшие изменения результатов. Это в точности напоминает серийную зависимость в выборках данных: эффективный размер снижается, если снижается эффективное количество проведенных тестов. Поскольку многие из тестов коррелируют друг с другом, 20 проведенных соответствуют 5–10 «реальным» независимым тестам. Учитывая серийную зависимость между тестами, вероятность с поправкой на оптимизацию составит около 0,15, а не 0,3104. Поскольку природа и точная величина серийной зависимости тестов неизвестны, менее консервативное заключение об оптимизации не может быть рассчитано напрямую, а только может быть примерно оценено.
В некоторых случаях, например в моделях множественной регрессии, существуют точные математические формулы для расчета статистических параметров с учетом процесса подгонки (оптимизации), что делает излишними поправки на оптимизацию.
Трактовка статистических показателей
В примере 1 представлен тест с проверкой системы, в примере 2 – оптимизация на данных из выборки. При обсуждении результатов мы возвращаемся к естественному порядку проведения тестов, т. е. сначала оптимизация, а потом проверка.
Результаты оптимизации. В табл. 4–2 показаны результаты анализа данных из выборки. За 5 лет периода оптимизации система провела 118 сделок (n = 118), средняя сделка дала прибыль в $740,97, и сделки были весьма различными: стандартное отклонение выборки составило около $3811. Таким образом, во многих сделках убытки составляли тысячи долларов, в других такого же масштаба достигали прибыли. Степень прибыльности легко оценить по столбцу «Прибыль/Убыток», в котором встречается немало убытков в $2500 (на этом уровне активировалась защитная остановка) и значительное количество прибылей, многие более $5000, а некоторые даже более $10 000. Ожидаемое стандартное отклонение средней прибыли в сделке показывает, что если бы такие расчеты многократно проводились на схожих выборках, то среднее колебалось бы в пределах десяти процентов, и многие выборки показывали бы среднюю прибыльность в размере $740 ± 350.
T-критерий для наилучшего решения составил 2,1118 при статистической значимости 0,0184. Это весьма впечатляющий результат. Если бы тест проводился только один раз (без оптимизации), то вероятность случайно достичь такого значения была бы около 2 %, что позволяет заключить, что система с большой вероятностью находит «скрытую неэффективность» рынка и имеет шанс на успех в реальной торговле. Впрочем, не забывайте: исследовались лучшие 20 наборов параметров. Если скорректировать статистическую значимость, то значение составит около 0,31, что вовсе не так хорошо – эффективность вполне может оказаться случайной. Следовательно, система имеет некоторые шансы на выживание в реальной торговле, однако в ее провале не будет ничего удивительного.
Серийная корреляция между сделками составляла всего 0,0479 при значимости 0,6083 – в данном контексте немного. Эти показатели говорят, что значительной серийной корреляции между сделками не наблюдалось, и вышеприведенный статистический анализ, скорее всего, справедлив.
За время проведения теста было 58 прибыльных сделок, т. е. доля прибыльных сделок составила около 49 %. Верхняя граница 99 %-ного доверительного интервала количества прибыльных сделок составила около 61 %, а нижняя – около 37 %. Это означает, что доля прибыльных сделок в популяции данных с вероятностью 99 % попала бы в интервал от 37 до 61 %. Фактически коррекция по оптимизации должна была бы расширить доверительный интервал; но мы этого не делали, поскольку не особенно интересовались показателем доли прибыльных сделок.
Результаты проверки. В табл. 4–1 содержатся данные и статистические заключения по тестированию модели на данных вне выборки. Поскольку все параметры уже определены при оптимизации и проводился всего один тест, мы не рассматривали ни оптимизацию, ни ее последствия. За период с 1.01.1995 по 1.01.1997 система провела 47 сделок, средняя сделка дала прибыль в $974, что выше, чем в выборке, использованной для оптимизации! Видимо, эффективность системы сохранилась.
Стандартное отклонение выборки составило более $6000, почти вдвое больше, чем в пределах выборки, по которой проводилась оптимизация. Следовательно, стандартное отклонение средней прибыли в сделке было около $890, что составляет немалую ошибку. С учетом небольшого размера выборки это приводит к снижению значения t-критерия по сравнению с полученным при оптимизации и к меньшей статистической значимости – около 14 %. Эти результаты не слишком плохи, но и не слишком хороши: вероятность нахождения «скрытой неэффективности» рынка составляет более 80 %. Но при этом серийная корреляция в тесте была значительно выше (ее вероятность составила 0,1572). Это означает, что такой серийной корреляции чисто случайно можно достичь лишь в 16 % случаев, даже если никакой реальной корреляции в данных нет. Следовательно, и t-критерий прибыли/убытка, скорее всего, переоценил статистическую значимость до некоторой степени (вероятно, на 20–30 %). Если размер выборки был бы меньше, то значение t составило бы около 0,18 вместо полученного 0,1392. Доверительный интервал для процента прибыльных сделок в популяции находился в пределах от 17 до приблизительно 53 %.
В общем, оценка показывает, что система, вероятно, сможет работать в будущем, но без особой уверенности в успехе. Учитывая, что в одном тесте вероятность случайности прибылей составила 31 %, в другом, независимом, – 14 % (с коррекцией на оптимизацию 18 %), шанс того, что средняя сделка будет выгодной и система в будущем сможет работать, остается неплохим.
Другие статистические методы и их использование
Этот раздел посвящен исключительно знакомству читателя с другими статистическими методами. Тем, кто желает серьезно заниматься разработкой и тестированием торговых систем, мы настоятельно рекомендуем обратить внимание на посвященную данным методам литературу.
Системы, полученные генетическими методами
Мы разрабатываем множество систем с использованием генетических алгоритмов. Популярной функцией пригодности системы (степени достижения желаемого результата) является общая прибыль системы. Но при этом общая прибыль не является лучшим из критериев качества системы! Система, которая использует только крупные обвалы рынка S&P 500, например, даст очень высокую общую прибыль и очень высокий процент прибыльных сделок, но кто может с уверенностью утверждать, что такая система полезна в практической торговле? Если система провела всего 2–3 сделки за 10 лет, чисто интуитивно нельзя ожидать ее стабильной работы в будущем или быть уверенным, что система вообще сможет совершать сделки. Частично проблема в том, что общая прибыль никак не учитывает количество сделок и их изменчивость.
Альтернативными показателями пригодности, лишенными некоторых недостатков общей прибыли, являются t-критерий и связанная с ним вероятность. При использовании t-критерия как функции пригодности (вместо простого поиска наиболее выгодного решения) смысл генетического развития систем состоит в создании систем с максимальной вероятностью прибылей в будущем или, что то же самое, с минимальной вероятностью прибылей, обусловленных случайностью или подгонкой под исторические данные. Этот подход работает весьма хорошо; t-критерий учитывает прибыль, размер выборки данных и количество совершенных сделок. Хотя все факторы важны, все же, чем больше сделок совершает система, тем выше t-показатель и больше вероятность устойчивости в будущем. Таким же образом системы, которые дают более стабильные сделки с минимальным разбросом, будут иметь лучший t-показатель и предпочтительнее систем, где разброс сделок велик. T-критерий включает в себя многие из параметров, определяющих качество торговой модели, и сводит их в одно число, для оптимизации которого можно применить генетический алгоритм.
Множественная регрессия
Еще одна часто применяемая методика – множественная регрессия. Рассмотрим анализ сравнения рынков; цель этого исследования в том, чтобы обнаружить на других рынках показатели поведения, которые указывали бы на текущее поведение данного рынка. Проведение различных регрессий – подходящий метод для анализа таких потенциальных связей; более того, существуют замечательные методы для тестирования и установки доверительных интервалов корреляций и весов регрессии (бета-чисел), генерируемых при анализе. Ввиду ограниченности объема главы, рекомендуем обратить внимание на книгу Мейерса (Meyers, 1986) – хорошее пособие по основам множественной регрессии.
Метод Монте-Карло
Есть еще один уникальный метод статистического анализа, который известен под названием метода Монте-Карло. Он состоит в проведении множественных тестов на искусственных данных, сконструированных так, чтобы обладать свойствами выборок, извлеченных из случайной популяции. За исключением случайности, эти данные настроены так, чтобы иметь основные характеристики популяции, из которой брались реальные образцы и относительно которой требуется сделать заключение. Это весьма мощный инструмент; красота моделирования по методу Монте-Карло состоит в том, что его можно провести, не нарушая основных положений статистического анализа (например, обеспечить нормальное распределение), что позволит избежать необоснованных выводов.
Тестирование вне пределов выборки
Еще один способ оценки системы – проводить тестирование вне пределов выборки. Несколько временных периодов резервируются для тестирования модели, которая была разработана и оптимизирована на данных из другого периода. Тестирование вне пределов выборки помогает понять, как ведет себя модель на данных, которые не использовались при ее разработке и оптимизации. Мы настоятельно рекомендуем применять этот метод. В приведенных выше примерах рассматривались тесты систем на оптимизационных выборках и вне их пределов. При тестировании вне пределов выборки не требуются коррекции статистики или процесса оптимизации. Тесты вне пределов выборки и тесты на нескольких выборках также могут дать информацию об изменении поведения рынка с течением времени.
Тестирование с прогонкой вперед
При тестировании с прогонкой вперед система оптимизируется на данных за несколько лет, затем моделируется торговля за следующий год. Потом система повторно оптимизируется на данных за несколько лет, со сдвигом окна оптимизации вперед, включая год ведения торговли, и процесс повторяется раз за разом, прогоняя систему через популяцию данных. Хотя этот метод требует огромного количества вычислений, он чрезвычайно полезен для изучения и тестирования торговых систем. Его основное преимущество в том, что он совмещает оптимизацию и проведение тестов вне пределов выборки. Все вышеописанные статистические методы, например проверка по критерию Стьюдента, могут быть использованы на тестах с прогонкой вперед просто и доступно, без необходимости вносить поправки на оптимизацию. Кроме того, тесты будут весьма правдоподобно моделировать процесс, происходящий в реальной торговле, – сначала ведется оптимизация, а затем система ведет торговлю на ранее неизвестных данных и время от времени повторно оптимизируется. Продвинутые разработчики встраивают процесс оптимизации в систему, создавая то, что можно назвать «адаптивной торговой моделью». В работе Мейерса (Meyers, 1997) подробно рассмотрен процесс тестирования с прогонкой вперед.
Системы, полученные генетическими методами
Мы разрабатываем множество систем с использованием генетических алгоритмов. Популярной функцией пригодности системы (степени достижения желаемого результата) является общая прибыль системы. Но при этом общая прибыль не является лучшим из критериев качества системы! Система, которая использует только крупные обвалы рынка S&P 500, например, даст очень высокую общую прибыль и очень высокий процент прибыльных сделок, но кто может с уверенностью утверждать, что такая система полезна в практической торговле? Если система провела всего 2–3 сделки за 10 лет, чисто интуитивно нельзя ожидать ее стабильной работы в будущем или быть уверенным, что система вообще сможет совершать сделки. Частично проблема в том, что общая прибыль никак не учитывает количество сделок и их изменчивость.
Альтернативными показателями пригодности, лишенными некоторых недостатков общей прибыли, являются t-критерий и связанная с ним вероятность. При использовании t-критерия как функции пригодности (вместо простого поиска наиболее выгодного решения) смысл генетического развития систем состоит в создании систем с максимальной вероятностью прибылей в будущем или, что то же самое, с минимальной вероятностью прибылей, обусловленных случайностью или подгонкой под исторические данные. Этот подход работает весьма хорошо; t-критерий учитывает прибыль, размер выборки данных и количество совершенных сделок. Хотя все факторы важны, все же, чем больше сделок совершает система, тем выше t-показатель и больше вероятность устойчивости в будущем. Таким же образом системы, которые дают более стабильные сделки с минимальным разбросом, будут иметь лучший t-показатель и предпочтительнее систем, где разброс сделок велик. T-критерий включает в себя многие из параметров, определяющих качество торговой модели, и сводит их в одно число, для оптимизации которого можно применить генетический алгоритм.
Множественная регрессия
Еще одна часто применяемая методика – множественная регрессия. Рассмотрим анализ сравнения рынков; цель этого исследования в том, чтобы обнаружить на других рынках показатели поведения, которые указывали бы на текущее поведение данного рынка. Проведение различных регрессий – подходящий метод для анализа таких потенциальных связей; более того, существуют замечательные методы для тестирования и установки доверительных интервалов корреляций и весов регрессии (бета-чисел), генерируемых при анализе. Ввиду ограниченности объема главы, рекомендуем обратить внимание на книгу Мейерса (Meyers, 1986) – хорошее пособие по основам множественной регрессии.
Метод Монте-Карло
Есть еще один уникальный метод статистического анализа, который известен под названием метода Монте-Карло. Он состоит в проведении множественных тестов на искусственных данных, сконструированных так, чтобы обладать свойствами выборок, извлеченных из случайной популяции. За исключением случайности, эти данные настроены так, чтобы иметь основные характеристики популяции, из которой брались реальные образцы и относительно которой требуется сделать заключение. Это весьма мощный инструмент; красота моделирования по методу Монте-Карло состоит в том, что его можно провести, не нарушая основных положений статистического анализа (например, обеспечить нормальное распределение), что позволит избежать необоснованных выводов.
Тестирование вне пределов выборки
Еще один способ оценки системы – проводить тестирование вне пределов выборки. Несколько временных периодов резервируются для тестирования модели, которая была разработана и оптимизирована на данных из другого периода. Тестирование вне пределов выборки помогает понять, как ведет себя модель на данных, которые не использовались при ее разработке и оптимизации. Мы настоятельно рекомендуем применять этот метод. В приведенных выше примерах рассматривались тесты систем на оптимизационных выборках и вне их пределов. При тестировании вне пределов выборки не требуются коррекции статистики или процесса оптимизации. Тесты вне пределов выборки и тесты на нескольких выборках также могут дать информацию об изменении поведения рынка с течением времени.
Тестирование с прогонкой вперед
При тестировании с прогонкой вперед система оптимизируется на данных за несколько лет, затем моделируется торговля за следующий год. Потом система повторно оптимизируется на данных за несколько лет, со сдвигом окна оптимизации вперед, включая год ведения торговли, и процесс повторяется раз за разом, прогоняя систему через популяцию данных. Хотя этот метод требует огромного количества вычислений, он чрезвычайно полезен для изучения и тестирования торговых систем. Его основное преимущество в том, что он совмещает оптимизацию и проведение тестов вне пределов выборки. Все вышеописанные статистические методы, например проверка по критерию Стьюдента, могут быть использованы на тестах с прогонкой вперед просто и доступно, без необходимости вносить поправки на оптимизацию. Кроме того, тесты будут весьма правдоподобно моделировать процесс, происходящий в реальной торговле, – сначала ведется оптимизация, а затем система ведет торговлю на ранее неизвестных данных и время от времени повторно оптимизируется. Продвинутые разработчики встраивают процесс оптимизации в систему, создавая то, что можно назвать «адаптивной торговой моделью». В работе Мейерса (Meyers, 1997) подробно рассмотрен процесс тестирования с прогонкой вперед.
Конец бесплатного ознакомительного фрагмента
