Страница:
М. А. Рябов, Е. Ю. Невская, Е. А. Сорокина, Т. Ф. Шешко
Сборник основных формул по химии
Краткий справочник студента
I. Общая химия
1. Основные понятия химии
Химия – наука о составе, строении, свойствах и превращениях веществ.
Атомно-молекулярное учение. Вещества состоят из химических частиц (молекул, атомов, ионов), которые имеют сложное строение и состоят из элементарных частиц (протонов, нейтронов, электронов).
Атом – нейтральная частица, состоящая из положительного ядра и электронов.
Молекула – устойчивая группа атомов, связанных химическими связями.
Химический элемент – вид атомов с одинаковым зарядом ядра. Элемент обозначают
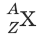где X – символ элемента, Z– порядковый номер элемента в Периодической системе элементов Д.И. Менделеева, A – массовое число. Порядковый номер Z равен заряду ядра атома, числу протонов в ядре атома и числу электронов в атоме. Массовое число A равно сумме чисел протонов и нейтронов в атоме. Число нейтронов равно разности A – Z.
Изотопы – атомы одного элемента, имеющие разные массовые числа.
Относительная атомная масса (Ar) – отношение средней массы атома элемента естественного изотопического состава к 1/12 массы атома изотопа углерода 12С.
Относительная молекулярная масса (Mr) – отношение средней массы молекулы вещества естественного изотопического состава к 1/12 части массы атома изотопа углерода 12С.
Атомная единица массы (а.е.м) – 1/12 часть массы атома изотопа углерода 12С. 1 а.е. м = 1,66 × 10-24 г.
Моль – количество вещества, содержащее столько структурных единиц (атомов, молекул, ионов), сколько содержится атомов в 0,012 кг изотопа углерода 12С. Моль – количество вещества, содержащее 6,02 • 1023 структурных единиц (атомов, молекул, ионов).
n = N/NA, где n – количество вещества (моль), N – число частиц, a NA – постоянная Авогадро. Количество вещества может обозначаться также и символом v.
Постоянная Авогадро NA = 6,02 • 1023 частиц/моль.
Молярная масса M (г/моль) – отношение массы вещества m(г) к количеству вещества n (моль):
М = m/n, откуда: m = М • n и n = m/М.
Молярный объем газа VM (л/моль) – отношение объема газа V (л) к количеству вещества этого газа n (моль). При нормальных условиях VM = 22,4 л/моль.
Нормальные условия: температура t = 0°C, или Т = 273 К, давление р = 1 атм = 760 мм. рт. ст. = 101 325 Па = 101,325 кПа.
VM = V/n, откуда: V = VM • n и n = V/VM.
В результате получается общая формула:
n = m/M = V/VM = N/NA.
Эквивалент – реальная или условная частица, взаимодействующая с одним атомом водорода, или замещающая его, или эквивалентная ему каким-либо другим способом.
Молярная масса эквивалентов Мэ – отношение массы вещества к количеству эквивалентов этого вещества: Мэ = m/n(экв).
В реакциях обмена зарядов молярная масса эквивалентов вещества
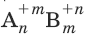с молярной массой М равна: Мэ = М/(n × m).
В окислительно-восстановительных реакциях молярная масса эквивалентов вещества с молярной массой М равна: Мэ = М/n(ē), где n(ē) – число переданных электронов.
Закон эквивалентов – массы реагирующих веществ 1 и 2 пропорциональны молярным массам их эквивалентов. m1/m2 = МЭ1/МЭ2, или m1/МЭ1 = m2/МЭ2, или n1 = n2, где m1 и m2 – массы двух веществ, МЭ1 и МЭ2 – молярные массы эквивалентов, n1 и n2 – количества эквивалентов этих веществ.
Для растворов закон эквивалентов может быть записан в следующем виде:
cЭ1 • V1 = cЭ2 • V2, где сЭ1, сЭ2, V1 и V2 – молярные концентрации эквивалентов и объемы растворов этих двух веществ.
Объединенный газовый закон: pV = nRT, где p – давление (Па, кПа), V – объем (м3, л), n – количество вещества газа (моль), T – температура (К), T (К) = t (°C) + 273, R – константа, R = 8,314 Дж/(К × моль), при этом Дж = Па • м3 = кПа • л.
Атомно-молекулярное учение. Вещества состоят из химических частиц (молекул, атомов, ионов), которые имеют сложное строение и состоят из элементарных частиц (протонов, нейтронов, электронов).
Атом – нейтральная частица, состоящая из положительного ядра и электронов.
Молекула – устойчивая группа атомов, связанных химическими связями.
Химический элемент – вид атомов с одинаковым зарядом ядра. Элемент обозначают
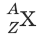
Изотопы – атомы одного элемента, имеющие разные массовые числа.
Относительная атомная масса (Ar) – отношение средней массы атома элемента естественного изотопического состава к 1/12 массы атома изотопа углерода 12С.
Относительная молекулярная масса (Mr) – отношение средней массы молекулы вещества естественного изотопического состава к 1/12 части массы атома изотопа углерода 12С.
Атомная единица массы (а.е.м) – 1/12 часть массы атома изотопа углерода 12С. 1 а.е. м = 1,66 × 10-24 г.
Моль – количество вещества, содержащее столько структурных единиц (атомов, молекул, ионов), сколько содержится атомов в 0,012 кг изотопа углерода 12С. Моль – количество вещества, содержащее 6,02 • 1023 структурных единиц (атомов, молекул, ионов).
n = N/NA, где n – количество вещества (моль), N – число частиц, a NA – постоянная Авогадро. Количество вещества может обозначаться также и символом v.
Постоянная Авогадро NA = 6,02 • 1023 частиц/моль.
Молярная масса M (г/моль) – отношение массы вещества m(г) к количеству вещества n (моль):
М = m/n, откуда: m = М • n и n = m/М.
Молярный объем газа VM (л/моль) – отношение объема газа V (л) к количеству вещества этого газа n (моль). При нормальных условиях VM = 22,4 л/моль.
Нормальные условия: температура t = 0°C, или Т = 273 К, давление р = 1 атм = 760 мм. рт. ст. = 101 325 Па = 101,325 кПа.
VM = V/n, откуда: V = VM • n и n = V/VM.
В результате получается общая формула:
n = m/M = V/VM = N/NA.
Эквивалент – реальная или условная частица, взаимодействующая с одним атомом водорода, или замещающая его, или эквивалентная ему каким-либо другим способом.
Молярная масса эквивалентов Мэ – отношение массы вещества к количеству эквивалентов этого вещества: Мэ = m/n(экв).
В реакциях обмена зарядов молярная масса эквивалентов вещества
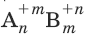
В окислительно-восстановительных реакциях молярная масса эквивалентов вещества с молярной массой М равна: Мэ = М/n(ē), где n(ē) – число переданных электронов.
Закон эквивалентов – массы реагирующих веществ 1 и 2 пропорциональны молярным массам их эквивалентов. m1/m2 = МЭ1/МЭ2, или m1/МЭ1 = m2/МЭ2, или n1 = n2, где m1 и m2 – массы двух веществ, МЭ1 и МЭ2 – молярные массы эквивалентов, n1 и n2 – количества эквивалентов этих веществ.
Для растворов закон эквивалентов может быть записан в следующем виде:
cЭ1 • V1 = cЭ2 • V2, где сЭ1, сЭ2, V1 и V2 – молярные концентрации эквивалентов и объемы растворов этих двух веществ.
Объединенный газовый закон: pV = nRT, где p – давление (Па, кПа), V – объем (м3, л), n – количество вещества газа (моль), T – температура (К), T (К) = t (°C) + 273, R – константа, R = 8,314 Дж/(К × моль), при этом Дж = Па • м3 = кПа • л.
2. Строение атома и Периодический закон
Корпускулярно-волновой дуализм материи – представление о том, что каждый объект может иметь и волновые, и корпускулярные свойства. Луи де Бройль предложил формулу, связывающую волновые и корпускулярные свойства объектов: λ = h/(mV), где h – постоянная Планка, λ – длина волны, которая соответствует каждому телу с массой m и скоростью V. Хотя волновые свойства существуют для всех объектов, но наблюдаться они могут лишь для микрообъектов, имеющих массы порядка массы атома и электрона.
Принцип неопределенности Гейзенберга: Δ(mVx) • Δх > h/2n или ΔVx • Δx > h/(2πm), где m – масса частицы, x – ее координата, Vx – скорость в направлении x, Δ – неопределенность, погрешность определения. Принцип неопределенности означает, что нельзя одновременно сколь угодно точно указать положение (координату x) и скорость (Vx) частицы.
Частицы с маленькими массами (атомы, ядра, электроны, молекулы) не являются частицами в понимании этого механикой Ньютона и не могут изучаться классической физикой. Они изучаются квантовой физикой.
Главное квантовое число n принимает значения 1, 2, 3, 4, 5, 6 и 7, соответствующие электронным уровням (слоям) К, L, M, N, О, Р и Q.
Уровень – пространство, где расположены электроны с одинаковым числом n. Электроны разных уровней пространственно и энергетически отделены друг от друга, поскольку число n определяет энергию электронов Е (чем больше n, тем больше Е) и расстояние R между электронами и ядром (чем больше n, тем больше R).
Орбитальное (побочное, азимутальное) квантовое число l принимает значения в зависимости от числа n: l = 0, 1,…(n – 1). Например, если n = 2, то l = 0, 1; если n = 3, то l = 0, 1, 2. Число l характеризует подуровень (подслой).
Подуровень – пространство, где расположены электроны с определенными n и l. Подуровни данного уровня обозначаются в зависимости от числа l: s – если l = 0, p – если l = 1, d – если l = 2, f – если l = 3. Подуровни данного атома обозначаются в зависимости от чисел n и l, например: 2s (п = 2, l = 0), 3d (n = 3, l = 2) и т. д. Подуровни данного уровня имеют разную энергию (чем больше l, тем больше Е): Es< E < ЕА < … и разную форму орбиталей, составляющих эти подуровни: s-орбиталь имеет форму шара, p-орбиталь имеет форму гантели и т. д.
Магнитное квантовое число m1 характеризует ориентацию орбитального магнитного момента, равного l, в пространстве относительно внешнего магнитного поля и принимает значения: – l,…-1, 0, 1,…l, т. е. всего (2l + 1) значение. Например, если l = 2, то m1 = -2, -1, 0, 1, 2.
Орбиталь (часть подуровня) – пространство, где расположены электроны (не более двух) с определенными n, l, m1. Подуровень содержит 2l+1 орбиталь. Например, d – подуровень содержит пять d-орбиталей. Орбитали одного подуровня, имеющие разные числа m1, имеют одинаковую энергию.
Магнитное спиновое число ms характеризует ориентацию собственного магнитного момента электрона s, равного ½, относительно внешнего магнитного поля и принимает два значению: +½ и _½.
Электроны в атоме занимают уровни, подуровни и орбитали согласно следующим правилам.
Правило Паули: в одном атоме два электрона не могут иметь четыре одинаковых квантовых числа. Они должны отличаться по меньшей мере одним квантовым числом.
Из правила Паули следует, что на орбитали могут располагаться не более двух электронов, на подуровне может содержаться не более 2(2l + 1) электронов, на уровне содержится не более 2n2 электронов.
Правило Клечковского: заполнение электронных подуровней осуществляется в порядке возрастания суммы (n + l), а в случае одинаковой суммы (n + l) – в порядке возрастания числа n.
Графическая форма правила Клечковского.
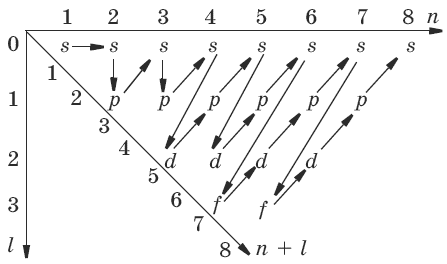Согласно правилу Клечковского, заполнение подуровней осуществляется в следующем порядке: 1s, 2s, 2р, 3s, Зр, 4s, 3d, 4р, 5s, 4d, 5р, 6s, 4f, 5d, 6p, 7s, 5f, 6d, 7p, 8s,…
Хотя заполнение подуровней происходит по правилу Клечковского, в электронной формуле подуровни записываются последовательно по уровням: 1s, 2s, 2p, 3s, 3p, 3d, 4s, 4р, 4d, 4f и т. д. Таким образом, электронная формула атома брома записывается следующим образом: Br(35ē) 1s22s22p63s23p63d104s24p5.
Электронные конфигурации ряда атомов отличаются от предсказанных по правилу Клечковского. Так, для Сr и Cu:
Сr(24ē) 1s22s22p63s23p63d54s1 и Cu(29ē) 1s22s22p63s23p63d104s1.
Правило Хунда (Гунда): заполнение ор-биталей данного подуровня осуществляется так, чтобы суммарный спин был максимален. Орбитали данного подуровня заполняются сначала по одному электрону.
Электронные конфигурации атомов можно записать по уровням, подуровням, ор-биталям. Например, электронная формула Р(15ē) может быть записана:
а) по уровням)2)8)5;
б) по подуровням 1s22s22p63s23p3;
в) по орбиталям
Примеры электронных формул некоторых атомов и ионов:
V(23ē) 1s22s22p63s23p63d34s2;
V3+(20ē) 1s22s22p63s23p63d24s0.
Принцип неопределенности Гейзенберга: Δ(mVx) • Δх > h/2n или ΔVx • Δx > h/(2πm), где m – масса частицы, x – ее координата, Vx – скорость в направлении x, Δ – неопределенность, погрешность определения. Принцип неопределенности означает, что нельзя одновременно сколь угодно точно указать положение (координату x) и скорость (Vx) частицы.
Частицы с маленькими массами (атомы, ядра, электроны, молекулы) не являются частицами в понимании этого механикой Ньютона и не могут изучаться классической физикой. Они изучаются квантовой физикой.
Главное квантовое число n принимает значения 1, 2, 3, 4, 5, 6 и 7, соответствующие электронным уровням (слоям) К, L, M, N, О, Р и Q.
Уровень – пространство, где расположены электроны с одинаковым числом n. Электроны разных уровней пространственно и энергетически отделены друг от друга, поскольку число n определяет энергию электронов Е (чем больше n, тем больше Е) и расстояние R между электронами и ядром (чем больше n, тем больше R).
Орбитальное (побочное, азимутальное) квантовое число l принимает значения в зависимости от числа n: l = 0, 1,…(n – 1). Например, если n = 2, то l = 0, 1; если n = 3, то l = 0, 1, 2. Число l характеризует подуровень (подслой).
Подуровень – пространство, где расположены электроны с определенными n и l. Подуровни данного уровня обозначаются в зависимости от числа l: s – если l = 0, p – если l = 1, d – если l = 2, f – если l = 3. Подуровни данного атома обозначаются в зависимости от чисел n и l, например: 2s (п = 2, l = 0), 3d (n = 3, l = 2) и т. д. Подуровни данного уровня имеют разную энергию (чем больше l, тем больше Е): Es< E < ЕА < … и разную форму орбиталей, составляющих эти подуровни: s-орбиталь имеет форму шара, p-орбиталь имеет форму гантели и т. д.
Магнитное квантовое число m1 характеризует ориентацию орбитального магнитного момента, равного l, в пространстве относительно внешнего магнитного поля и принимает значения: – l,…-1, 0, 1,…l, т. е. всего (2l + 1) значение. Например, если l = 2, то m1 = -2, -1, 0, 1, 2.
Орбиталь (часть подуровня) – пространство, где расположены электроны (не более двух) с определенными n, l, m1. Подуровень содержит 2l+1 орбиталь. Например, d – подуровень содержит пять d-орбиталей. Орбитали одного подуровня, имеющие разные числа m1, имеют одинаковую энергию.
Магнитное спиновое число ms характеризует ориентацию собственного магнитного момента электрона s, равного ½, относительно внешнего магнитного поля и принимает два значению: +½ и _½.
Электроны в атоме занимают уровни, подуровни и орбитали согласно следующим правилам.
Правило Паули: в одном атоме два электрона не могут иметь четыре одинаковых квантовых числа. Они должны отличаться по меньшей мере одним квантовым числом.
Из правила Паули следует, что на орбитали могут располагаться не более двух электронов, на подуровне может содержаться не более 2(2l + 1) электронов, на уровне содержится не более 2n2 электронов.
Правило Клечковского: заполнение электронных подуровней осуществляется в порядке возрастания суммы (n + l), а в случае одинаковой суммы (n + l) – в порядке возрастания числа n.
Графическая форма правила Клечковского.
Хотя заполнение подуровней происходит по правилу Клечковского, в электронной формуле подуровни записываются последовательно по уровням: 1s, 2s, 2p, 3s, 3p, 3d, 4s, 4р, 4d, 4f и т. д. Таким образом, электронная формула атома брома записывается следующим образом: Br(35ē) 1s22s22p63s23p63d104s24p5.
Электронные конфигурации ряда атомов отличаются от предсказанных по правилу Клечковского. Так, для Сr и Cu:
Сr(24ē) 1s22s22p63s23p63d54s1 и Cu(29ē) 1s22s22p63s23p63d104s1.
Правило Хунда (Гунда): заполнение ор-биталей данного подуровня осуществляется так, чтобы суммарный спин был максимален. Орбитали данного подуровня заполняются сначала по одному электрону.
Электронные конфигурации атомов можно записать по уровням, подуровням, ор-биталям. Например, электронная формула Р(15ē) может быть записана:
а) по уровням)2)8)5;
б) по подуровням 1s22s22p63s23p3;
в) по орбиталям
V(23ē) 1s22s22p63s23p63d34s2;
V3+(20ē) 1s22s22p63s23p63d24s0.
3. Химическая связь
3.1. Метод валентных связей
Согласно методу валентных связей, связь между атомами А и В образуется с помощью общей пары электронов.
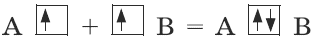
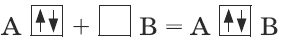
Насыщаемость ковалентной связи: атомы образуют ограниченное число связей, равное их валентности.
Гибридизация атомных орбиталей – смешение атомных орбиталей (АО) разных подуровней атома, электроны которых участвуют в образовании эквивалентных σ-связей. Эквивалентность гибридных орбиталей (ГО) объясняет эквивалентность образующихся химических связей. Например, в случае четырехвалентного атома углерода имеется один 2s– и три 2p-электрона. Чтобы объяснить эквивалентность четырех σ-связей, образованных углеродом в молекулах CH4, CF4 и т. д., атомные одна s- и три р-орбитали заменяют четырьмя эквивалентными гибридными sp3-орбиталями:
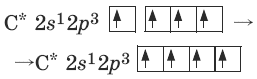Направленность ковалентной связи состоит в том, что она образуется в направлении максимального перекрывания орбиталей, образующих общую пару электронов.
В зависимости от типа гибридизации гибридные орбитали имеют определенное расположение в пространстве:
sp – линейное, угол между осями орби-талей 180°;
sp2 – треугольное, углы между осями орбиталей 120°;
sp3 – тетраэдрическое, углы между осями орбиталей 109°;
sp3d1 – тригонально-бипирамидальное, углы 90° и 120°;
sp2d1 – квадратное, углы между осями орбиталей 90°;
sp3d2 – октаэдрическое, углы между осями орбиталей 90°.
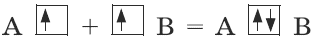
Ковалентная связь.
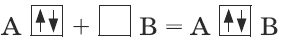
Донорно-ацепторная связь.
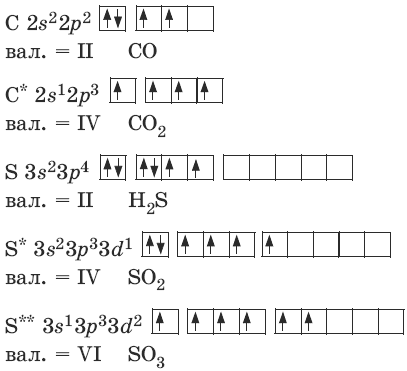
Валентность характеризует способность атомов образовывать химические связи и равна числу химических связей, образованных атомом. Согласно методу валентных связей, валентность равна числу общих пар электронов, а в случае ковалентной связи валентность равна числу неспаренных электронов на внешнем уровне атома в его основном или возбужденных состояниях.Валентность атомов
Например, для углерода и серы:Гибридизация атомных орбиталей – смешение атомных орбиталей (АО) разных подуровней атома, электроны которых участвуют в образовании эквивалентных σ-связей. Эквивалентность гибридных орбиталей (ГО) объясняет эквивалентность образующихся химических связей. Например, в случае четырехвалентного атома углерода имеется один 2s– и три 2p-электрона. Чтобы объяснить эквивалентность четырех σ-связей, образованных углеродом в молекулах CH4, CF4 и т. д., атомные одна s- и три р-орбитали заменяют четырьмя эквивалентными гибридными sp3-орбиталями:
В зависимости от типа гибридизации гибридные орбитали имеют определенное расположение в пространстве:
sp – линейное, угол между осями орби-талей 180°;
sp2 – треугольное, углы между осями орбиталей 120°;
sp3 – тетраэдрическое, углы между осями орбиталей 109°;
sp3d1 – тригонально-бипирамидальное, углы 90° и 120°;
sp2d1 – квадратное, углы между осями орбиталей 90°;
sp3d2 – октаэдрическое, углы между осями орбиталей 90°.
3.2. Теория молекулярных орбиталей
Согласно теории молекулярных орбита-лей, молекула состоит из ядер и электронов. В молекулах электроны находятся на молекулярных орбиталях (МО). МО внешних электронов имеют сложное строение и рассматриваются как линейная комбинация внешних орбиталей атомов, составляющих молекулу. Число образующихся МО равно числу АО, участвующих в их образовании. Энергии МО могут быть ниже (связывающие МО), равны (несвязывающие МО) или выше (разрыхляющие, антисвя-зывающие МО), чем энергии образующих их АО.
Условия взаимодействия АО
1. АО взаимодействуют, если имеют близкие энергии.
2. АО взаимодействуют, если они перекрываются.
3. АО взаимодействуют, если имеют соответствующую симметрию.
Для двухатомной молекулы АВ (или любой линейной молекулы) симметрия МО может быть:
σ, если данная МО имеет ось симметрии,
π, если данная МО имеет плоскость симметрии,
δ, если МО имеет две перпендикулярные плоскости симметрии.
Присутствие электронов на связывающих МО стабилизирует систему, так как уменьшает энергию молекулы по сравнению с энергией атомов. Стабильность молекулы характеризуется порядком связи n, равным: n = (nсв – nразр)/2, где nсв и nразр — числа электронов на связывающих и разрыхляющих орбиталях.
Заполнение МО электронами происходит по тем же правилам, что и заполнение АО в атоме, а именно: правилу Паули (на МО не может быть более двух электронов), правилу Хунда (суммарный спин должен быть максимален) и т. д.
Взаимодействие 1s-AO атомов первого периода (Н и Не) приводит к образованию связывающей σ-МО и разрыхляющей σ*-МО:
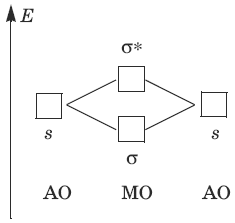Электронные формулы молекул, порядки связей n, экспериментальные энергии связей Е и межмолекулярные расстояния R для двухатомных молекул из атомов первого периода приведены в следующей таблице:
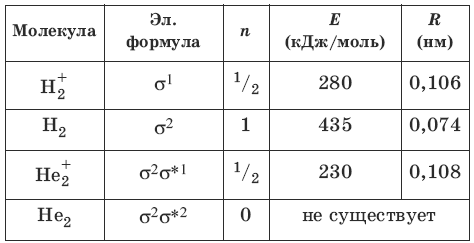Другие атомы второго периода содержат, помимо 2s-AO, также и 2рх-, 2рy– и 2рz-АО, которые при взаимодействии могут образовывать σ– и π-MO. Для атомов О, F и Ne энергии 2s– и 2р-АО существенно различаются, и можно пренебречь взаимодействием 2s-AO одного атома и 2р-АО другого атома, рассматривая взаимодействие между 2s-AO двух атомов отдельно от взаимодействия их 2р-АO. Схема МО для молекул O2, F2, Ne2 имеет следующий вид:
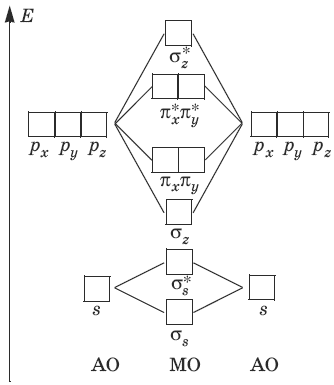Для атомов В, С, N энергии 2s– и 2р-АО близки по своим энергиям, и 2s-AO одного атома взаимодействует с 2рz-АО другого атома. Поэтому порядок МО в молекулах В2, С2 и N2 отличается от порядка МО в молекулах O2, F2 и Ne2. Ниже приведена схема МО для молекул В2, С2 и N2:
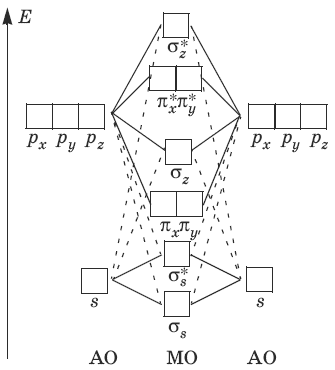На основании приведенных схем МО можно, например, записать электронные формулы молекул O2, O2+ и O2¯:
O2+(11ē)σs2σs*2σz2(πx2πy2)(πx*1πy*0)
n = 2 R = 0,121 нм;
O2(12ē)σs2σs*2σz2(πx2πy2)(πx*1πy*1)
n = 2,5 R = 0,112 нм;
O2¯(13ē)σs2σs*2σz2(πx2πy2)(πx*2πy*1)
n = 1,5 R = 0,126 нм.
В случае молекулы O2 теория МО позволяет предвидеть большую прочность этой молекулы, поскольку n = 2, характер изменения энергий связи и межъядерных расстояний в ряду O2+ – O2 – O2¯, а также парамагнетизм молекулы O2, на верхних МО которой имеются два неспаренных электрона.
Условия взаимодействия АО
1. АО взаимодействуют, если имеют близкие энергии.
2. АО взаимодействуют, если они перекрываются.
3. АО взаимодействуют, если имеют соответствующую симметрию.
Для двухатомной молекулы АВ (или любой линейной молекулы) симметрия МО может быть:
σ, если данная МО имеет ось симметрии,
π, если данная МО имеет плоскость симметрии,
δ, если МО имеет две перпендикулярные плоскости симметрии.
Присутствие электронов на связывающих МО стабилизирует систему, так как уменьшает энергию молекулы по сравнению с энергией атомов. Стабильность молекулы характеризуется порядком связи n, равным: n = (nсв – nразр)/2, где nсв и nразр — числа электронов на связывающих и разрыхляющих орбиталях.
Заполнение МО электронами происходит по тем же правилам, что и заполнение АО в атоме, а именно: правилу Паули (на МО не может быть более двух электронов), правилу Хунда (суммарный спин должен быть максимален) и т. д.
Взаимодействие 1s-AO атомов первого периода (Н и Не) приводит к образованию связывающей σ-МО и разрыхляющей σ*-МО:
O2+(11ē)σs2σs*2σz2(πx2πy2)(πx*1πy*0)
n = 2 R = 0,121 нм;
O2(12ē)σs2σs*2σz2(πx2πy2)(πx*1πy*1)
n = 2,5 R = 0,112 нм;
O2¯(13ē)σs2σs*2σz2(πx2πy2)(πx*2πy*1)
n = 1,5 R = 0,126 нм.
В случае молекулы O2 теория МО позволяет предвидеть большую прочность этой молекулы, поскольку n = 2, характер изменения энергий связи и межъядерных расстояний в ряду O2+ – O2 – O2¯, а также парамагнетизм молекулы O2, на верхних МО которой имеются два неспаренных электрона.
3.3. Некоторые виды связей
Ионная связь – электростатическая связь между ионами противоположных зарядов. Ионная связь может рассматриваться как предельный случай ковалентной полярной связи. Ионная связь образуется, если разница электроотрицательностей атомов ΔХ больше чем 1,5–2,0.
Ионная связь является ненаправленной ненасыщаемой связью. В кристалле NaCl ион Na+ притягивается всеми ионами Cl¯ и отталкивается всеми другими ионами Na+, независимо от направления взаимодействия и числа ионов. Это предопределяет большую устойчивость ионных кристаллов по сравнению с ионными молекулами.
Водородная связь – связь между атомом водорода одной молекулы и электроотрицательным атомом (F, CI, N) другой молекулы.
Существование водородной связи объясняет аномальные свойства воды: температура кипения воды гораздо выше, чем у ее химических аналогов: tкип(Н2O) = 100 °С, а tкип(H2S) = -61°C. Между молекулами H2S водородные связи не образуются.
Ионная связь является ненаправленной ненасыщаемой связью. В кристалле NaCl ион Na+ притягивается всеми ионами Cl¯ и отталкивается всеми другими ионами Na+, независимо от направления взаимодействия и числа ионов. Это предопределяет большую устойчивость ионных кристаллов по сравнению с ионными молекулами.
Водородная связь – связь между атомом водорода одной молекулы и электроотрицательным атомом (F, CI, N) другой молекулы.
Существование водородной связи объясняет аномальные свойства воды: температура кипения воды гораздо выше, чем у ее химических аналогов: tкип(Н2O) = 100 °С, а tкип(H2S) = -61°C. Между молекулами H2S водородные связи не образуются.
4. Закономерности протекания химических процессов
4.1. Термохимия
Энергия (Е) – способность производить работу. Механическая работа (А) совершается, например, газом при его расширении: А = р • ΔV.
Реакции, которые идут с поглощением энергии, – эндотермические.
Реакции, которые идут с выделением энергии, – экзотермические.
Виды энергии: теплота, свет, электрическая, химическая, ядерная энергия и др.
Типы энергии: кинетическая и потенциальная.
Кинетическая энергия – энергия движущегося тела, это работа, которую может совершить тело до достижения им покоя.
Теплота (Q) – вид кинетической энергии – связана с движением атомов и молекул. При сообщении телу массой (m) и удельной теплоемкостью (с) теплоты ΔQ его температура повышается на величину Δt: ΔQ = m • с • Δt, откуда Δt = ΔQ/(c • т).
Потенциальная энергия – энергия, приобретенная телом в результате изменения им или его составными частями положения в пространстве. Энергия химических связей – вид потенциальной энергии.
Первый закон термодинамики: энергия может переходить из одного вида в другой, но не может исчезать или возникать.
Внутренняя энергия (U) – сумма кинетической и потенциальной энергий частиц, составляющих тело. Поглощаемая в реакции теплота равна разности внутренней энергии продуктов реакции и реагентов (Q = ΔU = U2 – U1), при условии, что система не совершила работы над окружающей средой. Если реакция идет при постоянном давлении, то выделяющиеся газы совершают работу против сил внешнего давления, и поглощаемая в ходе реакции теплота равна сумме изменений внутренней энергии ΔU и работы А = р • ΔV. Эту поглощаемую при постоянном давлении теплоту называют изменением энтальпии: ΔН = ΔU + р • ΔV, определяя энтальпию как Н = U + pV. Реакции жидких и твердых веществ протекают без существенного изменения объема (ΔV = 0), так что для этих реакций ΔН близка к ΔU (ΔН = ΔU). Для реакций с изменением объема имеем ΔН > ΔU, если идет расширение, и ΔН < ΔU, если идет сжатие.
Изменение энтальпии обычно относят для стандартного состояния вещества: т. е. для чистого вещества в определенном (твердом, жидком или газообразном) состоянии, при давлении 1 атм = 101 325 Па, температуре 298 К и концентрации веществ 1 моль/л.
Стандартная энтальпия образования ΔНобр – теплота, выделяемая или поглощаемая при образовании 1 моль вещества из простых веществ, его составляющих, при стандартных условиях. Так, например, ΔНобр(NaCl) = -411 кДж/моль. Это означает, что в реакции Na(тв) + ½Cl2(г) = NaCl(тв) при образовании 1 моль NaCl выделяется 411 кДж энергии.
Стандартная энтальпия реакции ΔН – изменение энтальпии в ходе химической реакции, определяется по формуле: ΔН = ΔНобр(продуктов) – ΔНобр(реагентов).
Так для реакции NH3(г) + HCl(г) = NH4Cl(тв), зная ΔHo6p(NH3)=-46 кДж/моль, ΔHo6p(HCl) = -92 кДж/моль и ΔHo6p(NH4Cl) = -315 кДж/моль имеем:
ΔH = ΔHo6p(NH4Cl) – ΔHo6p(NH3) – ΔHo6p(HCl) = -315 – (-46) – (-92) = -177 кДж.
Если ΔН < 0, то реакция экзотермическая. Если ΔН > 0, то реакция эндотермическая.
Закон Гесса: стандартная энтальпия реакции зависит от стандартных энтальпий реагентов и продуктов и не зависит от пути протекания реакции.
Самопроизвольно идущие процессы могут быть не только экзотермическими, т. е. процессами с уменьшением энергии (ΔН < 0), но могут быть и эндотермическими процессами, т. е. процессами с увеличением энергии (ΔН > 0). Во всех этих процессах «беспорядок» системы увеличивается.
Энтропия S – физическая величина, характеризующая степень беспорядка системы. S – стандартная энтропия, ΔS – изменение стандартной энтропии. Если ΔS > 0, беспорядок растет, если AS < 0, то беспорядок системы уменьшается. Для процессов в которых растет число частиц, ΔS > 0. Для процессов, в которых число частиц уменьшается, ΔS < 0. Например, энтропия меняется в ходе реакций:
СаО(тв) + Н2O(ж) = Са(OH)2(тв), ΔS < 0;
CaCO3(тв) = СаО(тв) + CO2(г), ΔS > 0.
Самопроизвольно идут процессы с выделением энергии, т. е. для которых ΔН < 0, и с увеличением энтропии, т. е. для которых ΔS > 0. Учет обоих факторов приводит к выражению для энергии Гиббса: G = Н – TS или ΔG = ΔН – Т • ΔS. Реакции, в которых энергия Гиббса уменьшается, т. е. ΔG < 0, могут идти самопроизвольно. Реакции, в ходе которых энергия Гиббса увеличивается, т. е. ΔG > 0, самопроизвольно не идут. Условие ΔG = 0 значит, что между продуктами и реагентами установилось равновесие.
При низкой температуре, когда величина Т близка к нулю, идут лишь экзотермические реакции, так как TΔS – мало и ΔG = ΔН < 0. При высоких температурах значения TΔS велико, и, пренебрегая величиной ΔН, имеем ΔG = – TΔS, т. е. самопроизвольно будут идти процессы с увеличением энтропии, для которых ΔS > 0, a ΔG < 0. При этом чем больше по абсолютной величине значение ΔG, тем более полно проходит данный процесс.
Величина AG для той или иной реакции может быть определена по формуле:
ΔG = ΔСобр(продуктов) – ΔGoбp(реагентов).
При этом величины ΔGoбр, а также ΔНобр и ΔSoбр для большого числа веществ приведены в специальных таблицах.
Реакции, которые идут с поглощением энергии, – эндотермические.
Реакции, которые идут с выделением энергии, – экзотермические.
Виды энергии: теплота, свет, электрическая, химическая, ядерная энергия и др.
Типы энергии: кинетическая и потенциальная.
Кинетическая энергия – энергия движущегося тела, это работа, которую может совершить тело до достижения им покоя.
Теплота (Q) – вид кинетической энергии – связана с движением атомов и молекул. При сообщении телу массой (m) и удельной теплоемкостью (с) теплоты ΔQ его температура повышается на величину Δt: ΔQ = m • с • Δt, откуда Δt = ΔQ/(c • т).
Потенциальная энергия – энергия, приобретенная телом в результате изменения им или его составными частями положения в пространстве. Энергия химических связей – вид потенциальной энергии.
Первый закон термодинамики: энергия может переходить из одного вида в другой, но не может исчезать или возникать.
Внутренняя энергия (U) – сумма кинетической и потенциальной энергий частиц, составляющих тело. Поглощаемая в реакции теплота равна разности внутренней энергии продуктов реакции и реагентов (Q = ΔU = U2 – U1), при условии, что система не совершила работы над окружающей средой. Если реакция идет при постоянном давлении, то выделяющиеся газы совершают работу против сил внешнего давления, и поглощаемая в ходе реакции теплота равна сумме изменений внутренней энергии ΔU и работы А = р • ΔV. Эту поглощаемую при постоянном давлении теплоту называют изменением энтальпии: ΔН = ΔU + р • ΔV, определяя энтальпию как Н = U + pV. Реакции жидких и твердых веществ протекают без существенного изменения объема (ΔV = 0), так что для этих реакций ΔН близка к ΔU (ΔН = ΔU). Для реакций с изменением объема имеем ΔН > ΔU, если идет расширение, и ΔН < ΔU, если идет сжатие.
Изменение энтальпии обычно относят для стандартного состояния вещества: т. е. для чистого вещества в определенном (твердом, жидком или газообразном) состоянии, при давлении 1 атм = 101 325 Па, температуре 298 К и концентрации веществ 1 моль/л.
Стандартная энтальпия образования ΔНобр – теплота, выделяемая или поглощаемая при образовании 1 моль вещества из простых веществ, его составляющих, при стандартных условиях. Так, например, ΔНобр(NaCl) = -411 кДж/моль. Это означает, что в реакции Na(тв) + ½Cl2(г) = NaCl(тв) при образовании 1 моль NaCl выделяется 411 кДж энергии.
Стандартная энтальпия реакции ΔН – изменение энтальпии в ходе химической реакции, определяется по формуле: ΔН = ΔНобр(продуктов) – ΔНобр(реагентов).
Так для реакции NH3(г) + HCl(г) = NH4Cl(тв), зная ΔHo6p(NH3)=-46 кДж/моль, ΔHo6p(HCl) = -92 кДж/моль и ΔHo6p(NH4Cl) = -315 кДж/моль имеем:
ΔH = ΔHo6p(NH4Cl) – ΔHo6p(NH3) – ΔHo6p(HCl) = -315 – (-46) – (-92) = -177 кДж.
Если ΔН < 0, то реакция экзотермическая. Если ΔН > 0, то реакция эндотермическая.
Закон Гесса: стандартная энтальпия реакции зависит от стандартных энтальпий реагентов и продуктов и не зависит от пути протекания реакции.
Самопроизвольно идущие процессы могут быть не только экзотермическими, т. е. процессами с уменьшением энергии (ΔН < 0), но могут быть и эндотермическими процессами, т. е. процессами с увеличением энергии (ΔН > 0). Во всех этих процессах «беспорядок» системы увеличивается.
Энтропия S – физическая величина, характеризующая степень беспорядка системы. S – стандартная энтропия, ΔS – изменение стандартной энтропии. Если ΔS > 0, беспорядок растет, если AS < 0, то беспорядок системы уменьшается. Для процессов в которых растет число частиц, ΔS > 0. Для процессов, в которых число частиц уменьшается, ΔS < 0. Например, энтропия меняется в ходе реакций:
СаО(тв) + Н2O(ж) = Са(OH)2(тв), ΔS < 0;
CaCO3(тв) = СаО(тв) + CO2(г), ΔS > 0.
Самопроизвольно идут процессы с выделением энергии, т. е. для которых ΔН < 0, и с увеличением энтропии, т. е. для которых ΔS > 0. Учет обоих факторов приводит к выражению для энергии Гиббса: G = Н – TS или ΔG = ΔН – Т • ΔS. Реакции, в которых энергия Гиббса уменьшается, т. е. ΔG < 0, могут идти самопроизвольно. Реакции, в ходе которых энергия Гиббса увеличивается, т. е. ΔG > 0, самопроизвольно не идут. Условие ΔG = 0 значит, что между продуктами и реагентами установилось равновесие.
При низкой температуре, когда величина Т близка к нулю, идут лишь экзотермические реакции, так как TΔS – мало и ΔG = ΔН < 0. При высоких температурах значения TΔS велико, и, пренебрегая величиной ΔН, имеем ΔG = – TΔS, т. е. самопроизвольно будут идти процессы с увеличением энтропии, для которых ΔS > 0, a ΔG < 0. При этом чем больше по абсолютной величине значение ΔG, тем более полно проходит данный процесс.
Величина AG для той или иной реакции может быть определена по формуле:
ΔG = ΔСобр(продуктов) – ΔGoбp(реагентов).
При этом величины ΔGoбр, а также ΔНобр и ΔSoбр для большого числа веществ приведены в специальных таблицах.
4.2. Химическая кинетика
Скорость химической реакции (v) определяется изменением молярной концентрации реагирующих веществ в единицу времени:
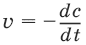где v – скорость реакции, с – молярная концентрация реагента, t – время.
Скорость химической реакции зависит от природы реагирующих веществ и условий протекания реакции (температуры, концентрации, присутствия катализатора и т. д.)
Влияние концентрации. В случае простых реакций скорость реакции пропорциональна произведению концентраций реагирующих веществ, взятых в степенях, равных их стехиометрическим коэффициентам.
Для реакции
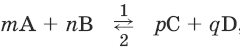где 1 и 2 соответственно направление прямой и обратной реакции:
v1 = k1 × [А]m × [В]n и
v2 = k2 × [C]p × [D]q
где v – скорость реакции, k – константа скорости, [А] – молярная концентрация вещества А.
Молекулярность реакции – число молекул, участвующих в элементарном акте реакции. Для простых реакций, например: mA + nB → рС + qD, молекулярность равна сумме коэффициентов (m + n). Реакции могут быть одномолекулярными, двумолекулярными и редко трехмолекулярными. Реакции более высокой молекулярности не встречаются.
Порядок реакции равен сумме показателей степеней концентрации в экспериментальном выражении скорости химической реакции. Так, для сложной реакции
mA + nB → рС + qD экспериментальное выражение скорости реакции имеет вид
v1 = k1 × [А]α × [В]β и порядок реакции равен (α + β). При этом α и β находятся экспериментально и могут не совпадать с m и n соответственно, поскольку уравнение сложной реакции представляет собой итог нескольких простых реакций.
Влияние температуры. Скорость реакции зависит от числа эффективных столкновений молекул. Увеличение температуры увеличивает число активных молекул, сообщая им необходимую для протекания реакции энергию активации Еакт и увеличивает скорость химической реакции.
Правило Вант-Гоффа. При увеличении температуры на 10° скорость реакции увеличивается в 2–4 раза. Математически это записывается в виде:
v2 = v1 × γ(t2 – t1)/10
где v1 и v2 – скорости реакции при начальной (t1) и конечной (t2) температурах, γ – температурный коэффициент скорости реакции, который показывает, во сколько раз увеличивается скорость реакции при увеличении температуры на 10°.
Более точно зависимость скорости реакции от температуры выражается уравнением Аррениуса:
k = A × e—E/(RT),
где k – константа скорости, А – постоянная, не зависящая от температуры, е = 2,71828, Е – энергия активации, R = 8,314 Дж/(К × моль) – газовая постоянная; Т – температура (К). Видно, что константа скорости увеличивается с увеличением температуры и уменьшением энергии активации.
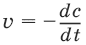
Скорость химической реакции зависит от природы реагирующих веществ и условий протекания реакции (температуры, концентрации, присутствия катализатора и т. д.)
Влияние концентрации. В случае простых реакций скорость реакции пропорциональна произведению концентраций реагирующих веществ, взятых в степенях, равных их стехиометрическим коэффициентам.
Для реакции
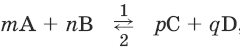
v1 = k1 × [А]m × [В]n и
v2 = k2 × [C]p × [D]q
где v – скорость реакции, k – константа скорости, [А] – молярная концентрация вещества А.
Молекулярность реакции – число молекул, участвующих в элементарном акте реакции. Для простых реакций, например: mA + nB → рС + qD, молекулярность равна сумме коэффициентов (m + n). Реакции могут быть одномолекулярными, двумолекулярными и редко трехмолекулярными. Реакции более высокой молекулярности не встречаются.
Порядок реакции равен сумме показателей степеней концентрации в экспериментальном выражении скорости химической реакции. Так, для сложной реакции
mA + nB → рС + qD экспериментальное выражение скорости реакции имеет вид
v1 = k1 × [А]α × [В]β и порядок реакции равен (α + β). При этом α и β находятся экспериментально и могут не совпадать с m и n соответственно, поскольку уравнение сложной реакции представляет собой итог нескольких простых реакций.
Влияние температуры. Скорость реакции зависит от числа эффективных столкновений молекул. Увеличение температуры увеличивает число активных молекул, сообщая им необходимую для протекания реакции энергию активации Еакт и увеличивает скорость химической реакции.
Правило Вант-Гоффа. При увеличении температуры на 10° скорость реакции увеличивается в 2–4 раза. Математически это записывается в виде:
v2 = v1 × γ(t2 – t1)/10
где v1 и v2 – скорости реакции при начальной (t1) и конечной (t2) температурах, γ – температурный коэффициент скорости реакции, который показывает, во сколько раз увеличивается скорость реакции при увеличении температуры на 10°.
Более точно зависимость скорости реакции от температуры выражается уравнением Аррениуса:
k = A × e—E/(RT),
где k – константа скорости, А – постоянная, не зависящая от температуры, е = 2,71828, Е – энергия активации, R = 8,314 Дж/(К × моль) – газовая постоянная; Т – температура (К). Видно, что константа скорости увеличивается с увеличением температуры и уменьшением энергии активации.