Страница:
В генераторе Шаубергера, рис. 5, как и в ранее рассмотренных устройствах, на корпус всей машины действует реактивная движущая сила, направленная вдоль оси вращения, а ее величина соответствует силе, которая обеспечивает крутящий момент ротора. В отличие от генератора, показанного на рис. 3, для того, чтобы генератор энергии «не взлетал», вход воды в ротор расположен таким образом, что сила, создаваемая вдоль оси вращения, прижимает аппарат к земле.
Известны и другие похожие решения: вход реактивной рабочей массы организован вдоль оси вращения ротора, а ее выход – в плоскости вращения ротора, то есть, перпендикулярно оси вращения ротора.
Итак, принцип Шаубергера позволяет получать пару сил: крутящий момент, и движущую силу, действующую на корпус устройства в целом. При такой схеме, рабочее вещество не выбрасывается во внешнюю среду, а используется в замкнутом цикле. При сравнительном анализе идеи, показанной на рис. 1 и принципа Шаубергера, можно сделать вывод о больших перспективах второго решения. Вместо поглощения энергии линейного реактивного импульса «глушителем», в машинах Шаубергера используется ее преобразование в крутящий момент. В том случае, если этот крутящий момент не требуется, его можно устранить, разместив на одной платформе несколько силовых установок, попарно встречного вращения.
Таким образом, с учетом простоты схемы Шаубергера, и истории ее развития с 1930 года, можно предположить, что использование ракетной техники в современном мире есть часть массовой дезинформации человечества о наших реальных возможностях. Далее мы перейдем к рассмотрению других простых работоспособных конструкций движителей нового типа, что даст читателям дополнительные факты и позволит сделать выводы. Фактически, нас обманывают, заставляя верить в то, что нет альтернативы ракетам.
Глава 2
Глава 3
Глава 4
Глава 5
Глава 6
Известны и другие похожие решения: вход реактивной рабочей массы организован вдоль оси вращения ротора, а ее выход – в плоскости вращения ротора, то есть, перпендикулярно оси вращения ротора.
Итак, принцип Шаубергера позволяет получать пару сил: крутящий момент, и движущую силу, действующую на корпус устройства в целом. При такой схеме, рабочее вещество не выбрасывается во внешнюю среду, а используется в замкнутом цикле. При сравнительном анализе идеи, показанной на рис. 1 и принципа Шаубергера, можно сделать вывод о больших перспективах второго решения. Вместо поглощения энергии линейного реактивного импульса «глушителем», в машинах Шаубергера используется ее преобразование в крутящий момент. В том случае, если этот крутящий момент не требуется, его можно устранить, разместив на одной платформе несколько силовых установок, попарно встречного вращения.
Таким образом, с учетом простоты схемы Шаубергера, и истории ее развития с 1930 года, можно предположить, что использование ракетной техники в современном мире есть часть массовой дезинформации человечества о наших реальных возможностях. Далее мы перейдем к рассмотрению других простых работоспособных конструкций движителей нового типа, что даст читателям дополнительные факты и позволит сделать выводы. Фактически, нас обманывают, заставляя верить в то, что нет альтернативы ракетам.
Глава 2
Крыло в замкнутом потоке
Рассмотрим простое крыло, имеющее профиль Жуковского – Чаплыгина, который впервые был предложен в 1910 году. До этого изобретения, крылья самолетов делали плоскими, а подъемная сила возникала за счет угла наклона крыла, простым реактивным отражением набегающего потока воздуха.
Подъемная сила крыла, имеющего профиль Жуковского – Чаплыгина, обусловлена разностью давления среды на крыло сверху и снизу, поскольку давление зависит от относительной скорости движения крыла и среды. На рис. 6 показано, что верхнюю поверхность крыла поток среды обтекает по большему пути, чем нижнюю.
Рис. 6. Эффект подъемной силы крыла
Поток стремится сохранять свою целостность, поэтому, его скорость относительно верхней выпуклой поверхности крыла выше, чем относительная скорость вдоль плоской нижней поверхности крыла. Разность давления среды на крыло (градиент) поднимает крыло вверх (вытесняет в сторону меньшего давления среды).
Не играет роли, движется ли крыло в среде, или поток среды (воздуха, воды и т. п.) обтекает крыло. Можно сказать, что здесь «работает геометрия»: путь относительного движения среды по верхней поверхности крыла больше, чем по нижней. Данная система не является реактивной, поэтому ее применение в движителях замкнутого цикла представляется весьма перспективным.
На рис. 6 (справа) показано, что крыло, установленное внутри аэродинамической трубы на упругих амортизаторах, демонстрирует наличие подъемной силы при продувании трубы. При этом, на весь корпус трубы действует вертикальная сила.
Предположим, что мы создали циркулирующий поток среды (газ или жидкость) в замкнутом корпусе, похожем на бублик (тороид). Поставим внутри потока несколько крыльев, радиально, как показано на рис. 7.
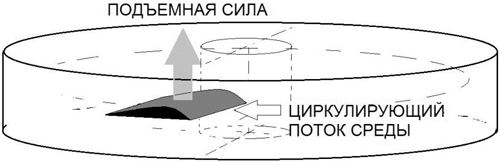Рис. 7. Крыло в замкнутом потоке среды
Мы получим простое решение, которое может быть проверено экспериментально, и иметь перспективы внедрения в аэрокосмической технике. Некоторые технические проблемы есть, но они решаются. Например, проходя в области крыла, линейный поток среды меняется, и в нем возникают турбулентности. Для выравнивания потока, позади крыла необходимо устанавливать плоские или трубчатые элементы (ламинаризаторы). Величина подъемной силы зависит от скорости движения потока относительно крыла, хотя ее направление, в данном случае, будет неизменным. Величину силы можно регулировать. Разумеется, замедление или ускорение циркулирующего потока среды потребует расхода энергии насоса, вентилятора или другого привода движения потока среды.
Далее, мы рассмотрим аналогичную перспективную схему, более экономную, с точки зрения энергетики, чем крыло, находящееся в замкнутом потоке среды.
Подъемная сила крыла, имеющего профиль Жуковского – Чаплыгина, обусловлена разностью давления среды на крыло сверху и снизу, поскольку давление зависит от относительной скорости движения крыла и среды. На рис. 6 показано, что верхнюю поверхность крыла поток среды обтекает по большему пути, чем нижнюю.
Поток стремится сохранять свою целостность, поэтому, его скорость относительно верхней выпуклой поверхности крыла выше, чем относительная скорость вдоль плоской нижней поверхности крыла. Разность давления среды на крыло (градиент) поднимает крыло вверх (вытесняет в сторону меньшего давления среды).
Не играет роли, движется ли крыло в среде, или поток среды (воздуха, воды и т. п.) обтекает крыло. Можно сказать, что здесь «работает геометрия»: путь относительного движения среды по верхней поверхности крыла больше, чем по нижней. Данная система не является реактивной, поэтому ее применение в движителях замкнутого цикла представляется весьма перспективным.
На рис. 6 (справа) показано, что крыло, установленное внутри аэродинамической трубы на упругих амортизаторах, демонстрирует наличие подъемной силы при продувании трубы. При этом, на весь корпус трубы действует вертикальная сила.
Предположим, что мы создали циркулирующий поток среды (газ или жидкость) в замкнутом корпусе, похожем на бублик (тороид). Поставим внутри потока несколько крыльев, радиально, как показано на рис. 7.
Мы получим простое решение, которое может быть проверено экспериментально, и иметь перспективы внедрения в аэрокосмической технике. Некоторые технические проблемы есть, но они решаются. Например, проходя в области крыла, линейный поток среды меняется, и в нем возникают турбулентности. Для выравнивания потока, позади крыла необходимо устанавливать плоские или трубчатые элементы (ламинаризаторы). Величина подъемной силы зависит от скорости движения потока относительно крыла, хотя ее направление, в данном случае, будет неизменным. Величину силы можно регулировать. Разумеется, замедление или ускорение циркулирующего потока среды потребует расхода энергии насоса, вентилятора или другого привода движения потока среды.
Далее, мы рассмотрим аналогичную перспективную схему, более экономную, с точки зрения энергетики, чем крыло, находящееся в замкнутом потоке среды.
Глава 3
Эффект Магнуса и сила Лоренца
Аналогично крылу Жуковского – Чаплыгина, сила Магнуса возникает за счет разности давления потока среды на поверхность вращающегося цилиндра. Данный эффект был открыт немецким ученым Г. Г. Магнусом (H. G. Magnus) в 1852 году. На рис. 8 показана схема сложения векторов скоростей потока среды и поверхности вращающегося цилиндра.
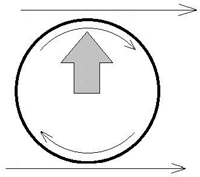Рис. 8. Эффект Магнуса для вращающегося цилиндра
В верхней части цилиндра (вид с торца), направление движения потока среды и поверхности вращающегося цилиндра совпадают, а в нижней части цилиндра, его поверхность движется навстречу потоку среды. Поскольку поток в нижней части вращающегося цилиндра тормозится его поверхностью, движущейся навстречу потоку, то динамическое давление потока уменьшается, а увеличивается статическое давление среды на поверхность, в соответствии с законом Бернулли о полном давлении потока. В результате, давление среды на верхнюю часть вращающегося цилиндра становится меньше, чем на нижнюю часть цилиндра. Возникает подъемная сила, как и при эффекте крыла, имеющего профиль Жуковского – Чаплыгина.
Эффект Магнуса хорошо известен футболистам и теннисистам, который используют его для создания криволинейной траектории полета закрученного мяча. При «крученом ударе», мяч летит прямолинейно, но вращается вокруг своей оси. В полете, на него набегает поток воздуха, что создает эффект Магнуса, и траектория полета искривляется. В результате такого удара, мяч летит по кривой, и попадает не туда, где его ждут…
Предположим, что мы сконструировали замкнутый поток движущейся среды (воздуха, воды и т. п.), в котором поставлены несколько вращающихся цилиндров, как показано на рис. 9. Допустим, что вращение каждого цилиндра обеспечивает независимый электропривод, с регулируемой скоростью и направлением вращения.
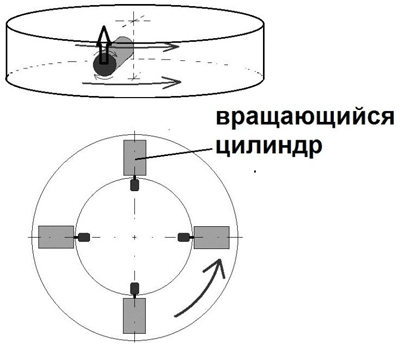Рис. 9. Движитель на основе эффекта Магнуса
В отличие от конструкции с крылом, установленным в потоке движущейся среды, данная схема имеет важное преимущество: величину и направление осевой подъемной силы, можно менять за счет изменений величины скорости и направления вращения цилиндров. Скорость и направление циркулирующего потока можно не менять, что дает значительные преимущества по быстродействию и маневренности данного транспортного средства. Движитель данного типа может быть установлен вертикально или горизонтально, создавая силу тяги.
Интересная аналогия с эффектом Магнуса возникает при рассмотрении электромагнитного явления, известного, как сила Лоренца: на проводник с током, находящийся в магнитном поле, действует сила, в направлении, показанном на рис. 10. О причине появления данной силы, ранее не было однозначного объяснения. Предполагая аналогии с эффектом Магнуса, можно трактовать силу Лоренца, как результат градиента давления эфирной среды. В докладе [1] это было впервые показано, 1996 год.
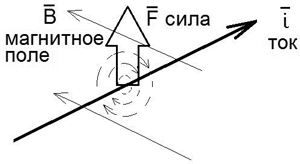Рис. 10. Сила Лоренца, как результат градиента давления эфира
Однако, на схеме рис. 10, мы получаем картину, обратную суперпозиции векторов, которая была показана на рис. 8. Сила Магнуса действует на цилиндр, вращающийся в потоке среды, в направлении согласованного движения поверхности цилиндра и среды. На рис. 10 показано, что сила Лоренца действует в направлении встречной суперпозиции векторов. Почему?
Дело в том, что вектора на рис. 10 показаны условно, согласно принятым обозначениям векторов электрического тока (потока положительно заряженных частиц) и магнитного поля. Направление движения реальных потоков электронов и эфирных частиц (вектора магнитных полей) отличаются от условных обозначений. Принципиально, эффект создается аналогично эффекту Магнуса, за счет градиента давления среды, обусловленного разной относительной скоростью, но электромагнитные системы используют эфирную среду, а не воздух или воду.
Важно отметить, что электрон или другая заряженная частица, которая при движении создает магнитное поле, является вращающимся объектом. Было бы точнее, считать ее линейное перемещение винтовой линией, правой или левой спиралью, в зависимости от знака электрического заряда данной частицы материи.
О структуре электрона написано немало, но мне хотелось бы рекомендовать читателю работу отца и сына Поляковых [4]. Данные авторы рассматривали в своей книге «Экспериментальная гравитоника» строение электрона, и показали, что он может быть представлен, как замкнутый на себя фотон круговой поляризации, то есть, как динамический процесс движения электромагнитной волны круговой поляризации в замкнутом тороидальном пространстве. Позже, мы раскроем данный вопрос подробнее. Здесь только коротко отметим, что, при таком рассмотрении, появление магнитного поля, при движении заряженной частицы в эфире, имеет явную аналогию с возмущение физической среды, которое возникает при движении в данной среде вращающегося цилиндра или шара.
Можно сказать, что взаимодействие внешнего магнитного поля, поперек которого движется электрически заряженная частица, с ее собственным магнитным полем, отклоняет частицу таким же образом, как и поток воздуха отклоняет закрученный мяч, а именно, благодаря созданию градиента давления среды на движущуюся в ней частицу материи.
В таком случае, силы Лоренца и силы Ампера являются внешними силами, по отношению к проводникам с током, на которые они действуют, то есть, могут обеспечить их движение в пространстве.
Эти интересные аналогии между аэродинамикой и эфиродинамикой дают много конструктивных идей.
В верхней части цилиндра (вид с торца), направление движения потока среды и поверхности вращающегося цилиндра совпадают, а в нижней части цилиндра, его поверхность движется навстречу потоку среды. Поскольку поток в нижней части вращающегося цилиндра тормозится его поверхностью, движущейся навстречу потоку, то динамическое давление потока уменьшается, а увеличивается статическое давление среды на поверхность, в соответствии с законом Бернулли о полном давлении потока. В результате, давление среды на верхнюю часть вращающегося цилиндра становится меньше, чем на нижнюю часть цилиндра. Возникает подъемная сила, как и при эффекте крыла, имеющего профиль Жуковского – Чаплыгина.
Эффект Магнуса хорошо известен футболистам и теннисистам, который используют его для создания криволинейной траектории полета закрученного мяча. При «крученом ударе», мяч летит прямолинейно, но вращается вокруг своей оси. В полете, на него набегает поток воздуха, что создает эффект Магнуса, и траектория полета искривляется. В результате такого удара, мяч летит по кривой, и попадает не туда, где его ждут…
Предположим, что мы сконструировали замкнутый поток движущейся среды (воздуха, воды и т. п.), в котором поставлены несколько вращающихся цилиндров, как показано на рис. 9. Допустим, что вращение каждого цилиндра обеспечивает независимый электропривод, с регулируемой скоростью и направлением вращения.
В отличие от конструкции с крылом, установленным в потоке движущейся среды, данная схема имеет важное преимущество: величину и направление осевой подъемной силы, можно менять за счет изменений величины скорости и направления вращения цилиндров. Скорость и направление циркулирующего потока можно не менять, что дает значительные преимущества по быстродействию и маневренности данного транспортного средства. Движитель данного типа может быть установлен вертикально или горизонтально, создавая силу тяги.
Интересная аналогия с эффектом Магнуса возникает при рассмотрении электромагнитного явления, известного, как сила Лоренца: на проводник с током, находящийся в магнитном поле, действует сила, в направлении, показанном на рис. 10. О причине появления данной силы, ранее не было однозначного объяснения. Предполагая аналогии с эффектом Магнуса, можно трактовать силу Лоренца, как результат градиента давления эфирной среды. В докладе [1] это было впервые показано, 1996 год.
Однако, на схеме рис. 10, мы получаем картину, обратную суперпозиции векторов, которая была показана на рис. 8. Сила Магнуса действует на цилиндр, вращающийся в потоке среды, в направлении согласованного движения поверхности цилиндра и среды. На рис. 10 показано, что сила Лоренца действует в направлении встречной суперпозиции векторов. Почему?
Дело в том, что вектора на рис. 10 показаны условно, согласно принятым обозначениям векторов электрического тока (потока положительно заряженных частиц) и магнитного поля. Направление движения реальных потоков электронов и эфирных частиц (вектора магнитных полей) отличаются от условных обозначений. Принципиально, эффект создается аналогично эффекту Магнуса, за счет градиента давления среды, обусловленного разной относительной скоростью, но электромагнитные системы используют эфирную среду, а не воздух или воду.
Важно отметить, что электрон или другая заряженная частица, которая при движении создает магнитное поле, является вращающимся объектом. Было бы точнее, считать ее линейное перемещение винтовой линией, правой или левой спиралью, в зависимости от знака электрического заряда данной частицы материи.
О структуре электрона написано немало, но мне хотелось бы рекомендовать читателю работу отца и сына Поляковых [4]. Данные авторы рассматривали в своей книге «Экспериментальная гравитоника» строение электрона, и показали, что он может быть представлен, как замкнутый на себя фотон круговой поляризации, то есть, как динамический процесс движения электромагнитной волны круговой поляризации в замкнутом тороидальном пространстве. Позже, мы раскроем данный вопрос подробнее. Здесь только коротко отметим, что, при таком рассмотрении, появление магнитного поля, при движении заряженной частицы в эфире, имеет явную аналогию с возмущение физической среды, которое возникает при движении в данной среде вращающегося цилиндра или шара.
Можно сказать, что взаимодействие внешнего магнитного поля, поперек которого движется электрически заряженная частица, с ее собственным магнитным полем, отклоняет частицу таким же образом, как и поток воздуха отклоняет закрученный мяч, а именно, благодаря созданию градиента давления среды на движущуюся в ней частицу материи.
В таком случае, силы Лоренца и силы Ампера являются внешними силами, по отношению к проводникам с током, на которые они действуют, то есть, могут обеспечить их движение в пространстве.
Эти интересные аналогии между аэродинамикой и эфиродинамикой дают много конструктивных идей.
Глава 4
Электрокинетические движители
Исходя из концепции «градиента эфирного давления», рассмотрим эффект Ампера, то есть, явление притяжения или отталкивания проводников с током, рис. 11.
Рис. 11. Эффект Ампера для проводников с током
Известно, что, при согласованном движении токов в параллельных проводниках, они притягиваются, а при встречных токах – отталкиваются. Очевидно, что векторное сложение и вычитание магнитных потоков имеет смысл, как увеличение или уменьшение относительной скорости движения эфирных частиц, что и создает градиент давления эфирной среды. Можно ли построить движитель, использующий данный градиент давления окружающей среды?
Согласно Амперу, результирующая сила, для параллельных проводников, равна нулю. Этот факт, достаточно долгое время, был причиной невнимания изобретателей и конструкторов к технологии создания электрокинетических движителей.
Анализ сил, возникающих в непараллельных проводниках, например, в Y-образном проводнике, был впервые проведен в 1844 году известным физиком – математиком Германом Г. Грассманом. Он показал, что случай параллельных проводников, рассмотренный Ампером, есть только частный случай, а в общем случае, результирующие силы для проводников с током могут быть не равны нулю.
На рис. 12 показаны вектора сил, действующих на участки тока в области Y-образной «вилки», формулу для расчета которых анализировал Грассман. В данном случае, суммарная сила, действующая на Y-образный участок проводников с током, не равна нулю, то есть, проводники образуют Y-образный движитель.
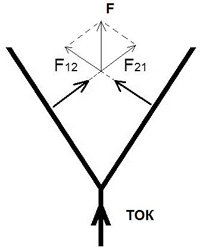Рис. 12. Силы в Y-образном проводнике электрического тока
Это еще одно проявление силовых эффектов, возникающих за счет разности давления среды, то есть градиента давления эфира.
Используя аналогии между явлениями гидродинамики, аэродинамики и эфиродинамики, можно конструировать различные движители. Аналогами Y-образного привода являются так называемые «электрокинетические движители Сигалова» [5], которые представляет собой V-образный или U-образный участок проводника электрического тока, рис. 13.
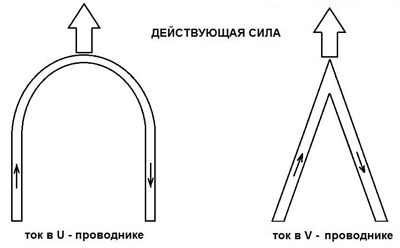Рис. 13. Эффект Сигалова в проводниках сложной формы
Данные явления, обычно, объясняют, как взаимодействие токов в проводнике сложной формы с собственным магнитным полем, то есть, силой Лоренца. Причину возникновения силы Лоренца мы уже рассматривали ранее, как результат градиента давления эфира, схема показана на рис. 10. Следовательно, электрокинетические движители представляют собой один из вариантов эфироплавательных движителей, использующих градиент давления окружающей эфирной среды для создания активной движущей силы в заданном направлении.
В работах Сигалова [4] рассмотрены и другие проводники сложной формы: П-образный, Г-образный и так далее. Предлагаю рассмотреть еще один интересный вариант: проводник с током в форме кардиоиды, рис. 14.
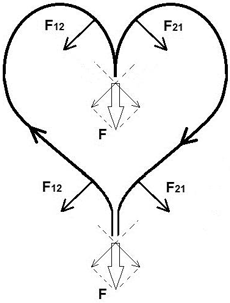Рис. 14. Силы в контуре тока, имеющего форму кардиоиды
Данный контур с током похож на V-образный вариант, причем, силы отталкивания двух соседних участков проводника на входе тока в контур создают силу, которая сонаправлена с результирующей силой, образуемой в области внутреннего изгиба кардиоиды. Весьма перспективная схема, на мой взгляд. Эксперименты в моей домашней лаборатории 1991–1996 года показали достаточно хорошие результаты.
Проводники питания, в данной схеме, могут быть скручены в витую пару. Проводник может быть один, или контур может быть изготовлен как многовитковая катушка. При наблюдениях действующих сил F12 и F21, целесообразно не закреплять проводники на каркасе, но при измерениях движущей силы проводники необходимо закрепить, например, на жесткой пластине.
Эксперименты с такими движителями простые, но они дают разные результаты при различной постановке эксперимента, то есть, на величину движущей силы влияет несколько факторов. Механические аналогии электрокинетических движителей, которые также могут иметь практическое применение в аэрокосмической технике, помогают понять, почему результаты экспериментов с электрокинетическими движителями зависят не только от силы тока, но и от импульсного режима работы (тока в проводниках).
Известно, что, при согласованном движении токов в параллельных проводниках, они притягиваются, а при встречных токах – отталкиваются. Очевидно, что векторное сложение и вычитание магнитных потоков имеет смысл, как увеличение или уменьшение относительной скорости движения эфирных частиц, что и создает градиент давления эфирной среды. Можно ли построить движитель, использующий данный градиент давления окружающей среды?
Согласно Амперу, результирующая сила, для параллельных проводников, равна нулю. Этот факт, достаточно долгое время, был причиной невнимания изобретателей и конструкторов к технологии создания электрокинетических движителей.
Анализ сил, возникающих в непараллельных проводниках, например, в Y-образном проводнике, был впервые проведен в 1844 году известным физиком – математиком Германом Г. Грассманом. Он показал, что случай параллельных проводников, рассмотренный Ампером, есть только частный случай, а в общем случае, результирующие силы для проводников с током могут быть не равны нулю.
На рис. 12 показаны вектора сил, действующих на участки тока в области Y-образной «вилки», формулу для расчета которых анализировал Грассман. В данном случае, суммарная сила, действующая на Y-образный участок проводников с током, не равна нулю, то есть, проводники образуют Y-образный движитель.
Это еще одно проявление силовых эффектов, возникающих за счет разности давления среды, то есть градиента давления эфира.
Используя аналогии между явлениями гидродинамики, аэродинамики и эфиродинамики, можно конструировать различные движители. Аналогами Y-образного привода являются так называемые «электрокинетические движители Сигалова» [5], которые представляет собой V-образный или U-образный участок проводника электрического тока, рис. 13.
Данные явления, обычно, объясняют, как взаимодействие токов в проводнике сложной формы с собственным магнитным полем, то есть, силой Лоренца. Причину возникновения силы Лоренца мы уже рассматривали ранее, как результат градиента давления эфира, схема показана на рис. 10. Следовательно, электрокинетические движители представляют собой один из вариантов эфироплавательных движителей, использующих градиент давления окружающей эфирной среды для создания активной движущей силы в заданном направлении.
В работах Сигалова [4] рассмотрены и другие проводники сложной формы: П-образный, Г-образный и так далее. Предлагаю рассмотреть еще один интересный вариант: проводник с током в форме кардиоиды, рис. 14.
Данный контур с током похож на V-образный вариант, причем, силы отталкивания двух соседних участков проводника на входе тока в контур создают силу, которая сонаправлена с результирующей силой, образуемой в области внутреннего изгиба кардиоиды. Весьма перспективная схема, на мой взгляд. Эксперименты в моей домашней лаборатории 1991–1996 года показали достаточно хорошие результаты.
Проводники питания, в данной схеме, могут быть скручены в витую пару. Проводник может быть один, или контур может быть изготовлен как многовитковая катушка. При наблюдениях действующих сил F12 и F21, целесообразно не закреплять проводники на каркасе, но при измерениях движущей силы проводники необходимо закрепить, например, на жесткой пластине.
Эксперименты с такими движителями простые, но они дают разные результаты при различной постановке эксперимента, то есть, на величину движущей силы влияет несколько факторов. Механические аналогии электрокинетических движителей, которые также могут иметь практическое применение в аэрокосмической технике, помогают понять, почему результаты экспериментов с электрокинетическими движителями зависят не только от силы тока, но и от импульсного режима работы (тока в проводниках).
Глава 5
Криволинейное движение тела
Всем хорошо знакомы силы инерции, возникающие при ускорении или торможении движущегося тела. В терминах эфиродинамики, можно сказать, что «эфир проявляет себя» при ускорении тел. Впрочем, существование эфирной упругой среды можно обнаружить и для неподвижных тел, в процессах их упругой деформации (растяжения или сжатия межатомных связей), но мы рассмотрим эти эффекты позже.
Ускорение криволинейного движения зависит от кривизны траектории (радиуса), а создаваемая при измерении траектории центробежная сила F определяется по простой формуле, второй закон Ньютона:
F = ma (F.1)
где F – сила, m – масса движущегося тела, а – ускорение криволинейного движения.
Сила F зависит от ускорения, а оно является функцией скорости и радиуса кривизны траектории движения тела, имеющего инерциальную массу. При движении тела по окружности, создается одинаковая сила F во всех радиальных направлениях. При движении тела по криволинейной траектории переменного радиуса, величина ускорения и силы будет меняться на разных участках траектории. В сумме, результирующая сила может быть ненулевая, что создает движущую силу в одном преимущественном направлении.
Использовать данную идею можно разными конструктивными методами, например, на рис. 15 предлагается схема движителя Вейника, в котором по криволинейной траектории переменного радиуса катаются металлические шарики [6]. В одном из экспериментов Вейника, в конструкции БМ-28, по криволинейной траектории, примерно 45 мм диаметром, двигалось 8 металлических шариков диаметром 8 мм. Вращение обеспечивал электропривод, на его оси было установлено «водило» – диск, в котором сделано 8 радиальных каналов для шариков. Шарики могли свободно менять свой радиус вращения внутри канала. Очевидно, что, при вращении, центробежная сила прижимает шарики к внешнему кольцу, которое установлено с эксцентриситетом: ось внешнего кольца, ограничивающего радиус вращения шариков, не совпадает с осью мотора. Эксцентриситет траектории движения шариков, в данной конструкции А.И. Вейник, был равен 0,7 мм. При скорости вращения порядка 21000 оборотов в минуту, устройство создавало движущую силу около 1,4·10-4 (Н), направленную перпендикулярно оси вращения мотора, в направлении эксцентриситета орбиты шариков.
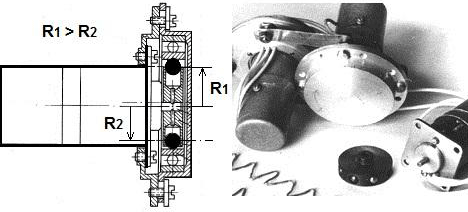Рис. 15. Движитель Вейника
На фото (справа на рис. 15) показана парная конструкция движителя Вейника. Сочетание двух приводов встречного вращения позволяет компенсировать реакцию крутящего момента, сохраняя одинаковое направление движущей силы F в обоих движителях. Эксцентриситет орбит шариков обоих приводов должен быть ориентирован в одном направлении.
Данный эксперимент Вейника был воспроизведен в ООО «Лаборатория Новых Технологий Фарадей» в 2002 году. Отметим, что работа движителя, разработанного в нашей лаборатории, сопровождалась значительной вибрацией, поэтому, увеличение эксцентриситета или скорости вращения было затруднительно. Силы, действующие в данной конструкции, были незначительны. Теоретически, рассматривался один из вариантов модернизации данной схемы: предлагалось добавить в конструкцию резиновый (упругий) обод, к которому центробежная сила должна прижимать вращающиеся шарики. Изучив вопрос надежности конструкции и перспективы данного метода, было решено найти другое техническое решение концепции движителя, использующего криволинейное ускоренное движение рабочего вещества, то есть, инерциальной массы.
Схема с применением жидкого рабочего вещества, движущегося по криволинейной замкнутой траектории переменного радиуса, была рассмотрена мной в 1996 году, [1]. Жидкое рабочее вещество, в отличие от металлических шариков, более удобно для применения в данной схеме. Разумеется, в данном случае, следует оптимизировать три фактора: увеличить плотность жидкости (рабочую массу при том же объеме), увеличить скорость движения рабочей массы, и обеспечить упругость взаимодействия. Предположим, что на поворотном участке трубопровода (корпуса), по U-образной траектории, с ускорением движется жидкое рабочее вещество, то есть, некоторая инерциальная масса, рис. 16.
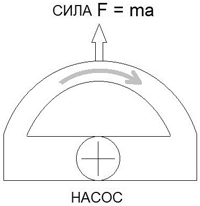Рис. 16. Центробежная сила, возникающая при криволинейном движении жидкости по трубе
Очевидно, что на частицы жидкости действует сила F = ma, согласно второго закона Ньютона. Данная сила прижимает рабочую жидкость к внутренней поверхности трубы на радиусе поворота.
Вернемся к электрокинетическим конструкциям. Эффекты Сигалова – это варианты проявления законов Грассмана для постоянных токов в проводнике сложной формы. Однако, есть и частный случай данного явления: мощная движущая сила возникает при импульсе тока в V-образном или U-образном проводнике.
На мой взгляд, этот случай не относится к эффекту Ампера – Грассмана, то есть, к взаимодействию тока и магнитного поля, а является результатом возникновения центробежной силы в электрокинетических движителях, по аналогии с концепцией движителя, показанной на рис. 16.
При таком рассмотрении, импульсный электрокинетический эффект может найти большее практическое применение, чем электрокинетические движители постоянного тока. Дело в том, что фронт импульса, то есть, волна смещения электронов в проводнике при включении тока, перемещается по проводнику со скоростью более сотен километров в секунду. Такой сдвиг вещества небольшой массы, но имеющей большую скорость, создает мощный кратковременный импульс движущей силы. При установлении постоянного тока, центробежные силы очень малы, так как реальная скорость движения электронов в проводнике составляет всего около 0,1 мм в секунду.
В связи с этим, реализация идеи с насосом и жидким циркулирующим рабочим веществом, рис. 16, не представляет большого практического интереса. Высокочастотный импульсный электрокинетический эффект, при наличии мощного источника электрической энергии, может быть намного эффективнее, чем любые механические устройства, за счет большой скорости распространения фронта импульса электрического тока в проводнике.
Масса частиц рабочего вещества – это второй фактор увеличения центробежной силы, согласно формуле F.1. Электроны имеют очень маленькую инерциальную массу.
Интересно было бы организовать эксперименты по изучению импульсного электрокинетического эффекта в U-образном контуре для протонов (ионизированного водорода), поскольку они в 1836 раз тяжелее электронов. Впрочем, более удобным для практического применения может оказаться конструктивный вариант U-образного импульсного электрокинетического движителя, рабочим веществом которого является электролит. В таком случае, движитель будет похож на электролитический конденсатор необычной формы, с импульсным источником питания.
Ускорение криволинейного движения зависит от кривизны траектории (радиуса), а создаваемая при измерении траектории центробежная сила F определяется по простой формуле, второй закон Ньютона:
F = ma (F.1)
где F – сила, m – масса движущегося тела, а – ускорение криволинейного движения.
Сила F зависит от ускорения, а оно является функцией скорости и радиуса кривизны траектории движения тела, имеющего инерциальную массу. При движении тела по окружности, создается одинаковая сила F во всех радиальных направлениях. При движении тела по криволинейной траектории переменного радиуса, величина ускорения и силы будет меняться на разных участках траектории. В сумме, результирующая сила может быть ненулевая, что создает движущую силу в одном преимущественном направлении.
Использовать данную идею можно разными конструктивными методами, например, на рис. 15 предлагается схема движителя Вейника, в котором по криволинейной траектории переменного радиуса катаются металлические шарики [6]. В одном из экспериментов Вейника, в конструкции БМ-28, по криволинейной траектории, примерно 45 мм диаметром, двигалось 8 металлических шариков диаметром 8 мм. Вращение обеспечивал электропривод, на его оси было установлено «водило» – диск, в котором сделано 8 радиальных каналов для шариков. Шарики могли свободно менять свой радиус вращения внутри канала. Очевидно, что, при вращении, центробежная сила прижимает шарики к внешнему кольцу, которое установлено с эксцентриситетом: ось внешнего кольца, ограничивающего радиус вращения шариков, не совпадает с осью мотора. Эксцентриситет траектории движения шариков, в данной конструкции А.И. Вейник, был равен 0,7 мм. При скорости вращения порядка 21000 оборотов в минуту, устройство создавало движущую силу около 1,4·10-4 (Н), направленную перпендикулярно оси вращения мотора, в направлении эксцентриситета орбиты шариков.
На фото (справа на рис. 15) показана парная конструкция движителя Вейника. Сочетание двух приводов встречного вращения позволяет компенсировать реакцию крутящего момента, сохраняя одинаковое направление движущей силы F в обоих движителях. Эксцентриситет орбит шариков обоих приводов должен быть ориентирован в одном направлении.
Данный эксперимент Вейника был воспроизведен в ООО «Лаборатория Новых Технологий Фарадей» в 2002 году. Отметим, что работа движителя, разработанного в нашей лаборатории, сопровождалась значительной вибрацией, поэтому, увеличение эксцентриситета или скорости вращения было затруднительно. Силы, действующие в данной конструкции, были незначительны. Теоретически, рассматривался один из вариантов модернизации данной схемы: предлагалось добавить в конструкцию резиновый (упругий) обод, к которому центробежная сила должна прижимать вращающиеся шарики. Изучив вопрос надежности конструкции и перспективы данного метода, было решено найти другое техническое решение концепции движителя, использующего криволинейное ускоренное движение рабочего вещества, то есть, инерциальной массы.
Схема с применением жидкого рабочего вещества, движущегося по криволинейной замкнутой траектории переменного радиуса, была рассмотрена мной в 1996 году, [1]. Жидкое рабочее вещество, в отличие от металлических шариков, более удобно для применения в данной схеме. Разумеется, в данном случае, следует оптимизировать три фактора: увеличить плотность жидкости (рабочую массу при том же объеме), увеличить скорость движения рабочей массы, и обеспечить упругость взаимодействия. Предположим, что на поворотном участке трубопровода (корпуса), по U-образной траектории, с ускорением движется жидкое рабочее вещество, то есть, некоторая инерциальная масса, рис. 16.
Очевидно, что на частицы жидкости действует сила F = ma, согласно второго закона Ньютона. Данная сила прижимает рабочую жидкость к внутренней поверхности трубы на радиусе поворота.
Вернемся к электрокинетическим конструкциям. Эффекты Сигалова – это варианты проявления законов Грассмана для постоянных токов в проводнике сложной формы. Однако, есть и частный случай данного явления: мощная движущая сила возникает при импульсе тока в V-образном или U-образном проводнике.
На мой взгляд, этот случай не относится к эффекту Ампера – Грассмана, то есть, к взаимодействию тока и магнитного поля, а является результатом возникновения центробежной силы в электрокинетических движителях, по аналогии с концепцией движителя, показанной на рис. 16.
При таком рассмотрении, импульсный электрокинетический эффект может найти большее практическое применение, чем электрокинетические движители постоянного тока. Дело в том, что фронт импульса, то есть, волна смещения электронов в проводнике при включении тока, перемещается по проводнику со скоростью более сотен километров в секунду. Такой сдвиг вещества небольшой массы, но имеющей большую скорость, создает мощный кратковременный импульс движущей силы. При установлении постоянного тока, центробежные силы очень малы, так как реальная скорость движения электронов в проводнике составляет всего около 0,1 мм в секунду.
В связи с этим, реализация идеи с насосом и жидким циркулирующим рабочим веществом, рис. 16, не представляет большого практического интереса. Высокочастотный импульсный электрокинетический эффект, при наличии мощного источника электрической энергии, может быть намного эффективнее, чем любые механические устройства, за счет большой скорости распространения фронта импульса электрического тока в проводнике.
Масса частиц рабочего вещества – это второй фактор увеличения центробежной силы, согласно формуле F.1. Электроны имеют очень маленькую инерциальную массу.
Интересно было бы организовать эксперименты по изучению импульсного электрокинетического эффекта в U-образном контуре для протонов (ионизированного водорода), поскольку они в 1836 раз тяжелее электронов. Впрочем, более удобным для практического применения может оказаться конструктивный вариант U-образного импульсного электрокинетического движителя, рабочим веществом которого является электролит. В таком случае, движитель будет похож на электролитический конденсатор необычной формы, с импульсным источником питания.
Глава 6
Гироскоп переменного радиуса
Рассмотрим отдельно варианты конструкции движителей, использующих «принцип гироскопа переменного радиуса». Данный принцип был предложен и подробно описан в книге «Экспериментальная гравитоника» [4].
Первый этап экспериментальных исследований, Спартак Михайлович Поляков проводил с помощью механического устройства, в котором создавалось орбитальное движение вращающихся тел (гироскопов), в сочетании с изменением их радиуса орбиты (прецессия). На фотографии рис. 17 показана экспериментальная установка «Елка», с четырьмя гироскопами, которая использовалась в 1984–1986 годы для изучения силовых эффектов в лаборатории Полякова. В данной конструкции, вращалась сама обойма гироскопов (орбитальное вращение), и каждый из них мог быть выключен или включен отдельно, причем, в разном направлении собственного вращения. Общая масса конструкции составляла 32 кг, масса четырех гироскопов 6,4 кг, источник питания моторов – внешний, регулируемый.
Рис. 17. Гироскопы движителя «Елка»
Результаты экспериментов Полякова показаны на графиках рис. 18 и рис. 19.
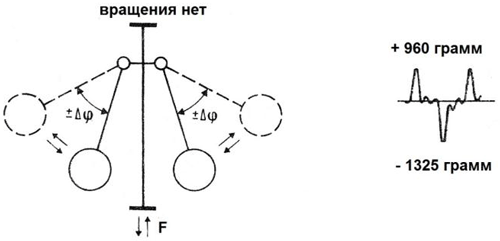Рис. 18. Калибровка устройства в эксперименте Полякова
Рис. 19. Силы, возникающие при прецессии гироскопов в эксперименте Полякова
Перед тем, как проверять силовые эффекты, возникающие за счет прецессии вращающихся гироскопов, Поляков калибровал систему. На рис. 18 показаны результаты измерений, которые были сделаны при отсутствии орбитального вращения. В данном случае, измерительная система показывает наличие реактивной силы, которая возникает только за счет «качания» гироскопов вверх и вниз, при отсутствии орбитального вращения.
При этом, центр масс системы смещается, так как изменяется положение гироскопов. Таким образом, автор определяет «динамический ноль» системы. Не имеет значения включены или выключены гироскопы, если нет осевого вращения. Суммарная сила, действующая вдоль оси «Елки», интегрированная за несколько «циклов качаний» гироскопов, будет равна нулю.
При наличии осевого вращения включенных гироскопов, создаются несимметричные силовые эффекты импульсного характера, рис. 19.
При такой траектории движения гироскопов, на весь корпус экспериментального устройства действуют импульсы, возникающие при переводе орбитально вращающегося гироскопа на меньший радиус вращения. Измерения показали, что суммарный импульс тяги, действующий на корпус устройства, с учетом калибровки относительно «динамического нуля», направлен вдоль оси вращения вверх, и достигал 573 грамма.
Итак, в соответствии с методом Полякова, рабочую массу (гироскоп) приводят во вращательное движение, а затем изменяют радиус вращения гироскопа, который является управляемым параметром вращения рабочей массы. Во время уменьшения радиуса вращения рабочего тела возникает кратковременный импульс тяги, направленный вдоль оси вращения. Очевидно, что изменение радиуса вращения рабочей массы в данном случае может носить только периодический характер, следовательно, создаваемая сила тяги имеет импульсный характер. В процессе возврата рабочей массы в начальное положение, характеризуемое максимальным радиусом вращения, импульс тяги отсутствует.
Первый этап экспериментальных исследований, Спартак Михайлович Поляков проводил с помощью механического устройства, в котором создавалось орбитальное движение вращающихся тел (гироскопов), в сочетании с изменением их радиуса орбиты (прецессия). На фотографии рис. 17 показана экспериментальная установка «Елка», с четырьмя гироскопами, которая использовалась в 1984–1986 годы для изучения силовых эффектов в лаборатории Полякова. В данной конструкции, вращалась сама обойма гироскопов (орбитальное вращение), и каждый из них мог быть выключен или включен отдельно, причем, в разном направлении собственного вращения. Общая масса конструкции составляла 32 кг, масса четырех гироскопов 6,4 кг, источник питания моторов – внешний, регулируемый.
Результаты экспериментов Полякова показаны на графиках рис. 18 и рис. 19.
Перед тем, как проверять силовые эффекты, возникающие за счет прецессии вращающихся гироскопов, Поляков калибровал систему. На рис. 18 показаны результаты измерений, которые были сделаны при отсутствии орбитального вращения. В данном случае, измерительная система показывает наличие реактивной силы, которая возникает только за счет «качания» гироскопов вверх и вниз, при отсутствии орбитального вращения.
При этом, центр масс системы смещается, так как изменяется положение гироскопов. Таким образом, автор определяет «динамический ноль» системы. Не имеет значения включены или выключены гироскопы, если нет осевого вращения. Суммарная сила, действующая вдоль оси «Елки», интегрированная за несколько «циклов качаний» гироскопов, будет равна нулю.
При наличии осевого вращения включенных гироскопов, создаются несимметричные силовые эффекты импульсного характера, рис. 19.
При такой траектории движения гироскопов, на весь корпус экспериментального устройства действуют импульсы, возникающие при переводе орбитально вращающегося гироскопа на меньший радиус вращения. Измерения показали, что суммарный импульс тяги, действующий на корпус устройства, с учетом калибровки относительно «динамического нуля», направлен вдоль оси вращения вверх, и достигал 573 грамма.
Итак, в соответствии с методом Полякова, рабочую массу (гироскоп) приводят во вращательное движение, а затем изменяют радиус вращения гироскопа, который является управляемым параметром вращения рабочей массы. Во время уменьшения радиуса вращения рабочего тела возникает кратковременный импульс тяги, направленный вдоль оси вращения. Очевидно, что изменение радиуса вращения рабочей массы в данном случае может носить только периодический характер, следовательно, создаваемая сила тяги имеет импульсный характер. В процессе возврата рабочей массы в начальное положение, характеризуемое максимальным радиусом вращения, импульс тяги отсутствует.