Встречаются такие термины, которые характеризуют, как кажется, именно данный смех. Среди них «радостный», «истерический», «убийственный», «исступлённый» и т.п. Но и их нельзя назвать строго квалификационными. Значение их расплывчато, и они опять-таки не столько говорят о том, чем является сам по себе этот смех, сколько сравнивают его с чем-то: состоянием радости, истерики, исступления и т.п.
Все это, конечно, не случайно, и дело не в недостаточной проницательности тех, кто пытался описать смех. Источник затруднений — в сложности смеха, отражающей сложность и многообразие тех движений души, внешним проявлением которых он является. Именно это имеет, как кажется, в виду Лосев, когда он заканчивает своё описание смеха Соловьёва определением человека как «смеющегося существа». Если смех связан с человеческой сущностью, он столь же сложен, как и сама эта сущность. Классификация смеха оказывается в итоге исследованием человека со всеми вытекающими из этого трудностями.
Речь шла только о смехе, но все это относится и к другим проявлениям сложной внутренней жизни человека.
И в заключение — один пример явно несостоятельной классификации, грубо нарушающей требования, предъявляемые к делению.
Писатель Х.Л.Борхес приводит отрывок из «некой китайской энциклопедии». В нем даётся классификация животных и говорится, что они «подразделяются на: а) принадлежащих императору; б) бальзамированных; в) приручённых; г) молочных поросят; д) сирен; е) сказочных; ж) бродячих собак; з) заключённых в настоящую классификацию; и) буйствующих, как в безумии; к) неисчислимых; л) нарисованных очень тонкой кисточкой из верблюжьей шерсти; м) и прочих; н) только что разбивших кувшин; о) издалека кажущихся мухами».
Чем поражает эта классификация? Почему с самого начала становится очевидным, что подобным образом нельзя рассуждать ни о животных, ни о чем-либо ином?
Дело, разумеется, не в отдельных рубриках, какими бы необычными они ни казались. Каждая из них имеет вполне определённое конкретное содержание. В числе животных упоминаются, правда, фантастические существа — сказочные животные и сирены, но это делается, пожалуй, с целью отличить реально существующих животных от существующих только в воображении. К животным относятся и нарисованные, но мы и в самом деле обычно называем их животными.
Невозможными являются не отдельные указанные разновидности животных, а как раз соединение их в одну группу, перечисление их друг за другом, так что рядом встают живые и умершие животные, буйствующие и нарисованные, фантастические и приручённые, классифицируемые и только что разбившие кувшин. Сразу возникает чувство, что нет такой единой плоскости, на которой удалось бы разместить все эти группы, нет общего, однородного пространства, в котором могли бы встретиться все перечисленные животные.
Классификация всегда устанавливает определённый порядок. Она разбивает рассматриваемую область объектов на группы, чтобы упорядочить эту область и сделать её хорошо обозримой. Но классификация животных из «энциклопедии» не только не намечает определённой системы, но, напротив, разрушает даже те представления о гранях между группами животных, которые у нас есть. В сущности, эта классификация нарушает все те требования, которые предъявляются к разделению какого-то множества объектов на составляющие его группы. Вместо системы она вносит несогласованность и беспорядок.
Ясно, что классификация вообще не придерживается никакого твёрдого основания, в ней нет даже намёка на единство и неизменность основания в ходе деления. Каждая новая группа животных выделяется на основе собственных своеобразных признаков, безотносительно к тому, по каким признакам обособляются другие группы. Связь между группами оказывается почти полностью разрушенной, никакой координации и субординации между ними установить невозможно. Можно предполагать, что сирены относятся к сказочным животным, а молочные поросята и бродячие собаки не принадлежат ни к тем, ни к другим. Но относятся ли сирены, сказочные животные, молочные поросята и бродячие животные к тем животным, что буйствуют, как в безумии, или к неисчислимым, или к тем, которые нарисованы тонкой кисточкой? Как соотносятся между собой животные, только что разбившие кувшин, и животные, издалека кажущиеся мухами? На подобные вопросы невозможно ответить, да их и бессмысленно задавать, поскольку очевидно, что никакого единого принципа в основе этой классификации не лежит. Далее, члены деления здесь не исключают друг друга. Всех перечисленных животных можно нарисовать, многие из них издалека могут казаться мухами, все они включены в классификацию и т.д. Относительно того, что перечисленные виды животных исчерпывают множество всех животных, можно говорить только с натяжкой: те животные, которые не упоминаются прямо, свалены в кучу в рубрике «и прочие». И наконец, очевидны скачки, допускаемые в данном делении. Различаются как будто сказочные и реально существующие животные, но вместо особого упоминания последних перечисляются их отдельные виды — поросята и собаки, причём не все поросята, а только молочные, и не все собаки, а лишь бродячие.
Классификации, подобные этой, настолько сумбурны, что возникает даже сомнение, следует ли вообще считать их делениями каких-то понятий. О возможности усовершенствования таких классификаций, придании им хотя бы видимости системы и порядка не приходится и говорить.
Но что интересно, даже такого рода деления, отличающиеся путаницей и невнятностью, иногда могут оказываться практически небесполезными. Неправильно делить, к примеру, обувь на мужскую, женскую и резиновую (или детскую), но во многих обувных магазинах она именно так делится, и это не ставит нас в тупик. Нет ничего невозможного в предположении, что и классификация животных, подобная взятой из «энциклопедии», может служить каким-то практическим, разнородным по самой своей природе целям. Теоретически, с точки зрения логики, она никуда не годится. Однако далеко не все, что используется повседневно, находится на уровне требований высокой теории и отвечает стандартам безупречной логики.
Нужно стремиться к логическому совершенству, но не следует быть педантичным и отбрасывать с порога все, что представляется логически не вполне совершённым.
Глава 4
1. ПРОСТЫЕ И СЛОЖНЫЕ ВЫСКАЗЫВАНИЯ.
2. УСЛОВНОЕ ВЫСКАЗЫВАНИЕ, ИМПЛИКАЦИЯ, ЭКВИВАЛЕНТНОСТЬ
Все это, конечно, не случайно, и дело не в недостаточной проницательности тех, кто пытался описать смех. Источник затруднений — в сложности смеха, отражающей сложность и многообразие тех движений души, внешним проявлением которых он является. Именно это имеет, как кажется, в виду Лосев, когда он заканчивает своё описание смеха Соловьёва определением человека как «смеющегося существа». Если смех связан с человеческой сущностью, он столь же сложен, как и сама эта сущность. Классификация смеха оказывается в итоге исследованием человека со всеми вытекающими из этого трудностями.
Речь шла только о смехе, но все это относится и к другим проявлениям сложной внутренней жизни человека.
И в заключение — один пример явно несостоятельной классификации, грубо нарушающей требования, предъявляемые к делению.
Писатель Х.Л.Борхес приводит отрывок из «некой китайской энциклопедии». В нем даётся классификация животных и говорится, что они «подразделяются на: а) принадлежащих императору; б) бальзамированных; в) приручённых; г) молочных поросят; д) сирен; е) сказочных; ж) бродячих собак; з) заключённых в настоящую классификацию; и) буйствующих, как в безумии; к) неисчислимых; л) нарисованных очень тонкой кисточкой из верблюжьей шерсти; м) и прочих; н) только что разбивших кувшин; о) издалека кажущихся мухами».
Чем поражает эта классификация? Почему с самого начала становится очевидным, что подобным образом нельзя рассуждать ни о животных, ни о чем-либо ином?
Дело, разумеется, не в отдельных рубриках, какими бы необычными они ни казались. Каждая из них имеет вполне определённое конкретное содержание. В числе животных упоминаются, правда, фантастические существа — сказочные животные и сирены, но это делается, пожалуй, с целью отличить реально существующих животных от существующих только в воображении. К животным относятся и нарисованные, но мы и в самом деле обычно называем их животными.
Невозможными являются не отдельные указанные разновидности животных, а как раз соединение их в одну группу, перечисление их друг за другом, так что рядом встают живые и умершие животные, буйствующие и нарисованные, фантастические и приручённые, классифицируемые и только что разбившие кувшин. Сразу возникает чувство, что нет такой единой плоскости, на которой удалось бы разместить все эти группы, нет общего, однородного пространства, в котором могли бы встретиться все перечисленные животные.
Классификация всегда устанавливает определённый порядок. Она разбивает рассматриваемую область объектов на группы, чтобы упорядочить эту область и сделать её хорошо обозримой. Но классификация животных из «энциклопедии» не только не намечает определённой системы, но, напротив, разрушает даже те представления о гранях между группами животных, которые у нас есть. В сущности, эта классификация нарушает все те требования, которые предъявляются к разделению какого-то множества объектов на составляющие его группы. Вместо системы она вносит несогласованность и беспорядок.
Ясно, что классификация вообще не придерживается никакого твёрдого основания, в ней нет даже намёка на единство и неизменность основания в ходе деления. Каждая новая группа животных выделяется на основе собственных своеобразных признаков, безотносительно к тому, по каким признакам обособляются другие группы. Связь между группами оказывается почти полностью разрушенной, никакой координации и субординации между ними установить невозможно. Можно предполагать, что сирены относятся к сказочным животным, а молочные поросята и бродячие собаки не принадлежат ни к тем, ни к другим. Но относятся ли сирены, сказочные животные, молочные поросята и бродячие животные к тем животным, что буйствуют, как в безумии, или к неисчислимым, или к тем, которые нарисованы тонкой кисточкой? Как соотносятся между собой животные, только что разбившие кувшин, и животные, издалека кажущиеся мухами? На подобные вопросы невозможно ответить, да их и бессмысленно задавать, поскольку очевидно, что никакого единого принципа в основе этой классификации не лежит. Далее, члены деления здесь не исключают друг друга. Всех перечисленных животных можно нарисовать, многие из них издалека могут казаться мухами, все они включены в классификацию и т.д. Относительно того, что перечисленные виды животных исчерпывают множество всех животных, можно говорить только с натяжкой: те животные, которые не упоминаются прямо, свалены в кучу в рубрике «и прочие». И наконец, очевидны скачки, допускаемые в данном делении. Различаются как будто сказочные и реально существующие животные, но вместо особого упоминания последних перечисляются их отдельные виды — поросята и собаки, причём не все поросята, а только молочные, и не все собаки, а лишь бродячие.
Классификации, подобные этой, настолько сумбурны, что возникает даже сомнение, следует ли вообще считать их делениями каких-то понятий. О возможности усовершенствования таких классификаций, придании им хотя бы видимости системы и порядка не приходится и говорить.
Но что интересно, даже такого рода деления, отличающиеся путаницей и невнятностью, иногда могут оказываться практически небесполезными. Неправильно делить, к примеру, обувь на мужскую, женскую и резиновую (или детскую), но во многих обувных магазинах она именно так делится, и это не ставит нас в тупик. Нет ничего невозможного в предположении, что и классификация животных, подобная взятой из «энциклопедии», может служить каким-то практическим, разнородным по самой своей природе целям. Теоретически, с точки зрения логики, она никуда не годится. Однако далеко не все, что используется повседневно, находится на уровне требований высокой теории и отвечает стандартам безупречной логики.
Нужно стремиться к логическому совершенству, но не следует быть педантичным и отбрасывать с порога все, что представляется логически не вполне совершённым.
Глава 4
ВЫСКАЗЫВАНИЯ
1. ПРОСТЫЕ И СЛОЖНЫЕ ВЫСКАЗЫВАНИЯ.
ОТРИЦАНИЕ, КОНЪЮНКЦИЯ, ДИЗЪЮНКЦИЯ
Высказывание — грамматически правильное предложение, взятое вместе с выражаемым им смыслом (содержанием) и являющееся истинным или ложным.
Высказывание — более сложное образование, чем имя. При разложении высказываний на части, мы всегда получаем те или иные имена. Скажем, высказывание «Солнце есть звезда» включает в качестве своих частей имена «Солнце» и «звезда».
Понятие высказывания — одно из ключевых в логике. Как таковое, оно не допускает точного определения, в равной мере приложимого в разных её разделах. Ясно, что всякое высказывание описывает определённую ситуацию, что-то утверждая или отрицая о ней, и является истинным или ложным.
Высказывание считается истинным, если даваемое им описание соответствует реальной ситуации, и ложным, если не соответствует ей. «Истина» и «ложь» называются истинностными значениями высказывания.
Из отдельных высказываний разными способами можно строить новые высказывания. Так, из высказываний «Дует ветер» и «Идёт дождь» можно образовать более сложные высказывания «Дует ветер и идёт дождь», «Либо дует ветер, либо идёт дождь», «Если идёт дождь, дует ветер» и т.п. Слова «и», «либо, либо», «если, то» и т.п., служащие для образования сложных высказываний, называются логическими связками.
Высказывание называется простым, если оно не включает других высказываний в качестве своих частей.
Высказывание является сложным, если оно получено с помощью логических связок из нескольких более простых высказываний.
Может показаться, что знакомство с высказываниями естественнее всего начать с изучения простых высказываний и их частей, и уже затем приступить к изучению того, как из простых высказываний образуются сложные. В логике, однако, подход является обратным. Сначала рассматриваются способы построения сложных высказываний из более простых, при этом простое высказывание берётся как неразложимое далее целое (как «атом»), и только затем переходят к выявлению строения простых высказываний. Анализ структуры сложных высказываний предшествует анализу структуры простых. Объясняется это следующим: для того, чтобы понимать способы сочетания высказываний, вовсе не обязательно знать, что такое простое высказывание; достаточно учитывать только то, что последнее имеет определённое значение истинности. Простые высказывания чрезвычайно разнообразны, выявление составляющих их частей во многом зависит от принятого способа их анализа. Некоторые логические связи между высказываниями не зависят от строения простых высказываний. Разумно поэтому поступить так, как если бы мы знали все о простых высказываниях, т.е. оставить вопрос об их структуре на время в стороне и заняться логическими связями высказываний. Последняя задача является относительно лёгкой.
Та часть логики, в которой описываются логические связи высказываний, не зависящие от структуры простых высказываний, называется общей теорией дедукции.
Перейдём теперь к рассмотрению наиболее важных способов построения сложных высказываний.
Отрицание — логическая связка, с помощью которой из данного высказывания получается новое, причём, если исходное высказывание истинно, его отрицание будет ложным, и наоборот. Отрицательное высказывание состоит из исходного высказывания и отрицания, выражаемого обычно словами «не», «неверно, что». Отрицательное высказывание является, таким образом, сложным высказыванием: оно включает в качестве своей части отличное от него высказывание. Например, отрицанием высказывания «10 — чётное число» является высказывание «10 не есть чётное число» (или: «Неверно, что 10 есть чётное число»).
Будем обозначать высказывания буквами А, В, С, …, отрицание высказывания — символом ~. Полный смысл понятия отрицания высказывания задаётся условием: если высказывание Л истинно, его отрицание А ложно, и если А ложно, его отрицание, ~А, истинно. Например, так как высказывание «1 есть целое положительное число» истинно, его отрицание «1 не является целым положительным числом» ложно, а так как «1 есть простое число» ложно, его отрицание «1 не есть простое число» истинно.
Определению отрицания можно придать форму таблицы истинности, в которой «и» означает «истинно» и «л» — «ложно».

В результате соединения двух высказываний при помощи слова «и», мы получаем сложное высказывание, называемое конъюнкцией. Высказывания, соединяемые таким способом, называются членами конъюнкции. Например, если высказывания «Сегодня жарко» и «Вчера было холодно» соединить связкой «и» получится конъюнкция «Сегодня жарко и вчера было холодно».
Конъюнкция истинна только в случае, когда оба входящих в неё высказывания являются истинными; если хотя бы один из её членов ложен, то и вся конъюнкция ложна.
Высказывание А может быть либо истинным, либо ложным, и то же самое можно сказать о высказывании В. Следовательно, возможны четыре пары значений истинности для этих высказываний.
Обозначим конъюнкцию символом &. Таблица истинности для конъюнкции приведена ниже.

Определение конъюнкции, как и определения других логических связок, служащих для образования сложных высказываний, основывается на следующих двух предположениях:
1) каждое высказывание (как простое, так и сложное) имеет одно и только одно из двух значений истинности: оно является либо истинным, либо ложным;
2) истинностное значение сложного высказывания зависит только от истинностных значений входящих в него высказываний и способа их логической связи между собой.
Эти предположения кажутся простыми. Приняв их, нужно, однако, отбросить идею, что, наряду с истинными и ложными высказываниями, могут существовать также высказывания неопределённые с точки зрения своего истинностного значения (такие, как, скажем, «Через пять лет в это время будет идти дождь с громом» и т.п.). Нужно отказаться также от того, что истинностное значение сложного высказывания зависит от «связи по смыслу» соединяемых высказываний.
В обычном языке два высказывания соединяются союзом «и», когда они связаны между собой по содержанию, или смыслу. Характер этой связи не вполне ясен, но понятно, что мы не рассматривали бы конъюнкцию «Он шёл в пальто и я шёл в университет» как выражение, имеющее смысл и способное быть истинным или ложным. Хотя высказывания «2 — простое число» и «Москва — большой город» истинны, мы не склонны считать истинной также их конъюнкцию «2 — простое число и Москва — большой город», поскольку составляющие её высказывания не связаны между собою по смыслу.
Упрощая значение конъюнкции и других логических связок и отказываясь для этого от неясного понятия «связь высказываний по смыслу», логика делает значение этих связок одновременно и более широким, и более ясным.
Соединяя два высказывания с помощью слова «или», мы получаем дизъюнкцию этих высказываний. Высказывания, образующие дизъюнкцию, называются членами дизъюнкции.
Слово «или» в повседневном языке имеет два разных смысла. Иногда оно означает «одно или другое или оба», а иногда «одно или другое, но не оба вместе». Высказывание «В этом сезоне я хочу пойти на „Пиковую даму“ или на „Аиду“» допускает возможность двукратного посещения оперы. В высказывании же «Он учится в Московском или в Саратовском университете» подразумевается, что упоминаемый человек учится только в одном из этих университетов.
Первый смысл «или» называется неисключающим. Взятая в этом смысле дизъюнкция двух высказываний означает только, что по крайней мере одно из этих высказываний истинно, независимо от того, истинны они оба или нет. Взятая во втором, исключающем, смысле дизъюнкция двух высказываний утверждает, что одно из них истинно, а второе — ложно.
Символ v будет обозначать дизъюнкцию в неисключающем смысле, для дизъюнкции в исключающем смысле будет использоваться символ V. Таблицы для двух видов дизъюнкции показывают, что неисключающая дизъюнкция истинна, когда хотя бы одно из входящих в неё высказываний истинно, и ложна, только когда оба её члена ложны; исключающая дизъюнкция истинна, когда истинным является только один из её членов, и она ложна, когда оба её члена истинны или оба ложны.
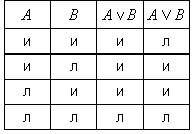
В логике и математике слово «или» всегда употребляется в неисключающем значении.
Разложение некоторого высказывания на простые, далее неразложимые части даёт два вида выражений, называемых собственными и несобственными символами. Особенность собственных символов в том, что они имеют какое-то содержание, даже взятые сами по себе. К ним относятся имена (обозначающие некоторые объекты), переменные (отсылающие к какой-то области объектов), высказывания (описывающие какие-то ситуации и являющиеся истинными или ложными). Несобственные символы не имеют самостоятельного содержания, но в сочетании с одним или несколькими собственными символами образуют сложные выражения, уже имеющие самостоятельное содержание. К несобственным символам относятся, в частности, логические связки, используемые для образования сложных высказываний из простых: «… и …», «… или …», «либо …, либо …», «если …, то …», «… тогда и только тогда, когда …», «ни …, ни …», «не …, а …», «…, но не …», «неверно, что …» и т.п. Само по себе слово, скажем «или», не обозначает никакого объекта. Но в совокупности с двумя собственными, обозначающими символами это слово даёт новый обозначающий символ: из двух высказываний «Письмо получено» и «Телеграмма отправлена» — новое высказывание «Письмо получено или телеграмма отправлена».
Центральная задача логики — отделение правильных схем рассуждения от неправильных и систематизация первых. Логическая правильность определяется логической формой. Для её выявления нужно отвлечься от содержательных частей рассуждения (собственных символов) и сосредоточить внимание на несобственных символах, представляющих эту форму в чистом виде. Отсюда интерес формальной логики к таким, обычно не привлекающим внимания, словам, как «и», «или», «если, то» и т.п.[1]
Высказывание — более сложное образование, чем имя. При разложении высказываний на части, мы всегда получаем те или иные имена. Скажем, высказывание «Солнце есть звезда» включает в качестве своих частей имена «Солнце» и «звезда».
Понятие высказывания — одно из ключевых в логике. Как таковое, оно не допускает точного определения, в равной мере приложимого в разных её разделах. Ясно, что всякое высказывание описывает определённую ситуацию, что-то утверждая или отрицая о ней, и является истинным или ложным.
Высказывание считается истинным, если даваемое им описание соответствует реальной ситуации, и ложным, если не соответствует ей. «Истина» и «ложь» называются истинностными значениями высказывания.
Из отдельных высказываний разными способами можно строить новые высказывания. Так, из высказываний «Дует ветер» и «Идёт дождь» можно образовать более сложные высказывания «Дует ветер и идёт дождь», «Либо дует ветер, либо идёт дождь», «Если идёт дождь, дует ветер» и т.п. Слова «и», «либо, либо», «если, то» и т.п., служащие для образования сложных высказываний, называются логическими связками.
Высказывание называется простым, если оно не включает других высказываний в качестве своих частей.
Высказывание является сложным, если оно получено с помощью логических связок из нескольких более простых высказываний.
Может показаться, что знакомство с высказываниями естественнее всего начать с изучения простых высказываний и их частей, и уже затем приступить к изучению того, как из простых высказываний образуются сложные. В логике, однако, подход является обратным. Сначала рассматриваются способы построения сложных высказываний из более простых, при этом простое высказывание берётся как неразложимое далее целое (как «атом»), и только затем переходят к выявлению строения простых высказываний. Анализ структуры сложных высказываний предшествует анализу структуры простых. Объясняется это следующим: для того, чтобы понимать способы сочетания высказываний, вовсе не обязательно знать, что такое простое высказывание; достаточно учитывать только то, что последнее имеет определённое значение истинности. Простые высказывания чрезвычайно разнообразны, выявление составляющих их частей во многом зависит от принятого способа их анализа. Некоторые логические связи между высказываниями не зависят от строения простых высказываний. Разумно поэтому поступить так, как если бы мы знали все о простых высказываниях, т.е. оставить вопрос об их структуре на время в стороне и заняться логическими связями высказываний. Последняя задача является относительно лёгкой.
Та часть логики, в которой описываются логические связи высказываний, не зависящие от структуры простых высказываний, называется общей теорией дедукции.
Перейдём теперь к рассмотрению наиболее важных способов построения сложных высказываний.
Отрицание — логическая связка, с помощью которой из данного высказывания получается новое, причём, если исходное высказывание истинно, его отрицание будет ложным, и наоборот. Отрицательное высказывание состоит из исходного высказывания и отрицания, выражаемого обычно словами «не», «неверно, что». Отрицательное высказывание является, таким образом, сложным высказыванием: оно включает в качестве своей части отличное от него высказывание. Например, отрицанием высказывания «10 — чётное число» является высказывание «10 не есть чётное число» (или: «Неверно, что 10 есть чётное число»).
Будем обозначать высказывания буквами А, В, С, …, отрицание высказывания — символом ~. Полный смысл понятия отрицания высказывания задаётся условием: если высказывание Л истинно, его отрицание А ложно, и если А ложно, его отрицание, ~А, истинно. Например, так как высказывание «1 есть целое положительное число» истинно, его отрицание «1 не является целым положительным числом» ложно, а так как «1 есть простое число» ложно, его отрицание «1 не есть простое число» истинно.
Определению отрицания можно придать форму таблицы истинности, в которой «и» означает «истинно» и «л» — «ложно».

В результате соединения двух высказываний при помощи слова «и», мы получаем сложное высказывание, называемое конъюнкцией. Высказывания, соединяемые таким способом, называются членами конъюнкции. Например, если высказывания «Сегодня жарко» и «Вчера было холодно» соединить связкой «и» получится конъюнкция «Сегодня жарко и вчера было холодно».
Конъюнкция истинна только в случае, когда оба входящих в неё высказывания являются истинными; если хотя бы один из её членов ложен, то и вся конъюнкция ложна.
Высказывание А может быть либо истинным, либо ложным, и то же самое можно сказать о высказывании В. Следовательно, возможны четыре пары значений истинности для этих высказываний.
Обозначим конъюнкцию символом &. Таблица истинности для конъюнкции приведена ниже.

Определение конъюнкции, как и определения других логических связок, служащих для образования сложных высказываний, основывается на следующих двух предположениях:
1) каждое высказывание (как простое, так и сложное) имеет одно и только одно из двух значений истинности: оно является либо истинным, либо ложным;
2) истинностное значение сложного высказывания зависит только от истинностных значений входящих в него высказываний и способа их логической связи между собой.
Эти предположения кажутся простыми. Приняв их, нужно, однако, отбросить идею, что, наряду с истинными и ложными высказываниями, могут существовать также высказывания неопределённые с точки зрения своего истинностного значения (такие, как, скажем, «Через пять лет в это время будет идти дождь с громом» и т.п.). Нужно отказаться также от того, что истинностное значение сложного высказывания зависит от «связи по смыслу» соединяемых высказываний.
В обычном языке два высказывания соединяются союзом «и», когда они связаны между собой по содержанию, или смыслу. Характер этой связи не вполне ясен, но понятно, что мы не рассматривали бы конъюнкцию «Он шёл в пальто и я шёл в университет» как выражение, имеющее смысл и способное быть истинным или ложным. Хотя высказывания «2 — простое число» и «Москва — большой город» истинны, мы не склонны считать истинной также их конъюнкцию «2 — простое число и Москва — большой город», поскольку составляющие её высказывания не связаны между собою по смыслу.
Упрощая значение конъюнкции и других логических связок и отказываясь для этого от неясного понятия «связь высказываний по смыслу», логика делает значение этих связок одновременно и более широким, и более ясным.
Соединяя два высказывания с помощью слова «или», мы получаем дизъюнкцию этих высказываний. Высказывания, образующие дизъюнкцию, называются членами дизъюнкции.
Слово «или» в повседневном языке имеет два разных смысла. Иногда оно означает «одно или другое или оба», а иногда «одно или другое, но не оба вместе». Высказывание «В этом сезоне я хочу пойти на „Пиковую даму“ или на „Аиду“» допускает возможность двукратного посещения оперы. В высказывании же «Он учится в Московском или в Саратовском университете» подразумевается, что упоминаемый человек учится только в одном из этих университетов.
Первый смысл «или» называется неисключающим. Взятая в этом смысле дизъюнкция двух высказываний означает только, что по крайней мере одно из этих высказываний истинно, независимо от того, истинны они оба или нет. Взятая во втором, исключающем, смысле дизъюнкция двух высказываний утверждает, что одно из них истинно, а второе — ложно.
Символ v будет обозначать дизъюнкцию в неисключающем смысле, для дизъюнкции в исключающем смысле будет использоваться символ V. Таблицы для двух видов дизъюнкции показывают, что неисключающая дизъюнкция истинна, когда хотя бы одно из входящих в неё высказываний истинно, и ложна, только когда оба её члена ложны; исключающая дизъюнкция истинна, когда истинным является только один из её членов, и она ложна, когда оба её члена истинны или оба ложны.

В логике и математике слово «или» всегда употребляется в неисключающем значении.
Разложение некоторого высказывания на простые, далее неразложимые части даёт два вида выражений, называемых собственными и несобственными символами. Особенность собственных символов в том, что они имеют какое-то содержание, даже взятые сами по себе. К ним относятся имена (обозначающие некоторые объекты), переменные (отсылающие к какой-то области объектов), высказывания (описывающие какие-то ситуации и являющиеся истинными или ложными). Несобственные символы не имеют самостоятельного содержания, но в сочетании с одним или несколькими собственными символами образуют сложные выражения, уже имеющие самостоятельное содержание. К несобственным символам относятся, в частности, логические связки, используемые для образования сложных высказываний из простых: «… и …», «… или …», «либо …, либо …», «если …, то …», «… тогда и только тогда, когда …», «ни …, ни …», «не …, а …», «…, но не …», «неверно, что …» и т.п. Само по себе слово, скажем «или», не обозначает никакого объекта. Но в совокупности с двумя собственными, обозначающими символами это слово даёт новый обозначающий символ: из двух высказываний «Письмо получено» и «Телеграмма отправлена» — новое высказывание «Письмо получено или телеграмма отправлена».
Центральная задача логики — отделение правильных схем рассуждения от неправильных и систематизация первых. Логическая правильность определяется логической формой. Для её выявления нужно отвлечься от содержательных частей рассуждения (собственных символов) и сосредоточить внимание на несобственных символах, представляющих эту форму в чистом виде. Отсюда интерес формальной логики к таким, обычно не привлекающим внимания, словам, как «и», «или», «если, то» и т.п.[1]
2. УСЛОВНОЕ ВЫСКАЗЫВАНИЕ, ИМПЛИКАЦИЯ, ЭКВИВАЛЕНТНОСТЬ
Условное высказывание — сложное высказывание, формулируемое обычно с помощью связки «если …, то …» и устанавливающее, что одно событие, состояние и т.п. является в том или ином смысле основанием или условием для другого. Например: «Если есть огонь, то есть дым», «Если число делится на 9, оно делится на 3» и т.п.
Условное высказывание слагается из двух простых высказываний. То, которому предпослано слово «если», называется основанием, или антецедентом (предыдущим); высказывание, идущее после слова «то», называется следствием, или консеквентом (последующим).
Утверждая условное высказывание, мы прежде всего имеем в виду, что не может быть так, чтобы то, о чем говорится в его основании, имело место, а то, о чем говорится в следствии, отсутствовало. Иными словами, не может случиться, чтобы антецедент был истинным, а консеквент — ложным.
В терминах условного высказывания обычно определяются понятия достаточного и необходимого условия: антецедент (основание) есть достаточное условие для консеквента (следствия), а консеквент — необходимое условие для антецедента. Например, истинность условного высказывания «Если выбор рационален, то выбирается лучшая из имеющихся альтернатив» означает, что рациональность — достаточное основание для избрания лучшей из имеющихся возможностей, и что выбор такой возможности есть необходимое условие его рациональности.
Типичной функцией условного высказывания является обоснование одного высказывания ссылкой на другое высказывание. К примеру, то, что серебро электропроводно, можно обосновать ссылкой на то, что оно металл: «Если серебро — металл, оно электропроводно».
Выражаемую условным высказыванием связь обосновывающего и обосновываемого (основания и следствия) трудно охарактеризовать в общем виде и только иногда природа её относительно ясна. Эта связь может быть, в частности, связью логического следования, имеющей место между посылками и заключением правильного умозаключения («Если все живые многоклеточные существа смертны, а медуза является таким существом, то она смертна»). Связь может представлять собой закон природы («Если тело подвергнуть трению, оно начнёт нагреваться») или причинную связь («Если Луна в новолуние находится в узле своей орбиты, наступает солнечное затмение»). Рассматриваемая связь может иметь также характер социальной закономерности, правила, традиции и т.п. («Если меняется общество, меняется также человек», «Если совет разумен, он должен быть выполнен»).
Со связью, выражаемой условным высказыванием, обычно соединяется убеждение, что консеквент с определённой необходимостью «вытекает» из антецедента и что имеется некоторый общий закон, сформулировав который, мы могли бы логически вывести консеквент из антецедента.
Условное высказывание слагается из двух простых высказываний. То, которому предпослано слово «если», называется основанием, или антецедентом (предыдущим); высказывание, идущее после слова «то», называется следствием, или консеквентом (последующим).
Утверждая условное высказывание, мы прежде всего имеем в виду, что не может быть так, чтобы то, о чем говорится в его основании, имело место, а то, о чем говорится в следствии, отсутствовало. Иными словами, не может случиться, чтобы антецедент был истинным, а консеквент — ложным.
В терминах условного высказывания обычно определяются понятия достаточного и необходимого условия: антецедент (основание) есть достаточное условие для консеквента (следствия), а консеквент — необходимое условие для антецедента. Например, истинность условного высказывания «Если выбор рационален, то выбирается лучшая из имеющихся альтернатив» означает, что рациональность — достаточное основание для избрания лучшей из имеющихся возможностей, и что выбор такой возможности есть необходимое условие его рациональности.
Типичной функцией условного высказывания является обоснование одного высказывания ссылкой на другое высказывание. К примеру, то, что серебро электропроводно, можно обосновать ссылкой на то, что оно металл: «Если серебро — металл, оно электропроводно».
Выражаемую условным высказыванием связь обосновывающего и обосновываемого (основания и следствия) трудно охарактеризовать в общем виде и только иногда природа её относительно ясна. Эта связь может быть, в частности, связью логического следования, имеющей место между посылками и заключением правильного умозаключения («Если все живые многоклеточные существа смертны, а медуза является таким существом, то она смертна»). Связь может представлять собой закон природы («Если тело подвергнуть трению, оно начнёт нагреваться») или причинную связь («Если Луна в новолуние находится в узле своей орбиты, наступает солнечное затмение»). Рассматриваемая связь может иметь также характер социальной закономерности, правила, традиции и т.п. («Если меняется общество, меняется также человек», «Если совет разумен, он должен быть выполнен»).
Со связью, выражаемой условным высказыванием, обычно соединяется убеждение, что консеквент с определённой необходимостью «вытекает» из антецедента и что имеется некоторый общий закон, сформулировав который, мы могли бы логически вывести консеквент из антецедента.
Конец бесплатного ознакомительного фрагмента
