Страница:
Грубо оценив, что вероятность попасть под автомобиль, выиграть пять тысяч в спортлото или дожить до ста двадцати лет лежит где-то далеко за пределами одной миллионной, вы будете смело ходить по улицам, откажетесь, имея лотерейный билет, от осмотра продающейся дачи и не станете откладывать написание своих мемуаров до 2070 года. Таков вывод, который можно сделать, сталкиваясь с малыми вероятностями.
Но наш совет – не делать и обратного.
Не стоит всегда принимать во внимание и те вероятности, которые больше одной миллионной. Жизнь была бы очень утомительной.
По данным метеорологической статистики, солнечное утро сменяется дождливым днём с вероятностью, лежащей в пределах 0,01—0,001. С этим считаться, вообще говоря, надо. Но риск промокнуть не более драматичен, чем насморк, да дождь можно и переждать. С другой стороны, таскать с собой дождевой зонтик в хорошую погоду – значит неминуемо подвергнуться насмешкам. Поэтому захватить зонтик стоит лишь тогда, когда по небу гуляют тёмные и подозрительные облака. Вероятно, так поступает большинство читателей. Разумеется, более серьёзно стоит отнестись к вероятности дурной погоды при отправлении в далёкую морскую прогулку на лёгком паруснике.
Таким образом, оценка вероятности события – вещь, несомненно, полезная и нужная. Следует стараться определить её как можно более обстоятельно, скажем поинтересоваться прогнозом погоды, постучать по барометру и посмотреть, падает или повышается давление. А окончательное решение принимать, соразмеряя вероятность неприятности с ценой риска. Задуматься о вероятности риска, приучить себя прикидывать величину этой вероятности полезно для людей обеих крайностей – и тех, кто неоправданно рискует, и тех, кто неоправданно осторожничает.
Привычка оценивать вероятности может оказаться полезной для обнаружения противоречий, ошибок и, мягко выражаясь, уклонений от истины.
О художественной правде
Математик спешит на свидание
Треугольник Паскаля
Но наш совет – не делать и обратного.
Не стоит всегда принимать во внимание и те вероятности, которые больше одной миллионной. Жизнь была бы очень утомительной.
По данным метеорологической статистики, солнечное утро сменяется дождливым днём с вероятностью, лежащей в пределах 0,01—0,001. С этим считаться, вообще говоря, надо. Но риск промокнуть не более драматичен, чем насморк, да дождь можно и переждать. С другой стороны, таскать с собой дождевой зонтик в хорошую погоду – значит неминуемо подвергнуться насмешкам. Поэтому захватить зонтик стоит лишь тогда, когда по небу гуляют тёмные и подозрительные облака. Вероятно, так поступает большинство читателей. Разумеется, более серьёзно стоит отнестись к вероятности дурной погоды при отправлении в далёкую морскую прогулку на лёгком паруснике.
Таким образом, оценка вероятности события – вещь, несомненно, полезная и нужная. Следует стараться определить её как можно более обстоятельно, скажем поинтересоваться прогнозом погоды, постучать по барометру и посмотреть, падает или повышается давление. А окончательное решение принимать, соразмеряя вероятность неприятности с ценой риска. Задуматься о вероятности риска, приучить себя прикидывать величину этой вероятности полезно для людей обеих крайностей – и тех, кто неоправданно рискует, и тех, кто неоправданно осторожничает.
Привычка оценивать вероятности может оказаться полезной для обнаружения противоречий, ошибок и, мягко выражаясь, уклонений от истины.
О художественной правде
Вы читаете рассказ.
А вот какую. Я думаю, что, если этот же самый отрывок перепишет хороший беллетрист, сущность дела не изменится. Ни самые что ни на есть художественные описания природы, ни попытки проникновения в психологию героев не смогли бы спасти пошлого сюжета. Почему, собственно, пошлого?
Да по той причине, что он неправдоподобен. Написанное непохоже на правду потому, что происшедшее невероятно. А невероятное есть невозможное – это ведь главный тезис нашей книги.
Каждое отдельное событие, изложенное в отрывке, само по себе имеет небольшую, но значимую вероятность. Самая маленькая из них – это выпасть из самолёта из-за несовершенства дверей. Пусть авиаинженеры фыркнут от негодования, но, наверное, один-два подобных случая за историю авиации были.
Остаться живым при свободном падении?.. Насколько мне не изменяет память, такие происшествия также фигурируют в истории воздухоплавания.
Встретиться случайно с пропавшей без вести любимой супругой? Что ж, и такое событие не исключено.
В отрывке же все эти крайне маловероятные события происходят одновременно. А вероятность сложного события, как мы знаем, равняется произведению составляющих его элементов. Значит, если вероятность каждого из событий одна миллионная (с этой вероятностью мы условились считаться), то вероятность нашего рассказа измеряется единицей, поделённой на единицу с восемнадцатью нулями. А это уж, простите, стопроцентная невозможность.
Разумный человек обычно делит события на правдоподобные и выдуманные без учёта данных теории. В критических рецензиях писатели иногда обвиняются в том, что они не считаются с художественной правдой. Мы же часто убеждаемся, что нарушения художественной правды – это просто использование крайне невероятного сюжета, невероятного в самом что ни на есть математическом смысле этого слова.
А вот рассказ Ю. Нагибина «Перекур». Что же происходит в рассказе? А примерно то же, что и в моём рассказе, только без падения героя из самолёта. Сорокапятилетний герой после двадцатилетнего перерыва понял, что по-настоящему он любил лишь один раз. Хотя любовь была всего лишь каких-то там двадцать лет назад, она вспыхнула вновь, и с пожаром в груди Климов едет в поезде на далёкий полустанок, где протекал в своё время его юношеский роман. Приехал, сошёл с поезда, зашагал через лес, а Маруся тут как тут. «Надо же было ей так точно рассчитать!» – пишет читатель Квашнин. Автор письма совершенно справедливо говорит: «Когда через двадцать лет герой выходит на полустанке и ровно в тот же час, минуту и секунду здесь же оказывается и героиня, читатель прищуривает глаза: хитро придумано – и перестаёт верить многому».
Примеров, подобных моему «сочинению» или вот этому рассказу Нагибина, нет числа. Авторов обвиняют в художественной неправде. А их стоит осуждать лишь за незнание теоремы умножения вероятностей. Они иногда оперируют несколькими маловероятными (но всё же возможными) событиями и достигают сногсшибательного эффекта (а вместе с ним и отхода от художественной правды), заставляя эти события пересекаться.
Подобные приёмы можно оправдать лишь в том случае, когда автор и не пытается убедить нас, что так было, а просто придумывает такие события, что у читателя дух захватывает. Прочитав подобную книгу, мы иногда говорим: «Бог мой, какая чушь, но до чего здорово закручено!» Блестящий пример такого произведения – «Сердца трех» Джека Лондона. Одна завязка что стоит, когда автор приводит в одно время и в одно место двух братьев и сестру, которые ничего не знают о связывающих их родственных узах.
«Но ведь и в шедеврах литературы случайности играют важную роль», – скажет читатель. Несомненно. Но это случайности, которые могут произойти; события, вероятность которых вполне значима. Скажем, у Л. Толстого раненый Болконский оказывается в хирургической палате рядом с Курагиным. Толстому нужна была эта встреча, чтобы показать душевный перелом князя Андрея. Вероятно ли это событие? Без сомнения. Офицерских палат вблизи поля боя было немного, а может быть, даже и одна. Вероятность очутиться в одной палате двум офицерам, грубо говоря, равняется вероятности быть раненными в один день. Если раненых офицеров в этот день был один процент, то вероятность попасть в один процент для каждого из них равняется 0,01, а обоих сразу – 0,0001; вполне разумное число, с которым надо считаться.
Нисколько не сомневаюсь, что Л. Толстой этих вычислений не производил. Но настоящий художник чувствует правду без расчётов.
Я далёк от мысли писать инструкцию литераторам, как добиваться художественной правды в произведениях. Мне хотелось лишь подчеркнуть, что важным элементом жизненности произведений является приемлемое значение вероятности происходящих событий.
Пока использование невероятных пересечений приводит лишь к пустяковым результатам, вроде встречи потерявших друг друга влюблённых, то бог уж с ним: читатель развлечётся, а то, что такого в жизни не бывает, он и сам знает. Лишний рассказ или роман такого рода вреда не принесёт, хотя, конечно, и вкладом в литературу не будет.
Но в ряде случаев авторы используют пересечения сюжетных линий для того, чтобы подвести читателя к мысли, что происшедшее есть явление высшего порядка. Они прекрасно понимают, что если останутся в рамках законов природы, то сюжет их «не проходит». И, вместо того чтобы сказать «не проходит» – значит, нет такого, – намекают, что, мол, «по законам, конечно, “не проходит”, а вот у меня прошло, значит, не все подчиняется этим законам, есть что-то и сверх законов».
К счастью, откровенно религиозные или мистические произведения сейчас не в моде, и романов или рассказов, в которых чудесные явления преподносились бы на полном серьёзе, в последнее время тоже нет.
Мы говорили о нарушении художественной правды из-за непонимания теоремы об умножении вероятностей, из-за отнесения события, вероятность которого практически равна нулю, к событиям возможным. Но более распространённым является другое заблуждение, а именно поиск детерминистского истолкования явлений, носящих случайный характер.
Можно с большой уверенностью утверждать, что есть категория людей, у которых не совсем правильные представления о случайности.
Человеческому разуму свойственно возвышенное объяснение случайным явлениям. Иногда можно услышать: «Попал, бедняга, под автомобиль. Значит, так ему на роду было написано». Встречаются суждения по поводу несчастного случая более глубокомысленные: «Человек был плохой. Мать родную из дому выгнал. Как жил плохо, так и кончил плохо». Во всём этом имеется в виду, что в жизни есть какая-то сила, способная мстить человеку за дурные его поступки. Религиозному человеку мораль подобного типа весьма близка. Рационалистически же мыслящему ясно, что никакого закономерного воздаяния со стороны судьбы, бога, рока и пр. не существует. Однако романам и повестям, подводящим читателей к мысли: «Что-то в этом есть!» или: «От судьбы не уйдёшь!» – нет числа. За примерами ходить не приходится, но, чтобы не быть голословным, напомним про роман Макса Фриша «Ното Фабер», в котором герой был наказан за то, что во время фашизма он бросил свою жену-еврейку.
Судьба расправилась с героем основательно, хотя и неоригинально (было такое уже в древнегреческой литературе). Что же она сделала с этим трусливым немцем? А вот что. Ей угодно было, чтобы он спустя двадцать лет познакомился с молодой красивой девушкой и влюбился в эту девушку. Далее судьба разъяснила герою, что он согрешил со своей родной дочерью, которая родилась после того, как он сбежал от своей супруги. Герой был доведён до такой степени отчаяния, что покончил жизнь самоубийством.
В конце концов можно было рассказать сей драматический случай, изложив его под флагом «чего только в жизни не бывает». Правда, и в этом случае вряд ли роман можно было удостоить названия художественно правдивого, ибо случай уж очень редкий и нетипичный. Но всё же это бы ещё куда ни шло. Но Макс Фриш не для этого написал свой роман, а захотел встать в ряды авторов, заставляющих судьбу раздавать награды и шлёпки в пропорции с делами героев. Позиция не заслуживает уважения. Ничем она не отличается от направленности сочинений откровенно религиозных авторов.
С моей точки зрения, любой писатель, который вмешивает «перст судьбы» в жизнь своих героев, никогда не может написать стоящую вещь. Разумеется, всегда проще командовать героями, если перипетии романа определяются тем, кто с кем «случайно» встретился, кто в какой момент догадался погибнуть или спастись… Легко навести героя на путь истинный, заставив его сломать ногу в то время, когда он направляется свершить прелюбодеяние или идёт на рынок загнать налево продукцию своего завода. Гораздо труднее обосновать сюжет романа психологией героев и социальным фоном, на котором развиваются события. А только на этом пути рождаются стоящие художественные произведения.
Все попытки даже самых великих писателей, таких, как Л. Толстой, создать литературное произведение, в котором случайности были бы возведены в ранг предопределенностей судьбы, кончались крахом. Анна Каренина бросается под поезд вовсе не потому, что судьба наказывает её за измену супругу. Вся ткань романа показывает, что такой конец естествен для Анны, что он возможен лишь потому, что Анна принадлежит к обществу именно с такой, а не иной моралью. Читателю ясно – будь Анна не Анной или принадлежи она не к российскому дворянству, а к другой среде, конец романа был бы иным, и отмщение не состоялось бы.
И одна из задач нашей книги, темой которой является вероятность, как раз и состоит в том, чтобы развенчать всяческую разновидность фатализма, предостеречь читателя от поисков обоснования событий там, где это обоснование невозможно, где события являются чисто случайными.
В своей очень интересной статье, посвящённой мифотворчеству Томаса Манна, Станислав Лем показывает, что непонимание законов случая лежит в основе многих мифов. Лем приводит характерный пример. Жители одной африканской страны верят в то, что львы делятся на две категории: на львов, которые просто львы, и на львов, в которых переселились души умерших людей. Обыкновенные львы кушают людей, а львы с человеческой душой не питаются своими духовными родственниками.
Таким образом случайность изгоняется, и трапезы львов получают своё истолкование. К сожалению, миф не даёт нам возможности заранее узнать, с каким львом мы имеем дело; его категория выясняется лишь после его обеда.
Понимание законов вероятности ставит все на свои места и является важнейшим оружием против мифов, против религии, против фатализма.
С одной стороны, нельзя и не надо искать объяснения случайным событиям, вероятность которых хотя и мала, но вполне разумна. Скажем, очень соблазнительно приписать всесильности материнской любви чудесное избавление от гибели её ребёнка. Ребёнок играл под балконом, мать отозвала его, а через пять секунд от карниза оторвался огромный кусок штукатурки и упал на то самое место, где играло дитя. Так и хочется сказать, что «Сердце матери – вещун», или «Материнская любовь – большая сила», или «Бог не допустил гибели невинного младенчика» и т.д. и т.п. Но происшедшее не нуждается в таких ремарках, ибо вероятность события вполне приемлема и иного объяснения не требует.
С другой – владение законами вероятности позволяет с уверенностью отнести определённый класс событий к невозможным. И если большое число случайных линий все же пересеклось, вероятность события ничтожно мала, а невозможное событие все же совершилось, то, значит, не «что-то в этом есть», а «что-то здесь не так!».
«Мотор самолёта работал с перебоями, по крайней мере так казалось Николаю Петровичу. Шёл он на совсем небольшой высоте. Пролетали засыпанную снегом деревушку, видны были люди, копошившиеся около застрявшего в сугробе грузовика. Вдалеке был виден город, до которого лету оставалось каких-нибудь минут десять-пятнадцать.Не буду дальше демонстрировать свои беллетристические таланты. (Демонстрация того, что писать плохие рассказы может каждый, не являлась моей целью.) Какую же мысль собираюсь я провести на примере только что изложенной, «захватывающей» истории?
В самолёте было чертовски холодно, ноги застыли. Николай Петрович вылез из своего кресла и стал двигаться в крошечном пространстве тамбура, отбивая ногами незамысловатую чечётку. Машина попала в воздушную яму, её тряхнуло раз, другой. Николай Петрович потерял равновесие, его бросило на дверь самолёта. Он приготовился встретить основательный удар, но удар оказался неожиданно мягким, и Николай Петрович почувствовал, что проваливается в пустоту и, прежде чем успел сообразить, что случилось, полетел вниз навстречу белой земле.
Ужас сжал сердце, мелькнуло: «Вот и все, дурацкая гибель». Но инстинкт самосохранения вступил в свои права. Наполовину подсознательно тело стремилось принять позу, наиболее безопасную при падении. «Ногами вперёд», – только успел он подумать и потерял сознание.
…У Веры Аркадьевны сегодня был свободный день. Сначала она собиралась заняться мелкими домашними делами. Начала с уборки комнаты. Случайно взгляд упал на лыжи, которые простояли без дела всю войну, да ещё три зимы, которые так незаметно пробежали после Дня Победы. Форточка была открыта, из окна пахнуло свежим холодным воздухом. «Нет, не годится так, – сказала себе Вера Аркадьевна, – я сознательно лишаю себя всех жизненных радостей. Это глупо и никому не нужно. Осталась жива, моя дорогая, и давай живи».
Через пятнадцать минут в синем лыжном костюме, с лыжами в руках Вера Аркадьевна уже выходила из дому. Ещё десять минут – последний большой дом был пройден, город кончился, можно было встать на лыжи и отправиться куда глаза глядят. Перед Верой Аркадьевной простиралась гладкая белая скатерть снега, лыжни были засыпаны, и дорогу можно было выбирать любую. Ровная гладь показалась ей скучной, и она направилась в ту сторону, где виднелись несколько занесённых снегом стогов сена.
Низко летел самолёт. Вера Аркадьевна взглянула вверх. От самолёта отделилась фигура. «Какой опасный прыжок! – подумала она. – Но почему же не открывается парашют? Земля уж совсем близко. Ну хватит шутки шутить… Аааах!»
Падение свершилось совсем близко, в каких-нибудь 200—300 метрах от Веры Аркадьевны. Человек упал в снег и не был виден. Несколько взмахов палками, несколько резких скольжений, и Вера Аркадьевна была у стога. Лихорадочно работая руками, лыжей, палкой, она добралась через немногие минуты до человека, одетого в обычный костюм. Лишь смутно мелькнуло: «Значит, несчастный случай, никакой он не парашютист. Может быть, живой ещё». Она приложила ухо к сердцу и услышала, да, ошибки быть не могло: сердце едва-едва, но билось. Что же теперь делать? Одна она не дотащит этого крупного мужчину до города. Но судьба решительно пошла на помощь Николаю Петровичу (читателю уже ясно, что это был он). Она не остановилась на полдороге. Вдалеке виднелась группа лыжников. Напрягая голос, Вера Аркадьевна позвала на помощь…
В больнице она нервно ходила по коридору, ожидая, что скажут доктора.
«Почему я так нервничаю? Можно подумать, что речь идёт о близком мне человеке. Это, наверное, меня волнует его чудесное спасение.
Дверь палаты открылась, и вышел улыбающийся доктор. «Можете зайти, – сказал он. – Больной хочет видеть, кто его спас».
Вера Аркадьевна зашла в комнату. Спасённый смотрел на неё пристально. Сначала во взоре было одно лишь любопытство, оно сменилось недоверием, изумлением, восторгом.
– Бог мой! – прошептал Николай Петрович. – Вера, это сон!
Добежав остающиеся несколько шагов до его кровати, Вера Аркадьевна упала на колени и, смотря в такие близкие единственные любимые глаза, ответила:
– Милый мой, это не сон. Это ты, это я… Я знала, я чувствовала.
Нам остаётся рассказать читателю, присутствующему при счастливой развязке этой драмы войны, почему целых три года муж и жена не могли разыскать друг друга…»
А вот какую. Я думаю, что, если этот же самый отрывок перепишет хороший беллетрист, сущность дела не изменится. Ни самые что ни на есть художественные описания природы, ни попытки проникновения в психологию героев не смогли бы спасти пошлого сюжета. Почему, собственно, пошлого?
Да по той причине, что он неправдоподобен. Написанное непохоже на правду потому, что происшедшее невероятно. А невероятное есть невозможное – это ведь главный тезис нашей книги.
Каждое отдельное событие, изложенное в отрывке, само по себе имеет небольшую, но значимую вероятность. Самая маленькая из них – это выпасть из самолёта из-за несовершенства дверей. Пусть авиаинженеры фыркнут от негодования, но, наверное, один-два подобных случая за историю авиации были.
Остаться живым при свободном падении?.. Насколько мне не изменяет память, такие происшествия также фигурируют в истории воздухоплавания.
Встретиться случайно с пропавшей без вести любимой супругой? Что ж, и такое событие не исключено.
Разумный человек обычно делит события на правдоподобные и выдуманные без учёта данных теории. В критических рецензиях писатели иногда обвиняются в том, что они не считаются с художественной правдой. Мы же часто убеждаемся, что нарушения художественной правды – это просто использование крайне невероятного сюжета, невероятного в самом что ни на есть математическом смысле этого слова.
А вот рассказ Ю. Нагибина «Перекур». Что же происходит в рассказе? А примерно то же, что и в моём рассказе, только без падения героя из самолёта. Сорокапятилетний герой после двадцатилетнего перерыва понял, что по-настоящему он любил лишь один раз. Хотя любовь была всего лишь каких-то там двадцать лет назад, она вспыхнула вновь, и с пожаром в груди Климов едет в поезде на далёкий полустанок, где протекал в своё время его юношеский роман. Приехал, сошёл с поезда, зашагал через лес, а Маруся тут как тут. «Надо же было ей так точно рассчитать!» – пишет читатель Квашнин. Автор письма совершенно справедливо говорит: «Когда через двадцать лет герой выходит на полустанке и ровно в тот же час, минуту и секунду здесь же оказывается и героиня, читатель прищуривает глаза: хитро придумано – и перестаёт верить многому».
Примеров, подобных моему «сочинению» или вот этому рассказу Нагибина, нет числа. Авторов обвиняют в художественной неправде. А их стоит осуждать лишь за незнание теоремы умножения вероятностей. Они иногда оперируют несколькими маловероятными (но всё же возможными) событиями и достигают сногсшибательного эффекта (а вместе с ним и отхода от художественной правды), заставляя эти события пересекаться.
Подобные приёмы можно оправдать лишь в том случае, когда автор и не пытается убедить нас, что так было, а просто придумывает такие события, что у читателя дух захватывает. Прочитав подобную книгу, мы иногда говорим: «Бог мой, какая чушь, но до чего здорово закручено!» Блестящий пример такого произведения – «Сердца трех» Джека Лондона. Одна завязка что стоит, когда автор приводит в одно время и в одно место двух братьев и сестру, которые ничего не знают о связывающих их родственных узах.
«Но ведь и в шедеврах литературы случайности играют важную роль», – скажет читатель. Несомненно. Но это случайности, которые могут произойти; события, вероятность которых вполне значима. Скажем, у Л. Толстого раненый Болконский оказывается в хирургической палате рядом с Курагиным. Толстому нужна была эта встреча, чтобы показать душевный перелом князя Андрея. Вероятно ли это событие? Без сомнения. Офицерских палат вблизи поля боя было немного, а может быть, даже и одна. Вероятность очутиться в одной палате двум офицерам, грубо говоря, равняется вероятности быть раненными в один день. Если раненых офицеров в этот день был один процент, то вероятность попасть в один процент для каждого из них равняется 0,01, а обоих сразу – 0,0001; вполне разумное число, с которым надо считаться.
Нисколько не сомневаюсь, что Л. Толстой этих вычислений не производил. Но настоящий художник чувствует правду без расчётов.
Я далёк от мысли писать инструкцию литераторам, как добиваться художественной правды в произведениях. Мне хотелось лишь подчеркнуть, что важным элементом жизненности произведений является приемлемое значение вероятности происходящих событий.
Пока использование невероятных пересечений приводит лишь к пустяковым результатам, вроде встречи потерявших друг друга влюблённых, то бог уж с ним: читатель развлечётся, а то, что такого в жизни не бывает, он и сам знает. Лишний рассказ или роман такого рода вреда не принесёт, хотя, конечно, и вкладом в литературу не будет.
Но в ряде случаев авторы используют пересечения сюжетных линий для того, чтобы подвести читателя к мысли, что происшедшее есть явление высшего порядка. Они прекрасно понимают, что если останутся в рамках законов природы, то сюжет их «не проходит». И, вместо того чтобы сказать «не проходит» – значит, нет такого, – намекают, что, мол, «по законам, конечно, “не проходит”, а вот у меня прошло, значит, не все подчиняется этим законам, есть что-то и сверх законов».
К счастью, откровенно религиозные или мистические произведения сейчас не в моде, и романов или рассказов, в которых чудесные явления преподносились бы на полном серьёзе, в последнее время тоже нет.
Мы говорили о нарушении художественной правды из-за непонимания теоремы об умножении вероятностей, из-за отнесения события, вероятность которого практически равна нулю, к событиям возможным. Но более распространённым является другое заблуждение, а именно поиск детерминистского истолкования явлений, носящих случайный характер.
Можно с большой уверенностью утверждать, что есть категория людей, у которых не совсем правильные представления о случайности.
Человеческому разуму свойственно возвышенное объяснение случайным явлениям. Иногда можно услышать: «Попал, бедняга, под автомобиль. Значит, так ему на роду было написано». Встречаются суждения по поводу несчастного случая более глубокомысленные: «Человек был плохой. Мать родную из дому выгнал. Как жил плохо, так и кончил плохо». Во всём этом имеется в виду, что в жизни есть какая-то сила, способная мстить человеку за дурные его поступки. Религиозному человеку мораль подобного типа весьма близка. Рационалистически же мыслящему ясно, что никакого закономерного воздаяния со стороны судьбы, бога, рока и пр. не существует. Однако романам и повестям, подводящим читателей к мысли: «Что-то в этом есть!» или: «От судьбы не уйдёшь!» – нет числа. За примерами ходить не приходится, но, чтобы не быть голословным, напомним про роман Макса Фриша «Ното Фабер», в котором герой был наказан за то, что во время фашизма он бросил свою жену-еврейку.
Судьба расправилась с героем основательно, хотя и неоригинально (было такое уже в древнегреческой литературе). Что же она сделала с этим трусливым немцем? А вот что. Ей угодно было, чтобы он спустя двадцать лет познакомился с молодой красивой девушкой и влюбился в эту девушку. Далее судьба разъяснила герою, что он согрешил со своей родной дочерью, которая родилась после того, как он сбежал от своей супруги. Герой был доведён до такой степени отчаяния, что покончил жизнь самоубийством.
В конце концов можно было рассказать сей драматический случай, изложив его под флагом «чего только в жизни не бывает». Правда, и в этом случае вряд ли роман можно было удостоить названия художественно правдивого, ибо случай уж очень редкий и нетипичный. Но всё же это бы ещё куда ни шло. Но Макс Фриш не для этого написал свой роман, а захотел встать в ряды авторов, заставляющих судьбу раздавать награды и шлёпки в пропорции с делами героев. Позиция не заслуживает уважения. Ничем она не отличается от направленности сочинений откровенно религиозных авторов.
С моей точки зрения, любой писатель, который вмешивает «перст судьбы» в жизнь своих героев, никогда не может написать стоящую вещь. Разумеется, всегда проще командовать героями, если перипетии романа определяются тем, кто с кем «случайно» встретился, кто в какой момент догадался погибнуть или спастись… Легко навести героя на путь истинный, заставив его сломать ногу в то время, когда он направляется свершить прелюбодеяние или идёт на рынок загнать налево продукцию своего завода. Гораздо труднее обосновать сюжет романа психологией героев и социальным фоном, на котором развиваются события. А только на этом пути рождаются стоящие художественные произведения.
Все попытки даже самых великих писателей, таких, как Л. Толстой, создать литературное произведение, в котором случайности были бы возведены в ранг предопределенностей судьбы, кончались крахом. Анна Каренина бросается под поезд вовсе не потому, что судьба наказывает её за измену супругу. Вся ткань романа показывает, что такой конец естествен для Анны, что он возможен лишь потому, что Анна принадлежит к обществу именно с такой, а не иной моралью. Читателю ясно – будь Анна не Анной или принадлежи она не к российскому дворянству, а к другой среде, конец романа был бы иным, и отмщение не состоялось бы.
И одна из задач нашей книги, темой которой является вероятность, как раз и состоит в том, чтобы развенчать всяческую разновидность фатализма, предостеречь читателя от поисков обоснования событий там, где это обоснование невозможно, где события являются чисто случайными.
В своей очень интересной статье, посвящённой мифотворчеству Томаса Манна, Станислав Лем показывает, что непонимание законов случая лежит в основе многих мифов. Лем приводит характерный пример. Жители одной африканской страны верят в то, что львы делятся на две категории: на львов, которые просто львы, и на львов, в которых переселились души умерших людей. Обыкновенные львы кушают людей, а львы с человеческой душой не питаются своими духовными родственниками.
Таким образом случайность изгоняется, и трапезы львов получают своё истолкование. К сожалению, миф не даёт нам возможности заранее узнать, с каким львом мы имеем дело; его категория выясняется лишь после его обеда.
Понимание законов вероятности ставит все на свои места и является важнейшим оружием против мифов, против религии, против фатализма.
С одной стороны, нельзя и не надо искать объяснения случайным событиям, вероятность которых хотя и мала, но вполне разумна. Скажем, очень соблазнительно приписать всесильности материнской любви чудесное избавление от гибели её ребёнка. Ребёнок играл под балконом, мать отозвала его, а через пять секунд от карниза оторвался огромный кусок штукатурки и упал на то самое место, где играло дитя. Так и хочется сказать, что «Сердце матери – вещун», или «Материнская любовь – большая сила», или «Бог не допустил гибели невинного младенчика» и т.д. и т.п. Но происшедшее не нуждается в таких ремарках, ибо вероятность события вполне приемлема и иного объяснения не требует.
С другой – владение законами вероятности позволяет с уверенностью отнести определённый класс событий к невозможным. И если большое число случайных линий все же пересеклось, вероятность события ничтожно мала, а невозможное событие все же совершилось, то, значит, не «что-то в этом есть», а «что-то здесь не так!».
Математик спешит на свидание
– Ты не забыл, что завтра мы идём в консерваторию?
– Ну конечно, нет.
– Заедешь за мной?
– Дел невпроворот. Давай мне билет, я приду один.
– Вот так всегда. Опять подруги надо мной посмеются. Завела, скажут, кавалера, который с тобою и показаться не желает.
– Ну ладно, давай встретимся. Где?
– У входа в продуктовый, что поближе к Никитским воротам.
– Так это на другой стороне улицы.
– Конечно. Мне не хочется, чтобы видели, как я тебя жду.
– Неизвестно, кто кого будет ждать… Но знаешь, завтра мне и правда время рассчитать трудно. От 18.00 до 19.00 я буду на месте как штык, а точнее – не скажу.
– Выходит, я час тебя буду ждать?
– Я и говорю: встретимся на месте.
– Не хочу.
– Тогда предлагаю компромиссное решение. Оба приходим между 17.40 и 18.40. И ждём не более двадцати минут.
– А если ты придёшь в 18.00, а я в 18.30?
– Значит, я буду уже в зале.
– Да так мы никогда не встретимся на улице.
– Вероятность встречи довольно значительная. Хочешь, подсчитаю?
– Да не берись за карандаш, горе ты моё. И надо было влюбиться в математика…
Я, конечно, был бы рад продолжить рассказ о радостях и горестях влюблённых математика и девушки, далёкой от чисел и интегралов. Тут бездна интересных психологических моментов. Но увы! Тема книги вынуждает вернуться к «сухой» науке.
Как же действительно подсчитать вероятность встречи математика с его любимой? Мы уже выяснили, что вероятность – это отношение числа благоприятных случаев к общему числу событий. А здесь как быть? Ведь встреча может состояться или не состояться в любой момент часового интервала.
Благоприятным исходом рассматриваемой задачи является мгновение встречи. Но мгновений бесконечно много. Ведь часовой интервал я могу разбить на минуты, на секунды и даже на микросекунды. Значит, здесь бесконечное число исходов, а не два, как в опыте с монетой, и не шесть, как в опыте с кубиком (игральной костью). Как же определяются вероятности в задачах такого рода? Оказывается, геометрическим путём. А поскольку геометрия требует наглядности, нам придётся прибегнуть к нехитрому рисунку.
Отложим по горизонтали время прибытия девушки на свидание. На вертикальной прямой отметим минуты появления нашего героя. Если бы не было условия – ждать не более двадцати минут, то встреча могла бы произойти в любой точке квадрата, обнимающего часовые ожидания. При наличии же дополнительного условия моменты встречи попадут в заштрихованную область. Пожалуйста, проверяйте.
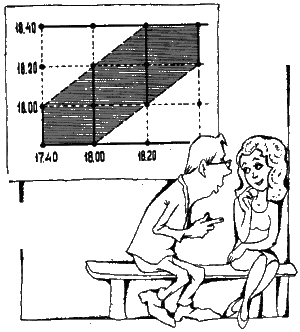Девушка пришла без двадцати шесть. Встреча состоится, если кавалер явится до шести. Этому соответствует первый отрезок.
Девушка пришла в 18.00. Встреча состоится, если кавалер явится от 17.40 до 18.20. Такой встречи соответствует второй отрезок, построенный на рисунке.
Если девушка пришла в 18.20, то встреча состоится при условии, если математик явится к продуктовому магазину между 18.00 часами и крайним сроком – 18.40. Вот вам третий отрезок.
Теперь ещё одна точка, и заштрихованная область будет готова: девушка успела прибежать на свидание в 18.40. Она застанет своего возлюбленного, если он явился не раньше 18.20.
Что же дальше? Где же искомая вероятность? Нетрудно догадаться, что она будет равняться частному от деления площади заштрихованной области на площадь всего квадрата.
По сути дела, определение вероятности остаётся тем же – благоприятные варианты относятся ко всем возможным. Но если ранее мерой было число случаев, то теперь мерой является площадь на графике.
Два незаштрихованных треугольника образуют квадрат со стороной, соответствующей 40 минутам. Его площадь 40. Таким образом, искомую вероятность получим, поделив (3600-1600) на 3600. Итого 5/9.
Будем надеяться, что математик встретится со своей девушкой.
Применение теории вероятностей к событиям с непрерывным рядом исходов намного расширяет её возможности.
Одной из исторически первых задач такого рода была проблема, поставленная и решённая французским естествоиспытателем XVIII века Бюффоном.
На большом листе бумаги начерчен ряд параллельных линий. Наобум бросается игла, длина которой много меньше расстояния между линиями на бумаге. Игла может пересечь одну из линий, а может очутиться и между линиями. Надо оценить вероятность того, что пересечение произойдёт.
Предполагается, что центр иглы с равной вероятностью может попасть в любое место бумажного листа. Так же точно считается, что угол наклона иглы к начерченным линиям может принять какое угодно значение. Если игла попадёт на середину между линиями, то она не пересечёт линии, как бы она ни оказалась повёрнутой. Если же центр иглы очутился вблизи линии, то пересечение не произойдёт, если игла установится параллельно линии или около того, и напротив, игла пересечёт линию, если образует угол, близкий к прямому. Получается так: чем ближе к линии попадёт центр иглы, тем больше вероятность её пересечения.
Задача может быть решена без всякой математики. Попробуйте свои силы.
– Ну конечно, нет.
– Заедешь за мной?
– Дел невпроворот. Давай мне билет, я приду один.
– Вот так всегда. Опять подруги надо мной посмеются. Завела, скажут, кавалера, который с тобою и показаться не желает.
– Ну ладно, давай встретимся. Где?
– У входа в продуктовый, что поближе к Никитским воротам.
– Так это на другой стороне улицы.
– Конечно. Мне не хочется, чтобы видели, как я тебя жду.
– Неизвестно, кто кого будет ждать… Но знаешь, завтра мне и правда время рассчитать трудно. От 18.00 до 19.00 я буду на месте как штык, а точнее – не скажу.
– Выходит, я час тебя буду ждать?
– Я и говорю: встретимся на месте.
– Не хочу.
– Тогда предлагаю компромиссное решение. Оба приходим между 17.40 и 18.40. И ждём не более двадцати минут.
– А если ты придёшь в 18.00, а я в 18.30?
– Значит, я буду уже в зале.
– Да так мы никогда не встретимся на улице.
– Вероятность встречи довольно значительная. Хочешь, подсчитаю?
– Да не берись за карандаш, горе ты моё. И надо было влюбиться в математика…
Я, конечно, был бы рад продолжить рассказ о радостях и горестях влюблённых математика и девушки, далёкой от чисел и интегралов. Тут бездна интересных психологических моментов. Но увы! Тема книги вынуждает вернуться к «сухой» науке.
Как же действительно подсчитать вероятность встречи математика с его любимой? Мы уже выяснили, что вероятность – это отношение числа благоприятных случаев к общему числу событий. А здесь как быть? Ведь встреча может состояться или не состояться в любой момент часового интервала.
Благоприятным исходом рассматриваемой задачи является мгновение встречи. Но мгновений бесконечно много. Ведь часовой интервал я могу разбить на минуты, на секунды и даже на микросекунды. Значит, здесь бесконечное число исходов, а не два, как в опыте с монетой, и не шесть, как в опыте с кубиком (игральной костью). Как же определяются вероятности в задачах такого рода? Оказывается, геометрическим путём. А поскольку геометрия требует наглядности, нам придётся прибегнуть к нехитрому рисунку.
Отложим по горизонтали время прибытия девушки на свидание. На вертикальной прямой отметим минуты появления нашего героя. Если бы не было условия – ждать не более двадцати минут, то встреча могла бы произойти в любой точке квадрата, обнимающего часовые ожидания. При наличии же дополнительного условия моменты встречи попадут в заштрихованную область. Пожалуйста, проверяйте.
Девушка пришла в 18.00. Встреча состоится, если кавалер явится от 17.40 до 18.20. Такой встречи соответствует второй отрезок, построенный на рисунке.
Если девушка пришла в 18.20, то встреча состоится при условии, если математик явится к продуктовому магазину между 18.00 часами и крайним сроком – 18.40. Вот вам третий отрезок.
Теперь ещё одна точка, и заштрихованная область будет готова: девушка успела прибежать на свидание в 18.40. Она застанет своего возлюбленного, если он явился не раньше 18.20.
Что же дальше? Где же искомая вероятность? Нетрудно догадаться, что она будет равняться частному от деления площади заштрихованной области на площадь всего квадрата.
По сути дела, определение вероятности остаётся тем же – благоприятные варианты относятся ко всем возможным. Но если ранее мерой было число случаев, то теперь мерой является площадь на графике.
Два незаштрихованных треугольника образуют квадрат со стороной, соответствующей 40 минутам. Его площадь 40. Таким образом, искомую вероятность получим, поделив (3600-1600) на 3600. Итого 5/9.
Будем надеяться, что математик встретится со своей девушкой.
Применение теории вероятностей к событиям с непрерывным рядом исходов намного расширяет её возможности.
Одной из исторически первых задач такого рода была проблема, поставленная и решённая французским естествоиспытателем XVIII века Бюффоном.
На большом листе бумаги начерчен ряд параллельных линий. Наобум бросается игла, длина которой много меньше расстояния между линиями на бумаге. Игла может пересечь одну из линий, а может очутиться и между линиями. Надо оценить вероятность того, что пересечение произойдёт.
Предполагается, что центр иглы с равной вероятностью может попасть в любое место бумажного листа. Так же точно считается, что угол наклона иглы к начерченным линиям может принять какое угодно значение. Если игла попадёт на середину между линиями, то она не пересечёт линии, как бы она ни оказалась повёрнутой. Если же центр иглы очутился вблизи линии, то пересечение не произойдёт, если игла установится параллельно линии или около того, и напротив, игла пересечёт линию, если образует угол, близкий к прямому. Получается так: чем ближе к линии попадёт центр иглы, тем больше вероятность её пересечения.
Задача может быть решена без всякой математики. Попробуйте свои силы.
Треугольник Паскаля
Однажды я медленно шёл по Парижу, разглядывал витрины магазинов и читал вывески. Цветастая надпись над входом грязновато-серого здания настойчиво приглашала зайти и попытать счастья. Я удивился, что игорный дом работает среди бела дня, – это не соответствовало сведениям, почерпнутым мною из классической литературы – и… я зашёл. Взору представилась поразительная картина: десятки людей стояли лицом к стене, и перед каждым находился цветной ящик. Подойдя ближе, я увидел, что они либо нажимали кнопку, либо дёргали за ручку, будто заводя заглохший лодочный мотор.
Через несколько минут я понял, в чём дело: люди играли с автоматами. Зрелище это неприятное, но великолепное поле для наблюдений психолога. Человек играет с судьбой. Один на один. Все побочные обстоятельства отсеяны. Нет ни соперничеств, ни личной неприязни, ни необходимости скрывать свои чувства.
Есть автоматы, у которых вы можете выиграть только конфетку или сигареты, есть такие, которые играют на деньги, и, наконец, существует возможность наслаждаться игрой безгранично, вступив в единоборство с автоматом, выигрыш у которого даёт лишь право дальнейшей игры. Бессмысленно, не правда ли? Но вот так оно есть. Эти автоматы вы можете найти в любом баре, в любом кафе любого города Америки и Западной Европы.
В чём же состоит игра? В принципе она сводится к следующему. Выпускается на волю шарик, который под действием силы тяжести или щелчка пружины движется по доске, на которой установлены препятствия. От каждой преграды шарик может отскочить куда попало. Получив несколько десятков таких случайных щелчков, шарик добирается до дна ящика и успокаивается в каком-то положении.
В зависимости от формы преград и от того, как они установлены, разные места дна ящика будут достижимы в различной степени. Определив из многочисленных опытов значения вероятностей окончания путешествия шарика в том или ином конечном пункте, нетрудно построить правила игры, которые позволят автомату уверенно обыгрывать своего живого партнёра.
Через несколько минут я понял, в чём дело: люди играли с автоматами. Зрелище это неприятное, но великолепное поле для наблюдений психолога. Человек играет с судьбой. Один на один. Все побочные обстоятельства отсеяны. Нет ни соперничеств, ни личной неприязни, ни необходимости скрывать свои чувства.
Есть автоматы, у которых вы можете выиграть только конфетку или сигареты, есть такие, которые играют на деньги, и, наконец, существует возможность наслаждаться игрой безгранично, вступив в единоборство с автоматом, выигрыш у которого даёт лишь право дальнейшей игры. Бессмысленно, не правда ли? Но вот так оно есть. Эти автоматы вы можете найти в любом баре, в любом кафе любого города Америки и Западной Европы.
В чём же состоит игра? В принципе она сводится к следующему. Выпускается на волю шарик, который под действием силы тяжести или щелчка пружины движется по доске, на которой установлены препятствия. От каждой преграды шарик может отскочить куда попало. Получив несколько десятков таких случайных щелчков, шарик добирается до дна ящика и успокаивается в каком-то положении.
В зависимости от формы преград и от того, как они установлены, разные места дна ящика будут достижимы в различной степени. Определив из многочисленных опытов значения вероятностей окончания путешествия шарика в том или ином конечном пункте, нетрудно построить правила игры, которые позволят автомату уверенно обыгрывать своего живого партнёра.