(М)берут иные меры центральной тенденции – моду или медиану.
Дисперсия (D)характеризует отклонения от средней величины в данной выборке. Вычисление дисперсии позляет избежать нулевой суммы конкретных разниц (d= Х – М)не через их абсолютные величины, а через их возведение в квадрат:
 где
d= |Х – М|,
М– среднее выборки,
X– конкретное значение,
N– число значений.
где
d= |Х – М|,
М– среднее выборки,
X– конкретное значение,
N– число значений.
Стандартное отклонение(б). Из-за возведения в квадрат отдельных отклонений dпри вычислении дисперсии полученная величина оказывается далекой от первоначальных отклонений и потому не дает о них наглядного представления. Чтобы этого избежать и получить характеристику, сопоставимую со средним отклонением, проделывают обратную математическую операцию – из дисперсии извлекают квадратный корень. Его положительное значение и принимается за меру изменчивости, именуемую среднеквадратическим, или стандартным, отклонением:

где d= |Х– М|, М– среднее выборки, X– конкретное значение, N– число значений.
МД, Dи ? применимы для интервальных и пропорционных данных. Для порядковых данных в качестве меры изменчивости обычно берут полуквартильное отклонение (Q),именуемое еще полуквартильным коэффициентом. Вычисляется этот показатель следующим образом. Вся область распределения данных делится на четыре равные части. Если отсчитывать наблюдения начиная от минимальной величины на измерительной шкале, то первая четверть шкалы называется первым квартилем, а точка, отделяющая его от остальной части шкалы, обозначается символом QvВторые 25 % распределения – второй квартиль, а соответствующая точка на шкале – Q2. Между третьей и четвертой четвертями распределения расположена точка Q3.Полуквартильный коэффициент определяется как половина интервала между первым и третьим квартилями:
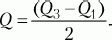 При симметричном распределении точка
Q2совпадет с медианой (а следовательно, и со средним), и тогда можно вычислить коэффициент
Qдля характеристики разброса данных относительно середины распределения. При несимметричном распределении этого недостаточно. Тогда дополнительно вычисляют коэффициенты для левого и правого участков:
При симметричном распределении точка
Q2совпадет с медианой (а следовательно, и со средним), и тогда можно вычислить коэффициент
Qдля характеристики разброса данных относительно середины распределения. При несимметричном распределении этого недостаточно. Тогда дополнительно вычисляют коэффициенты для левого и правого участков:
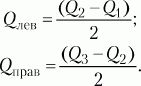
7.3. Вторичная статистическая обработка данных
Тема 8. Интерпретация и представление результатов психологических исследований
8.1. Интерпретация и обобщение результатов исследования
8.2. Формы представления результатов исследования
Дисперсия (D)характеризует отклонения от средней величины в данной выборке. Вычисление дисперсии позляет избежать нулевой суммы конкретных разниц (d= Х – М)не через их абсолютные величины, а через их возведение в квадрат:

Стандартное отклонение(б). Из-за возведения в квадрат отдельных отклонений dпри вычислении дисперсии полученная величина оказывается далекой от первоначальных отклонений и потому не дает о них наглядного представления. Чтобы этого избежать и получить характеристику, сопоставимую со средним отклонением, проделывают обратную математическую операцию – из дисперсии извлекают квадратный корень. Его положительное значение и принимается за меру изменчивости, именуемую среднеквадратическим, или стандартным, отклонением:

где d= |Х– М|, М– среднее выборки, X– конкретное значение, N– число значений.
МД, Dи ? применимы для интервальных и пропорционных данных. Для порядковых данных в качестве меры изменчивости обычно берут полуквартильное отклонение (Q),именуемое еще полуквартильным коэффициентом. Вычисляется этот показатель следующим образом. Вся область распределения данных делится на четыре равные части. Если отсчитывать наблюдения начиная от минимальной величины на измерительной шкале, то первая четверть шкалы называется первым квартилем, а точка, отделяющая его от остальной части шкалы, обозначается символом QvВторые 25 % распределения – второй квартиль, а соответствующая точка на шкале – Q2. Между третьей и четвертой четвертями распределения расположена точка Q3.Полуквартильный коэффициент определяется как половина интервала между первым и третьим квартилями:
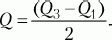
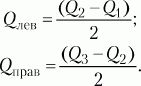
7.3. Вторичная статистическая обработка данных
К вторичным относят такие методы статистической обработки, с помощью которых на базе первичных данных выявляют скрытые в них статистические закономерности. Вторичные методы можно подразделить на способы оценки значимости различий и способы установления статистических взаимосвязей.
Способы оценки значимости различий.Для сравнения выборочных средних величин, принадлежащих к двум совокупностям данных, и для решения вопроса о том, отличаются ли средние значения статистически достоверно друг от друга, используют t-критерий Стьюдента. Его формула выглядит следующим образом:
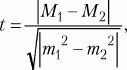 где
М1, М2– выборочные средние значения сравниваемых выборок,
m1, m2– интегрированные показатели отклонений частных значений из двух сравниваемых выборок, вычисляются по следующим формулам:
где
М1, М2– выборочные средние значения сравниваемых выборок,
m1, m2– интегрированные показатели отклонений частных значений из двух сравниваемых выборок, вычисляются по следующим формулам:
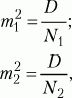 где
D1, D2– дисперсии первой и второй выборок,
N1, N2– число значений в первой и второй выборках.
где
D1, D2– дисперсии первой и второй выборок,
N1, N2– число значений в первой и второй выборках.
После вычисления значения показателя tпо таблице критических значений (см. Статистическое приложение 1), заданного числа степеней свободы ( N1 + N2 – 2) и избранной вероятности допустимой ошибки (0,05, 0,01, 0,02, 001 и т.д.) находят табличное значение t.Если вычисленное значение tбольше или равно табличному, делают вывод о том, что сравниваемые средние значения двух выборок статистически достоверно различаются с вероятностью допустимой ошибки, меньшей или равной избранной.
Если в процессе исследования встает задача сравнить неабсолютные средние величины, частотные распределения данных, то используется ?2 критерий(см. Приложение 2). Его формула выглядит следующим образом:
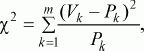 где
Pk– частоты распределения в первом замере,
Vk– частоты распределения во втором замере,
m– общее число групп, на которые разделились результаты замеров.
где
Pk– частоты распределения в первом замере,
Vk– частоты распределения во втором замере,
m– общее число групп, на которые разделились результаты замеров.
После вычисления значения показателя ?2по таблице критических значений (см. Статистическое приложение 2), заданного числа степеней свободы ( m– 1) и избранной вероятности допустимой ошибки (0,05, 0,0 ?2 tбольше или равно табличному) делают вывод о том, что сравниваемые распределения данных в двух выборках статистически достоверно различаются с вероятностью допустимой ошибки, меньшей или равной избранной.
Для сравнения дисперсий двух выборок используется F-критерийФишера. Его формула выглядит следующим образом:
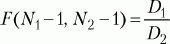
где D1, D2 – дисперсии первой и второй выборок, N1, N2 – число значений в первой и второй выборках.
После вычисления значения показателя Fпо таблице критических значений (см. Статистическое приложение 3), заданного числа степеней свободы ( N1 – 1, N2– 1) находится Fкр. Если вычисленное значение Fбольше или равно табличному, делают вывод о том, что различие дисперсий в двух выборках статистически достоверно.
Способы установления статистических взаимосвязей.Предыдущие показатели характеризуют совокупность данных по какому-либо одному признаку. Этот изменяющийся признак называют переменной величиной или просто переменной. Меры связивыявляют соотношения между двумя переменными или между двумя выборками. Эти связи, или корреляции, определяют через вычисление коэффициентов корреляции. Однако наличие корреляции не означает, что между переменными существует причинная (или функциональная) связь. Функциональная зависимость – это частный случай корреляции. Даже если связь причинна, корреляционные показатели не могут указать, какая из двух переменных является причиной, а какая – следствием. Кроме того, любая обнаруженная в психологических исследованиях связь, как правило, существует благодаря и другим переменным, а не только двум рассматриваемым. К тому же взаимосвязи психологических признаков столь сложны, что их обусловленность одной причиной вряд ли состоятельна, они детерминированы множеством причин.
По тесноте связи можно выделить следующие виды корреляции: полная, высокая, выраженная, частичная; отсутствие корреляции. Эти виды корреляций определяют в зависимости от значения коэффициента корреляции.
При полнойкорреляции его абсолютные значения равны или очень близки к 1. В этом случае устанавливается обязательная взаимозависимость между переменными. Здесь вероятна функциональная зависимость.
Высокаякорреляция устанавливается при абсолютном значении коэффициента 0,8–0,9. Выраженнаякорреляция считается при абсолютном значении коэффициента 0,6–0,7. Частичнаякорреляция существует при абсолютном значении коэффициента 0,4–0,5.
Абсолютные значения коэффициента корреляции менее 0,4 свидетельствуют об очень слабой корреляционной связи и, как правило, в расчет не принимаются. Отсутствие корреляцииконстатируется при значении коэффициента 0.
Кроме того, в психологии при оценке тесноты связи используют так называемую «частную» классификацию корреляционных связей. Она ориентирована не на абсолютную величину коэффициентов корреляции, а на уровень значимости этой величины при определенном объеме выборки. Эта классификация применяется при статистической оценке гипотез. При данном подходе предполагается, что чем больше выборка, тем меньшее значение коэффициента корреляции может быть принято для признания достоверности связей, а для малых выборок даже абсолютно большое значение коэффициента может оказаться недостоверным. [86]
По направленностивыделяют следующие виды корреляционных связей: положительная (прямая) и отрицательная (обратная). Положительная(прямая) корреляционная связь регистрируется при коэффициенте со знаком «плюс»: при увеличении значения одной переменной наблюдается увеличение другой. Отрицательная(обратная) корреляция имеет место при значении коэффициента со знаком «минус». Это означает обратную зависимость: увеличение значения одной переменной влечет за собой уменьшение другой.
По формеразличают следующие виды корреляционных связей: прямолинейную и криволинейную. При прямолинейнойсвязи равномерным изменениям одной переменной соответствуют равномерные изменения другой. Если говорить не только о корреляциях, но и о функциональных зависимостях, то такие формы зависимости называют пропорциональными. В психологии строго прямолинейные связи – явление редкое. При криволинейнойсвязи равномерное изменение одного признака сочетается с неравномерным изменением другого. Эта ситуация для психологии типична.
Коэффициент линейной корреляции по К. Пирсону (r)вычисляется c помощью следующей формулы:
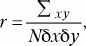
где х– отклонение отдельного значения Xот среднего выборки (Мх), у– отклонение отдельного значения Y отсреднего выборки (Му), Ьх– стандартное отклонение для X, ? y– стандартное отклонение для Y, N– число пар значений Xи Y.
Оценка значимости коэффициента корреляции проводится по таблице (см. Статистическое приложение 4).
При сравнении порядковых данных применяется коэффициент ранговой корреляции по Ч. Спирмену (R):
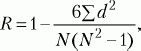
где d– разность рангов (порядковых мест) двух величин, N– число сравниваемых пар величин двух переменных (X и Y).
Оценка значимости коэффициента корреляции проводится по таблице (см. Статистическое приложение 5).
Внедрение в научные исследования автоматизированных средств обработки данных позволяет быстро и точно определять любые количественные характеристики любых массивов данных. Разработаны различные программы для компьютеров, по которым можно проводить соответствующий статистический анализ практически любых выборок. Из массы статистических приемов в психологии наибольшее распространение получили следующие: 1) комплексное вычисление статистик; 2) корреляционный анализ; 3) дисперсионный анализ; 4) регрессионный анализ; 5) факторный анализ; 6) таксономический (кластерный) анализ; 7) шкалирование. Познакомиться с характеристиками этих методов можно в специальной литературе («Статистические методы в педагогике и психологии» Стенли Дж., Гласа Дж. (М., 1976), «Математическая психология» Г.В. Суходольского (СПб., 1997), «Математические методы психологического исследования» А.Д. Наследова (СПб., 2005) и др.).
Способы оценки значимости различий.Для сравнения выборочных средних величин, принадлежащих к двум совокупностям данных, и для решения вопроса о том, отличаются ли средние значения статистически достоверно друг от друга, используют t-критерий Стьюдента. Его формула выглядит следующим образом:
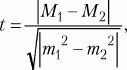
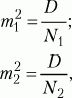
После вычисления значения показателя tпо таблице критических значений (см. Статистическое приложение 1), заданного числа степеней свободы ( N1 + N2 – 2) и избранной вероятности допустимой ошибки (0,05, 0,01, 0,02, 001 и т.д.) находят табличное значение t.Если вычисленное значение tбольше или равно табличному, делают вывод о том, что сравниваемые средние значения двух выборок статистически достоверно различаются с вероятностью допустимой ошибки, меньшей или равной избранной.
Если в процессе исследования встает задача сравнить неабсолютные средние величины, частотные распределения данных, то используется ?2 критерий(см. Приложение 2). Его формула выглядит следующим образом:
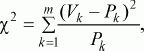
После вычисления значения показателя ?2по таблице критических значений (см. Статистическое приложение 2), заданного числа степеней свободы ( m– 1) и избранной вероятности допустимой ошибки (0,05, 0,0 ?2 tбольше или равно табличному) делают вывод о том, что сравниваемые распределения данных в двух выборках статистически достоверно различаются с вероятностью допустимой ошибки, меньшей или равной избранной.
Для сравнения дисперсий двух выборок используется F-критерийФишера. Его формула выглядит следующим образом:
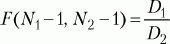
где D1, D2 – дисперсии первой и второй выборок, N1, N2 – число значений в первой и второй выборках.
После вычисления значения показателя Fпо таблице критических значений (см. Статистическое приложение 3), заданного числа степеней свободы ( N1 – 1, N2– 1) находится Fкр. Если вычисленное значение Fбольше или равно табличному, делают вывод о том, что различие дисперсий в двух выборках статистически достоверно.
Способы установления статистических взаимосвязей.Предыдущие показатели характеризуют совокупность данных по какому-либо одному признаку. Этот изменяющийся признак называют переменной величиной или просто переменной. Меры связивыявляют соотношения между двумя переменными или между двумя выборками. Эти связи, или корреляции, определяют через вычисление коэффициентов корреляции. Однако наличие корреляции не означает, что между переменными существует причинная (или функциональная) связь. Функциональная зависимость – это частный случай корреляции. Даже если связь причинна, корреляционные показатели не могут указать, какая из двух переменных является причиной, а какая – следствием. Кроме того, любая обнаруженная в психологических исследованиях связь, как правило, существует благодаря и другим переменным, а не только двум рассматриваемым. К тому же взаимосвязи психологических признаков столь сложны, что их обусловленность одной причиной вряд ли состоятельна, они детерминированы множеством причин.
По тесноте связи можно выделить следующие виды корреляции: полная, высокая, выраженная, частичная; отсутствие корреляции. Эти виды корреляций определяют в зависимости от значения коэффициента корреляции.
При полнойкорреляции его абсолютные значения равны или очень близки к 1. В этом случае устанавливается обязательная взаимозависимость между переменными. Здесь вероятна функциональная зависимость.
Высокаякорреляция устанавливается при абсолютном значении коэффициента 0,8–0,9. Выраженнаякорреляция считается при абсолютном значении коэффициента 0,6–0,7. Частичнаякорреляция существует при абсолютном значении коэффициента 0,4–0,5.
Абсолютные значения коэффициента корреляции менее 0,4 свидетельствуют об очень слабой корреляционной связи и, как правило, в расчет не принимаются. Отсутствие корреляцииконстатируется при значении коэффициента 0.
Кроме того, в психологии при оценке тесноты связи используют так называемую «частную» классификацию корреляционных связей. Она ориентирована не на абсолютную величину коэффициентов корреляции, а на уровень значимости этой величины при определенном объеме выборки. Эта классификация применяется при статистической оценке гипотез. При данном подходе предполагается, что чем больше выборка, тем меньшее значение коэффициента корреляции может быть принято для признания достоверности связей, а для малых выборок даже абсолютно большое значение коэффициента может оказаться недостоверным. [86]
По направленностивыделяют следующие виды корреляционных связей: положительная (прямая) и отрицательная (обратная). Положительная(прямая) корреляционная связь регистрируется при коэффициенте со знаком «плюс»: при увеличении значения одной переменной наблюдается увеличение другой. Отрицательная(обратная) корреляция имеет место при значении коэффициента со знаком «минус». Это означает обратную зависимость: увеличение значения одной переменной влечет за собой уменьшение другой.
По формеразличают следующие виды корреляционных связей: прямолинейную и криволинейную. При прямолинейнойсвязи равномерным изменениям одной переменной соответствуют равномерные изменения другой. Если говорить не только о корреляциях, но и о функциональных зависимостях, то такие формы зависимости называют пропорциональными. В психологии строго прямолинейные связи – явление редкое. При криволинейнойсвязи равномерное изменение одного признака сочетается с неравномерным изменением другого. Эта ситуация для психологии типична.
Коэффициент линейной корреляции по К. Пирсону (r)вычисляется c помощью следующей формулы:
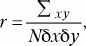
где х– отклонение отдельного значения Xот среднего выборки (Мх), у– отклонение отдельного значения Y отсреднего выборки (Му), Ьх– стандартное отклонение для X, ? y– стандартное отклонение для Y, N– число пар значений Xи Y.
Оценка значимости коэффициента корреляции проводится по таблице (см. Статистическое приложение 4).
При сравнении порядковых данных применяется коэффициент ранговой корреляции по Ч. Спирмену (R):
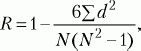
где d– разность рангов (порядковых мест) двух величин, N– число сравниваемых пар величин двух переменных (X и Y).
Оценка значимости коэффициента корреляции проводится по таблице (см. Статистическое приложение 5).
Внедрение в научные исследования автоматизированных средств обработки данных позволяет быстро и точно определять любые количественные характеристики любых массивов данных. Разработаны различные программы для компьютеров, по которым можно проводить соответствующий статистический анализ практически любых выборок. Из массы статистических приемов в психологии наибольшее распространение получили следующие: 1) комплексное вычисление статистик; 2) корреляционный анализ; 3) дисперсионный анализ; 4) регрессионный анализ; 5) факторный анализ; 6) таксономический (кластерный) анализ; 7) шкалирование. Познакомиться с характеристиками этих методов можно в специальной литературе («Статистические методы в педагогике и психологии» Стенли Дж., Гласа Дж. (М., 1976), «Математическая психология» Г.В. Суходольского (СПб., 1997), «Математические методы психологического исследования» А.Д. Наследова (СПб., 2005) и др.).
Тема 8. Интерпретация и представление результатов психологических исследований
8.1. Интерпретация и обобщение результатов исследования
Методы интерпретации данных корректнее называть подходами, поскольку они являются в первую очередь объяснительными принципами, предопределяющими направление интерпретации результатов исследования. В научной практике получили развитие генетический, структурный, функциональный, комплексный и системный подходы. Использование того или иного метода не означает отбрасывания других.
Генетическийподход – это способ исследования и объяснения явлений (в том числе психических), основанный на анализе их развития как в онтогенетическом, так и филогенетическом планах. При этом требуется установление: 1) начальных условий возникновения явления; 2) главных этапов и 3) основных тенденций его развития. Цель генетического подхода – выявление связи изучаемых явлений во времени, прослеживание перехода от низших форм к высшим.
Чаще всего генетический подход применяется при интерпретации результатов в психологии развития: сравнительной, возрастной, исторической. Любое лонгитюдное исследование предполагает применение рассматриваемого подхода.
Генетический подход рассматривается как методическая реализация одного из основных принципов психологии, а именно принципа развития. [87]При таком видении другие варианты реализации этого принципа рассматриваются как модификации генетического подхода (исторический и эволюционный подходы).
Структурныйподход – направление, ориентированное на выявление и описание структуры объектов (явлений). Для него характерно: углубленное внимание к описанию актуального состояния объектов; выяснение внутренне присущих им вневременных свойств; интерес не к изолированным фактам, а к отношениям между ними. В итоге строится система взаимосвязей между элементами объекта на различных уровнях его организации. [88]
Достоинством структурного подхода является возможность наглядного представления результатов в виде различных моделей. Эти модели могут даваться в форме описаний, перечня элементов, графической схемы, классификации и пр. Примеры подобного моделирования можно найти у З. Фрейда, Г. Айзенка и др.
Структурный подход часто применяется в исследованиях, посвященных изучению конституциональной организации психики и ее материального субстрата – нервной системы. Данный подход привел к созданию И.П. Павловым типологии высшей нервной деятельности, который затем был развит Б.М. Тепловым и В.Д. Небылицыным. Структурные модели человеческой психики в пространственном и функциональном аспектах представлены в работах В.А. Ганзена, [89]В.В. Никандрова [90]и др.
Функциональныйподход ориентирован на выявление и изучение функций объектов (явлений). Он применяется главным образом при изучении связей объекта со средой. Этот подход исходит из принципа саморегуляции и поддержания равновесия объектов действительности. Примерами реализации функционального подхода в истории науки являются такие известные направления, как функциональная психология и бихевиоризм. Классическим образцом воплощения функционального подхода в психологии является динамическая теория поля К. Левина. В современной психологии функциональный подход обогащается компонентами структурного и генетического анализа. Общеизвестным считается представление о многоуровневости и многофазности всех психических функций человека, действующих одновременно на всех уровнях как единое целое. Элементы структур большинство авторов соответствующих моделей рассматривают также и как функциональные единицы, олицетворяющие определенные связи человека с действительностью.
Комплексныйподход – это направление, рассматривающее объект исследования как совокупность компонентов, подлежащих изучению с помощью соответствующей совокупности методов. Компоненты могут быть как относительно однородными частями целого, так и его разнородными сторонами, характеризующими изучаемый объект в разных аспектах.
Часто комплексный подход предполагает изучение сложного объекта методами различных наук, т. е. организацию междисциплинарного исследования. Очевидно, что он предполагает применение в той или иной мере и всех предыдущих интерпретационных методов.
Яркий пример реализации комплексного подхода в науке – концепция человекознания, согласно которой человек как объект изучения подлежит скоординированному исследованию большого комплекса наук. В психологии эта идея комплексности изучения человека была четко сформулирована Б.Г. Ананьевым. [91]Человек рассматривается одновременно как представитель биологического вида (индивид), носитель сознания и активный элемент познавательной и преобразующей действительность деятельности (субъект), субъект социальных отношений (личность) и уникальное единство социально значимых биологических, социальных и психологических особенностей (индивидуальность).
Системныйподход – это методологическое направление в изучении реальности, рассматривающее любой ее фрагмент как систему. Основателем системного подхода как неотъемлемого методологического и методического компонента научного познания можно считать австрийского ученого, переехавшего в США, Л. Берталанфи, разработавшего общую теорию систем. [92]Система есть некоторая целостность, взаимодействующая с окружающей средой и состоящая из множества элементов, находящихся между собой в некоторых отношениях и связях. Организация этих связей между элементами называется структурой. Элемент – мельчайшая часть системы, сохраняющая ее свойства в пределах данной системы. Дальнейшее расчленение этой части ведет к потере соответствующих свойств. Свойства элементов определяются их положением в структуре и, в свою очередь, определяют свойства системы. Но свойства системы не сводятся к сумме свойств элементов. Система как целое синтезирует (объединяет и обобщает) свойства частей и элементов, в результате чего она обладает свойствами более высокого уровня организации, которые во взаимодействии с другими системами могут представать как ее функции. Любая система может рассматриваться, с одной стороны, как объединение более простых (мелких) подсистем со своими свойствами и функциями, а с другой – как подсистема более сложных (крупных) систем.
Системные исследования осуществляются с помощью системных анализа и синтеза. В процессе анализа система выделяется из среды, определяются ее состав (набор элементов), структура, функции, интегральные свойства и характеристики, системообразующие факторы, взаимосвязи со средой. В процессе синтеза создается модель реальной системы, повышается уровень обобщения и абстракции описания системы, определяются полнота ее состава и структур, закономерности развития и поведения.
Описание объектов как систем, т. е. системные описания, выполняют те же функции, что и любые другие научные описания, – объяснительную и прогнозирующую. Но еще важнее, что системные описания выполняют функцию интеграции знаний об объектах.
Системный подход в психологии позволяет вскрыть общность психических явлений с другими явлениями действительности. Это дает возможность обогащения психологии идеями, фактами, методами других наук и, наоборот, проникновения психологических данных в другие области знания. Он позволяет интегрировать и систематизировать психологические знания, сокращать объем и повышать наглядность описаний, уменьшать субъективизм в интерпретации психических явлений, помогает увидеть пробелы в знаниях о конкретных объектах, определить задачи дальнейших исследований, а иногда и предсказать свойства объектов, информация о которых отсутствует, путем экстраполяции и интерполяции имеющихся сведений.
Рассмотренные выше подходы являются фактически органичными компонентами системного подхода. Некоторые авторы сопоставляют эти подходы с соответствующими уровнями качеств человека, составляющих предмет психологического исследования (В.П. Кузьмин [93]и др.).
В настоящее время большинство научных исследований проводится в русле системного подхода. Наиболее полное освещение применительно к психологии системный подход нашел в работах В.А. Ганзена, [94]А.А. Крылова, [95]Б.Ф. Ломова, [96]А. Раппопорта [97]и др.
Генетическийподход – это способ исследования и объяснения явлений (в том числе психических), основанный на анализе их развития как в онтогенетическом, так и филогенетическом планах. При этом требуется установление: 1) начальных условий возникновения явления; 2) главных этапов и 3) основных тенденций его развития. Цель генетического подхода – выявление связи изучаемых явлений во времени, прослеживание перехода от низших форм к высшим.
Чаще всего генетический подход применяется при интерпретации результатов в психологии развития: сравнительной, возрастной, исторической. Любое лонгитюдное исследование предполагает применение рассматриваемого подхода.
Генетический подход рассматривается как методическая реализация одного из основных принципов психологии, а именно принципа развития. [87]При таком видении другие варианты реализации этого принципа рассматриваются как модификации генетического подхода (исторический и эволюционный подходы).
Структурныйподход – направление, ориентированное на выявление и описание структуры объектов (явлений). Для него характерно: углубленное внимание к описанию актуального состояния объектов; выяснение внутренне присущих им вневременных свойств; интерес не к изолированным фактам, а к отношениям между ними. В итоге строится система взаимосвязей между элементами объекта на различных уровнях его организации. [88]
Достоинством структурного подхода является возможность наглядного представления результатов в виде различных моделей. Эти модели могут даваться в форме описаний, перечня элементов, графической схемы, классификации и пр. Примеры подобного моделирования можно найти у З. Фрейда, Г. Айзенка и др.
Структурный подход часто применяется в исследованиях, посвященных изучению конституциональной организации психики и ее материального субстрата – нервной системы. Данный подход привел к созданию И.П. Павловым типологии высшей нервной деятельности, который затем был развит Б.М. Тепловым и В.Д. Небылицыным. Структурные модели человеческой психики в пространственном и функциональном аспектах представлены в работах В.А. Ганзена, [89]В.В. Никандрова [90]и др.
Функциональныйподход ориентирован на выявление и изучение функций объектов (явлений). Он применяется главным образом при изучении связей объекта со средой. Этот подход исходит из принципа саморегуляции и поддержания равновесия объектов действительности. Примерами реализации функционального подхода в истории науки являются такие известные направления, как функциональная психология и бихевиоризм. Классическим образцом воплощения функционального подхода в психологии является динамическая теория поля К. Левина. В современной психологии функциональный подход обогащается компонентами структурного и генетического анализа. Общеизвестным считается представление о многоуровневости и многофазности всех психических функций человека, действующих одновременно на всех уровнях как единое целое. Элементы структур большинство авторов соответствующих моделей рассматривают также и как функциональные единицы, олицетворяющие определенные связи человека с действительностью.
Комплексныйподход – это направление, рассматривающее объект исследования как совокупность компонентов, подлежащих изучению с помощью соответствующей совокупности методов. Компоненты могут быть как относительно однородными частями целого, так и его разнородными сторонами, характеризующими изучаемый объект в разных аспектах.
Часто комплексный подход предполагает изучение сложного объекта методами различных наук, т. е. организацию междисциплинарного исследования. Очевидно, что он предполагает применение в той или иной мере и всех предыдущих интерпретационных методов.
Яркий пример реализации комплексного подхода в науке – концепция человекознания, согласно которой человек как объект изучения подлежит скоординированному исследованию большого комплекса наук. В психологии эта идея комплексности изучения человека была четко сформулирована Б.Г. Ананьевым. [91]Человек рассматривается одновременно как представитель биологического вида (индивид), носитель сознания и активный элемент познавательной и преобразующей действительность деятельности (субъект), субъект социальных отношений (личность) и уникальное единство социально значимых биологических, социальных и психологических особенностей (индивидуальность).
Системныйподход – это методологическое направление в изучении реальности, рассматривающее любой ее фрагмент как систему. Основателем системного подхода как неотъемлемого методологического и методического компонента научного познания можно считать австрийского ученого, переехавшего в США, Л. Берталанфи, разработавшего общую теорию систем. [92]Система есть некоторая целостность, взаимодействующая с окружающей средой и состоящая из множества элементов, находящихся между собой в некоторых отношениях и связях. Организация этих связей между элементами называется структурой. Элемент – мельчайшая часть системы, сохраняющая ее свойства в пределах данной системы. Дальнейшее расчленение этой части ведет к потере соответствующих свойств. Свойства элементов определяются их положением в структуре и, в свою очередь, определяют свойства системы. Но свойства системы не сводятся к сумме свойств элементов. Система как целое синтезирует (объединяет и обобщает) свойства частей и элементов, в результате чего она обладает свойствами более высокого уровня организации, которые во взаимодействии с другими системами могут представать как ее функции. Любая система может рассматриваться, с одной стороны, как объединение более простых (мелких) подсистем со своими свойствами и функциями, а с другой – как подсистема более сложных (крупных) систем.
Системные исследования осуществляются с помощью системных анализа и синтеза. В процессе анализа система выделяется из среды, определяются ее состав (набор элементов), структура, функции, интегральные свойства и характеристики, системообразующие факторы, взаимосвязи со средой. В процессе синтеза создается модель реальной системы, повышается уровень обобщения и абстракции описания системы, определяются полнота ее состава и структур, закономерности развития и поведения.
Описание объектов как систем, т. е. системные описания, выполняют те же функции, что и любые другие научные описания, – объяснительную и прогнозирующую. Но еще важнее, что системные описания выполняют функцию интеграции знаний об объектах.
Системный подход в психологии позволяет вскрыть общность психических явлений с другими явлениями действительности. Это дает возможность обогащения психологии идеями, фактами, методами других наук и, наоборот, проникновения психологических данных в другие области знания. Он позволяет интегрировать и систематизировать психологические знания, сокращать объем и повышать наглядность описаний, уменьшать субъективизм в интерпретации психических явлений, помогает увидеть пробелы в знаниях о конкретных объектах, определить задачи дальнейших исследований, а иногда и предсказать свойства объектов, информация о которых отсутствует, путем экстраполяции и интерполяции имеющихся сведений.
Рассмотренные выше подходы являются фактически органичными компонентами системного подхода. Некоторые авторы сопоставляют эти подходы с соответствующими уровнями качеств человека, составляющих предмет психологического исследования (В.П. Кузьмин [93]и др.).
В настоящее время большинство научных исследований проводится в русле системного подхода. Наиболее полное освещение применительно к психологии системный подход нашел в работах В.А. Ганзена, [94]А.А. Крылова, [95]Б.Ф. Ломова, [96]А. Раппопорта [97]и др.
8.2. Формы представления результатов исследования
Завершением любой исследовательской работы является представление результатов в той форме, которая принята научным сообществом. Следует различать две основные формы представления результатов: квалификационную и научно-исследовательскую.
Квалификационная работа– курсовая, дипломная работа, диссертация и т. д. – служит для того, чтобы студент, аспирант или соискатель, представив свое научное исследование, получил документ, удостоверяющий уровень компетентности. Требования к таким работам, способу их оформления и представления результатов изложены в соответствующих инструкциях и положениях, принятых учеными советами.
Результаты научно-исследовательской работы– это результаты, полученные в ходе исследовательской деятельности ученого. Представление научных результатов обычно происходит в трех формах: 1) устные изложения; 2) публикации; 3) электронные версии. В любой их этих форм присутствует описание. В. А. Ганзен под описанием понимает любую форму представления информации о полученных в исследовании результатах. [98]
Различают следующие варианты представления информации: вербальная форма (текст, речь), символическая (знаки, формулы), графическая (схемы, графики), предметнообразная (макеты, вещественные модели, фильмы и др.).
Вербальнаяформа – наиболее распространенный вариант представления описаний. Любое научное сообщение – это прежде всего текст, организованный по определенным правилам. Различают два вида текстов: на естественномязыке («природном», обыденном) и на научномязыке. Обычно представление результатов научного исследования является текстом «смешанного» вида, где в естественную речевую структуру включены фрагменты, сформулированные на строго научном языке. Эти языки нельзя строго разграничить: научные термины входят в повседневное обращение, а наука черпает из естественного языка слова для обозначения вновь открытых сторон реальности. Но в отличие от обыденного употребления каждый научный термин имеет однозначное предметное содержание. В психологии в качестве научных терминов употребляются такие слова, как «личность», «внимание», «чувство» и т. п. Здесь грань между научной и обыденной терминологией весьма тонка, что порождает дополнительную трудность для автора-психолога.
Главное требование к научному тексту – последовательность и логичность изложения. Автор должен по возможности не загружать текст избыточной информацией, но может использовать метафоры, примеры, для того чтобы привлечь внимание к особо значимому для понимания сути звену рассуждений. Научный текст в отличие от литературного текста или повседневной речи очень клиширован – в нем преобладают устойчивые структуры и обороты (в этом он сходен с «канцеляритом» – бюрократическим языком деловых бумаг). Роль таких штампов чрезвычайно важна, поскольку внимание читателя не отвлекается на литературные изыски или неправильности изложения, а сосредоточивается на значимой информации: суждениях, умозаключениях, доказательствах, цифрах, формулах. «Наукообразные» штампы на самом деле играют важную роль «рамок», стандартной установки для нового научного содержания.
Текст состоит из высказываний. Каждое высказывание имеет определенную логическую форму. Существуют основные логические формы высказывания: 1) индуктивное – обобщающее некоторый эмпирический материал; 2) дедуктивное – логический вывод от общего к частному или описание алгоритма; 3) аналогия – «трансдукция»; 4) толкование или комментарий – «перевод», раскрытие содержания одного текста посредством создания другого.
Геометрические(пространственно-образные) описания являются традиционным способом кодирования научной информации. Поскольку геометрическое описание дополняет и поясняет текст, оно «привязано» к описанию языковому. Геометрическое описание наглядно. Оно позволяет одновременно представить систему отношений между отдельными переменными, исследуемыми в эксперименте. Информационная емкость геометрического описания очень велика.
В психологии используется несколько основных форм графическогопредставления научной информации. Для первичного представления данных используются следующие графические формы: диаграммы, гистограммы и полигоны распределения, а также различные графики.
Начальным способом представления данных является изображение распределения. Для этого используют гистограммы и полигоны распределения. Часто для наглядности распределение показателя в экспериментальной и контрольной группах изображают на одном рисунке.
Гистограмма– это «столбчатая» диаграмма частотного распределения признака на выборке. При построении гистограмм на оси абсцисс откладывают значения измеряемой величины, а на оси ординат – частоты или относительные частоты встречаемости данного диапазона величины в выборке.
В полигоне распределенияколичество испытуемых, имеющих данную величину признака (или попавших в определенный интервал величины), обозначают точкой с координатами. Точки соединяются отрезками прямой. Перед тем как строить полигон распределения или гистограмму, исследователь должен разбить диапазон измеряемой величины, если признак дан в шкале интервалов или отношений, на равные отрезки. Рекомендуют использовать не менее пяти, но не более десяти градаций. В случае использования шкалы наименований или порядковой шкалы такой проблемы не возникает.
Если исследователь хочет нагляднее представить соотношение между различными величинами, например доли испытуемых с разными качественными особенностями, то ему выгоднее использовать диаграмму.В секторной круговой диаграмме величина каждого сектора пропорциональна величине встречаемости каждого типа. Величина круговой диаграммы может отображать относительный объем выборки или значимость признака.
Квалификационная работа– курсовая, дипломная работа, диссертация и т. д. – служит для того, чтобы студент, аспирант или соискатель, представив свое научное исследование, получил документ, удостоверяющий уровень компетентности. Требования к таким работам, способу их оформления и представления результатов изложены в соответствующих инструкциях и положениях, принятых учеными советами.
Результаты научно-исследовательской работы– это результаты, полученные в ходе исследовательской деятельности ученого. Представление научных результатов обычно происходит в трех формах: 1) устные изложения; 2) публикации; 3) электронные версии. В любой их этих форм присутствует описание. В. А. Ганзен под описанием понимает любую форму представления информации о полученных в исследовании результатах. [98]
Различают следующие варианты представления информации: вербальная форма (текст, речь), символическая (знаки, формулы), графическая (схемы, графики), предметнообразная (макеты, вещественные модели, фильмы и др.).
Вербальнаяформа – наиболее распространенный вариант представления описаний. Любое научное сообщение – это прежде всего текст, организованный по определенным правилам. Различают два вида текстов: на естественномязыке («природном», обыденном) и на научномязыке. Обычно представление результатов научного исследования является текстом «смешанного» вида, где в естественную речевую структуру включены фрагменты, сформулированные на строго научном языке. Эти языки нельзя строго разграничить: научные термины входят в повседневное обращение, а наука черпает из естественного языка слова для обозначения вновь открытых сторон реальности. Но в отличие от обыденного употребления каждый научный термин имеет однозначное предметное содержание. В психологии в качестве научных терминов употребляются такие слова, как «личность», «внимание», «чувство» и т. п. Здесь грань между научной и обыденной терминологией весьма тонка, что порождает дополнительную трудность для автора-психолога.
Главное требование к научному тексту – последовательность и логичность изложения. Автор должен по возможности не загружать текст избыточной информацией, но может использовать метафоры, примеры, для того чтобы привлечь внимание к особо значимому для понимания сути звену рассуждений. Научный текст в отличие от литературного текста или повседневной речи очень клиширован – в нем преобладают устойчивые структуры и обороты (в этом он сходен с «канцеляритом» – бюрократическим языком деловых бумаг). Роль таких штампов чрезвычайно важна, поскольку внимание читателя не отвлекается на литературные изыски или неправильности изложения, а сосредоточивается на значимой информации: суждениях, умозаключениях, доказательствах, цифрах, формулах. «Наукообразные» штампы на самом деле играют важную роль «рамок», стандартной установки для нового научного содержания.
Текст состоит из высказываний. Каждое высказывание имеет определенную логическую форму. Существуют основные логические формы высказывания: 1) индуктивное – обобщающее некоторый эмпирический материал; 2) дедуктивное – логический вывод от общего к частному или описание алгоритма; 3) аналогия – «трансдукция»; 4) толкование или комментарий – «перевод», раскрытие содержания одного текста посредством создания другого.
Геометрические(пространственно-образные) описания являются традиционным способом кодирования научной информации. Поскольку геометрическое описание дополняет и поясняет текст, оно «привязано» к описанию языковому. Геометрическое описание наглядно. Оно позволяет одновременно представить систему отношений между отдельными переменными, исследуемыми в эксперименте. Информационная емкость геометрического описания очень велика.
В психологии используется несколько основных форм графическогопредставления научной информации. Для первичного представления данных используются следующие графические формы: диаграммы, гистограммы и полигоны распределения, а также различные графики.
Начальным способом представления данных является изображение распределения. Для этого используют гистограммы и полигоны распределения. Часто для наглядности распределение показателя в экспериментальной и контрольной группах изображают на одном рисунке.
Гистограмма– это «столбчатая» диаграмма частотного распределения признака на выборке. При построении гистограмм на оси абсцисс откладывают значения измеряемой величины, а на оси ординат – частоты или относительные частоты встречаемости данного диапазона величины в выборке.
В полигоне распределенияколичество испытуемых, имеющих данную величину признака (или попавших в определенный интервал величины), обозначают точкой с координатами. Точки соединяются отрезками прямой. Перед тем как строить полигон распределения или гистограмму, исследователь должен разбить диапазон измеряемой величины, если признак дан в шкале интервалов или отношений, на равные отрезки. Рекомендуют использовать не менее пяти, но не более десяти градаций. В случае использования шкалы наименований или порядковой шкалы такой проблемы не возникает.
Если исследователь хочет нагляднее представить соотношение между различными величинами, например доли испытуемых с разными качественными особенностями, то ему выгоднее использовать диаграмму.В секторной круговой диаграмме величина каждого сектора пропорциональна величине встречаемости каждого типа. Величина круговой диаграммы может отображать относительный объем выборки или значимость признака.
