Леоненков Александр. Самоучитель UML

   Для выделения или идентификации компонентов предметной области было предложено несколько способов и правил. Сам этот процесс получил название концептуализации предметной области. При этом под компонентой понимают некоторую абстрактную единицу, которая обладает функциональностью, т. е. может выполнять определенные действия, связанные с решением поставленных задач. На предварительном этапе концептуализации рекомендуется использовать так называемые CRC-карточки (Component, Responsibility, Collaborator– компонента, обязанность, сотрудники) [1]. Для каждой выделенной компоненты предметной области разрабатывается собственная CRC-карточка (рис. 1.6).

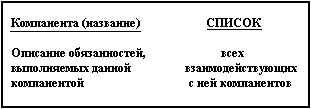    Рис. 1.6.Общий вид CRC-карточки для описания компонентов предметной области
   Появление методологии ООАП потребовало, с одной стороны, разработки различных средств концептуализации предметной области, а с другой – соответствующих специалистов, которые владели бы этой методологией. На данном этапе появляется относительно новый тип специалиста, который получил название аналитика или архитектора. Наряду со специалистами по предметной области аналитик участвует в построении концептуальной схемы будущей программы, которая затем преобразуется программистами в код. При этом отдельные компоненты выбираются таким образом, чтобы при последующей разработке их было удобно представить в форме классов и объектов. В этом случае немаловажное значение приобретает и сам язык представления информации о концептуальной схеме предметной области.
   Разделение процесса разработки сложных программных приложений на отдельные этапы способствовало становлению концепции жизненного цикла программы. Под жизненным циклом (ЖЦ) программы понимают совокупность взаимосвязанных и следующих во времени этапов, начиная от разработки требований к ней и заканчивая полным отказом от ее использования. Стандарт ISO/IEC 12207, хотя и описывает общую структуру ЖЦ программы, не конкретизирует детали выполнения тех или иных этапов. Согласно принятым взглядам ЖЦ программы состоит из следующих этапов:

   • Анализа предметной области и формулировки требований к программе
   • Проектирования структуры программы
   • Реализации программы в кодах (собственно программирования)
   • Внедрения программы
   • Сопровождения программы
   • Отказа от использования программы

   На этапе анализа предметной области и .формулировки требований осуществляется определение функций, которые должна выполнять разрабатываемая программа, а также концептуализация предметной области. Эту работу выполняют аналитики совместно со специалистами предметной области. Результатом данного этапа должна являться некоторая концептуальная схема, содержащая описание основных компонентов и тех функций, которые они должны выполнять.
   Этап проектирования структуры программы заключается в разработке детальной схемы будущей программы, на которой указываются классы, их свойства и методы, а также различные взаимосвязи между ними. Как правило, на этом этапе могут участвовать в работе аналитики, архитекторы и отдельные квалифицированные программисты. Результатом данного этапа должна стать детализированная схема программы, на которой указываются все классы и взаимосвязи между ними в процессе функционирования программы. Согласно методологии ООАП, именно данная схема должна "служить исходной информацией для написания программного кода.
   Этап программирования вряд ли нуждается в уточнении, поскольку является наиболее традиционным для программистов. Появление инструментариев быстрой разработки приложений (Rapid Application Development, RAD) позволило существенно сократить время, и затраты на выполнение этого этапа. Результатом данного этапа является программное приложение, которое обладает требуемой функциональностью и способно решать нужные задачи в конкретной предметной области.
   Этапы внедрения и сопровождения программы связаны с необходимостью настройки и конфигурирования среды программы, а также с устранением возникших в процессе ее использования ошибок. Иногда в качестве отдельного этапа выделяют тестирование программы, под которым понимают проверку работоспособности программы на некоторой совокупности исходных данных или при некоторых специальных режимах эксплуатации. Результатом этих этапов является повышение надежности Программного приложения, исключающего возникновение критических ситуаций или нанесение ущерба компании, использующей данное приложение.
    Примечание 8
   Методология ООАП тесно связана с концепцией автоматизированной разработки программного обеспечения (Computer Aided Software Engineering, CASE). Появление первых CASE-средств было встречено с определенной настороженностью. Со временем появились как восторженные Отзывы об их применении, так и критические оценки их возможностей. Причин для столь противоречивых мнений было несколько. Первая из них заключается в том, что ранние CASE-средства были простой надстройкой над некоторой системой управления базами данных (СУБД). Хотя визуализация процесса разработки концептуальной схемы БД имеет немаловажное значение, она не решает проблем разработки приложений других типов.
   Вторая причина имеет более сложную природу, поскольку связана с графической нотацией, реализованной в том или ином CASE-средстве. Если языки программирования имеют строгий синтаксис, то попытки предложить подходящий синтаксис для визуального представления концептуальных схем БД были восприняты далеко неоднозначно. Появилось несколько подходов, которые более подробно будут рассмотрены в главе 2. На этом фоне появление унифицированного языка моделирования (Unified Modeling Language, UML), который ориентирован на решение задач первых двух этапов ЖЦ программ, было воспринято с большим оптимизмом всем сообществом корпоративных программистов.
    Примечание 9
   Последнее, на что следует обратить внимание, это осознание необходимости построения предварительной модели программной системы, которую, согласно современным концепциям ООАП, следует считать результатом первых этапов ЖЦ программы. Поскольку язык UML даже в своем названии имеет отношение к моделированию, следует дополнительно остановиться на целом ряде достаточно важных вопросов. Таким образом, мы переходим к теме, которая традиционно не рассматривается в изданиях по ООАП, но имеющая самое прямое отношение к процессу построения моделей и, собственно, моделированию. Речь идет о методологии системного анализа и системного моделирования.

1.4. Методология системного анализа и системного моделирования

   Системный анализ как научное направление имеет более давнюю историю, чем ООП и ООАП, и собственный предмет исследования. Центральным понятием системного анализа является понятие системы, под которой понимается совокупность объектов, компонентов или элементов произвольной природы, образующих некоторую целостность. Определяющей предпосылкой выделения некоторой совокупности как системы является возникновение у нее новых свойств, которых не имеют составляющие ее элементы. Примеров систем можно привести достаточно много – это персональный компьютер, автомобиль, человек, биосфера, программа и др. Более ортодоксальная точка зрения предполагает, что все окружающие нас предметы являются системами.
   Важнейшими характеристиками любой системы являются ее структура и процесс функционирования. Под структурой системы понимают устойчивую во времени совокупность взаимосвязей между ее элементами или компонентами. Именно структура связывает воедино все элементы и препятствует распаду системы на отдельные компоненты. Структура системы может отражать самые различные взаимосвязи, в том числе и вложенность элементов одной системы в другую. В этом случае принято называть более мелкую или вложенную систему подсистемой, а более крупную – метасистемой.
   Процесс функционирования системы тесно связан с изменением ее свойств или поведения во времени. При этом важной характеристикой системы является ее состояние, под которым понимается совокупность свойств или признаков, которые в каждый момент времени отражают наиболее существенные особенности поведения системы.
   Рассмотрим следующий пример. В качестве системы представим себе «Автомобиль». Для этого случая система охлаждения двигателя будет являться подсистемой «Автомобиля». С одной стороны, двигатель является элементом системы «Автомобиль». С другой стороны, двигатель сам является системой, состоящей из отдельных компонентов, таких как цилиндры, свечи зажигания и др. Поэтому система «Двигатель» также будет являться подсистемой системы «Автомобиль».
   Структура системы «Автомобиль» может быть описана с разных точек зрения. Наиболее общее представление о структуре этой системы дает механическая схема устройства того или иного автомобиля. Взаимодействие элементов в этом случае носит механический характер. Состояние автомобиля можно рассматривать также с различных точек зрения, наиболее общей из которых является характеристика автомобиля как исправного или неисправного. Очевидно, что каждое из этих состояний в отдельных ситуациях может быть детализировано. Например, состояние «неисправный» может быть конкретизировано в состояния «неисправность двигателя», «неисправность аккумулятора», «отсутствие подачи топлива» и пр. Важно иметь четкое представление, что подобная детализация должна быть адекватна решаемой задаче.
   Процесс функционирования системы отражает поведение системы во времени и может быть представлен как последовательное изменение ее состояний: Если система изменяет одно свое состояние на другое, то принято говорить, что система переходит из одного состояния в другое. Совокупность признаков или условий изменения состояний системы в этом случае называется переходом. Для системы с дискретными состояниями процесс функционирования может быть представлен в виде последовательности состояний с соответствующими переходами. Более точное графическое описание процесса функционирования систем будет дано в главе 2.
   Методология системного анализа служит концептуальной основой системно-ориентированной декомпозиции предметной области. В этом случае исходными компонентами концептуализации являются системы и взаимосвязи между ними. При этом понятие системы является более общим, чем понятия классов и объектов в ООАП. Результатом системного анализа является построение некоторой модели системы или предметной области.
   Понятие модели столь широко используется в повседневной жизни, что приобрело очень много смысловых оттенков. Это и «Дом моделей» известного кутюрье, и модель престижной марки автомобиля, и модель политического руководства, и математическая модель колебаний маятника. Применительно к программным системам нас будет интересовать только то понятие модели, которое используется в системном анализе. А именно, под моделью будем понимать некоторое представление о системе, отражающее наиболее существенные закономерности ее структуры и процесса функционирования и зафиксированное на некотором языке или в другой форме.
   Примеров моделей можно привести достаточно много. Например, аэродинамическая модель гоночного автомобиля или проектируемого самолета, модель ракетного двигателя, модель колебательной .системы, модель системы электроснабжения региона, модель избирательной компании и др.
   Общим свойством всех моделей является их подобие оригинальной системе или системе-оригиналу. Важность построения моделей заключается в возможности их использования для получения информации о свойствах или поведении системы-оригинала. При этом процесс построения и последующего применения моделей для получения информации о системе-оригинале получил название моделирование.
    Примечание 10
   Наиболее общей моделью системы является так называемая модель «черного ящика». В этом случае система представляется в виде прямоугольника, внутреннее устройство которого скрыто от аналитика или неизвестно. Однако система не является полностью изолированной от внешней среды, поскольку последняя оказывает на систему некоторые информационные или материальные воздействия. Такие воздействия получили название входных воздействий. В свою очередь, система также оказывает на среду или другие системы определенные информационные или материальные воздействия, которые получили название выходных воздействий. Графически данная модель может быть изображена следующим образом (рис. 1.7).

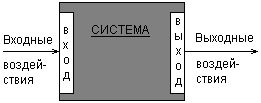    Рис. 1.7.Графическое изображение модели системы в виде «черного ящика»
   Ценность моделей, подобных модели «черного ящика», весьма условна. Невольно может возникнуть ассоциация с «Черным квадратом». Однако если оценка изобразительных особенностей последнего не входит в задачи системного анализа, то общая модель системы содержит некоторую важную инфомацию о функциональных особенностях данной системы, которые дают представление о ее поведении. Действительно, кроме самой общей информации о том, на какие воздействия реагирует система, и как проявляется эта реакция на окружающие объекты и системы, другой информации мы получить не можем. В рамках системного анализа разработаны определенные методологические средства, позволяющие выполнить дальнейшую конкретизацию общей модели системы. Некоторые из графических средств представления моделей систем будут рассмотрены в главе 2.
   Процесс разработки адекватных моделей и их последующего конструктивного применения требует не только знания общей методологии системного анализа, но и наличия соответствующих изобразительных средств или языков для фиксации результатов моделирования и их документирования. Очевидно, что естественный язык не вполне подходит для этой цели, поскольку обладает неоднозначностью и неопределенностью. Для построения моделей были разработаны достаточно серьезные теоретические методы, основанные на развитии математических и логических средств моделирования, а также предложены различные формальные и графические нотации, отражающие специфику решаемых задач. Важно представлять, что унификация любого языка моделирования тесно связана с методологией системного моделирования, т. е. с системой воззрений и принципов рассмотрения сложных явлений и объектов как моделей сложных систем.
   Сложность системы и, соответственно, ее модели может быть рассмотрена с различных точек зрения. Прежде всего, можно выделить сложность структуры системы, которая характеризуется количеством элементов системы и различными типами взаимосвязей между этими элементами. Если количество элементов превышает некоторое пороговое значение, которое не является строго фиксированным, то такая система может быть названа сложной. Например, если программная СУБД насчитывает более 100 отдельных форм ввода и вывода информации, то многие программисты сочтут ее сложной. Транспортная система современных мегаполисов также может служить примером сложной системы.
   Вторым аспектом сложности является сложность процесса функционирования системы. Это может быть связано как с непредсказуемым характером поведения системы, так и невозможностью формального представления правил преобразования входных воздействий в выходные. В качестве примеров сложных программных систем можно привести современные операционные системы, которым присущи черты сложности как структуры, так и поведения.

ГЛАВА 2 Исторический обзор развития методологии объектно-ориентированного анализа и проектирования сложных систем

2.1. Предыстория. Математические основы

   Представление различных понятий окружающего нас мира при помощи графической символики уходит своими истоками в глубокую древность. В качестве примеров можно привести условные обозначения знаков Зодиака, магические символы различных оккультных доктрин, графические изображения геометрических фигур на плоскости и в пространстве. Важным достоинством той или иной графической нотации является возможность образного закрепления содержательного смысла или семантики отдельных понятий, что существенно упрощает процесс общения между посвященными в соответствующие теории и идеологии.

Теория множеств

   Как одну из наиболее известных систем графических символов, оказавших непосредственное влияние на развитие научного мышления, следует отметить язык диаграмм английского логика Джона Венна (1834-1923). В настоящее время диаграммы Венна применяются для иллюстрации основных теоретико-множественных операций, которые являются предметом специального раздела математики – теории множеств. Поскольку многие общие идеи моделирования систем имеют адекватное описание в терминологии теории множеств, рассмотрим основные понятия данной теории, имеющие отношение к современным концепциям и технологиям исследования сложных систем.
   Исходным понятием теории множеств является само понятие множество, под которым принято понимать некоторую совокупность объектов, хорошо различимых нашей мыслью или интуицией. При этом не делается никаких предположений ни о природе этих объектов, ни о способе их включения в данную совокупность. Отдельные объекты, составляющие то или иное множество, называют элементами данного множества. Вопрос «Почему мы рассматриваем ту или иную совокупность элементов как множество?» не требует ответа, поскольку в общее определение множества не входят никакие дополнительные условия на включение отдельных элементов в множество. Если нам хочется, например, рассмотреть множество, состоящее из трех элементов: «солнце, море, апельсин», то никто не сможет запретить это сделать.
   Примеров конкретных множеств можно привести достаточно много. Это и множество квартир жилого дома, и множество натуральных чисел, с которого начинается знакомство каждого ребенка с великим таинством счета. Совокупность компьютеров в офисе тоже представляет собой множество, хотя, возможно, они и соединены между собою в сеть. Множество живущих на планете людей, как и множество звезд на небосводе, тоже могут служить примерами множеств, хотя природа их существенно различна.
    Примечание 11
   В теории множеств используется специальное соглашение, по которому множества обозначаются прописными буквами латинского алфавита, и традиция эта настолько общепризнана, что не возникает никакого сомнения в ее целесообразности. При этом отдельные элементы обозначаются строчными буквами, иногда с индексами, которые вносят некоторую упорядоченность в последовательность рассмотрения этих элементов. Важно понимать, что какой бы то ни было порядок, вообще говоря, не входит в исходное определение множества. Таким образом, множество, например, квартир 100-квартирного жилого дома с использованием специальных обозначений можно записать следующим образом: A={aj, 02, а3, ..., а{00}. Здесь фигурные скобки служат обозначением совокупности элементов, каждый из которых имеет свой уникальный числовой индекс. Важно понимать, что для данного конкретного множества элемент ato обозначает отдельную квартиру в рассматриваемом жилом доме. При этом вовсе необязательно, чтобы номер этой квартиры был равен 10, хотя с точки зрения удобства это было бы желательно.
   Принято называть элементы отдельного множества принадлежащими данному множеству. Данный факт записывается при помощи специального символа "е", который так и называется – символ принадлежности. Например, запись а10ьА означает тот простой факт, что отдельная квартира (возможно, с номером 10) принадлежит рассматриваемому множеству квартир некоторого жилого дома.
   Следующим важным понятием, которое служит прототипом многих более конкретных терминов при моделировании сложных систем, является понятие подмножества. Казалось бы, интуитивно и здесь нет ничего неясного. Если есть некоторая совокупность, рассматриваемая как множество, то любая ее часть и будет являться подмножеством. Так, например, совокупность квартир на первом этаже жилого дома есть ничто иное, как подмножество рассматриваемого нами примера. Ситуация становится не столь тривиальной, если рассматривать множество абстрактных понятий, таких как сущность или класс.
   Для обозначения подмножества используется специальный символ. Если утверждается, что множество А является подмножеством множества В, то это записывается как Аа В. Запоминать подобные значки не всегда удобно, поэтому со временем была предложена специальная система графических обозначений.
   Как же используются диаграммы Венна в теории множеств? Оказывается, тот факт, что некоторая совокупность элементов образует множество, можно обозначить графически в виде круга. В этом случае окружность имеет содержательный смысл или, выражаясь более точным языком, семантику границы данного множества. Очевидно, что рассмотрение отношения включения элементов одного множества в другое можно изобразить графически следующим образом (рис. 2.1). На этом рисунке большему множеству В соответствует внешний круг, а меньшему множеству (подмножеству) А – внутренний.

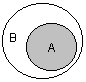    Рис. 2.1.Диаграмма Венна для отношения включения двух множеств
   Подобным образом можно изобразить и основные теоретико-множественные операции. Так, пересечением двух множеств А и В называется некоторое третье множество С, которое состоит из тех и только тех элементов двух исходных множеств, которые одновременно принадлежат и множеству А, и множеству В. Для этой операции также имеется специальное обозначение: С= А о В. Например, если в качестве множества А для операции пересечения рассмотреть множество сотрудников некоторой фирмы, а в качестве множества В – множество всех мужчин, то нетрудно догадаться, что множество С будет состоять из элементов -± всех сотрудников мужского пола данной фирмы. Операция пересечения множеств также может быть проиллюстрирована с помощью диаграмм Венна (рис. 2.2). На этом рисунке условно изображены два множества А и В, затененной области как раз и соответствует множество С, являющееся пересечением множеств А и В.

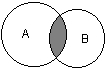    Рис. 2.2Диаграмма Венна для пересечения двух множеств
   Следующей операцией, которая также допускает наглядную интерпретацию, является операция объединения множеств. Под объединением двух множеств А и В понимается некоторое третье множество, пусть это будет D, которое состоит из тех и только тех элементов, которые принадлежат или А, или В, или им обоим одновременно. Конечно, специальное обозначение есть и для этой операции: D= AuB. Так, если в качестве множества А рассмотреть множество, состоящее из клавиатуры и мыши, а в качестве множества В – множество, состоящее из системного блока и монитора, то нетрудно догадаться, что их объединение, т. е. множество D, образует основные составляющие персонального компьютера. И для этой операции имеется условное графическое представление (рис. 2.3). На этом рисунке объединению двух исходных множеств также соответствует затемненная область, только размеры и форма ее отличаются от случая пересечения двух множеств на предыдущем рисунке.

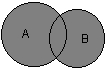    Рис. 2.3.Диаграмма Венна для объединения двух множеств
    Примечание 12
   Последнее, на что следовало бы обратить внимание при столь кратком знакомстве с основами теории множеств – это на так называемые понятия мощности множества и отношения множеств. Хотя существуют и другие операции над множествами, а также целый ряд дополнительных понятий, их рассмотрение выходит за рамки настоящей книги. Что касается понятия мощности множества, то данный термин важен для анализа кратности связей, поскольку ассоциируется с количеством элементов отдельного множества. В случае конечного множества ситуация очень простая, поскольку мощность конечного множества равна количеству элементов этого множества. Таким образом, возвращаясь к примеру с множеством А квартир жилого дома, можно сказать, что его мощность равна 100.
   Ситуация усложняется, когда рассматриваются бесконечные множества, т. е. множества, не являющиеся конечными. Не вдаваясь в технические детали, которые послужили источником драматичного по своим последствиям кризиса основ математики, ограничим наше рассмотрение бесконечными множествами счетной мощности. Такими множествами принято считать множества, содержащие бесконечное число элементов, которые, однако, можно перенумеровать натуральными числами 1, 2, 3 и т. д. При этом важно иметь в виду, что достичь последнего элемента при такой нумерации принципиально невозможно, иначе множество окажется конечным. Например, есть все основания считать множество всех звезд бесконечным, хотя многие из них имеют свое уникальное название. С другой стороны, множество всех возможных комбинаций из 8 символов, которые могут служить для ввода некоторого пароля, конечное, хотя и достаточно большое. Или, говоря строгим языком, это множество имеет конечную мощность.
    Примечание 13
   Наконец, было упомянуто и следующее понятие, различные аспекты которого будут служить темой рассмотрения во всех последующих главах. Это фундаментальное понятие отношения множеств, которое часто заменяется терминами связь или соотношение. Данный термин ведет свое происхождение от теории множеств и служит для обозначения любого подмножества упорядоченных кортежей, построенных из элементов некоторых исходных множеств. При этом под кортежем понимается просто набор или список элементов, важно только, чтобы они были упорядочены. Другими словами, если рассматривать первый элемент кортежа, то он всегда будет первым в списке элементов, второй элемент кортежа будет вторым элементом в списке и т. д. Можно ли это записать с использованием специальных обозначений?