Страница:
Хотя и существует некоторая неоднозначность в принятых обозначениях, кортеж из двух элементов удобно обозначать как <a1, a2>, из трех элементов – <a1, a2, a3> и т. д. При этом отдельные элементы могут принадлежать как одному и тому же множеству, так и различным множествам. Важно иметь в виду, что порядок выбора элементов для построения кортежей строго фиксирован для конкретной задачи. Речь идет о том, что первый элемент всегда выбирается из первого множества, второй – из второго, и т. д:
Отношение в этом случае будет характеризовать способ или семантику выбора отдельных элементов из одного или нескольких множеств для подобного упорядоченного списка. В этом смысле взаимосвязь является частным случаем отношения, о чем будет сказано в последующем. К сожалению, диаграммы Венна не предназначены для иллюстрации отношений в общем случае. Однако отношения послужили исходной идеей для развития другой теории, которая даже в своем названии несет отпечаток графической нотации, а именно – теории графов. В этой связи наиболее важным является тот факт, что теоретико-множественные отношения послужили также основой для разработки реляционной алгебры в теории реляционных баз данных. Развитие последней привело к тому, что в последние годы именно реляционные СУБД конкретных фирм доминируют на рынке соответствующего программного обеспечения.
Теория графов
Семантические сети
2.2. Диаграммы структурного системного анализа
Диаграммы «сущность-связь»
Диаграммы функционального моделирования
Отношение в этом случае будет характеризовать способ или семантику выбора отдельных элементов из одного или нескольких множеств для подобного упорядоченного списка. В этом смысле взаимосвязь является частным случаем отношения, о чем будет сказано в последующем. К сожалению, диаграммы Венна не предназначены для иллюстрации отношений в общем случае. Однако отношения послужили исходной идеей для развития другой теории, которая даже в своем названии несет отпечаток графической нотации, а именно – теории графов. В этой связи наиболее важным является тот факт, что теоретико-множественные отношения послужили также основой для разработки реляционной алгебры в теории реляционных баз данных. Развитие последней привело к тому, что в последние годы именно реляционные СУБД конкретных фирм доминируют на рынке соответствующего программного обеспечения.
Теория графов
Граф можно рассматривать как графическую нотацию для бинарного отношения двух множеств. Бинарное отношение состоит из таких кортежей или списков элементов, которые содержат только два элемента некоторого множества. Хотя основные понятия теории графов получили свое развитие задолго до появления теории множеств как самостоятельной научной дисциплины, формальное определение графа удобно представить в теоретико-множественных терминах.
Графом называется совокупность двух множеств: множества точек или вершин и множества соединяющих их линий или ребер. Формально граф задается в виде двух множеств: G=(V, Е), где V={v1v2, ..., vn} – множество вершин графа, а Е={е1, е2, ..., еm} – множество ребер графа. Натуральное число n определяет общее количество вершин конкретного графа, а натуральное число m – общее количество ребер графа. Следует заметить, в общем случае не все вершины графа могут соединяться между собой, что ставит в соответствие каждому графу некоторое бинарное отношение PQ, состоящее из всех пар вида <vi, vj>, где vi, vj = V. При этом пара <vi, vj> и, соответственно, пара <vj, vi> принадлежат отношению PG в том и только в том случае, если вершины vi и vj соединяются в графе G некоторым ребром ek=Е. Вершины графа изображаются точками, а ребра – отрезками прямых линий. Рядом с вершинами и ребрами записываются соответствующие номера или идентификаторы, позволяющие их идентифицировать однозначным образом.
Примечание 14
Ниже представлены два примера конкретных графов (рис. 2.4). При этом первый из них (рис. 2.4, а) является неориентированным графом, а второй (рис. 2.4, б) – ориентированным графом. Как нетрудно заметить, для неориентированного графа ребро е1 соединяет вершины v1 и v2, ребро е2 – вершины v1 и v3, а ребро e3 – вершины v2 и v3 и т. д. Последнее ребро, e8, соединяет вершины v4 и v5, тем самым задается описание графа в целом. Других ребер данный граф не содержит, как не содержит других вершин, не изображенных на рисунке. Так, хотя ребра е6 и e7 визуально пересекаются, но точка их пересечения не является вершиной графа.
Для ориентированного графа (рис. 2.4, б) ситуация несколько иная. А именно, вершины v1 и v2 соединены дугой е1, для которой вершина v2 является началом дуги, а вершина v1 – концом этой дуги. Далее дуга е2 соединяет вершины v1 и v4, при этом началом дуги e2 является вершина v1, а концом – вершина v4.
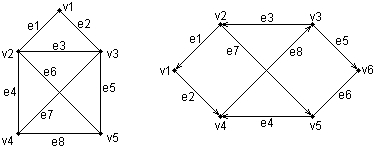Рис. 2.4.Примеры неориентированного (а) и ориентированного (б) графов
Графы широко применяются для представления различной информации о структуре систем и процессов. Примерами подобных графических моделей могут служить: схемы автомобильных дорог, соединяющих отдельные населенные пункты; схемы телекоммуникаций, используемых для передачи информации между отдельными узлами; схемы программ, на которых указываются варианты ветвления вычислительного процесса. Общим для всех конкретных подобных моделей является возможность представления информации в графическом виде в форме соответствующего графа. При этом отдельные модели, как правило, обладают дополнительной семантикой и специальными обозначениями, характерными для той или иной предметной области.
Важными понятиями теории графов являются понятия маршрута и пути, которые ассоциируются с последовательным перемещением от вершины к вершине по соединяющим их ребрам или дугам. Для неориентированного графа маршрут определяется как конечная или бесконечная упорядоченная последовательность ребер S=<, esl, es2, ..., esk>>, таких, что каждые два соседних ребра имеют общую вершину. Нас будут интересовать только конечные маршруты S=<es1, es2, ..., esk>, т. е. такие маршруты, которые состоят из конечного числа ребер. При этом ребро esl принято считать началом маршрута S, а ребро esk – концом маршрута S. Для ориентированного графа соответствующая последовательность дуг S=<es1, es2, ..., esk> называется ориентированным маршрутом, если две соседние дуги имеют общую вершину, которая является концом предыдущей и началом последующей дуги.
Примерами маршрутов для неориентированного графа (рис. 2.4, а) являются последовательности ребер: S1=<e1, e2 e5, e8>, S2=<e1, e2, е3, e1>, S3=<e3, e5, e8>. Если в маршруте не повторяются ни ребра, ни вершины, как в случае S1 и S3, то такой неориентированный маршрут называется простой цепью.
Примерами ориентированных маршрутов для графа (рис. 2.4, б) являются такие последовательности дуг: S1=<e2, e8, e5>, S2=<e3, e7, e6>, S3=<e8, e3, e7, e4, e8>. Если в ориентированном маршруте не повторяются ни ребра, ни вершины, как в случае S1 и S2, то такой ориентированный маршрут называется путем. Последнее понятие также иногда применяется для обозначения простой цепи в неориентированных графах и для определения специального класса графов, так называемых деревьев. В общем случае деревья служат для графического представления иерархических структур или иерархий, занимающих важное место в ООАП.
Деревом в теории графов называется такой граф D=<V, E>, между любыми двумя вершинами которого существует единственная простая цепь, т. е. неориентированный маршрут, у которого вершины и ребра не повторяются. Применительно к ориентированным графам соответствующее определение является более сложным, поскольку основывается на выделении некоторой специальной вершины v0, которая получила специальное название корневой вершины или просто – корня. В этом случае ориентированный граф D=<V, Е> называется ориентированным деревом или сокращенно – деревом, если между корнем дерева v0 и любой другой вершиной существует единственный путь, берущий начало в v0. Ниже представлены два примера деревьев: неориентированного дерева (рис. 2.5, а) и ориентированного дерева (рис. 2.5, б).
В случае неориентированного дерева (рис. 2.5, а) любая из вершин графа может быть выбрана в качестве корня. Подобный выбор определяется специфическими особенностями решаемой задачи. Так, вершина v1 может рассматриваться в качестве корня неориентированного дерева, поскольку между v1 и любой другой вершиной дерева всегда существует единственная простая цепь по определению (или, что менее строго, единственный неориентированный путь).
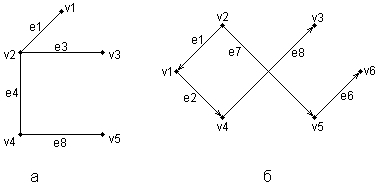Рис. 2.5.Примеры неориентированного (а) и ориентированного (б) деревьев
Для случая ориентированного дерева (рис. 2.5, б) вершина v2 является единственным его корнем и имеет специальное обозначение v0. Единственность корня в ориентированном дереве следует из того факта, что ориентированный путь всегда имеет единственную вершину, которая является его началом. Поскольку в теории графов имеет значение только наличие или отсутствие связей между отдельными вершинами, деревья, как правило, изображаются специальным образом в виде иерархической структуры. При этом корень дерева изображается самой верхней вершиной в данной иерархии. Далее следуют вершины уровня 1, которые связаны с корнем одним ребром или одной дугой. Следующий уровень будет иметь номер 2, поскольку соответствующие вершины должны быть связаны с корнем двумя последовательными ребрами или дугами. Процесс построения иерархического дерева продолжается до тех пор, пока не будут рассмотрены вершины, которые не связаны с другими вершинами, кроме рассмотренных, или из которых не выходит ни одна дуга. В этом случае самые нижние вершины иногда называют листьями дерева. Важно иметь в виду, что в теории графов дерево «растет» вниз, а не вверх, как в реальной жизни.
Изображенные выше деревья (рис. 2.5) можно преобразовать к виду иерархий. Например, неориентированное дерево (рис. 2.5, а) может быть представлено в виде иерархического дерева следующим образом (рис. 2.6, а). В этом случае корнем иерархии является вершина v1. Ориентированное дерево (рис. 2.5, б) также может быть изображено в форме иерархического дерева (рис. 2.6, б), однако такое представление является единственным.
В первом случае (рис. 2.6, а) вершина v2 образует первый уровень иерархии, вершины v4 и v3 – второй уровень иерархии, вершина v5 – третий и последний уровень иерархии. При этом листьями данного неориентированного дерева являются вершины v3 и v5. Во втором случае (рис. 2.6, б) вершины v1 и v5 образуют первый уровень иерархии, вершины v4 и v6 – второй уровень иерархии, вершина v3 – третий и последний уровень иерархии. Листьями данного ориентированного дерева являются вершины v3 и v6.
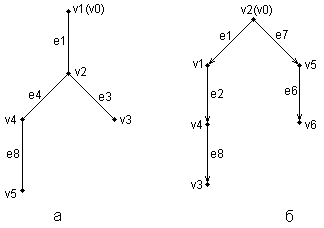Рис. 2.6.Иерархические схемы неориентированного дерева (а) и ориентированного дерева (б)
В заключение следует заметить, что в теории графов разработаны различные методы анализа отдельных классов графов и алгоритмы построения специальных графических объектов, рассмотрение которых выходит за рамки настоящей книги. Для получения дополнительной информации по данной теме можно рекомендовать обратиться к специальной литературе по теории графов, где эти вопросы рассмотрены более подробно. В дальнейшем нас будет интересовать отдельное направление в теории графов, которое связано с явным включением семантики в традиционные обозначения и получившее самостоятельное развитие в форме семантических сетей.
Графом называется совокупность двух множеств: множества точек или вершин и множества соединяющих их линий или ребер. Формально граф задается в виде двух множеств: G=(V, Е), где V={v1v2, ..., vn} – множество вершин графа, а Е={е1, е2, ..., еm} – множество ребер графа. Натуральное число n определяет общее количество вершин конкретного графа, а натуральное число m – общее количество ребер графа. Следует заметить, в общем случае не все вершины графа могут соединяться между собой, что ставит в соответствие каждому графу некоторое бинарное отношение PQ, состоящее из всех пар вида <vi, vj>, где vi, vj = V. При этом пара <vi, vj> и, соответственно, пара <vj, vi> принадлежат отношению PG в том и только в том случае, если вершины vi и vj соединяются в графе G некоторым ребром ek=Е. Вершины графа изображаются точками, а ребра – отрезками прямых линий. Рядом с вершинами и ребрами записываются соответствующие номера или идентификаторы, позволяющие их идентифицировать однозначным образом.
Примечание 14
Ниже представлены два примера конкретных графов (рис. 2.4). При этом первый из них (рис. 2.4, а) является неориентированным графом, а второй (рис. 2.4, б) – ориентированным графом. Как нетрудно заметить, для неориентированного графа ребро е1 соединяет вершины v1 и v2, ребро е2 – вершины v1 и v3, а ребро e3 – вершины v2 и v3 и т. д. Последнее ребро, e8, соединяет вершины v4 и v5, тем самым задается описание графа в целом. Других ребер данный граф не содержит, как не содержит других вершин, не изображенных на рисунке. Так, хотя ребра е6 и e7 визуально пересекаются, но точка их пересечения не является вершиной графа.
Для ориентированного графа (рис. 2.4, б) ситуация несколько иная. А именно, вершины v1 и v2 соединены дугой е1, для которой вершина v2 является началом дуги, а вершина v1 – концом этой дуги. Далее дуга е2 соединяет вершины v1 и v4, при этом началом дуги e2 является вершина v1, а концом – вершина v4.
Графы широко применяются для представления различной информации о структуре систем и процессов. Примерами подобных графических моделей могут служить: схемы автомобильных дорог, соединяющих отдельные населенные пункты; схемы телекоммуникаций, используемых для передачи информации между отдельными узлами; схемы программ, на которых указываются варианты ветвления вычислительного процесса. Общим для всех конкретных подобных моделей является возможность представления информации в графическом виде в форме соответствующего графа. При этом отдельные модели, как правило, обладают дополнительной семантикой и специальными обозначениями, характерными для той или иной предметной области.
Важными понятиями теории графов являются понятия маршрута и пути, которые ассоциируются с последовательным перемещением от вершины к вершине по соединяющим их ребрам или дугам. Для неориентированного графа маршрут определяется как конечная или бесконечная упорядоченная последовательность ребер S=<, esl, es2, ..., esk>>, таких, что каждые два соседних ребра имеют общую вершину. Нас будут интересовать только конечные маршруты S=<es1, es2, ..., esk>, т. е. такие маршруты, которые состоят из конечного числа ребер. При этом ребро esl принято считать началом маршрута S, а ребро esk – концом маршрута S. Для ориентированного графа соответствующая последовательность дуг S=<es1, es2, ..., esk> называется ориентированным маршрутом, если две соседние дуги имеют общую вершину, которая является концом предыдущей и началом последующей дуги.
Примерами маршрутов для неориентированного графа (рис. 2.4, а) являются последовательности ребер: S1=<e1, e2 e5, e8>, S2=<e1, e2, е3, e1>, S3=<e3, e5, e8>. Если в маршруте не повторяются ни ребра, ни вершины, как в случае S1 и S3, то такой неориентированный маршрут называется простой цепью.
Примерами ориентированных маршрутов для графа (рис. 2.4, б) являются такие последовательности дуг: S1=<e2, e8, e5>, S2=<e3, e7, e6>, S3=<e8, e3, e7, e4, e8>. Если в ориентированном маршруте не повторяются ни ребра, ни вершины, как в случае S1 и S2, то такой ориентированный маршрут называется путем. Последнее понятие также иногда применяется для обозначения простой цепи в неориентированных графах и для определения специального класса графов, так называемых деревьев. В общем случае деревья служат для графического представления иерархических структур или иерархий, занимающих важное место в ООАП.
Деревом в теории графов называется такой граф D=<V, E>, между любыми двумя вершинами которого существует единственная простая цепь, т. е. неориентированный маршрут, у которого вершины и ребра не повторяются. Применительно к ориентированным графам соответствующее определение является более сложным, поскольку основывается на выделении некоторой специальной вершины v0, которая получила специальное название корневой вершины или просто – корня. В этом случае ориентированный граф D=<V, Е> называется ориентированным деревом или сокращенно – деревом, если между корнем дерева v0 и любой другой вершиной существует единственный путь, берущий начало в v0. Ниже представлены два примера деревьев: неориентированного дерева (рис. 2.5, а) и ориентированного дерева (рис. 2.5, б).
В случае неориентированного дерева (рис. 2.5, а) любая из вершин графа может быть выбрана в качестве корня. Подобный выбор определяется специфическими особенностями решаемой задачи. Так, вершина v1 может рассматриваться в качестве корня неориентированного дерева, поскольку между v1 и любой другой вершиной дерева всегда существует единственная простая цепь по определению (или, что менее строго, единственный неориентированный путь).
Для случая ориентированного дерева (рис. 2.5, б) вершина v2 является единственным его корнем и имеет специальное обозначение v0. Единственность корня в ориентированном дереве следует из того факта, что ориентированный путь всегда имеет единственную вершину, которая является его началом. Поскольку в теории графов имеет значение только наличие или отсутствие связей между отдельными вершинами, деревья, как правило, изображаются специальным образом в виде иерархической структуры. При этом корень дерева изображается самой верхней вершиной в данной иерархии. Далее следуют вершины уровня 1, которые связаны с корнем одним ребром или одной дугой. Следующий уровень будет иметь номер 2, поскольку соответствующие вершины должны быть связаны с корнем двумя последовательными ребрами или дугами. Процесс построения иерархического дерева продолжается до тех пор, пока не будут рассмотрены вершины, которые не связаны с другими вершинами, кроме рассмотренных, или из которых не выходит ни одна дуга. В этом случае самые нижние вершины иногда называют листьями дерева. Важно иметь в виду, что в теории графов дерево «растет» вниз, а не вверх, как в реальной жизни.
Изображенные выше деревья (рис. 2.5) можно преобразовать к виду иерархий. Например, неориентированное дерево (рис. 2.5, а) может быть представлено в виде иерархического дерева следующим образом (рис. 2.6, а). В этом случае корнем иерархии является вершина v1. Ориентированное дерево (рис. 2.5, б) также может быть изображено в форме иерархического дерева (рис. 2.6, б), однако такое представление является единственным.
В первом случае (рис. 2.6, а) вершина v2 образует первый уровень иерархии, вершины v4 и v3 – второй уровень иерархии, вершина v5 – третий и последний уровень иерархии. При этом листьями данного неориентированного дерева являются вершины v3 и v5. Во втором случае (рис. 2.6, б) вершины v1 и v5 образуют первый уровень иерархии, вершины v4 и v6 – второй уровень иерархии, вершина v3 – третий и последний уровень иерархии. Листьями данного ориентированного дерева являются вершины v3 и v6.
В заключение следует заметить, что в теории графов разработаны различные методы анализа отдельных классов графов и алгоритмы построения специальных графических объектов, рассмотрение которых выходит за рамки настоящей книги. Для получения дополнительной информации по данной теме можно рекомендовать обратиться к специальной литературе по теории графов, где эти вопросы рассмотрены более подробно. В дальнейшем нас будет интересовать отдельное направление в теории графов, которое связано с явным включением семантики в традиционные обозначения и получившее самостоятельное развитие в форме семантических сетей.
Семантические сети
Семантические сети получили свое развитие в рамках научного направления, связанного с представлением знаний для моделирования рассуждений человека. Эта область научных исследований возникла в рамках общей проблематики искусственного интеллекта и была ориентирована на разработку специальных языков и графических средств для представления декларативных или, что менее точно, статических знаний о предметной области. Результаты исследований в области семантических сетей в последующем были конкретизированы и успешно использованы при построении концептуальных моделей и схем реляционных баз данных.
В общем случае под семантической сетью понимают некоторый граф Gs= =(Vs, Es), в котором множество вершин Vs и множество ребер Es разделены на отдельные типы, обладающие специальной семантикой, характерной для той или иной предметной области. В данной ситуации множество вершин может соответствовать объектам или сущностям рассматриваемой предметной области и иметь вместо номеров вершин соответствующие явные имена этих сущностей. Подобные имена должны позволять однозначно идентифицировать соответствующие объекты, при этом общих формальных правил записи имен не существует. Множество ребер также делится на различные типы, которые соответствуют различным видам связей между сущностями рассматриваемой предметной области.
Так, при построении семантической сети для представления знаний о рабочем персонале некоторой компании в качестве объектов целесообразно выбрать отдельных сотрудников, каждого из которых идентифицировать собственным именем и фамилией. Дополнительно в сети могут присутствовать такие объекты, как рабочие проекты и подразделения компании. В качестве семантических связей можно выделить такие виды, как должностное подчинение сотрудников, участие сотрудников в работе над проектами, принадлежность сотрудников тому или иному подразделению компании.
Важной особенностью семантических сетей является разработка специальных графических обозначений для представления отдельных типов вершин и ребер. При этом вершины не изображаются, как ранее – точками, а имеют вид прямоугольников, овалов, окружностей и других геометрических фигур, конкретный вид которых определяет тот или иной тип сущностей предметной области. Более разнообразным становится и изображение ребер, приобретающих вид различных линий со стрелками или без них, а также имеющих специальные обозначения или украшения в виде условных значков. Соответствующая система обозначений, предназначенная для представления информации об отдельных аспектах моделируемой предметной области, получила название графической нотации.
Примечание 15
В качестве конкретного варианта представления информации в виде семантической сети рассмотрим дальнейшее развитие примера с классом «Автомобиль» из главы 1. Фрагмент семантической сети, которая описывает иерархию классов данной предметной области, может быть изображен следующим образом (рис. 2.7). На данном рисунке отдельные вершины семантической сети изображаются прямоугольниками с закругленными концами и служат для условного обозначения классов данной предметной области. Соединяющие вершины ребра имеют вполне определенный смысл или семантику. А именно, они явно указывают, что вершина или класс, расположенные на рисунке ниже, являются подклассом того класса уровнем выше, с которым имеется связь в форме соединяющего их ребра.
Например, классы «Легковой автомобиль» и «Грузовой автомобиль» являются подклассами класса «Автомобиль», а классы «Модель ВАЗ-21083» и «Модель ВАЗ-21099» являются подклассами класса «Легковой автомобиль производства ВАЗ». Ребра или связи данной семантической сети имеют единственный тип, определяемый семантикой включения классов друг в друга. Поэтому никаких дополнительных обозначений они не содержат.
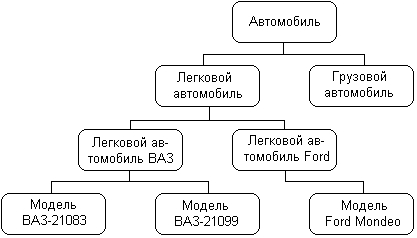Рис 2.7.Фрагмент семантической сети для представления иерархии классов «Автомобиль»
Примечание 16
Построение моделей сложных систем, отражающих десятки различных типов объектов и связей между ними, привело в конце 80-х годов к появлению большого числа различных графических нотаций, которые в той или иной степени были ориентированы на решение специальных классов задач. Сложилась парадоксальная ситуация, которая получила название «войны методов». Многие подходы, хотя и имели общие истоки, совершенно игнорировали другие альтернативные способы представления семантической информации. Наибольшее распространение в эти годы получил подход к моделированию программных систем, который назвали системным структурным анализом (ССА). Поскольку многие идеи ССА оказали непосредственное влияние на развитие языка UML, а используемая графическая нотация была реализована в некоторых CASE-средствах, ниже приводится краткая характеристика основных компонентов данного направления графического моделирования программных систем.
В общем случае под семантической сетью понимают некоторый граф Gs= =(Vs, Es), в котором множество вершин Vs и множество ребер Es разделены на отдельные типы, обладающие специальной семантикой, характерной для той или иной предметной области. В данной ситуации множество вершин может соответствовать объектам или сущностям рассматриваемой предметной области и иметь вместо номеров вершин соответствующие явные имена этих сущностей. Подобные имена должны позволять однозначно идентифицировать соответствующие объекты, при этом общих формальных правил записи имен не существует. Множество ребер также делится на различные типы, которые соответствуют различным видам связей между сущностями рассматриваемой предметной области.
Так, при построении семантической сети для представления знаний о рабочем персонале некоторой компании в качестве объектов целесообразно выбрать отдельных сотрудников, каждого из которых идентифицировать собственным именем и фамилией. Дополнительно в сети могут присутствовать такие объекты, как рабочие проекты и подразделения компании. В качестве семантических связей можно выделить такие виды, как должностное подчинение сотрудников, участие сотрудников в работе над проектами, принадлежность сотрудников тому или иному подразделению компании.
Важной особенностью семантических сетей является разработка специальных графических обозначений для представления отдельных типов вершин и ребер. При этом вершины не изображаются, как ранее – точками, а имеют вид прямоугольников, овалов, окружностей и других геометрических фигур, конкретный вид которых определяет тот или иной тип сущностей предметной области. Более разнообразным становится и изображение ребер, приобретающих вид различных линий со стрелками или без них, а также имеющих специальные обозначения или украшения в виде условных значков. Соответствующая система обозначений, предназначенная для представления информации об отдельных аспектах моделируемой предметной области, получила название графической нотации.
Примечание 15
В качестве конкретного варианта представления информации в виде семантической сети рассмотрим дальнейшее развитие примера с классом «Автомобиль» из главы 1. Фрагмент семантической сети, которая описывает иерархию классов данной предметной области, может быть изображен следующим образом (рис. 2.7). На данном рисунке отдельные вершины семантической сети изображаются прямоугольниками с закругленными концами и служат для условного обозначения классов данной предметной области. Соединяющие вершины ребра имеют вполне определенный смысл или семантику. А именно, они явно указывают, что вершина или класс, расположенные на рисунке ниже, являются подклассом того класса уровнем выше, с которым имеется связь в форме соединяющего их ребра.
Например, классы «Легковой автомобиль» и «Грузовой автомобиль» являются подклассами класса «Автомобиль», а классы «Модель ВАЗ-21083» и «Модель ВАЗ-21099» являются подклассами класса «Легковой автомобиль производства ВАЗ». Ребра или связи данной семантической сети имеют единственный тип, определяемый семантикой включения классов друг в друга. Поэтому никаких дополнительных обозначений они не содержат.
Примечание 16
Построение моделей сложных систем, отражающих десятки различных типов объектов и связей между ними, привело в конце 80-х годов к появлению большого числа различных графических нотаций, которые в той или иной степени были ориентированы на решение специальных классов задач. Сложилась парадоксальная ситуация, которая получила название «войны методов». Многие подходы, хотя и имели общие истоки, совершенно игнорировали другие альтернативные способы представления семантической информации. Наибольшее распространение в эти годы получил подход к моделированию программных систем, который назвали системным структурным анализом (ССА). Поскольку многие идеи ССА оказали непосредственное влияние на развитие языка UML, а используемая графическая нотация была реализована в некоторых CASE-средствах, ниже приводится краткая характеристика основных компонентов данного направления графического моделирования программных систем.
2.2. Диаграммы структурного системного анализа
Под структурным системным анализом принято понимать метод исследования системы, который начинается с наиболее общего ее описания с последующей детализацией представления отдельных аспектов ее поведения и функционирования. При этом общая модель системы строится в виде некоторой иерархической структуры, которая отражает различные уровни абстракции с ограниченным числом компонентов на каждом из уровней. Одним из главных принципов структурного системного анализа является выделение на каждом из уровней абстракции только наиболее существенных компонентов или элементов системы.
В рамках данного направления программной инженерии принято рассматривать три графические нотации, получивших названия диаграмм: диаграммы «сущность-связь» (Entity-Relationship Diagrams, ERD), диаграммы функционального моделирования (Structured Analysis and Design Technique, SADT) и диаграммы потоков данных (Data Flow Diagrams, DFD).
В рамках данного направления программной инженерии принято рассматривать три графические нотации, получивших названия диаграмм: диаграммы «сущность-связь» (Entity-Relationship Diagrams, ERD), диаграммы функционального моделирования (Structured Analysis and Design Technique, SADT) и диаграммы потоков данных (Data Flow Diagrams, DFD).
Диаграммы «сущность-связь»
Данная нотация была предложена П. Ченом (P. Chen) в его известной работе 1976 года [17] и получила дальнейшее развитие в работах Р. Баркера [16] (R. Barker). Диаграммы «сущность-связь» (ERD) предназначены для графического представления моделей данных разрабатываемой программной системы и предлагают некоторый набор стандартных обозначений для определения данных и отношений между ними. С помощью этого вида диаграмм можно описать отдельные компоненты концептуальной модели данных и совокупность взаимосвязей между ними, имеющих важное значение для разрабатываемой системы.
Основными понятиями данной нотации являются понятия сущности и связи. При этом под сущностью (entity) понимается произвольное множество реальных или абстрактных объектов, каждый из которых обладает одинаковыми свойствами и характеристиками. В этом случае каждый рассматриваемый объект может являться экземпляром одной и только одной сущности, должен иметь уникальное имя или идентификатор, а также отличаться от других экземпляров данной сущности.
Примерами сущностей могут быть: банк, клиент банка, счет клиента, аэропорт, пассажир, рейс, компьютер, терминал, автомобиль, водитель. Каждая из сущностей может рассматриваться с различной степенью детализации и на различном уровне абстракции, что определяется конкретной постановкой задачи. Для графического представления сущностей используются специальные обозначения (рис. 2.8).
Рис. 2.8.Графические изображения для обозначения сущностей
Связь (relationship) определяется как отношение или некоторая ассоциация между отдельными сущностями. Примерами связей могут являться родственные отношения типа «отец-сын» или производственные отношения типа «начальник-подчиненный». Другой тип связей задается отношениями «иметь в собственности» или «обладать свойством». Различные типы связей графически изображаются в форме ромба с соответствующим именем данной связи (рис. 2.9).
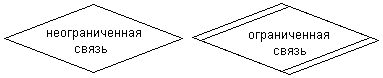Рис. 2.9.Графические изображения для обозначения связей
Графическая модель данных строится таким образом, чтобы связи между отдельными сущностями отражали не только семантический характер соответствующего отношения, но и дополнительные аспекты обязательности связей, а также кратность участвующих в данных отношениях экземпляров сущностей.
Рассмотрим в качестве простого примера ситуацию, которая описывается двумя сущностями: «Сотрудник» и «Компания». При этом в качестве связи естественно. использовать отношение принадлежности сотрудника данной компании. Если учесть соображения о том, что в компании работают несколько сотрудников, и эти сотрудники не могут быть работниками других компаний, то данная информация может быть представлена графически в виде следующей диаграммы «сущность-связь» (рис. 2.10). На данном рисунке буква "N" около связи означает тот факт, что в компании могут работать более одного сотрудника, при этом значение N заранее не фиксируется. Цифра "1" на другом конце связи означает, что сотрудник может работать только в одной конкретной компании, т. е. не допускается прием на работу сотрудников по совместительству из других компаний или учреждений.
Рис. 2.10.Диаграмма «сущность-связь» для примера сотрудников некоторой компании
Несколько иная ситуация складывается в случае рассмотрения сущностей «сотрудник» и «проект», и связи «участвует в работе над проектом» (рис. 2.11). Поскольку в общем случае один сотрудник может участвовать в разработке нескольких проектов, а в разработке одного проекта могут принимать участие несколько сотрудников, то данная связь является многозначной. Данный факт специально отражается на диаграмме указанием букв "N" и "М" около соответствующих сущностей, при этом выбор конкретных букв не является принципиальным.
Рис. 2.11.Диаграмма «сущность-связь» для примера сотрудников, участвующих в работе над проектами
Рассмотренные две диаграммы могут быть объединены в одну, на которой будет представлена информация о сотрудниках компании, участвующих в разработке проектов данной компании (рис. 2.12). При этом может быть введена дополнительная связь, характеризующая проекты данной компании.
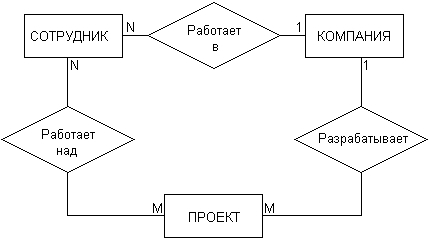Рис. 2.12.Диаграмма «сущность-связь» для общего примера компании
Примечание 17
Ограниченность ERD проявляется при конкретизации концептуальной модели в более детальное представление моделируемой программной системы, которое кроме статических связей должно содержать информацию о поведении или функционировании отдельных ее компонентов. Для этих целей в рамках ССА используется другой тип диаграмм, получивших название диаграмм потоков данных. А сейчас перейдем к диаграммам SADT.
Основными понятиями данной нотации являются понятия сущности и связи. При этом под сущностью (entity) понимается произвольное множество реальных или абстрактных объектов, каждый из которых обладает одинаковыми свойствами и характеристиками. В этом случае каждый рассматриваемый объект может являться экземпляром одной и только одной сущности, должен иметь уникальное имя или идентификатор, а также отличаться от других экземпляров данной сущности.
Примерами сущностей могут быть: банк, клиент банка, счет клиента, аэропорт, пассажир, рейс, компьютер, терминал, автомобиль, водитель. Каждая из сущностей может рассматриваться с различной степенью детализации и на различном уровне абстракции, что определяется конкретной постановкой задачи. Для графического представления сущностей используются специальные обозначения (рис. 2.8).
Связь (relationship) определяется как отношение или некоторая ассоциация между отдельными сущностями. Примерами связей могут являться родственные отношения типа «отец-сын» или производственные отношения типа «начальник-подчиненный». Другой тип связей задается отношениями «иметь в собственности» или «обладать свойством». Различные типы связей графически изображаются в форме ромба с соответствующим именем данной связи (рис. 2.9).
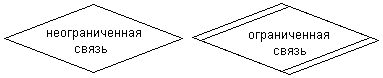
Графическая модель данных строится таким образом, чтобы связи между отдельными сущностями отражали не только семантический характер соответствующего отношения, но и дополнительные аспекты обязательности связей, а также кратность участвующих в данных отношениях экземпляров сущностей.
Рассмотрим в качестве простого примера ситуацию, которая описывается двумя сущностями: «Сотрудник» и «Компания». При этом в качестве связи естественно. использовать отношение принадлежности сотрудника данной компании. Если учесть соображения о том, что в компании работают несколько сотрудников, и эти сотрудники не могут быть работниками других компаний, то данная информация может быть представлена графически в виде следующей диаграммы «сущность-связь» (рис. 2.10). На данном рисунке буква "N" около связи означает тот факт, что в компании могут работать более одного сотрудника, при этом значение N заранее не фиксируется. Цифра "1" на другом конце связи означает, что сотрудник может работать только в одной конкретной компании, т. е. не допускается прием на работу сотрудников по совместительству из других компаний или учреждений.
Несколько иная ситуация складывается в случае рассмотрения сущностей «сотрудник» и «проект», и связи «участвует в работе над проектом» (рис. 2.11). Поскольку в общем случае один сотрудник может участвовать в разработке нескольких проектов, а в разработке одного проекта могут принимать участие несколько сотрудников, то данная связь является многозначной. Данный факт специально отражается на диаграмме указанием букв "N" и "М" около соответствующих сущностей, при этом выбор конкретных букв не является принципиальным.
Рассмотренные две диаграммы могут быть объединены в одну, на которой будет представлена информация о сотрудниках компании, участвующих в разработке проектов данной компании (рис. 2.12). При этом может быть введена дополнительная связь, характеризующая проекты данной компании.
Примечание 17
Ограниченность ERD проявляется при конкретизации концептуальной модели в более детальное представление моделируемой программной системы, которое кроме статических связей должно содержать информацию о поведении или функционировании отдельных ее компонентов. Для этих целей в рамках ССА используется другой тип диаграмм, получивших название диаграмм потоков данных. А сейчас перейдем к диаграммам SADT.
Диаграммы функционального моделирования
Начало разработки диаграмм функционального моделирования относится к середине 1960-х годов, когда Дуглас Т. Росс предложил специальную технику моделирования, получившую название SADT (Structured Analysis & Design Technique). Военно-воздушные силы США использовали методику SADT в качестве части своей программы интеграции компьютерных и промышленных технологий (Integrated Computer Aided Manufacturing, ICAM) и назвали ее IDEFO (Icam DEFinition). Целью программы ICAM было увеличение эффективности компьютерных технологий в сфере проектирования новых средств вооружений и ведения боевых действий. Одним из результатов этих исследований являлся вывод о том, что описательные языки не эффективны для документирования и моделирования процессов функционирования сложных систем. Подобные описания на естественном языке не обеспечивают требуемого уровня непротиворечивости и полноты, имеющих доминирующее значение при решении задач моделирования.
В рамках программы ICAM было разработано несколько графических языков моделирования, которые получили следующие названия:
В начале 1990 года специально образованная группа пользователей IDEF (IDEF Users Group), в сотрудничестве с Национальным институтом по стандартизации и технологии США (National Institutes for Standards and Technology, NIST), предприняла попытку создания стандарта для IDEFO и IDEF1X. Эта попытка оказалась успешной и завершилась принятием в 1993 году стандарта правительства США, известного как FIPS для данных двух технологий IDEFO и IDEF1X. В течение последующих лет этот стандарт продолжал активно развиваться и послужил основой для реализации в некоторых первых CASE-средствах.
Методология IDEF-SADT представляет собой совокупность методов, правил и процедур, предназначенных для построения функциональной модели сиетемы какой-либо предметной области. Функциональная модель SADT отображает структуру процессов функционирования системы и ее отдельных подсистем, т. е. выполняемые ими действия и связи между этими действиями. Для этой цели строятся специальные модели, которые позволяют в наглядной форме представить последовательность определенных действий. Исходными строительными блоками любой модели IDEFO процесса являются деятельность (activity) и стрелки (arrows).
Рассмотрим кратко эти основные понятия методологии IDEF-SADT, которые используются при построении диаграмм функционального моделирования. Деятельность представляет собой некоторое действие или набор действий, которые имеют фиксированную цель и приводят к некоторому конечному результату. Иногда деятельность называют просто процессом. Модели IDEFO отслеживают различные виды деятельности системы, их описание и взаимодействие с другими процессами. На диаграммах деятельность или процесс изображается прямоугольником, который называется блоком. Стрелка служит для обозначения некоторого носителя или воздействия, которые обеспечивают перенос данных или объектов от одной деятельности к другой. Стрелки также необходимы для описания того, что именно производит деятельность и какие ресурсы она потребляет. Это так называемые роли стрелок – ICOM – сокращение первых букв от названий соответствующих стрелок IDEFO. При этом различают стрелки четырех видов:
В рамках программы ICAM было разработано несколько графических языков моделирования, которые получили следующие названия:
• Нотация IDEF0 – для документирования процессов производства и отображения информации об использовании ресурсов на каждом из этапов проектирования систем.Нотация IDEF2 никогда не была полностью реализована. Нотация IDEF1 в 1985 году была расширена и переименована в IDEF1X. Методология IDEF-SADT, нашла применение в правительственных и коммерческих организациях, поскольку на тот период времени вполне удовлетворяла различным требованиям, предъявляемым к моделированию широкого класса систем.
• Нотация IDEF1 – для документирования информации о производственном окружении систем.
• Нотация IDEF2 – для документирования поведения системы во времени.
• Нотация IDEF3 – специально для моделирования бизнес-процессов.
В начале 1990 года специально образованная группа пользователей IDEF (IDEF Users Group), в сотрудничестве с Национальным институтом по стандартизации и технологии США (National Institutes for Standards and Technology, NIST), предприняла попытку создания стандарта для IDEFO и IDEF1X. Эта попытка оказалась успешной и завершилась принятием в 1993 году стандарта правительства США, известного как FIPS для данных двух технологий IDEFO и IDEF1X. В течение последующих лет этот стандарт продолжал активно развиваться и послужил основой для реализации в некоторых первых CASE-средствах.
Методология IDEF-SADT представляет собой совокупность методов, правил и процедур, предназначенных для построения функциональной модели сиетемы какой-либо предметной области. Функциональная модель SADT отображает структуру процессов функционирования системы и ее отдельных подсистем, т. е. выполняемые ими действия и связи между этими действиями. Для этой цели строятся специальные модели, которые позволяют в наглядной форме представить последовательность определенных действий. Исходными строительными блоками любой модели IDEFO процесса являются деятельность (activity) и стрелки (arrows).
Рассмотрим кратко эти основные понятия методологии IDEF-SADT, которые используются при построении диаграмм функционального моделирования. Деятельность представляет собой некоторое действие или набор действий, которые имеют фиксированную цель и приводят к некоторому конечному результату. Иногда деятельность называют просто процессом. Модели IDEFO отслеживают различные виды деятельности системы, их описание и взаимодействие с другими процессами. На диаграммах деятельность или процесс изображается прямоугольником, который называется блоком. Стрелка служит для обозначения некоторого носителя или воздействия, которые обеспечивают перенос данных или объектов от одной деятельности к другой. Стрелки также необходимы для описания того, что именно производит деятельность и какие ресурсы она потребляет. Это так называемые роли стрелок – ICOM – сокращение первых букв от названий соответствующих стрелок IDEFO. При этом различают стрелки четырех видов: