Однако анализ опыта показывает, что законы механики здесь не пострадали. Дело в том, что человек целиком в этом опыте не вращается. Одна его часть – туловище, поворачивается справа налево, а рука с гантелью, обладая существенным моментом инерции, в результате поворачивается слева направо. Можно было упростить этот опыт, сделав его, правда, более уязвимым для разоблачения, просто вращая руку с гантелью над головой. Туловище в этом случае стало бы вращаться в противоположную сторону.
Сбивает с толку в этих опытах то, что мы справедливо подмечаем вращение туловища, а то, что рука с гантелью тоже совершает вращательное движение вокруг оси вращения скамьи Жуковского, не учитываем.
Так как кинетический момент системы до начала движения был равен нулю, то таким же он остается и во время движения частей тела человека, потому что внешние моменты (со стороны других тел) на нас при этом не действуют.
Надо заметить, что кошки в падении инстинктивно используют этот закон механики (закон сохранения кинетического момента системы) для приземления на лапы из любого положения. Мгновенно оценивая ситуацию, кошка понимает, куда ей нужно повернуться, и начинает быстро вращать вытянутым хвостом в противоположную сторону. Если кошка почему-либо без хвоста, или он у нее короткий, то животное начинает вращать задней частью туловища, совсем как мы вращали над головой руку с гантелью. И делает это кошка до тех пор, пока не повернется всеми четырьмя (или, по крайней мере, двумя передними) лапами вниз.
Рссмотрим другой парадоксальный опыт.
Поставим скамью Жуковского чуть наклонно, подложив, например, с одной стороны под нее книгу. Затем встанем на этот диск, выпрямившись поровнее. И почувствуем, что... начинаем раскручиваться! Сами, без каких-нибудь телодвижений или посторонней помощи. Обычно удержаться на таком все ускоряющем свое вращение диске более минуты невозможно, и человек в самых нелепых позах слетает на пол.
В чем же здесь дело? Стоя вертикально, человек инстиктивно смещает давление своих подошв на верхнюю половину диска. Диск при этом, конечно же, проворачивается, чтобы груз, то есть человек, занял наиболее низкое положение, согласно известному принципу наименьшего действия (минимума потенциальной энергии). Человек опять же инстиктивно пытается снова стать прямо, и весь описанный цикл повторяется. Так человек раскручивает диск все быстрее, пока тот не сбросит его на пол.
Однако, если поставить на этот диск статую, то она, разумеется, раскручиваться не будет, иначе мы получим самый настоящий вечный двигатель. Так вот, если человек хочет удержать себя от раскручивания, то он должен стоять на этом наклонном диске как статуя – тоже наклонно. Но, как показал опыт, человеку это очень трудно сделать.
И в этом опыте законы механики дают вращению объяснение. Диск вращает внешняя сила – вес тела человека. Линия действия этой силы не проходит через ось вращения, поэтому-то она и вызывает момент, вращающий диск с человеком.
5.11. Вопрос. Какую мощность может развить человек?
Ответ. Тут вопрос в том, в течение какого времени эта мощность развивается и какая при этом энергия выделяется – механическая или тепловая.
В справочниках по физике можно прочесть, что средняя мощность человека– это 150–300 ватт. Давайте остановимся на меньшей цифре и проверим это утверждение.
Что такое 150 Вт применительно к человеку? Это мощность, которую развивает человек, непрерывно каждые 2 секунды поднимая пудовую гирю. Попробуйте проделать это упражнение хотя бы 3 минуты и, если вы не профессиональный гиревик, то поймете, что такое 150 Вт! Замерьте время, в течение которого вы осиливаете это упражнение, а затем поделите на это время 6–8 часов – время рабочего дня. Полученная двух, а то и трехзначная цифра покажет, во сколько раз преувеличены возможности человека.
Меньшие мощности человек переносит легче. Измерять их лучше всего на велотренажере, где мощность прямо высвечивается на табло. На современных велотренажерах вы можете даже получить работу в джоулях, совершенную за тот или иной промежуток времени. Так вот, работая и отдыхая в течение рабочего дня, сложите полученную сумму работ, поделите ее на продолжительность вашего рабочего дня в секундах и получите вашу среднюю мощность в ваттах. Не огорчайтесь, если получится очень малая цифра – к сожалению, это так и есть, если только вы не олимпийский чемпион по велоспорту.
Кстати, о чемпионах. Очень сильные люди, например штангисты, при рывке штанги двумя руками (первое движение двоеборья) могут развить мощность до 1,5–2 кВт и более, но очень кратковременно, не более 2–3 секунд. А средняя мощность обычного человека за 6–8 часов близка к мощности карманного фонарика и равна нескольким ваттам. Спокойно едущий велосипедист развивает мощность до 20 Вт, но попробуйте непрерывно проехать около 7 часов!
А как же справочные данные по средней мощности человека? Видимо, авторы справочника имели в виду не механическую, а тепловую мощность. Если раздетый человек стоит в ледяной проточной воде, то выделяемая им мощность на согревание воды будет поболее 300 Вт! В холодное время года средняя тепловая мощность человека больше, а в теплое – меньше. Поэтому зимой, особенно на холоде, человек ест больше, предпочитая калорийную жирную пищу. И очень небольшая часть энергии, выделяемой пищей в результате ее «сгорания» в организме, менее 6–8 %, выделяется в виде механической энергии.
Даже лошадь в среднем развивает мощность от 0,1 до 0,5 лошадиной силы. Следует помнить, что для определения эталона мощности – лошадиной силы или 736 Вт, была загнана насмерть за несколько часов одна из самых сильных лошадей!
5.12. Вопрос. Иногда говорят, что вращающийся маховик весит меньше неподвижного; может ли это быть?
Ответ. Действительно, в печати иногда появляются сообщения о том, что вращающийся с высокой скоростью маховик «теряет в весе». Это явление объясняют действием некой «антигравитации».
Если попробовать взвесить вращающийся маховик на чаше весов, то действительно можно обнаружить обескураживающее явление – кажущееся убавление веса маховика, причем существенное. Если предположить, что весы невероятно точны, а маховик вращается также с невероятной скоростью, то, согласно положениям релятивистской механики, возможно некоторое увеличение массы маховика за счет накопленной в нем энергии. Но чем же можно объяснить уменьшение веса?
Рассмотрим вращающийся маховик, нижняя плоскость которого находится вблизи плоскости чаши весов (рис. 34). Опыт проводится в воздухе, поэтому в щели между маховиком и чашей весов, а также над маховиком образуется разрежение, так как воздух отгоняется наружу как в центробежном насосе. Воздух, отгоняемый наружу верхней плоскостью вращающегося маховика, создает разрежение, «втягивающее» маховик вверх. Внешняя сила давления воздуха снизу на чашу весов (так как давление воздуха здесь выше, чем у верхнего торца маховика) нарушает равновесие весов, якобы уменьшая массу килограммового маховика на десятки граммов.
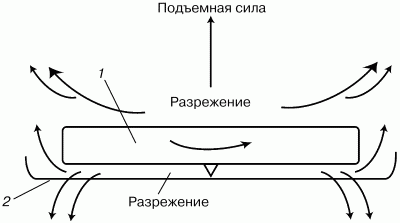Рис. 34. Почему вращающийся в воздухе маховик весит меньше неподвижного:
1– маховик;
2– чаша весов.
Весьма точные опыты по взвешиванию вращающегося маховика гироскопа проводились и в вакууме, где было также обнаружено уменьшение веса маховика, но уже всего на миллиграммы [11, с.144].
Тщательная проверка этого парадокса в Институте Механики РАН показала, что объясняется он вполне «земными» причинами. Прежде всего, вибрация, которой неизбежно сопровождается вращение маховика, оказывает влияние на чувствительные элементы весов – их призмы. При этом сопротивление в призмах то уменьшается, то растет в зависимости от направления ускорений при вибрации. В результате при ходе коромысла весов в сторону маховика призмы из-за дополнительной нагрузки более затрублены в показаниях, чем при обратном ходе, когда они разгружены. Поэтому чаша весов с неподвижными гирями при вибрациях перевешивает «активную» вибрирующую чашу.
Такими образом, нет оснований полагать, что вращающийся маховик будет иметь массу меньше неподвижного.
5.13. Вопрос. Можно ли сдвинуть ось вращения Земли, ускорить или замедлить ее вращение, находясь на ней самой?
Ответ. Вопрос этот несколько похож на вопрос 5.10 потому, что его можно сформулировать и так: «Можно ли внутренними моментами изменить значение кинетического момента Земли?»
Согласно законам механики этого, конечно, сделать нельзя. Но если дополнительные устройства, необходимые для этого, не считать принадлежащими самой Земле, то принципиально можно и замедлить и убыстрить вращение Земли, как и сместить на определенный угол ось ее вращения.
В действительности каждый наш шаг, движение каждой молекулы уже изменяют упомянутые параметры вращения Земли на ничтожно малые значения, если, конечно, считать нас самих или эту молекулу, не входящими в «состав» Земли. Речь идет о том, как не будучи ограниченными в технических и финансовых возможностях, изменить упомянутые параметры в ощутимых пределах.
Для увеличения или уменьшения частоты вращения Земли, иначе говоря, для изменения продолжительности суток можно в районе полюса, удобнее в районе Южного географического полюса, так как там суша, установить соосно самой Земле громадный маховик с приводом его вращения в ту или другую сторону. Сам привод, например огромный электродвигатель, естественно, закреплен на Земле, а маховик посажен на его вал (рис. 35). Раскручивая маховик в сторону вращения Земли, мы реактивным моментом, передающимся Земле корпусом двигателя, замедляем угловую скорость планеты. Разгоняя маховик в противоположную сторону, мы увеличиваем угловую скорость вращения Земли. Однако в любом случае кинетический момент системы «Земля – маховик» останется постоянным. Заметим, что существует похожий способ ориентирования космических аппаратов, и маховичные устройства для этого называются гиродинами.
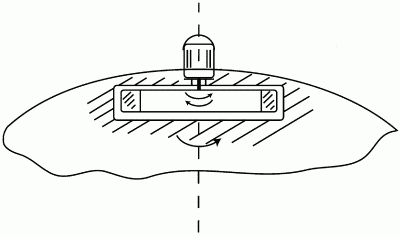Рис. 35. Маховик в недрах Антарктиды, вращающийся соосно Земле.
Если разместить столь же крупный маховик в районе экватора (рис. 36) и раскрутить его, то вектор его кинетического момента, складываясь с вектором кинетического момента Земли, образует новое направление суммарного вектора, который изменит положение оси вращения Земли. Вот мы и сумели обойтись без жюль-верновской стрельбы из сверхпушки, которая, как оказалось, мало чем смогла бы помочь в изменении положения земной оси.
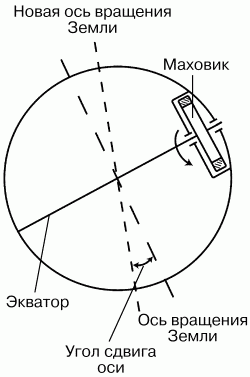Рис. 36. Схема расположения маховика на Земле для поворота оси Земли.
5.14. Вопрос. Можно ли, находясь на самой Земле, использовать энергию вращения Земли?
Ответ. О том, что это можно сделать, находясь на Луне, уже было сказано. Луна постоянно отнимает от энергии вращения Земли огромные величины. Но можно ли сделать это, находясь на самой Земле?
Поместим на полюсе Земли платформу и плашмя положим на нее неподвижный маховик в опорах – подшипниках (рис. 37). Угловые скорости маховика и Земли будут совпадать. Затем каким-нибудь мощным манипулятором ухватим маховик за опоры и перевернем его на другую сторону.
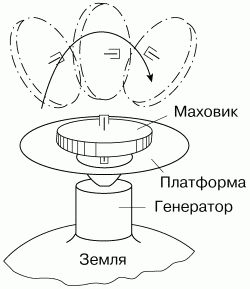Рис. 37. Маховик на платформе на полюсе Земли.
Угловая скорость маховика по величине сохранится, но направлена она будет уже в другую сторону. Платформа будет вращаться в сторону, противоположную вращению Земли, и ее относительная угловая скорость будет равна удвоенной угловой скорости Земли.
Включаем генератор и отбираем энергию, пока угловые скорости Земли и платформы не совпадут. После этого опять поворачиваем маховик, как блин на сковороде, и опять «снимаем» разность угловых скоростей генератором. И будем поступать так, пока Земля не перестанет вращаться!
Неужели действительно таким образом можно использовать энергию вращения Земли? Ответ на этот вопрос можно получить из следующего опыта.
Встанем на скамью Жуковского, держа в руках за неподвижную ось переднее колесо велосипеда, желательно побольше диаметром и помассивнее (рис. 38). Прижимая колесо к себе шиной, раскрутимся на скамье до угловой скорости, которую легко сможем выдержать не падая. Затем, отодвинув колесо от себя, перевернем его за ось на 180 градусов на другую сторону. Колесо будет вращаться в подшипниках на оси с той же угловой скоростью, что и раньше, только в другую сторону. Затормозим колесо, прижав его к себе шиной, тем самым отобрав у него кинетическую энергию вращения. Теперь опять перевернем это колесо, опять же тормозя его и отбирая кинетическую энергию.
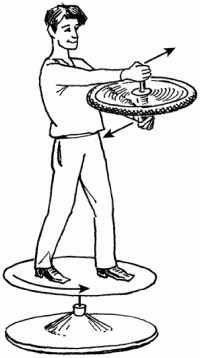Рис. 38. Опыт, имитирующий отбор энергии от вращающейся Земли.
Этим опытом мы смоделируем предполагаемое использование энергии вращения Земли с помощью переворачиваемого маховика. Обратим внимание на то, что угловая скорость скамьи Жуковского, имитирующей Землю, не уменьшается (не учитывая, конечно, потери в подшипниках на собственное вращение), несмотря на то, что после каждого переворота колеса мы тормозим его, отбирая кинетическую энергию.
Интересно, какое объяснение дадут этому «неправдоподобному» опыту сами ученики. Можно только добавить, что будем считать упомянутый мощный манипулятор, который, как руками, сможет подхватить маховик за подшипники и перевернуть его, технически исполнимым.
Объяснение этого парадокса заключается в том, что, переворачивая маховик, мы вызываем гироскопический момент, разгоняющий Землю. Вновь «скрепляя» Землю с маховиком после его переворота, мы Землю тормозим. Поэтому скорость вращения Земли при переворачивании маховика никак не изменится. А энергия, затраченная на «переворот» маховика, перейдет в тепло при его соприкосновении с Землей.
Так что энергии от вращения Земли, находясь на ней самой, получить нельзя.
Список использованной и рекомендуемой литературы
Сбивает с толку в этих опытах то, что мы справедливо подмечаем вращение туловища, а то, что рука с гантелью тоже совершает вращательное движение вокруг оси вращения скамьи Жуковского, не учитываем.
Так как кинетический момент системы до начала движения был равен нулю, то таким же он остается и во время движения частей тела человека, потому что внешние моменты (со стороны других тел) на нас при этом не действуют.
Надо заметить, что кошки в падении инстинктивно используют этот закон механики (закон сохранения кинетического момента системы) для приземления на лапы из любого положения. Мгновенно оценивая ситуацию, кошка понимает, куда ей нужно повернуться, и начинает быстро вращать вытянутым хвостом в противоположную сторону. Если кошка почему-либо без хвоста, или он у нее короткий, то животное начинает вращать задней частью туловища, совсем как мы вращали над головой руку с гантелью. И делает это кошка до тех пор, пока не повернется всеми четырьмя (или, по крайней мере, двумя передними) лапами вниз.
Рссмотрим другой парадоксальный опыт.
Поставим скамью Жуковского чуть наклонно, подложив, например, с одной стороны под нее книгу. Затем встанем на этот диск, выпрямившись поровнее. И почувствуем, что... начинаем раскручиваться! Сами, без каких-нибудь телодвижений или посторонней помощи. Обычно удержаться на таком все ускоряющем свое вращение диске более минуты невозможно, и человек в самых нелепых позах слетает на пол.
В чем же здесь дело? Стоя вертикально, человек инстиктивно смещает давление своих подошв на верхнюю половину диска. Диск при этом, конечно же, проворачивается, чтобы груз, то есть человек, занял наиболее низкое положение, согласно известному принципу наименьшего действия (минимума потенциальной энергии). Человек опять же инстиктивно пытается снова стать прямо, и весь описанный цикл повторяется. Так человек раскручивает диск все быстрее, пока тот не сбросит его на пол.
Однако, если поставить на этот диск статую, то она, разумеется, раскручиваться не будет, иначе мы получим самый настоящий вечный двигатель. Так вот, если человек хочет удержать себя от раскручивания, то он должен стоять на этом наклонном диске как статуя – тоже наклонно. Но, как показал опыт, человеку это очень трудно сделать.
И в этом опыте законы механики дают вращению объяснение. Диск вращает внешняя сила – вес тела человека. Линия действия этой силы не проходит через ось вращения, поэтому-то она и вызывает момент, вращающий диск с человеком.
5.11. Вопрос. Какую мощность может развить человек?
Ответ. Тут вопрос в том, в течение какого времени эта мощность развивается и какая при этом энергия выделяется – механическая или тепловая.
В справочниках по физике можно прочесть, что средняя мощность человека– это 150–300 ватт. Давайте остановимся на меньшей цифре и проверим это утверждение.
Что такое 150 Вт применительно к человеку? Это мощность, которую развивает человек, непрерывно каждые 2 секунды поднимая пудовую гирю. Попробуйте проделать это упражнение хотя бы 3 минуты и, если вы не профессиональный гиревик, то поймете, что такое 150 Вт! Замерьте время, в течение которого вы осиливаете это упражнение, а затем поделите на это время 6–8 часов – время рабочего дня. Полученная двух, а то и трехзначная цифра покажет, во сколько раз преувеличены возможности человека.
Меньшие мощности человек переносит легче. Измерять их лучше всего на велотренажере, где мощность прямо высвечивается на табло. На современных велотренажерах вы можете даже получить работу в джоулях, совершенную за тот или иной промежуток времени. Так вот, работая и отдыхая в течение рабочего дня, сложите полученную сумму работ, поделите ее на продолжительность вашего рабочего дня в секундах и получите вашу среднюю мощность в ваттах. Не огорчайтесь, если получится очень малая цифра – к сожалению, это так и есть, если только вы не олимпийский чемпион по велоспорту.
Кстати, о чемпионах. Очень сильные люди, например штангисты, при рывке штанги двумя руками (первое движение двоеборья) могут развить мощность до 1,5–2 кВт и более, но очень кратковременно, не более 2–3 секунд. А средняя мощность обычного человека за 6–8 часов близка к мощности карманного фонарика и равна нескольким ваттам. Спокойно едущий велосипедист развивает мощность до 20 Вт, но попробуйте непрерывно проехать около 7 часов!
А как же справочные данные по средней мощности человека? Видимо, авторы справочника имели в виду не механическую, а тепловую мощность. Если раздетый человек стоит в ледяной проточной воде, то выделяемая им мощность на согревание воды будет поболее 300 Вт! В холодное время года средняя тепловая мощность человека больше, а в теплое – меньше. Поэтому зимой, особенно на холоде, человек ест больше, предпочитая калорийную жирную пищу. И очень небольшая часть энергии, выделяемой пищей в результате ее «сгорания» в организме, менее 6–8 %, выделяется в виде механической энергии.
Даже лошадь в среднем развивает мощность от 0,1 до 0,5 лошадиной силы. Следует помнить, что для определения эталона мощности – лошадиной силы или 736 Вт, была загнана насмерть за несколько часов одна из самых сильных лошадей!
5.12. Вопрос. Иногда говорят, что вращающийся маховик весит меньше неподвижного; может ли это быть?
Ответ. Действительно, в печати иногда появляются сообщения о том, что вращающийся с высокой скоростью маховик «теряет в весе». Это явление объясняют действием некой «антигравитации».
Если попробовать взвесить вращающийся маховик на чаше весов, то действительно можно обнаружить обескураживающее явление – кажущееся убавление веса маховика, причем существенное. Если предположить, что весы невероятно точны, а маховик вращается также с невероятной скоростью, то, согласно положениям релятивистской механики, возможно некоторое увеличение массы маховика за счет накопленной в нем энергии. Но чем же можно объяснить уменьшение веса?
Рассмотрим вращающийся маховик, нижняя плоскость которого находится вблизи плоскости чаши весов (рис. 34). Опыт проводится в воздухе, поэтому в щели между маховиком и чашей весов, а также над маховиком образуется разрежение, так как воздух отгоняется наружу как в центробежном насосе. Воздух, отгоняемый наружу верхней плоскостью вращающегося маховика, создает разрежение, «втягивающее» маховик вверх. Внешняя сила давления воздуха снизу на чашу весов (так как давление воздуха здесь выше, чем у верхнего торца маховика) нарушает равновесие весов, якобы уменьшая массу килограммового маховика на десятки граммов.
Весьма точные опыты по взвешиванию вращающегося маховика гироскопа проводились и в вакууме, где было также обнаружено уменьшение веса маховика, но уже всего на миллиграммы [11, с.144].
Тщательная проверка этого парадокса в Институте Механики РАН показала, что объясняется он вполне «земными» причинами. Прежде всего, вибрация, которой неизбежно сопровождается вращение маховика, оказывает влияние на чувствительные элементы весов – их призмы. При этом сопротивление в призмах то уменьшается, то растет в зависимости от направления ускорений при вибрации. В результате при ходе коромысла весов в сторону маховика призмы из-за дополнительной нагрузки более затрублены в показаниях, чем при обратном ходе, когда они разгружены. Поэтому чаша весов с неподвижными гирями при вибрациях перевешивает «активную» вибрирующую чашу.
Такими образом, нет оснований полагать, что вращающийся маховик будет иметь массу меньше неподвижного.
5.13. Вопрос. Можно ли сдвинуть ось вращения Земли, ускорить или замедлить ее вращение, находясь на ней самой?
Ответ. Вопрос этот несколько похож на вопрос 5.10 потому, что его можно сформулировать и так: «Можно ли внутренними моментами изменить значение кинетического момента Земли?»
Согласно законам механики этого, конечно, сделать нельзя. Но если дополнительные устройства, необходимые для этого, не считать принадлежащими самой Земле, то принципиально можно и замедлить и убыстрить вращение Земли, как и сместить на определенный угол ось ее вращения.
В действительности каждый наш шаг, движение каждой молекулы уже изменяют упомянутые параметры вращения Земли на ничтожно малые значения, если, конечно, считать нас самих или эту молекулу, не входящими в «состав» Земли. Речь идет о том, как не будучи ограниченными в технических и финансовых возможностях, изменить упомянутые параметры в ощутимых пределах.
Для увеличения или уменьшения частоты вращения Земли, иначе говоря, для изменения продолжительности суток можно в районе полюса, удобнее в районе Южного географического полюса, так как там суша, установить соосно самой Земле громадный маховик с приводом его вращения в ту или другую сторону. Сам привод, например огромный электродвигатель, естественно, закреплен на Земле, а маховик посажен на его вал (рис. 35). Раскручивая маховик в сторону вращения Земли, мы реактивным моментом, передающимся Земле корпусом двигателя, замедляем угловую скорость планеты. Разгоняя маховик в противоположную сторону, мы увеличиваем угловую скорость вращения Земли. Однако в любом случае кинетический момент системы «Земля – маховик» останется постоянным. Заметим, что существует похожий способ ориентирования космических аппаратов, и маховичные устройства для этого называются гиродинами.
Если разместить столь же крупный маховик в районе экватора (рис. 36) и раскрутить его, то вектор его кинетического момента, складываясь с вектором кинетического момента Земли, образует новое направление суммарного вектора, который изменит положение оси вращения Земли. Вот мы и сумели обойтись без жюль-верновской стрельбы из сверхпушки, которая, как оказалось, мало чем смогла бы помочь в изменении положения земной оси.
5.14. Вопрос. Можно ли, находясь на самой Земле, использовать энергию вращения Земли?
Ответ. О том, что это можно сделать, находясь на Луне, уже было сказано. Луна постоянно отнимает от энергии вращения Земли огромные величины. Но можно ли сделать это, находясь на самой Земле?
Поместим на полюсе Земли платформу и плашмя положим на нее неподвижный маховик в опорах – подшипниках (рис. 37). Угловые скорости маховика и Земли будут совпадать. Затем каким-нибудь мощным манипулятором ухватим маховик за опоры и перевернем его на другую сторону.
Угловая скорость маховика по величине сохранится, но направлена она будет уже в другую сторону. Платформа будет вращаться в сторону, противоположную вращению Земли, и ее относительная угловая скорость будет равна удвоенной угловой скорости Земли.
Включаем генератор и отбираем энергию, пока угловые скорости Земли и платформы не совпадут. После этого опять поворачиваем маховик, как блин на сковороде, и опять «снимаем» разность угловых скоростей генератором. И будем поступать так, пока Земля не перестанет вращаться!
Неужели действительно таким образом можно использовать энергию вращения Земли? Ответ на этот вопрос можно получить из следующего опыта.
Встанем на скамью Жуковского, держа в руках за неподвижную ось переднее колесо велосипеда, желательно побольше диаметром и помассивнее (рис. 38). Прижимая колесо к себе шиной, раскрутимся на скамье до угловой скорости, которую легко сможем выдержать не падая. Затем, отодвинув колесо от себя, перевернем его за ось на 180 градусов на другую сторону. Колесо будет вращаться в подшипниках на оси с той же угловой скоростью, что и раньше, только в другую сторону. Затормозим колесо, прижав его к себе шиной, тем самым отобрав у него кинетическую энергию вращения. Теперь опять перевернем это колесо, опять же тормозя его и отбирая кинетическую энергию.
Этим опытом мы смоделируем предполагаемое использование энергии вращения Земли с помощью переворачиваемого маховика. Обратим внимание на то, что угловая скорость скамьи Жуковского, имитирующей Землю, не уменьшается (не учитывая, конечно, потери в подшипниках на собственное вращение), несмотря на то, что после каждого переворота колеса мы тормозим его, отбирая кинетическую энергию.
Интересно, какое объяснение дадут этому «неправдоподобному» опыту сами ученики. Можно только добавить, что будем считать упомянутый мощный манипулятор, который, как руками, сможет подхватить маховик за подшипники и перевернуть его, технически исполнимым.
Объяснение этого парадокса заключается в том, что, переворачивая маховик, мы вызываем гироскопический момент, разгоняющий Землю. Вновь «скрепляя» Землю с маховиком после его переворота, мы Землю тормозим. Поэтому скорость вращения Земли при переворачивании маховика никак не изменится. А энергия, затраченная на «переворот» маховика, перейдет в тепло при его соприкосновении с Землей.
Так что энергии от вращения Земли, находясь на ней самой, получить нельзя.
Список использованной и рекомендуемой литературы
1.
Аппель П.Теоретическая механика. – М.: Физматгиз, 1960.
2. Асламазов Л. Г., Варламов А. А.Удивительная физика. – М.: Добросвет, 2002.
3. Бронштэн В. А.Гипотезы о звездах и Вселенной. – М.: Наука, 1974.
4. Выгодский М. Я.Галилей и инквизиция. – М-Л.: Гостехтеориздат,1934.
5. Галилей Галилео.Беседы и математические доказательства... – М-Л.: Гостехтеориздат, 1934.
6. Галилей Галилео.Избранные труды. – М.: Наука, 1964.
7. Гарднер М.Теория относительности для миллионов. – М.: Атомиздат, 1979.
8. Герц Г.Принципы механики, изложенные в новой связи. – М.: АН СССР, 1959.
9. Григорьев В. К, Мякишев Г. Л.Силы в природе. – М.: Наука, 1977.
10. Григорьян А. Т.Механика от античности до наших дней. – М.: Наука, 1974.
11. Гулиа Н. В.Инерция. – М.: Наука, 1982.
12. Гулиа Н. В.Накопители энергии. – М.: Наука, 1980.
13. Гулиа Н. В.Удивительная физика. О чем умолчали учебники. – М.:НЦЭНАС, 2003.
14. Гюйгенс X.О центробежной силе. Три мемуара по механике. – М.: АН СССР, 1951.
15. Даламбер Ж. Л.Динамика. Трактат. – М-Л.: Гостехтеориздат, 1950.
16. Декарт Р.Избранные произведения. – М.: АН СССР, 1950.
17. Ишлинскии А. Ю.Механика относительного движения и силы инерции. – М.: Наука, 1981.
18. Калашников Н. П., Смондырев М. А.Основы физики. Т.1. -М.: Дрофа, 2003.
19. Коперник Николай.О вращениях небесных сфер. – М.: Наука, 1964.
20. Ньютон И.Математические начала натуральной философии. – СПб., 1915.
21. Павлов В. А.Гироскопический эффект. – Л.: Судостроение, 1978.
22. Перельман Я. И.Занимательная физика. Кн.1. – М.: Наука, 1979.
23. Перельман Я. И.Занимательная физика. Кн.2. – М.: Наука, 1986.
24. Суорц Кл. Э.Необыкновенная физика обыкновенных явлений. Т.1. -М.: Наука, 1986.
25. Тарг С. М.Краткий курс теоретической механики. – М.: Наука, 1970.
26. Физика (Механика) / Под ред. Г. Д. Мякишева. – М.: Просвещение, 1995.
27. Эйлер Л.Основы динамики точки. – М-Л.: ОНТИ, 1938.
28. Эйнштейн А.Физика и реальность. – М.: Наука, 1965.
2. Асламазов Л. Г., Варламов А. А.Удивительная физика. – М.: Добросвет, 2002.
3. Бронштэн В. А.Гипотезы о звездах и Вселенной. – М.: Наука, 1974.
4. Выгодский М. Я.Галилей и инквизиция. – М-Л.: Гостехтеориздат,1934.
5. Галилей Галилео.Беседы и математические доказательства... – М-Л.: Гостехтеориздат, 1934.
6. Галилей Галилео.Избранные труды. – М.: Наука, 1964.
7. Гарднер М.Теория относительности для миллионов. – М.: Атомиздат, 1979.
8. Герц Г.Принципы механики, изложенные в новой связи. – М.: АН СССР, 1959.
9. Григорьев В. К, Мякишев Г. Л.Силы в природе. – М.: Наука, 1977.
10. Григорьян А. Т.Механика от античности до наших дней. – М.: Наука, 1974.
11. Гулиа Н. В.Инерция. – М.: Наука, 1982.
12. Гулиа Н. В.Накопители энергии. – М.: Наука, 1980.
13. Гулиа Н. В.Удивительная физика. О чем умолчали учебники. – М.:НЦЭНАС, 2003.
14. Гюйгенс X.О центробежной силе. Три мемуара по механике. – М.: АН СССР, 1951.
15. Даламбер Ж. Л.Динамика. Трактат. – М-Л.: Гостехтеориздат, 1950.
16. Декарт Р.Избранные произведения. – М.: АН СССР, 1950.
17. Ишлинскии А. Ю.Механика относительного движения и силы инерции. – М.: Наука, 1981.
18. Калашников Н. П., Смондырев М. А.Основы физики. Т.1. -М.: Дрофа, 2003.
19. Коперник Николай.О вращениях небесных сфер. – М.: Наука, 1964.
20. Ньютон И.Математические начала натуральной философии. – СПб., 1915.
21. Павлов В. А.Гироскопический эффект. – Л.: Судостроение, 1978.
22. Перельман Я. И.Занимательная физика. Кн.1. – М.: Наука, 1979.
23. Перельман Я. И.Занимательная физика. Кн.2. – М.: Наука, 1986.
24. Суорц Кл. Э.Необыкновенная физика обыкновенных явлений. Т.1. -М.: Наука, 1986.
25. Тарг С. М.Краткий курс теоретической механики. – М.: Наука, 1970.
26. Физика (Механика) / Под ред. Г. Д. Мякишева. – М.: Просвещение, 1995.
27. Эйлер Л.Основы динамики точки. – М-Л.: ОНТИ, 1938.
28. Эйнштейн А.Физика и реальность. – М.: Наука, 1965.