Страница:
2. В дремучем Муромском лесу из-под земли бьют два источника мертвой воды: № 1 и № 2. Из источника № 1 мертвую воду может взять каждый, а источник № 2 находится в пещере Кощея, в которую никто, кроме самого Кощея, попасть не может.
На вкус и цвет мертвая вода ничем не отличается от обыкновенной, однако если человек выпьет из какого-нибудь источника, он через сутки умрет. Правда, если он выпьет из источника № 1, спасти его может только одно: если он в течение суток выпьет яд из источника № 2. А если он сразу выпьет яд из источника № 2, то ему уже ничто не поможет.
Иванушка-дурачок вызвал Кощея на дуэль. Условия дуэли были такие: каждый приносит с собой кружку с жидкостью и дает ее выпить своему противнику. Кощей обрадовался: «Ура! Я дам яд № 2, и Иванушка-дурачок не сможет спастись! А сам выпью яд из источника № 1, который Иванушка-дурачок мне принесет, затем выпью свой яд № 2 и спасусь!»
В назначенный день оба противника встретились в условленном месте. Они честно обменялись кружками и выпили то, что в них было. Каковы же были радость и удивление обитателей Муромского леса, когда оказалось, что Кощей умер, а Иванушка-дурачок остался жив! Догадайтесь, как?
3. На волшебной яблоне выросли 15 бананов и 20 апельсинов. Если сорвать один из плодов – вырастет такой же, если одновременно сорвать два одинаковых плода – вырастет апельсин, а если одновременно сорвать два разных плода – вырастет банан. Ася срывала плоды, и в конце концов на яблоне остался ровно один плод. Можете ли вы определить, какой это был плод?
4. Мальчик плотно прижал грань синего карандаша к грани желтого карандаша. Один сантиметр (в длину) прижатой грани синего карандаша, считая от нижнего конца, запачкан краской. Желтый карандаш мальчик держит неподвижно, а синий, продолжая прижимать к желтому, опускает на 1 см, затем возвращает в прежнее положение, опять опускает на 1 см и опять возвращает в прежнее положение; 3 раза он так опускает и 3 раза поднимает синий карандаш (6 движений). Допустим, что за это время краска не высыхает и не истощается. На сколько сантиметров в длину окажется запачканным желтый карандаш после шестого движения?
5. Решите задачу из немецкого рукописного трактата из мюнхенского собрания (XV век).
«Некто имеет работников и деньги. Если он даст каждому работнику 5 монет, у него остается 30, а если 7 монет, то не хватит 30. Спрашивается, сколько у него работников?»
6. Решите уравнение
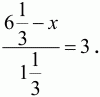
Высшая лига
1 тур
2 тур
3 тур
4 тур
5 тур
6 тур
7 тур
8 тур
9 тур
10 тур
Суперлига
1 тур
2 тур
3 тур
4 тур
5 тур
6 тур
7 тур
На вкус и цвет мертвая вода ничем не отличается от обыкновенной, однако если человек выпьет из какого-нибудь источника, он через сутки умрет. Правда, если он выпьет из источника № 1, спасти его может только одно: если он в течение суток выпьет яд из источника № 2. А если он сразу выпьет яд из источника № 2, то ему уже ничто не поможет.
Иванушка-дурачок вызвал Кощея на дуэль. Условия дуэли были такие: каждый приносит с собой кружку с жидкостью и дает ее выпить своему противнику. Кощей обрадовался: «Ура! Я дам яд № 2, и Иванушка-дурачок не сможет спастись! А сам выпью яд из источника № 1, который Иванушка-дурачок мне принесет, затем выпью свой яд № 2 и спасусь!»
В назначенный день оба противника встретились в условленном месте. Они честно обменялись кружками и выпили то, что в них было. Каковы же были радость и удивление обитателей Муромского леса, когда оказалось, что Кощей умер, а Иванушка-дурачок остался жив! Догадайтесь, как?
3. На волшебной яблоне выросли 15 бананов и 20 апельсинов. Если сорвать один из плодов – вырастет такой же, если одновременно сорвать два одинаковых плода – вырастет апельсин, а если одновременно сорвать два разных плода – вырастет банан. Ася срывала плоды, и в конце концов на яблоне остался ровно один плод. Можете ли вы определить, какой это был плод?
4. Мальчик плотно прижал грань синего карандаша к грани желтого карандаша. Один сантиметр (в длину) прижатой грани синего карандаша, считая от нижнего конца, запачкан краской. Желтый карандаш мальчик держит неподвижно, а синий, продолжая прижимать к желтому, опускает на 1 см, затем возвращает в прежнее положение, опять опускает на 1 см и опять возвращает в прежнее положение; 3 раза он так опускает и 3 раза поднимает синий карандаш (6 движений). Допустим, что за это время краска не высыхает и не истощается. На сколько сантиметров в длину окажется запачканным желтый карандаш после шестого движения?
5. Решите задачу из немецкого рукописного трактата из мюнхенского собрания (XV век).
«Некто имеет работников и деньги. Если он даст каждому работнику 5 монет, у него остается 30, а если 7 монет, то не хватит 30. Спрашивается, сколько у него работников?»
6. Решите уравнение
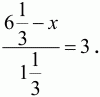
Высшая лига
1 тур
1. Найдите значение выражения (a ? a ? a – b ? b ? b): (а ? а + a ? b + b ? b), если а = 17, Ь = 14.
2. Решите уравнение 72: (38 ? 26: (17–92: х)) = 2.
3. Расставьте вместо букв цифры так, чтобы получилось верное равенство (разным буквам соответствуют разные цифры): У – Р = А: В = Н ? Е = Н + И = Е.
4. Из села по дороге в полдень вышла Таня со скоростью 6 км/ч. В 13 ч 00 мин вслед за ней вышел Игорь со скоростью 8 км/ч. А в 14 ч 00 мин из того же села вдогонку на велосипеде выехала Света. С какой скоростью должна ехать Света, чтобы догнать Игоря в тот момент, когда Игорь догонит Таню?
5. В команде 7 мальчиков и 6 девочек. Вначале все мальчики обменялись рукопожатиями друг с другом. Затем каждый мальчик обменялся рукопожатием с каждой девочкой. А вот девочки друг другу руки решили не жать. Сколько всего было рукопожатий?
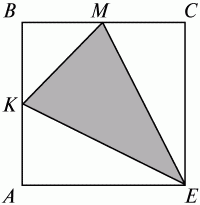
6. Дан квадрат АВСЕ со стороной 4 см. Точка К – середина стороны АВ, точка М – середина стороны ВС. Найдите площадь треугольника МКЕ.
2. Решите уравнение 72: (38 ? 26: (17–92: х)) = 2.
3. Расставьте вместо букв цифры так, чтобы получилось верное равенство (разным буквам соответствуют разные цифры): У – Р = А: В = Н ? Е = Н + И = Е.
4. Из села по дороге в полдень вышла Таня со скоростью 6 км/ч. В 13 ч 00 мин вслед за ней вышел Игорь со скоростью 8 км/ч. А в 14 ч 00 мин из того же села вдогонку на велосипеде выехала Света. С какой скоростью должна ехать Света, чтобы догнать Игоря в тот момент, когда Игорь догонит Таню?
5. В команде 7 мальчиков и 6 девочек. Вначале все мальчики обменялись рукопожатиями друг с другом. Затем каждый мальчик обменялся рукопожатием с каждой девочкой. А вот девочки друг другу руки решили не жать. Сколько всего было рукопожатий?
6. Дан квадрат АВСЕ со стороной 4 см. Точка К – середина стороны АВ, точка М – середина стороны ВС. Найдите площадь треугольника МКЕ.
2 тур
1. На могиле Диофанта (древнегреческий математик) имеется надпись: «Шестую часть его жизни заняло детство, двенадцатую – отрочество, седьмую – юность. Затем протекла половина его жизни, после чего он женился. Через 5 лет у него родился сын, а когда сыну минуло 4 года, Диофант скончался». Сколько лет жил Диофант?
2. Найдите х, если 54 км/ч = х м/с.
3. Алеша дал Боре столько яблок, сколько у Бори было. Потом Боря дал Алеше столько яблок, сколько у того стало. После этого у мальчиков оказалось по 4 яблока. Сколько яблок было у каждого первоначально?
4. Дядя Федор, кот Матроскин, Шарик и почтальон Печкин поспорили: кто больше выпьет молока. После того, как молоко было выпито, каждый из них высказался:
Дядя Федор: «А все-таки я не оказался последним!» Кот Матроскин: «Я выпил не больше, но и не меньше всех». Шарик: «Я маленький, поэтому выпил меньше всех». Почтальон Печкин: «Я вас всех победил!» Один из них сказал неправду. Кто победил в соревновании, и кто сказал неправду?
5. Вычислите 7288: 8 + 6363: 7 – 2000 + 1000: 250 + 276.
6. Частное равно 100. Делимое уменьшили на делитель. Узнайте новое частное.
2. Найдите х, если 54 км/ч = х м/с.
3. Алеша дал Боре столько яблок, сколько у Бори было. Потом Боря дал Алеше столько яблок, сколько у того стало. После этого у мальчиков оказалось по 4 яблока. Сколько яблок было у каждого первоначально?
4. Дядя Федор, кот Матроскин, Шарик и почтальон Печкин поспорили: кто больше выпьет молока. После того, как молоко было выпито, каждый из них высказался:
Дядя Федор: «А все-таки я не оказался последним!» Кот Матроскин: «Я выпил не больше, но и не меньше всех». Шарик: «Я маленький, поэтому выпил меньше всех». Почтальон Печкин: «Я вас всех победил!» Один из них сказал неправду. Кто победил в соревновании, и кто сказал неправду?
5. Вычислите 7288: 8 + 6363: 7 – 2000 + 1000: 250 + 276.
6. Частное равно 100. Делимое уменьшили на делитель. Узнайте новое частное.
3 тур
1. Найдите наибольшее целое число, дающее при делении на 13 неполное частное 17.
2. Сколько существует натуральных двузначных чисел, у которых первая цифра в два раза больше второй?
3. Найдите закономерность в последовательности чисел и определите, сколько в этой последовательности трехзначных чисел: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55...
4. Три землекопа за 2 ч выкопали три ямы. Сколько ям выкопают шесть землекопов за 5 ч?
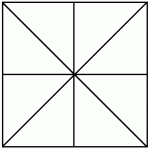
5. Сколько треугольников «спрятано» на рисунке?
6. Летела стая гусей, а навстречу им летит один гусь и говорит: «Здравствуйте, сто гусей!» А передний старый гусь ему и отвечает: «Нет, нас не сто гусей! Вот, если б нас было еще столько, да еще полстолька, да еще четверть столько, да ты, гусь, то было бы сто гусей, а теперь... Вот и рассчитай-ка, сколько нас?»
2. Сколько существует натуральных двузначных чисел, у которых первая цифра в два раза больше второй?
3. Найдите закономерность в последовательности чисел и определите, сколько в этой последовательности трехзначных чисел: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55...
4. Три землекопа за 2 ч выкопали три ямы. Сколько ям выкопают шесть землекопов за 5 ч?
5. Сколько треугольников «спрятано» на рисунке?
4 тур
1. 3 кедровых ореха можно обменять на 2 лимона, а 3 лимона можно обменять на 4 яблока. Сколько кедровых орехов можно обменять на 16 яблок?
2. Из цифр 0, 2, 3, 5, 8 составьте все трехзначные числа, сумма цифр в каждом из которых равна 8 (цифры в числе могут повторяться).
3. Путь, пройденный туристом за один день, оказался в три раза больше, чем половина оставшегося пути. Какую часть всего пути прошел турист за день?
4. Придумайте задачу, которая решалась бы с помощью уравнения 2 ? (х + 1) + х = 32.
5. Найдите площадь треугольника, изображенного на рисунке. Площадь одной клетки равна 1.
6. В токарном цехе вытачиваются детали из стальных заготовок, из одной заготовки – деталь. Стружки, оставшиеся после обработки трех заготовок, можно переплавить и получить ровно одну заготовку. Сколько всего деталей можно сделать из 9-ти заготовок? А из 14-ти? Сколько нужно взять заготовок, чтобы получить 40 деталей?
2. Из цифр 0, 2, 3, 5, 8 составьте все трехзначные числа, сумма цифр в каждом из которых равна 8 (цифры в числе могут повторяться).
3. Путь, пройденный туристом за один день, оказался в три раза больше, чем половина оставшегося пути. Какую часть всего пути прошел турист за день?
4. Придумайте задачу, которая решалась бы с помощью уравнения 2 ? (х + 1) + х = 32.
5. Найдите площадь треугольника, изображенного на рисунке. Площадь одной клетки равна 1.
5 тур
1. Сумма шести различных натуральных чисел равна 22. Найдите эти числа.
2. Пятиклассникам очень понравилась поездка в Великий Устюг, и они решили поехать туда снова, дабы навестить веселых Дедов Морозов. Ежемесячно каждый ученик вносил определенное количество рублей (без копеек), одинаковое для всех, и в течение пяти месяцев было собрано 49 685 р. Сколько было в группе учеников, и какую сумму внес каждый?
3. Четыре подруги пришли на каток, каждая со своим братом. Они разбились на пары и начали кататься. Оказалось, что в каждой паре «кавалер» выше «дамы» и никто не катается со своей сестрой. Самым высоким в компании был Юра Воробьев, следующим по росту – Андрей Егоров, потом Люся Егорова, Сережа Петров, Оля Петрова, Дима Крымов, Инна Крымоваи Аня Воробьева. Определите, кто с кем катался?
4. Простые числа имеют только два различных делителя – единицу и само это число. Найдите первые три числа, имеющие ровно три различных делителя. Догадаетесь ли вы, какие числа имеют только три различных делителя?
5. Полный бидон с молоком весит 34 кг, а наполненный до половины – 17 кг 500 г. Сколько весит пустой бидон?
6. Из литра молока получают 150 г сливок, а из литра сливок – 300 г масла. Сколько масла получится из 100 л молока?
2. Пятиклассникам очень понравилась поездка в Великий Устюг, и они решили поехать туда снова, дабы навестить веселых Дедов Морозов. Ежемесячно каждый ученик вносил определенное количество рублей (без копеек), одинаковое для всех, и в течение пяти месяцев было собрано 49 685 р. Сколько было в группе учеников, и какую сумму внес каждый?
3. Четыре подруги пришли на каток, каждая со своим братом. Они разбились на пары и начали кататься. Оказалось, что в каждой паре «кавалер» выше «дамы» и никто не катается со своей сестрой. Самым высоким в компании был Юра Воробьев, следующим по росту – Андрей Егоров, потом Люся Егорова, Сережа Петров, Оля Петрова, Дима Крымов, Инна Крымоваи Аня Воробьева. Определите, кто с кем катался?
4. Простые числа имеют только два различных делителя – единицу и само это число. Найдите первые три числа, имеющие ровно три различных делителя. Догадаетесь ли вы, какие числа имеют только три различных делителя?
5. Полный бидон с молоком весит 34 кг, а наполненный до половины – 17 кг 500 г. Сколько весит пустой бидон?
6. Из литра молока получают 150 г сливок, а из литра сливок – 300 г масла. Сколько масла получится из 100 л молока?
6 тур
1. На почтовом ящике написано: «Выемка писем производится пять раз в день с 7 до 19 ч». И действительно, первый раз почтальон забирает почту в 7 ч утра, а последний – в 7 ч вечера. Через какие интервалы времени вынимают письма из ящика?
2. Вычислите 66 509 + 141 404: (39 839 – 39 793) + 1985.
3. В классе учится меньше чем 50 школьников. За контрольную работу седьмая часть учеников получила пятерки, третья – четверки, половина – тройки. Остальные работы были оценены как неудовлетворительные. Сколько всего учащихся в классе?
4. Ковбой Билл зашел в бар и попросил у бармена бутылку виски за 3 доллара и 6 коробков непромокаемых спичек, цену которых он не знал. Бармен потребовал с него 11 долларов 80 центов (1 доллар – 100 центов), и в ответ на это Билл вытащил револьвер. Тогда бармен пересчитал стоимость покупки и исправил ошибку. Как Билл догадался, что бармен пытался его обсчитать?
5. Однажды на лестнице была найдена странная тетрадь. В ней было записано четыре утверждения:
«В этой тетради ровно одно неверное утверждение»;
«В этой тетради ровно два неверных утверждения»;
«В этой тетради ровно три неверных утверждения»;
«В этой тетради ровно четыре неверных утверждения».
Есть ли среди этих утверждений верные, и если да, то какие?
6. Вася взял у товарища книгу на три дня. В первый день он прочел полкниги, во второй – треть оставшихся страниц, а в третий день прочитал половину прочитанного за первые два дня. Успел ли Вася прочитать всю книгу за три дня? Ответ обоснуйте.
2. Вычислите 66 509 + 141 404: (39 839 – 39 793) + 1985.
3. В классе учится меньше чем 50 школьников. За контрольную работу седьмая часть учеников получила пятерки, третья – четверки, половина – тройки. Остальные работы были оценены как неудовлетворительные. Сколько всего учащихся в классе?
4. Ковбой Билл зашел в бар и попросил у бармена бутылку виски за 3 доллара и 6 коробков непромокаемых спичек, цену которых он не знал. Бармен потребовал с него 11 долларов 80 центов (1 доллар – 100 центов), и в ответ на это Билл вытащил револьвер. Тогда бармен пересчитал стоимость покупки и исправил ошибку. Как Билл догадался, что бармен пытался его обсчитать?
5. Однажды на лестнице была найдена странная тетрадь. В ней было записано четыре утверждения:
«В этой тетради ровно одно неверное утверждение»;
«В этой тетради ровно два неверных утверждения»;
«В этой тетради ровно три неверных утверждения»;
«В этой тетради ровно четыре неверных утверждения».
Есть ли среди этих утверждений верные, и если да, то какие?
6. Вася взял у товарища книгу на три дня. В первый день он прочел полкниги, во второй – треть оставшихся страниц, а в третий день прочитал половину прочитанного за первые два дня. Успел ли Вася прочитать всю книгу за три дня? Ответ обоснуйте.
7 тур
1. – Еще веревочку? – спросила мать, вытаскивая руки из лоханки с бельем. – Можно подумать, что я вся веревочная. Только и слышишь: веревочку да веревочку. Ведь я вчера дала тебе порядочный клубок. Куда ты ее девала?
– Во-первых, половину ты сама взяла обратно. Половину того, что осталось, взял у меня Том, чтобы удить в канаве колюшек. Осталось совсем немного, да из того еще папа взял половину для починки подтяжек, которые лопнули у него от смеха, когда случилась беда с автомобилем. А после понадобилось еще сестре взять две пятых оставшегося, чтобы завязать свои волосы узлом.
– Что же ты сделала с остальной веревочкой?
– С остальной? Остальной-то было всего-навсего 30 см! Вот и устраивай телефон из такого обрывка...
Какую же длину имела веревочка первоначально?
2. Ира, Наташа, Алеша и Витя собирали грибы. Наташа собрала больше всех, Ира не меньше всех, а Алеша – больше, чем Витя. Верно ли, что девочки собрали грибов больше, чем мальчики?
3. Чему равна площадь треугольника со сторонами 8, 7 и 15?
4. Пять первоклассников стояли в шеренгу и держали 37 флажков. У всех справа от Таты – 14 флажков, справа от Яши – 32, справа от Веры – 20, справа от Максима – 8. Сколько флажков у Даши?
5. Как при помощи чашечных весов без гирь разделить 24 кг гвоздей на две части – 9 и 15 кг?
6. Решите уравнение
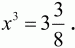
– Во-первых, половину ты сама взяла обратно. Половину того, что осталось, взял у меня Том, чтобы удить в канаве колюшек. Осталось совсем немного, да из того еще папа взял половину для починки подтяжек, которые лопнули у него от смеха, когда случилась беда с автомобилем. А после понадобилось еще сестре взять две пятых оставшегося, чтобы завязать свои волосы узлом.
– Что же ты сделала с остальной веревочкой?
– С остальной? Остальной-то было всего-навсего 30 см! Вот и устраивай телефон из такого обрывка...
Какую же длину имела веревочка первоначально?
2. Ира, Наташа, Алеша и Витя собирали грибы. Наташа собрала больше всех, Ира не меньше всех, а Алеша – больше, чем Витя. Верно ли, что девочки собрали грибов больше, чем мальчики?
3. Чему равна площадь треугольника со сторонами 8, 7 и 15?
4. Пять первоклассников стояли в шеренгу и держали 37 флажков. У всех справа от Таты – 14 флажков, справа от Яши – 32, справа от Веры – 20, справа от Максима – 8. Сколько флажков у Даши?
5. Как при помощи чашечных весов без гирь разделить 24 кг гвоздей на две части – 9 и 15 кг?
6. Решите уравнение
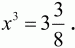
8 тур
1. Шли три крестьянина и зашли на постоялый двор отдохнуть и пообедать. Заказали хозяйке сварить картофель, а сами заснули. Хозяйка сварила картофель, но не стала будить постояльцев, а поставила миску с картофелем на стол и ушла. Проснулся один крестьянин, увидел картофель и, чтобы не будить товарищей, сосчитал картофель, съел свою долю и снова заснул. Вскоре проснулся другой; ему невдомек было, что один из товарищей уже съел свою долю, поэтому он сосчитал весь оставшийся картофель, съел третью часть и опять заснул. После него проснулся третий; полагая, что он проснулся первым, он сосчитал весь оставшийся в миске картофель и съел третью часть. Тут проснулись его товарищи и увидели, что в миске осталось 8 картофелин. Тогда только объяснилось дело. Сосчитайте, сколько картофелин подала на стол хозяйка?
2. Во время стоянки между двумя рейсами матросу исполнилось 20 лет. По этому случаю в кают-компании собрались все шесть членов команды.
– Я вдвое старше юнги и на 6 лет старше машиниста, – сказал рулевой.
– А я на столько же старше юнги, на сколько моложе машиниста, – заметил боцман. – Кроме того, я на 4 года старше матроса.
– Средний возраст команды – 28 лет, – дал справку капитан.
Сколько лет капитану?
3. В шахматном турнире участвовали 40 игроков, и каждый сыграл с каждым по одной партии. Сколько было сыграно партий?
4. Два пильщика должны распилить бревно, длина которого 5 1/2 м, на полуметровые чурки. Во сколько минут они сделают это, если распиловка бревна поперек продолжается каждый раз 2 1/2 мин?
5. В 100-значном числе 12345678901234567890...1234567890 вычеркнули все цифры, стоящие на нечетных местах; в полученном 50-значном числе вновь вычеркнули все цифры, стоящие на нечетных местах, и т. д. Вычеркивание продолжалось до тех пор, пока было что вычеркивать. Какая цифра была вычеркнута последней?
6. Докажите, что разность 9100– 7100делится на 10.
2. Во время стоянки между двумя рейсами матросу исполнилось 20 лет. По этому случаю в кают-компании собрались все шесть членов команды.
– Я вдвое старше юнги и на 6 лет старше машиниста, – сказал рулевой.
– А я на столько же старше юнги, на сколько моложе машиниста, – заметил боцман. – Кроме того, я на 4 года старше матроса.
– Средний возраст команды – 28 лет, – дал справку капитан.
Сколько лет капитану?
3. В шахматном турнире участвовали 40 игроков, и каждый сыграл с каждым по одной партии. Сколько было сыграно партий?
4. Два пильщика должны распилить бревно, длина которого 5 1/2 м, на полуметровые чурки. Во сколько минут они сделают это, если распиловка бревна поперек продолжается каждый раз 2 1/2 мин?
5. В 100-значном числе 12345678901234567890...1234567890 вычеркнули все цифры, стоящие на нечетных местах; в полученном 50-значном числе вновь вычеркнули все цифры, стоящие на нечетных местах, и т. д. Вычеркивание продолжалось до тех пор, пока было что вычеркивать. Какая цифра была вычеркнута последней?
6. Докажите, что разность 9100– 7100делится на 10.
9 тур
1. На столе лежат в ряд четыре фигуры: треугольник, круг, прямоугольник и ромб. Они окрашены в разные цвета: красный, синий, желтый, зеленый. Известно, что красная фигура лежит где-то между синей и зеленой; непосредственно справа от желтой фигуры лежит ромб; круг лежит правее и треугольника, и ромба; треугольник лежит не с краю; синяя и желтая фигуры лежат не рядом. Определите, какого цвета какая фигура. Укажите все возможные решения.
2. Найдите значение выражения Зх3+ 2х2+ х, если
3. Два города, А и В, находятся на расстоянии 300 км друг от друга. Из этих городов одновременно выезжают друг другу навстречу два велосипедиста и мчатся, не останавливаясь, каждый со скоростью 50 км/ч. Но вместе с первым велосипедистом из города^ вылетает муха, пролетающая в час 120 км. Муха опережает первого велосипедиста, летит навстречу второму, выехавшему из В. Встретив его, она сразу поворачивает назад к велосипедисту А. Повстречав его, опять летит обратно навстречу велосипедисту В, и так продолжает она свои полеты взад и вперед до тех пор, пока велосипедисты не съехались. Тогда она успокоилась и села одному из велосипедистов на шапку. Сколько километров пролетела муха?
4. Школьник сказал своему приятелю Вите:
– У нас в классе семнадцать человек. И, представь, каждый из них дружит ровно с пятью одноклассниками.
– Не может этого быть, – сразу ответил Витя.
Почему он так решил?
5. Женю, Леву и Гришу рассадили так, что Женя мог видеть Леву и Гришу, Лева-только Гришу, а Гриша – никого. Потом из мешка, в котором лежали две белые и три черные шапки (содержимое мешка было известно мальчикам), достали и надели на каждого шапку неизвестного ему цвета, а две шапки остались в мешке (какие именно – мальчикам неизвестно).
Женя сказал, что он не может определить цвет своей шапки. Лева слышал ответ Жени и сказал, что и у него не хватает данных для определения цвета своей шапки. Мог ли Гриша на основании этих ответов определить цвет своей шапки? Если нет, то почему; если да, то как?
6. «То» да «это», да половина «того» да «этого» – сколько это будет процентов от трех четвертей «того» да «этого»?
2. Найдите значение выражения Зх3+ 2х2+ х, если
4. Школьник сказал своему приятелю Вите:
– У нас в классе семнадцать человек. И, представь, каждый из них дружит ровно с пятью одноклассниками.
– Не может этого быть, – сразу ответил Витя.
Почему он так решил?
5. Женю, Леву и Гришу рассадили так, что Женя мог видеть Леву и Гришу, Лева-только Гришу, а Гриша – никого. Потом из мешка, в котором лежали две белые и три черные шапки (содержимое мешка было известно мальчикам), достали и надели на каждого шапку неизвестного ему цвета, а две шапки остались в мешке (какие именно – мальчикам неизвестно).
Женя сказал, что он не может определить цвет своей шапки. Лева слышал ответ Жени и сказал, что и у него не хватает данных для определения цвета своей шапки. Мог ли Гриша на основании этих ответов определить цвет своей шапки? Если нет, то почему; если да, то как?
6. «То» да «это», да половина «того» да «этого» – сколько это будет процентов от трех четвертей «того» да «этого»?
10 тур
1. На экзамене преподаватель предлагает студенту пять вопросов, на которые надо ответить «да» или «нет». Студент знает, что ответов «да» больше, чем «нет», и что преподаватель никогда не задает три вопроса подряд, требующие одинакового ответа. Из содержания первого и последнего вопросов ему ясно, что ответы на них должны быть противоположны. Единственный вопрос, ответ на который ему известен, – второй. И этот ответ – «нет». Какими должны быть ответы на эти пять вопросов?
2. В меню входят: овощной суп или бульон на первое, бифштекс, цыпленок или рыба на второе и компот или мороженое на третье. Полный обед состоит из одного блюда на первое, одного блюда на второе и одного блюда на третье.
а) Сколько может быть различных полных обедов?
б) Сколько может быть полных обедов с бифштексом в качестве второго?
3. Имеется девять монет, о которых известно, что восемь из них имеют одинаковый вес, а девятая несколько тяжелее остальных. Покажите, что более тяжелая монета может быть отделена от остальных посредством двух взвешиваний на чашечных весах (без гирь).
4. Изготовление книги включает в себя несколько стадий: сначала ее набирают, затем печатают и наконец делают к ней обложку и переплетают. Допустим, что наборщик берет 6 долларов (600 центов) в час, бумага стоит 1/4 цента за лист, печатник берет 11 центов за каждую минуту работы его пресса, обложка стоит 28 центов и переплетчик берет 15 центов за переплетение каждой книги. Допустим теперь, что издатель хочет напечатать книгу, для которой требуется 300 ч работы наборщика, 220 листов бумаги на один экземпляр и 5 мин работы одного печатного пресса на каждый экземпляр. Найдите стоимость издания одного экземпляра книги.
5. Что больше и на сколько: 20 % от 30 или 30 % от 20?
6. Маша съедает коробку конфет за 5 мин, а Даша – за 6 мин. За какое время будут съедены все конфеты, если Маша и Даша займутся решением данного вопроса одновременно?
2. В меню входят: овощной суп или бульон на первое, бифштекс, цыпленок или рыба на второе и компот или мороженое на третье. Полный обед состоит из одного блюда на первое, одного блюда на второе и одного блюда на третье.
а) Сколько может быть различных полных обедов?
б) Сколько может быть полных обедов с бифштексом в качестве второго?
3. Имеется девять монет, о которых известно, что восемь из них имеют одинаковый вес, а девятая несколько тяжелее остальных. Покажите, что более тяжелая монета может быть отделена от остальных посредством двух взвешиваний на чашечных весах (без гирь).
4. Изготовление книги включает в себя несколько стадий: сначала ее набирают, затем печатают и наконец делают к ней обложку и переплетают. Допустим, что наборщик берет 6 долларов (600 центов) в час, бумага стоит 1/4 цента за лист, печатник берет 11 центов за каждую минуту работы его пресса, обложка стоит 28 центов и переплетчик берет 15 центов за переплетение каждой книги. Допустим теперь, что издатель хочет напечатать книгу, для которой требуется 300 ч работы наборщика, 220 листов бумаги на один экземпляр и 5 мин работы одного печатного пресса на каждый экземпляр. Найдите стоимость издания одного экземпляра книги.
5. Что больше и на сколько: 20 % от 30 или 30 % от 20?
6. Маша съедает коробку конфет за 5 мин, а Даша – за 6 мин. За какое время будут съедены все конфеты, если Маша и Даша займутся решением данного вопроса одновременно?
Суперлига
1 тур
1. В пруд пустили 30 щук, которые постепенно поедали друг друга. Щука считается сытой, если она съела 3 щук (сытых или голодных). Каково наибольшее число щук, которые могут насытиться?
2. В бочке 10 литров бензина. Как отлить из нее 6 литров с помощью девятилитрового ведра и пятилитрового бидона?
3. Отец старше сына в 4 раза, а сумма их возрастов составляет 50 лет. Через сколько лет отец станет втрое старше сына?
4. Расставьте в записи 4 ? 12 + 18:6 + 3 скобки так, чтобы получилось: а) число 50; б) наименьшее возможное число; в) наибольшее возможное число.
5. При сложении двух целых чисел ученик по ошибке поставил во втором слагаемом лишний нуль на конце и получил в сумме 6641 вместо 2411. Определите слагаемые.
6. При делении одного числа на другое получилось в частном 28 и в остатке 84. Как изменится частное и как изменится остаток, если делимое и делитель уменьшить в 7 раз?
2. В бочке 10 литров бензина. Как отлить из нее 6 литров с помощью девятилитрового ведра и пятилитрового бидона?
3. Отец старше сына в 4 раза, а сумма их возрастов составляет 50 лет. Через сколько лет отец станет втрое старше сына?
4. Расставьте в записи 4 ? 12 + 18:6 + 3 скобки так, чтобы получилось: а) число 50; б) наименьшее возможное число; в) наибольшее возможное число.
5. При сложении двух целых чисел ученик по ошибке поставил во втором слагаемом лишний нуль на конце и получил в сумме 6641 вместо 2411. Определите слагаемые.
6. При делении одного числа на другое получилось в частном 28 и в остатке 84. Как изменится частное и как изменится остаток, если делимое и делитель уменьшить в 7 раз?
2 тур
1. Куб со стороной 1 м распилили на кубики со стороной 1 см. Получившиеся кубики выложили вряд. Чему равна длина ряда?
2. Применяя знаки арифметических действий и, возможно, скобки, запишите восемью двойками число 200 (разрешено использовать такие числа, как 22, 222, 2222 и т. д.).
3. Во сколько раз увеличится трехзначное число, если справа к нему приписать такое же число? Ответ подтвердите двумя примерами.
4. Докажите, что из любых трех целых чисел можно найти два, сумма которых делится на 2.
5. Сошлись два пастуха, Иван и Петр. Иван и говорит Петру: «Отдай-ка ты мне одну овцу, тогда у меня будет овец ровно вдвое больше, чем у тебя!» А Петр ему отвечает: «Нет! Лучше ты мне отдай одну овцу, тогда у нас будет овец поровну!» Сколько же было у каждого овец?
6. На прямоугольном торте лежит круглая шоколадка, причем отнюдь не посередке. Как разрезать торт на две равные части так, чтобы и шоколадка тоже разделилась ровно пополам?
2. Применяя знаки арифметических действий и, возможно, скобки, запишите восемью двойками число 200 (разрешено использовать такие числа, как 22, 222, 2222 и т. д.).
3. Во сколько раз увеличится трехзначное число, если справа к нему приписать такое же число? Ответ подтвердите двумя примерами.
4. Докажите, что из любых трех целых чисел можно найти два, сумма которых делится на 2.
5. Сошлись два пастуха, Иван и Петр. Иван и говорит Петру: «Отдай-ка ты мне одну овцу, тогда у меня будет овец ровно вдвое больше, чем у тебя!» А Петр ему отвечает: «Нет! Лучше ты мне отдай одну овцу, тогда у нас будет овец поровну!» Сколько же было у каждого овец?
6. На прямоугольном торте лежит круглая шоколадка, причем отнюдь не посередке. Как разрезать торт на две равные части так, чтобы и шоколадка тоже разделилась ровно пополам?
3 тур
1. В коробке лежат 4 цветных карандаша и 10 простых. Берут из этой коробки наугад несколько карандашей. Какое наименьшее число карандашей надо взять из коробки, чтобы среди них с гарантией оказалось не менее: а) двух цветных; б) трех простых?
2. Поблизости один от другого расположены два населенных пункта, А и В. Все жители А говорят только правду, а жители В всегда лгут. Жители А и В посещают друг друга. Ты находишься в каком-то из этих пунктов. Какой вопрос (только один) ты можешь задать первому встретившемуся тебе в этом пункте человеку, чтобы по ответу на этот вопрос ты мог установить, А это или В?
3. Два мальчика играли в шашки. Положение первого игрока стало ухудшаться. Пока он обдумывал очередной ход, второй игрок рассматривал доску, на которой стояли шашки. Оказалось, что пустых клеток на доске было втрое больше, чем занятых шашками, и что у него на две шашки больше, чем у первого игрока. Сколько шашек у каждого игрока было в это время на доске?
4. Школьники ехали на автомашине из деревни в город. Когда они проехали 3/4 пути, автомашина была остановлена для ремонта. Оставшуюся часть пути школьники проделали пешком, затратив на это времени в четыре раза больше, чем они ехали на автомашине. Во сколько раз быстрей ехали школьники на автомашине, чем шли пешком?
5. Дано трехзначное число ABB, произведение цифр которого – двузначное число AC, произведение цифр этого числа равно С (здесь цифры в записи числа заменены буквами; одинаковым буквам соответствуют одинаковые цифры, разным – разные). Определите исходное число.
6. Ребята принесли из леса по полной корзинке грибов. Всего было собрано 289 грибов, причем в каждой корзинке их оказалось одинаковое количество. Сколько было ребят?
2. Поблизости один от другого расположены два населенных пункта, А и В. Все жители А говорят только правду, а жители В всегда лгут. Жители А и В посещают друг друга. Ты находишься в каком-то из этих пунктов. Какой вопрос (только один) ты можешь задать первому встретившемуся тебе в этом пункте человеку, чтобы по ответу на этот вопрос ты мог установить, А это или В?
3. Два мальчика играли в шашки. Положение первого игрока стало ухудшаться. Пока он обдумывал очередной ход, второй игрок рассматривал доску, на которой стояли шашки. Оказалось, что пустых клеток на доске было втрое больше, чем занятых шашками, и что у него на две шашки больше, чем у первого игрока. Сколько шашек у каждого игрока было в это время на доске?
4. Школьники ехали на автомашине из деревни в город. Когда они проехали 3/4 пути, автомашина была остановлена для ремонта. Оставшуюся часть пути школьники проделали пешком, затратив на это времени в четыре раза больше, чем они ехали на автомашине. Во сколько раз быстрей ехали школьники на автомашине, чем шли пешком?
5. Дано трехзначное число ABB, произведение цифр которого – двузначное число AC, произведение цифр этого числа равно С (здесь цифры в записи числа заменены буквами; одинаковым буквам соответствуют одинаковые цифры, разным – разные). Определите исходное число.
6. Ребята принесли из леса по полной корзинке грибов. Всего было собрано 289 грибов, причем в каждой корзинке их оказалось одинаковое количество. Сколько было ребят?
4 тур
1. Упростите выражение (2 + х – 1 + Зх): (7х + 6 – 3х – 5).
2. Восстановите недостающие цифры:
3. На колхозном рынке продаются два арбуза разных размеров. Первый в диаметре 40 см, а второй – 80 см. Первый арбуз стоит 30 р., второй арбуз стоит 180 р. Какой из арбузов выгоднее купить и почему?
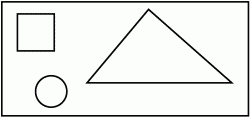
4. Перед нами толстая дощечка с тремя отверстиями: квадратным, треугольным и круглым (на рисунке дан вид сверху). Может ли существовать одна затычка такой формы, чтобы закрывать все эти отверстия? Если да, то опишите ее. Если нет – обоснуйте невозможность создания такой затычки.
5. Со стартовой площадки вылетел на север вертолет. Пролетев в северном направлении 100 км, он повернул на восток. Пролетев в эту сторону 100 км, вертолет сделал новый поворот – на юг и прошел в южном направлении 100 км. Затем он повернул на запад и, пролетев 100 км, опустился. Спрашивается: где расположено место спуска вертолета относительно стартовой площадки – к западу, к востоку, к северу или югу? Подсказка: Земля имеет форму, близкую к шару, а потому вертолет не вернется на стартовую площадку!
6. Сколько существует трехзначных натуральных чисел с четными цифрами, таких, что: а) цифры в числе не повторяются; б) цифры в числе могут повторяться; в) ровно две цифры в числе повторяются?
2. Восстановите недостающие цифры:
4. Перед нами толстая дощечка с тремя отверстиями: квадратным, треугольным и круглым (на рисунке дан вид сверху). Может ли существовать одна затычка такой формы, чтобы закрывать все эти отверстия? Если да, то опишите ее. Если нет – обоснуйте невозможность создания такой затычки.
6. Сколько существует трехзначных натуральных чисел с четными цифрами, таких, что: а) цифры в числе не повторяются; б) цифры в числе могут повторяться; в) ровно две цифры в числе повторяются?
5 тур
1. Сможете ли вы найти четыре целых числа, сумма и произведение которых являются нечетными числами?
2. Первый вторник месяца Митя провел в Смоленске, а первый вторник после первого понедельника – в Вологде. В следующем месяце Митя первый вторник провел в Пскове, а первый вторник после первого понедельника – во Владимире. Сможете ли вы определить, какого числа и какого месяца Митя был в каждом из городов?
3. Сколько нечетных чисел заключено между 300 и 700?
4. Имеются 6 запертых чемоданов и 6 ключей к ним. При этом неизвестно, к какому чемодану подходит какой ключ. Сколько попыток вы попросите вам предоставить, чтобы наверняка открыть все чемоданы?
5. В турнире участвовали пять шахматистов. Известно, что каждый сыграл с остальными по одной партии и все набрали разное количество очков; занявший 1-е место не сделал ни одной ничьей; занявший 2-е место не проиграл ни одной партии; занявший 4-е место не выиграл ни одной партии. Определите результаты всех партий турнира.
6. Начнем считать пальцы на правой руке: первый – мизинец, второй – безымянный, третий – средний, четвертый – указательный, пятый – большой, шестой – снова указательный, седьмой – снова средний, восьмой – безымянный, девятый – мизинец, десятый – безымянный и т. д. Какой палец будет по счету 1992-м?
2. Первый вторник месяца Митя провел в Смоленске, а первый вторник после первого понедельника – в Вологде. В следующем месяце Митя первый вторник провел в Пскове, а первый вторник после первого понедельника – во Владимире. Сможете ли вы определить, какого числа и какого месяца Митя был в каждом из городов?
3. Сколько нечетных чисел заключено между 300 и 700?
4. Имеются 6 запертых чемоданов и 6 ключей к ним. При этом неизвестно, к какому чемодану подходит какой ключ. Сколько попыток вы попросите вам предоставить, чтобы наверняка открыть все чемоданы?
5. В турнире участвовали пять шахматистов. Известно, что каждый сыграл с остальными по одной партии и все набрали разное количество очков; занявший 1-е место не сделал ни одной ничьей; занявший 2-е место не проиграл ни одной партии; занявший 4-е место не выиграл ни одной партии. Определите результаты всех партий турнира.
6. Начнем считать пальцы на правой руке: первый – мизинец, второй – безымянный, третий – средний, четвертый – указательный, пятый – большой, шестой – снова указательный, седьмой – снова средний, восьмой – безымянный, девятый – мизинец, десятый – безымянный и т. д. Какой палец будет по счету 1992-м?
6 тур
1. Найдите, какую цифру обозначает каждая буква в следующем равенстве: АХА= БАХ.
2. Сколько нулей на конце этого числа: 1 ? 2 ? 3 ? 4... ? 50?
3. Некоторое число уменьшили на 7, потом уменьшили в 10 раз и получили число, которое на 34 меньше исходного. Найдите исходное число.
4. Яша идет от дома до школы 30 мин, а его брат Петя 40 мин. Петя вышел из дома на 5 мин раньше Яши. Через сколько минут Яша догонит Петю?
5. Пятиклассники ехали на автомашине из деревни в город. Когда они проехали 4/5 пути, автомашина была остановлена для ремонта. Оставшуюся часть пути пятиклассники проделали пешком, затратив на это времени в 3 раза больше, чем они ехали на автомашине. Во сколько раз быстрей ехали пятиклассники на автомашине, чем шли пешком?
6. Сколько квадратов «спрятано» на рисунке?
2. Сколько нулей на конце этого числа: 1 ? 2 ? 3 ? 4... ? 50?
3. Некоторое число уменьшили на 7, потом уменьшили в 10 раз и получили число, которое на 34 меньше исходного. Найдите исходное число.
4. Яша идет от дома до школы 30 мин, а его брат Петя 40 мин. Петя вышел из дома на 5 мин раньше Яши. Через сколько минут Яша догонит Петю?
5. Пятиклассники ехали на автомашине из деревни в город. Когда они проехали 4/5 пути, автомашина была остановлена для ремонта. Оставшуюся часть пути пятиклассники проделали пешком, затратив на это времени в 3 раза больше, чем они ехали на автомашине. Во сколько раз быстрей ехали пятиклассники на автомашине, чем шли пешком?
6. Сколько квадратов «спрятано» на рисунке?
7 тур
1. На доске написаны шесть чисел: 1, 2, 3, 4, 5, 6. За один ход разрешается к любым двум из них одновременно добавлять по единице. Можно ли за несколько ходов все числа сделать равными? Ответ обоснуйте.
2. Разрежьте квадрат на пять треугольников так, чтобы площадь одного из этих треугольников равнялась сумме площадей оставшихся.
3. Дорога от дома до школы занимает у Пети 20 мин. Однажды по дороге в школу он вспомнил, что забыл дома ручку. Если теперь он продолжит свой путь с той же скоростью, то придет в школу за 3 мин до звонка, а если вернется домой за ручкой, то, идя с той же скоростью, опоздает к началу урока на 7 мин. Какую часть пути он прошел до того, как вспомнил о ручке?
4. 20 черных коров и 15 рыжих дают за неделю столько молока, сколько 12 черных коров и 20 рыжих. У каких коров больше удои: у черных или у рыжих? Ответ обоснуйте.
5. Если написать любое двузначное число, а затем поменять местами в этом числе цифры и вычесть из большего числа меньшее, то получится число, которое делится на 9. Почему?
2. Разрежьте квадрат на пять треугольников так, чтобы площадь одного из этих треугольников равнялась сумме площадей оставшихся.
3. Дорога от дома до школы занимает у Пети 20 мин. Однажды по дороге в школу он вспомнил, что забыл дома ручку. Если теперь он продолжит свой путь с той же скоростью, то придет в школу за 3 мин до звонка, а если вернется домой за ручкой, то, идя с той же скоростью, опоздает к началу урока на 7 мин. Какую часть пути он прошел до того, как вспомнил о ручке?
4. 20 черных коров и 15 рыжих дают за неделю столько молока, сколько 12 черных коров и 20 рыжих. У каких коров больше удои: у черных или у рыжих? Ответ обоснуйте.
5. Если написать любое двузначное число, а затем поменять местами в этом числе цифры и вычесть из большего числа меньшее, то получится число, которое делится на 9. Почему?