Страница:
Андрей Николаевич Павлов
Математические олимпиады по лигам. 5–9 классы
Предисловие
Когда мы слышим слово «олимпиада», то ассоциируем его с сильными учащимися, отличниками. Подобный подход оправдан, если речь идет о городских, районных, областных, республиканских, Всероссийских и Международных математических олимпиадах. На таких уровнях сама цель олимпиад – выявление одаренных и нестандартно мыслящих учащихся, определение сильнейших из них. Однако задачи внутришкольных олимпиад нам видятся гораздо шире.
В книге представлен опыт автора по проведению олимпиад в лицее г. Лобни Московской области. Их отличительная особенность: в олимпиадах участвуют все! Причем термин «все» следует понимать в буквальном смысле слова, а именно как 100 %-ный охват учащихся, без исключений. С этим связаны и дифференцирование заданий по уровню сложности, и включение в олимпиады, помимо нестандартных, чисто технических заданий (примеры, уравнения, типовые задачи и т. д.).
Рассмотрим основное содержание и правила проведения наиболее популярных олимпиад, которые и вошли в книгу.
В книге представлен опыт автора по проведению олимпиад в лицее г. Лобни Московской области. Их отличительная особенность: в олимпиадах участвуют все! Причем термин «все» следует понимать в буквальном смысле слова, а именно как 100 %-ный охват учащихся, без исключений. С этим связаны и дифференцирование заданий по уровню сложности, и включение в олимпиады, помимо нестандартных, чисто технических заданий (примеры, уравнения, типовые задачи и т. д.).
Рассмотрим основное содержание и правила проведения наиболее популярных олимпиад, которые и вошли в книгу.
Олимпиады по лигам (5–6 классы)
Новая и чрезвычайно интересная форма внеклассной работы по предмету. Учителя, знающие, как устроены лиги в чемпионатах страны по различным видам спорта, без труда разберутся в этой системе.
Принцип проведения игры прост. Сначала дается общее задание для всех, по результатам которого определяется, кто в какой лиге (второй, первой, высшей или суперлиге) начинает играть.
Далее выбирается день недели, в который постоянно будут проходить соревнования. Выбор дня определяется действующим расписанием. Желательно, чтобы все классы параллели имели одинаковое количество уроков в этот день (напоминаем, что в олимпиаде участвуют все).
Для лучшего понимания рассмотрим правила игры на конкретном примере.
Пусть в параллели пятых классов 53 человека. После предварительного тура 10 человек определены в суперлигу, 15 – в высшую, 15 – в первую и 13 – во вторую. Определен постоянный день игр – четверг.
В первый такой четверг соревнуются участники второй лиги (вторая лига, 1 тур). Они решают шесть заданий за 40–60 мин (время определяется учителем). После проведения первого тура и проверки работ участники, занявшие первые пять мест, переходят в первую лигу. Остальные 8 человек получают места с 53 по 46.
В следующий четверг соревнуются 20 человек (15 человек, определенных первоначально в первую лигу плюс пятеро перешедших из второй лиги). После проверки работ происходит следующее: лучшие 5 участников переходят в высшую лигу; остальные 15 человек получают места с 45 по 31; 5 участников, занявших последние места (в нашем примере 41–45 места), переходят во вторую лигу.
В следующий (третий) четверг соревнуются 20 человек (15 человек, определенных изначально в высшую лигу плюс пятеро перешедших из первой лиги). После проверки работ, как и в предыдущем случае: 5 лучших участников переходят в суперлигу; остальные 15 человек получают места с 30 по 16; 5 участников, занявших 26–30 места, переходят в первую лигу.
В четвертый четверг проходит первый тур суперлиги. Все участники в итоге получают места с 1 по 15, причем участники, занявшие 11–15 места, переходят в высшую лигу.
Затем по тем же правилам проходит второй тур в каждой из четырех лиг, затем третий и т. д.
Если учащийся по болезни или по другим причинам пропускает какой-нибудь тур своей лиги, то он набирает 0 баллов и выбывает в более низшую лигу (а если он во второй лиге – просто занимает последнее место).
В книге представлено два комплекса олимпиад по лигам:
1. Олимпиады по лигам (5–6 классы), адаптированные под учебник Г. В. Дорофеева и Л. Г. Петерсон. Учителя математики знают, что если пятиклассники учатся по учебному комплекту Г. В. Дорофеева и Л. Г. Петерсон, то за 5 класс проходится чуть ли не вся программа 6 класса. Это нашло свое отражение в содержании задач.
Всего в лигах предусмотрено 10 туров. Итоговые результаты подводятся просто (лучше всего это сделать в Excel). Пусть некоторый учащийся в течение десяти туров занимал места: ах, а2, ах... а. Из данных чисел отбрасываются лучший и худший результаты, а далее считается среднее арифметическое оставшихся 8 чисел:
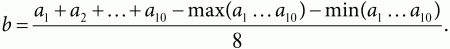У кого меньше число Ь, тот и выиграл (для сортировки участников по местам можно применить известную в Excel команду РАНГ). Небольшое пояснение: лучший результат отбрасывается, так как бывает случайное попадание учащегося в высшую лигу и суперлигу перед первым туром, а худший результат учащийся также может показать случайно, например, вследствие пропуска по болезни.
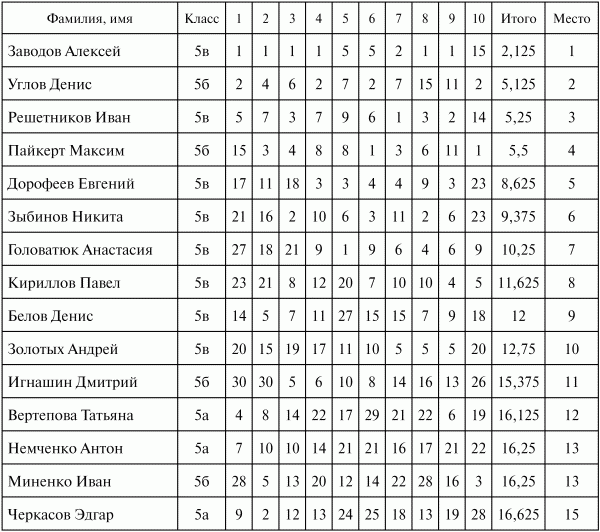
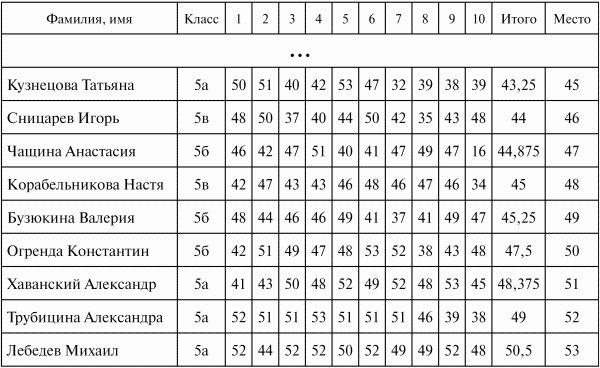
Итоговая таблица может выглядеть так:
2. Олимпиады по лигам (5–6 классы), адаптированные под учебник Н. Я. Виленкина и др.
Эти олимпиады четко разделены на два вида:
стандартная лига (примеры, уравнения, типовые задачи и т. д.);
олимпиадная лига (нестандартные задания).
Разделение связано с тем, что в учебном комплекте Н. Я. Виленкина и др. практически отсутствуют задачи на развитие логического мышления (правда, это не является недостатком учебника, просто он преследует другие дидактические цели). А потому есть смысл разделить математическое соревнование учащихся на две части.
Итоги подводятся так же, как и при проведении олимпиад, адаптированных под учебник Г. В. Дорофеева и Л. Г. Петерсон. Те же 10 туров, та же формула для подведения итогов.
Практика показала, что детям очень нравится такое соревнование. Неожиданным и одновременно приятным было то обстоятельство, что учащиеся, занимающие последние места, рвались на игру не хуже «обитателей суперлиги» и также живо обсуждали каждый промежуточный итог игры.
Выражаю большую благодарность своим коллегам: Наталье Михайловне Дорофеевой и Ольге Алексеевне Коржовой, которые вместе с автором книги разработали данную форму проведения математических олимпиад.
Принцип проведения игры прост. Сначала дается общее задание для всех, по результатам которого определяется, кто в какой лиге (второй, первой, высшей или суперлиге) начинает играть.
Далее выбирается день недели, в который постоянно будут проходить соревнования. Выбор дня определяется действующим расписанием. Желательно, чтобы все классы параллели имели одинаковое количество уроков в этот день (напоминаем, что в олимпиаде участвуют все).
Для лучшего понимания рассмотрим правила игры на конкретном примере.
Пусть в параллели пятых классов 53 человека. После предварительного тура 10 человек определены в суперлигу, 15 – в высшую, 15 – в первую и 13 – во вторую. Определен постоянный день игр – четверг.
В первый такой четверг соревнуются участники второй лиги (вторая лига, 1 тур). Они решают шесть заданий за 40–60 мин (время определяется учителем). После проведения первого тура и проверки работ участники, занявшие первые пять мест, переходят в первую лигу. Остальные 8 человек получают места с 53 по 46.
В следующий четверг соревнуются 20 человек (15 человек, определенных первоначально в первую лигу плюс пятеро перешедших из второй лиги). После проверки работ происходит следующее: лучшие 5 участников переходят в высшую лигу; остальные 15 человек получают места с 45 по 31; 5 участников, занявших последние места (в нашем примере 41–45 места), переходят во вторую лигу.
В следующий (третий) четверг соревнуются 20 человек (15 человек, определенных изначально в высшую лигу плюс пятеро перешедших из первой лиги). После проверки работ, как и в предыдущем случае: 5 лучших участников переходят в суперлигу; остальные 15 человек получают места с 30 по 16; 5 участников, занявших 26–30 места, переходят в первую лигу.
В четвертый четверг проходит первый тур суперлиги. Все участники в итоге получают места с 1 по 15, причем участники, занявшие 11–15 места, переходят в высшую лигу.
Затем по тем же правилам проходит второй тур в каждой из четырех лиг, затем третий и т. д.
Если учащийся по болезни или по другим причинам пропускает какой-нибудь тур своей лиги, то он набирает 0 баллов и выбывает в более низшую лигу (а если он во второй лиге – просто занимает последнее место).
В книге представлено два комплекса олимпиад по лигам:
1. Олимпиады по лигам (5–6 классы), адаптированные под учебник Г. В. Дорофеева и Л. Г. Петерсон. Учителя математики знают, что если пятиклассники учатся по учебному комплекту Г. В. Дорофеева и Л. Г. Петерсон, то за 5 класс проходится чуть ли не вся программа 6 класса. Это нашло свое отражение в содержании задач.
Всего в лигах предусмотрено 10 туров. Итоговые результаты подводятся просто (лучше всего это сделать в Excel). Пусть некоторый учащийся в течение десяти туров занимал места: ах, а2, ах... а. Из данных чисел отбрасываются лучший и худший результаты, а далее считается среднее арифметическое оставшихся 8 чисел:
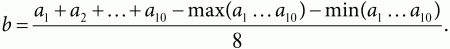
Итоговая таблица может выглядеть так:
Эти олимпиады четко разделены на два вида:
стандартная лига (примеры, уравнения, типовые задачи и т. д.);
олимпиадная лига (нестандартные задания).
Разделение связано с тем, что в учебном комплекте Н. Я. Виленкина и др. практически отсутствуют задачи на развитие логического мышления (правда, это не является недостатком учебника, просто он преследует другие дидактические цели). А потому есть смысл разделить математическое соревнование учащихся на две части.
Итоги подводятся так же, как и при проведении олимпиад, адаптированных под учебник Г. В. Дорофеева и Л. Г. Петерсон. Те же 10 туров, та же формула для подведения итогов.
Практика показала, что детям очень нравится такое соревнование. Неожиданным и одновременно приятным было то обстоятельство, что учащиеся, занимающие последние места, рвались на игру не хуже «обитателей суперлиги» и также живо обсуждали каждый промежуточный итог игры.
Выражаю большую благодарность своим коллегам: Наталье Михайловне Дорофеевой и Ольге Алексеевне Коржовой, которые вместе с автором книги разработали данную форму проведения математических олимпиад.
Финальная игра (5–6 классы)
Игра названа финальной, так как ее рекомендуется проводить в качестве итоговой к олимпиадам по лигам. В ней соревнуются между собой учащиеся, занявшие одинаковые места в своих классах. Так, из вышеприведенной таблицы следует, что первое место в 5а классе заняла Вертепова Татьяна, в 5б – Углов Денис, в 5в – Заводов Алексей. Значит, в финальной игре они и соревнуются между собой. В нашем случае получаем следующую таблицу участников:
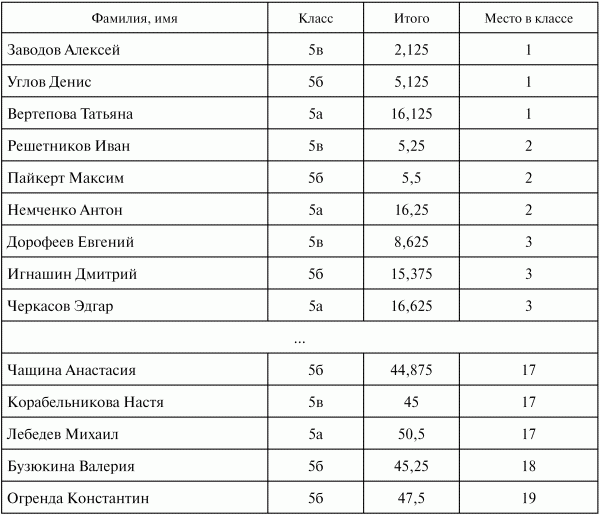В книге приведено 17 вариантов финальной игры. Если в классе более 17 человек, что характерно для общеобразовательных школ, то задания для последующих вариантов можно взять из учебника или дидактических материалов.
Финальную игру можно провести независимо от олимпиад по лигам; в этом случае за основу берутся учебные показатели учащихся.
Финальную игру можно провести независимо от олимпиад по лигам; в этом случае за основу берутся учебные показатели учащихся.
Межклассные математические олимпиады
Соревнуются учащиеся 5–9 классов. Привлекать 10–11 классы вряд ли целесообразно ввиду их профилизации.
В книге вы найдете задания трех межклассных олимпиад.
На межклассную математическую олимпиаду № 1 от каждого класса представляются две команды. Общая численность двух команд – не более 12 человек.
За каждое задание можно получить: 0 очков (—), 1 очко ( + ), 2 очка ( + ), 3 очка ( + ).
Очки, набранные командой № 1, умножаются на 1, 5.
В олимпиаду входят:
кроссворд;
технические задания (примеры, уравнения, неравенства и т. д.);
задачи на сообразительность;
геометрические задания;
задачи по комбинаторике.
Класс может выставить на олимпиаду более двух команд (скажем, одну первую и две вторых). В этом случае будет засчитан лучший из результатов. Например, если команда № 1 набрала 11 очков, команда № 2а – 12 очков, команда № 26–14 очков, то класс в целом получает 11 1, 5 + 14 = 30, 5 очков. Время выполнения работы – 60 мин.
На олимпиаду № 2 от каждого класса должны быть представлены три команды: № 1 – самая сильная, № 2 и № 3. В каждой команде должно быть не более 6 человек. Класс может представить более трех команд, например, две команды под № 3. В этом случае будет засчитан лучший из результатов.
Каждой команде выдается листок с заданиями. Около каждого задания стоит количество очков, которое может получить команда в случае верного решения и верного ответа. На решение заданий также отводится 60 мин.
А на олимпиаду № 3 каждый класс представляет 4 команды. В команде не более 6 человек.
Команда № 1 решает 4 олимпиадных задачи, по 5 очков каждая. Команда № 2 решает 5 технически сложных заданий (примеры, уравнения, неравенства, системы, типовые задачи), по 4 очка каждое. Командам № 3 и № 4 предлагается соответственно 6 заданий по 3 очка и 7 заданий по 2 очка, причем задания для команды № 4 взяты из дидактических материалов для общеобразовательных классов. Время выполнения работы – 45–60 мин.
Решения всех задач олимпиад должны быть четкими и подробными. В случае если несколько команд набирают одинаковое количество очков, то оцениваются оформление, рациональность и красота решения.
Важно отметить, что в соревновании принимают участие и слабые учащиеся, причем каждый из них понимает: успех класса от него зависит не меньше, чем от отличников!
Ответы на все задания помещены в конце книги, поэтому в содержании к каждой рубрике приводятся две страницы. Первая указывает место расположения задания, вторая – в скобках – ответ.
В книге вы найдете задания трех межклассных олимпиад.
На межклассную математическую олимпиаду № 1 от каждого класса представляются две команды. Общая численность двух команд – не более 12 человек.
За каждое задание можно получить: 0 очков (—), 1 очко ( + ), 2 очка ( + ), 3 очка ( + ).
Очки, набранные командой № 1, умножаются на 1, 5.
В олимпиаду входят:
кроссворд;
технические задания (примеры, уравнения, неравенства и т. д.);
задачи на сообразительность;
геометрические задания;
задачи по комбинаторике.
Класс может выставить на олимпиаду более двух команд (скажем, одну первую и две вторых). В этом случае будет засчитан лучший из результатов. Например, если команда № 1 набрала 11 очков, команда № 2а – 12 очков, команда № 26–14 очков, то класс в целом получает 11 1, 5 + 14 = 30, 5 очков. Время выполнения работы – 60 мин.
На олимпиаду № 2 от каждого класса должны быть представлены три команды: № 1 – самая сильная, № 2 и № 3. В каждой команде должно быть не более 6 человек. Класс может представить более трех команд, например, две команды под № 3. В этом случае будет засчитан лучший из результатов.
Каждой команде выдается листок с заданиями. Около каждого задания стоит количество очков, которое может получить команда в случае верного решения и верного ответа. На решение заданий также отводится 60 мин.
А на олимпиаду № 3 каждый класс представляет 4 команды. В команде не более 6 человек.
Команда № 1 решает 4 олимпиадных задачи, по 5 очков каждая. Команда № 2 решает 5 технически сложных заданий (примеры, уравнения, неравенства, системы, типовые задачи), по 4 очка каждое. Командам № 3 и № 4 предлагается соответственно 6 заданий по 3 очка и 7 заданий по 2 очка, причем задания для команды № 4 взяты из дидактических материалов для общеобразовательных классов. Время выполнения работы – 45–60 мин.
Решения всех задач олимпиад должны быть четкими и подробными. В случае если несколько команд набирают одинаковое количество очков, то оцениваются оформление, рациональность и красота решения.
Важно отметить, что в соревновании принимают участие и слабые учащиеся, причем каждый из них понимает: успех класса от него зависит не меньше, чем от отличников!
Ответы на все задания помещены в конце книги, поэтому в содержании к каждой рубрике приводятся две страницы. Первая указывает место расположения задания, вторая – в скобках – ответ.
Олимпиады по лигам (5–6 классы), адаптированные под учебник Г. В. Дорофеева и Л. Г. Петерсон
Вторая лига
1 тур
1. Вычислите 4506 ? 7568.
2. Периметр квадрата равен 12 м. Найдите площадь квадрата.
3. Найдите значение выражения a: b – с при а = 34 128 120, b= 1703, с = 400.
4. Решите уравнение 148 – 7 ? х = 36.
5. Аня прошла 2 км за 31 мин, а Оля – 4 км за 1 ч. Скорость какой девочки больше и почему?
6. Четыре страны имеют форму треугольников. Нарисуйте, как расположены страны одна относительно другой, если у каждой из них есть общие границы с тремя другими.
2. Периметр квадрата равен 12 м. Найдите площадь квадрата.
3. Найдите значение выражения a: b – с при а = 34 128 120, b= 1703, с = 400.
4. Решите уравнение 148 – 7 ? х = 36.
5. Аня прошла 2 км за 31 мин, а Оля – 4 км за 1 ч. Скорость какой девочки больше и почему?
6. Четыре страны имеют форму треугольников. Нарисуйте, как расположены страны одна относительно другой, если у каждой из них есть общие границы с тремя другими.
2 тур
1. Во сколько раз число 9801 больше, чем 99?
2. Частное равно 7, делимое на 14 больше частного. Найдите делитель.
3. Сколько миллиметров в 4 км?
4. Решите уравнение 4752: (1010 – 2х) = 11.
5. Поставьте между цифрами любые арифметические знаки и скобки, чтобы получить верное равенство: 7 7 7 7 = 8.
6. В семье четверо детей. Им 5, 8, 13 и 15 лет, а зовут их Аня, Юра, Света и Лена. Сколько лет каждому из них, если одна девочка ходит в детский сад, Аня старше, чем Юра, а сумма лет Ани и Светы делится на три?
2. Частное равно 7, делимое на 14 больше частного. Найдите делитель.
3. Сколько миллиметров в 4 км?
4. Решите уравнение 4752: (1010 – 2х) = 11.
5. Поставьте между цифрами любые арифметические знаки и скобки, чтобы получить верное равенство: 7 7 7 7 = 8.
6. В семье четверо детей. Им 5, 8, 13 и 15 лет, а зовут их Аня, Юра, Света и Лена. Сколько лет каждому из них, если одна девочка ходит в детский сад, Аня старше, чем Юра, а сумма лет Ани и Светы делится на три?
3 тур
1. На сколько произведение чисел 308 и 22 больше их частного?
2. Найдите сумму цифр числах = 1 ? 2 ? 3 ? 4 ? 5 ? 6 ? 7.
3. Сколько метров в 1 см?
4. Подберите такое натуральное число х, чтобы выполнялось равенство 12 – х = х ? х.
5. Встретились три друга – Белов, Серов и Чернов. Чернов сказал другу, одетому в серый костюм: «Интересно, что на одном из нас белый костюм, на другом – серый и на третьем – черный, но на каждом костюм цвета, не соответствующего фамилии». Какой цвет костюма у каждого из друзей?
6. Угадайте два следующих числа в ряду: 5, 8, 14, 26, 50...
2. Найдите сумму цифр числах = 1 ? 2 ? 3 ? 4 ? 5 ? 6 ? 7.
3. Сколько метров в 1 см?
4. Подберите такое натуральное число х, чтобы выполнялось равенство 12 – х = х ? х.
5. Встретились три друга – Белов, Серов и Чернов. Чернов сказал другу, одетому в серый костюм: «Интересно, что на одном из нас белый костюм, на другом – серый и на третьем – черный, но на каждом костюм цвета, не соответствующего фамилии». Какой цвет костюма у каждого из друзей?
6. Угадайте два следующих числа в ряду: 5, 8, 14, 26, 50...
4 тур
1. Вычислите 75 764 376: 94–86 004.
2. Решите уравнение 737 – 14 (38 – х) = 205.
3. Запишите двойку тремя пятерками.
4. Кот в сапогах поймал четырех щук и еще половину улова. Сколько щук поймал Кот в сапогах?
5. Как в зале расставить 10 кресел так, чтобы у каждой из четырех стен кресел было поровну? При этом: 1) кресла должны стоять только вдоль стен; 2) если кресло стоит в углу зала, то считается, что оно стоит вдоль сразу двух стен.
6. Три девочки – Соня, Оля и Полина – одновременно сели есть конфеты. Оля и Соня съели вдвоем 11 конфет, Полина и Оля – 15, а Соня и Полина – 14. Сколько конфет съели все три девочки вместе?
2. Решите уравнение 737 – 14 (38 – х) = 205.
3. Запишите двойку тремя пятерками.
4. Кот в сапогах поймал четырех щук и еще половину улова. Сколько щук поймал Кот в сапогах?
5. Как в зале расставить 10 кресел так, чтобы у каждой из четырех стен кресел было поровну? При этом: 1) кресла должны стоять только вдоль стен; 2) если кресло стоит в углу зала, то считается, что оно стоит вдоль сразу двух стен.
6. Три девочки – Соня, Оля и Полина – одновременно сели есть конфеты. Оля и Соня съели вдвоем 11 конфет, Полина и Оля – 15, а Соня и Полина – 14. Сколько конфет съели все три девочки вместе?
5 тур
1. Вычислите 34 128 120: 1703 – 240.
2. Чему равна величина 3х – 1, если 2х + 1 = 7?
3. Все стороны треугольника равны, а его периметр равен 180 см. Найдите площадь квадрата, сторона которого равна стороне треугольника.
4. Сколько минут содержится в 7/10 ч?
5. Нарисуйте какой-нибудь круг. Начертите 4 прямые так, чтобы круг был поделен на 6 частей.
6. Найдите сумму всех двузначных натуральных чисел, которые при делении на 30 дают в остатке 3.
2. Чему равна величина 3х – 1, если 2х + 1 = 7?
3. Все стороны треугольника равны, а его периметр равен 180 см. Найдите площадь квадрата, сторона которого равна стороне треугольника.
4. Сколько минут содержится в 7/10 ч?
5. Нарисуйте какой-нибудь круг. Начертите 4 прямые так, чтобы круг был поделен на 6 частей.
6. Найдите сумму всех двузначных натуральных чисел, которые при делении на 30 дают в остатке 3.
6 тур
1. Когда три подруги – Надя, Валя и Маша – вышли гулять, на них были белое, красное и синее платья. Туфли их были тех же трех цветов, но только у Нади цвета туфель и платья совпадают. При этом у Вали ни платье, ни туфли не были синими, а Маша – в красных туфлях. Определите цвет платьев и туфель каждой из подруг.
2. Башенные часы отбивают три удара за 12 с. В течение какого времени они пробьют шесть ударов?
3. Баба Яга в своей избушке на курьих ножках завела сказочных животных. Все они, кроме двух, – Говорящие Коты; все, кроме двух, – Мудрые Совы; остальные – Усатые Тараканы. Сколько обитателей в избушке у Бабы Яги (саму Бабу Ягу в расчет не принимать)?
4. Какими должны быть два следующих числа в последовательности: 10, 8, 11, 9, 12, 10, 13...?
5. У каких двузначных чисел сумма цифр равна 10?
6. – У меня зазвонил телефон.
– Кто говорит?
– Слон.
... А потом позвонил Крокодил...
... А потом позвонили Зайчатки...
... А потом позвонили Мартышки...
... А потом позвонил Медведь...
... А потом позвонили Цапли...
... Итак, у Слона, Крокодила, Зайчаток, Мартышек, Медведя, Цапель и у меня установлены телефоны. Каждые два телефонных аппарата соединены проводом. Сколько для этого понадобилось проводов?
2. Башенные часы отбивают три удара за 12 с. В течение какого времени они пробьют шесть ударов?
3. Баба Яга в своей избушке на курьих ножках завела сказочных животных. Все они, кроме двух, – Говорящие Коты; все, кроме двух, – Мудрые Совы; остальные – Усатые Тараканы. Сколько обитателей в избушке у Бабы Яги (саму Бабу Ягу в расчет не принимать)?
4. Какими должны быть два следующих числа в последовательности: 10, 8, 11, 9, 12, 10, 13...?
5. У каких двузначных чисел сумма цифр равна 10?
6. – У меня зазвонил телефон.
– Кто говорит?
– Слон.
... А потом позвонил Крокодил...
... А потом позвонили Зайчатки...
... А потом позвонили Мартышки...
... А потом позвонил Медведь...
... А потом позвонили Цапли...
... Итак, у Слона, Крокодила, Зайчаток, Мартышек, Медведя, Цапель и у меня установлены телефоны. Каждые два телефонных аппарата соединены проводом. Сколько для этого понадобилось проводов?
7 тур
1. Какое число больше: 3/7 или 1/2?
2. Вычислите 2504 ? 706.
3. Решите уравнение Зх + 4 – х – 1 – 2х – 3 = 0.
4. Сколько существует двузначных чисел, которые делятся без остатка на 5?
5. Федя всегда говорит правду, а Вадим всегда лжет. Какой вопрос надо им задать, чтобы они дали на него одинаковые ответы?
6. Десяти собакам и кошкам скормили 56 галет. Каждой кошке досталось 5 галет, а каждой собаке – 6. Сколько было собак?
2. Вычислите 2504 ? 706.
3. Решите уравнение Зх + 4 – х – 1 – 2х – 3 = 0.
4. Сколько существует двузначных чисел, которые делятся без остатка на 5?
5. Федя всегда говорит правду, а Вадим всегда лжет. Какой вопрос надо им задать, чтобы они дали на него одинаковые ответы?
6. Десяти собакам и кошкам скормили 56 галет. Каждой кошке досталось 5 галет, а каждой собаке – 6. Сколько было собак?
8 тур
1. В магазине продается сладкая кукуруза в разных банках. В первой банке 300 г кукурузы, и стоит она 18 р. Во второй банке 400 г кукурузы, и стоит она 23 р. Какую банку выгоднее купить и почему?
2. Найдите значение выражения а ? (а + Ь): с при а = 104, b = 23, с = 127.
3. Решите уравнение х + 2х + 3х + 4х + 5х + 6х + 7х = 56.
4. Какой должна быть следующая фигурка в ряду:
5. Во дворе живут 3 девочки и 4 мальчика. Сколькими способами из них можно составить команду, состоящую из двух девочек и двух мальчиков?
6. Найдите такие два натуральных числа, разность кубов которых равна 19.
2. Найдите значение выражения а ? (а + Ь): с при а = 104, b = 23, с = 127.
3. Решите уравнение х + 2х + 3х + 4х + 5х + 6х + 7х = 56.
4. Какой должна быть следующая фигурка в ряду:
6. Найдите такие два натуральных числа, разность кубов которых равна 19.
9 тур
1. Запишите число 30 тремя тройками.
2. Найдите двузначное число, произведение цифр которого равно сумме этих цифр.
3. Можно ли испечь такой торт, который может быть разделен одним прямолинейным разрезом на 4 части?
4. В двух пачках всего 30 тетрадей. Если бы из первой пачки переложили во вторую 2 тетради, то в первой пачке стало бы вдвое больше тетрадей, чем во второй. Сколько тетрадей было в каждой пачке?
5. Вычислите 1/3 + 2/5 – 1/15. Ответ запишите в виде несократимой дроби.
6. Трое туристов должны перебраться с одного берега реки на другой. В их распоряжении старая лодка, которая может выдержать нагрузку всего в 100 кг. Вес одного из туристов 45 кг, второго – 50 кг, третьего – 80 кг. Как должны они действовать, чтобы перебраться на другой берег?
2. Найдите двузначное число, произведение цифр которого равно сумме этих цифр.
3. Можно ли испечь такой торт, который может быть разделен одним прямолинейным разрезом на 4 части?
4. В двух пачках всего 30 тетрадей. Если бы из первой пачки переложили во вторую 2 тетради, то в первой пачке стало бы вдвое больше тетрадей, чем во второй. Сколько тетрадей было в каждой пачке?
5. Вычислите 1/3 + 2/5 – 1/15. Ответ запишите в виде несократимой дроби.
6. Трое туристов должны перебраться с одного берега реки на другой. В их распоряжении старая лодка, которая может выдержать нагрузку всего в 100 кг. Вес одного из туристов 45 кг, второго – 50 кг, третьего – 80 кг. Как должны они действовать, чтобы перебраться на другой берег?
10 тур
1. Мальчик лег спать в 19 ч вечера, поставив будильник так, чтобы он прозвенел в 9 ч утра. Сколько времени проспит мальчик?
2. Делимое в шесть раз больше делителя, а делитель в шесть раз больше частного. Чему равно делимое?
3. Может ли произведение двух чисел быть меньше меньшего из сомножителей? Если нет, то почему? А если да, то приведите хотя бы один пример.
4. На поляну прилетело 35 ворон. Неожиданно вороны взлетели и разделились на две стаи: одна стая уселась на ветви старой березы, а другая – на ольху. Через некоторое время с березы на ольху перелетело 5 ворон, столько же ворон совсем улетело с березы, после чего на березе осталось вдвое больше ворон, чем на ольхе. Сколько ворон было в каждой из двух стай первоначально?
5. Скорость течения реки 2 км/ч. На сколько больше скорость движения катера по течению этой реки, чем против течения, при постоянной собственной скорости катера?
6. Вычислите
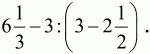
2. Делимое в шесть раз больше делителя, а делитель в шесть раз больше частного. Чему равно делимое?
3. Может ли произведение двух чисел быть меньше меньшего из сомножителей? Если нет, то почему? А если да, то приведите хотя бы один пример.
4. На поляну прилетело 35 ворон. Неожиданно вороны взлетели и разделились на две стаи: одна стая уселась на ветви старой березы, а другая – на ольху. Через некоторое время с березы на ольху перелетело 5 ворон, столько же ворон совсем улетело с березы, после чего на березе осталось вдвое больше ворон, чем на ольхе. Сколько ворон было в каждой из двух стай первоначально?
5. Скорость течения реки 2 км/ч. На сколько больше скорость движения катера по течению этой реки, чем против течения, при постоянной собственной скорости катера?
6. Вычислите
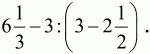
Первая лига
1 тур
1. Вычислите 828 828: 138 – 5644.
2. Найдите значение выражения (х + у ? z): t – f, если х = 450 044, у = 203, z =470, t =6, f = 999.
3. Подберите такое натуральное число х, чтобы х ? х + х = 992.
4. Запишите самое большое трехзначное число, сумма цифр которого равна 15.
5. Точки А, В, С, лежат на одной прямой. Длина отрезка АВ равна 6 см, длина отрезка ВС равна 8 см. Чему может равняться длина отрезка АС?
6. Скорость катера по течению 48 км/ч, а против течения 40 км/ч. Чему равна скорость течения?
2. Найдите значение выражения (х + у ? z): t – f, если х = 450 044, у = 203, z =470, t =6, f = 999.
3. Подберите такое натуральное число х, чтобы х ? х + х = 992.
4. Запишите самое большое трехзначное число, сумма цифр которого равна 15.
5. Точки А, В, С, лежат на одной прямой. Длина отрезка АВ равна 6 см, длина отрезка ВС равна 8 см. Чему может равняться длина отрезка АС?
6. Скорость катера по течению 48 км/ч, а против течения 40 км/ч. Чему равна скорость течения?
2 тур
1. Вычислите 809 ? 43–97 + 13 662 000: 27 000.
2. Найдите значение выражения х + 6 + 5х – 4 – 2х + 3 – 4х, если х = 307.
3. Восстановите запись: * 8 ? * = 8**. Укажите все решения.
4. Сколько прямоугольников, считая большой, «спрятано» на рисунке?
5. Если бы Аня купила 3 тетради, то у нее осталось бы 5 р., а если бы Аня купила 4 тетради, то ей не хватило бы 5 р. Сколько денег было у Ани?
6. Найдите наименьшее натуральное пятизначное число, которое делится на 9, и чтобы первая цифра была 7 и все цифры различны.
2. Найдите значение выражения х + 6 + 5х – 4 – 2х + 3 – 4х, если х = 307.
3. Восстановите запись: * 8 ? * = 8**. Укажите все решения.
4. Сколько прямоугольников, считая большой, «спрятано» на рисунке?
6. Найдите наименьшее натуральное пятизначное число, которое делится на 9, и чтобы первая цифра была 7 и все цифры различны.
3 тур
1. Вычислите 35 ? 202 – 51 948: (1577 – 44 ? 35) + 334.
2. Нарисуйте отрезок АВ длиной 4 см. Отметьте середину отрезка-точку С. Отметьте точку D – середину отрезка АС. На луче DC отметьте точку Е так, чтобы длина отрезка DE была равна 7 см. Чему равно расстояние от В до Е?
3. Разрежьте фигуру, изображенную на рисунке, на 4 одинаковые части.
4. Турист прошел половину пути, затем треть оставшегося пути, после чего ему осталось пройти 6 км. Чему равен весь путь туриста?
5. Мастер за 8 ч делает 80 деталей, а его ученик за 5 ч делает 25 деталей. За сколько часов они изготовят 45 деталей, если будут работать вместе?
6. В мастерской по пошиву одежды от куска сукна в 200 см ежедневно, начиная с 1 декабря, отрезали по 2 дм. Когда был отрезан последний кусок?
2. Нарисуйте отрезок АВ длиной 4 см. Отметьте середину отрезка-точку С. Отметьте точку D – середину отрезка АС. На луче DC отметьте точку Е так, чтобы длина отрезка DE была равна 7 см. Чему равно расстояние от В до Е?
3. Разрежьте фигуру, изображенную на рисунке, на 4 одинаковые части.
5. Мастер за 8 ч делает 80 деталей, а его ученик за 5 ч делает 25 деталей. За сколько часов они изготовят 45 деталей, если будут работать вместе?
6. В мастерской по пошиву одежды от куска сукна в 200 см ежедневно, начиная с 1 декабря, отрезали по 2 дм. Когда был отрезан последний кусок?
4 тур
1. Решите уравнение 18 408: (268 ? 75–19 746) – х = 42.
2. В этом примере умножения больше половины цифр заменено звездочками. Восстановите недостающие цифры:
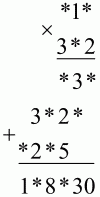3. Какой угол составляют между собой часовая и минутная стрелки часов в 16 ч?
4. Строительный кирпич весит 4 кг. Сколько весит игрушечный кирпичик из того же материала, все размеры которого в 2 раза меньше?
5. На уроке физкультуры ученики выстроились в линейку на расстоянии 1 м друг от друга. Вся линейка растянулась на 21 м. Сколько было учеников?
6. В школе 368 учащихся. Докажите, что среди учащихся этой школы обязательно найдутся хотя бы два ученика, отмечающие свой день рождения в один и тот же день.
2. В этом примере умножения больше половины цифр заменено звездочками. Восстановите недостающие цифры:
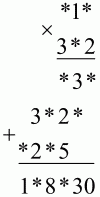
4. Строительный кирпич весит 4 кг. Сколько весит игрушечный кирпичик из того же материала, все размеры которого в 2 раза меньше?
5. На уроке физкультуры ученики выстроились в линейку на расстоянии 1 м друг от друга. Вся линейка растянулась на 21 м. Сколько было учеников?
6. В школе 368 учащихся. Докажите, что среди учащихся этой школы обязательно найдутся хотя бы два ученика, отмечающие свой день рождения в один и тот же день.
5 тур
1. Вычислите 66 509 + 141 404: (39 839 – 39 793) + 1985.
2. Решите уравнение 12х + 4 – 5х + 21 = 8x.
3. На какую цифру оканчивается число 42004(произведение 2004 четверок)?
4. 2/5 числа равны 12. Найдите: а) само число; б) 60 % этого числа.
5. Найдите длину стороны квадрата, если его площадь численно равна периметру.
6. Сейчас Сереже 11 лет, а Вове 1 год. Сколько лет будет Сереже и Вове, когда Сережа станет втрое старше Вовы?
2. Решите уравнение 12х + 4 – 5х + 21 = 8x.
3. На какую цифру оканчивается число 42004(произведение 2004 четверок)?
4. 2/5 числа равны 12. Найдите: а) само число; б) 60 % этого числа.
5. Найдите длину стороны квадрата, если его площадь численно равна периметру.
6. Сейчас Сереже 11 лет, а Вове 1 год. Сколько лет будет Сереже и Вове, когда Сережа станет втрое старше Вовы?
6 тур
1. Вычислите (2 ? 3 ? 4 ? 5 ? 6 ? 7 ? 8 ? 9): (1 2 ? 3 ? 4 ? 5 ? 6 ? 7 ? 8).
2. Подберите число n так, чтобы уравнение nx + 1 = х не имело решений.
3. Мачеха, уезжая на бал, дала Золушке мешок, в котором были перемешаны мак и просо, и велела перебрать их. Когда Золушка уезжала на бал, она оставила три мешка: в одном было просо, в другом – мак, а в третьем – еще не разобранная смесь. Чтобы не перепутать мешки, Золушка к каждому из них прикрепила по табличке: «Мак», «Просо» и «Смесь».
Мачеха вернулась с бала первой и нарочно поменяла местами таблички так, чтобы на каждом мешке оказалась неправильная надпись. Ученик Феи успел предупредить Золушку, что теперь ни одна надпись на мешках не соответствует действительности. Тогда Золушка достала только одно-единственное зернышко из одного мешка и, посмотрев на него, сразу догадалась, где что лежит. Как она это сделала?
4. Кувшин = бутылка + стакан; два кувшина = семь стаканов; бутылка = чашка + два стакана; бутылка = сколько чашек?
5. В кабинете со звуконепроницаемыми стенами висят настенные часы, которые бьют каждые полчаса (один удар) и каждый час (столько ударов, сколько показывает часовая стрелка). Однажды, открыв дверь в кабинет, хозяин услышал один удар часов. После этого хозяин не уходил из кабинета. Через полчаса часы в кабинете пробили еще раз – опять один удар. Спустя полчаса – еще один удар. Наконец, еще через полчаса часы снова пробили один раз. Какое время показывали часы, когда хозяин входил в кабинет?
6. В соревновании участвовали 50 стрелков. Первый выбил 60 очков; второй – 80; третий – среднее арифметическое очков первых двух; четвертый – среднее арифметическое очков первых трех. Каждый следующий выбил среднее арифметическое очков всех предыдущих. Сколько очков выбил 50-й стрелок?
2. Подберите число n так, чтобы уравнение nx + 1 = х не имело решений.
3. Мачеха, уезжая на бал, дала Золушке мешок, в котором были перемешаны мак и просо, и велела перебрать их. Когда Золушка уезжала на бал, она оставила три мешка: в одном было просо, в другом – мак, а в третьем – еще не разобранная смесь. Чтобы не перепутать мешки, Золушка к каждому из них прикрепила по табличке: «Мак», «Просо» и «Смесь».
Мачеха вернулась с бала первой и нарочно поменяла местами таблички так, чтобы на каждом мешке оказалась неправильная надпись. Ученик Феи успел предупредить Золушку, что теперь ни одна надпись на мешках не соответствует действительности. Тогда Золушка достала только одно-единственное зернышко из одного мешка и, посмотрев на него, сразу догадалась, где что лежит. Как она это сделала?
4. Кувшин = бутылка + стакан; два кувшина = семь стаканов; бутылка = чашка + два стакана; бутылка = сколько чашек?
5. В кабинете со звуконепроницаемыми стенами висят настенные часы, которые бьют каждые полчаса (один удар) и каждый час (столько ударов, сколько показывает часовая стрелка). Однажды, открыв дверь в кабинет, хозяин услышал один удар часов. После этого хозяин не уходил из кабинета. Через полчаса часы в кабинете пробили еще раз – опять один удар. Спустя полчаса – еще один удар. Наконец, еще через полчаса часы снова пробили один раз. Какое время показывали часы, когда хозяин входил в кабинет?
6. В соревновании участвовали 50 стрелков. Первый выбил 60 очков; второй – 80; третий – среднее арифметическое очков первых двух; четвертый – среднее арифметическое очков первых трех. Каждый следующий выбил среднее арифметическое очков всех предыдущих. Сколько очков выбил 50-й стрелок?
7 тур
1. Вычислите 612 228 + (53 007 – 52 275: 615).
2. Подберите такое натуральное число х, чтобы х(х + 1)(х + 2) = 720.
3. Сколько раз в течение суток часовая и минутная стрелки составляют прямой угол?
4. Найдите двузначное число, которое в семь раз больше цифры его единиц.
5. Тане не хватало 7 р., а Гале – 2 р., чтобы купить по коробке цветных карандашей. Когда они сложили свои деньги, их не хватило даже на покупку одной коробки. Сколько стоит коробка карандашей?
6. Собака погналась за лисицей, которая была на расстоянии 30 м от нее. Скачок собаки равен 2 м, скачок лисицы 1 м. В то время как лисица делает 3 скачка, собака делает 2 скачка. Какое расстояние должна пробежать собака, чтобы догнать лисицу?
2. Подберите такое натуральное число х, чтобы х(х + 1)(х + 2) = 720.
3. Сколько раз в течение суток часовая и минутная стрелки составляют прямой угол?
4. Найдите двузначное число, которое в семь раз больше цифры его единиц.
5. Тане не хватало 7 р., а Гале – 2 р., чтобы купить по коробке цветных карандашей. Когда они сложили свои деньги, их не хватило даже на покупку одной коробки. Сколько стоит коробка карандашей?
6. Собака погналась за лисицей, которая была на расстоянии 30 м от нее. Скачок собаки равен 2 м, скачок лисицы 1 м. В то время как лисица делает 3 скачка, собака делает 2 скачка. Какое расстояние должна пробежать собака, чтобы догнать лисицу?
8 тур
1. Напишите наименьшее натуральное число, составленное из всех цифр, которое делится на 5.
2. Один из пяти братьев испек маме пирог. Никита сказал: «Это Глеб или Игорь». Глеб сказал: «Это сделал не я и не Дима». Игорь сказал: «Вы оба шутите». Андрей сказал: «Нет, один из них сказал правду, а другой обманул». Дима сказал: «Нет, Андрей, ты не прав». Мама знает, что трое из ее сыновей всегда говорят правду. Кто испек пирог?
3. Известно, что в январе четыре пятницы и четыре понедельника. На какой день недели приходится 1 января?
4. Расставьте 24 человека в 6 рядов так, чтобы каждый ряд состоял из 5 человек.
5. Эта старинная задача была известна еще в Древнем Риме. Богатый сенатор, умирая, оставил жену в ожидании ребенка. После смерти сенатора выяснилось, что на свое имущество, равное 210 талантам, он составил следующее завещание: «В случае рождения сына отдать мальчику две трети состояния (то есть 140 талантов), а остальную треть (то есть 70 талантов) – матери; в случае же рождения дочери отдать девочке одну треть состояния (то есть 70 талантов), а остальные две трети (то есть 140 талантов) – матери».
У вдовы сенатора родились близнецы – мальчик и девочка. Такой возможности завещатель не предусмотрел. Как можно разделить имущество между тремя наследниками с наибольшим приближением к условию завещания?
6. Решите уравнение (х – 2)/3 + 2 = 4.
2. Один из пяти братьев испек маме пирог. Никита сказал: «Это Глеб или Игорь». Глеб сказал: «Это сделал не я и не Дима». Игорь сказал: «Вы оба шутите». Андрей сказал: «Нет, один из них сказал правду, а другой обманул». Дима сказал: «Нет, Андрей, ты не прав». Мама знает, что трое из ее сыновей всегда говорят правду. Кто испек пирог?
3. Известно, что в январе четыре пятницы и четыре понедельника. На какой день недели приходится 1 января?
4. Расставьте 24 человека в 6 рядов так, чтобы каждый ряд состоял из 5 человек.
5. Эта старинная задача была известна еще в Древнем Риме. Богатый сенатор, умирая, оставил жену в ожидании ребенка. После смерти сенатора выяснилось, что на свое имущество, равное 210 талантам, он составил следующее завещание: «В случае рождения сына отдать мальчику две трети состояния (то есть 140 талантов), а остальную треть (то есть 70 талантов) – матери; в случае же рождения дочери отдать девочке одну треть состояния (то есть 70 талантов), а остальные две трети (то есть 140 талантов) – матери».
У вдовы сенатора родились близнецы – мальчик и девочка. Такой возможности завещатель не предусмотрел. Как можно разделить имущество между тремя наследниками с наибольшим приближением к условию завещания?
6. Решите уравнение (х – 2)/3 + 2 = 4.
9 тур
1. Вычислите
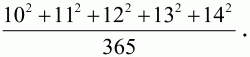2. Решите уравнение
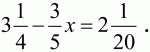3. Припишите к числу 10 справа и слева одну и ту же цифру так, чтобы полученное четырехзначное число делилось на 12.
4. Гена пошел с папой в тир. Договорились, что Гена делает 5 выстрелов и за каждое попадание в цель получает право сделать еще 2 выстрела. Всего Гена сделал 17 выстрелов. Сколько раз он попал в цель?
5. Как-то в минуту отдыха друзья-мушкетеры – Атос, Портос, Арамис и дАртаньян решили померяться силой при перетягивании каната. Портос с д Артаньяном легко перетянули Атоса с Арамисом. Но когда Портос встал в паре с Атосом, то победа против Арамиса с дАртаньяном досталась им уже не так легко. Когда же Портос с Арамисом оказались против Атоса с дАртаньяном, то ни одна из этих пар не смогла одолеть друг друга. Можете ли вы определить, как мушкетеры распределяются по силе?
6. Ваня и Вася – братья-близнецы. Один из них всегда говорит правду, а другой всегда лжет. Вы можете задать только один вопрос одному из братьев, на который он ответит «да» или «нет». Попробуйте выяснить, как зовут каждого из близнецов.
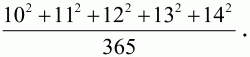
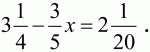
4. Гена пошел с папой в тир. Договорились, что Гена делает 5 выстрелов и за каждое попадание в цель получает право сделать еще 2 выстрела. Всего Гена сделал 17 выстрелов. Сколько раз он попал в цель?
5. Как-то в минуту отдыха друзья-мушкетеры – Атос, Портос, Арамис и дАртаньян решили померяться силой при перетягивании каната. Портос с д Артаньяном легко перетянули Атоса с Арамисом. Но когда Портос встал в паре с Атосом, то победа против Арамиса с дАртаньяном досталась им уже не так легко. Когда же Портос с Арамисом оказались против Атоса с дАртаньяном, то ни одна из этих пар не смогла одолеть друг друга. Можете ли вы определить, как мушкетеры распределяются по силе?
6. Ваня и Вася – братья-близнецы. Один из них всегда говорит правду, а другой всегда лжет. Вы можете задать только один вопрос одному из братьев, на который он ответит «да» или «нет». Попробуйте выяснить, как зовут каждого из близнецов.
10 тур
1. Угол в 12 3/4 градуса рассматривают в лупу, дающую четырехкратное увеличение. Какой величины покажется угол?