Причина “чуда” ясна всякому, кто знаком с законами отражения света: ведь тут имеются три пары параллельных зеркал и десять пар зеркал, поставленных под углом; неудивительно, что они дают такое множество отражений. Еще любопытнее те оптические эффекты, которые были достигнуты на Парижской выставке в так называемом “Дворце миражей”. Устроители этого “дворца” присоединили к бесчисленным отражениям еще мгновенную перемену всей картины. Они как бы устроили подвижный, огромных размеров калейдоскоп, внутри которого помещались зрители.
Перемена обстановки в этом “Дворце миражей” достигалась следующим образом: зеркальные стены на некотором расстоянии от ребер разрезаны вдоль, и полученный угол может вращаться вокруг оси, заменяясь другим. Из рис. 107 видно, что можно произвести три замены, соответствующие углам 1, 2 и 3. Теперь представьте себе, что все углы, обозначенные цифрой 1, заключают в себе обстановку тропического леса, все углы 2 — обстановку арабского зала, а углы 3 — индийского храма.
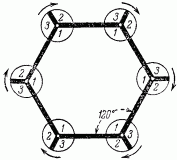Рис. 107.
Рис. 108. Секрет “Дворца миражей”.
Одним движением скрытого механизма, поворачивающего углы, тропический лес превращается в храм или в арабский зал. Весь секрет “волшебства” основан на таком простом физическом явлении, как отражение световых лучей.
“Представьте себе отряд солдат, идущий по местности, разделенной прямой границей на две полосы, из которых одна гладкая, ровная и удобная для ходьбы, другая — кочковатая, затруднительная, так что ходьба по ней не может совершаться столь быстро. Предположим сверх того, что фронт отряда составляет угол с пограничной линией между двумя полосами, так что солдаты достигают этой границы не все одновременно, а последовательно один за другим. Тогда каждый солдат, переступив границу, очутится на почве, по которой он не может более подвигаться так быстро, как до того времени. Он не сможет уже держаться на одной линии с остальной частью шеренги, еще находящейся на лучшей почве, и будет от нее отставать с каждой секундой все больше. Так как каждый солдат, достигая границы, испытывает одинаковое затруднение в ходьбе, то если солдаты не нарушат строя, не рассеются, а будут продолжать маршировать правильной колонной, вся та часть колонны, которая переступила границу, будет неизбежно отставать от остальной и составит с ней поэтому тупой угол в точке пересечения границы. И так как необходимость ходить в ногу, не перебивая дороги друг другу, заставит каждого солдата шагать прямо перед собой, под прямым углом к новому фронту, то путь, который он пройдет по переходе границы, будет, во-первых, перпендикулярен к новому фронту, а во-вторых, так относиться к тому пути, какой был бы пройден в случае отсутствия замедления, как новая скорость к прежней”.
Рис. 109. Опыт, поясняющий преломление света.
В малом виде вы можете воспроизвести это наглядное подобие преломления света у себя на столе. Накройте половину стола скатертью (рис. 109) и, слегка наклонив стол, заставьте скатываться по нему пару колесиков, наглухо посаженных на общую ось (например, от сломанного детского паровоза или другой игрушки). Если направление движения колес и край скатерти составляют прямой угол, преломления пути не происходит. Вы имеете в этом случае иллюстрацию оптического правила: луч, перпендикулярный к плоскости раздела сред, не преломляется. При направлении, наклонном к краю скатерти, путь колес изламывается на этом краю, т. е. на границе между средами с различной скоростью движения в них. Легко заметить, что при переходе из части стола, где скорость движения больше (непокрытая часть), в ту часть, где скорость меньше (скатерть), направление пути (“луч”) приближается к “перпендикуляру падения”. В обратном случае наблюдается удаление от этого перпендикуляра.
Из этого можно, между прочим, почерпнуть важное указание, вскрывающее сущность рассматриваемого явления, а именно, что преломление обусловлено различием скорости света в обеих средах. Чем больше различие в скорости, тем значительнее преломление; так называемый “показатель преломления”, характеризующий величину излома лучей, есть не что иное, как отношение этих скоростей. Когда вы читаете, что показатель преломления при переходе из воздуха в воду есть 4/3, то вы, вместе с тем, узнаёте, что свет движется в воздухе примерно в 1,3 раза скорее, чем в воде.
А в связи с этим находится и другая поучительная особенность распространения света. Если в случае отражения световой луч следует кратчайшим путем, то в случае преломления он избирает скорейший путь: никакое другое направление не приводит луч так скоро к “месту назначения”, как этот изломанный путь.
Рис. 110. Задача о кавалеристе. Найти скорейший путь из A в С.
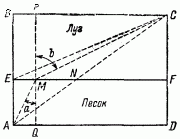Рис. 111. Решение задачи о кавалеристе. Скорейший путь АМС.
Уделим минуту внимания еще одному примеру. Кавалерист должен прибыть с донесением из точки А к палатке командира в точке C (рис. 110). Его отделяют от палатки полоса глубокого песка и полоса луга, разграниченные между собой прямой линией EF, По песчаной почве лошадь движется вдвое медленнее, чем по лугу. Какой же путь должен выбрать кавалерист, чтобы достигнуть палатки в кратчайшее время?
Рис. 112. Что такое синус? Отношение m к радиусу есть синус угла 1, отношение n к радиусу — синус угла 2.
На первый взгляд кажется, что самый скорый путь — прямая линия, проведенная от A до С. Но это совершенно ошибочно, и я не думаю, чтобы нашелся кавалерист, который выбрал бы такой путь. Медленное движение по песку наведет его на правильную мысль сократить эту медленную часть пути, прорезав песчаную полосу по менее косой линии; конечно, тем самым удлинится вторая часть пути — по лугу; но так как по лугу можно двигаться вдвое быстрее, то удлинение пути не перевесит полученной выгоды, и в общем итоге путь будет проделан в меньший промежуток времени. Другими словами, путь кавалериста должен преломиться на границе обоих родов почвы и притом так, чтобы путь по лугу составлял с перпендикуляром к границе больший угол, чем путь по песчаной почве.
Кто знаком с геометрией, именно с теоремой Пифагора, тот может проверить, что прямой путь AC действительно не является путем скорейшим и что при тех размерах для ширины полос и расстояний, которые мы здесь имеем в виду, можно скорее достичь цели, если направиться, например, по ломаной АЕС (рис. 111).
На рис. 110 указано, что ширина песчаной полосы 2 км, луговой — 3 км, а расстояние ВС — 7 км. Тогда вся длина AC (рис. 111) равна, по теореме Пифагора, корень(52 + 72) = корень(74) = 8,60 км. Часть AN — путь по песку — этого отрезка составляет, как легко сообразить, 2/5 этой величины, т. е. 3,44 км. Так как по песку движение происходит вдвое медленнее, чем по лугу, то 3,44 км песчаного пути равнозначны, в смысле требуемого времени, 6,88 км по лугу. И, следовательно, весь смешанный путь по прямой АС, равный 8,60 км, соответствует 12,04 км пути по лугу.
Сделаем такое же “приведение к лугу” и для ломаного пути АЕС. Часть АЕ = 2 км и соответствует 4 км пути по лугу. Часть ЕС = корень(32 + 72) = корень(58) = 7,61 км. Итого весь ломаный путь AEC отвечает 4 + 7,61 = 11,61 км.
Итак, “короткий” прямой путь соответствует 12,04 км движения по лугу, а “длинный” ломаный — всего только 11,61 км по той же почве. “Длинный” путь, как видите, дает выгоду в 12,04 — 11,61 = 0,43, почти в полкилометра!
Но мы не указали еще самого быстрого пути. Быстрейший путь, как учит теория, будет тот, при котором (нам придется здесь обратиться к услугам тригонометрии) синус угла b относится к синусу угла A, как скорость на лугу относится к скорости на песке, т. е. как 2:1. Другими словами, нужно выбрать направление так, чтобы sin b был вдвое больше sin а. Для этого нужно перешагнуть границу между полосами в такой точке m, которая находится в одном километре от Е. Действительно, тогда sin b = 6/(корень(32 + 62)), sin a = 1/(корень(1 + 22)), отношение sin b / sin a = (6 / корень(45)) / (1 / (3*корень(5))) = (6/(3*корень(5))) / (1/корень(5)) = 2, т. е. как раз отношению скоростей.
А какова будет в таком случае “приведенная к лугу” длина пути? Вычислим: AM = корень(22 + 12). что отвечает 4,47 км пути по лугу. МС = корень(45) = 6,71 км. Длина всего пути 4,47 + 6,71 = 11,18, т. е. на 860 км короче прямолинейного пути, который, как мы уже знаем, соответствует 12,04 км.
Вы видите, какие выгоды доставляет при данных условиях изламывание пути. Световой луч как раз и избирает такой скорейший путь, потому что закон преломления света строго удовлетворяет требованию математического решения задачи: синус угла преломления относится к синусу угла падения, как скорость света в новой среде к скорости его в покидаемой среде; с другой стороны, это отношение равно показателю преломления света в указанных средах.
Объединяя в одно правило особенности и отражения и преломления, мы можем сказать, что световой луч во всех случаях следует по быстрейшему пути, т. е. подчиняется правилу, которое физики называют “принципом скорейшего прихода” (принцип Ферма).
Если среда неоднородна и ее преломляющая способность меняется постепенно, как, например, в нашей атмосфере, то и в таком случае вполне осуществляется быстрейший приход. Этим объясняется то небольшое искривление лучей небесных светил в атмосфере, которое на языке астрономов называется “атмосферной рефракцией”. В атмосфере, постепенно уплотняющейся книзу, луч света изгибается так, что вогнутость его обращена к Земле. Тогда луч остается дольше в высоких слоях, которые слабее замедляют его путь, и проводит меньше времени в “медленных” низких слоях, в итоге он приходит к цели быстрее, чем по пути строго прямолинейному.
Принцип быстрейшего прихода (принцип Ферма) справедлив не для одних лишь световых явлений: ему в полной мере подчиняется также распространение звука и всех вообще волнообразных движений, какова бы ни была природа этих волн.
Читатель, без сомнения, желал бы узнать, чем объясняется это свойство волнообразных движений. Приведу поэтому относящиеся сюда соображения, высказанные выдающимся современным физиком Шредингером [В докладе, прочитанном в Стокгольме при получении Нобелевской премии (в 1933 г.)]. Он исходит из знакомого уже нам примера марширующих солдат и имеет в виду случай движения светового луча в среде постепенно изменяющейся плотности.
“Пусть, — пишет он, — для того, чтобы сохранить строгую правильность фронта, солдаты соединены длинным шестом, который каждый из них крепко удерживает в руках. Команда гласит: всем бежать возможно быстрее! Если характер почвы медленно меняется от точки к точке, то сначала, скажем, правое, а позднее левое крыло фронта будет подвигаться быстрее — и поворот фронта осуществится сам собой. Мы заметим при этом, что пройденный путь — не прямолинейный, а искривленный. То, что путь этот строго совпадает с кратчайшим в смысле времени прибытия в данный пункт при заданных свойствах почвы, — довольно понятно, так как ведь каждый солдат старался подвигаться как можно быстрее”.
“ — Но кто же зажег огонь? — спросил моряк.
— Солнце, — ответил Спилетт.
Журналист не шутил. Действительно, Солнце доставило огонь, которым так восторгался моряк. Он не верил своим глазам и был до того изумлен, что даже не мог расспрашивать инженера.
— Значит, у вас было зажигательное стекло? — спросил инженера Герберт.
— Нет, но я его изготовил.
И он его показал. Это были просто два стекла, снятые инженером со своих часов и часов Спилетта. Он соединил их края глиной, предварительно наполнив водой, и таким образом получилась настоящая зажигательная чечевица, с помощью которой, сосредоточив солнечные лучи на сухом мхе, инженер добыл огонь”.
Читатель пожелает, я думаю, узнать, зачем нужно заполнять водой пространство между часовыми стеклами: разве наполненная воздухом двояковыпуклая чечевица не сосредоточивает лучей?
Именно нет. Часовое стекло ограничено двумя параллельными (концентрическими) поверхностями — наружной и внутренней; а известно из физики, что, проходя через среду, ограниченную такими поверхностями, лучи почти не изменяют своего направления. Проходя затем через второе такое же стекло, они и здесь не отклоняются, а следовательно, не собираются в фокусе. Чтобы сосредоточить лучи в одной точке, необходимо заполнить пространство между стеклами каким-нибудь прозрачным веществом, которое преломляло бы лучи сильнее, нежели воздух. Так и поступил инженер в романе Жюля Верна.
Обыкновенный графин с водой, если имеет шарообразную форму, также может служить зажигательной чечевицей. Это знали уже древние, которые заметили и то, что сама вода при этом остается холодной. Случалось даже, что стоящий на открытом окне графин с водой зажигал занавески, скатерть, обугливал стол. Те огромные шаровые бутылки с окрашенной водой, которые, по старинному обычаю, украшали раньше витрины аптек, могли быть иногда причиной настоящих катастроф, вызывая возгорание легко воспламеняющихся веществ, расположенных поблизости.
Небольшой круглой колбой, наполненной водой, можно даже при небольших размерах колбы довести до кипения воду, налитую на часовое стеклышко: для этого достаточна колба сантиметров в 12 диаметром. При 15 см в фокусе [Фокус помещается при этом весьма близко к колбе] получается температура 120°. Зажечь папироску с помощью колбы с водой так же легко, как и стеклянной чечевицей, о которой еще Ломоносов в своем стихотворении “О пользе стекла” писал:
Любопытно, что зажигательное действие стеклянных чечевиц известно было еще древним грекам, более чем за тысячелетие раньше изобретения очков и зрительных труб. О нем упоминает Аристофан в знаменитой комедии “Облака”. Сократ предлагает Стрептиаду задачу:
“Если бы кто писал обязательство на тебя в пяти талантах, как бы ты уничтожил оное?
Стрептиад. Нашел я, как истребить обязательство, да такой способ, что ты и сам признаешь его прехитрым! Видал ты, конечно, в аптеках камень прекрасный, прозрачный, которым зажигают?
Сократ. Зажигательное стекло?
Стрептиад. Точно так.
Сократ. Что же далее?
Стрептиад. Пока нотариус пишет, я, став позади его, направлю лучи Солнца на обязательство, да слова-то все и растоплю…”
Напомню для пояснения, что греки времен Аристофана писали на навощенных дощечках, которые от тепла легко растапливались.
Ледяная чечевица сослужила хорошую службу в жюль-верновом “Путешествии капитана Гаттераса”. Доктор Клоубони таким именно образом зажег костер, когда путники потеряли огниво и очутились без огня, при страшном морозе в 48 градусов.
— “Это несчастье, — сказал Гаттерас доктору.
— Да, — отвечал тот.
— У нас нет даже подзорной трубы, с которой мы могли бы снять чечевицу и добыть огня.
— Знаю, — ответил доктор, — и очень жаль, что нет: солнечные лучи достаточно сильны, чтобы зажечь трут.
— Что делать, придется утолить голод сырой медвежатиной, — заметил Гаттерас.
— Да, — задумчиво проговорил доктор, — в крайнем случае. Но отчего бы нам не…
— Что вы задумали? — полюбопытствовал Гаттерас.
— Мне пришла в голову мысль…
— Мысль? — воскликнул боцман. — Если вам пришла мысль, значит, мы спасены!
— Не знаю, как удастся, — колебался доктор.
— Что же вы придумали? — спросил Гаттерас.
— У нас нет чечевицы, но мы ее изготовим.
— Как? — поинтересовался боцман.
— Отшлифуем из куска льда.
— Неужели вы полагаете…
— Отчего бы и нет? Ведь нужно только, чтобы лучи Солнца были сведены в одну точку, а для этой цели лед может заменить нам лучший хрусталь. Только я предпочел бы кусочек пресноводного льда: он крепче и прозрачнее.
— Вот, если не ошибаюсь, эта ледяная глыба, — указал боцман на льдину шагах в ста от путешественников — судя по ее цвету, есть как раз то, что вам надо.
— Вы правы. Возьмите-ка свой топор. Пойдемте друзья мои.
Все трое направились к указанной ледяной глыбе Действительно, лед оказался пресноводным.
Доктор велел отрубить кусок льда, имеющий фут в диаметре и начал обравнивать его топором. Потом отделал его ножом, наконец постепенно отшлифовал рукою. Получилась прозрачная чечевица, словно из лучшего хрусталя. Солнце было довольно яркое. Доктор подставил чечевицу его лучам и сосредоточил их на труте. Через несколько секунд трут загорелся”.
Рис 113. “Доктор сосредоточил лучи Солнца на труте”.
Рассказ Жюля Верна не совсем фантастичен: опыты зажигания дерева при помощи ледяной чечевицы, впервые успешно выполненные в Англии с весьма большой чечевицей еще в 1763 г., с тех пор неоднократно производились с полным успехом. Конечно, трудно изготовить прозрачную ледяную чечевицу с помощью таких орудий, как топор, нож и “просто рука” (при 48-градусном морозе!), но можно изготовить ледяную чечевицу проще: налить воды в чашку надлежащей формы и заморозить, а затем, слегка подогрев чашку, вынуть из нее готовую чечевицу.
Рис. 114. Чашка для изготовления ледяной чечевицы.
Проделывая подобный опыт, не забывайте, что он удается лишь в ясный морозный день и на открытом воздухе, но не в комнате за оконным стеклом: стекло поглощает значительную часть энергии солнечных лучей и остающейся недостаточно, чтобы вызвать значительное нагревание.
Поучительный опыт этот впервые проделан был знаменитым борцом за независимость Соединенных Штатов Веньямином Франклином, обессмертившим себя, как физик, изобретением громоотвода. “Я взял у портного несколько квадратных кусочков сукна различных цветов, — писал он. — Между ними были: черный, темно-синий, светло-синий, зеленый, пурпуровый, красный, белый и различные другие цвета и оттенки. В одно светлое солнечное утро я положил все эти куски на снег. Через несколько часов черный кусок, нагревшийся сильнее других, погрузился так глубоко, что лучи Солнца более его не достигали; темно-синий погрузился почти настолько же, как и черный; светло-синий гораздо менее; остальные цвета опустились тем менее, чем они светлее. Белый же остался на поверхности, т. е. вовсе не опустился”.
“К чему годна была бы теория, если бы из нее нельзя было извлечь никакой пользы? — восклицает он по этому поводу и продолжает: — Разве не можем мы из этого опыта вывести то, что черное платье в теплом солнечном климате менее годно, чем белое, так как оно на солнце сильнее нагревает наше тело, и если мы при этом еще будем делать движения, которые сами по себе нас согревают, то образуется излишняя теплота? Не должны ли мужские и женские летние шляпы быть белого цвета, чтобы устранить ту жару, которая вызывает у некоторых солнечный удар?… Далее, вычерненные стены не могут разве поглотить в течение дня столько солнечной теплоты, чтобы ночью остаться до некоторой степени теплыми и предохранить фрукты от мороза? Не может разве внимательный наблюдатель натолкнуться еще и на другие частности большей или меньшей важности?”
Каковы могут быть эти выводы и полезные применения, показывает пример немецкой южно-полярной экспедиции 1903 г. на корабле “Гаусс”. Судно вмерзло в лед, и все обычные способы освобождения не привели ни к каким результатам. Взрывчатые вещества и пилы, пущенные в дело, удалили всего несколько сотен кубометров льда и не освободили корабля. Тогда обратились к помощи солнечных лучей: из темной золы и угля устроили на льду полосу в 2 км длины и в десяток метров ширины; она вела от корабля до ближайшей широкой щели во льду. Стояли ясные долгие дни полярного лета, и солнечные лучи сделали то, чего не могли сделать динамит и пила. Лед, подтаяв, сломался вдоль насыпанной полосы, и корабль освободился от льда.
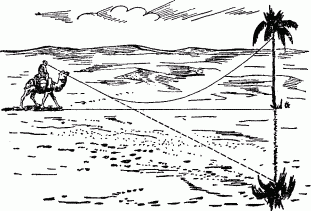Рис. 115. Как возникает мираж в пустыне. Этот рисунок, обычно воспроизводимый в учебниках, представляет путь светового луча наклоненным к земле преувеличенно круто.
Правильнее было бы, впрочем, сказать, что нагретый слой воздуха близ раскаленной почвы отражает лучи не наподобие зеркала, а наподобие водной поверхности, рассматриваемой из глубины воды. Здесь происходит не простое отражение, а то, что на языке физики называется “внутренним отражением”. Для этого необходимо, чтобы луч света вступал в воздушные слои очень полого — более полого, чем показано на нашем упрощенном рис. 115; иначе не будет превзойден “предельный угол” падения луча, а без этого не получается внутреннего отражения.
Отметим попутно один пункт этой теории, могущий породить недоразумение. Изложенное объяснение требует такого расположения воздушных слоев, при котором более плотные слои находились бы выше, чем менее плотные. Мы знаем, однако, что плотный, тяжелый воздух стремится опуститься и вытеснить лежащий под ним легкий слой газа вверх. Как же может существовать то расположение слоев плотного и разреженного воздуха, которое необходимо для появления миража?
Перемена обстановки в этом “Дворце миражей” достигалась следующим образом: зеркальные стены на некотором расстоянии от ребер разрезаны вдоль, и полученный угол может вращаться вокруг оси, заменяясь другим. Из рис. 107 видно, что можно произвести три замены, соответствующие углам 1, 2 и 3. Теперь представьте себе, что все углы, обозначенные цифрой 1, заключают в себе обстановку тропического леса, все углы 2 — обстановку арабского зала, а углы 3 — индийского храма.
Одним движением скрытого механизма, поворачивающего углы, тропический лес превращается в храм или в арабский зал. Весь секрет “волшебства” основан на таком простом физическом явлении, как отражение световых лучей.
Почему и как преломляется свет?
То, что при переходе из одной среды в другую луч света преломляется, многим представляется странным капризом природы. Кажется непонятным, почему свет не сохраняет в новой среде первоначального своего направления, а избирает ломаный путь. Кто так думает, тот, вероятно, с удовлетворением узнает, что луч света претерпевает, в сущности, то же самое, что происходит и с марширующей колонной бойцов, пересекающей границу между почвой, удобной для ходьбы, и почвой неудобной. Вот что говорит об этом Джон Гершель, знаменитый астроном и физик прошлого века.“Представьте себе отряд солдат, идущий по местности, разделенной прямой границей на две полосы, из которых одна гладкая, ровная и удобная для ходьбы, другая — кочковатая, затруднительная, так что ходьба по ней не может совершаться столь быстро. Предположим сверх того, что фронт отряда составляет угол с пограничной линией между двумя полосами, так что солдаты достигают этой границы не все одновременно, а последовательно один за другим. Тогда каждый солдат, переступив границу, очутится на почве, по которой он не может более подвигаться так быстро, как до того времени. Он не сможет уже держаться на одной линии с остальной частью шеренги, еще находящейся на лучшей почве, и будет от нее отставать с каждой секундой все больше. Так как каждый солдат, достигая границы, испытывает одинаковое затруднение в ходьбе, то если солдаты не нарушат строя, не рассеются, а будут продолжать маршировать правильной колонной, вся та часть колонны, которая переступила границу, будет неизбежно отставать от остальной и составит с ней поэтому тупой угол в точке пересечения границы. И так как необходимость ходить в ногу, не перебивая дороги друг другу, заставит каждого солдата шагать прямо перед собой, под прямым углом к новому фронту, то путь, который он пройдет по переходе границы, будет, во-первых, перпендикулярен к новому фронту, а во-вторых, так относиться к тому пути, какой был бы пройден в случае отсутствия замедления, как новая скорость к прежней”.
В малом виде вы можете воспроизвести это наглядное подобие преломления света у себя на столе. Накройте половину стола скатертью (рис. 109) и, слегка наклонив стол, заставьте скатываться по нему пару колесиков, наглухо посаженных на общую ось (например, от сломанного детского паровоза или другой игрушки). Если направление движения колес и край скатерти составляют прямой угол, преломления пути не происходит. Вы имеете в этом случае иллюстрацию оптического правила: луч, перпендикулярный к плоскости раздела сред, не преломляется. При направлении, наклонном к краю скатерти, путь колес изламывается на этом краю, т. е. на границе между средами с различной скоростью движения в них. Легко заметить, что при переходе из части стола, где скорость движения больше (непокрытая часть), в ту часть, где скорость меньше (скатерть), направление пути (“луч”) приближается к “перпендикуляру падения”. В обратном случае наблюдается удаление от этого перпендикуляра.
Из этого можно, между прочим, почерпнуть важное указание, вскрывающее сущность рассматриваемого явления, а именно, что преломление обусловлено различием скорости света в обеих средах. Чем больше различие в скорости, тем значительнее преломление; так называемый “показатель преломления”, характеризующий величину излома лучей, есть не что иное, как отношение этих скоростей. Когда вы читаете, что показатель преломления при переходе из воздуха в воду есть 4/3, то вы, вместе с тем, узнаёте, что свет движется в воздухе примерно в 1,3 раза скорее, чем в воде.
А в связи с этим находится и другая поучительная особенность распространения света. Если в случае отражения световой луч следует кратчайшим путем, то в случае преломления он избирает скорейший путь: никакое другое направление не приводит луч так скоро к “месту назначения”, как этот изломанный путь.
Когда длинный путь проходится быстрее, чем короткий?
Но неужели ломаный путь может быстрее привести к цели, чем прямой? Да, в тех случаях, когда скорость движения в различных частях пути различна. Вспомните, что приходится делать жителям деревни, расположенной между двумя железнодорожными станциями в соседстве с одной из них. Чтобы попасть скорее на дальнюю станцию, они едут на лошади сначала в обратном направлении, к ближайшей станции, там садятся в поезд и едут на место назначения. Им короче было бы, разумеется, прямо ехать туда на лошади, но они предпочитают более длинный путь на лошади и в вагоне, потому что он приводит к цели скорее.Уделим минуту внимания еще одному примеру. Кавалерист должен прибыть с донесением из точки А к палатке командира в точке C (рис. 110). Его отделяют от палатки полоса глубокого песка и полоса луга, разграниченные между собой прямой линией EF, По песчаной почве лошадь движется вдвое медленнее, чем по лугу. Какой же путь должен выбрать кавалерист, чтобы достигнуть палатки в кратчайшее время?
На первый взгляд кажется, что самый скорый путь — прямая линия, проведенная от A до С. Но это совершенно ошибочно, и я не думаю, чтобы нашелся кавалерист, который выбрал бы такой путь. Медленное движение по песку наведет его на правильную мысль сократить эту медленную часть пути, прорезав песчаную полосу по менее косой линии; конечно, тем самым удлинится вторая часть пути — по лугу; но так как по лугу можно двигаться вдвое быстрее, то удлинение пути не перевесит полученной выгоды, и в общем итоге путь будет проделан в меньший промежуток времени. Другими словами, путь кавалериста должен преломиться на границе обоих родов почвы и притом так, чтобы путь по лугу составлял с перпендикуляром к границе больший угол, чем путь по песчаной почве.
Кто знаком с геометрией, именно с теоремой Пифагора, тот может проверить, что прямой путь AC действительно не является путем скорейшим и что при тех размерах для ширины полос и расстояний, которые мы здесь имеем в виду, можно скорее достичь цели, если направиться, например, по ломаной АЕС (рис. 111).
На рис. 110 указано, что ширина песчаной полосы 2 км, луговой — 3 км, а расстояние ВС — 7 км. Тогда вся длина AC (рис. 111) равна, по теореме Пифагора, корень(52 + 72) = корень(74) = 8,60 км. Часть AN — путь по песку — этого отрезка составляет, как легко сообразить, 2/5 этой величины, т. е. 3,44 км. Так как по песку движение происходит вдвое медленнее, чем по лугу, то 3,44 км песчаного пути равнозначны, в смысле требуемого времени, 6,88 км по лугу. И, следовательно, весь смешанный путь по прямой АС, равный 8,60 км, соответствует 12,04 км пути по лугу.
Сделаем такое же “приведение к лугу” и для ломаного пути АЕС. Часть АЕ = 2 км и соответствует 4 км пути по лугу. Часть ЕС = корень(32 + 72) = корень(58) = 7,61 км. Итого весь ломаный путь AEC отвечает 4 + 7,61 = 11,61 км.
Итак, “короткий” прямой путь соответствует 12,04 км движения по лугу, а “длинный” ломаный — всего только 11,61 км по той же почве. “Длинный” путь, как видите, дает выгоду в 12,04 — 11,61 = 0,43, почти в полкилометра!
Но мы не указали еще самого быстрого пути. Быстрейший путь, как учит теория, будет тот, при котором (нам придется здесь обратиться к услугам тригонометрии) синус угла b относится к синусу угла A, как скорость на лугу относится к скорости на песке, т. е. как 2:1. Другими словами, нужно выбрать направление так, чтобы sin b был вдвое больше sin а. Для этого нужно перешагнуть границу между полосами в такой точке m, которая находится в одном километре от Е. Действительно, тогда sin b = 6/(корень(32 + 62)), sin a = 1/(корень(1 + 22)), отношение sin b / sin a = (6 / корень(45)) / (1 / (3*корень(5))) = (6/(3*корень(5))) / (1/корень(5)) = 2, т. е. как раз отношению скоростей.
А какова будет в таком случае “приведенная к лугу” длина пути? Вычислим: AM = корень(22 + 12). что отвечает 4,47 км пути по лугу. МС = корень(45) = 6,71 км. Длина всего пути 4,47 + 6,71 = 11,18, т. е. на 860 км короче прямолинейного пути, который, как мы уже знаем, соответствует 12,04 км.
Вы видите, какие выгоды доставляет при данных условиях изламывание пути. Световой луч как раз и избирает такой скорейший путь, потому что закон преломления света строго удовлетворяет требованию математического решения задачи: синус угла преломления относится к синусу угла падения, как скорость света в новой среде к скорости его в покидаемой среде; с другой стороны, это отношение равно показателю преломления света в указанных средах.
Объединяя в одно правило особенности и отражения и преломления, мы можем сказать, что световой луч во всех случаях следует по быстрейшему пути, т. е. подчиняется правилу, которое физики называют “принципом скорейшего прихода” (принцип Ферма).
Если среда неоднородна и ее преломляющая способность меняется постепенно, как, например, в нашей атмосфере, то и в таком случае вполне осуществляется быстрейший приход. Этим объясняется то небольшое искривление лучей небесных светил в атмосфере, которое на языке астрономов называется “атмосферной рефракцией”. В атмосфере, постепенно уплотняющейся книзу, луч света изгибается так, что вогнутость его обращена к Земле. Тогда луч остается дольше в высоких слоях, которые слабее замедляют его путь, и проводит меньше времени в “медленных” низких слоях, в итоге он приходит к цели быстрее, чем по пути строго прямолинейному.
Принцип быстрейшего прихода (принцип Ферма) справедлив не для одних лишь световых явлений: ему в полной мере подчиняется также распространение звука и всех вообще волнообразных движений, какова бы ни была природа этих волн.
Читатель, без сомнения, желал бы узнать, чем объясняется это свойство волнообразных движений. Приведу поэтому относящиеся сюда соображения, высказанные выдающимся современным физиком Шредингером [В докладе, прочитанном в Стокгольме при получении Нобелевской премии (в 1933 г.)]. Он исходит из знакомого уже нам примера марширующих солдат и имеет в виду случай движения светового луча в среде постепенно изменяющейся плотности.
“Пусть, — пишет он, — для того, чтобы сохранить строгую правильность фронта, солдаты соединены длинным шестом, который каждый из них крепко удерживает в руках. Команда гласит: всем бежать возможно быстрее! Если характер почвы медленно меняется от точки к точке, то сначала, скажем, правое, а позднее левое крыло фронта будет подвигаться быстрее — и поворот фронта осуществится сам собой. Мы заметим при этом, что пройденный путь — не прямолинейный, а искривленный. То, что путь этот строго совпадает с кратчайшим в смысле времени прибытия в данный пункт при заданных свойствах почвы, — довольно понятно, так как ведь каждый солдат старался подвигаться как можно быстрее”.
Новые Робинзоны
Без сомнения, вы знаете, как герои романа Жюля Верна “Таинственный остров”, заброшенные на необитаемую землю, добыли огонь без спичек и огнива. Робинзону явилась на помощь молния, зажегшая дерево, новым же Робинзонам Жюля Верна помогла не случайность, а находчивость сведущего инженера и твердое знание им законов физики. Помните, как удивился наивный моряк Пенкроф, когда, возвратившись с охоты, нашел инженера и журналиста перед пылающим костром.“ — Но кто же зажег огонь? — спросил моряк.
— Солнце, — ответил Спилетт.
Журналист не шутил. Действительно, Солнце доставило огонь, которым так восторгался моряк. Он не верил своим глазам и был до того изумлен, что даже не мог расспрашивать инженера.
— Значит, у вас было зажигательное стекло? — спросил инженера Герберт.
— Нет, но я его изготовил.
И он его показал. Это были просто два стекла, снятые инженером со своих часов и часов Спилетта. Он соединил их края глиной, предварительно наполнив водой, и таким образом получилась настоящая зажигательная чечевица, с помощью которой, сосредоточив солнечные лучи на сухом мхе, инженер добыл огонь”.
Читатель пожелает, я думаю, узнать, зачем нужно заполнять водой пространство между часовыми стеклами: разве наполненная воздухом двояковыпуклая чечевица не сосредоточивает лучей?
Именно нет. Часовое стекло ограничено двумя параллельными (концентрическими) поверхностями — наружной и внутренней; а известно из физики, что, проходя через среду, ограниченную такими поверхностями, лучи почти не изменяют своего направления. Проходя затем через второе такое же стекло, они и здесь не отклоняются, а следовательно, не собираются в фокусе. Чтобы сосредоточить лучи в одной точке, необходимо заполнить пространство между стеклами каким-нибудь прозрачным веществом, которое преломляло бы лучи сильнее, нежели воздух. Так и поступил инженер в романе Жюля Верна.
Обыкновенный графин с водой, если имеет шарообразную форму, также может служить зажигательной чечевицей. Это знали уже древние, которые заметили и то, что сама вода при этом остается холодной. Случалось даже, что стоящий на открытом окне графин с водой зажигал занавески, скатерть, обугливал стол. Те огромные шаровые бутылки с окрашенной водой, которые, по старинному обычаю, украшали раньше витрины аптек, могли быть иногда причиной настоящих катастроф, вызывая возгорание легко воспламеняющихся веществ, расположенных поблизости.
Небольшой круглой колбой, наполненной водой, можно даже при небольших размерах колбы довести до кипения воду, налитую на часовое стеклышко: для этого достаточна колба сантиметров в 12 диаметром. При 15 см в фокусе [Фокус помещается при этом весьма близко к колбе] получается температура 120°. Зажечь папироску с помощью колбы с водой так же легко, как и стеклянной чечевицей, о которой еще Ломоносов в своем стихотворении “О пользе стекла” писал:
Следует заметить, однако, что зажигательное действие водяных линз значительно слабее, чем стеклянных. Это связано, во-первых, с тем, что преломление света в воде гораздо меньше, чем в стекле, во-вторых, вода в сильной степени поглощает инфракрасные лучи, которые играют большую роль в нагревании тел.
Мы пламень солнечный стеклом здесь получаем
И Прометею тем безбедно подражаем.
Ругаясь подлости нескладных оных врак,
Небесным без греха огнем курим табак.
Любопытно, что зажигательное действие стеклянных чечевиц известно было еще древним грекам, более чем за тысячелетие раньше изобретения очков и зрительных труб. О нем упоминает Аристофан в знаменитой комедии “Облака”. Сократ предлагает Стрептиаду задачу:
“Если бы кто писал обязательство на тебя в пяти талантах, как бы ты уничтожил оное?
Стрептиад. Нашел я, как истребить обязательство, да такой способ, что ты и сам признаешь его прехитрым! Видал ты, конечно, в аптеках камень прекрасный, прозрачный, которым зажигают?
Сократ. Зажигательное стекло?
Стрептиад. Точно так.
Сократ. Что же далее?
Стрептиад. Пока нотариус пишет, я, став позади его, направлю лучи Солнца на обязательство, да слова-то все и растоплю…”
Напомню для пояснения, что греки времен Аристофана писали на навощенных дощечках, которые от тепла легко растапливались.
Как добыть огонь с помощью льда?
Материалом для двояковыпуклой линзы, а следовательно, и для добывания огня, может послужить также лед, если он достаточно прозрачен. При этом лед, преломляя лучи, сам не нагревается и не тает. Показатель преломления льда лишь немногим меньше, чем у воды, и если, как мы видели, можно добыть огонь с помощью шара, наполненного водой, то возможно сделать это и с помощью чечевицы из льда.Ледяная чечевица сослужила хорошую службу в жюль-верновом “Путешествии капитана Гаттераса”. Доктор Клоубони таким именно образом зажег костер, когда путники потеряли огниво и очутились без огня, при страшном морозе в 48 градусов.
— “Это несчастье, — сказал Гаттерас доктору.
— Да, — отвечал тот.
— У нас нет даже подзорной трубы, с которой мы могли бы снять чечевицу и добыть огня.
— Знаю, — ответил доктор, — и очень жаль, что нет: солнечные лучи достаточно сильны, чтобы зажечь трут.
— Что делать, придется утолить голод сырой медвежатиной, — заметил Гаттерас.
— Да, — задумчиво проговорил доктор, — в крайнем случае. Но отчего бы нам не…
— Что вы задумали? — полюбопытствовал Гаттерас.
— Мне пришла в голову мысль…
— Мысль? — воскликнул боцман. — Если вам пришла мысль, значит, мы спасены!
— Не знаю, как удастся, — колебался доктор.
— Что же вы придумали? — спросил Гаттерас.
— У нас нет чечевицы, но мы ее изготовим.
— Как? — поинтересовался боцман.
— Отшлифуем из куска льда.
— Неужели вы полагаете…
— Отчего бы и нет? Ведь нужно только, чтобы лучи Солнца были сведены в одну точку, а для этой цели лед может заменить нам лучший хрусталь. Только я предпочел бы кусочек пресноводного льда: он крепче и прозрачнее.
— Вот, если не ошибаюсь, эта ледяная глыба, — указал боцман на льдину шагах в ста от путешественников — судя по ее цвету, есть как раз то, что вам надо.
— Вы правы. Возьмите-ка свой топор. Пойдемте друзья мои.
Все трое направились к указанной ледяной глыбе Действительно, лед оказался пресноводным.
Доктор велел отрубить кусок льда, имеющий фут в диаметре и начал обравнивать его топором. Потом отделал его ножом, наконец постепенно отшлифовал рукою. Получилась прозрачная чечевица, словно из лучшего хрусталя. Солнце было довольно яркое. Доктор подставил чечевицу его лучам и сосредоточил их на труте. Через несколько секунд трут загорелся”.
Рассказ Жюля Верна не совсем фантастичен: опыты зажигания дерева при помощи ледяной чечевицы, впервые успешно выполненные в Англии с весьма большой чечевицей еще в 1763 г., с тех пор неоднократно производились с полным успехом. Конечно, трудно изготовить прозрачную ледяную чечевицу с помощью таких орудий, как топор, нож и “просто рука” (при 48-градусном морозе!), но можно изготовить ледяную чечевицу проще: налить воды в чашку надлежащей формы и заморозить, а затем, слегка подогрев чашку, вынуть из нее готовую чечевицу.
Проделывая подобный опыт, не забывайте, что он удается лишь в ясный морозный день и на открытом воздухе, но не в комнате за оконным стеклом: стекло поглощает значительную часть энергии солнечных лучей и остающейся недостаточно, чтобы вызвать значительное нагревание.
С помощью солнечных лучей
Проделайте еще опыт, тоже легко выполнимый в зимнее время. Положите на снег, заливаемый солнечным светом, два одинаковой величины лоскутка ткани, светлый и черный. Через час или два вы убедитесь, что черный лоскуток погрузился в снег, между тем как светлый остался на прежнем уровне. Доискаться причины подобного различия нетрудно: под черным лоскутком снег тает сильнее, так как темная ткань поглощает большую часть падающих на нее солнечных лучей; светлая же, напротив, большую часть их рассеивает и потому слабее нагревается, нежели черная.Поучительный опыт этот впервые проделан был знаменитым борцом за независимость Соединенных Штатов Веньямином Франклином, обессмертившим себя, как физик, изобретением громоотвода. “Я взял у портного несколько квадратных кусочков сукна различных цветов, — писал он. — Между ними были: черный, темно-синий, светло-синий, зеленый, пурпуровый, красный, белый и различные другие цвета и оттенки. В одно светлое солнечное утро я положил все эти куски на снег. Через несколько часов черный кусок, нагревшийся сильнее других, погрузился так глубоко, что лучи Солнца более его не достигали; темно-синий погрузился почти настолько же, как и черный; светло-синий гораздо менее; остальные цвета опустились тем менее, чем они светлее. Белый же остался на поверхности, т. е. вовсе не опустился”.
“К чему годна была бы теория, если бы из нее нельзя было извлечь никакой пользы? — восклицает он по этому поводу и продолжает: — Разве не можем мы из этого опыта вывести то, что черное платье в теплом солнечном климате менее годно, чем белое, так как оно на солнце сильнее нагревает наше тело, и если мы при этом еще будем делать движения, которые сами по себе нас согревают, то образуется излишняя теплота? Не должны ли мужские и женские летние шляпы быть белого цвета, чтобы устранить ту жару, которая вызывает у некоторых солнечный удар?… Далее, вычерненные стены не могут разве поглотить в течение дня столько солнечной теплоты, чтобы ночью остаться до некоторой степени теплыми и предохранить фрукты от мороза? Не может разве внимательный наблюдатель натолкнуться еще и на другие частности большей или меньшей важности?”
Каковы могут быть эти выводы и полезные применения, показывает пример немецкой южно-полярной экспедиции 1903 г. на корабле “Гаусс”. Судно вмерзло в лед, и все обычные способы освобождения не привели ни к каким результатам. Взрывчатые вещества и пилы, пущенные в дело, удалили всего несколько сотен кубометров льда и не освободили корабля. Тогда обратились к помощи солнечных лучей: из темной золы и угля устроили на льду полосу в 2 км длины и в десяток метров ширины; она вела от корабля до ближайшей широкой щели во льду. Стояли ясные долгие дни полярного лета, и солнечные лучи сделали то, чего не могли сделать динамит и пила. Лед, подтаяв, сломался вдоль насыпанной полосы, и корабль освободился от льда.
Старое и новое о миражах
Вероятно, всем известно, в чем заключается физическая причина обыкновенного миража. Раскаленный зноем песок пустыни приобретает зеркальные свойства оттого, что прилегающий к нему нагретый слой воздуха имеет меньшую плотность, нежели вышележащие слои. Наклонный луч света от весьма далекого предмета, достигнув этого воздушного слоя, искривляет в нем свой путь так, что в дальнейшем следовании он вновь удаляется от земли и попадает в глаз наблюдателя, словно отразившись от зеркала под очень большим углом падения. И наблюдателю кажется, что перед ним расстилается в пустыне водная гладь, отражающая прибрежные предметы (рис. 115).Правильнее было бы, впрочем, сказать, что нагретый слой воздуха близ раскаленной почвы отражает лучи не наподобие зеркала, а наподобие водной поверхности, рассматриваемой из глубины воды. Здесь происходит не простое отражение, а то, что на языке физики называется “внутренним отражением”. Для этого необходимо, чтобы луч света вступал в воздушные слои очень полого — более полого, чем показано на нашем упрощенном рис. 115; иначе не будет превзойден “предельный угол” падения луча, а без этого не получается внутреннего отражения.
Отметим попутно один пункт этой теории, могущий породить недоразумение. Изложенное объяснение требует такого расположения воздушных слоев, при котором более плотные слои находились бы выше, чем менее плотные. Мы знаем, однако, что плотный, тяжелый воздух стремится опуститься и вытеснить лежащий под ним легкий слой газа вверх. Как же может существовать то расположение слоев плотного и разреженного воздуха, которое необходимо для появления миража?