Как разрешить спор? Выход один. Надо задать значения ?, ? и ? и свести проблему к решению типовой задачи линейного целочисленного программирования, которая формулируется следующим образом. Найти целочисленные значения zi?0 (i=1,2,…,8), такие, что удовлетворяются шесть вышеприведенных неравенств, и такие, что минимум функции
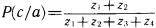
достигает своего максимума.
Если задача решена и минимум Р(с/а) есть ? и этот минимум удовлетворяет неравенству ???, то верен силлогизм бабушки. А если ???<?, то верен силлогизм Сумбурука. Если же ?<?, то и бабушка, и Сумбурук ошиблись. Их силлогизмы будут ложными.
Значит, все зависит от того, как определены ?, ? и ?. Пусть для определения этих значений мы опросили четырех людей Ч1, Ч2, Ч3 и Ч4. Их ответы сведены в табл. 6.
Таблица 6
Интерпретация чисел в таблице следующая. Опрашиваемый считает, что можно говорить «почти все», когда явление это встречается не реже, чем в 95 случаях из 100. Аналогично интерпретируются и остальные элементы таблицы. В первом столбце стоят значения ?, во втором ?, а в третьем ?. Каждая строка может быть использована для решения задачи линейного программирования, которую мы сформулировали. Если решить возникающие четыре задачи, то выяснится, что силлогизм бабушки оказывается истинным во всех случаях, кроме третьего. В третьем случае прав Сумбурук, а бабушка ошибается.
Из сказанного ясно, что при исследовании нечетких силлогизмов (или D-cиллогизмов, как их принято называть) необходимо анализировать области в пространстве параметров ?, ?, ?, в которых будут истинны или ложны те или иные силлогизмы. В частности, для силлогизма бабушки доказывается следующее утверждение, которое естественно было бы назвать Теоремой бармена: «Силлогизм бабушки истинен только в тех точках параметрического пространства, в которых выполняется соотношение ??max[0,2?1/?, 1?(1??)(?+1/?)]». Но, наверное, ни бармен, ни Сумбурук не смогли бы так четко сформулировать нужный для разрешения их спора результат.
Рассуждая о споре в баре, мы незаметно сформулировали метод формального поиска оценок нечетких квантификаторов в схемах рассуждений. Ведь если вернуться к схемам предшествующего раздела, то становится ясным, что метод решения силлогизма бабушки вполне пригоден для поиска
2 в заключениях этих схем.
Коллекция схем
Глава пятая. ВЫВОД В БАЗЕ ЗНАНИЙ
Что такое интеллектуальная система
Продукционные системы
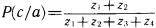
достигает своего максимума.
Если задача решена и минимум Р(с/а) есть ? и этот минимум удовлетворяет неравенству ???, то верен силлогизм бабушки. А если ???<?, то верен силлогизм Сумбурука. Если же ?<?, то и бабушка, и Сумбурук ошиблись. Их силлогизмы будут ложными.
Значит, все зависит от того, как определены ?, ? и ?. Пусть для определения этих значений мы опросили четырех людей Ч1, Ч2, Ч3 и Ч4. Их ответы сведены в табл. 6.
Таблица 6
Интерпретация чисел в таблице следующая. Опрашиваемый считает, что можно говорить «почти все», когда явление это встречается не реже, чем в 95 случаях из 100. Аналогично интерпретируются и остальные элементы таблицы. В первом столбце стоят значения ?, во втором ?, а в третьем ?. Каждая строка может быть использована для решения задачи линейного программирования, которую мы сформулировали. Если решить возникающие четыре задачи, то выяснится, что силлогизм бабушки оказывается истинным во всех случаях, кроме третьего. В третьем случае прав Сумбурук, а бабушка ошибается.
Из сказанного ясно, что при исследовании нечетких силлогизмов (или D-cиллогизмов, как их принято называть) необходимо анализировать области в пространстве параметров ?, ?, ?, в которых будут истинны или ложны те или иные силлогизмы. В частности, для силлогизма бабушки доказывается следующее утверждение, которое естественно было бы назвать Теоремой бармена: «Силлогизм бабушки истинен только в тех точках параметрического пространства, в которых выполняется соотношение ??max[0,2?1/?, 1?(1??)(?+1/?)]». Но, наверное, ни бармен, ни Сумбурук не смогли бы так четко сформулировать нужный для разрешения их спора результат.
Рассуждая о споре в баре, мы незаметно сформулировали метод формального поиска оценок нечетких квантификаторов в схемах рассуждений. Ведь если вернуться к схемам предшествующего раздела, то становится ясным, что метод решения силлогизма бабушки вполне пригоден для поиска
2 в заключениях этих схем.
Коллекция схем
Среди схем правдоподобных рассуждений встречаются не только те, которые мы расссмотрели и которые основаны на индуктивном выводе, аналогиях или нечетких квантификаторах. Многими исследователями предлагались и иные схемы. Их количество достаточно велико и продолжает расти. В этом разделе мы приведем (практически без комментариев) примеры схем, в основе которых лежат соображения, связанные с теорией вероятностей и аналогией, а также несколько схем, типичных для теории возможностей, активно развивающейся в последние годы ветви теории рассуждений.
Рассмотрим прежде всего схемы рассуждений, опирающиеся на свойства вероятностей, т.е. вероятностные схемы рассуждений.
Рассуждением, основанным, например, на схеме 2, может служить следующее: «С вероятностью, большей 0,7, при переохлаждении двигателя он не заводится с помощью стартера. Вероятность того, что он не заводится, меньше 0,5. Следовательно, вероятность того, что двигатель переохлажден, меньше min(1,1–0,7+0,5), т.е. меньше 0,8». Так же нетрудно придумать примеры и для других схем вероятностных рассуждений.
Рассмотрим две схемы рассуждения с учетом необходимых условий.
Значения q и r необходимости в этих схемах могут оцениваться в каких-то специальных единицах. Можно считать, например, что имеется лингвистическая шкала нечетких квантификаторов необходимости. Тогда q и r будут соответствовать некоторые интервалы или усредненные характеристики этих интервалов. В качестве примера рассуждения с учетом необходимых условий в соответствии со схемой 5 приведем следующее рассуждение: «Если у меня будет дача, то необходимо будет купить велосипед. Дача мне крайне необходима. Тогда покупка велосипеда для меня необходима».
Рассмотрим еще две схемы, в которых наряду с необходимостью учитывается возможность некоторых фактов, явлений или действий. Подобные схемы (как и две предшествующие) характерны для упоминавшейся теории возможностей.
Пример рассуждения, основанного на схеме 7: «Когда поднимается температура в реакторе, чрезвычайно необходимо понизить в нем давление. Возможность повышения температуры в реакторе высока. Следовательно, возможность того, что надо будет снижать давление в реакторе, либо больше нуля, либо больше той возможности, которая приписана событию повышения температуры». Альтернативный характер этого рассуждения обусловлен тем, что q и r при проведении его не были оценены количественно. Это не позволяет сделать окончательный альтернативный вывод в следствии.
Завершим раздел еще тремя схемами рассуждений, в которых учитывается возможная взаимосвязь А и В, а также некоторые соображения из рассуждений по аналогии.
Каждый, кого интересуют схемы правдоподобных рассуждений, может без труда увеличить нашу коллекцию, например, заимствовав их из книги Д. Пойи, приведенной в списке литературы. Нам же необходимо двигаться дальше к тем человеческим схемам рассуждений, в которых активно используются знания, хранящиеся в его памяти, т.е. к рассуждениям, на которые опирается интеллектуальная деятельность человека и ее моделирование в современных интеллектуальных системах.
Рассмотрим прежде всего схемы рассуждений, опирающиеся на свойства вероятностей, т.е. вероятностные схемы рассуждений.
Рассуждением, основанным, например, на схеме 2, может служить следующее: «С вероятностью, большей 0,7, при переохлаждении двигателя он не заводится с помощью стартера. Вероятность того, что он не заводится, меньше 0,5. Следовательно, вероятность того, что двигатель переохлажден, меньше min(1,1–0,7+0,5), т.е. меньше 0,8». Так же нетрудно придумать примеры и для других схем вероятностных рассуждений.
Рассмотрим две схемы рассуждения с учетом необходимых условий.
Значения q и r необходимости в этих схемах могут оцениваться в каких-то специальных единицах. Можно считать, например, что имеется лингвистическая шкала нечетких квантификаторов необходимости. Тогда q и r будут соответствовать некоторые интервалы или усредненные характеристики этих интервалов. В качестве примера рассуждения с учетом необходимых условий в соответствии со схемой 5 приведем следующее рассуждение: «Если у меня будет дача, то необходимо будет купить велосипед. Дача мне крайне необходима. Тогда покупка велосипеда для меня необходима».
Рассмотрим еще две схемы, в которых наряду с необходимостью учитывается возможность некоторых фактов, явлений или действий. Подобные схемы (как и две предшествующие) характерны для упоминавшейся теории возможностей.
Пример рассуждения, основанного на схеме 7: «Когда поднимается температура в реакторе, чрезвычайно необходимо понизить в нем давление. Возможность повышения температуры в реакторе высока. Следовательно, возможность того, что надо будет снижать давление в реакторе, либо больше нуля, либо больше той возможности, которая приписана событию повышения температуры». Альтернативный характер этого рассуждения обусловлен тем, что q и r при проведении его не были оценены количественно. Это не позволяет сделать окончательный альтернативный вывод в следствии.
Завершим раздел еще тремя схемами рассуждений, в которых учитывается возможная взаимосвязь А и В, а также некоторые соображения из рассуждений по аналогии.
Каждый, кого интересуют схемы правдоподобных рассуждений, может без труда увеличить нашу коллекцию, например, заимствовав их из книги Д. Пойи, приведенной в списке литературы. Нам же необходимо двигаться дальше к тем человеческим схемам рассуждений, в которых активно используются знания, хранящиеся в его памяти, т.е. к рассуждениям, на которые опирается интеллектуальная деятельность человека и ее моделирование в современных интеллектуальных системах.
Глава пятая. ВЫВОД В БАЗЕ ЗНАНИЙ
Приходится порой простые мысли
доказывать всерьез, как теоремы.
О. Сулейменов. От января до апреля
Что такое интеллектуальная система
Проблема моделирования человеческих рассуждений стала чрезвычайно актуальной в конце 70-х годов, когда в области искусственного интеллекта появились практически интересные системы. В последующие несколько лет возникла новая отрасль индустрии – производство интеллектуальных систем.
Причин скачкообразного развития работ по созданию систем искусственного интеллекта было несколько. Главнейшими из них можно считать три: необходимость создания ЭВМ пятого поколения, переход к роботизированным производствам и появление экспертных систем.
Как известно, ЭВМ пятого поколения отличаются от машин предыдущих поколений тем, что в них встроены функции программиста. По словесному заданию задачи, сформулированному на ограниченном профессиональном языке, эти ЭВМ способны сами построить необходимую рабочую программу (синтезировать ее из отдельных модулей, хранящихся в памяти ЭВМ) и выполнить ее. Для этого в состав ЭВМ должна входить база знаний, в которой хранится информация о закономерностях, присущих данной проблемной области, и методах решения характерных для нее задач. Кроме того, в состав ЭВМ должен входить специальный блок – решатель, в который встроены процедуры, подобные логическому выводу. С помощью решателя на основании сведений из базы знаний автоматически синтезируются нужные для пользователя программы. На рис. 29 приведена общая структура ЭВМ пятого поколения. Отметим, что процессор, показанный на рисунке, – это обычное арифметическое устройство с необходимой оперативной памятью, а внешняя память служит для хранения данных, нужных для решения задач. Таким образом, база знаний является новым специфическим блоком (как и система общения и решатель) в структуре ЭВМ пятого поколения.
Рис. 29.
В роботизированных производствах используются роботы третьего поколения. Они должны быть достаточно автономны в своих действиях и уметь выполнять необходимый набор операций в динамически изменяющихся условиях производства. Это означает, что они не могут довольствоваться набором встроенных в них программ жесткого поведения. Интеллектуальный уровень таких роботов должен быть достаточно высоким. В их систему управления необходимо включить специальный блок – планировщик, задачей которого является составление программы действий робота в тех реальных условиях окружающей среды, которые в данный момент наблюдаются рецепторной системой робота. Для планирования целесообразной деятельности робот третьего поколения должен обладать определенными знаниями о свойствах окружающей среды и методах достижения целей в ней. Эти знания хранятся в его базе знаний, показанной в общей структуре робота на рис. 30. Глядя на этот рисунок, легко установить аналогии со схемой, показанной на предыдущем рисунке. В ЭВМ пятого поколения и в роботах третьего поколения осуществляется планирование будущей деятельности: автоматический синтез программы, выполняемый решателем, и программа деятельности, создаваемая планировщиком. Оба блока работают на основе знаний, хранящихся в базе знаний.
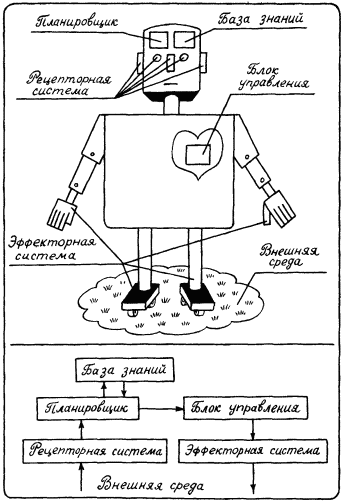Рис. 30.
Экспертные системы, структура которых показана на рис. 31, также содержат базу знаний и логический блок, функции которого похожи на функции решателя и планировщика. Задача логического блока состоит в поиске вывода, ответа на входное сообщение, поступившее в систему. В базе знаний хранится необходимая информация о проблемной области, в которой работает пользователь. Его запросы поступают на профессиональном ограниченном естественном языке. В системе общения они преобразуются во внутреннее представление, с которым работает логический блок. Это внутреннее представление преобразуется в запрос к базе знаний. Если прямого ответа на запрос в базе нет, то логический блок осуществляет поиск косвенной информации, получаемой из хранящейся в базе с помощью достоверного или правдоподобного вывода. Система объяснения (это специфический блок, отличающий экспертные системы от других интеллектуальных систем) при необходимости по требованию пользователя поясняет ему, как получена та информация, которая выдана в качестве ответа.
Рис. 31.
Мы хотим отметить, что ядром всех основных типов рассмотренных интеллектуальных систем являются база знаний и блок, осуществляющий вывод с помощью знаний (решатель, планировщик или логический блок). Этот вывод составляет основную процедуру, реализуемую в интеллектуальных системах.
Знания о внешнем мире могут иметь двоякую природу. Они могут содержать декларативное описание фактов и явлений внешнего мира, фиксирующее их наличие или отсутствие, а также основные связи и закономерности, в которые эти факты и явления входят. Но они могут содержать и процедурные описания того, как надо манипулировать с этими фактами и достигать целей, интересных для системы. Для описания знаний в интеллектуальных системах используются специальные языки описания знаний (ЯОЗ). Эти языки могут иметь различную природу. Нас будут интересовать (из-за темы данной книги) лишь языки логического типа. Простейшими видами таких ЯОЗ являются языки исчисления высказываний или исчисления предикатов вместе с теми процедурами вывода, которые для них известны. Однако в современных интеллектуальных системах такие языки используются довольно редко. Куда более распространены в них языки, основанные на продукциях. Продукции в общем виде можно записать в форме «Если…, то…». Сама по себе эта форма оказывается весьма характерной для фиксации знаний в различных областях человеческой деятельности. Вот несколько примеров текстов, взятых почти наугад из различных книг.
Химические реакции мы со школьных лет привыкли воспринимать в форме соотношений следующего вида:
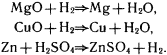
И т.д.
Покажем, как подобные утверждения можно записать в продукционной форме. Введем шесть сортов базовых элементов. К первому сорту отнесем металлы: Q1={Cu,Mg,Zn,…}. Ко второму – газы: Q2={H2,О,N,…}, к третьему – воду: Q3={H2O}. Четвертый сорт составляют окиси: Q4={MgO,CuО,…}. Пятый сорт образуют кислоты: Q5={H2SO4,HCl,…}. Наконец, шестой сорт образуют соли: Q6={ZnSO4,NaCl,…}. Зададим два базовых отображения. Первое отображает элементы из Q4 в элементы Q1. С его помощью для окисей выделяются основания. Второе отображение сопоставляет с именами веществ (под веществом будем понимать металл, газ, окись, воду, кислоту или соль) их химические формулы. Введем еще два оператора, которые будем использовать в продукциях: A(q) и E(q). Оператор A(q) добавляет в базу знаний q, а оператор E(q) убирает q из базы. Выпишем первый тип продукций для описания химических реакций.
Эта продукция годится для описания двух из приведенных выше химических реакций. Для описания третьей реакции используем другой тип продукций.
Вспомним программу «Логик-теоретик», которую мы обсуждали в третьей главе. Она была основана на том, что при доказательстве равенства двух выражений в исчислении высказываний использовалось понятие различия в двух выражениях и подбирались такие преобразования, которые эти различия устраняли. Для соотнесения различий с преобразованиями была построена таблица, в которой указывалось, какие преобразования какие различия устраняют. От этой таблицы чрезвычайно легко перейти к продукционной системе. Если i есть номер различия, a F* – одно из преобразований, то запись i
F* соответствует утверждению, что при наличии различия i можно применить преобразование F*.
Два последних примера показывают, что продукциями являются не только те выражения, которые имеют форму «Если…, то…», но и многие другие выражения. К ним, по сути, сводятся все каузальные, т.е. причинно-cледственные утверждения, подобные тем, которые мы обсуждали в предшествующей главе. К ним же относятся и любые схемы вывода типа «посылки – следствие». Замкнутые системы правил типа законов короля Павзолия, описанных в романе Пьера Луиса «Приключения короля Павзолия»[9], также могут рассматриваться как особая форма продукций. Даже такие утверждения, как знаменитое «Если звезды зажигают, значит, это кому-то нужно» (В. Маяковский), можно рассматривать как продукцию.
Продукционные системы получили при представлении знаний в последнее время наибольшее распространение. Поэтому посвятим им специальный раздел нашей книги.
Причин скачкообразного развития работ по созданию систем искусственного интеллекта было несколько. Главнейшими из них можно считать три: необходимость создания ЭВМ пятого поколения, переход к роботизированным производствам и появление экспертных систем.
Как известно, ЭВМ пятого поколения отличаются от машин предыдущих поколений тем, что в них встроены функции программиста. По словесному заданию задачи, сформулированному на ограниченном профессиональном языке, эти ЭВМ способны сами построить необходимую рабочую программу (синтезировать ее из отдельных модулей, хранящихся в памяти ЭВМ) и выполнить ее. Для этого в состав ЭВМ должна входить база знаний, в которой хранится информация о закономерностях, присущих данной проблемной области, и методах решения характерных для нее задач. Кроме того, в состав ЭВМ должен входить специальный блок – решатель, в который встроены процедуры, подобные логическому выводу. С помощью решателя на основании сведений из базы знаний автоматически синтезируются нужные для пользователя программы. На рис. 29 приведена общая структура ЭВМ пятого поколения. Отметим, что процессор, показанный на рисунке, – это обычное арифметическое устройство с необходимой оперативной памятью, а внешняя память служит для хранения данных, нужных для решения задач. Таким образом, база знаний является новым специфическим блоком (как и система общения и решатель) в структуре ЭВМ пятого поколения.
В роботизированных производствах используются роботы третьего поколения. Они должны быть достаточно автономны в своих действиях и уметь выполнять необходимый набор операций в динамически изменяющихся условиях производства. Это означает, что они не могут довольствоваться набором встроенных в них программ жесткого поведения. Интеллектуальный уровень таких роботов должен быть достаточно высоким. В их систему управления необходимо включить специальный блок – планировщик, задачей которого является составление программы действий робота в тех реальных условиях окружающей среды, которые в данный момент наблюдаются рецепторной системой робота. Для планирования целесообразной деятельности робот третьего поколения должен обладать определенными знаниями о свойствах окружающей среды и методах достижения целей в ней. Эти знания хранятся в его базе знаний, показанной в общей структуре робота на рис. 30. Глядя на этот рисунок, легко установить аналогии со схемой, показанной на предыдущем рисунке. В ЭВМ пятого поколения и в роботах третьего поколения осуществляется планирование будущей деятельности: автоматический синтез программы, выполняемый решателем, и программа деятельности, создаваемая планировщиком. Оба блока работают на основе знаний, хранящихся в базе знаний.
Экспертные системы, структура которых показана на рис. 31, также содержат базу знаний и логический блок, функции которого похожи на функции решателя и планировщика. Задача логического блока состоит в поиске вывода, ответа на входное сообщение, поступившее в систему. В базе знаний хранится необходимая информация о проблемной области, в которой работает пользователь. Его запросы поступают на профессиональном ограниченном естественном языке. В системе общения они преобразуются во внутреннее представление, с которым работает логический блок. Это внутреннее представление преобразуется в запрос к базе знаний. Если прямого ответа на запрос в базе нет, то логический блок осуществляет поиск косвенной информации, получаемой из хранящейся в базе с помощью достоверного или правдоподобного вывода. Система объяснения (это специфический блок, отличающий экспертные системы от других интеллектуальных систем) при необходимости по требованию пользователя поясняет ему, как получена та информация, которая выдана в качестве ответа.
Мы хотим отметить, что ядром всех основных типов рассмотренных интеллектуальных систем являются база знаний и блок, осуществляющий вывод с помощью знаний (решатель, планировщик или логический блок). Этот вывод составляет основную процедуру, реализуемую в интеллектуальных системах.
Знания о внешнем мире могут иметь двоякую природу. Они могут содержать декларативное описание фактов и явлений внешнего мира, фиксирующее их наличие или отсутствие, а также основные связи и закономерности, в которые эти факты и явления входят. Но они могут содержать и процедурные описания того, как надо манипулировать с этими фактами и достигать целей, интересных для системы. Для описания знаний в интеллектуальных системах используются специальные языки описания знаний (ЯОЗ). Эти языки могут иметь различную природу. Нас будут интересовать (из-за темы данной книги) лишь языки логического типа. Простейшими видами таких ЯОЗ являются языки исчисления высказываний или исчисления предикатов вместе с теми процедурами вывода, которые для них известны. Однако в современных интеллектуальных системах такие языки используются довольно редко. Куда более распространены в них языки, основанные на продукциях. Продукции в общем виде можно записать в форме «Если…, то…». Сама по себе эта форма оказывается весьма характерной для фиксации знаний в различных областях человеческой деятельности. Вот несколько примеров текстов, взятых почти наугад из различных книг.
1. Если Академия заблагорассудит присоединить к себе ученого русского или иностранца, который не столько еще известен, чтобы мог требовать чести быть почетным членом, но своими полезными сочинениями или познаниями, или же ревностию и старанием, оказав полезные Академии услуги, обратил на себя отличное внимание, то она принимает его в корреспонденты, которые также разделяются на русских и иностранных. (Устав Санкт-Петербургской Академии наук 1836 года, № 85)Число подобных примеров можно увеличивать до бесконечности. Они показывают, что представление фрагментов наших знаний о внешнем мире и действиях в нем в виде продукций имеет весьма большое распространение. Часть специалистов по интеллектуальным системам считает, что запись знаний в виде систем продукций носит универсальный характер – любые знания можно записать в такой форме. Они приводят немало примеров, когда знания, внешне не имеющие продукционной формы, удается перевести в систему продукций. Вот один из таких примеров.
2. Если враг не сдается, то его уничтожают. Если кто к нам с мечем придет, то от меча и погибнет. (Высказывания полководцев.)
3. Если температура в верхней зоне превысит 75°, то необходимо открыть задвижку № 7. (Из инструкции.)
Химические реакции мы со школьных лет привыкли воспринимать в форме соотношений следующего вида:
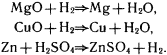
И т.д.
Покажем, как подобные утверждения можно записать в продукционной форме. Введем шесть сортов базовых элементов. К первому сорту отнесем металлы: Q1={Cu,Mg,Zn,…}. Ко второму – газы: Q2={H2,О,N,…}, к третьему – воду: Q3={H2O}. Четвертый сорт составляют окиси: Q4={MgO,CuО,…}. Пятый сорт образуют кислоты: Q5={H2SO4,HCl,…}. Наконец, шестой сорт образуют соли: Q6={ZnSO4,NaCl,…}. Зададим два базовых отображения. Первое отображает элементы из Q4 в элементы Q1. С его помощью для окисей выделяются основания. Второе отображение сопоставляет с именами веществ (под веществом будем понимать металл, газ, окись, воду, кислоту или соль) их химические формулы. Введем еще два оператора, которые будем использовать в продукциях: A(q) и E(q). Оператор A(q) добавляет в базу знаний q, а оператор E(q) убирает q из базы. Выпишем первый тип продукций для описания химических реакций.
F* соответствует утверждению, что при наличии различия i можно применить преобразование F*.Два последних примера показывают, что продукциями являются не только те выражения, которые имеют форму «Если…, то…», но и многие другие выражения. К ним, по сути, сводятся все каузальные, т.е. причинно-cледственные утверждения, подобные тем, которые мы обсуждали в предшествующей главе. К ним же относятся и любые схемы вывода типа «посылки – следствие». Замкнутые системы правил типа законов короля Павзолия, описанных в романе Пьера Луиса «Приключения короля Павзолия»[9], также могут рассматриваться как особая форма продукций. Даже такие утверждения, как знаменитое «Если звезды зажигают, значит, это кому-то нужно» (В. Маяковский), можно рассматривать как продукцию.
Продукционные системы получили при представлении знаний в последнее время наибольшее распространение. Поэтому посвятим им специальный раздел нашей книги.
Продукционные системы
Анализ структур ЭВМ пятого поколения, роботов автономного типа и экспертных систем приводит к обобщенной структуре, показанной на рис. 32. Эта схема при условии, что система R представляет собой продукционную систему, может послужить основой для классификации типов продукций. На ней показано взаимодействие «рассуждающей» системы с внешним миром и базой знаний, из которой рассуждающая система может черпать накопленную ранее информацию о закономерностях этого мира и его состояниях. Из внешнего мира в рассуждающую систему приходит сиюминутная, текущая информация о наблюдаемых в этом мире фактах и явлениях. А из базы знаний поступает информация, имеющая более фундаментальное значение. Она может описывать законы внешнего мира, правила действий в нем, целевые структуры или ожидаемые отклики внешнего мира на те или иные воздействия на него. В памяти рассуждающей системы хранится текущая информация, связанная с ходом рассуждений. Со временем она либо исчезает, либо передается для хранения в базу знаний. Последнее происходит лишь в том случае, когда в процессе рассуждений появилась информация, которая может оказаться полезной для рассуждающей системы в будущем.
Рис. 32.
Теперь приступим к классификации продукций.
1. Продукции типа AWBR. В левой части продукции стоит информация, поступившая из внешнего мира, а в правой – сведения о вытекающих из этой информации изменениях в рассуждающей системе. Эти изменения сказываются на ходе рассуждений. Например, рассуждая утром о выборе места воскресного отдыха, вы вдруг слышите по радио сообщение о том, что в середине дня ожидается сильная гроза. Это сообщение и есть AW. В ответ на него может измениться весь ход ваших рассуждений о планах отдыха. Сразу же будут отброшены варианты, связанные с пребыванием за городом на открытом воздухе, а другие варианты приобретут куда больший вес. Это изменение предпочтительности вариантов отдыха характеризуется правой частью продукции BR. Сама продукция для данного случая могла бы выглядеть, например, следующим образом: «Если на улице идет дождь или гроза или они ожидаются в течение дня, то вместо прогулки лучше пойти в музей или кино».
В качестве AW может выступать не только некоторое сообщение о W или некоторый факт, имеющий место во внешнем мире, но и прямое воздействие из внешнего мира на рассуждающую систему. Но что бы ни стояло в левой части продукции ABWR, в ее правой части стоят некоторые операторы, меняющие ход самих рассуждений.
2. Продукции типа AWBK. Такие продукции отражают ситуацию передачи некоторого сообщения из внешнего мира для запоминания в базе знаний. Примером продукции такого типа может служить приказание, которое отдает командир разведчику: «Все, что увидишь интересного в окрестности переправы, запомни, а потом передай через связного». Это приказание можно переписать в стандартной продукционной форме: «Если F есть интересный факт, относящийся к району переправы, то F надо запомнить и передать со связным». При работе с продукциями такого типа рассуждающая система выступает в роли отделения связи, передающего сообщение от одного абонента другому. Правда, в этом отделении связи может происходить перлюстрация корреспонденции. Рассуждающая система может при необходимости воспользоваться информацией о AW и BK для своих целей.
3. Продукции типа AKBW. В этом случае рассуждающая система также выступает в виде отделения связи. Только теперь выдача сообщения происходит из базы знаний во внешний мир. Примером возникновения подобной продукции может служить обнаружение в базе знаний противоречивой информации. Пусть некто X знает, что у его приятеля Y пятеро детей. Но встретившийся X знакомый Z утверждает, что по его сведениям у Y не пятеро детей, а трое. Такое противоречие может заставить «рассуждающую систему X» реализовать продукцию, в которой АК характеризует факт наличия противоречивой информации о числе детей у Y, a BW – некоторое действие, которое X предпринимает в связи с этим. Например, BW может соответствовать разговору X по телефону с Y, в ходе которого X попытается выяснить истинное количество детей у Y.
4. Продукции типа ARBK. Они соответствуют тому, что некоторый факт, полученный рассуждающей системой, передается на хранение в базу знаний. Интерпретация продукций такого типа очевидна.
5. Продукции типа AKBR. Подобно продукциям предшествующего типа эти продукции описывают обмен информацией при работе рассуждающей системы. Необходимая для рассуждений информация выбирается из базы знаний и передается для обработки в рассуждающую систему.
6. Продукции типа AWBW. Эти продукции обычно называют продукциями непосредственного отклика. Левая их часть AWописывает некоторую наблюдаемую ситуацию во внешнем мире или воздействие внешнего мира на рассуждающую систему. Правая часть продукции описывает действие, которое поступает от системы в окружающий ее мир. Выполнение подобных продукций чем-то напоминает мгновенный отклик, возникающий при рефлекторных процессах (например, при отдергивании руки, когда она касается чего-то горячего). Рассуждающая система в этих случаях просто не успевает срабатывать. Она лишь транслирует информацию об AW и BW адресатам.
7. Продукции типа ARBW. Они описывают те воздействия на внешний мир, которые порождает результат работы рассуждающей системы. «Подумай, прежде чем делать» – мудрый совет, призывающий того, к кому он обращен, воспользоваться продукцией данного типа, а не продукцией непосредственного отклика.
8. Продукции типа ARBR. Это внутренние продукции рассуждающей системы. Они описывают промежуточные шаги процесса вывода и не влияют непосредственно на содержимое базы знаний и состояния внешнего мира. Эти продукции описывают единичные шаги многошаговых процессов рассуждений.
9. Продукции типа АКВК. Они описывают процедуры преобразования знаний в базе знаний: обобщение знаний, получение новых знаний из ранее известных с помощью логического вывода, установление закономерностей между знаниями на основании обработки сведений о единичных фактах, хранящихся в базе знаний, и т.п. Рассуждающая система в этом случае используется лишь в качестве инструмента, с помощью которого происходит изменение состояния базы знаний.
Сказанное наводит на мысль, что продукции могут иметь весьма различное значение. В качестве их левых и правых частей могут выступать и некоторые утверждения, и действия. Возможны не только те интерпретации, которые мы привели выше, но и ряд других. Например, продукции типа AWBK можно трактовать как способ описания шагов общения между пользователем и системой в диалоговом режиме. Тогда AW будет интерпретироваться как вопрос пользователя, а ВK – как ответ системы. При смене спрашивающего и отвечающего надо использовать для описания шага диалога продукции типа AKBW.
Продукционной системой будем называть любую совокупность продукций, в которую могут входить продукции любого из перечисленных выше типов.
Часто вместо продукций типа ?? рассматривают более сложные конструкции. В общей форме продукции имеют вид
i, П, P, A B, Q.
Здесь АВ – обычная продукция «Если …, то …», которая носит название ядра продукции. Элемент Р характеризует внешние условия или условия применимости продукции, определяемые факторами, не входящими непосредственно в А, например целями, которые стоят перед рассуждающей системой. Условия Р позволяют из всех продукций, у которых в левой части ядра стоит А, отбирать нужную часть продукций.
Элемент П характеризует сферу проблемной области базы знаний или предусловия применимости продукции. Эти предусловия ничем не отличаются от Р, но выделяют подсистемы продукций на ранг выше тех, которые выделяют условия. Предусловия задают формальную систему, в рамках которой будут проводиться логические рассуждения. Поясним эту мысль на примере. В обычном мире лошади не летают. Поэтому продукция «Если х лошадь, то она летать не может» в обычном мире всегда имеет место. Но если мы от обычного мира перейдем к миру греческих мифов, то продукция «Если лошадь есть Пегас, то она летает» станет верной. В мире же русской сказки продукция «Если лошадь есть Конек-Горбунок, то она летает» принимается без всякой критики. В приведенном примере предусловия П должны развести между собой обычный мир, мир греческих мифов и мир русской сказки.
Теперь приступим к классификации продукций.
1. Продукции типа AW
BR. В левой части продукции стоит информация, поступившая из внешнего мира, а в правой – сведения о вытекающих из этой информации изменениях в рассуждающей системе. Эти изменения сказываются на ходе рассуждений. Например, рассуждая утром о выборе места воскресного отдыха, вы вдруг слышите по радио сообщение о том, что в середине дня ожидается сильная гроза. Это сообщение и есть AW. В ответ на него может измениться весь ход ваших рассуждений о планах отдыха. Сразу же будут отброшены варианты, связанные с пребыванием за городом на открытом воздухе, а другие варианты приобретут куда больший вес. Это изменение предпочтительности вариантов отдыха характеризуется правой частью продукции BR. Сама продукция для данного случая могла бы выглядеть, например, следующим образом: «Если на улице идет дождь или гроза или они ожидаются в течение дня, то вместо прогулки лучше пойти в музей или кино».В качестве AW может выступать не только некоторое сообщение о W или некоторый факт, имеющий место во внешнем мире, но и прямое воздействие из внешнего мира на рассуждающую систему. Но что бы ни стояло в левой части продукции AB
WR, в ее правой части стоят некоторые операторы, меняющие ход самих рассуждений.2. Продукции типа AW
BK. Такие продукции отражают ситуацию передачи некоторого сообщения из внешнего мира для запоминания в базе знаний. Примером продукции такого типа может служить приказание, которое отдает командир разведчику: «Все, что увидишь интересного в окрестности переправы, запомни, а потом передай через связного». Это приказание можно переписать в стандартной продукционной форме: «Если F есть интересный факт, относящийся к району переправы, то F надо запомнить и передать со связным». При работе с продукциями такого типа рассуждающая система выступает в роли отделения связи, передающего сообщение от одного абонента другому. Правда, в этом отделении связи может происходить перлюстрация корреспонденции. Рассуждающая система может при необходимости воспользоваться информацией о AW и BK для своих целей.3. Продукции типа AK
BW. В этом случае рассуждающая система также выступает в виде отделения связи. Только теперь выдача сообщения происходит из базы знаний во внешний мир. Примером возникновения подобной продукции может служить обнаружение в базе знаний противоречивой информации. Пусть некто X знает, что у его приятеля Y пятеро детей. Но встретившийся X знакомый Z утверждает, что по его сведениям у Y не пятеро детей, а трое. Такое противоречие может заставить «рассуждающую систему X» реализовать продукцию, в которой АК характеризует факт наличия противоречивой информации о числе детей у Y, a BW – некоторое действие, которое X предпринимает в связи с этим. Например, BW может соответствовать разговору X по телефону с Y, в ходе которого X попытается выяснить истинное количество детей у Y.4. Продукции типа AR
BK. Они соответствуют тому, что некоторый факт, полученный рассуждающей системой, передается на хранение в базу знаний. Интерпретация продукций такого типа очевидна.5. Продукции типа AK
BR. Подобно продукциям предшествующего типа эти продукции описывают обмен информацией при работе рассуждающей системы. Необходимая для рассуждений информация выбирается из базы знаний и передается для обработки в рассуждающую систему.6. Продукции типа AW
BW. Эти продукции обычно называют продукциями непосредственного отклика. Левая их часть AWописывает некоторую наблюдаемую ситуацию во внешнем мире или воздействие внешнего мира на рассуждающую систему. Правая часть продукции описывает действие, которое поступает от системы в окружающий ее мир. Выполнение подобных продукций чем-то напоминает мгновенный отклик, возникающий при рефлекторных процессах (например, при отдергивании руки, когда она касается чего-то горячего). Рассуждающая система в этих случаях просто не успевает срабатывать. Она лишь транслирует информацию об AW и BW адресатам.7. Продукции типа AR
BW. Они описывают те воздействия на внешний мир, которые порождает результат работы рассуждающей системы. «Подумай, прежде чем делать» – мудрый совет, призывающий того, к кому он обращен, воспользоваться продукцией данного типа, а не продукцией непосредственного отклика.8. Продукции типа AR
BR. Это внутренние продукции рассуждающей системы. Они описывают промежуточные шаги процесса вывода и не влияют непосредственно на содержимое базы знаний и состояния внешнего мира. Эти продукции описывают единичные шаги многошаговых процессов рассуждений.9. Продукции типа АК
ВК. Они описывают процедуры преобразования знаний в базе знаний: обобщение знаний, получение новых знаний из ранее известных с помощью логического вывода, установление закономерностей между знаниями на основании обработки сведений о единичных фактах, хранящихся в базе знаний, и т.п. Рассуждающая система в этом случае используется лишь в качестве инструмента, с помощью которого происходит изменение состояния базы знаний.Сказанное наводит на мысль, что продукции могут иметь весьма различное значение. В качестве их левых и правых частей могут выступать и некоторые утверждения, и действия. Возможны не только те интерпретации, которые мы привели выше, но и ряд других. Например, продукции типа AW
BK можно трактовать как способ описания шагов общения между пользователем и системой в диалоговом режиме. Тогда AW будет интерпретироваться как вопрос пользователя, а ВK – как ответ системы. При смене спрашивающего и отвечающего надо использовать для описания шага диалога продукции типа AKBW.Продукционной системой будем называть любую совокупность продукций, в которую могут входить продукции любого из перечисленных выше типов.
Часто вместо продукций типа ?
? рассматривают более сложные конструкции. В общей форме продукции имеют видi, П, P, A
B, Q.Здесь А
В – обычная продукция «Если …, то …», которая носит название ядра продукции. Элемент Р характеризует внешние условия или условия применимости продукции, определяемые факторами, не входящими непосредственно в А, например целями, которые стоят перед рассуждающей системой. Условия Р позволяют из всех продукций, у которых в левой части ядра стоит А, отбирать нужную часть продукций.Элемент П характеризует сферу проблемной области базы знаний или предусловия применимости продукции. Эти предусловия ничем не отличаются от Р, но выделяют подсистемы продукций на ранг выше тех, которые выделяют условия. Предусловия задают формальную систему, в рамках которой будут проводиться логические рассуждения. Поясним эту мысль на примере. В обычном мире лошади не летают. Поэтому продукция «Если х лошадь, то она летать не может» в обычном мире всегда имеет место. Но если мы от обычного мира перейдем к миру греческих мифов, то продукция «Если лошадь есть Пегас, то она летает» станет верной. В мире же русской сказки продукция «Если лошадь есть Конек-Горбунок, то она летает» принимается без всякой критики. В приведенном примере предусловия П должны развести между собой обычный мир, мир греческих мифов и мир русской сказки.