2б. Если некоторое частное утверждение общего утверждения находится с ним в тексте одновременно и содержит посылки, более частные, чем общее утверждение, то этот частный случай есть исключение из общего утверждения. Примером такой схемы рассуждений может служить вывод о том, что в общественном транспорте военнослужащий не обязан отдавать честь вышестоящему начальнику, так как в уставе одновременно содержится общее требование отдачи чести военнослужащим при встрече со старшим по званию, а также частное требование, указывающее конкретные условия (посылки), при которых честь не отдается.
2в. В предшествующем случае посылки частного утверждения входили в посылки общего утверждения, но приводили к другому заключению, отменяющему общее. Но возможен случай, когда заключение частного утверждения не только не отменяет общее, но как бы усиливает его. Проиллюстрируем это на примере закона о хищениях, который вполне мог бы быть в уголовном кодексе некоторой страны: «При хищении имущества граждан преступник несет наказание в виде тюремного заключения от двух до пяти лет. При хищении в особо крупных размерах срок его наказания от семи до девяти лет.» В этом примере второе утверждение по форме является частным, а первое общим. Однако заключение второго утверждения усиливает заключение первого.
Два последних типа герменевтических рассуждений весьма часто используются в юриспруденции, усиливая и смягчая наказания в зависимости от тех или иных конкретных посылок, входящих, как правило, в посылки общих утверждений.
3. Этот герменевтический прием рассуждения весьма распространен в юриспруденции всех стран. Если в некотором месте текста, когда говорится о чем-то и допускается, что это что-то необходимо следует из посылок q1 и q2, а в другом месте этого текста говорится о том же самом, но в качестве необходимой посылки указывается лишь q1, то и в первом случае посылку q2 можно опустить.
4. Если в тексте содержатся два утверждения, противоречащие друг другу, то либо в тексте имеется утверждение, примиряющее их, либо такое утверждение надо построить, введя в противоречащие утверждения такую посылку, которая «разводит» их и снимает их противоречивость. Этот прием весьма хитроумно использовали талмудисты для устранения вопиющего противоречия, связанного с указаниями срока употребления опресноков во время пасхи. В книге «Второзаконие» в одной и той же главе говорится, что опресноки надо употреблять в пищу и шесть и семь дней. Ситуация исключительно тяжелая. Но вот как талмудисты преодолели ее. По учению фарисеев первый сноп нового урожая торжественно приносился в храм на второй день пасхи. После его освящения в храме разрешалось есть хлеб нового урожая. Учитывая это обстоятельство, талмудисты устранили противоречие, добавив к заключениям о том, что опресноки надо есть шесть дней и что опресноки надо есть семь дней, посылки о типе муки, используемой при выпечке опресноков. Если это мука получена из зерен старого урожая, то такие опресноки можно есть все семь пасхальных дней, а если для их приготовления используется мука из зерен нового урожая, то число дней потребления опресноков, естественно, сокращается до шести.
К сожалению, процедуры поиска дополнительных посылок, «разводящих» противоречивые высказывания, до сих пор не созданы. Если бы это удалось, то многие проблемы сохранения непротиворечивости баз данных и баз знаний в современных интеллектуальных системах, а также непротиворечивости рассуждений, опирающихся на факты и знания, были бы решены.
5. Если в ряду однотипных утверждений что-то упоминается ранее, то оно автоматически переносится на все последующие утверждения. Если бы этот прием герменевтики перенести на текст известной русской сказки «Терем-Теремок», то можно было бы существенно сократить ее текст, ибо повтор всего диалога с вновь пришедшим к теремку персонажем не нужен. Достаточно лишь последней его части, отличающей его от предшествующего диалога. Правда, тогда бы потерялась вся прелесть и привлекательность этой сказки.
Наверное, читатель уже уловил суть герменевтических схем. Конечно, в отличие от строгих силлогистических рассуждений, сомнение в справедливости которых возможно лишь при очень тщательном их анализе, правильность герменевтических рассуждений можно подвергнуть критике «с ходу». Однако с их помощью удается объяснить многие особенности человеческих рассуждений, которые, как мы уже неоднократно подчеркивали, не являются в большинстве своем рассуждениями, порождаемыми формальными системами. Именно поэтому мы рассмотрим еще несколько «экзотических» схем рассуждений.
Разнообразные логические системы, родившиеся в Индии, Китае, Японии и других странах, дают немало примеров моделей рассуждений, которые не принимаются теми, кто считает необходимым, чтобы в основе логической системы дедуктивного типа лежала идея формальной системы. Здесь не место давать сколь-нибудь глубокий анализ систем Востока, в которых логика тесно переплетается с философией, а зачастую и с религией. Наша задача состоит лишь в том, чтобы у читателя сложилось представление, что многие особенности человеческих рассуждений (прежде всего опирающихся на правосторонние механизмы), никак не отражаемые в логических теориях Европы, находят место в теориях, рожденных в Азии.
Этим системам ничуть не были чужды идеи чисто дедуктивных рассуждений по типу силлогистики Аристотеля. Вот как звучит дошедший до нас из глубины веков разговор философа Махинды, посланца царя Ашоки, ревностного проповедника и распространителя буддизма, с царем Цейлона Ланка Деванампиятиссом. В этом разговоре Махинда проверяет логические способности царя Цейлона, ибо для восприятия философии буддизма, по мнению Ашоки, требуется определенный уровень логического мышления, способности к рассуждениям логического типа:
В этом рассуждении второе утверждение найдено по аналогии с первым наблюдением. Третье утверждение есть переход от частного к общему. Четвертое утверждение устанавливает связь по общности (аналогии) между первым и вторым утверждением. Наконец, общее заключение выводится из всего предшествующего. Таким образом, в пятичленном рассуждении, приведенном нами, используются одновременно индуктивные и дедуктивные рассуждения, а также вывод по аналогии.
Не чужды были буддийским мыслителям и герменевтические схемы. Они, например, широко пользовались так называемым «принципом куропаток», который звучал так: «Если в тексте о чем-то говорится как о множестве, то число элементов множества равно трем». Этот странный принцип обосновывается тем, что по закону о жертвоприношениях количество жертвенных животных (в том числе и куропаток) никак не ограничивалось. С другой стороны, имел место закон, запрещающий убийство. Коллизия этих двух требований и породила конформистский «принцип куропаток».
В философском учении школы хуаянь, процветавшей в Китае, имеются элементы логики, в которой закон тождества понимается не статично, как в силлогистике Аристотеля, а диалектически. В такой форме закон тождества звучит следующим образом: «Всякое Q есть Q и одновременно не есть Q». В учении о мире дхарм говорится:
Попытки ввести диалектику в схемы логических рассуждений делались, конечно, не только на Востоке, но и в Европе. Достаточно вспомнить Гегеля с его диалектическим методом. Но до сих пор так и не удалось создать формальную систему, в рамках которой описывались бы законы рассуждения, опирающиеся на диалектику. Это дело будущего. И, возможно, для этого потребуется расширение самого понятия формальной системы.
А сейчас мы переходим к описанию двух мощных формальных дедуктивных систем, порожденных наукой Нового времени. Именно эти системы впервые позволили автоматизировать ряд характерных для человека способов рассуждений, опирающихся на схему дедуктивного вывода.
Глава третья. АВТОМАТИЗАЦИЯ ДОСТОВЕРНЫХ РАССУЖДЕНИЙ
Исчисление высказываний
2в. В предшествующем случае посылки частного утверждения входили в посылки общего утверждения, но приводили к другому заключению, отменяющему общее. Но возможен случай, когда заключение частного утверждения не только не отменяет общее, но как бы усиливает его. Проиллюстрируем это на примере закона о хищениях, который вполне мог бы быть в уголовном кодексе некоторой страны: «При хищении имущества граждан преступник несет наказание в виде тюремного заключения от двух до пяти лет. При хищении в особо крупных размерах срок его наказания от семи до девяти лет.» В этом примере второе утверждение по форме является частным, а первое общим. Однако заключение второго утверждения усиливает заключение первого.
Два последних типа герменевтических рассуждений весьма часто используются в юриспруденции, усиливая и смягчая наказания в зависимости от тех или иных конкретных посылок, входящих, как правило, в посылки общих утверждений.
3. Этот герменевтический прием рассуждения весьма распространен в юриспруденции всех стран. Если в некотором месте текста, когда говорится о чем-то и допускается, что это что-то необходимо следует из посылок q1 и q2, а в другом месте этого текста говорится о том же самом, но в качестве необходимой посылки указывается лишь q1, то и в первом случае посылку q2 можно опустить.
4. Если в тексте содержатся два утверждения, противоречащие друг другу, то либо в тексте имеется утверждение, примиряющее их, либо такое утверждение надо построить, введя в противоречащие утверждения такую посылку, которая «разводит» их и снимает их противоречивость. Этот прием весьма хитроумно использовали талмудисты для устранения вопиющего противоречия, связанного с указаниями срока употребления опресноков во время пасхи. В книге «Второзаконие» в одной и той же главе говорится, что опресноки надо употреблять в пищу и шесть и семь дней. Ситуация исключительно тяжелая. Но вот как талмудисты преодолели ее. По учению фарисеев первый сноп нового урожая торжественно приносился в храм на второй день пасхи. После его освящения в храме разрешалось есть хлеб нового урожая. Учитывая это обстоятельство, талмудисты устранили противоречие, добавив к заключениям о том, что опресноки надо есть шесть дней и что опресноки надо есть семь дней, посылки о типе муки, используемой при выпечке опресноков. Если это мука получена из зерен старого урожая, то такие опресноки можно есть все семь пасхальных дней, а если для их приготовления используется мука из зерен нового урожая, то число дней потребления опресноков, естественно, сокращается до шести.
К сожалению, процедуры поиска дополнительных посылок, «разводящих» противоречивые высказывания, до сих пор не созданы. Если бы это удалось, то многие проблемы сохранения непротиворечивости баз данных и баз знаний в современных интеллектуальных системах, а также непротиворечивости рассуждений, опирающихся на факты и знания, были бы решены.
5. Если в ряду однотипных утверждений что-то упоминается ранее, то оно автоматически переносится на все последующие утверждения. Если бы этот прием герменевтики перенести на текст известной русской сказки «Терем-Теремок», то можно было бы существенно сократить ее текст, ибо повтор всего диалога с вновь пришедшим к теремку персонажем не нужен. Достаточно лишь последней его части, отличающей его от предшествующего диалога. Правда, тогда бы потерялась вся прелесть и привлекательность этой сказки.
Наверное, читатель уже уловил суть герменевтических схем. Конечно, в отличие от строгих силлогистических рассуждений, сомнение в справедливости которых возможно лишь при очень тщательном их анализе, правильность герменевтических рассуждений можно подвергнуть критике «с ходу». Однако с их помощью удается объяснить многие особенности человеческих рассуждений, которые, как мы уже неоднократно подчеркивали, не являются в большинстве своем рассуждениями, порождаемыми формальными системами. Именно поэтому мы рассмотрим еще несколько «экзотических» схем рассуждений.
Разнообразные логические системы, родившиеся в Индии, Китае, Японии и других странах, дают немало примеров моделей рассуждений, которые не принимаются теми, кто считает необходимым, чтобы в основе логической системы дедуктивного типа лежала идея формальной системы. Здесь не место давать сколь-нибудь глубокий анализ систем Востока, в которых логика тесно переплетается с философией, а зачастую и с религией. Наша задача состоит лишь в том, чтобы у читателя сложилось представление, что многие особенности человеческих рассуждений (прежде всего опирающихся на правосторонние механизмы), никак не отражаемые в логических теориях Европы, находят место в теориях, рожденных в Азии.
Этим системам ничуть не были чужды идеи чисто дедуктивных рассуждений по типу силлогистики Аристотеля. Вот как звучит дошедший до нас из глубины веков разговор философа Махинды, посланца царя Ашоки, ревностного проповедника и распространителя буддизма, с царем Цейлона Ланка Деванампиятиссом. В этом разговоре Махинда проверяет логические способности царя Цейлона, ибо для восприятия философии буддизма, по мнению Ашоки, требуется определенный уровень логического мышления, способности к рассуждениям логического типа:
– Как называется это дерево, о царь?Результатом этой проверки Махинда был, несомненно, доволен. Условия для распространения буддизма оказались на Цейлоне вполне подходящими, ибо царь Ланка Деванампиятисс вполне справился с задачами выделения классов сущностей и выявления тех жергоновых отношений, которые между ними имеются. Он даже оказался способным на силлогистические заключения! Этот пример показывает, что в Индии периода развития буддийского учения логика уже достигла уровня силлогистики. Однако в ней не был сделан решающий шаг: не совершился переход к замкнутой дедуктивной системе. Силлогистические заключения остались всего лишь одним из приемов для проведения рассуждений. Интересно, что в буддийской логике силлогизм был не трехчленным, как у Аристотеля (две посылки и заключение), а пятичленным. Но его пятичленность определялась не тем, что использовались сориты с четырьмя посылками, а тем, что он представлял собой как бы два силлогизма Аристотеля, сцепленные друг с другом. Рассмотрим пример такого рассуждения.
– Это дерево называется манго.
– Существуют ли здесь еще деревья манго, кроме этого?
– Существует множество деревьев манго.
– А существуют ли здесь другие деревья, кроме этого дерева манго и других деревьев манго?
– Существует множество деревьев, о достопочтенный, но это деревья, которые не есть деревья манго.
– А существует ли здесь, кроме других деревьев манго и тех деревьев, которые не есть деревья манго, еще другие деревья?
– Вот это дерево манго, о достопочтенный.
– Есть ли здесь люди твоего рода, о царь?
– Здесь много людей моего рода, о достопочтенный.
– А есть ли здесь кто-либо, не принадлежащий к твоему роду, о царь?
– Да, их здесь еще больше, чем людей моего рода.
– А есть ли здесь кто-либо, кроме людей твоего рода и других?
– Это я, о достопочтенный.
В этом рассуждении второе утверждение найдено по аналогии с первым наблюдением. Третье утверждение есть переход от частного к общему. Четвертое утверждение устанавливает связь по общности (аналогии) между первым и вторым утверждением. Наконец, общее заключение выводится из всего предшествующего. Таким образом, в пятичленном рассуждении, приведенном нами, используются одновременно индуктивные и дедуктивные рассуждения, а также вывод по аналогии.
Не чужды были буддийским мыслителям и герменевтические схемы. Они, например, широко пользовались так называемым «принципом куропаток», который звучал так: «Если в тексте о чем-то говорится как о множестве, то число элементов множества равно трем». Этот странный принцип обосновывается тем, что по закону о жертвоприношениях количество жертвенных животных (в том числе и куропаток) никак не ограничивалось. С другой стороны, имел место закон, запрещающий убийство. Коллизия этих двух требований и породила конформистский «принцип куропаток».
В философском учении школы хуаянь, процветавшей в Китае, имеются элементы логики, в которой закон тождества понимается не статично, как в силлогистике Аристотеля, а диалектически. В такой форме закон тождества звучит следующим образом: «Всякое Q есть Q и одновременно не есть Q». В учении о мире дхарм говорится:
«Мир дхарм ши это мир явлений, которые изменчивы, многообразны, отличны друг от друга, все события и предметы этого мира взаимосвязаны. Мир дхарм не является миром сущностей, неизменных и вечных. Этот мир есть некоторая единая субстанция. И оба мира неотделимы друг от друга, взаимозависимы, образуют единое неразрывное целое. Ши и ли взаимно обусловлены, взаимно тождественны и различны (выделено нами)».В этой позиции предугаданы многие законы, которые позже стали изучаться в диалектической логике. В настоящее время эта логика находится в стадии становления, в стадии поиска формального аппарата, который позволил бы ей достичь того же уровня формализации, который достигнут в формальных логиках, отражающих человеческие рассуждения о мире явлений, в котором нет диалектических переходов. Но уже в древности философы и мыслители пытались в своих логических построениях преодолеть статичность и метафизичность описываемого мира и выдвигать положения, подобные тем, которые приняты в философской системе хуаянь или сформулированы в древнеиндийской сутре Ланкаватра: «Вещи не такие, как они выглядят, но и не другие».
Попытки ввести диалектику в схемы логических рассуждений делались, конечно, не только на Востоке, но и в Европе. Достаточно вспомнить Гегеля с его диалектическим методом. Но до сих пор так и не удалось создать формальную систему, в рамках которой описывались бы законы рассуждения, опирающиеся на диалектику. Это дело будущего. И, возможно, для этого потребуется расширение самого понятия формальной системы.
А сейчас мы переходим к описанию двух мощных формальных дедуктивных систем, порожденных наукой Нового времени. Именно эти системы впервые позволили автоматизировать ряд характерных для человека способов рассуждений, опирающихся на схему дедуктивного вывода.
Глава третья. АВТОМАТИЗАЦИЯ ДОСТОВЕРНЫХ РАССУЖДЕНИЙ
Где меч силлогизма горел и сверкал,
Проверенный чистым рассудком,
И что же? Сражение он проиграл
Во славу иным прибауткам!
Н. Заболоцкий. Битва слонов
Исчисление высказываний
Под высказыванием будем понимать утверждение, относительно которого в любой момент можно сказать, является оно истинным или ложным, или по крайней мере предполагать, что ему может быть приписана такая интерпретация. Например, фразы «Пик Коммунизма есть высочайшая вершина СССР», «Все жители земли имеют рост более двух метров», «В Африке находятся более десяти еще неизвестных захоронений фараонов Египта» являются высказываниями. Первое из них истинно, второе – ложно (легко приводятся конкретные опровергающие примеры), а относительно третьей фразы мы не можем говорить, является она истинной или ложной, так как наши знания о еще не найденных погребениях фараонов пока недостаточны. Но мы вполне можем предполагать, что это высказывание, ибо оно обязательно либо истинно, либо ложно.
Не всякие фразы на естественном языке могут быть высказываниями. Например, утверждение «Девушка была очень красивой» таковым не является. Одни мужчины могут согласиться с мнением, высказанным в этой фразе, т.е. посчитать, что это утверждение истинно, но другие могут и не принять данной точки зрения, т.е. посчитать утверждение ложным. Такого рода утверждения в рамках формальной системы, называемой исчислением высказываний, не рассматриваются.
О формальной системе речь шла во второй главе, и читатели, наверное, помнят, что такие системы задаются как четверки, состоящие из множества базовых элементов Т, множества синтаксических правил L, множества аксиом Q и множества правил вывода R. Поэтому, если мы хотим рассматривать исчисление высказываний как формальную систему, то должны задать указанные четыре множества.
В качестве элементов множества Т будут выступать элементарные высказывания, обозначаемые малыми латинскими буквами. Считать или не считать некоторое высказывание элементарным, зависит от нашей воли. Как станет ясно из дальнейшего, этот вопрос не имеет принципиального значения в рамках той дедуктивной системы, которую мы строим. Для описания процедур построения производных высказываний из элементарных, т.е. синтаксических, правил надо предварительно ввести знаки логических связок. В качестве таких связок будут выступать уже известные по первой главе конъюнкция, дизъюнкция и отрицание, которые будем обозначать &,
и 
(иногда заменяя, как и ранее, этот последний знак чертой сверху буквы, соответствующей элементарному высказыванию), а также новая связка, называемая импликацией, которую будем обозначать 
.
Сформулируем теперь совокупность синтаксических правил для исчисления высказываний.
1. Всякое элементарное высказывание является правильной совокупностью (будем говорить далее правильной формулой).
2. Если ? и ? являются правильными формулами, то правильными формулами являются также?, (?&?), (??) и (??).
3. Других правильных формул в исчислении высказываний нет.
Между знаками логических связок, &, и и конструкциями естественного языка существует некоторая связь, которую проиллюстрируем на примерах. Воспользуемся стихотворением Давида Самойлова «Пестель, поэт и Анна». Вот его начало:
Вспомним, что такое конъюнкция и дизъюнкция. Во второй главе, определяя эти связки, мы говорили, что ?&? является истинным, если истинны оба утверждения ? и ?, а ?? является истинным, если истинно хотя бы одно из утверждений ? или ?. Такое определение связок позволяет перейти от структуры, в которой используются союзы И и ИЛИ, к записи ((a&(bc))&d), которая согласно синтаксическим правилам исчисления высказываний является правильной формулой этого исчисления. Правда, внимательные читатели могут усмотреть в этом переходе некоторую некорректность. Дело в том, что выражение ?? является истинным и тогда, когда одновременно ? и ? истинны. Но подобный случай в нашем примере невозможен. Анна либо шила, либо вышивала. Одновременно делать то и другое она не могла. Другими словами, одновременная истинность ? и ? должна была бы давать сигнал о ложности такого утверждения, а дизъюнкция утверждает, что оно истинно. Эту ситуацию можно исправить, введя связку, называемую разделительной дизъюнкцией. Но мы этого делать не будем, так как такая связка есть комбинация более простых связок, которые мы уже ввели: (?&?)(?&?).
Проверим, достигаем ли мы нужной цели с помощью данной комбинации. Если ? и ? ложны, то ложны правильные формулы (?&?) и (?&?) и, следовательно, по свойству дизъюнкции ложна и вся большая формула. Если же ? и ? одновременно истинны, то опять обе конъюнкции ложны, так как в них входят ложные высказывания, получающиеся из истинных путем отрицания, и, следовательно, вся дизъюнкция опять является ложной. И лишь тогда, когда из двух высказываний ? и ? одно истинно, а другое ложно, мы получаем истинность всего высказывания. После этого уточнения правильная формула исчисления высказываний, соответствующая нашему примеру, примет вид ((а&((b&c)(b&c)))&d).
Рассмотрим еще одну цитату из того же стихотворения: «…Если трон находится в стране в руках деспо?та, тогда дворянства первая забота сменить основы власти и закон». Введем два элементарных высказывания: g – «Трон находится в стране в руках деспо?та» и h – «Дворянства первая забота сменить основы власти и закон». Тогда логическая структура всего высказывания может быть представлена в виде (ЕСЛИ g ТОГДА h). Для перехода к правильной формуле исчисления высказываний воспользуемся импликацией. Раньше она не встречалась. По определению выражение ?? истинно во всех случаях, кроме того, когда ? истинно, а ? ложно. Другими словами, из истинности ? в импликации, которая является истинной, всегда следует истинность ?.
Исследуем запись (gh). Если g истинно, то h должно быть истинно, если фраза, которая вложена Д. Самойловым в уста Пестеля, является истинной. Это хорошо, но что будет в случае, когда утверждение g ложно? Для импликации это означает, что как при истинности h, так и при его ложности вся фраза в целом остается истинной. Другими словами, если неверно, что «Трон находится в стране в руках деспо?та», то дворянство может менять основы власти и закона, а может этого и не делать. Всё равно сложное высказывание будет сохранять свою истинность. Если же мы потребуем, чтобы при ложности g всегда было бы ложным и все высказывание целиком, сохраняя остальные свойства импликации, то мы опять вернемся к конъюнкции.
Наверное, самым разумным с точки зрения здравого смысла было бы вообще отказаться от определения истинности или ложности выражения (ЕСЛИ ? ТОГДА ?), когда ? является ложным. Ибо для выводов в этом случае нет никакой информации. Во второй главе мы использовали знак выводимости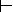
. Вот с его-то помощью и можно формализовать случай, когда в записи g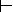h из истинности g всегда следует истинность h, а при ложности g ничего сказать нельзя. Но знак выводимости не является логической связкой и не входит в синтаксис исчисления высказываний. Поэтому, оставаясь в рамках этого исчисления, мы вынуждены пользоваться импликацией.
И еще одно замечание, касающееся импликации. Эта связка, как и разделительная дизъюнкция, может быть сведена к комбинации других связок, имеющихся в исчислении. Читатели легко могут убедиться в справедливости замены ?? на ??. Однако по ряду причин в исчислении высказываний в его классической форме импликация сохраняется как самостоятельная связка[5].
Не нужно думать, что переход от фраз на естественном языке к соответствующим им правильным формулам исчисления высказываний столь прост. На этом пути стоит немало трудностей, И прежде всего потому, что частицы и союзы языка типа НЕ, И, ИЛИ, ТО, ЕСЛИ и т.п. не являются однозначными свидетельствами наличия похожих на них связок. Цитата из стихотворения «Смерть поэта» Д. Самойлова иллюстрирует это положение:
Мы ввели множество базовых элементов и множество синтаксических правил. Теперь необходимо ввести множество аксиом. В логике в качестве множества аксиом выбирают обычно совокупность правильных формул, которые являются общезначимыми (или тождественно истинными). Высказывания, описываемые этими формулами, таковы, что они всегда истинны. Вот пример такого множества формул:
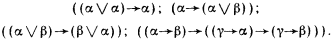
Читатели могут сами убедиться в том, что при всех комбинациях истинности и ложности формул ?, ? и ? четыре выписанные аксиомы всегда являются истинными. Такие аксиомы принято называть абсолютными или логическими.
Перейдем к описанию правил вывода R. Вспомним, что Аристотель, создавая свои силлогистические правила, добивался того, чтобы из истинных посылок всегда следовали истинные заключения. Если в качестве аксиом используются абсолютные аксиомы, то правила вывода должны обладать тем свойством, что их применение не должно нарушать истинность. Другими словами, из тождественно истинных формул должны выводиться лишь тождественно истинные формулы. Введем, учитывая это, два правила вывода исчисления высказываний.
Первое правило носит название правило подстановки. Согласно ему в формулу, которая уже выведена, можно вместо некоторого высказывания подставить любое другое при непременном условии, что эта подстановка сделана во всех местах вхождения заменяемого высказывания в данную формулу. Такая подстановка сохраняет свойство формулы быть тождественно истинной. Если в аксиому (?(??)) вместо ? подставить любую формулу, например (?&?), то формула ((?&?)((?&?)?)) останется тождественно истинной, что легко доказывается перебором всех комбинаций истинностных значений ? и ? и проверкой того, что для всех них полученная формула остается истинной.
Второе правило называется модус поненс (лат. modus ponens) или правило заключения и выглядит следующим образом: если ? и (??) являются истинными формулами, то формула ? также истинна. Если ? является истинной, то истинность (??) означает, что ? является истинной. Поэтому правило заключения не портит истинности выводимых формул.
Мы полностью описали исчисление высказываний. Заметим еще раз, что оно устроено так, что в результате выводов из аксиом получаются лишь тождественно истинные формулы. Можно показать, что система логических аксиом может быть выбрана таким образом, что для любой тождественно истинной формулы всегда найдется цепочка выводов (логических рассуждений), с помощью которой она будет выведена из системы аксиом путем применения правил подстановки и заключения. Другими словами, может быть построена полная система аксиом, из которой будут выводиться все тождественно истинные формулы и только они. Как показали исследования логиков, таких полных систем аксиом существует много. Система из четырех аксиом, которую мы только что рассмотрели является полной. Ее предложил известный немецкий математик и логик Д. Гильберт.
Подобное свойство исчисления высказываний позволяет достаточно легко ответить на кардинальный вопрос, возникающий для любой формальной системы: принадлежит ли некоторая правильная формула к множеству формул, выводимых в данной формальной системе? Для ответа на этот вопрос надо построить таблицу, в которой в левой части перечислены все возможные комбинации значений истины и лжи для высказываний, входящих в эту формулу (легко видеть, что при n различных таких высказываниях число комбинаций будет равно 2n), а в правой части выписаны значения истинности проверяемой формулы. Если правый столбец состоит только из значений «истина», то формула выводима в исчислении высказываний. В противном случае ее выводимость не имеет места.
Пусть, например, надо узнать, выводима ли в исчислении высказываний формула ((??)?). В эту формулу входит одно высказывание ?. Поэтому нужно проверить лишь две комбинации истинности: когда ? истинно и когда оно ложно. В первом случае по свойству импликации первая скобка является истинной, ибо ? ложно. Но тогда истинна и вся формула, ибо импликация истинна, когда истинны ее левая и правая части. Если же ? ложно, то первая скобка является ложной, так как левая часть импликации (??) истинна, а правая ложна. Но тогда вся формула является истинной. Тем самым доказано, что интересующая нас формула является тождественно истинной и, следовательно, выводимой в исчислении высказываний.
Не всякие фразы на естественном языке могут быть высказываниями. Например, утверждение «Девушка была очень красивой» таковым не является. Одни мужчины могут согласиться с мнением, высказанным в этой фразе, т.е. посчитать, что это утверждение истинно, но другие могут и не принять данной точки зрения, т.е. посчитать утверждение ложным. Такого рода утверждения в рамках формальной системы, называемой исчислением высказываний, не рассматриваются.
О формальной системе речь шла во второй главе, и читатели, наверное, помнят, что такие системы задаются как четверки, состоящие из множества базовых элементов Т, множества синтаксических правил L, множества аксиом Q и множества правил вывода R. Поэтому, если мы хотим рассматривать исчисление высказываний как формальную систему, то должны задать указанные четыре множества.
В качестве элементов множества Т будут выступать элементарные высказывания, обозначаемые малыми латинскими буквами. Считать или не считать некоторое высказывание элементарным, зависит от нашей воли. Как станет ясно из дальнейшего, этот вопрос не имеет принципиального значения в рамках той дедуктивной системы, которую мы строим. Для описания процедур построения производных высказываний из элементарных, т.е. синтаксических, правил надо предварительно ввести знаки логических связок. В качестве таких связок будут выступать уже известные по первой главе конъюнкция, дизъюнкция и отрицание, которые будем обозначать &,
и (иногда заменяя, как и ранее, этот последний знак чертой сверху буквы, соответствующей элементарному высказыванию), а также новая связка, называемая импликацией, которую будем обозначать .Сформулируем теперь совокупность синтаксических правил для исчисления высказываний.
1. Всякое элементарное высказывание является правильной совокупностью (будем говорить далее правильной формулой).
2. Если ? и ? являются правильными формулами, то правильными формулами являются также
?, (?&?), (??) и (??).3. Других правильных формул в исчислении высказываний нет.
Между знаками логических связок
, &, и и конструкциями естественного языка существует некоторая связь, которую проиллюстрируем на примерах. Воспользуемся стихотворением Давида Самойлова «Пестель, поэт и Анна». Вот его начало:В этом четверостишии можно выделить четыре элементарных высказывания: a – «Там Анна пела с самого утра», b – «Что-то (Анна) шила», с – «Что-то (Анна) вышивала», d – «Песня, долетая со двора, ему невольно сердце волновала». В скобках мы ввели субъект, отсутствующий во второй строке приведенного отрывка. Общая логическая структура всего четверостишия может быть описана следующим образом: (а И (b ИЛИ c) И d). Большими буквами мы выделили союзы, которые в явной форме присутствуют в тексте Д. Самойлова. Можно ли от этой записи перейти к логическим связкам?
Там Анна пела с самого утра
И что-то шила или вышивала.
И песня, долетая со двора,
Ему невольно сердце волновала.
Вспомним, что такое конъюнкция и дизъюнкция. Во второй главе, определяя эти связки, мы говорили, что ?&? является истинным, если истинны оба утверждения ? и ?, а ?
? является истинным, если истинно хотя бы одно из утверждений ? или ?. Такое определение связок позволяет перейти от структуры, в которой используются союзы И и ИЛИ, к записи ((a&(bc))&d), которая согласно синтаксическим правилам исчисления высказываний является правильной формулой этого исчисления. Правда, внимательные читатели могут усмотреть в этом переходе некоторую некорректность. Дело в том, что выражение ?? является истинным и тогда, когда одновременно ? и ? истинны. Но подобный случай в нашем примере невозможен. Анна либо шила, либо вышивала. Одновременно делать то и другое она не могла. Другими словами, одновременная истинность ? и ? должна была бы давать сигнал о ложности такого утверждения, а дизъюнкция утверждает, что оно истинно. Эту ситуацию можно исправить, введя связку, называемую разделительной дизъюнкцией. Но мы этого делать не будем, так как такая связка есть комбинация более простых связок, которые мы уже ввели: (?&?)(?&?).Проверим, достигаем ли мы нужной цели с помощью данной комбинации. Если ? и ? ложны, то ложны правильные формулы (
?&?) и (?&?) и, следовательно, по свойству дизъюнкции ложна и вся большая формула. Если же ? и ? одновременно истинны, то опять обе конъюнкции ложны, так как в них входят ложные высказывания, получающиеся из истинных путем отрицания, и, следовательно, вся дизъюнкция опять является ложной. И лишь тогда, когда из двух высказываний ? и ? одно истинно, а другое ложно, мы получаем истинность всего высказывания. После этого уточнения правильная формула исчисления высказываний, соответствующая нашему примеру, примет вид ((а&((b&c)(b&c)))&d).Рассмотрим еще одну цитату из того же стихотворения: «…Если трон находится в стране в руках деспо?та, тогда дворянства первая забота сменить основы власти и закон». Введем два элементарных высказывания: g – «Трон находится в стране в руках деспо?та» и h – «Дворянства первая забота сменить основы власти и закон». Тогда логическая структура всего высказывания может быть представлена в виде (ЕСЛИ g ТОГДА h). Для перехода к правильной формуле исчисления высказываний воспользуемся импликацией. Раньше она не встречалась. По определению выражение ?
? истинно во всех случаях, кроме того, когда ? истинно, а ? ложно. Другими словами, из истинности ? в импликации, которая является истинной, всегда следует истинность ?.Исследуем запись (g
h). Если g истинно, то h должно быть истинно, если фраза, которая вложена Д. Самойловым в уста Пестеля, является истинной. Это хорошо, но что будет в случае, когда утверждение g ложно? Для импликации это означает, что как при истинности h, так и при его ложности вся фраза в целом остается истинной. Другими словами, если неверно, что «Трон находится в стране в руках деспо?та», то дворянство может менять основы власти и закона, а может этого и не делать. Всё равно сложное высказывание будет сохранять свою истинность. Если же мы потребуем, чтобы при ложности g всегда было бы ложным и все высказывание целиком, сохраняя остальные свойства импликации, то мы опять вернемся к конъюнкции.Наверное, самым разумным с точки зрения здравого смысла было бы вообще отказаться от определения истинности или ложности выражения (ЕСЛИ ? ТОГДА ?), когда ? является ложным. Ибо для выводов в этом случае нет никакой информации. Во второй главе мы использовали знак выводимости
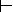. Вот с его-то помощью и можно формализовать случай, когда в записи g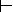h из истинности g всегда следует истинность h, а при ложности g ничего сказать нельзя. Но знак выводимости не является логической связкой и не входит в синтаксис исчисления высказываний. Поэтому, оставаясь в рамках этого исчисления, мы вынуждены пользоваться импликацией.И еще одно замечание, касающееся импликации. Эта связка, как и разделительная дизъюнкция, может быть сведена к комбинации других связок, имеющихся в исчислении. Читатели легко могут убедиться в справедливости замены ?
? на ??. Однако по ряду причин в исчислении высказываний в его классической форме импликация сохраняется как самостоятельная связка[5].Не нужно думать, что переход от фраз на естественном языке к соответствующим им правильным формулам исчисления высказываний столь прост. На этом пути стоит немало трудностей, И прежде всего потому, что частицы и союзы языка типа НЕ, И, ИЛИ, ТО, ЕСЛИ и т.п. не являются однозначными свидетельствами наличия похожих на них связок. Цитата из стихотворения «Смерть поэта» Д. Самойлова иллюстрирует это положение:
Встречающиеся здесь И и ИЛИ не являются прямыми аналогами связок исчисления высказываний.
И не ведал я, было ли это
Отпеванием времени года,
Воспеваньем страны и народа
Или просто кончиной поэта.
Мы ввели множество базовых элементов и множество синтаксических правил. Теперь необходимо ввести множество аксиом. В логике в качестве множества аксиом выбирают обычно совокупность правильных формул, которые являются общезначимыми (или тождественно истинными). Высказывания, описываемые этими формулами, таковы, что они всегда истинны. Вот пример такого множества формул:
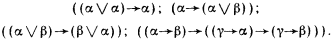
Читатели могут сами убедиться в том, что при всех комбинациях истинности и ложности формул ?, ? и ? четыре выписанные аксиомы всегда являются истинными. Такие аксиомы принято называть абсолютными или логическими.
Перейдем к описанию правил вывода R. Вспомним, что Аристотель, создавая свои силлогистические правила, добивался того, чтобы из истинных посылок всегда следовали истинные заключения. Если в качестве аксиом используются абсолютные аксиомы, то правила вывода должны обладать тем свойством, что их применение не должно нарушать истинность. Другими словами, из тождественно истинных формул должны выводиться лишь тождественно истинные формулы. Введем, учитывая это, два правила вывода исчисления высказываний.
Первое правило носит название правило подстановки. Согласно ему в формулу, которая уже выведена, можно вместо некоторого высказывания подставить любое другое при непременном условии, что эта подстановка сделана во всех местах вхождения заменяемого высказывания в данную формулу. Такая подстановка сохраняет свойство формулы быть тождественно истинной. Если в аксиому (?
(??)) вместо ? подставить любую формулу, например (?&?), то формула ((?&?)((?&?)?)) останется тождественно истинной, что легко доказывается перебором всех комбинаций истинностных значений ? и ? и проверкой того, что для всех них полученная формула остается истинной.Второе правило называется модус поненс (лат. modus ponens) или правило заключения и выглядит следующим образом: если ? и (?
?) являются истинными формулами, то формула ? также истинна. Если ? является истинной, то истинность (??) означает, что ? является истинной. Поэтому правило заключения не портит истинности выводимых формул.Мы полностью описали исчисление высказываний. Заметим еще раз, что оно устроено так, что в результате выводов из аксиом получаются лишь тождественно истинные формулы. Можно показать, что система логических аксиом может быть выбрана таким образом, что для любой тождественно истинной формулы всегда найдется цепочка выводов (логических рассуждений), с помощью которой она будет выведена из системы аксиом путем применения правил подстановки и заключения. Другими словами, может быть построена полная система аксиом, из которой будут выводиться все тождественно истинные формулы и только они. Как показали исследования логиков, таких полных систем аксиом существует много. Система из четырех аксиом, которую мы только что рассмотрели является полной. Ее предложил известный немецкий математик и логик Д. Гильберт.
Подобное свойство исчисления высказываний позволяет достаточно легко ответить на кардинальный вопрос, возникающий для любой формальной системы: принадлежит ли некоторая правильная формула к множеству формул, выводимых в данной формальной системе? Для ответа на этот вопрос надо построить таблицу, в которой в левой части перечислены все возможные комбинации значений истины и лжи для высказываний, входящих в эту формулу (легко видеть, что при n различных таких высказываниях число комбинаций будет равно 2n), а в правой части выписаны значения истинности проверяемой формулы. Если правый столбец состоит только из значений «истина», то формула выводима в исчислении высказываний. В противном случае ее выводимость не имеет места.
Пусть, например, надо узнать, выводима ли в исчислении высказываний формула ((
??)?). В эту формулу входит одно высказывание ?. Поэтому нужно проверить лишь две комбинации истинности: когда ? истинно и когда оно ложно. В первом случае по свойству импликации первая скобка является истинной, ибо ? ложно. Но тогда истинна и вся формула, ибо импликация истинна, когда истинны ее левая и правая части. Если же ? ложно, то первая скобка является ложной, так как левая часть импликации (??) истинна, а правая ложна. Но тогда вся формула является истинной. Тем самым доказано, что интересующая нас формула является тождественно истинной и, следовательно, выводимой в исчислении высказываний.