Это знаменитое предсказание впервые было сделано в 1824 году великим французским физиком Никола Карно. Он показал, что все тела во Вселенной меняют свою температуру – горячие остывают, а холодные нагреваются. Таким образом, они выравнивают свою температуру. Это всё равно что разделить богатое наследство поровну между всеми бедными родственниками; результатом будет общая нищета. Так и нас всех в конце концов должен охватить холод мирового пространства.
Правда, проблеск надежды появился, когда Эрнст Резерфорд и другие учёные открыли радиоактивность. Радиоактивные атомы, распадаясь, казалось, смогут поддерживать огонь на Солнце ещё довольно долго. Эта приятная новость означала, что Солнце, с одной стороны, много моложе, а с другой – много старше, чем предполагал лорд Кельвин. Но всё равно это всего лишь отсрочка. Всё, что учёные могут нам предложить, это 1 500 000 000 лет. Потом всё равно замёрзнем.
Когда на смену средневековым суевериям пришло просвещение, первыми науками, которые выделились и самоопределились, были математика, астрономия и физика. К началу девятнадцатого столетия всё было поставлено на свои места; Солнечная система вращалась так сонно и плавно, что Лаплас сумел убедить Наполеона в том, что бог, который бы присматривал за ней, вообще не нужен. Гравитация работала, как часы, а часы работали, как гравитация. Химия, которая, как и электричество во времена Бенджамена Франклина, была лишь набором бессвязных экспериментальных данных, превратилась в науку после того, как Лавуазье открыл, что огонь не вещь, а процесс, что-то происходящее с вещами. Эта мысль была настолько выше понимания широкой публики, что её автора в 1794 году гильотинировали. Появился Дальтон и показал, что любую вещь можно раздробить на очень-очень маленькие атомы, атомы объединяются в молекулы, и всё идёт по плану. С Фарадея и Максвелла заняло своё место в новом научном порядке и электричество (оказалось, что это то же самое, что магнетизм).
Примерно к 1880 году выяснилось, что мир прекрасно объяснён наукой. Метафизика всё ещё что-то бормотала во сне. Теология всё ещё произносила проповеди. Она пыталась оспаривать многие открытия науки, особенно в геологии и в новой эволюционной теории жизни. Но наука уже обращала на это мало внимания.
Потому что всё было очень просто. Есть время и пространство – вещи слишком очевидные, чтобы их объяснять. Есть материя, сделанная из маленьких твёрдых атомов, похожих на крошечные зёрнышки. Всё это движется, подчиняясь закону всемирного тяготения. Туманности сгущаются в звёзды, звёзды извергают планеты, планеты остывают, на них зарождается жизнь, она развивается и становится разумной, появляются сперва человекообразные обезьяны, потом епископ Уилберфорс и, наконец, профессор Гексли.
Осталось несколько небольших неясностей, например вопрос о том, что же такое на самом деле пространство и материя, и время, и жизнь, и разум. Но все эти вещи Герберт Спенсер очень кстати догадался назвать непознаваемыми, запер в ящик письменного стола и там оставил.
Всё было объяснено механическим Железным Детерминизмом. Оставался только этот противный скелет в ящике письменного стола. Да было ещё что-то странное и таинственное в электричестве, которое было не то чтобы просто вещь, но и не то чтобы просто выдумка. Была ещё странная загадка о «действии на расстояний», и электричество её только усугубляло. Как только добирается тяготение от Земли до Солнца? Если в пространстве нет ничего, то каким образом свет долетает к нам от Солнца за восемь минут и даже от Сириуса – за восемь лет? Даже изобретение «эфира», этакого универсального желе, по которому ходят волны, рябь и дрожь, не избавляло науку от некоторой неубедительности.
И вот, как раз на пороге XX столетия всё здание начало рушиться.
Первым предупреждением, что не всё ладно, было открытие икс-лучей. Открыл их Рентген, и с тех пор большинство физиков называют их рентгеновскими. Сэр Уильям Крукс, экспериментируя с трубками, наполненными разрежённым газом, открыл «лучистую материю» так же случайно, как Колумб открыл Америку. Британское правительство сразу же пожаловало Круксу дворянство, но было уже поздно. Дело было сделано.
Затем последовали работы целой школы исследователей радиоактивности. Венцом их были труды Резерфорда, который революционизировал теорию строения вещества. Я хорошо знал Резерфорда – мы с ним в течение семи лет были коллегами по Мак-Гиллскому университету – и могу подтвердить, что он действовал без заранее обдуманного намерения потрясти основы Вселенной. Но сделал он именно это, за что его тоже в своё время произвели в лорды.
Не следует путать труды Резерфорда по ядерной физике с теорией пространства и времени, которую создал Эйнштейн. Резерфорд ни разу в жизни не сослался на Эйнштейна. Даже когда он работал в Кавендишской лаборатории и, проявляя чёрную неблагодарность, разбивал те самые атомы, которые его прославили, даже тогда ему ничего не было нужно от Эйнштейна. Я однажды спросил Резерфорда (это было в 1923 году, всемирная слава Эйнштейна была в зените), что он думает о теории относительности. «А, чепуха! – ответил он. – Для нашей работы это не нужно!» Его биограф и почитатель, профессор Ив, рассказывает, что, когда немецкий физик Вин сказал Резерфорду, что ни один англосакс не понимает теории относительности, Резерфорд ответил: «Естественно, у нас слишком много здравого смысла».
Но всё же главные неприятности начались именно с Эйнштейна. В 1905 году он объявил, что абсолютного покоя нет. И с тех пор его не стало. Но только после первой мировой войны на Эйнштейна набросилась читающая публика, и полки в магазинах стали ломиться от книжек «про относительность».
Эйнштейн нокаутировал пространство и время так же, как Резерфорд нокаутировал вещество. Общий взгляд теории относительности на пространство очень прост. Эйнштейн всем объяснил, что нет такого места, как «здесь». «Но ведь я-то здесь, – скажете вы. – Здесь – как раз то место, где я сейчас сижу». Но ведь вы двигаетесь! Земля вертится, и вы на ней вертитесь. Вместе с Землёй вы движетесь вокруг Солнца, а вместе с Солнцем – вслед за «далёкой галактикой», которая сама мчится со скоростью 26 000 миль в секунду. Так что же это за место – «здесь»? Как вы его отметите? Всё это очень напоминает рассказ о двух идиотах на рыбалке. Один из них говорит другому: «Слушай, надо заметить то место, где мы вытащили эту здоровую рыбину», а тот ему отвечает: «Да я уже сделал отметину на борту лодки». Вот вам и «здесь»!
Открытие Эйнштейном кривизны пространства физики приветствовали взрывом аплодисментов, какие до тех пор можно было слышать только на бейсболе. Блестящий учёный, сэр Артур Эддингтон, который с пространством и временем обращается как поэт (даже его рассуждения о гравитации пронизаны юмором: он говорит, что идеальную возможность изучать тяготение имеет человек, падающий в лифте с двадцатого этажа), так вот, сэр Артур Эддингтои аплодировал громче всех. По его словам, без этой кривизны в пространстве разобраться вообще невозможно. Мы ползаем по своему пространству, как муха ползает по глобусу, думая, что он плоский. Тайны тяготения озадачивают нас (я не имею в виду тех немногих счастливцев, которым представился редкий случай упасть в лифте с двадцатого этажа. Но и на них откровение снизошло слишком поздно, а откровение заключается в следующем: мы и не падаем вовсе, а просто искривляемся). «Признайте кривизну пространства, – писал Эддингтон в 1927 году, – и таинственная сила исчезнет. Эйнштейн изгнал этого демона».
Но сейчас, четырнадцать лет спустя, начинает казаться, что Эйнштейна мало беспокоит, изогнуто пространство или нет. Ему это, по-видимому, всё равно. Один известный физик, руководящий факультетом в одном из крупнейших университетов, недавно написал мне по этому поводу: «Эйнштейн надеется, что общая теория, учитывающая некоторые свойства пространства, напоминающие то, что сейчас обычно называют кривизной, может в будущем оказаться более плодотворной, чем это, по-видимому, имеет место в настоящее время». Сказано чисто по-профессорски. Большинство же говорит просто, что Эйнштейн махнул рукой на кривое пространство. Всё равно что сэр Исаак Ньютон, зевнув, сказал бы: «Ах, вы об этом яблоке – а может быть, оно вовсе и не падало?»[99]
О существе математических доказательств
Новая классификация камней
К математической теории охоты
Сага о новом гормоне
Правда, проблеск надежды появился, когда Эрнст Резерфорд и другие учёные открыли радиоактивность. Радиоактивные атомы, распадаясь, казалось, смогут поддерживать огонь на Солнце ещё довольно долго. Эта приятная новость означала, что Солнце, с одной стороны, много моложе, а с другой – много старше, чем предполагал лорд Кельвин. Но всё равно это всего лишь отсрочка. Всё, что учёные могут нам предложить, это 1 500 000 000 лет. Потом всё равно замёрзнем.
Когда на смену средневековым суевериям пришло просвещение, первыми науками, которые выделились и самоопределились, были математика, астрономия и физика. К началу девятнадцатого столетия всё было поставлено на свои места; Солнечная система вращалась так сонно и плавно, что Лаплас сумел убедить Наполеона в том, что бог, который бы присматривал за ней, вообще не нужен. Гравитация работала, как часы, а часы работали, как гравитация. Химия, которая, как и электричество во времена Бенджамена Франклина, была лишь набором бессвязных экспериментальных данных, превратилась в науку после того, как Лавуазье открыл, что огонь не вещь, а процесс, что-то происходящее с вещами. Эта мысль была настолько выше понимания широкой публики, что её автора в 1794 году гильотинировали. Появился Дальтон и показал, что любую вещь можно раздробить на очень-очень маленькие атомы, атомы объединяются в молекулы, и всё идёт по плану. С Фарадея и Максвелла заняло своё место в новом научном порядке и электричество (оказалось, что это то же самое, что магнетизм).
Примерно к 1880 году выяснилось, что мир прекрасно объяснён наукой. Метафизика всё ещё что-то бормотала во сне. Теология всё ещё произносила проповеди. Она пыталась оспаривать многие открытия науки, особенно в геологии и в новой эволюционной теории жизни. Но наука уже обращала на это мало внимания.
Потому что всё было очень просто. Есть время и пространство – вещи слишком очевидные, чтобы их объяснять. Есть материя, сделанная из маленьких твёрдых атомов, похожих на крошечные зёрнышки. Всё это движется, подчиняясь закону всемирного тяготения. Туманности сгущаются в звёзды, звёзды извергают планеты, планеты остывают, на них зарождается жизнь, она развивается и становится разумной, появляются сперва человекообразные обезьяны, потом епископ Уилберфорс и, наконец, профессор Гексли.
Осталось несколько небольших неясностей, например вопрос о том, что же такое на самом деле пространство и материя, и время, и жизнь, и разум. Но все эти вещи Герберт Спенсер очень кстати догадался назвать непознаваемыми, запер в ящик письменного стола и там оставил.
Всё было объяснено механическим Железным Детерминизмом. Оставался только этот противный скелет в ящике письменного стола. Да было ещё что-то странное и таинственное в электричестве, которое было не то чтобы просто вещь, но и не то чтобы просто выдумка. Была ещё странная загадка о «действии на расстояний», и электричество её только усугубляло. Как только добирается тяготение от Земли до Солнца? Если в пространстве нет ничего, то каким образом свет долетает к нам от Солнца за восемь минут и даже от Сириуса – за восемь лет? Даже изобретение «эфира», этакого универсального желе, по которому ходят волны, рябь и дрожь, не избавляло науку от некоторой неубедительности.
И вот, как раз на пороге XX столетия всё здание начало рушиться.
Первым предупреждением, что не всё ладно, было открытие икс-лучей. Открыл их Рентген, и с тех пор большинство физиков называют их рентгеновскими. Сэр Уильям Крукс, экспериментируя с трубками, наполненными разрежённым газом, открыл «лучистую материю» так же случайно, как Колумб открыл Америку. Британское правительство сразу же пожаловало Круксу дворянство, но было уже поздно. Дело было сделано.
Затем последовали работы целой школы исследователей радиоактивности. Венцом их были труды Резерфорда, который революционизировал теорию строения вещества. Я хорошо знал Резерфорда – мы с ним в течение семи лет были коллегами по Мак-Гиллскому университету – и могу подтвердить, что он действовал без заранее обдуманного намерения потрясти основы Вселенной. Но сделал он именно это, за что его тоже в своё время произвели в лорды.
Не следует путать труды Резерфорда по ядерной физике с теорией пространства и времени, которую создал Эйнштейн. Резерфорд ни разу в жизни не сослался на Эйнштейна. Даже когда он работал в Кавендишской лаборатории и, проявляя чёрную неблагодарность, разбивал те самые атомы, которые его прославили, даже тогда ему ничего не было нужно от Эйнштейна. Я однажды спросил Резерфорда (это было в 1923 году, всемирная слава Эйнштейна была в зените), что он думает о теории относительности. «А, чепуха! – ответил он. – Для нашей работы это не нужно!» Его биограф и почитатель, профессор Ив, рассказывает, что, когда немецкий физик Вин сказал Резерфорду, что ни один англосакс не понимает теории относительности, Резерфорд ответил: «Естественно, у нас слишком много здравого смысла».
Но всё же главные неприятности начались именно с Эйнштейна. В 1905 году он объявил, что абсолютного покоя нет. И с тех пор его не стало. Но только после первой мировой войны на Эйнштейна набросилась читающая публика, и полки в магазинах стали ломиться от книжек «про относительность».
Эйнштейн нокаутировал пространство и время так же, как Резерфорд нокаутировал вещество. Общий взгляд теории относительности на пространство очень прост. Эйнштейн всем объяснил, что нет такого места, как «здесь». «Но ведь я-то здесь, – скажете вы. – Здесь – как раз то место, где я сейчас сижу». Но ведь вы двигаетесь! Земля вертится, и вы на ней вертитесь. Вместе с Землёй вы движетесь вокруг Солнца, а вместе с Солнцем – вслед за «далёкой галактикой», которая сама мчится со скоростью 26 000 миль в секунду. Так что же это за место – «здесь»? Как вы его отметите? Всё это очень напоминает рассказ о двух идиотах на рыбалке. Один из них говорит другому: «Слушай, надо заметить то место, где мы вытащили эту здоровую рыбину», а тот ему отвечает: «Да я уже сделал отметину на борту лодки». Вот вам и «здесь»!
Открытие Эйнштейном кривизны пространства физики приветствовали взрывом аплодисментов, какие до тех пор можно было слышать только на бейсболе. Блестящий учёный, сэр Артур Эддингтон, который с пространством и временем обращается как поэт (даже его рассуждения о гравитации пронизаны юмором: он говорит, что идеальную возможность изучать тяготение имеет человек, падающий в лифте с двадцатого этажа), так вот, сэр Артур Эддингтои аплодировал громче всех. По его словам, без этой кривизны в пространстве разобраться вообще невозможно. Мы ползаем по своему пространству, как муха ползает по глобусу, думая, что он плоский. Тайны тяготения озадачивают нас (я не имею в виду тех немногих счастливцев, которым представился редкий случай упасть в лифте с двадцатого этажа. Но и на них откровение снизошло слишком поздно, а откровение заключается в следующем: мы и не падаем вовсе, а просто искривляемся). «Признайте кривизну пространства, – писал Эддингтон в 1927 году, – и таинственная сила исчезнет. Эйнштейн изгнал этого демона».
Но сейчас, четырнадцать лет спустя, начинает казаться, что Эйнштейна мало беспокоит, изогнуто пространство или нет. Ему это, по-видимому, всё равно. Один известный физик, руководящий факультетом в одном из крупнейших университетов, недавно написал мне по этому поводу: «Эйнштейн надеется, что общая теория, учитывающая некоторые свойства пространства, напоминающие то, что сейчас обычно называют кривизной, может в будущем оказаться более плодотворной, чем это, по-видимому, имеет место в настоящее время». Сказано чисто по-профессорски. Большинство же говорит просто, что Эйнштейн махнул рукой на кривое пространство. Всё равно что сэр Исаак Ньютон, зевнув, сказал бы: «Ах, вы об этом яблоке – а может быть, оно вовсе и не падало?»[99]
О существе математических доказательств
Дж. Коэн[100]
Бертран Рассел определил математику как науку, в которой мы никогда не знаем, о чём говорим и насколько правильно то, что мы говорим. Известно, что математика широко применяется во многих других областях науки. Следовательно, и остальные учёные в большинстве своём не знают, о чём говорят и истина ли то, что они говорят.
Таким образом, одна из главных функций математического доказательства – создание надёжной основы для проникновения в суть вещей.
Аристотель относится к числу первых философов, занявшихся изучением математических доказательств. Он изобрёл силлогизм – приспособление, которое в силу своей абсолютной бесполезности привлекало внимание бесчисленного множества логиков и философов. Силлогизм состоит из первой посылки, второй посылки и заключения. Логики только и делают, что приходят к заключениям. Просто чудо, что они до сих пор не обошли всё кругом и не пришли туда, откуда вышли.
В первой посылке заключается истина, относящаяся к целому классу вещей, например: «Не все посылки верны». Во второй посылке утверждается, что интересующая нас вещь принадлежит к этому классу, например: «Последние четыре слова предыдущего предложения являются посылкой». Таким образом, мы приходим к заключению: «Не всегда верно, что не все посылки верны». Такова всеобъемлющая полнота, с которой логика обобщает явления повседневной жизни.
Опираясь на математические доказательства, учёные сумели соединить дотоле разрозненные области, термодинамику и технику связи, в новую дисциплину – теорию информации. «Информация», научным образом определённая, пропорциональна удивлению: чем удивительнее сообщение, тем больше информации оно содержит. Если, подняв телефонную трубку, человек услышит «алло», это его не очень удивит; значительно больше будет информация, если его вместо «алло» внезапно ударит током.
Колоссальные новые возможности открылись перед математическими доказательствами с развитием теории множеств в конце прошлого столетия и начале нынешнего. Автор сам недавно открыл одну теорему в теории множеств, которая заслуживает того, чтобы её здесь привести.
Теорема. Множество, единственным элементом которого является множество, может быть изоморфно множеству, единственным элементом которого является множество, все элементы которого образуют подгруппу элементов в множестве, которое является единственным элементом множества, с которым оно изоморфно.
Эту интуитивно очевидную теорему можно окольным путём вывести из теоремы об изоморфизме в теории групп.
Рассмотрим теперь логические системы. От простого набора теорем логическая система отличается так же, как готовое здание от груды кирпичей: в логической системе каждая последующая теорема опирается на предыдущую. Пойа отмечал, что заслуга Евклида состояла не в коллекционировании геометрических фактов, а в их логическом упорядочении. Если бы он просто свалил их в кучу, то прославился бы не больше, чем автор любого учебника по математике для средней школы.
Чтобы проиллюстрировать способы математических доказательств, мы приведём пример развёрнутой логической системы.
Лемма 1. Все лошади имеют одинаковую масть (докажем по индукции).
Доказательство. Очевидно, что одна лошадь имеет одинаковую масть. Обозначим через P (k) предположение, что k лошадей имеют одинаковую масть, и покажем, что из такого предположения вытекает, что k + 1 лошадей имеют ту же масть. Возьмём множество, состоящее из k + 1 лошадей, и удалим из него одну лошадь, тогда оставшиеся k лошадей по предположению имеют одинаковую масть. Вернём удалённую лошадь в множество, а вместо неё удалим другую. Получится снова табун из k лошадей. Согласно предположению, все они одной масти. Так мы переберём все k + 1 множеств, в каждом по k лошадей. Отсюда следует, что все лошади одной масти, т. е. предположение, что P (k) влечёт за собой P (k + 1). Но ранее мы уже показали, что предположение Р (1) выполняется всегда, значит, Р справедливо для любого k и все лошади имеют одинаковую масть.
Следствие I. Все предметы имеют одинаковую окраску.
Доказательство. В доказательстве леммы 1 никак не используется конкретная природа рассматриваемых объектов. Поэтому в утверждений «если Х — лошадь, то все Х имеют одинаковую окраску» можно заменить «лошадь» на «нечто» и тем самым доказать следствие. (Можно, кстати, заменить «нечто» на «ничто» без нарушения справедливости утверждения, но этого мы доказывать не будем.)
Следствие II. Все предметы белого цвета.
Доказательство. Если утверждение справедливо для всех X, то при подстановке любого конкретного Х оно сохраняет свою справедливость. В частности, если Х — слон, то все слоны одинакового цвета. Аксиоматически достоверным является существование белых слонов (см. Марк Твен, Похищение белого слона). Следовательно, все слоны белого цвета. Тогда из следствия I вытекает следствие II, что и требовалось доказать!
Теорема. Александр Великий не существовал.
Доказательство. Заметим для начала, что историки, очевидно, всегда говорят правду (поскольку они всегда ручаются за свои слова и поэтому, следовательно, не могут лгать). Отсюда исторически достоверным является утверждение: «Если Александр Великий существовал, то он ездил на вороном коне, которого звали Буцефал». Но, согласно следствию II, все предметы белые, и Александр не мог ездить на вороном коне. Поэтому для справедливости высказанного выше условного исторического утверждения необходимо, чтобы условие нарушалось. Следовательно, Александр Великий в действительности не существовал.
Из этого краткого обзора, посвящённого математическим доказательствам, не следует делать вывод, что всё уже доказано. Приведём два примера недоказанных теорем. Первый – это знаменитая гипотеза Голдбрика из теории чисел, которая утверждает, что каждое простое число можно представить в виде суммы двух чётных чисел. Этого нехитрого утверждения никто до сих пор не опроверг, но, несмотря на многовековые усилия математиков, никто и не доказал. Второй пример известен, хотя бы в интуитивной форме, всему цивилизованному миру. Это знаменитый первый закон Чизхолма: «Всё, что может испортиться, – портится».[101]
– И чего же тут трудного? – удивился Эйнштейн. – Две дюжины и 19 в квадрате.
– Мы считали: 10, 9, 8, 7, … – и сбились со счёта.
Использование ракет в мирных целях.
– Мой муж гений! – сказала госпожа Эйнштейн. – Он умеет делать абсолютно всё, кроме денег.
Бертран Рассел определил математику как науку, в которой мы никогда не знаем, о чём говорим и насколько правильно то, что мы говорим. Известно, что математика широко применяется во многих других областях науки. Следовательно, и остальные учёные в большинстве своём не знают, о чём говорят и истина ли то, что они говорят.
Таким образом, одна из главных функций математического доказательства – создание надёжной основы для проникновения в суть вещей.
Аристотель относится к числу первых философов, занявшихся изучением математических доказательств. Он изобрёл силлогизм – приспособление, которое в силу своей абсолютной бесполезности привлекало внимание бесчисленного множества логиков и философов. Силлогизм состоит из первой посылки, второй посылки и заключения. Логики только и делают, что приходят к заключениям. Просто чудо, что они до сих пор не обошли всё кругом и не пришли туда, откуда вышли.
В первой посылке заключается истина, относящаяся к целому классу вещей, например: «Не все посылки верны». Во второй посылке утверждается, что интересующая нас вещь принадлежит к этому классу, например: «Последние четыре слова предыдущего предложения являются посылкой». Таким образом, мы приходим к заключению: «Не всегда верно, что не все посылки верны». Такова всеобъемлющая полнота, с которой логика обобщает явления повседневной жизни.
Опираясь на математические доказательства, учёные сумели соединить дотоле разрозненные области, термодинамику и технику связи, в новую дисциплину – теорию информации. «Информация», научным образом определённая, пропорциональна удивлению: чем удивительнее сообщение, тем больше информации оно содержит. Если, подняв телефонную трубку, человек услышит «алло», это его не очень удивит; значительно больше будет информация, если его вместо «алло» внезапно ударит током.
Колоссальные новые возможности открылись перед математическими доказательствами с развитием теории множеств в конце прошлого столетия и начале нынешнего. Автор сам недавно открыл одну теорему в теории множеств, которая заслуживает того, чтобы её здесь привести.
Теорема. Множество, единственным элементом которого является множество, может быть изоморфно множеству, единственным элементом которого является множество, все элементы которого образуют подгруппу элементов в множестве, которое является единственным элементом множества, с которым оно изоморфно.
Эту интуитивно очевидную теорему можно окольным путём вывести из теоремы об изоморфизме в теории групп.
Рассмотрим теперь логические системы. От простого набора теорем логическая система отличается так же, как готовое здание от груды кирпичей: в логической системе каждая последующая теорема опирается на предыдущую. Пойа отмечал, что заслуга Евклида состояла не в коллекционировании геометрических фактов, а в их логическом упорядочении. Если бы он просто свалил их в кучу, то прославился бы не больше, чем автор любого учебника по математике для средней школы.
Чтобы проиллюстрировать способы математических доказательств, мы приведём пример развёрнутой логической системы.
Лемма 1. Все лошади имеют одинаковую масть (докажем по индукции).
Доказательство. Очевидно, что одна лошадь имеет одинаковую масть. Обозначим через P (k) предположение, что k лошадей имеют одинаковую масть, и покажем, что из такого предположения вытекает, что k + 1 лошадей имеют ту же масть. Возьмём множество, состоящее из k + 1 лошадей, и удалим из него одну лошадь, тогда оставшиеся k лошадей по предположению имеют одинаковую масть. Вернём удалённую лошадь в множество, а вместо неё удалим другую. Получится снова табун из k лошадей. Согласно предположению, все они одной масти. Так мы переберём все k + 1 множеств, в каждом по k лошадей. Отсюда следует, что все лошади одной масти, т. е. предположение, что P (k) влечёт за собой P (k + 1). Но ранее мы уже показали, что предположение Р (1) выполняется всегда, значит, Р справедливо для любого k и все лошади имеют одинаковую масть.
Следствие I. Все предметы имеют одинаковую окраску.
Доказательство. В доказательстве леммы 1 никак не используется конкретная природа рассматриваемых объектов. Поэтому в утверждений «если Х — лошадь, то все Х имеют одинаковую окраску» можно заменить «лошадь» на «нечто» и тем самым доказать следствие. (Можно, кстати, заменить «нечто» на «ничто» без нарушения справедливости утверждения, но этого мы доказывать не будем.)
Следствие II. Все предметы белого цвета.
Доказательство. Если утверждение справедливо для всех X, то при подстановке любого конкретного Х оно сохраняет свою справедливость. В частности, если Х — слон, то все слоны одинакового цвета. Аксиоматически достоверным является существование белых слонов (см. Марк Твен, Похищение белого слона). Следовательно, все слоны белого цвета. Тогда из следствия I вытекает следствие II, что и требовалось доказать!
Теорема. Александр Великий не существовал.
Доказательство. Заметим для начала, что историки, очевидно, всегда говорят правду (поскольку они всегда ручаются за свои слова и поэтому, следовательно, не могут лгать). Отсюда исторически достоверным является утверждение: «Если Александр Великий существовал, то он ездил на вороном коне, которого звали Буцефал». Но, согласно следствию II, все предметы белые, и Александр не мог ездить на вороном коне. Поэтому для справедливости высказанного выше условного исторического утверждения необходимо, чтобы условие нарушалось. Следовательно, Александр Великий в действительности не существовал.
Из этого краткого обзора, посвящённого математическим доказательствам, не следует делать вывод, что всё уже доказано. Приведём два примера недоказанных теорем. Первый – это знаменитая гипотеза Голдбрика из теории чисел, которая утверждает, что каждое простое число можно представить в виде суммы двух чётных чисел. Этого нехитрого утверждения никто до сих пор не опроверг, но, несмотря на многовековые усилия математиков, никто и не доказал. Второй пример известен, хотя бы в интуитивной форме, всему цивилизованному миру. Это знаменитый первый закон Чизхолма: «Всё, что может испортиться, – портится».[101]
– • • • —
«Выражение „Инфекционное заболевание“ означает прежде всего заболевание, подпадающее под действие подраздела 1 раздела 29 абсолютно или согласно определению одной из стадий такого заболевания, но в любом разделе части 4 настоящего Закона, применением которой заболевание или стадия заболевания исключаются из этого класса в соответствии с подразделом 2 упомянутого раздела 29, соответствующее выражение не означает такого заболевания или такого заболевания в такой стадии, как это может показаться».
Из британского «Закона об охране здоровья»
• • •
Правило тринадцатого удара, которое следует помнить, читая работу, обещающую слишком много: если часы пробили тринадцать раз, то это не только означает, что тринадцатый удар был неверным. Он порождает сомнения в верности каждого из первых двенадцати ударов.
Джон Мастерс
• • •
Одна знакомая просила Альберта Эйнштейна позвонить ей по телефону, но предупредила, что номер очень трудно запомнить: 24361.– И чего же тут трудного? – удивился Эйнштейн. – Две дюжины и 19 в квадрате.
• • •
• • •
• • •
В начале научной карьеры Эйнштейна один журналист спросил госпожу Эйнштейн, что она думает о своём муже.– Мой муж гений! – сказала госпожа Эйнштейн. – Он умеет делать абсолютно всё, кроме денег.
• • •
«…одной из главных причин потока научной литературы является то, что, когда исследователь достигает стадии, на которой он перестаёт видеть за деревьями лес, он слишком охотно склоняется к разрешению этой трудности путём перехода к изучению отдельных листьев».
«Ланцет», декабрь 1980 г.
Новая классификация камней
М. Дж. Оппенгейм
Ниже приводится классификация камней, применимая ко всем разновидностям и рекомендуемая для всеобщего использования. Эта классификация, с одной стороны, совершенно чёткая и жёсткая, с другой стороны – весьма гибкая и удобная. Кроме того, она подлинно научна, ибо опирается только на наблюдаемые свойства объектов и рассматривает эти объекты в нескольких различных планах, демонстрируя серьёзный и разносторонний подход к проблеме.
A2. Камень подземного происхождения. Типичный представитель – угольный камень (его называют также каменный уголь).
A3. Камень земного происхождения – могильный камень.
B2. Краеугольный камень – не претерпевавший перемещений с момента образования.
C2. Нефилософский камень – не обращающий металлы в золото.
D2. Нележачий камень, под который вода течёт.
E2. Камень в почках.
EЗ. Камень за пазухой.
Указания для практического применения нашей классификации при описании минералов:
1. Классификационный тип камня может быть при желании дополнен указанием цвета камня и высоты музыкального тона, издаваемого им при профессиональном простукивании геологическим молотком.
2. При описании камня все признаки следует располагать в порядке, обратном по отношению к Порядку, в котором они были перечислены выше.
– Теперь вы видите, – сказал Резерфорд, – что ничего не видно. А почему ничего не видно, вы сейчас увидите.
Дарвин играл на трубе перед своими тюльпанами. Никаких результатов.
Новое в системе водоснабжения.
Ниже приводится классификация камней, применимая ко всем разновидностям и рекомендуемая для всеобщего использования. Эта классификация, с одной стороны, совершенно чёткая и жёсткая, с другой стороны – весьма гибкая и удобная. Кроме того, она подлинно научна, ибо опирается только на наблюдаемые свойства объектов и рассматривает эти объекты в нескольких различных планах, демонстрируя серьёзный и разносторонний подход к проблеме.
A. Генетический план
A1. Камень небесного происхождения. Наиболее яркий представитель – лунный камень.A2. Камень подземного происхождения. Типичный представитель – угольный камень (его называют также каменный уголь).
A3. Камень земного происхождения – могильный камень.
B. Тектонический план
B1. Перекатный камень – претерпевавший перемещения с момента образования.B2. Краеугольный камень – не претерпевавший перемещений с момента образования.
C. Физико-химический план
C1. Философский камень – обращающий металлы, к которым он прикасается, в золото.C2. Нефилософский камень – не обращающий металлы в золото.
D. Кинематический план
D1. Лежачий камень, под который вода не течёт.D2. Нележачий камень, под который вода течёт.
Е. Функциональный план (отражающий роль камня в человеческом обществе)
E1. Камень на шее (разновидность: на сердце).E2. Камень в почках.
EЗ. Камень за пазухой.
Указания для практического применения нашей классификации при описании минералов:
1. Классификационный тип камня может быть при желании дополнен указанием цвета камня и высоты музыкального тона, издаваемого им при профессиональном простукивании геологическим молотком.
2. При описании камня все признаки следует располагать в порядке, обратном по отношению к Порядку, в котором они были перечислены выше.
Пример:
Автор настоящего сообщения недавно обнаружил фа-диез серо-бурый за пазухой лежачий нефилософский краеугольный могильный камень.– • • • —
Резерфорд демонстрировал слушателям распад радия. Экран то светился, то темнел.– Теперь вы видите, – сказал Резерфорд, – что ничего не видно. А почему ничего не видно, вы сейчас увидите.
• • •
Эразм Дарвин считал, что время от времени следует производить самые дикие эксперименты. Из них почти никогда ничего не выходит, но если они удаются, то результат бывает потрясающим.Дарвин играл на трубе перед своими тюльпанами. Никаких результатов.
• • •
К математической теории охоты
Г. Петард[102]
Простоты ради мы ограничимся рассмотрением только охоты на львов (Felis leo), живущих в пустыне Сахара. Перечисленные ниже методы с лёгкостью можно модифицировать и применять к другим плотоядным, обитающим в разных частях света.
2. Метод проективной геометрии. Без ограничения общности мы можем рассматривать пустыню Сахара как плоскость. Проектируем плоскость на линию, а линию – в точку, находящуюся внутри клетки. Лев проектируется в ту же точку,
3. Метод Больцано – Вейерштрасса. Рассекаем пустыню линией, проходящей с севера на юг. Лев находится либо в восточной части пустыни, либо в западной. Предположим для определённости, что он находится в западной части. Рассекаем её линией, идущей с запада на восток. Лев находится либо в северной части, либо в южной. Предположим для определённости, что он находится в южной части, рассекаем её линией, идущей с севера на юг. Продолжаем этот процесс до бесконечности, воздвигая после каждого шага крепкую решётку вдоль разграничительной линии. Площадь последовательно получаемых областей стремится к нулю, так что лев в конце концов оказывается окружённым решёткой произвольно малого периметра.
4. Комбинированный метод. Заметим, что пустыня представляет собой сепарабельное пространство. Оно содержит всюду плотное множество точек, из которого мы выбираем последовательность точек, имеющих пределом местоположение льва. Затем по этим точкам, захватив с собой необходимое снаряжение, крадучись, подбираемся к льву.
5. Топологический метод. Заметим, что связность тела льва во всяком случае не меньше, чем связность тора. Переводим пустыню в четырехмерное пространство. Согласно работе [103], в этом пространстве можно непрерывным образом выполнить такую деформацию, что по возвращении в трехмерное пространство лев окажется завязанным в узел. В таком состоянии он беспомощен.
6. Метод Коши, или функционально-теоретический. Рассмотрим льва как аналитическую функцию координат f(x) и запишем интеграл
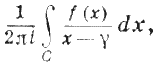где C – контур, ограничивающий пустыню, а γ – точка, в которой находится клетка. После вычисления интеграла получается f(γ), то есть лев в клетке.
2. Метод Шрёдингера. В любом случае существует положительная, отличная от нуля вероятность, что лев сам окажется в клетке. Сидите и ждите.
3. Метод ядерной физики. Поместите ручного льва в клетку и примените к нему и дикому льву обменный оператор Майорана[104]. Или предположим, что мы хотели поймать льва, а поймали львицу. Поместим тогда последнюю в клетку и применим к ней обменный оператор Гейзенберга, который обменивает спины.
2. Метод активации. Облучим пустыню медленными нейтронами. Внутри льва будет наведена радиоактивность, и он начнёт распадаться. Если подождать достаточно долго, лев не сможет оказать никакого сопротивления.[105]
Простоты ради мы ограничимся рассмотрением только охоты на львов (Felis leo), живущих в пустыне Сахара. Перечисленные ниже методы с лёгкостью можно модифицировать и применять к другим плотоядным, обитающим в разных частях света.
§ 1. Математические методы
1. Метод инверсивной геометрии. Помещаем в заданную точку пустыни клетку, входим в неё и запираем изнутри. Производим инверсию пространства по отношению к клетке. Теперь лев внутри клетки, а мы – снаружи.2. Метод проективной геометрии. Без ограничения общности мы можем рассматривать пустыню Сахара как плоскость. Проектируем плоскость на линию, а линию – в точку, находящуюся внутри клетки. Лев проектируется в ту же точку,
3. Метод Больцано – Вейерштрасса. Рассекаем пустыню линией, проходящей с севера на юг. Лев находится либо в восточной части пустыни, либо в западной. Предположим для определённости, что он находится в западной части. Рассекаем её линией, идущей с запада на восток. Лев находится либо в северной части, либо в южной. Предположим для определённости, что он находится в южной части, рассекаем её линией, идущей с севера на юг. Продолжаем этот процесс до бесконечности, воздвигая после каждого шага крепкую решётку вдоль разграничительной линии. Площадь последовательно получаемых областей стремится к нулю, так что лев в конце концов оказывается окружённым решёткой произвольно малого периметра.
4. Комбинированный метод. Заметим, что пустыня представляет собой сепарабельное пространство. Оно содержит всюду плотное множество точек, из которого мы выбираем последовательность точек, имеющих пределом местоположение льва. Затем по этим точкам, захватив с собой необходимое снаряжение, крадучись, подбираемся к льву.
5. Топологический метод. Заметим, что связность тела льва во всяком случае не меньше, чем связность тора. Переводим пустыню в четырехмерное пространство. Согласно работе [103], в этом пространстве можно непрерывным образом выполнить такую деформацию, что по возвращении в трехмерное пространство лев окажется завязанным в узел. В таком состоянии он беспомощен.
6. Метод Коши, или функционально-теоретический. Рассмотрим льва как аналитическую функцию координат f(x) и запишем интеграл
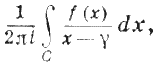
§ 2. Методы теоретической физики
1. Метод Дирака. Отмечаем, что дикие львы в пустыне Сахара являются величинами ненаблюдаемыми. Следовательно, все наблюдаемые львы в пустыне Сахара – ручные. Поимку ручного льва предоставляем читателю в качестве самостоятельного упражнения.2. Метод Шрёдингера. В любом случае существует положительная, отличная от нуля вероятность, что лев сам окажется в клетке. Сидите и ждите.
3. Метод ядерной физики. Поместите ручного льва в клетку и примените к нему и дикому льву обменный оператор Майорана[104]. Или предположим, что мы хотели поймать льва, а поймали львицу. Поместим тогда последнюю в клетку и применим к ней обменный оператор Гейзенберга, который обменивает спины.
§ 3. Методы экспериментальной физики
1. Термодинамический метод. Через пустыню натянем полупроницаемую мембрану, которая пропускает через себя всё, кроме льва.2. Метод активации. Облучим пустыню медленными нейтронами. Внутри льва будет наведена радиоактивность, и он начнёт распадаться. Если подождать достаточно долго, лев не сможет оказать никакого сопротивления.[105]
– • • • —
«Механитис – профессиональное заболевание тех, кто верит, что ответ математической задачи, которую он не может ни решить, ни даже сформулировать, легко будет найти, если получить доступ к достаточно дорогой вычислительной машине».
Б. Купман, Исследование операций, 4, 442 (1956).
Сага о новом гормоне
Норман Апплцвейг[106]
За последние месяцы мир узнал об открытии трех чудодейственных лекарств тремя ведущими фармацевтическими фирмами. При ближайшем рассмотрении выяснилось, что все три препарата – это один и тот же гормон. Если вам интересно узнать, как одно и то же химическое соединение получает несколько разных названий, давайте проследим за цепочкой событий, предшествующих созданию чудотворного средства.
Первым его обычно совершенно случайно открывает физиолог в погоне за двумя другими гормонами. Он даёт ему название, отражающее его функции в организме, и предсказывает, что новое соединение может оказаться полезным при лечении редкого заболевания крови. Переработав одну тонну свежих бычьих гланд, доставляемых прямо с бойни, он выделяет 10 граммов чистого гормона и отправляет их к специалисту по физхимии на анализ.
Физхимик обнаруживает, что 95% очищенного физиологом гормона составляют разного рода примеси, а остальные 5% содержат по крайней мере три разных соединения. Из одного такого соединения он успешно выделяет 10 миллиграммов чистого кристаллического гормона. На основе изучения его физических свойств он предсказывает возможную химическую структуру нового вещества и высказывает предположение, что его роль в организме, вероятнее всего, не совпадает с предсказаниями физиолога. Затем он даёт ему новое название и переправляет химику-органику для подтверждения своих предположений о структуре соединения;
За последние месяцы мир узнал об открытии трех чудодейственных лекарств тремя ведущими фармацевтическими фирмами. При ближайшем рассмотрении выяснилось, что все три препарата – это один и тот же гормон. Если вам интересно узнать, как одно и то же химическое соединение получает несколько разных названий, давайте проследим за цепочкой событий, предшествующих созданию чудотворного средства.
Первым его обычно совершенно случайно открывает физиолог в погоне за двумя другими гормонами. Он даёт ему название, отражающее его функции в организме, и предсказывает, что новое соединение может оказаться полезным при лечении редкого заболевания крови. Переработав одну тонну свежих бычьих гланд, доставляемых прямо с бойни, он выделяет 10 граммов чистого гормона и отправляет их к специалисту по физхимии на анализ.
Физхимик обнаруживает, что 95% очищенного физиологом гормона составляют разного рода примеси, а остальные 5% содержат по крайней мере три разных соединения. Из одного такого соединения он успешно выделяет 10 миллиграммов чистого кристаллического гормона. На основе изучения его физических свойств он предсказывает возможную химическую структуру нового вещества и высказывает предположение, что его роль в организме, вероятнее всего, не совпадает с предсказаниями физиолога. Затем он даёт ему новое название и переправляет химику-органику для подтверждения своих предположений о структуре соединения;