Страница:
Например, число 33B16 шестнадцатеричной системы счисления, в соответствии с (2.6) примет вид: 3 · 162 + 3 · 161 + В · 160 (В = 11).
При операциях с числами, представленными в различных системах счисления, необходимо указывать систему счисления числа, используя нижний индекс, например: 82710 – число 827 в десятичной системе; 11001110112 – число 1100111011 в двоичной системе; 14738 – число 1473 в восьмеричной системе; 33B16 – число 33В в шестнадцатеричной системе счисления.
Преобразование чисел, представленных в двоичной, восьмеричной и шестнадцатеричной системах счисления, в десятичную осуществляется достаточно просто. Для этого необходимо записать число в развернутой форме в соответствии с выражением (2.1) и вычислить его значение. Например:
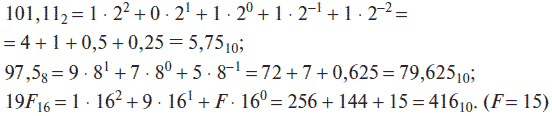Преобразование чисел, представленных в десятичной системе счисления, в двоичную, восьмеричную и шестнадцатеричную системы счисления – более сложная процедура, которая может осуществляться различными способами: деления, умножения, вычитания и т. д. При этом необходимо учитывать, что способы перевода целых десятичных чисел и правильных дробей будут различаться. Для перевода целого десятичного числа, например 5310, в двоичную систему можно использовать способ деления, а десятичной правильной дроби, например 0,7510, в двоичную систему – способ умножения. Результаты действий отобразим в соответствующих табл. 2.1 и 2.2.
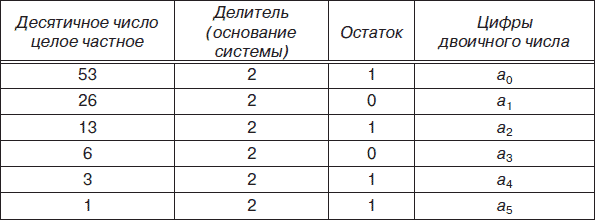Таким образом, 5310 = 1101012.
Таким образом, 0,7510 = 0,112.
Перевод чисел из одной системы счисления в другую достаточно просто реализуется с помощью компьютерных программ Калькулятор и MS Excel. Однако следует заметить, что данные программы осуществляют перевод только целых чисел.
Преобразуем число AF16 с помощью компьютерного калькулятора в двоичную, восьмеричную и десятичную системы счисления. Запустим программу Калькулятор с помощью команды: [Кнопка Пуск – Программы – Стандартные – Калькулятор]. После запуска программ выполним команду: [Вид – Инженерный]. У калькулятора имеется четыре опционные кнопки, расположенные слева вверху под индикатором вывода результата вычислений. При активизации кнопки Hex осуществляется преобразование числа, отображаемого в поле ввода, и результата вычислений калькулятора в шестнадцатеричную систему счисления, Dec – в десятичную, Oct – в восьмеричную, Bin – в двоичную систему счисления. Активизируем кнопку Hex и введем число АF16. Последовательно переключая кнопки Bin, Oct и Dec, получим следующие результаты: АF16 = 101011112 = 2578 = 17510. На рис. 2.5 показан результат преобразования числа AF16 в число 2578.
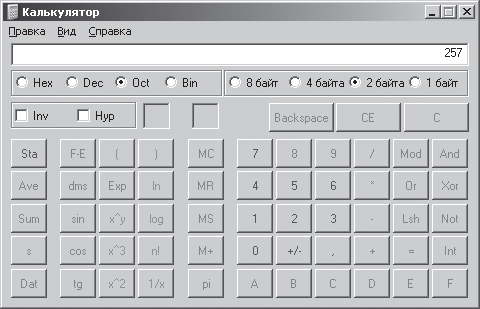Рис. 2.5. Программа «Калькулятор»
Последовательность действий при преобразовании шестнадцатеричного числа AF16 в двоичную, восьмеричную и десятичную системы счисления с помощью программы MS Excel аналогична преобразованию числа 1997 в римскую систему счисления, но здесь необходимо учесть, что вместо функции «Римское» необходимо использовать функции «ШЕСТН.В.ДВ», «ШЕСТН.В.ВОСЬМ», «ШЕСТН.В.ДЕС» категории «Инженерные» (см. рис. 2.2).
2.2. Арифметические операции над числами, представленными в различных системах счисления
2.3. Представление чисел в компьютере
Упражнения для самостоятельного выполнения
Глава 3
3.1. Кодирование текстовой информации
При операциях с числами, представленными в различных системах счисления, необходимо указывать систему счисления числа, используя нижний индекс, например: 82710 – число 827 в десятичной системе; 11001110112 – число 1100111011 в двоичной системе; 14738 – число 1473 в восьмеричной системе; 33B16 – число 33В в шестнадцатеричной системе счисления.
Преобразование чисел, представленных в двоичной, восьмеричной и шестнадцатеричной системах счисления, в десятичную осуществляется достаточно просто. Для этого необходимо записать число в развернутой форме в соответствии с выражением (2.1) и вычислить его значение. Например:
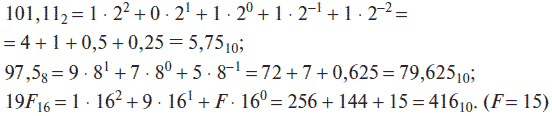
Таблица 2.1
Таблица 2.2
Перевод чисел из одной системы счисления в другую достаточно просто реализуется с помощью компьютерных программ Калькулятор и MS Excel. Однако следует заметить, что данные программы осуществляют перевод только целых чисел.
Преобразуем число AF16 с помощью компьютерного калькулятора в двоичную, восьмеричную и десятичную системы счисления. Запустим программу Калькулятор с помощью команды: [Кнопка Пуск – Программы – Стандартные – Калькулятор]. После запуска программ выполним команду: [Вид – Инженерный]. У калькулятора имеется четыре опционные кнопки, расположенные слева вверху под индикатором вывода результата вычислений. При активизации кнопки Hex осуществляется преобразование числа, отображаемого в поле ввода, и результата вычислений калькулятора в шестнадцатеричную систему счисления, Dec – в десятичную, Oct – в восьмеричную, Bin – в двоичную систему счисления. Активизируем кнопку Hex и введем число АF16. Последовательно переключая кнопки Bin, Oct и Dec, получим следующие результаты: АF16 = 101011112 = 2578 = 17510. На рис. 2.5 показан результат преобразования числа AF16 в число 2578.
Последовательность действий при преобразовании шестнадцатеричного числа AF16 в двоичную, восьмеричную и десятичную системы счисления с помощью программы MS Excel аналогична преобразованию числа 1997 в римскую систему счисления, но здесь необходимо учесть, что вместо функции «Римское» необходимо использовать функции «ШЕСТН.В.ДВ», «ШЕСТН.В.ВОСЬМ», «ШЕСТН.В.ДЕС» категории «Инженерные» (см. рис. 2.2).
2.2. Арифметические операции над числами, представленными в различных системах счисления
Арифметические операции во всех позиционных системах счисления выполняются по одним и тем же правилам. Для проведения арифметических операций над числами, представленными в различных системах счисления, необходимо предварительно преобразовать их в одну систему счисления и учесть то, что перенос в следующий разряд при операции сложения и заем из старшего разряда при операции вычитания определяется величиной основания системы счисления.
Арифметические операции в двоичной системе счисления основаны на таблицах сложения, вычитания и умножения одноразрядных двоичных чисел.
При сложении двух единиц происходит переполнение разряда и производится перенос единицы в старший разряд, при вычитании 0–1 производится заем из старшего разряда, в таблице «Вычитание» этот заем обозначен 1 с чертой над цифрой.
Ниже приведены примеры выполнения арифметических операций над числами, представленными в различных системах счисления:
Арифметические операции над целыми числами, представленными в различных системах счисления, достаточно просто реализуются с помощью программ Калькулятор и MS Excel.
Арифметические операции в двоичной системе счисления основаны на таблицах сложения, вычитания и умножения одноразрядных двоичных чисел.
При сложении двух единиц происходит переполнение разряда и производится перенос единицы в старший разряд, при вычитании 0–1 производится заем из старшего разряда, в таблице «Вычитание» этот заем обозначен 1 с чертой над цифрой.
2.3. Представление чисел в компьютере
Числовые данные обрабатываются в компьютере в двоичной системе счисления. Числа хранятся в памяти компьютера в двоичном коде, т. е. в виде последовательности нулей и единиц, и могут быть представлены в формате с фиксированной или плавающей запятой.
Целые числа хранятся в памяти в формате с фиксированной запятой. При таком формате представления чисел для хранения целых неотрицательных чисел отводится регистр памяти, состоящий из восьми ячеек памяти (8 бит). Каждому разряду ячейки памяти соответствует всегда один и тот же разряд числа, а запятая находится справа после младшего разряда и вне разрядной сетки. Например, число 110011012 будет храниться в регистре памяти следующим образом:
Максимальное значение целого неотрицательного числа, которое может храниться в регистре в формате с фиксированной запятой, можно определить из формулы: 2n – 1, где п – число разрядов числа. Максимальное число при этом будет равно 28 – 1 = 25510 = 111111112и минимальное 010 = 000000002. Таким образом, диапазон изменения целых неотрицательных чисел будет находиться в пределах от 0 до 25510.
В отличие от десятичной системы в двоичной системе счисления при компьютерном представлении двоичного числа отсутствуют символы, обозначающие знак числа: положительный (+) или отрицательный (-), поэтому для представления целых чисел со знаком в двоичной системе используются два формата представления числа: формат значения числа со знаком и формат дополнительного кода. В первом случае для хранения целых чисел со знаком отводится два регистра памяти (16 бит), причем старший разряд (крайний слева) используется под знак числа: если число положительное, то в знаковый разряд записывается 0, если число отрицательное, то – 1. Например, число 53610 = 00000010000110002 будет представлено в регистрах памяти в следующем виде:
а отрицательное число -53610 = 10000010000110002 в виде:
Максимальное положительное число или минимальное отрицательное в формате значения числа со знаком (с учетом представления одного разряда под знак) равно 2n-1 – 1 = 216-1 – 1 = 215 – 1 = 3276710 = 1111111111111112 и диапазон чисел будет находиться в пределах от -3276710 до 32767.
Наиболее часто для представления целых чисел со знаком в двоичной системе применяется формат дополнительного кода, который позволяет заменить арифметическую операцию вычитания в компьютере операцией сложения, что существенно упрощает структуру микропроцессора и увеличивает его быстродействие.
Для представления целых отрицательных чисел в таком формате используется дополнительный код, который представляет собой дополнение модуля отрицательного числа до нуля. Перевод целого отрицательного числа в дополнительный код осуществляется с помощью следующих операций:
1) модуль числа записать прямым кодом в п (п = 16) двоичных разрядах;
2) получить обратный код числа (инвертировать все разряды числа, т. е. все единицы заменить на нули, а нули – на единицы);
3) к полученному обратному коду прибавить единицу к младшему разряду.
Например, для числа -53610 в таком формате модуль будет равен 00000010000110002, обратный код – 1111110111100111, а дополнительный код – 1111110111101000. Проверим полученное значение дополнительного кода с помощью калькулятора. Для этого введем значение модуля числа -53610, т. е. число 53610, и с помощью опционной кнопки Bin преобразуем это число, представленное в десятичной системе счисления, в двоичную систему, предварительно установив опционную кнопку 2 байта. Нажав кнопку Not калькулятора, получим обратный код числа, а прибавив к обратному коду двоичную единицу, – дополнительный код. Окончательный результат получим в поле окна программы Калькулятор (рис. 2.6). Можно поступить еще проще: набрав на калькуляторе число -53610 и активизировав кнопку Bin, получить дополнительной код этого числа в двоичной системе счисления.
Рис. 2.6. Результат получения дополнительного кода
Необходимо помнить, что дополнительный код положительного числа – само число.
Для хранения целых чисел со знаком помимо 16-разрядного компьютерного представления, когда используются два регистра памяти (такой формат числа называется также форматом коротких целых чисел со знаком), применяются форматы средних и длинных целых чисел со знаком. Для представления чисел в формате средних чисел используется четыре регистра (4 х 8 = 32 бит), а для представления чисел в формате длинных чисел – восемь регистров (8 х 8 = 64 бита). Диапазоны значений для формата средних и длинных чисел будут соответственно равны: -(231 – 1) … + 231 – 1 и -(263-1) … + 263 – 1.
Компьютерное представление чисел в формате с фиксированной запятой имеет свои преимущества и недостатки. К преимуществам относятся простота представления чисел и алгоритмов реализации арифметических операций, к недостаткам – конечный диапазон представления чисел, который может быть недостаточным для решения многих задач практического характера (математических, экономических, физических и т. д.).
Вещественные числа (конечные и бесконечные десятичные дроби) обрабатываются и хранятся в компьютере в формате с плавающей запятой. При таком формате представления числа положение запятой в записи может изменяться. Любое вещественное число Къ формате с плавающей запятой может быть представлено в виде:
где А – мантисса числа; h – основание системы счисления; р – порядок числа.
Выражение (2.7) для десятичной системы счисления примет вид:
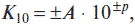для двоичной —
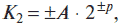для восьмеричной —
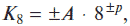для шестнадцатеричной —
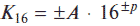и т. д.
Такая форма представления числа также называется нормальной. С изменением порядка запятая в числе смещается, т. е. как бы плавает влево или вправо. Поэтому нормальную форму представления чисел называют формой с плавающей запятой. Десятичное число 15,5, например, в формате с плавающей запятой может быть представлено в виде: 0,155 · 102; 1,55 · 101; 15,5 · 100; 155,0 · 10-1; 1550,0 · 10-2 и т. д. Эта форма записи десятичного числа 15,5 с плавающей запятой не используется при написании компьютерных программ и вводе их в компьютер (устройства ввода компьютеров воспринимают только линейную запись данных). Исходя из этого выражение (2.7) для представления десятичных чисел и ввода их в компьютер преобразовывают к виду
где Р – порядок числа,
т. е. вместо основания системы счисления 10 пишут букву Е, вместо запятой – точку, и знак умножения не ставится. Таким образом, число 15,5 в формате с плавающей запятой и линейной записи (компьютерное представление) будет записано в виде: 0.155Е2; 1.55Е1; 15.5Е0; 155.0Е-1; 1550.0Е-2 и т.д.
Независимо от системы счисления любое число в форме с плавающей запятой может быть представлено бесконечным множеством чисел. Такая форма записи называется ненормализованной. Для однозначного представления чисел с плавающей запятой используют нормализованную форму записи числа, при которой мантисса числа должна отвечать условию
где |А| — абсолютное значение мантиссы числа.
Условие (2.9) означает, что мантисса должна быть правильной дробью и иметь после запятой цифру, отличную от нуля, или, другими словами, если после запятой в мантиссе стоит не нуль, то число называется нормализованным. Так, число 15,5 в нормализованном виде (нормализованная мантисса) в форме с плавающей запятой будет выглядеть следующим образом: 0,155 · 102, т. е. нормализованная мантисса будет A = 0,155 и порядок Р = 2, или в компьютерном представлении числа 0.155Е2.
Числа в форме с плавающей запятой имеют фиксированный формат и занимают в памяти компьютера четыре (32 бит) или восемь байт (64 бит). Если число занимает в памяти компьютера 32 разряда, то это число обычной точности, если 64 разряда, то это число двойной точности. При записи числа с плавающей запятой выделяются разряды для хранения знака мантиссы, знака порядка, мантиссы и порядка. Количество разрядов, которое отводится под порядок числа, определяет диапазон изменения чисел, а количество разрядов, отведенных для хранения мантиссы, – точность, с которой задается число.
При выполнении арифметических операций (сложение и вычитание) над числами, представленными в формате с плавающей запятой, реализуется следующий порядок действий (алгоритм) :
1) производится выравнивание порядков чисел, над которыми совершаются арифметические операции (порядок меньшего по модулю числа увеличивается до величины порядка большего по модулю числа, мантисса при этом уменьшается в такое же количество раз);
2) выполняются арифметические операции над мантиссами чисел;
3) производится нормализация полученного результата.
Поясним сказанное выше на примерах.
Решение.
Проведем выравнивание порядков и сложение мантисс 0,05 · 103 + 0,8 · 103 = 0,85 · 103. Полученная мантисса 0,85 является нормализованной, так как удовлетворяет условию (2.9).
Решение.
Проведем выравнивание порядков и сложение мантисс: 0,01 · 23 + 0,1 · 23 = 0,11 · 23. Полученная мантисса 0,11 является нормализованной, так как удовлетворяет условию (2.9).
Целые числа хранятся в памяти в формате с фиксированной запятой. При таком формате представления чисел для хранения целых неотрицательных чисел отводится регистр памяти, состоящий из восьми ячеек памяти (8 бит). Каждому разряду ячейки памяти соответствует всегда один и тот же разряд числа, а запятая находится справа после младшего разряда и вне разрядной сетки. Например, число 110011012 будет храниться в регистре памяти следующим образом:
В отличие от десятичной системы в двоичной системе счисления при компьютерном представлении двоичного числа отсутствуют символы, обозначающие знак числа: положительный (+) или отрицательный (-), поэтому для представления целых чисел со знаком в двоичной системе используются два формата представления числа: формат значения числа со знаком и формат дополнительного кода. В первом случае для хранения целых чисел со знаком отводится два регистра памяти (16 бит), причем старший разряд (крайний слева) используется под знак числа: если число положительное, то в знаковый разряд записывается 0, если число отрицательное, то – 1. Например, число 53610 = 00000010000110002 будет представлено в регистрах памяти в следующем виде:
Наиболее часто для представления целых чисел со знаком в двоичной системе применяется формат дополнительного кода, который позволяет заменить арифметическую операцию вычитания в компьютере операцией сложения, что существенно упрощает структуру микропроцессора и увеличивает его быстродействие.
Для представления целых отрицательных чисел в таком формате используется дополнительный код, который представляет собой дополнение модуля отрицательного числа до нуля. Перевод целого отрицательного числа в дополнительный код осуществляется с помощью следующих операций:
1) модуль числа записать прямым кодом в п (п = 16) двоичных разрядах;
2) получить обратный код числа (инвертировать все разряды числа, т. е. все единицы заменить на нули, а нули – на единицы);
3) к полученному обратному коду прибавить единицу к младшему разряду.
Например, для числа -53610 в таком формате модуль будет равен 00000010000110002, обратный код – 1111110111100111, а дополнительный код – 1111110111101000. Проверим полученное значение дополнительного кода с помощью калькулятора. Для этого введем значение модуля числа -53610, т. е. число 53610, и с помощью опционной кнопки Bin преобразуем это число, представленное в десятичной системе счисления, в двоичную систему, предварительно установив опционную кнопку 2 байта. Нажав кнопку Not калькулятора, получим обратный код числа, а прибавив к обратному коду двоичную единицу, – дополнительный код. Окончательный результат получим в поле окна программы Калькулятор (рис. 2.6). Можно поступить еще проще: набрав на калькуляторе число -53610 и активизировав кнопку Bin, получить дополнительной код этого числа в двоичной системе счисления.
Необходимо помнить, что дополнительный код положительного числа – само число.
Для хранения целых чисел со знаком помимо 16-разрядного компьютерного представления, когда используются два регистра памяти (такой формат числа называется также форматом коротких целых чисел со знаком), применяются форматы средних и длинных целых чисел со знаком. Для представления чисел в формате средних чисел используется четыре регистра (4 х 8 = 32 бит), а для представления чисел в формате длинных чисел – восемь регистров (8 х 8 = 64 бита). Диапазоны значений для формата средних и длинных чисел будут соответственно равны: -(231 – 1) … + 231 – 1 и -(263-1) … + 263 – 1.
Компьютерное представление чисел в формате с фиксированной запятой имеет свои преимущества и недостатки. К преимуществам относятся простота представления чисел и алгоритмов реализации арифметических операций, к недостаткам – конечный диапазон представления чисел, который может быть недостаточным для решения многих задач практического характера (математических, экономических, физических и т. д.).
Вещественные числа (конечные и бесконечные десятичные дроби) обрабатываются и хранятся в компьютере в формате с плавающей запятой. При таком формате представления числа положение запятой в записи может изменяться. Любое вещественное число Къ формате с плавающей запятой может быть представлено в виде:
Выражение (2.7) для десятичной системы счисления примет вид:
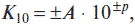
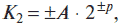
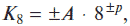
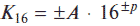
Такая форма представления числа также называется нормальной. С изменением порядка запятая в числе смещается, т. е. как бы плавает влево или вправо. Поэтому нормальную форму представления чисел называют формой с плавающей запятой. Десятичное число 15,5, например, в формате с плавающей запятой может быть представлено в виде: 0,155 · 102; 1,55 · 101; 15,5 · 100; 155,0 · 10-1; 1550,0 · 10-2 и т. д. Эта форма записи десятичного числа 15,5 с плавающей запятой не используется при написании компьютерных программ и вводе их в компьютер (устройства ввода компьютеров воспринимают только линейную запись данных). Исходя из этого выражение (2.7) для представления десятичных чисел и ввода их в компьютер преобразовывают к виду
т. е. вместо основания системы счисления 10 пишут букву Е, вместо запятой – точку, и знак умножения не ставится. Таким образом, число 15,5 в формате с плавающей запятой и линейной записи (компьютерное представление) будет записано в виде: 0.155Е2; 1.55Е1; 15.5Е0; 155.0Е-1; 1550.0Е-2 и т.д.
Независимо от системы счисления любое число в форме с плавающей запятой может быть представлено бесконечным множеством чисел. Такая форма записи называется ненормализованной. Для однозначного представления чисел с плавающей запятой используют нормализованную форму записи числа, при которой мантисса числа должна отвечать условию
Условие (2.9) означает, что мантисса должна быть правильной дробью и иметь после запятой цифру, отличную от нуля, или, другими словами, если после запятой в мантиссе стоит не нуль, то число называется нормализованным. Так, число 15,5 в нормализованном виде (нормализованная мантисса) в форме с плавающей запятой будет выглядеть следующим образом: 0,155 · 102, т. е. нормализованная мантисса будет A = 0,155 и порядок Р = 2, или в компьютерном представлении числа 0.155Е2.
Числа в форме с плавающей запятой имеют фиксированный формат и занимают в памяти компьютера четыре (32 бит) или восемь байт (64 бит). Если число занимает в памяти компьютера 32 разряда, то это число обычной точности, если 64 разряда, то это число двойной точности. При записи числа с плавающей запятой выделяются разряды для хранения знака мантиссы, знака порядка, мантиссы и порядка. Количество разрядов, которое отводится под порядок числа, определяет диапазон изменения чисел, а количество разрядов, отведенных для хранения мантиссы, – точность, с которой задается число.
При выполнении арифметических операций (сложение и вычитание) над числами, представленными в формате с плавающей запятой, реализуется следующий порядок действий (алгоритм) :
1) производится выравнивание порядков чисел, над которыми совершаются арифметические операции (порядок меньшего по модулю числа увеличивается до величины порядка большего по модулю числа, мантисса при этом уменьшается в такое же количество раз);
2) выполняются арифметические операции над мантиссами чисел;
3) производится нормализация полученного результата.
Поясним сказанное выше на примерах.
Пример 1
Произведем сложение двух чисел 0,5 · 102 и 0,8 · 103 в формате с плавающей запятой.Решение.
Проведем выравнивание порядков и сложение мантисс 0,05 · 103 + 0,8 · 103 = 0,85 · 103. Полученная мантисса 0,85 является нормализованной, так как удовлетворяет условию (2.9).
Пример 2
Произведем сложение двух чисел 0,1 · 22 и 0,1 · 23 в формате с плавающей запятой.Решение.
Проведем выравнивание порядков и сложение мантисс: 0,01 · 23 + 0,1 · 23 = 0,11 · 23. Полученная мантисса 0,11 является нормализованной, так как удовлетворяет условию (2.9).
Упражнения для самостоятельного выполнения
1. Перевести числа, записанные в римской системе счисления, в числа десятичной системы счисления:
a) XL; б) СХХХ; в) CDXXVIII; г) CMLXXVI; д) MCMLII; е) MMV.
2. Используя программу MS Excel, реализовать автоматический перевод чисел из десятичной системы счисления в римскую.
3. Создать и заполнить все ячейки следующей таблицы, используя табличный процессор MS Excel.
4. Используя формулы (2.1) —(2.6) записать в развернутом виде числа:
a) K10 = 12355; б) К8 = 321476; в) К2 = 101110011;
г) K16 = 143D5; е) K10 = 769,314; ж) К8 = 0,1734;
з) K2 = 100101,011; и) K16 = ЗА1,5С1.
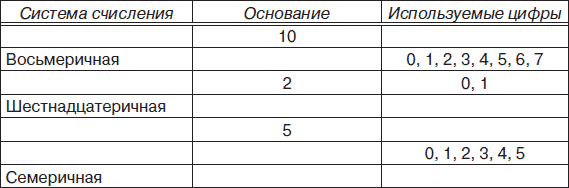
5. Заполнить все строки следующей таблицы.
6. Правильно ли записаны числа в соответствующих системах счисления:
а) К2 = 100200; б) K16 = CD1; в) K10 = F,345; г) K8 = -122453?
7. Какие из чисел 3D716, 100101112, 3758 и 134245 являются наибольшим и наименьшим?
8. Перевести числа 23410, 100010, 30,7510, 9,810 в двоичную, восьмеричную и шестнадцатеричную системы счисления.
9. Перевести числа 100012, 1010,012, 1111112, 1001110,0112 в десятичную, восьмеричную и шестнадцатеричную системы счисления.
10. Перевести числа 2716, D,1B16, 4116, 25E,816 в двоичную, восьмеричную и десятичную системы счисления.
11. Перевести числа 2378, 10508, 33,758, 0,7568 в двоичную, десятичную и шестнадцатеричную системы счисления.
12. Какое число следует и предшествует каждому из приведенных ниже чисел:
а) 1213; б) 9А16; в) 10011012; г) 7358 д) 23410; е) 1356; ж) 2589?
13. Выполнить арифметические действия:
а) 468 + 1358; г) 2128 – 1658; ж) 128 · 1378;
б) 10101112 + 1012; д) 10110012 – 101112; з) 110121012;
в) 1АЕ16 + 32В16; е) 10C16 – D16; и) 3D16 · 1A16.
14. Создать и заполнить в MS Excel таблицу, записав десятичные числа в заданном компьютерном представлении:
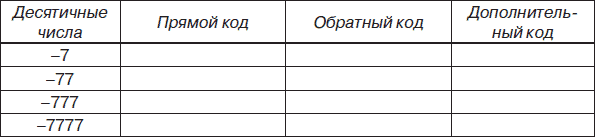
15. Создать и заполнить в MS Excel таблицу, записав десятичные числа в прямом, обратном и дополнительных кодах в 16-разрядном компьютерном представлении:
16. Представить заданные числа в форме с плавающей запятой и нормализованном виде:
а) 234,67810; б) 102410; в) 3576910; г) 0,12610;
д) 1112; е) 478; ж) 1DC16.
17. Произвести сложение, вычитание и умножение следующих чисел в формате с плавающей запятой:
а) 0,537 · 102 и 0,25 · 101; б) 0,1 · 21 и 0,1 · 2-2.
a) XL; б) СХХХ; в) CDXXVIII; г) CMLXXVI; д) MCMLII; е) MMV.
2. Используя программу MS Excel, реализовать автоматический перевод чисел из десятичной системы счисления в римскую.
3. Создать и заполнить все ячейки следующей таблицы, используя табличный процессор MS Excel.
a) K10 = 12355; б) К8 = 321476; в) К2 = 101110011;
г) K16 = 143D5; е) K10 = 769,314; ж) К8 = 0,1734;
з) K2 = 100101,011; и) K16 = ЗА1,5С1.
5. Заполнить все строки следующей таблицы.
а) К2 = 100200; б) K16 = CD1; в) K10 = F,345; г) K8 = -122453?
7. Какие из чисел 3D716, 100101112, 3758 и 134245 являются наибольшим и наименьшим?
8. Перевести числа 23410, 100010, 30,7510, 9,810 в двоичную, восьмеричную и шестнадцатеричную системы счисления.
9. Перевести числа 100012, 1010,012, 1111112, 1001110,0112 в десятичную, восьмеричную и шестнадцатеричную системы счисления.
10. Перевести числа 2716, D,1B16, 4116, 25E,816 в двоичную, восьмеричную и десятичную системы счисления.
11. Перевести числа 2378, 10508, 33,758, 0,7568 в двоичную, десятичную и шестнадцатеричную системы счисления.
12. Какое число следует и предшествует каждому из приведенных ниже чисел:
а) 1213; б) 9А16; в) 10011012; г) 7358 д) 23410; е) 1356; ж) 2589?
13. Выполнить арифметические действия:
а) 468 + 1358; г) 2128 – 1658; ж) 128 · 1378;
б) 10101112 + 1012; д) 10110012 – 101112; з) 110121012;
в) 1АЕ16 + 32В16; е) 10C16 – D16; и) 3D16 · 1A16.
14. Создать и заполнить в MS Excel таблицу, записав десятичные числа в заданном компьютерном представлении:
а) 234,67810; б) 102410; в) 3576910; г) 0,12610;
д) 1112; е) 478; ж) 1DC16.
17. Произвести сложение, вычитание и умножение следующих чисел в формате с плавающей запятой:
а) 0,537 · 102 и 0,25 · 101; б) 0,1 · 21 и 0,1 · 2-2.
Глава 3
Кодирование текстовой и графической информации
3.1. Кодирование текстовой информации
При вводе текстовой информации в компьютер символы (буквы, цифры, знаки) кодируются с помощью различных кодовых систем, которые состоят из набора кодовых таблиц, размещенных на соответствующих страницах стандартов для кодирования текстовой информации. В таких таблицах каждому символу присваивается определенный числовой код в шестнадцатеричной или десятичной системе счисления, т. е. кодовые таблицы отражают соответствие между изображениями символов и числовыми кодами и предназначены для кодирования и декодирования текстовой информации. При вводе текстовой информации с помощью клавиатуры компьютера каждый вводимый символ подвергается кодированию, т. е. преобразуется в числовой код, при выводе текстовой информации на устройство вывода компьютера (дисплей, принтер или плоттер) по числовому коду символа строится его изображение. Присвоение символу определенного числового кода является результатом соглашения между соответствующими организациями разных стран. В настоящее время нет единой универсальной кодовой таблицы, удовлетворяющей буквам национальных алфавитов разных стран.
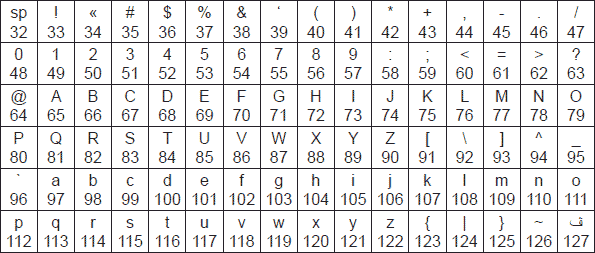
Современные кодовые таблицы включают в себя международную и национальную части, т. е. содержат буквы латинского и национального алфавитов, цифры, знаки арифметических операций и препинания, математические и управляющие символы, символы псевдографики. Международная часть кодовой таблицы, базирующаяся на стандарте ASCII (American Standard Code for Information Interchange), кодирует первую половину символов кодовой таблицы с числовыми кодами от 0 до 7F16, или в десятичной системе счисления от 0 до 127. При этом коды от 0 до 2016 (0 ÷ 3210) отведены функциональным клавишам (F1, F2, F3 и т. д.) клавиатуры персонального компьютера. На рис. 3.1 приведена международная часть кодовых таблиц, основанная на стандарте ASCII. Ячейки таблиц пронумерованы соответственно в десятичной и шестнадцатеричной системе счисления.
а)
б)
Рис 3.1. Международная часть кодовой таблицы (стандарт ASCII) с номерами ячеек, представленных в десятичной (а) и шестнадцатеричной (б) системе счисления
Национальная часть кодовых таблиц содержит коды национальных алфавитов, которую называют также таблицей наборов символов (charset).
В настоящее время для поддержки букв русского алфавита (кириллицы) существует несколько кодовых таблиц (кодировок), которые используются различными операционными системами, что является существенным недостатком и в ряде случаев приводит к проблемам, связанным с операциями декодирования числовых значений символов. В табл. 3.1 приведены названия кодовых страниц (стандартов), на которых размещены кодовые таблицы (кодировки) кириллицы.
Одним из первых стандартов кодирования кириллицы на компьютерах был стандарт КОИ8-Р. Национальная часть кодовой таблицы этого стандарта приведена на рис. 3.2.
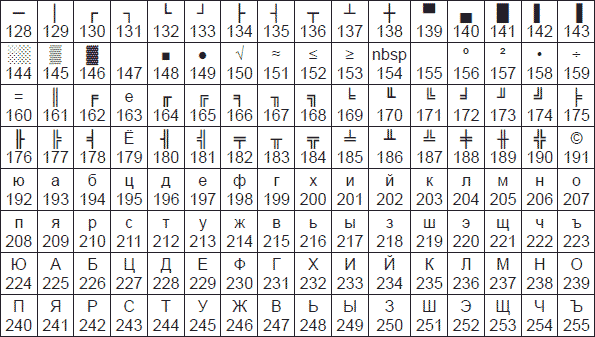Рис. 3.2. Национальная часть кодовой таблицы стандарта КОИ8-Р
В настоящее время применяется и кодовая таблица, размещенная на странице СР866 стандарта кодирования текстовой информации, которая используется в операционной системе MS DOS или сеансе работы MS DOS для кодирования кириллицы (рис. 3.3, а).
а)
б)
Рис. 3.3. Национальная часть кодовой таблицы, размещенная на странице СР866 (а) и на странице СР1251 (б) стандарта кодирования текстовой информации
В настоящее время для кодирования кириллицы наибольшее распространение получила кодовая таблица, размещенная на странице СР1251 соответствующего стандарта, которая используется в операционных системах семейства Windows фирмы Microsoft (рис. 3.2, б). Во всех представленных кодовых таблицах, кроме таблицы стандарта Unicode, для кодирования одного символа отводится 8 двоичных разрядов (8 бит).
В конце прошлого века появился новый международный стандарт Unicode, в котором один символ представляется двухбайтовым двоичным кодом. Применение этого стандарта – продолжение разработки универсального международного стандарта, позволяющего решить проблему совместимости национальных кодировок символов. С помощью данного стандарта можно закодировать 216 = 65536 различных символов. На рис. 3.4 приведена кодовая таблица 0400 (русский алфавит) стандарта Unicode.
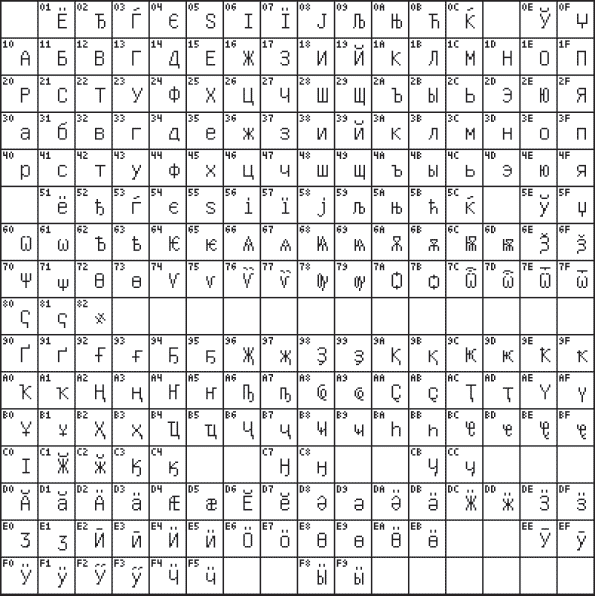Рис. 3.4. Кодовая таблица 0400 стандарта Unicode
Поясним сказанное, касающееся кодирования текстовой информации, на примере.
Последовательности шестнадцатеричного и двоичного кода слова «Компьютер» на основе кодировочной таблицы СР1251 (см. рис. 3.3, б) будут выглядеть следующим образом:
Данная кодовая последовательность в кодировках СР866 и КОИ8-Р приведет к отображению следующих символов:
Для преобразования русскоязычных текстовых документов из одного стандарта кодирования текстовой информации в другой используются специальные программы – конверторы. Конверторы обычно встраиваются в другие программы. Примером может служить программа браузер – Internet Explorer (IE), которая имеет встроенный конвертор. Программа браузер – это специальная программа для просмотра содержимого Web-страниц в глобальной компьютерной сети Интернет. Воспользуемся этой программой для подтверждения полученного в примере 3.1 результата отображения символов. Для этого выполним следующие действия.
1. Запустим программу Блокнот (NotePad). Программа Блокнот в операционной системе Windows ХР запускается с помощью команды: [Кнопка Пуск – Программы – Стандартные – Блокнот]. В открывшемся окне программы Блокнот напечатаем слово «Компьютер» с использованием синтаксиса языка разметки гипертекстовых документов – HTML (Hyper Text Markup Language). Этот язык используется для создания документов в Интернете. Текст должен выглядеть следующим образом: <h1>Компыотер</h1>, где <h1> и </h1> теги (специальные конструкции) языка HTML для разметки заголовков. На рис. 3.5 представлен результат этих действий.
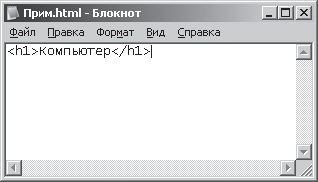Рис. 3.5. Отображение текста в окне Блокнот
Сохраним этот текст, выполнив команду: [Файл – Сохранить как…] в соответствующей папке компьютера, при сохранении текста файлу присвоим имя – Прим, с расширением файла. html.
2. Запустим программу Internet Explorer, выполнив команду: [Кнопка Пуск – Программы – Internet Explorer]. При запуске программы появится окно, представленное на рис. 3.6
Рис. 3.6. Окно доступа в автономный режим
Выберем и активизируем кнопку Автономно при этом не произойдет подключение компьютера к глобальной сети Интернет. Появится основное окно программы Microsoft Internet Explorer, представленное на рис. 3.7.
Рис. 3.7. Основное окно Microsoft Internet Explorer
Выполним следующую команду: [Файл – Открыть], появится окно (рис. 3.8), в котором необходимо указать имя файла и нажать кнопку ОК или нажать кнопку Обзор… и найти файл Прим.html.
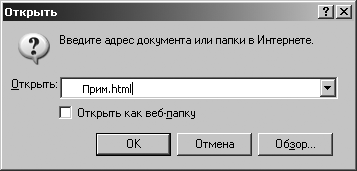Рис. 3.8. Окно «Открыть»
Основное окно программы Internet Explorer примет вид, показанный на рис. 3.9. В окне отобразится слово «Компьютер». Далее, используя верхнее меню программы Internet Explorer, выполним следующую команду: [Вид – Кодировка – Кириллица (DOS)]. После выполнения этой команды в окне программы Internet Ехplorer отобразятся символы, показанные на рис. 3.10. При выполнении команды: [Вид – Кодировка – Кириллица (KOI8-R) ] в окне программы Internet Explorer отобразятся символы, показанные на рис. 3.11.
Рис. 3.9. Символы, отображаемые при кодировке СР1251
Современные кодовые таблицы включают в себя международную и национальную части, т. е. содержат буквы латинского и национального алфавитов, цифры, знаки арифметических операций и препинания, математические и управляющие символы, символы псевдографики. Международная часть кодовой таблицы, базирующаяся на стандарте ASCII (American Standard Code for Information Interchange), кодирует первую половину символов кодовой таблицы с числовыми кодами от 0 до 7F16, или в десятичной системе счисления от 0 до 127. При этом коды от 0 до 2016 (0 ÷ 3210) отведены функциональным клавишам (F1, F2, F3 и т. д.) клавиатуры персонального компьютера. На рис. 3.1 приведена международная часть кодовых таблиц, основанная на стандарте ASCII. Ячейки таблиц пронумерованы соответственно в десятичной и шестнадцатеричной системе счисления.
а)
Национальная часть кодовых таблиц содержит коды национальных алфавитов, которую называют также таблицей наборов символов (charset).
В настоящее время для поддержки букв русского алфавита (кириллицы) существует несколько кодовых таблиц (кодировок), которые используются различными операционными системами, что является существенным недостатком и в ряде случаев приводит к проблемам, связанным с операциями декодирования числовых значений символов. В табл. 3.1 приведены названия кодовых страниц (стандартов), на которых размещены кодовые таблицы (кодировки) кириллицы.
Таблица 3.1
В настоящее время применяется и кодовая таблица, размещенная на странице СР866 стандарта кодирования текстовой информации, которая используется в операционной системе MS DOS или сеансе работы MS DOS для кодирования кириллицы (рис. 3.3, а).
а)
В настоящее время для кодирования кириллицы наибольшее распространение получила кодовая таблица, размещенная на странице СР1251 соответствующего стандарта, которая используется в операционных системах семейства Windows фирмы Microsoft (рис. 3.2, б). Во всех представленных кодовых таблицах, кроме таблицы стандарта Unicode, для кодирования одного символа отводится 8 двоичных разрядов (8 бит).
В конце прошлого века появился новый международный стандарт Unicode, в котором один символ представляется двухбайтовым двоичным кодом. Применение этого стандарта – продолжение разработки универсального международного стандарта, позволяющего решить проблему совместимости национальных кодировок символов. С помощью данного стандарта можно закодировать 216 = 65536 различных символов. На рис. 3.4 приведена кодовая таблица 0400 (русский алфавит) стандарта Unicode.
Поясним сказанное, касающееся кодирования текстовой информации, на примере.
Пример 3.1
Закодировать слово «Компьютер» в виде последовательности десятичных и шестнадцатеричных чисел, используя кодировку СР1251. Какие символы будут отображены в кодовых таблицах СР866 и КОИ8-Р при использовании полученного кода.Последовательности шестнадцатеричного и двоичного кода слова «Компьютер» на основе кодировочной таблицы СР1251 (см. рис. 3.3, б) будут выглядеть следующим образом:
1. Запустим программу Блокнот (NotePad). Программа Блокнот в операционной системе Windows ХР запускается с помощью команды: [Кнопка Пуск – Программы – Стандартные – Блокнот]. В открывшемся окне программы Блокнот напечатаем слово «Компьютер» с использованием синтаксиса языка разметки гипертекстовых документов – HTML (Hyper Text Markup Language). Этот язык используется для создания документов в Интернете. Текст должен выглядеть следующим образом: <h1>Компыотер</h1>, где <h1> и </h1> теги (специальные конструкции) языка HTML для разметки заголовков. На рис. 3.5 представлен результат этих действий.
Сохраним этот текст, выполнив команду: [Файл – Сохранить как…] в соответствующей папке компьютера, при сохранении текста файлу присвоим имя – Прим, с расширением файла. html.
2. Запустим программу Internet Explorer, выполнив команду: [Кнопка Пуск – Программы – Internet Explorer]. При запуске программы появится окно, представленное на рис. 3.6
Выберем и активизируем кнопку Автономно при этом не произойдет подключение компьютера к глобальной сети Интернет. Появится основное окно программы Microsoft Internet Explorer, представленное на рис. 3.7.
Выполним следующую команду: [Файл – Открыть], появится окно (рис. 3.8), в котором необходимо указать имя файла и нажать кнопку ОК или нажать кнопку Обзор… и найти файл Прим.html.
Основное окно программы Internet Explorer примет вид, показанный на рис. 3.9. В окне отобразится слово «Компьютер». Далее, используя верхнее меню программы Internet Explorer, выполним следующую команду: [Вид – Кодировка – Кириллица (DOS)]. После выполнения этой команды в окне программы Internet Ехplorer отобразятся символы, показанные на рис. 3.10. При выполнении команды: [Вид – Кодировка – Кириллица (KOI8-R) ] в окне программы Internet Explorer отобразятся символы, показанные на рис. 3.11.