

Таким образом, полученные с помощью программы Internet Explorer последовательности символов совпадают с последовательностями символов, полученных с помощью кодовых таблиц СР866 и КОИ8-Р в примере 3.1.
3.2. Кодирование графической информации
Графическая информация, представленная в виде рисунков, фотографий, слайдов, подвижных изображений (анимация, видео), схем, чертежей, может создаваться и редактироваться с помощью компьютера, при этом она соответствующим образом кодируется. В настоящее время существует достаточно большое количество прикладных программ для обработки графической информации, но все они реализуют три вида компьютерной графики: растровую, векторную и фрактальную.
Если более пристально рассмотреть графическое изображение на экране монитора компьютера, то можно увидеть большое количество разноцветных точек (пикселов – от англ. pixel, образованного от picture element – элемент изображения), которые, будучи собраны вместе, и образуют данное графическое изображение. Из этого можно сделать вывод: графическое изображение в компьютере определенным образом кодируется и должно быть представлено в виде графического файла. Файл является основной структурной единицей организации и хранения данных в компьютере и в данном случае должен содержать информацию о том, как представить этот набор точек на экране монитора.
Файлы, созданные на основе векторной графики, содержат информацию в виде математических зависимостей (математических функций, описывающих линейные зависимости) и соответствующих данных о том, как построить изображение объекта с помощью отрезков линий (векторов) при выводе его на экран монитора компьютера.
Файлы, созданные на основе растровой графики, предполагают хранение данных о каждой отдельной точке изображения. Для отображения растровой графики не требуется сложных математических расчетов, достаточно лишь получить данные о каждой точке изображения (ее координаты и цвет) и отобразить их на экране монитора компьютера.
В процессе кодирования изображения производится его пространственная дискретизация, т. е. изображение разбивается на отдельные точки и каждой точке задается код цвета (желтый, красный, синий и т. д.). Для кодирования каждой точки цветного графического изображения применяется принцип декомпозиции произвольного цвета на основные его составляющие, в качестве которых используют три основных цвета: красный (английское слово Red, обозначают буквой К), зеленый (Green, обозначают буквой G), синий (Blue, обозначают букой В). Любой цвет точки, воспринимаемый человеческим глазом, можно получить путем аддитивного (пропорционального) сложения (смешения) трех основных цветов – красного, зеленого и синего. Такая система кодирования называется цветовой системой RGB. Файлы графических изображений, в которых применяется цветовая система RGB, представляют каждую точку изображения в виде цветового триплета – трех числовых величин R, G и В, соответствующих интенсивностям красного, зеленого и синего цветов. Процесс кодирования графического изображения осуществляется с помощью различных технических средств (сканера, цифрового фотоаппарата, цифровой видеокамеры и т. д.); в результате получается растровое изображение. При воспроизведении цветных графических изображений на экране цветного монитора компьютера цвет каждой точки (пикселя) такого изображения получается путем смешения трех основных цветов R,G и B.
Качество растрового изображения определяется двумя основными параметрами – разрешением (количеством точек по горизонтали и вертикали) и используемой палитрой цветов (количеством задаваемых цветов для каждой точки изображения). Разрешение задается указанием числа точек по горизонтали и по вертикали, например 800 на 600 точек.
Между количеством цветов, задаваемых точке растрового изображения, и количеством информации, которое необходимо выделить для хранения цвета точки, существует зависимость, определяемая соотношением (формула Р. Хартли) :
 где I – количество информации; N – количество цветов, задаваемых точке.
где I – количество информации; N – количество цветов, задаваемых точке.
Количество информации, необходимое для хранения цвета точки, называют также глубиной цвета, или качеством цветопередачи.
Так, если количество цветов, задаваемых для точки изображения, N = 256, то количество информации необходимое для ее хранения (глубина цвета) в соответствии с формулой (3.1) будет равно I = 8 бит.
В компьютерах для отображения графической информации используются различные графические режимы работы монитора. Здесь необходимо отметить, что кроме графического режима работы монитора есть также текстовый режим, при котором экран монитора условно разбивается на 25 строк по 80 символов в строке. Эти графические режимы характеризуются разрешением экрана монитора и качеством цветопередачи (глубиной цвета). Для установки графического режима экрана монитора в операционной системе MS Windows ХР необходимо выполнить команду: [Кнопка Пуск – Настройка – Панель управления – Экран]. В появившемся диалоговом окне «Свойства: Экран» (рис. 3.12) необходимо выбрать вкладку «Параметры» и с помощью ползунка «Разрешение экрана» выбрать соответствующее разрешение экрана (800 на 600 точек, 1024 на 768 точек и т. д.). С помощью раскрывающегося списка «Качество цветопередачи» можно выбрать глубину цвета – «Самое высокое (32 бита)», «Среднее (16 бит)» и т. д., при этом количество цветов, задаваемых каждой точке изображения, будет соответственно равно 232 (4294967296), 216 (65536) и т. д.
 Рис. 3.12. Диалоговое окно «Свойства: Экран»
Рис. 3.12. Диалоговое окно «Свойства: Экран»
Для реализации каждого из графических режимов экрана монитора необходим определенный информационный объем видеопамяти компьютера. Необходимый информационный объем видеопамяти (V) определяется из соотношения
 где К – количество точек изображения на экране монитора (К = А · В); А – количество точек по горизонтали на экране монитора; В – количество точек по вертикали на экране монитора; I – количество информации (глубина цвета).
где К – количество точек изображения на экране монитора (К = А · В); А – количество точек по горизонтали на экране монитора; В – количество точек по вертикали на экране монитора; I – количество информации (глубина цвета).
Так, если экран монитора имеет разрешающую способность 1024 на 768 точек и палитру, состоящую из 65 536 цветов, то глубина цвета в соответствии с формулой (3.1) составит I = log265 538 = 16 бит, количество точек изображения будет равно: К = 1024 х 768 = 786432, и требуемый информационный объем видеопамяти в соответствии с (3.2) будет равен
V = 786432 · 16 бит = 12582912 бит = 1572864 байт = 1536 Кбайт = 1,5 Мбайт.
В заключение необходимо заметить, что кроме перечисленныхарактеристик важнейшими характеристиками монитора являются геометрические размеры его экрана и точки изображения. Геометрические размеры экрана задаются величиной диагонали монитора. Величина диагонали мониторов задается в дюймах (1 дюйм = 1" = 25,4 мм) и может принимать значения, равные: 14", 15", 17", 21" т. д. Современные технологии производства мониторов могут обеспечить размер точки изображения равный 0,22 мм.
Таким образом, для каждого монитора существует физически максимально возможная разрешающая способность экрана, определяемая величиной его диагонали и размером точки изображения.
Если более пристально рассмотреть графическое изображение на экране монитора компьютера, то можно увидеть большое количество разноцветных точек (пикселов – от англ. pixel, образованного от picture element – элемент изображения), которые, будучи собраны вместе, и образуют данное графическое изображение. Из этого можно сделать вывод: графическое изображение в компьютере определенным образом кодируется и должно быть представлено в виде графического файла. Файл является основной структурной единицей организации и хранения данных в компьютере и в данном случае должен содержать информацию о том, как представить этот набор точек на экране монитора.
Файлы, созданные на основе векторной графики, содержат информацию в виде математических зависимостей (математических функций, описывающих линейные зависимости) и соответствующих данных о том, как построить изображение объекта с помощью отрезков линий (векторов) при выводе его на экран монитора компьютера.
Файлы, созданные на основе растровой графики, предполагают хранение данных о каждой отдельной точке изображения. Для отображения растровой графики не требуется сложных математических расчетов, достаточно лишь получить данные о каждой точке изображения (ее координаты и цвет) и отобразить их на экране монитора компьютера.
В процессе кодирования изображения производится его пространственная дискретизация, т. е. изображение разбивается на отдельные точки и каждой точке задается код цвета (желтый, красный, синий и т. д.). Для кодирования каждой точки цветного графического изображения применяется принцип декомпозиции произвольного цвета на основные его составляющие, в качестве которых используют три основных цвета: красный (английское слово Red, обозначают буквой К), зеленый (Green, обозначают буквой G), синий (Blue, обозначают букой В). Любой цвет точки, воспринимаемый человеческим глазом, можно получить путем аддитивного (пропорционального) сложения (смешения) трех основных цветов – красного, зеленого и синего. Такая система кодирования называется цветовой системой RGB. Файлы графических изображений, в которых применяется цветовая система RGB, представляют каждую точку изображения в виде цветового триплета – трех числовых величин R, G и В, соответствующих интенсивностям красного, зеленого и синего цветов. Процесс кодирования графического изображения осуществляется с помощью различных технических средств (сканера, цифрового фотоаппарата, цифровой видеокамеры и т. д.); в результате получается растровое изображение. При воспроизведении цветных графических изображений на экране цветного монитора компьютера цвет каждой точки (пикселя) такого изображения получается путем смешения трех основных цветов R,G и B.
Качество растрового изображения определяется двумя основными параметрами – разрешением (количеством точек по горизонтали и вертикали) и используемой палитрой цветов (количеством задаваемых цветов для каждой точки изображения). Разрешение задается указанием числа точек по горизонтали и по вертикали, например 800 на 600 точек.
Между количеством цветов, задаваемых точке растрового изображения, и количеством информации, которое необходимо выделить для хранения цвета точки, существует зависимость, определяемая соотношением (формула Р. Хартли) :

Количество информации, необходимое для хранения цвета точки, называют также глубиной цвета, или качеством цветопередачи.
Так, если количество цветов, задаваемых для точки изображения, N = 256, то количество информации необходимое для ее хранения (глубина цвета) в соответствии с формулой (3.1) будет равно I = 8 бит.
В компьютерах для отображения графической информации используются различные графические режимы работы монитора. Здесь необходимо отметить, что кроме графического режима работы монитора есть также текстовый режим, при котором экран монитора условно разбивается на 25 строк по 80 символов в строке. Эти графические режимы характеризуются разрешением экрана монитора и качеством цветопередачи (глубиной цвета). Для установки графического режима экрана монитора в операционной системе MS Windows ХР необходимо выполнить команду: [Кнопка Пуск – Настройка – Панель управления – Экран]. В появившемся диалоговом окне «Свойства: Экран» (рис. 3.12) необходимо выбрать вкладку «Параметры» и с помощью ползунка «Разрешение экрана» выбрать соответствующее разрешение экрана (800 на 600 точек, 1024 на 768 точек и т. д.). С помощью раскрывающегося списка «Качество цветопередачи» можно выбрать глубину цвета – «Самое высокое (32 бита)», «Среднее (16 бит)» и т. д., при этом количество цветов, задаваемых каждой точке изображения, будет соответственно равно 232 (4294967296), 216 (65536) и т. д.

Для реализации каждого из графических режимов экрана монитора необходим определенный информационный объем видеопамяти компьютера. Необходимый информационный объем видеопамяти (V) определяется из соотношения

Так, если экран монитора имеет разрешающую способность 1024 на 768 точек и палитру, состоящую из 65 536 цветов, то глубина цвета в соответствии с формулой (3.1) составит I = log265 538 = 16 бит, количество точек изображения будет равно: К = 1024 х 768 = 786432, и требуемый информационный объем видеопамяти в соответствии с (3.2) будет равен
V = 786432 · 16 бит = 12582912 бит = 1572864 байт = 1536 Кбайт = 1,5 Мбайт.
В заключение необходимо заметить, что кроме перечисленныхарактеристик важнейшими характеристиками монитора являются геометрические размеры его экрана и точки изображения. Геометрические размеры экрана задаются величиной диагонали монитора. Величина диагонали мониторов задается в дюймах (1 дюйм = 1" = 25,4 мм) и может принимать значения, равные: 14", 15", 17", 21" т. д. Современные технологии производства мониторов могут обеспечить размер точки изображения равный 0,22 мм.
Таким образом, для каждого монитора существует физически максимально возможная разрешающая способность экрана, определяемая величиной его диагонали и размером точки изображения.
Упражнения для самостоятельного выполнения
1. С помощью программы MS Excel преобразовать кодовые таблицы ASCII, СР866, СР1251, КОИ8-Р к таблицам вида: в ячейки первого столбца таблиц записать в алфавитном порядке заглавные, а затем строчные буквы латиницы и кириллицы, в ячейки второго столбца – соответствующие буквам коды в десятичной системе счисления, в ячейки третьего столбца – соответствующие буквам коды в шестнадцатеричной системе счисления. Значения кодов необходимо выбрать из соответствующих кодовых таблиц.
2. Закодировать и записать в виде последовательности чисел в десятичной и шестнадцатеричной системе счисления следующие слова:
a) Internet Explorer, б) Microsoft Office; в) CorelDRAW.
Кодирование произвести с помощью модернизированной кодировочной таблицы ASCII, полученной в предыдущем упражнении.
3. Декодировать с помощью модернизированной кодировочной таблицы КОИ8-Р последовательности чисел записанных в шестнадцатеричной системе счисления:
а) FC CB DA C9 D3 D4 C5 CE C3 C9 D1;
б) EB CF CE C6 CF D2 CD C9 DA CD;
в) FC CB D3 D0 D2 C5 D3 C9 CF CE C9 DA CD.
4. Как будет выглядеть слово «Кибернетика», записанное в кодировке СР1251, при использовании кодировок СР866 и КОИ8-Р? Проверить полученные результаты с помощью программы Internet Explorer.
5. Используя кодовую таблицу, приведенную на рис. 3.1а, декодировать следующие кодовые последовательности, записанные в двоичной системе счисления:
а) 01010111 01101111 01110010 01100100;
б) 01000101 01111000 01100011 01100101 01101100;
в) 01000001 01100011 01100011 01100101 01110011 01110011.
6. Определить информационный объем слова «Экономика», закодированного с помощью кодовых таблиц СР866, СР1251, Unicode и КОИ8-Р.
7. Определить информационный объем файла, полученного в результате сканирования цветного изображения размером 12x12 см. Разрешающая способность сканера, используемого при сканировании данного изображения, равна 600 dpi. Сканер задает глубину цвета точки изображения равной 16 бит.
Разрешающая способность сканера 600 dpi (dotper inch – точек на дюйм) определяет возможность сканера с такой разрешающей способностью на отрезке длиной 1 дюйм различить 600 точек.
8. Определить информационный объем файла, полученного в результате сканирования цветного изображения размером А4. Разрешающая способность сканера, используемого при сканировании данного изображения, равна 1200 dpi. Сканер задает глубину цвета точки изображения равной 24 бит.
9. Определить количество цветов в палитре при глубине цвета 8, 16, 24 и 32 бита.
10. Определить требуемый объем видеопамяти для графических режимов экрана монитора 640 на 480, 800 на 600, 1024 на 768 и 1280 на 1024 точек при глубине цвета точки изображения 8, 16, 24 и 32 бита. Результаты свести в таблицу. Разработать в MS Excel программу для автоматизации расчетов.
11. Определить максимальное число цветов, которое допустимо использовать для хранения изображения размером 32 на 32 точки, если в компьютере выделено под изображение 2 Кбайт памяти.
12. Определить максимально возможную разрешающую способность экрана монитора, имеющего длину диагонали 15" и размер точки изображения 0,28 мм.
13. Какие графические режимы работы монитора может обеспечить видеопамять объемом 64 Мбайт?
2. Закодировать и записать в виде последовательности чисел в десятичной и шестнадцатеричной системе счисления следующие слова:
a) Internet Explorer, б) Microsoft Office; в) CorelDRAW.
Кодирование произвести с помощью модернизированной кодировочной таблицы ASCII, полученной в предыдущем упражнении.
3. Декодировать с помощью модернизированной кодировочной таблицы КОИ8-Р последовательности чисел записанных в шестнадцатеричной системе счисления:
а) FC CB DA C9 D3 D4 C5 CE C3 C9 D1;
б) EB CF CE C6 CF D2 CD C9 DA CD;
в) FC CB D3 D0 D2 C5 D3 C9 CF CE C9 DA CD.
4. Как будет выглядеть слово «Кибернетика», записанное в кодировке СР1251, при использовании кодировок СР866 и КОИ8-Р? Проверить полученные результаты с помощью программы Internet Explorer.
5. Используя кодовую таблицу, приведенную на рис. 3.1а, декодировать следующие кодовые последовательности, записанные в двоичной системе счисления:
а) 01010111 01101111 01110010 01100100;
б) 01000101 01111000 01100011 01100101 01101100;
в) 01000001 01100011 01100011 01100101 01110011 01110011.
6. Определить информационный объем слова «Экономика», закодированного с помощью кодовых таблиц СР866, СР1251, Unicode и КОИ8-Р.
7. Определить информационный объем файла, полученного в результате сканирования цветного изображения размером 12x12 см. Разрешающая способность сканера, используемого при сканировании данного изображения, равна 600 dpi. Сканер задает глубину цвета точки изображения равной 16 бит.
Разрешающая способность сканера 600 dpi (dotper inch – точек на дюйм) определяет возможность сканера с такой разрешающей способностью на отрезке длиной 1 дюйм различить 600 точек.
8. Определить информационный объем файла, полученного в результате сканирования цветного изображения размером А4. Разрешающая способность сканера, используемого при сканировании данного изображения, равна 1200 dpi. Сканер задает глубину цвета точки изображения равной 24 бит.
9. Определить количество цветов в палитре при глубине цвета 8, 16, 24 и 32 бита.
10. Определить требуемый объем видеопамяти для графических режимов экрана монитора 640 на 480, 800 на 600, 1024 на 768 и 1280 на 1024 точек при глубине цвета точки изображения 8, 16, 24 и 32 бита. Результаты свести в таблицу. Разработать в MS Excel программу для автоматизации расчетов.
11. Определить максимальное число цветов, которое допустимо использовать для хранения изображения размером 32 на 32 точки, если в компьютере выделено под изображение 2 Кбайт памяти.
12. Определить максимально возможную разрешающую способность экрана монитора, имеющего длину диагонали 15" и размер точки изображения 0,28 мм.
13. Какие графические режимы работы монитора может обеспечить видеопамять объемом 64 Мбайт?
Глава 4
Логические основы компьютерной техники
4.1. Логические переменные и логические операции
Информация (данные, машинные команды и т. д.) в компьютере представлена в двоичной системе счисления, в которой используется две цифры – 0 и 1. Электрический сигнал, проходящий по электронным схемам и соединительным проводникам (шинам) компьютера, может принимать значения 1 (высокий уровень электрического напряжения) и 0 (низкий уровень электрического напряжения) и рассматривается как импульсный сигнал, который математически может быть описан в виде двоичной переменной, принимающей также значения 0 или 1. Для решения различных логических задач, например, связанных с анализом и синтезом цифровых схем и электронных блоков компьютера, широко используются логические функции и логические операции с двоичными переменными, которые называются также логическими переменными.
Логические переменные изучаются в специальном разделе математики, который носит название алгебры логики (высказываний), или булевой алгебры. Булева алгебра названа по имени английского математика Джорджа Буля (1815–1864), внесшего значительный вклад в разработку алгебры логики. Предметом изучения алгебры логики являются высказывания, при этом анализу подвергается истинность или ложность высказываний, а не их смысловое содержание. Простые высказывания в алгебре логики обозначаются заглавными латинскими буквами: А, В, С, D,… и т. д. Составные высказывания на естественном языке образуются с помощью союзов. В алгебре логики эти союзы заменяются логическими операциями. В соответствии с алгеброй логики любое составное высказывание можно рассматривать как логическую функцию F(А, В, С, …), аргументами которой являются логические переменные А, В, С… (простые высказывания). Логические функции и логические переменные (аргументы) принимают только два значения: «истина», которая обозначается логической единицей – 1 и «ложь», обозначаемая логическим нулем – 0. Логическую функцию называют также предикатом.
Действия, совершаемые над логическими переменными для получения определенных логических функций, называются логическими операциями. В алгебре логики используются следующие логические операции.
1. Логическая операция ИНВЕРСИЯ (отрицание). В естественных языках соответствует словам неверно, ложь или частице не, в языках программирования обозначается Not, в алгебре логики обозначается
 Инверсия каждому простому высказыванию ставит в соответствие составное высказывание, заключающееся в том, что исходное высказывание отрицается.
Инверсия каждому простому высказыванию ставит в соответствие составное высказывание, заключающееся в том, что исходное высказывание отрицается.
Математическая запись данной операции для логической переменной А будет иметь вид:
 2. Логическая операция КОНЪЮНКЦИЯ (логическое умножение). В естественных языках соответствует союзу и, в языках программирования обозначается And, в алгебре логики обозначается & .
2. Логическая операция КОНЪЮНКЦИЯ (логическое умножение). В естественных языках соответствует союзу и, в языках программирования обозначается And, в алгебре логики обозначается & .
Конъюнкция каждым простым высказываниям ставит в соответствие составное высказывание, являющееся только тогда истинным, когда являются истинными простые высказывания, образующие составное высказывание.
Математическая запись данной операции для логических переменных Д В, С, … будет иметь вид:
F = A & B & C & …
3. Логическая операция ДИЗЪЮНКЦИЯ (логическое сложение). В естественных языках соответствует союзу или, в языках программирования обозначается Or, в алгебре логики обозначается V.
Дизъюнкция каждым простым высказываниям ставит в соответствие составное высказывание, являющееся только тогда истинным, когда хотя бы одно из образующих его высказываний является истинным.
Математическая запись данной операции для логических переменных A, В, С, … будет иметь вид:
F = AvBvC…
4. Логическая операция ИМПЛИКАЦИЯ (логическое следование). В естественных языках соответствует обороту речи, если…, то …, в языках программирования обозначается If, в алгебре логики обозначается ⇒.
Импликация каждым простым высказываниям ставит в соответствие составное высказывание, являющееся ложным тогда и только тогда, когда первое высказывание истинно, а второе высказывание ложно.
Математическая запись данной операции для двух логических переменных А и В будет иметь вид:
F = A⇒B.
5. Логическая операция ЭКВИВАЛЕНЦИЯ (логическая равнозначность). В естественных языках соответствует обороту речи тогда и только тогда, в алгебре логики обозначается ⇔.
Эквиваленция каждым простым высказываниям ставит в соответствие составное высказывание, являющееся истинным тогда и только тогда, когда все простые высказывания, образующие составное высказывание, одновременно истинны или одновременно ложны.
Математическая запись данной операции для логических переменных A, В, С… будет иметь вид:
F = A⇔B⇔C⇔…
Логические переменные изучаются в специальном разделе математики, который носит название алгебры логики (высказываний), или булевой алгебры. Булева алгебра названа по имени английского математика Джорджа Буля (1815–1864), внесшего значительный вклад в разработку алгебры логики. Предметом изучения алгебры логики являются высказывания, при этом анализу подвергается истинность или ложность высказываний, а не их смысловое содержание. Простые высказывания в алгебре логики обозначаются заглавными латинскими буквами: А, В, С, D,… и т. д. Составные высказывания на естественном языке образуются с помощью союзов. В алгебре логики эти союзы заменяются логическими операциями. В соответствии с алгеброй логики любое составное высказывание можно рассматривать как логическую функцию F(А, В, С, …), аргументами которой являются логические переменные А, В, С… (простые высказывания). Логические функции и логические переменные (аргументы) принимают только два значения: «истина», которая обозначается логической единицей – 1 и «ложь», обозначаемая логическим нулем – 0. Логическую функцию называют также предикатом.
Действия, совершаемые над логическими переменными для получения определенных логических функций, называются логическими операциями. В алгебре логики используются следующие логические операции.
1. Логическая операция ИНВЕРСИЯ (отрицание). В естественных языках соответствует словам неверно, ложь или частице не, в языках программирования обозначается Not, в алгебре логики обозначается

Математическая запись данной операции для логической переменной А будет иметь вид:

Конъюнкция каждым простым высказываниям ставит в соответствие составное высказывание, являющееся только тогда истинным, когда являются истинными простые высказывания, образующие составное высказывание.
Математическая запись данной операции для логических переменных Д В, С, … будет иметь вид:
F = A & B & C & …
3. Логическая операция ДИЗЪЮНКЦИЯ (логическое сложение). В естественных языках соответствует союзу или, в языках программирования обозначается Or, в алгебре логики обозначается V.
Дизъюнкция каждым простым высказываниям ставит в соответствие составное высказывание, являющееся только тогда истинным, когда хотя бы одно из образующих его высказываний является истинным.
Математическая запись данной операции для логических переменных A, В, С, … будет иметь вид:
F = AvBvC…
4. Логическая операция ИМПЛИКАЦИЯ (логическое следование). В естественных языках соответствует обороту речи, если…, то …, в языках программирования обозначается If, в алгебре логики обозначается ⇒.
Импликация каждым простым высказываниям ставит в соответствие составное высказывание, являющееся ложным тогда и только тогда, когда первое высказывание истинно, а второе высказывание ложно.
Математическая запись данной операции для двух логических переменных А и В будет иметь вид:
F = A⇒B.
5. Логическая операция ЭКВИВАЛЕНЦИЯ (логическая равнозначность). В естественных языках соответствует обороту речи тогда и только тогда, в алгебре логики обозначается ⇔.
Эквиваленция каждым простым высказываниям ставит в соответствие составное высказывание, являющееся истинным тогда и только тогда, когда все простые высказывания, образующие составное высказывание, одновременно истинны или одновременно ложны.
Математическая запись данной операции для логических переменных A, В, С… будет иметь вид:
F = A⇔B⇔C⇔…
4.2. Основные законы алгебры логики и правила преобразования логических выражений
В алгебре логики имеются законы, которые записываются в виде соотношений. Логические законы позволяют производить равносильные (эквивалентные) преобразования логических выражений. Преобразования называются равносильными, если истинные значения исходной и полученной после преобразования логической функции совпадают при любых значениях входящих в них логических переменных.
Для простоты записи приведем основные законы алгебры логики для двух логических переменных А и В. Эти законы распространяются и на другие логические переменные.
1. Закон противоречия:
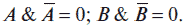 2. Закон исключенного третьего:
2. Закон исключенного третьего:
 3. Закон двойного отрицания:
3. Закон двойного отрицания:
 4. Законы де Моргана:
4. Законы де Моргана:
 5. Законы повторения: A & A = A; A v A = A; В & В = В; В v В = В.
5. Законы повторения: A & A = A; A v A = A; В & В = В; В v В = В.
6. Законы поглощения: A ∨ (A & B) = A; A & (A ∨ B) = A.
7. Законы исключения констант: A ∨ 1 = 1; A ∨ 0 = A; A & 1 = A; A & 0 = 0; B ∨ 1 = 1; B ∨ 0 = B; B & 1 = B; B & 0 = 0.
8. Законы склеивания:
 9. Закон контрапозиции: (A ⇔ B) = (B ⇔ A).
9. Закон контрапозиции: (A ⇔ B) = (B ⇔ A).
Для логических переменных справедливы и общематематические законы. Для простоты записи приведем общематематические законы для трех логических переменных A, В и С:
1. Коммутативный закон: A & B = B & A; A ∨ B = B ∨ A.
2. Ассоциативный закон: A & (B & C) = (A & B) & C; A ∨ (B ∨ C) = (A ∨ B) ∨ C.
3. Дистрибутивный закон: A & (B ∨ C) = (A & B) ∨ (A & C).
Как уже отмечалось, с помощью законов алгебры логики можно производить равносильные преобразования логических выражений с целью их упрощения. В алгебре логики на основе принятого соглашения установлены следующие правила (приоритеты) для выполнения логических операций: первыми выполняются операции в скобках, затем в следующем порядке: инверсия (отрицание), конъюнкция ( & ), дизъюнкция (v), импликация (⇒), эквиваленция (⇔)
Выполним преобразование, например, логической функции
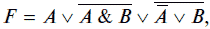 применив соответствующие законы алгебры логики.
применив соответствующие законы алгебры логики.

Для простоты записи приведем основные законы алгебры логики для двух логических переменных А и В. Эти законы распространяются и на другие логические переменные.
1. Закон противоречия:
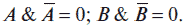



6. Законы поглощения: A ∨ (A & B) = A; A & (A ∨ B) = A.
7. Законы исключения констант: A ∨ 1 = 1; A ∨ 0 = A; A & 1 = A; A & 0 = 0; B ∨ 1 = 1; B ∨ 0 = B; B & 1 = B; B & 0 = 0.
8. Законы склеивания:

Для логических переменных справедливы и общематематические законы. Для простоты записи приведем общематематические законы для трех логических переменных A, В и С:
1. Коммутативный закон: A & B = B & A; A ∨ B = B ∨ A.
2. Ассоциативный закон: A & (B & C) = (A & B) & C; A ∨ (B ∨ C) = (A ∨ B) ∨ C.
3. Дистрибутивный закон: A & (B ∨ C) = (A & B) ∨ (A & C).
Как уже отмечалось, с помощью законов алгебры логики можно производить равносильные преобразования логических выражений с целью их упрощения. В алгебре логики на основе принятого соглашения установлены следующие правила (приоритеты) для выполнения логических операций: первыми выполняются операции в скобках, затем в следующем порядке: инверсия (отрицание), конъюнкция ( & ), дизъюнкция (v), импликация (⇒), эквиваленция (⇔)
Выполним преобразование, например, логической функции
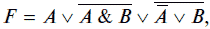

4.3. Логические функции и таблицы истинности
Соотношения между логическими переменными и логическими функциями в алгебре логики можно отобразить также с помощью соответствующих таблиц, которые носят название таблиц истинности. Таблицы истинности находят широкое применение, поскольку наглядно показывают, какие значения принимает логическая функция при всех сочетаниях значений ее логических переменных. Таблица истинности состоит из двух частей. Первая (левая) часть относится к логическим переменным и содержит полный перечень возможных комбинаций логических переменных А, В, С… и т. д. Вторая (правая) часть этой таблицы определяет выходные состояния как логическую функцию от комбинаций входных величин.
Например, для логической функции F = A v B v C (дизъюнкции) трех логических переменных А, В, и С таблица истинности будет иметь вид, показанный на рис. 4.1. Для записи значений логических переменных и логической функции данная таблица истинности содержит 8 строк и 4 столбца, т. е. число строк для записи значений аргументов и функции любой таблицы истинности будет равно 2n, где п – число аргументов логической функции, а число столбцов равно п + 1.
 Рис. 4.1. Таблица истинности для логической функции F = A v В v С
Рис. 4.1. Таблица истинности для логической функции F = A v В v С
Таблицу истинности можно составить для любой логической функции, например, на рис. 4.2 приведена таблица истинности логической функции F = A ⇔ B ⇔ C (эквиваленции).
Логические функции имеют соответствующие названия. Для двух двоичных переменных существует шестнадцать логических функций, названия которых приведены ниже. На рис. 4.3 представлена таблица, в которой приведены логические функции F1, F2, F3, … , F16 двух логических переменных A и В.
Функция F1 = 0 и называется функцией константы нуля, или генератора нуля.
 Рис. 4.2. Таблица истинности для логической функции F = A ⇔ B ⇔ C
Рис. 4.2. Таблица истинности для логической функции F = A ⇔ B ⇔ C
 Рис. 4.3. Логические функции F1, F2, F3,… F16 двух аргументов А и В
Рис. 4.3. Логические функции F1, F2, F3,… F16 двух аргументов А и В
Функция F2 = A & B называется функцией конъюнкции.
Функция
 называется функцией запрета по логической переменной А.
называется функцией запрета по логической переменной А.
Функция F4 = А называется функцией повторения по логической переменной А.
Функция
 называется функцией запрета по логической переменной В.
называется функцией запрета по логической переменной В.
Функция F6 = В называется функцией повторения по логической переменной В.
Функция
 называется функцией исключающее «ИЛИ».
называется функцией исключающее «ИЛИ».
Функция F8 = A v В называется функцией дизъюнкции.
Функция
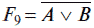 называется функцией Пирса.
называется функцией Пирса.
Функция
 называется функцией эквиваленции.
называется функцией эквиваленции.
Функция
 называется функцией отрицания (инверсии) по логической переменной В.
называется функцией отрицания (инверсии) по логической переменной В.
Функция F12 = B ⇒ A называется функцией импликации B ⇒ A.
Функция
 называется функцией отрицания (инверсии) по логической переменной А.
называется функцией отрицания (инверсии) по логической переменной А.
Функция F14 = A ⇒ B называется функцией импликации A ⇒ B.
Функция
 называется функцией Шеффера.
называется функцией Шеффера.
Функция F16 = 1 называется функцией генератора 1.
Среди перечисленных выше логических функций переменных можно выделить несколько логических функций, с помощью которых можно выразить другие логические функции. Операцию замены одной логической функции другой в алгебре логики называют операцией суперпозиции или методом суперпозиции. Например, функцию Шеффера можно выразить при помощи логических функций дизъюнкции и отрицания, используя закон де Моргана:
 Логические функции, с помощью которых можно выразить другие логические функции методом суперпозиции, называются базовыми логическими функциями. Такой набор базовых логических функций называется функционально полным набором логических функций. На практике наиболее широко в качестве такого набора используют три логических функции: конъюнкцию, дизъюнкцию и отрицание. Если логическая функция представлена с помощью базовых функций, то такая форма представления называется нормальной. В предыдущем примере логическая функция Шеффера, выраженная через базовые функции, представлена в нормальной форме.
Логические функции, с помощью которых можно выразить другие логические функции методом суперпозиции, называются базовыми логическими функциями. Такой набор базовых логических функций называется функционально полным набором логических функций. На практике наиболее широко в качестве такого набора используют три логических функции: конъюнкцию, дизъюнкцию и отрицание. Если логическая функция представлена с помощью базовых функций, то такая форма представления называется нормальной. В предыдущем примере логическая функция Шеффера, выраженная через базовые функции, представлена в нормальной форме.
При помощи набора базовых функций и соответствующих им технических устройств, реализующих эти логические функции, можно разработать и создать любое логическое устройство или систему.
В настоящее время существует достаточно много программных продуктов, с помощью которых можно реализовать различные логические функции и форму их представления, например в виде таблиц истинности. Логические функции широко используются и в программе MS Excel. Для вызова этих функций необходимо выполнить следующие команды: [Кнопка Пуск – Программы – MS Office ХР – Microsoft Excel] и далее команду: [Вставка – Функция]. В открывшемся окне (рис. 4.4) «Мастер функций – шаг 1 из 2», выберем: «Категория: „Логические“ и далее можно выбрать необходимую логическую функцию: ЕСЛИ, И, ИЛИ, ИСТИНА, ЛОЖЬ, НЕ. В этом же окне можно получить справку по каждой из этих функций.
 Рис. 4.4. Диалоговое окно «Мастер функций – шаг 1 из 2»
Рис. 4.4. Диалоговое окно «Мастер функций – шаг 1 из 2»
Как видно из рис. 4.4, в состав логических функций программы MS Excel входит функционально полный набор логических функций, состоящий из следующих логических функций: И (конъюнкция), ИЛИ (дизъюнкция), НЕ (отрицание). Таким образом, с помощью функционально полного набора логических функций программы MS Excel можно реализовать другие функции. Логическая функция ЕСЛИ (импликация), также входящая в логические функции MS Excel, выполняет логическую проверку и в зависимости от результата проверки выполняет одно из двух возможных действий. В данной программе она имеет следующий формат: = ЕСЛИ (арг1;арг2;арг3), где арг1 – логическое условие; арг2 – возвращаемое значение при условии, что значение аргумента арг1 выполняется (ИСТИНА); арг3 – возвращаемое значение при условии, что значение аргумента арг1 не выполняется (ЛОЖЬ). Например, если в произвольную ячейку листа программы MS Excel ввести выражение « = ЕСЛИ (А1 = 5; „пять“; „не пять“)», то при вводе числа 5 в ячейку А1 и нажатии клавиши «Enter» в ячейке А1 автоматически будет записано слово «пять», при вводе любого другого числа в ячейку А1 в ней запишется слово «не пять». Как уже отмечалось, с помощью логических функций программы MS Excel можно представить другие логические функции и соответствующие им таблицы истинности.
Реализуем с помощью логических функций ЕСЛИ и И модифицированную таблицу истинности логической функции F = А & В (конъюнкции), состоящую из двух строк и трех столбцов, которая позволяет при изменении значений (0 или 1) логических переменных А и В автоматически устанавливать, например, в ячейке Е6 значение функции F = А & В, соответствующее значениям этих логических переменных. Для этого в ячейку Е6 введем следующее выражение: «=ЕСЛИ(И(С6;D6);1;0)», тогда при вводе в ячейки С6 и D6 значений 0 или 1 в ячейке Е6 будет выполняться логическая функция F = А & В. Результат этих действий представлен на рис. 4.5.
 Рис. 4.5. Реализация модифицированной таблицы истинности логической функции F = A & В
Рис. 4.5. Реализация модифицированной таблицы истинности логической функции F = A & В
Например, для логической функции F = A v B v C (дизъюнкции) трех логических переменных А, В, и С таблица истинности будет иметь вид, показанный на рис. 4.1. Для записи значений логических переменных и логической функции данная таблица истинности содержит 8 строк и 4 столбца, т. е. число строк для записи значений аргументов и функции любой таблицы истинности будет равно 2n, где п – число аргументов логической функции, а число столбцов равно п + 1.

Таблицу истинности можно составить для любой логической функции, например, на рис. 4.2 приведена таблица истинности логической функции F = A ⇔ B ⇔ C (эквиваленции).
Логические функции имеют соответствующие названия. Для двух двоичных переменных существует шестнадцать логических функций, названия которых приведены ниже. На рис. 4.3 представлена таблица, в которой приведены логические функции F1, F2, F3, … , F16 двух логических переменных A и В.
Функция F1 = 0 и называется функцией константы нуля, или генератора нуля.


Функция F2 = A & B называется функцией конъюнкции.
Функция

Функция F4 = А называется функцией повторения по логической переменной А.
Функция

Функция F6 = В называется функцией повторения по логической переменной В.
Функция

Функция F8 = A v В называется функцией дизъюнкции.
Функция
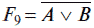
Функция

Функция

Функция F12 = B ⇒ A называется функцией импликации B ⇒ A.
Функция

Функция F14 = A ⇒ B называется функцией импликации A ⇒ B.
Функция

Функция F16 = 1 называется функцией генератора 1.
Среди перечисленных выше логических функций переменных можно выделить несколько логических функций, с помощью которых можно выразить другие логические функции. Операцию замены одной логической функции другой в алгебре логики называют операцией суперпозиции или методом суперпозиции. Например, функцию Шеффера можно выразить при помощи логических функций дизъюнкции и отрицания, используя закон де Моргана:

При помощи набора базовых функций и соответствующих им технических устройств, реализующих эти логические функции, можно разработать и создать любое логическое устройство или систему.
В настоящее время существует достаточно много программных продуктов, с помощью которых можно реализовать различные логические функции и форму их представления, например в виде таблиц истинности. Логические функции широко используются и в программе MS Excel. Для вызова этих функций необходимо выполнить следующие команды: [Кнопка Пуск – Программы – MS Office ХР – Microsoft Excel] и далее команду: [Вставка – Функция]. В открывшемся окне (рис. 4.4) «Мастер функций – шаг 1 из 2», выберем: «Категория: „Логические“ и далее можно выбрать необходимую логическую функцию: ЕСЛИ, И, ИЛИ, ИСТИНА, ЛОЖЬ, НЕ. В этом же окне можно получить справку по каждой из этих функций.

Как видно из рис. 4.4, в состав логических функций программы MS Excel входит функционально полный набор логических функций, состоящий из следующих логических функций: И (конъюнкция), ИЛИ (дизъюнкция), НЕ (отрицание). Таким образом, с помощью функционально полного набора логических функций программы MS Excel можно реализовать другие функции. Логическая функция ЕСЛИ (импликация), также входящая в логические функции MS Excel, выполняет логическую проверку и в зависимости от результата проверки выполняет одно из двух возможных действий. В данной программе она имеет следующий формат: = ЕСЛИ (арг1;арг2;арг3), где арг1 – логическое условие; арг2 – возвращаемое значение при условии, что значение аргумента арг1 выполняется (ИСТИНА); арг3 – возвращаемое значение при условии, что значение аргумента арг1 не выполняется (ЛОЖЬ). Например, если в произвольную ячейку листа программы MS Excel ввести выражение « = ЕСЛИ (А1 = 5; „пять“; „не пять“)», то при вводе числа 5 в ячейку А1 и нажатии клавиши «Enter» в ячейке А1 автоматически будет записано слово «пять», при вводе любого другого числа в ячейку А1 в ней запишется слово «не пять». Как уже отмечалось, с помощью логических функций программы MS Excel можно представить другие логические функции и соответствующие им таблицы истинности.
Реализуем с помощью логических функций ЕСЛИ и И модифицированную таблицу истинности логической функции F = А & В (конъюнкции), состоящую из двух строк и трех столбцов, которая позволяет при изменении значений (0 или 1) логических переменных А и В автоматически устанавливать, например, в ячейке Е6 значение функции F = А & В, соответствующее значениям этих логических переменных. Для этого в ячейку Е6 введем следующее выражение: «=ЕСЛИ(И(С6;D6);1;0)», тогда при вводе в ячейки С6 и D6 значений 0 или 1 в ячейке Е6 будет выполняться логическая функция F = А & В. Результат этих действий представлен на рис. 4.5.

4.4. Логические элементы и синтез логических схем
Сложные цифровые логические устройства, входящие в состав компьютера, состоят из ряда элементарных логических элементов, построенных на базе средств электронной техники. При производстве этих электронных логических элементов используют различные технологии и схемотехнические решения, такие как: ДТЛ (диодно-транзисторная логика), ТТЛ (транзисторно-транзисторная логика), ЭСЛ (эмиттерно-связанная логика), технологии, основанные на использовании полевых транзисторов, и т. д. Логические элементы позволяют реализовать любую логическую функцию. Входные и выходные сигналы логических элементов, соответствующие двум логическим состояниям 1 и 0, могут иметь один из двух установленных уровней электрического напряжения, который зависит от схемотехнического решения логического элемента. Например, для логических элементов, основанных на технологии ТТЛ, высокий уровень электрического напряжения (2,4 ÷ 5 В) соответствует значению логической единицы (истина), а низкий уровень (0 ÷ 0,4 В) – логическому нулю (ложь).
Три приведенных ниже логических элемента составляют функционально полную систему для проектирования цифровых логических устройств, в том числе и соответствующих логических блоков и устройств компьютера, поскольку реализуют функционально полный набор логических функций, состоящий из логических функций: И (конъюнкции), ИЛИ (дизъюнкции), НЕ (отрицания).
1. Логический элемент НЕ, который называется также инвертором, выполняет логическую операцию отрицания (инверсии).
 2. Логический элемент И, называемый также конъюнктором, выполняет операцию логического умножения (конъюнкции), теоретически может иметь бесконечное число входов, на практике ограничиваются числом входов от двух до восьми.
2. Логический элемент И, называемый также конъюнктором, выполняет операцию логического умножения (конъюнкции), теоретически может иметь бесконечное число входов, на практике ограничиваются числом входов от двух до восьми.
 3. Логический элемент ИЛИ, называемый также дизъюнктором, выполняет операцию логического сложения (дизъюнкции), теоретически может иметь бесконечное число входов, на практике ограничиваются числом входов от двух до восьми.
3. Логический элемент ИЛИ, называемый также дизъюнктором, выполняет операцию логического сложения (дизъюнкции), теоретически может иметь бесконечное число входов, на практике ограничиваются числом входов от двух до восьми.
 При проектировании цифровых логических устройств часто возникает задача по заданной таблице истинности записать выражение для логической функции и реализовать ее в виде логической схемы, состоящей из функционально полного набора логических элементов. Данную задачу называют также задачей синтеза логических схем или логических устройств.
При проектировании цифровых логических устройств часто возникает задача по заданной таблице истинности записать выражение для логической функции и реализовать ее в виде логической схемы, состоящей из функционально полного набора логических элементов. Данную задачу называют также задачей синтеза логических схем или логических устройств.
Синтез логических схем на основе функционально полного набора логических элементов состоит из представления логических функций, описывающих данные логические схемы в нормальных формах. Нормальной формой представления считается форма, полученная посредством суперпозиций вспомогательных логических функций – минтермов и макстернов.
Минтермом называют логическую функцию, которая принимает значение логической единицы только при одном значении логических переменных и значение логического нуля при других значениях логических переменных. Например, минтермами являются логические функции F2, F3, F5 и F9 (см. рис. 4.3).
Три приведенных ниже логических элемента составляют функционально полную систему для проектирования цифровых логических устройств, в том числе и соответствующих логических блоков и устройств компьютера, поскольку реализуют функционально полный набор логических функций, состоящий из логических функций: И (конъюнкции), ИЛИ (дизъюнкции), НЕ (отрицания).
1. Логический элемент НЕ, который называется также инвертором, выполняет логическую операцию отрицания (инверсии).



Синтез логических схем на основе функционально полного набора логических элементов состоит из представления логических функций, описывающих данные логические схемы в нормальных формах. Нормальной формой представления считается форма, полученная посредством суперпозиций вспомогательных логических функций – минтермов и макстернов.
Минтермом называют логическую функцию, которая принимает значение логической единицы только при одном значении логических переменных и значение логического нуля при других значениях логических переменных. Например, минтермами являются логические функции F2, F3, F5 и F9 (см. рис. 4.3).
Конец бесплатного ознакомительного фрагмента
