Страница:
Рис. 14. Рычаги 1-го и 2-го рода: груз и сила расположены по разные стороны от точки опоры
Несмотря на это отличие, соотношение сил и плеч на рычаге 2-го рода такое же, как на рычаге 1-го рода: сила и груз обратно пропорциональны длинам плеч[4]. В нашем случае, если для непосредственного поднятия двери нужно, например, 27 кг, а длина плеч 18 см и 162 см, то сила х, с которой вы должны действовать на конец рычага, определяется из пропорции
х: 27= 18: 162,
откуда
Ваше усилие должно быть не меньше 3 кг (не меньше потому, что сила в 3 кг только уравновешивает сопротивление двери).
Билетный автомат
Для продажи билетов, дающих право выйти на платформу, поставлены на некоторых вокзалах билетные автоматы; вы бросаете в щель автомата 10-копеечную монету – и из другой щели тотчас же выскакивает билет. Многие думают, что внутри автомата сложный механизм. Между тем приспособление здесь довольно простое: не что иное, как видоизменение известного уже вам рычага.
Взгляните на рис. 15, и секрет билетного автомата станет для вас ясен. Монета скатывается на конец рычажка и своим весом (и ударом) заставляет его опускаться. От этого противоположный, более короткий конец рычажка приподнимается, увлекая за собой пластинку, за которой на косом основании лежит стопка билетов. Пластинка поднимается ровно настолько, чтобы через образовавшуюся щелочку как раз мог проскользнуть один билетик. Вот и все нехитрое устройство автомата. Конечно, нужно подобрать длину плеч рычага так, чтобы вес и удар 10-копеечной монеты были достаточны для надлежащего поднятия пластинки. Монета меньшего веса не произведет этого действия. А кружок того же веса, но из другого материала будет иметь ведь другие размеры и, значит, не пройдет через монетную щелочку автомата.
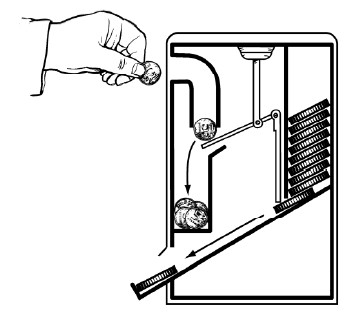Рис. 15. Устройство билетного автомата
Взгляните на рис. 15, и секрет билетного автомата станет для вас ясен. Монета скатывается на конец рычажка и своим весом (и ударом) заставляет его опускаться. От этого противоположный, более короткий конец рычажка приподнимается, увлекая за собой пластинку, за которой на косом основании лежит стопка билетов. Пластинка поднимается ровно настолько, чтобы через образовавшуюся щелочку как раз мог проскользнуть один билетик. Вот и все нехитрое устройство автомата. Конечно, нужно подобрать длину плеч рычага так, чтобы вес и удар 10-копеечной монеты были достаточны для надлежащего поднятия пластинки. Монета меньшего веса не произведет этого действия. А кружок того же веса, но из другого материала будет иметь ведь другие размеры и, значит, не пройдет через монетную щелочку автомата.
Ворот и шпиль
Кому не случалось видеть, как из глубоких колодцев поднимают полные ведра с помощью «ворота», при этом вращается вал, на который наматывается веревка: она-то и вытягивает ведро с водою.
Почему же таким способом легче вытаскивать тяжелое ведро, чем просто руками? Рассмотрим ворот внимательнее (рис. 16). Когда поворачивают колесо А в направлении стрелки, то в том же направлении поворачивается и вал.
Рис. 16. Как работает ворот
Проведем прямую NM через ось вала. Эту прямую мы можем рассматривать как рычаг, который вращается вокруг точки О. Сила приложена в точке М, а поднимаемый груз – в N (силы по разные стороны от точки опоры: это рычаг 1-го рода). Следовательно, сила, приложенная в точке М (т. е. к колесу), во столько раз меньше силы, приложенной в N (т. е. к валу), во сколько раз ON (радиус вала) меньше ОМ (радиуса колеса). Но радиус вала всегда в несколько раз меньше радиуса колеса; следовательно, на колесо приходится действовать с силою в несколько раз меньшею, чем вес полного ведра. Отсюда ясна выгода ворота. Если, например, радиус колеса 60 см, а радиус вала 11/2 см, то ведро с водой весом 12 кг можно уравновесить силою х, которая определяется из пропорции:
х: 12 = 7 1/2: 60,
откуда
Существуют вороты, приспособленные не для поднятия грузов, а для волочения; такой ворот называется шпилем, или кабестаном. Здесь вал – стоячий, а не лежачий, а вместо колеса имеются длинные шесты – «водила», которыми вращают вал. Нетрудно сообразить, что сила, с какой приходится напирать на конец водила, во столько раз меньше сопротивления груза (его трения об опору), во сколько раз радиус вала меньше длины водила.
Пусть, например, нужно передвигать груз, требующий без шпиля усилия в 500 кг; имеется шпиль с валом радиуса 21 см и с водилами длиною 3 1/2 м. Тогда усилие х, которое нужно приложить к концу водил, чтобы тащить груз, найдем из пропорции:
х: 500 = 21: 350,
откуда
Почему же таким способом легче вытаскивать тяжелое ведро, чем просто руками? Рассмотрим ворот внимательнее (рис. 16). Когда поворачивают колесо А в направлении стрелки, то в том же направлении поворачивается и вал.
Рис. 16. Как работает ворот
Проведем прямую NM через ось вала. Эту прямую мы можем рассматривать как рычаг, который вращается вокруг точки О. Сила приложена в точке М, а поднимаемый груз – в N (силы по разные стороны от точки опоры: это рычаг 1-го рода). Следовательно, сила, приложенная в точке М (т. е. к колесу), во столько раз меньше силы, приложенной в N (т. е. к валу), во сколько раз ON (радиус вала) меньше ОМ (радиуса колеса). Но радиус вала всегда в несколько раз меньше радиуса колеса; следовательно, на колесо приходится действовать с силою в несколько раз меньшею, чем вес полного ведра. Отсюда ясна выгода ворота. Если, например, радиус колеса 60 см, а радиус вала 11/2 см, то ведро с водой весом 12 кг можно уравновесить силою х, которая определяется из пропорции:
х: 12 = 7 1/2: 60,
откуда
Существуют вороты, приспособленные не для поднятия грузов, а для волочения; такой ворот называется шпилем, или кабестаном. Здесь вал – стоячий, а не лежачий, а вместо колеса имеются длинные шесты – «водила», которыми вращают вал. Нетрудно сообразить, что сила, с какой приходится напирать на конец водила, во столько раз меньше сопротивления груза (его трения об опору), во сколько раз радиус вала меньше длины водила.
Пусть, например, нужно передвигать груз, требующий без шпиля усилия в 500 кг; имеется шпиль с валом радиуса 21 см и с водилами длиною 3 1/2 м. Тогда усилие х, которое нужно приложить к концу водил, чтобы тащить груз, найдем из пропорции:
х: 500 = 21: 350,
откуда
Золотое правило механики
На вороте или на шпиле можно, значит, небольшою силою привести в движение значительный груз. Но скорость этого движения в таких случаях бывает невелика, – меньше, чем скорость, с какою движется приложенная к вороту сила.
Рассмотрим последний пример со шпилем: при одном полном обороте конец шеста, где приложена сила, описывает путь длиною
2 × 3,14 × 350 = 2200 см.
Тем временем вал сделает также один оборот, намотав на себя кусок веревки, длиною
2 × 3,14 × 21 = 130 см.
Следовательно, груз подтянется всего на 130 см. Сила прошла 2 200 см, а груз за то же время – только 130 см, т. е. почти в 17 раз меньше. Если сравните величину груза (500 кг) с величиною усилия, прилагаемого к шпилю (30 кг), то убедитесь, что между ними существует такое же отношение:
500: 30 = около 17.
Вы видите, что путь груза во столько же раз меньше пути силы, во сколько раз эта сила меньше груза. Другими словами: во сколько раз выигрывается в силе, во столько же раз теряется в скорости.
Рис. 17. Объяснение золотого правила механики
Это правило применимо не только к вороту или шпилю, но и к рычагу, и ко всякой вообще машине (его издавна называют «золотым правилом механики»).
Рассмотрим, например, рычаг, о котором говорилось на с. 51. Здесь выигрывается в силе в 3 раза, но зато, пока длинное плечо рычага (см. рис. 17) описывает своим концом большую дугу MN, конец короткого плеча описывает втрое меньшую дугу ОР. Следовательно, и в этом случае путь, проходимый грузом, меньше пути, проходимого в то же время силою, в 3 раза – во столько же раз, во сколько эта сила меньше груза.
Теперь вам станет понятно, почему в некоторых случаях выгодно пользоваться рычагами наоборот: действуя большою силой на короткое плечо, чтобы двигать маленький груз на конце длинного плеча. Какая выгода так поступать? Ведь мы теряем здесь в силе! Конечно, зато во столько же раз выигрываем в скорости. И когда нам необходима большая скорость, мы приобретаем ее этой ценой. Такие рычаги представляют кости наших рук (рис. 18): в них мускул прикреплен к короткому плечу рычага 2-го рода и приводит в быстрое движение кисть руки.
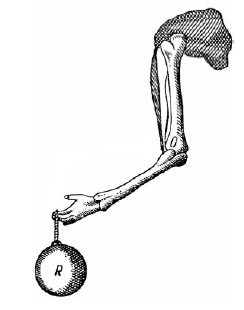
Рис. 18. Наша рука – рычаг. Какого рода?
В данном случае потеря силы вознаграждается выигрышем скорости. Мы были бы крайне медлительными существами, если бы кости нашего скелета были устроены как рычаги, выигрывающие в силе и, значит, теряющие в скорости.
Рассмотрим последний пример со шпилем: при одном полном обороте конец шеста, где приложена сила, описывает путь длиною
2 × 3,14 × 350 = 2200 см.
Тем временем вал сделает также один оборот, намотав на себя кусок веревки, длиною
2 × 3,14 × 21 = 130 см.
Следовательно, груз подтянется всего на 130 см. Сила прошла 2 200 см, а груз за то же время – только 130 см, т. е. почти в 17 раз меньше. Если сравните величину груза (500 кг) с величиною усилия, прилагаемого к шпилю (30 кг), то убедитесь, что между ними существует такое же отношение:
500: 30 = около 17.
Вы видите, что путь груза во столько же раз меньше пути силы, во сколько раз эта сила меньше груза. Другими словами: во сколько раз выигрывается в силе, во столько же раз теряется в скорости.
Рис. 17. Объяснение золотого правила механики
Это правило применимо не только к вороту или шпилю, но и к рычагу, и ко всякой вообще машине (его издавна называют «золотым правилом механики»).
Рассмотрим, например, рычаг, о котором говорилось на с. 51. Здесь выигрывается в силе в 3 раза, но зато, пока длинное плечо рычага (см. рис. 17) описывает своим концом большую дугу MN, конец короткого плеча описывает втрое меньшую дугу ОР. Следовательно, и в этом случае путь, проходимый грузом, меньше пути, проходимого в то же время силою, в 3 раза – во столько же раз, во сколько эта сила меньше груза.
Теперь вам станет понятно, почему в некоторых случаях выгодно пользоваться рычагами наоборот: действуя большою силой на короткое плечо, чтобы двигать маленький груз на конце длинного плеча. Какая выгода так поступать? Ведь мы теряем здесь в силе! Конечно, зато во столько же раз выигрываем в скорости. И когда нам необходима большая скорость, мы приобретаем ее этой ценой. Такие рычаги представляют кости наших рук (рис. 18): в них мускул прикреплен к короткому плечу рычага 2-го рода и приводит в быстрое движение кисть руки.
Рис. 18. Наша рука – рычаг. Какого рода?
В данном случае потеря силы вознаграждается выигрышем скорости. Мы были бы крайне медлительными существами, если бы кости нашего скелета были устроены как рычаги, выигрывающие в силе и, значит, теряющие в скорости.
Машины Архимеда
Учение о рычаге разработано было впервые древнегреческим математиком Архимедом, жившим в Сиракузах (Сицилия) за двести лет до нашей эры. Легенды, в которых, вероятно, кроется большая доля истины, повествуют о замечательных машинах, которые были придуманы им на основе рычага. Вот что рассказывает об этом древний историк Плутарх:
Рис. 19. Метательное орудие времен Архимеда: полевая баллиста
Рис. 20. Тяжелая осадная баллиста времен Архимеда
Рис. 21
«Марцел (римский полководец) приближался и по суше и морем. На суше войско шло под командою Аппия, а сам Марцел плыл во главе шестидесяти галер, о пяти рядах весел, со всякого рода метательными снарядами и оружием. Восемь судов, соединенных вместе, составляли род обширного помоста, на котором возвышалась стенобитная машина. Так плыл он к городу, доверяясь громадности и могуществу приспособлений и своей славе. Это однако не смутило Архимеда. Что все это значило в сравнении с его машинами?
«Однажды Архимед написал царю (сиракузскому) Гиерону, которому он был родственник и друг, что данною силой можно подвинуть какой угодно груз. Увлеченный жаром и силой доказательств, он прибавил, что если бы была другая земля, то, перейдя на нее, он сдвинул бы с места нашу. Удивленный Гиерон просил Архимеда осуществить задачу на практике и показать ему случай передвижения огромного груза малою силой. Архимед выбрал одну из царских галер; с великим трудом, работою многих рук, перевел ее на землю, посадил на нее много народу и нагрузил, как обычно. Сам же сел на некотором расстоянии; потом без усилия стал потихоньку двигать конец машины, состоявшей из блоков и веревок, и тянуть галеру, которая пошла, не качаясь, как если бы плыла по ровной поверхности моря. Царь, пораженный виденным и оценив могущество науки, пригласил Архимеда построить машины, пригодные для осады в случае ли нападения, или обороны.
Рис. 19. Метательное орудие времен Архимеда: полевая баллиста
«В настоящих обстоятельствах приготовления эти пришлись как нельзя более кстати для сиракузцев, которые вместе с изготовленными машинами имели в своей среде и самого их изобретателя.
«При двойной атаке римлян сиракузцы онемели, пораженные ужасом. Что могли они противопоставить таким силам, такой могущественной рати? Но Архимед пустил в ход свои машины. Сухопутная армия была поражена градом метательных снарядов и громадных камней, бросаемых с великой стремительностью. Ничто не могло противостоять их удару: они все низвергали перед собою и вносили смятение в ряды. Что касается флота, то вдруг с высоты стен опускались бревна и вследствие своего веса и приданной им скорости топили суда. Железные когти и клювы захватывали суда: подымали их в воздух носом вверх, кормою вниз и потом погружали в воду. Иные суда приводились во вращение и, кружась, попадали на подводные камни и утесы у подножия стен. Большая часть находившихся на судах погибала при этом. Ежеминутно видели какое-нибудь судно поднятым в воздухе над морем. Страшное зрелище!
Рис. 20. Тяжелая осадная баллиста времен Архимеда
«Достигнув стен, римляне воображали себя в безопасности, но они были под ударами. Камни падали на них сверху, стены отовсюду пускали в них копья. Они удалялись обратно, но летали новые метательные снаряды и поражали отступающих. Много воинов погибло, суда сталкивались между собою; причинить же какой-либо вред осаждаемым нельзя было: большая часть машин Архимеда была за стенами. Невидимая рука бросала тысячи зол в римлян.
Рис. 21
«Видя все это, Марцел отказался от нападения и исход осады решил предоставить времени.
«Таковы были величие души Архимеда, глубина его гения, неисчерпаемость его знаний».
Лошадиная сила и работа лошади
Мы часто слышим выражение «лошадиная сила» и привыкли к нему. Поэтому мало кто отдает себе отчет в том, что это старинное наименование совершенно неправильно. «Лошадиная сила» – не сила, а мощность и притом даже не лошадиная. Мощность – это работа, совершаемая двигателем каждую секунду. Лошадиная сила – мощность двигателя, совершающего ежесекундно 75 килограммометров работы; это значит, что двигатель в 1 лошадиную силу каждую секунду выполняет работу, одинаковую с работой поднятия 1 кг на высоту 75 м (или 75 кг на высоту 1 м). Это ничего не говорит о силе, затрачиваемой двигателем, а лишь о работе, т. е. о произведении силы на пройденный путь.
Может ли лошадь совершать при работе каждую секунду 75 килограммометров работы? В отдельные секунды она способна развить и большую мощность, например, перепрыгивая через препятствие, когда в течение 1–2 секунд поднимает груз своего веса (около 300–400 кг) на высоту метра. Но работать так в течение целого дня и длинного ряда дней, как работает механический двигатель, живая лошадь не может.
Мощность лошади далеко не достигает даже и одной «лошадиной силы».
Откуда же в таком случае взялось название «лошадиная сила», если нет соответствия с энергией лошади? Название это родилось случайно и вот при каких обстоятельствах.
Во времена Уатта, знаменитого изобретателя паровой машины, жил в Англии пивовар, пожелавший поставить у себя машину Уатта для приведения в действие водяного насоса. До той поры насос работал конной тягой, и заводчик поставил Уатту условие, чтобы машина была не менее производительна, чем лошадь. Уатт принял это требование.
Желая сравнить работу машины и лошади, пивовар выбрал самую сильную лошадь и приказал работникам стегать ее не жалея. При таких ненормальных условиях лошадь работала сверх сил и накачала столько воды, что, учитывая глубину, откуда воду брали, мощность лошади надо было оценить в 70 килограммометров.
Рис. 22. Джемс Уатт, изобретатель паровой машины
Уатт знал о хитрости заводчика, но знал также и высокую мощность своей паровой машины. Поэтому он принял преувеличенную оценку пивовара и даже поднял ее до 75 килограммометров. С тех пор и установился обычай считать механическую «лошадиную силу» равной 75 килограммометрам, хотя мощность живой лошади едва достигает 2/3 этой величины.
Может ли лошадь совершать при работе каждую секунду 75 килограммометров работы? В отдельные секунды она способна развить и большую мощность, например, перепрыгивая через препятствие, когда в течение 1–2 секунд поднимает груз своего веса (около 300–400 кг) на высоту метра. Но работать так в течение целого дня и длинного ряда дней, как работает механический двигатель, живая лошадь не может.
Мощность лошади далеко не достигает даже и одной «лошадиной силы».
Откуда же в таком случае взялось название «лошадиная сила», если нет соответствия с энергией лошади? Название это родилось случайно и вот при каких обстоятельствах.
Во времена Уатта, знаменитого изобретателя паровой машины, жил в Англии пивовар, пожелавший поставить у себя машину Уатта для приведения в действие водяного насоса. До той поры насос работал конной тягой, и заводчик поставил Уатту условие, чтобы машина была не менее производительна, чем лошадь. Уатт принял это требование.
Желая сравнить работу машины и лошади, пивовар выбрал самую сильную лошадь и приказал работникам стегать ее не жалея. При таких ненормальных условиях лошадь работала сверх сил и накачала столько воды, что, учитывая глубину, откуда воду брали, мощность лошади надо было оценить в 70 килограммометров.
Рис. 22. Джемс Уатт, изобретатель паровой машины
Уатт знал о хитрости заводчика, но знал также и высокую мощность своей паровой машины. Поэтому он принял преувеличенную оценку пивовара и даже поднял ее до 75 килограммометров. С тех пор и установился обычай считать механическую «лошадиную силу» равной 75 килограммометрам, хотя мощность живой лошади едва достигает 2/3 этой величины.
Искуснее Колумба
«Христофор Колумб был великий человек, – писал один школьник в своем классном сочинении. – Он открыл Америку и поставил яйцо». Оба подвига казались юному школьнику одинаково достойными изумления. Напротив, американский юморист Марк Твен не видел ничего удивительного в том, что Колумб открыл Америку: «Было бы удивительно, если бы он не нашел ее на месте».
Я осмеливаюсь думать, что не много стоит и второй подвиг великого мореплавателя. Вы знаете, как Колумб поставил яйцо? Попросту придавил его к столу, сломив скорлупу в нижней части. При этом он, разумеется, изменил форму яйца.
А как поставить яйцо, не меняя его формы?
Этой задачи отважный моряк так и не разрешил.
Между тем она несравненно легче, чем открытие Америки или даже самого крошечного островка. Укажу вам два способа: один – для вареных яиц, другой – для всяких.
Чтобы поставить вареное яйцо, достаточно закружить его пальцами одной руки или между ладонями рук, как кубарь или юла: яйцо завертится стоймя и будет сохранять стоячее положение до тех пор, пока вертится. После двух-трех проб опыт удается довольно легко.
Поставить указанным способом яйцо сырое нельзя: сырые яйца, как вы, вероятно, уже заметили, вертятся плохо. В этом состоит, между прочим, безошибочный способ отличить, не ломая скорлупы, вареное яйцо от сырого. Жидкое содержимое сырого яйца не увлекается в такое же быстрое вращение, как скорлупа, и потому словно тормозит его движение. Приходится искать другой способ ставить яйца. Способ этот существует. Яйцо ставят, например, на край горлышка бутылки и на него помещают пробку с воткнутыми в нее двумя вилками. Вся эта «система» (как выразился бы физик) довольно устойчива и сохраняет равновесие даже при осторожном наклонении бутылки.
Рис. 23
Но почему же пробка и яйцо не падают? По той же причине, почему не падает карандаш, отвесно поставленный на палец, если в него воткнуть перочинный нож: центр тяжести системы лежит ниже точки опоры. Это значит, что та точка, к которой приложен вес «системы», расположена ниже того места, на которое она опирается.
Теперь вас уже не удивит, почему так устойчиво качается в кольце игрушечный попугай и почему не опрокидываются всевозможные «ваньки-встаньки» (рис. 24).
Рис. 24
Я осмеливаюсь думать, что не много стоит и второй подвиг великого мореплавателя. Вы знаете, как Колумб поставил яйцо? Попросту придавил его к столу, сломив скорлупу в нижней части. При этом он, разумеется, изменил форму яйца.
А как поставить яйцо, не меняя его формы?
Этой задачи отважный моряк так и не разрешил.
Между тем она несравненно легче, чем открытие Америки или даже самого крошечного островка. Укажу вам два способа: один – для вареных яиц, другой – для всяких.
Чтобы поставить вареное яйцо, достаточно закружить его пальцами одной руки или между ладонями рук, как кубарь или юла: яйцо завертится стоймя и будет сохранять стоячее положение до тех пор, пока вертится. После двух-трех проб опыт удается довольно легко.
Поставить указанным способом яйцо сырое нельзя: сырые яйца, как вы, вероятно, уже заметили, вертятся плохо. В этом состоит, между прочим, безошибочный способ отличить, не ломая скорлупы, вареное яйцо от сырого. Жидкое содержимое сырого яйца не увлекается в такое же быстрое вращение, как скорлупа, и потому словно тормозит его движение. Приходится искать другой способ ставить яйца. Способ этот существует. Яйцо ставят, например, на край горлышка бутылки и на него помещают пробку с воткнутыми в нее двумя вилками. Вся эта «система» (как выразился бы физик) довольно устойчива и сохраняет равновесие даже при осторожном наклонении бутылки.
Рис. 23
Но почему же пробка и яйцо не падают? По той же причине, почему не падает карандаш, отвесно поставленный на палец, если в него воткнуть перочинный нож: центр тяжести системы лежит ниже точки опоры. Это значит, что та точка, к которой приложен вес «системы», расположена ниже того места, на которое она опирается.
Теперь вас уже не удивит, почему так устойчиво качается в кольце игрушечный попугай и почему не опрокидываются всевозможные «ваньки-встаньки» (рис. 24).
Рис. 24
Движение по кругу
Раскройте зонтик, уприте его концом в пол, закружите и бросьте внутрь мячик, скомканную бумагу, носовой платок – вообще что-нибудь легкое и неломкое. Произойдет нечто для вас неожиданное. Зонтик словно не пожелает принять подарка: мяч или бумажный ком выползут вверх, до краев зонтика, а оттуда полетят на пол.
Причину, которая в этом опыте выбросила мяч, принято называть «центробежной силой», хотя правильнее называть ее «инерцией». Она обнаруживается всякий раз, когда тело движется по круговому пути. Это не что иное, как один из случаев проявления инерции – стремления движущегося предмета сохранять направление и скорость своего движения.
Рис. 25
С таким проявлением инерции мы встречаемся гораздо чаще, чем сами подозреваем. Старинное оружие для метания камней – праща – работает по той же причине. Инерция кругового движения разрывает жернов, когда он заверчен слишком быстро и недостаточно прочен. Если вы ловки, она поможет вам выполнить фокус со стаканом, из которого вода не выливается, хотя он опрокинут вверх дном: для этого нужно только быстро взмахнуть стаканом над головой, описав круг. Инерция же помогает велосипедисту в цирке делать головокружительную «чертову петлю». Она же отделяет сливки от молока в так называемых «центробежных» сепараторах; она извлекает мед из сотов в центробежке и т. д.
Когда трамвайный вагон описывает кривую часть пути, например, при повороте из одной улицы в другую, то пассажиры непосредственно на себе ощущают силу, которая прижимает их по направлению к внешней стенке вагона. При достаточной скорости движения весь вагон мог бы быть опрокинут, если бы наружный рельс закругления не был предусмотрительно уложен выше внутреннего: благодаря этому вагон на повороте слегка наклоняется внутрь. Это звучит довольно странно: вагон, покосившийся набок, устойчивее, чем стоящий прямо!
Рис. 26
А между тем это так, и маленький опыт поможет вам уяснить себе, как происходит дело. Сверните картонный лист в виде широкого раструба, еще лучше, – возьмите, если в доме найдется, миску со стенками такой формы. Особенно пригодится для нашей цели конический абажур – стеклянный или жестяной – от электрической лампы. Вооружившись одним из этих предметов, пустите по нему монету, небольшой металлический кружочек или колечко от ключей. Они будут описывать круги по дну посуды, заметно наклоняясь при этом внутрь. По мере того как монета или колечко будут замедлять свое движение, они станут описывать все меньшие круги, приближаясь к центру посуды. Но легким поворотом посуды вы можете заставить монету снова катиться быстрее, и тогда она удаляется от центра, описывая большие круги. Если она разгонится очень сильно, то может и совсем выкатиться из посуды.
Для велосипедных состязаний на так называемом «велодроме» устраиваются особые круговые дорожки; вы можете видеть, что дорожки эти, особенно там, где они круто заворачивают, устроены с заметным уклоном к центру. Велосипед кружится по ним в сильно наклоненном положении, – как монета в вашей чашке, – и не только не опрокидывается, но, напротив, в таком именно положении приобретает особенную устойчивость. В цирках велосипедисты изумляют публику тем, что описывают круги по круто наклоненному настилу; вы понимаете теперь, что в этом нет ничего необычайного. Напротив, трудным искусством для велосипедиста было бы кружиться так по ровной, горизонтальной дорожке.
Причину, которая в этом опыте выбросила мяч, принято называть «центробежной силой», хотя правильнее называть ее «инерцией». Она обнаруживается всякий раз, когда тело движется по круговому пути. Это не что иное, как один из случаев проявления инерции – стремления движущегося предмета сохранять направление и скорость своего движения.
Рис. 25
С таким проявлением инерции мы встречаемся гораздо чаще, чем сами подозреваем. Старинное оружие для метания камней – праща – работает по той же причине. Инерция кругового движения разрывает жернов, когда он заверчен слишком быстро и недостаточно прочен. Если вы ловки, она поможет вам выполнить фокус со стаканом, из которого вода не выливается, хотя он опрокинут вверх дном: для этого нужно только быстро взмахнуть стаканом над головой, описав круг. Инерция же помогает велосипедисту в цирке делать головокружительную «чертову петлю». Она же отделяет сливки от молока в так называемых «центробежных» сепараторах; она извлекает мед из сотов в центробежке и т. д.
Когда трамвайный вагон описывает кривую часть пути, например, при повороте из одной улицы в другую, то пассажиры непосредственно на себе ощущают силу, которая прижимает их по направлению к внешней стенке вагона. При достаточной скорости движения весь вагон мог бы быть опрокинут, если бы наружный рельс закругления не был предусмотрительно уложен выше внутреннего: благодаря этому вагон на повороте слегка наклоняется внутрь. Это звучит довольно странно: вагон, покосившийся набок, устойчивее, чем стоящий прямо!
Рис. 26
А между тем это так, и маленький опыт поможет вам уяснить себе, как происходит дело. Сверните картонный лист в виде широкого раструба, еще лучше, – возьмите, если в доме найдется, миску со стенками такой формы. Особенно пригодится для нашей цели конический абажур – стеклянный или жестяной – от электрической лампы. Вооружившись одним из этих предметов, пустите по нему монету, небольшой металлический кружочек или колечко от ключей. Они будут описывать круги по дну посуды, заметно наклоняясь при этом внутрь. По мере того как монета или колечко будут замедлять свое движение, они станут описывать все меньшие круги, приближаясь к центру посуды. Но легким поворотом посуды вы можете заставить монету снова катиться быстрее, и тогда она удаляется от центра, описывая большие круги. Если она разгонится очень сильно, то может и совсем выкатиться из посуды.
Для велосипедных состязаний на так называемом «велодроме» устраиваются особые круговые дорожки; вы можете видеть, что дорожки эти, особенно там, где они круто заворачивают, устроены с заметным уклоном к центру. Велосипед кружится по ним в сильно наклоненном положении, – как монета в вашей чашке, – и не только не опрокидывается, но, напротив, в таком именно положении приобретает особенную устойчивость. В цирках велосипедисты изумляют публику тем, что описывают круги по круто наклоненному настилу; вы понимаете теперь, что в этом нет ничего необычайного. Напротив, трудным искусством для велосипедиста было бы кружиться так по ровной, горизонтальной дорожке.
Где легче всего?
Земной шар, на котором мы живем, вращается, и вследствие вращения Земли все вещи на ее поверхности становятся легче. Чем ближе к экватору, тем больший круг успевают сделать вещи за 24 часа, тем, значит, они быстрее вращаются и оттого больше теряют в весе. Если килограммовую гирю перенести с полюса на экватор и здесь вновь взвесить на пружинных весах, то обнаружится нехватка в весе на 5 г. Разница невелика, конечно, но чем тяжелее вещь, тем нехватка крупнее. Паровоз, приехавший из Архангельска в Одессу, становится здесь легче на 60 кг – вес взрослого человека. А линейный корабль в 20 тыс. тонн, прибывший из Белого моря в Черное, теряет здесь в весе ни мало, ни много – 80 тонн; это вес хорошего паровоза!
Рис. 27
Отчего так происходит? Оттого, что земной шар, вращаясь, стремится разбросать со своей поверхности все вещи, как зонтик в нашем опыте выкидывает брошенный в него мяч. Земной шар и скинул бы их, но этому мешает то, что он притягивает все вещи к себе. Мы называем это притяжение «тяжестью». Скинуть вещи с Земли вращение не может, а уменьшить вес их может. Вот почему вещи становятся немного легче вследствие вращения земного шара.
Рис. 27
Отчего так происходит? Оттого, что земной шар, вращаясь, стремится разбросать со своей поверхности все вещи, как зонтик в нашем опыте выкидывает брошенный в него мяч. Земной шар и скинул бы их, но этому мешает то, что он притягивает все вещи к себе. Мы называем это притяжение «тяжестью». Скинуть вещи с Земли вращение не может, а уменьшить вес их может. Вот почему вещи становятся немного легче вследствие вращения земного шара.
Если бы Земля вращалась быстрее…
Чем быстрее вращение, тем уменьшение веса должно становиться заметнее. Вычислено, что если бы Земля вращалась не так, как теперь, а в 17 раз быстрее, то на экваторе вещи потеряли бы свой вес целиком: они стали бы невесомы. А если бы Земля вращалась еще быстрее, то вещи потеряли бы весь свой вес не только на экваторе, но и в странах и морях, лежащих по обе его стороны.
Рис. 28
Подумайте только, что это значит: вещи потеряли бы свой вес! Ведь это значит, что не будет такой вещи, которой вы не могли бы поднять: паровозы, каменные глыбы, исполинские пушки, целые военные корабли со всеми машинами и орудиями вы поднимали бы – как перышко. А если бы вы их уронили – не опасно: они никого не раздавят. Не раздавят потому, что вовсе и не упали бы: ведь они ничего не весят! Они парили бы в воздухе там, где вы выпустили их из рук. Если бы, сидя в корзине воздушного шара, вы вздумали ронять свои вещи за борт, – они так и остались бы в воздухе. Удивительный был бы это мир! Прыгать вы могли бы так высоко, как и во сне не прыгали: выше самых высоких сооружений и гор. Но только не забывайте: подпрыгнуть легко, а назад спрыгнуть невозможно. Лишенные веса, вы на землю не упадете, а оттолкнуться в воздухе не от чего.
Будут и другие неудобства в этом мире. Сами сообразите, какие: все вещи – и малые и большие, – если они не прикреплены, будут подниматься от малейшего ветерка и носиться в воздухе. Люди, животные, автомобили, телеги, корабли – все беспорядочно металось бы в воздухе, ломая и калеча друг друга… Вот что произошло бы, если бы Земля вращалась значительно быстрее.
Рис. 28
Подумайте только, что это значит: вещи потеряли бы свой вес! Ведь это значит, что не будет такой вещи, которой вы не могли бы поднять: паровозы, каменные глыбы, исполинские пушки, целые военные корабли со всеми машинами и орудиями вы поднимали бы – как перышко. А если бы вы их уронили – не опасно: они никого не раздавят. Не раздавят потому, что вовсе и не упали бы: ведь они ничего не весят! Они парили бы в воздухе там, где вы выпустили их из рук. Если бы, сидя в корзине воздушного шара, вы вздумали ронять свои вещи за борт, – они так и остались бы в воздухе. Удивительный был бы это мир! Прыгать вы могли бы так высоко, как и во сне не прыгали: выше самых высоких сооружений и гор. Но только не забывайте: подпрыгнуть легко, а назад спрыгнуть невозможно. Лишенные веса, вы на землю не упадете, а оттолкнуться в воздухе не от чего.
Будут и другие неудобства в этом мире. Сами сообразите, какие: все вещи – и малые и большие, – если они не прикреплены, будут подниматься от малейшего ветерка и носиться в воздухе. Люди, животные, автомобили, телеги, корабли – все беспорядочно металось бы в воздухе, ломая и калеча друг друга… Вот что произошло бы, если бы Земля вращалась значительно быстрее.
Сжатие земного шара
Вращением Земли объясняется и то, что она, строго говоря, не представляет собой шара, а сплющена по направлению своей оси. Простой опыт уяснит нам, почему Земля приняла такую форму.
Конец бесплатного ознакомительного фрагмента