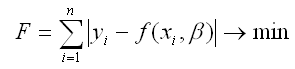Страница:
4) информационный этап, в процессе осуществления которого происходит сбор необходимых статистических данных, а также анализируется качество собранной информации;
5) этап идентификации модели, в ходе осуществления которого происходит статистический анализ модели и оцененивание неизвестных параметров. Данный этап непосредственно связан с проблемой идентифицируемостимодели, т. е. ответа на вопрос «Возможно ли восстановить значения неизвестных параметров модели по имеющимся исходным данным в соответствии с решением, принятым на этапе параметризацииβ». После положительного ответа на этот вопрос решается проблема идентификации модели, т. е. реализуется математически корректная процедура оценивания неизвестных параметров модели по имеющимся исходным данным;
6) этап оценки качества модели, в ходе осуществления которого проверяется достоверность и адекватность модели, т. е. определяется, насколько успешно решены задачи спецификации и идентификации модели, какова точность расчётов, полученных на её основе. Построенная модель должна быть адекватна реальному экономическому процессу. Если качество модели является неудовлетворительным, то происходит возврат ко второму этапу моделирования;
7) этап интерпретации результатов моделирования.
К наиболее распространённым эконометрическим моделям относятся:
1) модели потребительского и сберегательного потребления;
2) модели взаимосвязи риска и доходности ценных бумаг;
3) модели предложения труда;
4) макроэкономические модели (модель роста);
5) модели инвестиций;
6) маркетинговые модели;
7) модели валютных курсов и валютных кризисов и др.
Эконометрическое исследование связано с решением следующих проблем:
1) качественный анализ связей экономических переменных, т. е. определение зависимых (yi) и независимых (хi) переменных;
2) изучение соответствующего раздела экономической теории;
3) подбор данных;
4) спецификация формы связи между yi и хi;
5) оценка неизвестных параметров модели;
6) проверка ряда гипотез о свойствах распределения вероятностей для случайной компоненты (гипотезы о средней дисперсии и ковариации);
7) анализ мультиколлинеарности объясняющих переменных, оценка ее статистической значимости, определение переменных, ответственных за мультиколлинеарность;
8) введение фиктивных переменных;
9) выявление автокорреляции;
10) выявление тренда, циклической и случайной компонент;
11) проверка остатков модели на гетероскедастичность;
12) анализ структуры связей и построения системы одновременных уравнений;
13) проверка условия идентификации;
14) оценка параметров системы одновременных уравнений;
15) проблемы моделирования на основе системы временных рядов;
16) построение рекурсивных моделей, авторегрессионных моделей;
17) выработка управленческих решений
18) прогноз экономических показателей, характеризующих изучаемый процесс;
19) моделирование поведения процесса при различных значениях независимых (факторных) переменных.
7. Сбор статистических данных для оценивания параметров эконометрической модели
8. Классификация видов эконометрических переменных и типов данных. Проблемы, связанные с данными
9. Общая модель парной (однофакторной) регрессии
10. Нормальная линейная модель парной (однофакторной) регрессии
11. Критерии оценки неизвестных коэффициентов модели регрессии
5) этап идентификации модели, в ходе осуществления которого происходит статистический анализ модели и оцененивание неизвестных параметров. Данный этап непосредственно связан с проблемой идентифицируемостимодели, т. е. ответа на вопрос «Возможно ли восстановить значения неизвестных параметров модели по имеющимся исходным данным в соответствии с решением, принятым на этапе параметризацииβ». После положительного ответа на этот вопрос решается проблема идентификации модели, т. е. реализуется математически корректная процедура оценивания неизвестных параметров модели по имеющимся исходным данным;
6) этап оценки качества модели, в ходе осуществления которого проверяется достоверность и адекватность модели, т. е. определяется, насколько успешно решены задачи спецификации и идентификации модели, какова точность расчётов, полученных на её основе. Построенная модель должна быть адекватна реальному экономическому процессу. Если качество модели является неудовлетворительным, то происходит возврат ко второму этапу моделирования;
7) этап интерпретации результатов моделирования.
К наиболее распространённым эконометрическим моделям относятся:
1) модели потребительского и сберегательного потребления;
2) модели взаимосвязи риска и доходности ценных бумаг;
3) модели предложения труда;
4) макроэкономические модели (модель роста);
5) модели инвестиций;
6) маркетинговые модели;
7) модели валютных курсов и валютных кризисов и др.
Эконометрическое исследование связано с решением следующих проблем:
1) качественный анализ связей экономических переменных, т. е. определение зависимых (yi) и независимых (хi) переменных;
2) изучение соответствующего раздела экономической теории;
3) подбор данных;
4) спецификация формы связи между yi и хi;
5) оценка неизвестных параметров модели;
6) проверка ряда гипотез о свойствах распределения вероятностей для случайной компоненты (гипотезы о средней дисперсии и ковариации);
7) анализ мультиколлинеарности объясняющих переменных, оценка ее статистической значимости, определение переменных, ответственных за мультиколлинеарность;
8) введение фиктивных переменных;
9) выявление автокорреляции;
10) выявление тренда, циклической и случайной компонент;
11) проверка остатков модели на гетероскедастичность;
12) анализ структуры связей и построения системы одновременных уравнений;
13) проверка условия идентификации;
14) оценка параметров системы одновременных уравнений;
15) проблемы моделирования на основе системы временных рядов;
16) построение рекурсивных моделей, авторегрессионных моделей;
17) выработка управленческих решений
18) прогноз экономических показателей, характеризующих изучаемый процесс;
19) моделирование поведения процесса при различных значениях независимых (факторных) переменных.
7. Сбор статистических данных для оценивания параметров эконометрической модели
Первым этапом при проведении эконометрического исследования является сбор статистических данных об анализируемом объекте или процессе в виде конкретных значений эндогенных переменных и предопределенных переменных, входящих в спецификацию модели. Данная информация необходима для определения оценок неизвестных коэффициентов, входящих в эконометрическую модель.
Сбором статистических данных называется процесс получения исходных данных об элементах исследуемой совокупности и их свойствах, которые в дальнейшем становятся предметом статистической обработки и анализа.
В связи с многообразием статистических наблюдений, их принято классифицировать по следующим признаками:
1) по форме организации;
2) по времени регистрации фактов;
3) по признаку полноты охвата элементов изучаемой совокупности.
По форме организации выделяют отчётность и специально организованные статистические наблюдения.
Отчётностью называется основная организационная форма статистического наблюдения, которая состоит в сборе сведений от предприятий, учреждений и организаций о различных сторонах их деятельности на специальных бланках, называемых отчётами. В зависимости от продолжительности периода, относительно которого составляется отчётность, выделяют основную и текущую отчётность.
Основной отчётностью называется организационная форма статистического наблюдения, которая содержит наиболее широкий круг показателей, характеризующих все стороны деятельности предприятия. Основная отчётность также называется годовой.
Текущей отчётностью называется организационная форма статистического наблюдения, которая представляется предприятиями в течение года за различные по продолжительности промежутки времени.
По той причине, что существуют данные, которые принципиально невозможно получить на основе отчётности и данные, которые нецелесообразно включать в неё, используются специально организованные статистические наблюдения – различного рода обследования и переписи.
Статистическим обследованием называется такая форма специально организованного статистического наблюдения, при котором исследуемая совокупность явлений подвергается наблюдению в течение определённого периода времени.
Переписью называется такая форма специально организованного статистического наблюдения, при котором исследуемая совокупность явлений наблюдается на какую-либо дату.
По признаку времени регистрации фактов в эконометрике различают текущее (непрерывное) и дискретное (прерывное) статистическое наблюдение.
Текущим (непрерывным) статистическим наблюдением называется наблюдение, которое осуществляется во времени непрерывно. При этом отдельные явления, факты, события регистрируются по мере их возникновения.
Дискретным (прерывным) статистическим наблюдением называется наблюдение, при котором наблюдаемые явления, факты, события регистрируются через периоды времени, равной или неравной продолжительности. Дискретное наблюдение может быть периодическим и единовременным.
Периодическим наблюдением называется такая форма прерывного наблюдения, которая осуществляется через периоды времени равной продолжительности.
Единовременным наблюдением называется такая форма прерывного наблюдения, которое осуществляется через периоды времени неравной продолжительности или имеющие разовый характер.
В соответствии с признаком полноты охвата элементов изучаемой совокупности явлений, фактов, событий статистические наблюдения делятся на сплошные и несплошные наблюдения.
Сплошным наблюдением называется такая форма статистического наблюдения, при использовании которой учитываются все без исключения явления, факты, события, входящие в исследуемую совокупность.
Несплошным наблюдением называется такая форма статистического наблюдения, при использовании которой учитывается только некоторая часть явлений, фактов, событий, входящих в исследуемую совокупность.
Объективные причины использования несплошного наблюдения:
1) физическая невозможность или нецелесообразность осуществления сплошного наблюдения;
2) ограниченность исследователей во времени или средствах.
Выделяют несколько основных разновидностей несплошного наблюдения:
1) обследование основного массива характеризуется тем, что та часть исследуемой совокупности, которая подлежит наблюдению, устанавливается заранее. При этом отобранная часть единиц является преобладающей в объеме исследуемого объекта;
2) выборочное наблюдение характеризуется тем, что отбор той части единиц исследуемой совокупности, которая подлежит обследованию, производится строго в случайном порядке в соответствии с требованиями, установленными в теории вероятности;
3) анкетное наблюдение характеризуется тем, что лицам, от которых необходимо получить сведения, рассылают анкеты с просьбой заполнить их и возвратить обратно;
4) монографическое наблюдение характеризуется тем, что в составе исследуемой совокупности выделяются типические группы. В каждой подлежащей обследованию группе подвергают наблюдению одну (иногда две, три) типичную единицу. Установленные при наблюдении величины признаков рассматривают как типичные (средние) величины для группы в целом. Программа наблюдения при монографическом наблюдении обычно бывает достаточно широкой, т. е. охватывает большое число признаков.
Сбором статистических данных называется процесс получения исходных данных об элементах исследуемой совокупности и их свойствах, которые в дальнейшем становятся предметом статистической обработки и анализа.
В связи с многообразием статистических наблюдений, их принято классифицировать по следующим признаками:
1) по форме организации;
2) по времени регистрации фактов;
3) по признаку полноты охвата элементов изучаемой совокупности.
По форме организации выделяют отчётность и специально организованные статистические наблюдения.
Отчётностью называется основная организационная форма статистического наблюдения, которая состоит в сборе сведений от предприятий, учреждений и организаций о различных сторонах их деятельности на специальных бланках, называемых отчётами. В зависимости от продолжительности периода, относительно которого составляется отчётность, выделяют основную и текущую отчётность.
Основной отчётностью называется организационная форма статистического наблюдения, которая содержит наиболее широкий круг показателей, характеризующих все стороны деятельности предприятия. Основная отчётность также называется годовой.
Текущей отчётностью называется организационная форма статистического наблюдения, которая представляется предприятиями в течение года за различные по продолжительности промежутки времени.
По той причине, что существуют данные, которые принципиально невозможно получить на основе отчётности и данные, которые нецелесообразно включать в неё, используются специально организованные статистические наблюдения – различного рода обследования и переписи.
Статистическим обследованием называется такая форма специально организованного статистического наблюдения, при котором исследуемая совокупность явлений подвергается наблюдению в течение определённого периода времени.
Переписью называется такая форма специально организованного статистического наблюдения, при котором исследуемая совокупность явлений наблюдается на какую-либо дату.
По признаку времени регистрации фактов в эконометрике различают текущее (непрерывное) и дискретное (прерывное) статистическое наблюдение.
Текущим (непрерывным) статистическим наблюдением называется наблюдение, которое осуществляется во времени непрерывно. При этом отдельные явления, факты, события регистрируются по мере их возникновения.
Дискретным (прерывным) статистическим наблюдением называется наблюдение, при котором наблюдаемые явления, факты, события регистрируются через периоды времени, равной или неравной продолжительности. Дискретное наблюдение может быть периодическим и единовременным.
Периодическим наблюдением называется такая форма прерывного наблюдения, которая осуществляется через периоды времени равной продолжительности.
Единовременным наблюдением называется такая форма прерывного наблюдения, которое осуществляется через периоды времени неравной продолжительности или имеющие разовый характер.
В соответствии с признаком полноты охвата элементов изучаемой совокупности явлений, фактов, событий статистические наблюдения делятся на сплошные и несплошные наблюдения.
Сплошным наблюдением называется такая форма статистического наблюдения, при использовании которой учитываются все без исключения явления, факты, события, входящие в исследуемую совокупность.
Несплошным наблюдением называется такая форма статистического наблюдения, при использовании которой учитывается только некоторая часть явлений, фактов, событий, входящих в исследуемую совокупность.
Объективные причины использования несплошного наблюдения:
1) физическая невозможность или нецелесообразность осуществления сплошного наблюдения;
2) ограниченность исследователей во времени или средствах.
Выделяют несколько основных разновидностей несплошного наблюдения:
1) обследование основного массива характеризуется тем, что та часть исследуемой совокупности, которая подлежит наблюдению, устанавливается заранее. При этом отобранная часть единиц является преобладающей в объеме исследуемого объекта;
2) выборочное наблюдение характеризуется тем, что отбор той части единиц исследуемой совокупности, которая подлежит обследованию, производится строго в случайном порядке в соответствии с требованиями, установленными в теории вероятности;
3) анкетное наблюдение характеризуется тем, что лицам, от которых необходимо получить сведения, рассылают анкеты с просьбой заполнить их и возвратить обратно;
4) монографическое наблюдение характеризуется тем, что в составе исследуемой совокупности выделяются типические группы. В каждой подлежащей обследованию группе подвергают наблюдению одну (иногда две, три) типичную единицу. Установленные при наблюдении величины признаков рассматривают как типичные (средние) величины для группы в целом. Программа наблюдения при монографическом наблюдении обычно бывает достаточно широкой, т. е. охватывает большое число признаков.
8. Классификация видов эконометрических переменных и типов данных. Проблемы, связанные с данными
В эконометрических моделях в основном используются данные трёх типов:
1) пространственные данные (cross-sectional data);
2) временные ряды (time-series data);
3) панельные данные (panel data).
Пространственными данными называется совокупность экономической информации, которая характеризует различные объекты, однако полученной за один и тот же период или момент времени.
Пространственные данные являются выборочной совокупностью из некоторой генеральной совокупности. Примером пространственных данных может служить комплекс экономической информации по какому-либо предприятию (численность работников, объём производства, размер основных фондов), объёмах потребления продукции определённого вида, данные о ВВП различных стран в каком-либо конкретном году и т. д.
Временными данными называется совокупность экономической информации, которая характеризует один и тот же объект, но за разные периоды времени.
Отдельно взятый временной ряд можно рассматривать как выборку из бесконечного ряда значений показателей во времени. Примером временных данных могут служить данные о динамике индекса потребительских цен, ежедневные обменные курсы валют.
Отличия временных данных от пространственных данных:
1) единицы временных рядов подвержены явлению автокорреляции (зависимости между прошлыми и текущими наблюдениями временного ряда), т. е. они не являются статистически независимыми в отличие от единиц случайной пространственной выборки;
2) единицы временных рядов не являются одинаково распределёнными величинами;
3) в отличие от пространственных данных временные данные естественным образом упорядочены во времени.
Панельными данными называются данные, содержащие сведения об одном и том же множестве объектов за ряд последовательных периодов времени.
Панельные данные являются обобщением или комбинацией пространственных и временных данных. Примером панельных данных могут служить показатели хозяйственной деятельности совокупности предприятий, которые собираются каждый год. В этом случае мы получим массив данных, в котором содержатся и данные об однородных объектах за один и тот же период времени, и последовательные значения одной экономической переменной в различные периоды времени. Но если совокупность предприятий из года в год будет различна, то такие данные уже не будут панельными.
Набором признаков называется совокупность экономической информации, которая характеризует изучаемый процесс или объект.
Признаки взаимосвязаны между собой, и при этом они могут выступать в одной из двух ролей:
1) в роли результативного или зависимого признака;
2) в роли факторного или независимого признака.
В эконометрических моделях результативный признак называется объясняемой переменной, а факторный признак называется объясняющей переменной.
В эконометрическом моделировании выделяют следующие виды экономических переменных:
1) экзогенные или независимые переменные (х), значения которых задаются извне. В определённой степени экзогенные переменные поддаются управлению;
2) эндогенные или зависимые переменные (у), значения которых определяются внутри модели;
3) лаговые переменные – это экзогенные или эндогенные переменные, которые относятся к предыдущим моментам времени и находятся в эконометрической модели одновременно с переменными, относящимися к текущему моменту времени. Например, xt-1 – это лаговая экзогенная переменная, а yt-1 – это лаговая эндогенная переменная;
4) предопределённые или объясняющие переменные – это лаговые (xt-1) и текущие (х) экзогенные переменные, а также лаговые эндогенные переменные (yt-1).
5) фиктивные переменные используются в эконометрических моделях для характеристики явления или процесса, в отношении которого нет данных по качественному признаку;
6) переменные-заместители искусственно вводятся в эконометрическую модель для характеристики явления или процесса, который не может быть количественно охарактеризован. При этом переменная-заместитель тесно коррелирует с этим явлением.
В эконометрических исследованиях большое внимание уделяется проблеме данных, т. е. специальным методам работы при наличии данных с пропусками, влиянию агрегирования данных на эконометрические измерения. Зачастую по единицам исследуемой совокупности информация отсутствует, а в наличии имеются данные, характеризующие более крупные единицы (агрегаты). Следует отметить, что при агрегировании временных данных опасность искажения результатов измерений гораздо больше, чем при агрегировании пространных данных, потому что с одной стороны, добавляется эффект автокорреляции, а с другой – происходит погашение случайной компоненты.
1) пространственные данные (cross-sectional data);
2) временные ряды (time-series data);
3) панельные данные (panel data).
Пространственными данными называется совокупность экономической информации, которая характеризует различные объекты, однако полученной за один и тот же период или момент времени.
Пространственные данные являются выборочной совокупностью из некоторой генеральной совокупности. Примером пространственных данных может служить комплекс экономической информации по какому-либо предприятию (численность работников, объём производства, размер основных фондов), объёмах потребления продукции определённого вида, данные о ВВП различных стран в каком-либо конкретном году и т. д.
Временными данными называется совокупность экономической информации, которая характеризует один и тот же объект, но за разные периоды времени.
Отдельно взятый временной ряд можно рассматривать как выборку из бесконечного ряда значений показателей во времени. Примером временных данных могут служить данные о динамике индекса потребительских цен, ежедневные обменные курсы валют.
Отличия временных данных от пространственных данных:
1) единицы временных рядов подвержены явлению автокорреляции (зависимости между прошлыми и текущими наблюдениями временного ряда), т. е. они не являются статистически независимыми в отличие от единиц случайной пространственной выборки;
2) единицы временных рядов не являются одинаково распределёнными величинами;
3) в отличие от пространственных данных временные данные естественным образом упорядочены во времени.
Панельными данными называются данные, содержащие сведения об одном и том же множестве объектов за ряд последовательных периодов времени.
Панельные данные являются обобщением или комбинацией пространственных и временных данных. Примером панельных данных могут служить показатели хозяйственной деятельности совокупности предприятий, которые собираются каждый год. В этом случае мы получим массив данных, в котором содержатся и данные об однородных объектах за один и тот же период времени, и последовательные значения одной экономической переменной в различные периоды времени. Но если совокупность предприятий из года в год будет различна, то такие данные уже не будут панельными.
Набором признаков называется совокупность экономической информации, которая характеризует изучаемый процесс или объект.
Признаки взаимосвязаны между собой, и при этом они могут выступать в одной из двух ролей:
1) в роли результативного или зависимого признака;
2) в роли факторного или независимого признака.
В эконометрических моделях результативный признак называется объясняемой переменной, а факторный признак называется объясняющей переменной.
В эконометрическом моделировании выделяют следующие виды экономических переменных:
1) экзогенные или независимые переменные (х), значения которых задаются извне. В определённой степени экзогенные переменные поддаются управлению;
2) эндогенные или зависимые переменные (у), значения которых определяются внутри модели;
3) лаговые переменные – это экзогенные или эндогенные переменные, которые относятся к предыдущим моментам времени и находятся в эконометрической модели одновременно с переменными, относящимися к текущему моменту времени. Например, xt-1 – это лаговая экзогенная переменная, а yt-1 – это лаговая эндогенная переменная;
4) предопределённые или объясняющие переменные – это лаговые (xt-1) и текущие (х) экзогенные переменные, а также лаговые эндогенные переменные (yt-1).
5) фиктивные переменные используются в эконометрических моделях для характеристики явления или процесса, в отношении которого нет данных по качественному признаку;
6) переменные-заместители искусственно вводятся в эконометрическую модель для характеристики явления или процесса, который не может быть количественно охарактеризован. При этом переменная-заместитель тесно коррелирует с этим явлением.
В эконометрических исследованиях большое внимание уделяется проблеме данных, т. е. специальным методам работы при наличии данных с пропусками, влиянию агрегирования данных на эконометрические измерения. Зачастую по единицам исследуемой совокупности информация отсутствует, а в наличии имеются данные, характеризующие более крупные единицы (агрегаты). Следует отметить, что при агрегировании временных данных опасность искажения результатов измерений гораздо больше, чем при агрегировании пространных данных, потому что с одной стороны, добавляется эффект автокорреляции, а с другой – происходит погашение случайной компоненты.
9. Общая модель парной (однофакторной) регрессии
Общая модель парной регрессии характеризует связь между двумя переменными, которая проявляется как некоторая закономерность лишь в среднем в целом по совокупности наблюдений.
Регрессионным анализом называется определение аналитического выражения связи между исследуемыми переменными, в котором изменение результативной переменной происходит под влиянием факторной переменной.
Модель регрессии или уравнение регрессии позволяет количественно оценить взаимосвязь между исследуемыми переменными.
Предположим, что имеется набор значений двух переменных: yi (результативная переменная) и xi (факторная переменная). Между этими переменными существует зависимость вида: y = f (x).
Задача регрессионного анализа состоит в том, чтобы по данным наблюдений определить такую функцию ỹ = f (x), которая наилучшим образом описывала исследуемую зависимость между переменными.
Для определения аналитической формы зависимости между исследуемыми переменными применяются следующие методы:
1) графический метод или визуальная оценка характера связи. В этом случае на линейном графике по оси абсцисс откладываются значения факторной переменной х, а по оси ординат – значения результативной переменной у. Затем на пересечении соответствующих значений отмечаются точки. Полученный точечный график в системе координат (х, у) называется корреляционным полем. Линия, которая соединяет точки на графике, называется эмпирической линией. По её виду можно судить не только о наличии, но и о форме зависимости между изучаемыми переменными;
2) на основе теоретического и логического анализа природы изучаемых явлений, их социально-экономической сущности;
3) определение аналитической формы зависимости между переменными экспериментальным путём.
При исследовании зависимости между двумя переменными чаще всего используется линейная форма связи. Это связано с двумя обстоятельствами:
1) чёткая экономическая интерпретация параметров линейной модели регрессии;
2) в большинстве случаев нелинейные модели регрессии преобразуются к линейному виду.
Общий вид модели парной регрессии зависимости переменной у от переменной х:
yi=β0+β1xi+εi,
где yi– результативные переменные,
xi– факторные переменные,
β0, β1 – параметры модели регрессии, подлежащие оцениванию;
εi – случайная ошибка модели регрессии. Данная величина является случайной, она характеризует отклонения реальных значений результативных переменных от теоретических, рассчитанных по уравнению регрессии.
Присутствие случайной ошибки в модели регрессии порождено следующими источниками:
1) нерепрезентативность выборки. Модель парной регрессии в большинстве случаев является большим упрощением истинной зависимости между переменными, потому что в модель входит только одна факторная переменная, не способная полностью объяснить вариацию результативной переменной. При этом результативная переменная может быть подвержена влиянию множества других факторных переменных в гораздо большей степени;
2) ошибки, возникающие при измерении данных;
3) неправильная функциональная спецификация модели.
Коэффициент β1, входящий в модельпарной регрессии, называется коэффициентом регрессии. Он характеризует, на сколько в среднем изменится результативная переменная у при условии изменения факторной переменной х на единицу своего измерения. Знак коэффициента регрессии указывает на направление связи между переменными:
1) если β1›0, то связь между изучаемыми переменными (с уменьшением факторной переменной х уменьшается и результативная переменная у, и наоборот);
2) если β1‹0, то связь между изучаемыми переменными (с увеличением факторной переменной х результативная переменная у уменьшается, и наоборот).
Коэффициент β0, входящий в модель парной регрессии, трактуется как среднее значение результативной переменной у при условии, что факторная переменная х равна нулю. Но если факторная переменная не имеет и не может иметь нулевого значения, то подобная трактовка коэффициента β0 не имеет смысла.
Общий вид модели парной регрессии в матричном виде:
Y= X* β+ ε,
где
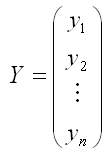– случайный вектор-столбец значений результативной переменной размерности n x 1;
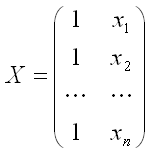– матрица значений факторной переменной размерности n x 2. Первый столбец является единичным, потому что в модели регрессии коэффициент β0 умножается на единицу;
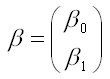– вектор-столбец неизвестных коэффициентов модели регрессии размерности 2 x 1;
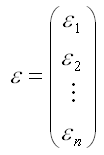– случайный вектор-столбец ошибок модели регрессии размерности n x 1.
Регрессионным анализом называется определение аналитического выражения связи между исследуемыми переменными, в котором изменение результативной переменной происходит под влиянием факторной переменной.
Модель регрессии или уравнение регрессии позволяет количественно оценить взаимосвязь между исследуемыми переменными.
Предположим, что имеется набор значений двух переменных: yi (результативная переменная) и xi (факторная переменная). Между этими переменными существует зависимость вида: y = f (x).
Задача регрессионного анализа состоит в том, чтобы по данным наблюдений определить такую функцию ỹ = f (x), которая наилучшим образом описывала исследуемую зависимость между переменными.
Для определения аналитической формы зависимости между исследуемыми переменными применяются следующие методы:
1) графический метод или визуальная оценка характера связи. В этом случае на линейном графике по оси абсцисс откладываются значения факторной переменной х, а по оси ординат – значения результативной переменной у. Затем на пересечении соответствующих значений отмечаются точки. Полученный точечный график в системе координат (х, у) называется корреляционным полем. Линия, которая соединяет точки на графике, называется эмпирической линией. По её виду можно судить не только о наличии, но и о форме зависимости между изучаемыми переменными;
2) на основе теоретического и логического анализа природы изучаемых явлений, их социально-экономической сущности;
3) определение аналитической формы зависимости между переменными экспериментальным путём.
При исследовании зависимости между двумя переменными чаще всего используется линейная форма связи. Это связано с двумя обстоятельствами:
1) чёткая экономическая интерпретация параметров линейной модели регрессии;
2) в большинстве случаев нелинейные модели регрессии преобразуются к линейному виду.
Общий вид модели парной регрессии зависимости переменной у от переменной х:
yi=β0+β1xi+εi,
где yi– результативные переменные,
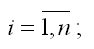
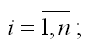
εi – случайная ошибка модели регрессии. Данная величина является случайной, она характеризует отклонения реальных значений результативных переменных от теоретических, рассчитанных по уравнению регрессии.
Присутствие случайной ошибки в модели регрессии порождено следующими источниками:
1) нерепрезентативность выборки. Модель парной регрессии в большинстве случаев является большим упрощением истинной зависимости между переменными, потому что в модель входит только одна факторная переменная, не способная полностью объяснить вариацию результативной переменной. При этом результативная переменная может быть подвержена влиянию множества других факторных переменных в гораздо большей степени;
2) ошибки, возникающие при измерении данных;
3) неправильная функциональная спецификация модели.
Коэффициент β1, входящий в модельпарной регрессии, называется коэффициентом регрессии. Он характеризует, на сколько в среднем изменится результативная переменная у при условии изменения факторной переменной х на единицу своего измерения. Знак коэффициента регрессии указывает на направление связи между переменными:
1) если β1›0, то связь между изучаемыми переменными (с уменьшением факторной переменной х уменьшается и результативная переменная у, и наоборот);
2) если β1‹0, то связь между изучаемыми переменными (с увеличением факторной переменной х результативная переменная у уменьшается, и наоборот).
Коэффициент β0, входящий в модель парной регрессии, трактуется как среднее значение результативной переменной у при условии, что факторная переменная х равна нулю. Но если факторная переменная не имеет и не может иметь нулевого значения, то подобная трактовка коэффициента β0 не имеет смысла.
Общий вид модели парной регрессии в матричном виде:
Y= X* β+ ε,
где
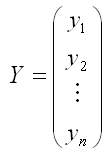
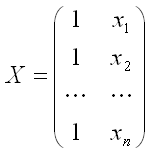
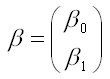
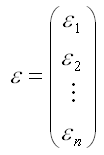
10. Нормальная линейная модель парной (однофакторной) регрессии
Общий вид нормальной (традиционной или классической) линейной модели парной (однофакторной) регрессии (Classical Normal Regression Model):
yi=β0+β1xi+εi,
где yi– результативные переменные,
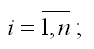xi – факторные переменные,
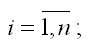β0, β1 – параметры модели регрессии, подлежащие оцениванию;
εi – случайная ошибка модели регрессии.
При построении нормальной линейной модели парной регрессии учитываются пять условий:
1) факторная переменная xi – неслучайная или детерминированная величина, которая не зависит от распределения случайной ошибки модели регрессии εi;
2) математическое ожидание случайной ошибки модели регрессии равно нулю во всех наблюдениях:
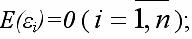3) дисперсия случайной ошибки модели регрессии постоянна для всех наблюдений:
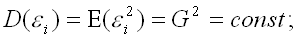4) между значениями случайных ошибок модели регрессии в любых двух наблюдениях отсутствует систематическая взаимосвязь, т. е. случайные ошибки модели регрессии не коррелированны между собой (ковариация случайных ошибок любых двух разных наблюдений равна нулю): Cov(εi,εj)=E(εi,εj)=0 (). Это условие выполняется в том случае, если исходные данные не являются временными рядами;
5) на основании третьего и четвёртого условий часто добавляется пятое условие, заключающееся в том, что случайная ошибка модели регрессии – это случайная величина, подчиняющейся нормальному закону распределения с нулевым математическим ожиданием и дисперсией G2: εi~N(0, G2).
Общий вид нормальной линейной модели парной регрессии в матричной форме:
Y= X* β+ ε,
где
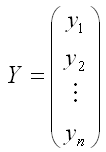– случайный вектор-столбец значений результативной переменной размерности n x 1;
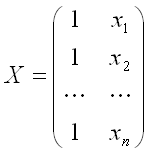– матрица значений факторной переменной размерности n x 2. Первый столбец является единичным, потому что в модели регрессии коэффициент β0 умножается на единицу;
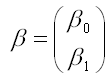– вектор-столбец неизвестных коэффициентов модели регрессии размерности 2 x 1;
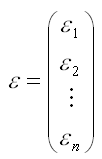– случайный вектор-столбец ошибок модели регрессии размерности n x 1.
Условия построения нормальной линейной модели парной регрессии, записанные в матричной форме:
1) факторная переменная xi – неслучайная или детерминированная величина, которая не зависит от распределения случайной ошибки модели регрессии βi;
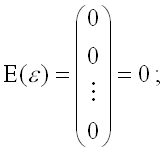2) математическое ожидание случайной ошибки модели регрессии равно нулю во всех наблюдениях:;
3) третье и четвёртое условия можно записать через ковариационную матрицы случайных ошибок нормальной линейной модели парной регрессии:
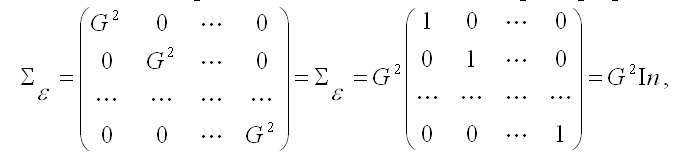
где G2 – дисперсия случайной ошибки модели регрессии ε;
In – единичная матрица размерности n x n.
Определение. Ковариацией называется показатель тесноты связи между переменными х и у, который рассчитывается по формуле:
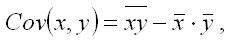где
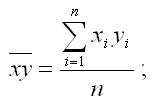– среднее арифметическое значение произведения факторного и результативного признаков;
Основными свойствами показателя ковариации являются:
а) ковариация переменной и константы равна нулю, т. е. cov(x,C)=0 (C=const);
б) ковариация переменной с самой собой равна дисперсии переменной, т. е. Cov(ε,ε)=G2(ε). По этой причине на диагонали ковариационной матрицы случайных ошибок нормальной линейной модели парной регрессии располагается дисперсия случайных ошибок;
4) случайная ошибка модели регрессии подчиняется нормальному закону распределения: εi~N(0, G2).
yi=β0+β1xi+εi,
где yi– результативные переменные,
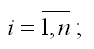
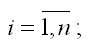
εi – случайная ошибка модели регрессии.
При построении нормальной линейной модели парной регрессии учитываются пять условий:
1) факторная переменная xi – неслучайная или детерминированная величина, которая не зависит от распределения случайной ошибки модели регрессии εi;
2) математическое ожидание случайной ошибки модели регрессии равно нулю во всех наблюдениях:
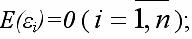
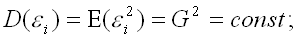
5) на основании третьего и четвёртого условий часто добавляется пятое условие, заключающееся в том, что случайная ошибка модели регрессии – это случайная величина, подчиняющейся нормальному закону распределения с нулевым математическим ожиданием и дисперсией G2: εi~N(0, G2).
Общий вид нормальной линейной модели парной регрессии в матричной форме:
Y= X* β+ ε,
где
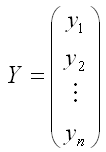
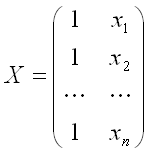
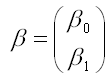
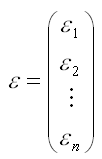
Условия построения нормальной линейной модели парной регрессии, записанные в матричной форме:
1) факторная переменная xi – неслучайная или детерминированная величина, которая не зависит от распределения случайной ошибки модели регрессии βi;
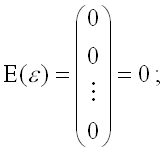
3) третье и четвёртое условия можно записать через ковариационную матрицы случайных ошибок нормальной линейной модели парной регрессии:
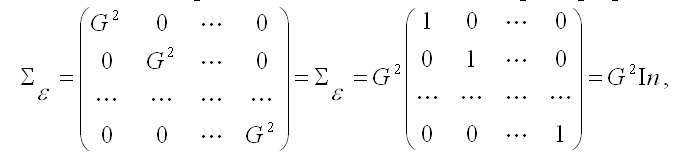
где G2 – дисперсия случайной ошибки модели регрессии ε;
In – единичная матрица размерности n x n.
Определение. Ковариацией называется показатель тесноты связи между переменными х и у, который рассчитывается по формуле:
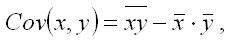
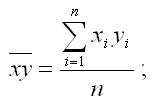
Основными свойствами показателя ковариации являются:
а) ковариация переменной и константы равна нулю, т. е. cov(x,C)=0 (C=const);
б) ковариация переменной с самой собой равна дисперсии переменной, т. е. Cov(ε,ε)=G2(ε). По этой причине на диагонали ковариационной матрицы случайных ошибок нормальной линейной модели парной регрессии располагается дисперсия случайных ошибок;
4) случайная ошибка модели регрессии подчиняется нормальному закону распределения: εi~N(0, G2).
11. Критерии оценки неизвестных коэффициентов модели регрессии
В ходе регрессионного анализа была подобрана форма связи, которая наилучшим образом отражает зависимость результативной переменной у от факторной переменной х:
y=f(x).
Необходимо оценить неизвестные коэффициенты модели регрессии β0…βn. Для определения оптимальных коэффициентов модели регрессии возможно применение следующих критериев:
1) критерий суммы квадратов отклонений наблюдаемых значений результативной переменной у от теоретических значений β (рассчитанных на основе функции регрессии f(x)):
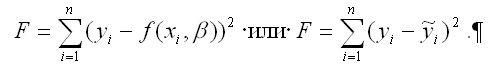Данный критерий определения оптимальных коэффициентов модели регрессии получил название метода наименьших квадратов или МНК. К основным преимуществам данного метода относятся:
а) все расчёты сводятся к механической процедуре нахождения коэффициентов;
б) доступность полученных математических выводов.
Недостаток метода наименьших квадратов заключается в излишней чувствительности оценок к резким выбросам, встречающимся в исходных данных.
Для определения оптимальных значений коэффициентов β0…βn необходимо минимизировать функционал F по данным параметрам:
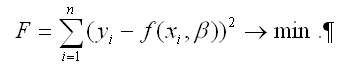Суть минимизации функционала наименьших квадратов F состоит в определении таких значений коэффициентов β0…βn, при которых сумма квадратов отклонений наблюдаемых значений результативной переменной у от теоретических значений β была бы минимальной;
2) критерий суммы модулей отклонений наблюдаемых значений результативной переменной у от теоретических значений β (рассчитанных на основе функции регрессии f(x)):
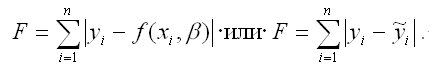Главное преимущество данного критерия заключается в устойчивости полученных оценок к резким выбросам в исходных данных, в отличие от метода наименьших квадратов.
К недостаткам данного критерия относятся:
а) сложности, возникающие в процессе вычислений;
б) зачастую большим отклонениям в исходных данных следует придавать больший вес для уравновешивания их в общей сумме наблюдений;
в) разным значениям оцениваемых коэффициентов β0…βn могут соответствовать одинаковые суммы модулей отклонений.
Для определения оптимальных значений коэффициентов β0…βn необходимо минимизировать функционал Fпо данным параметрам:
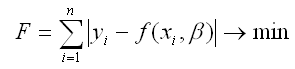Суть минимизации функционала F состоит в определении таких значений коэффициентов β0…βn, при которых сумма квадратов отклонений наблюдаемых значений результативной переменной у от теоретических значений β была бы минимальной;
y=f(x).
Необходимо оценить неизвестные коэффициенты модели регрессии β0…βn. Для определения оптимальных коэффициентов модели регрессии возможно применение следующих критериев:
1) критерий суммы квадратов отклонений наблюдаемых значений результативной переменной у от теоретических значений β (рассчитанных на основе функции регрессии f(x)):
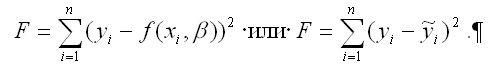
а) все расчёты сводятся к механической процедуре нахождения коэффициентов;
б) доступность полученных математических выводов.
Недостаток метода наименьших квадратов заключается в излишней чувствительности оценок к резким выбросам, встречающимся в исходных данных.
Для определения оптимальных значений коэффициентов β0…βn необходимо минимизировать функционал F по данным параметрам:
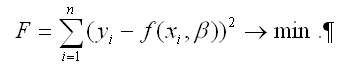
2) критерий суммы модулей отклонений наблюдаемых значений результативной переменной у от теоретических значений β (рассчитанных на основе функции регрессии f(x)):
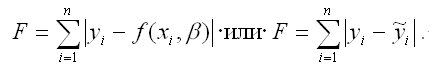
К недостаткам данного критерия относятся:
а) сложности, возникающие в процессе вычислений;
б) зачастую большим отклонениям в исходных данных следует придавать больший вес для уравновешивания их в общей сумме наблюдений;
в) разным значениям оцениваемых коэффициентов β0…βn могут соответствовать одинаковые суммы модулей отклонений.
Для определения оптимальных значений коэффициентов β0…βn необходимо минимизировать функционал Fпо данным параметрам: