Страница:
3) критерий, имеющий вид:
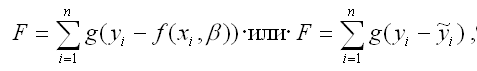 где g – это мера или вес, с которой отклонение (yi-f|xi,β|) входит в функционал F. В качестве примера веса g можно привести функцию Хубера, которая при малых значениях переменной х является квадратичной, а при больших значениях х – линейной:
где g – это мера или вес, с которой отклонение (yi-f|xi,β|) входит в функционал F. В качестве примера веса g можно привести функцию Хубера, которая при малых значениях переменной х является квадратичной, а при больших значениях х – линейной:
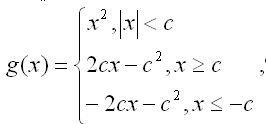
где с – ограничения функции.
Данный критерий определения наилучших оценок коэффициентов модели регрессии β0…βn является попыткой объединения достоинств двух предыдущих критериев. Основное преимущество данного критерия заключается в том, что оценки неизвестных коэффициентов, найденные с его помощью, являются более устойчивыми к случайным выбросам в исходных данных, чем оценки, полученные методом наименьших квадратов.
Для определения оптимальных значений коэффициентов β0…βn необходимо минимизировать функционал F по данным параметрам:
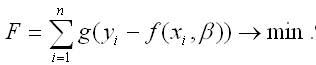 Суть минимизации функционала F состоит в определении таких значений коэффициентов β0…βn, при которых сумма квадратов отклонений наблюдаемых значений результативной переменной у от теоретических значений ỹ с учётом заданных весов g была бы минимальной.
Суть минимизации функционала F состоит в определении таких значений коэффициентов β0…βn, при которых сумма квадратов отклонений наблюдаемых значений результативной переменной у от теоретических значений ỹ с учётом заданных весов g была бы минимальной.
12. Оценивание неизвестных коэффициентов модели регрессии методом наименьших квадратов. Теорема Гаусса – Маркова
13. Система нормальных уравнений и явный вид ее решения при оценивании методом наименьших квадратов линейной модели парной регрессии
14. Оценка коэффициентов модели парной регрессии с помощью выборочного коэффициента регрессии
15. Оценка дисперсии случайной ошибки модели регрессии
16. Состоятельность и несмещённость МНК-оценок
17. Эффективность МНК-оценок МНК
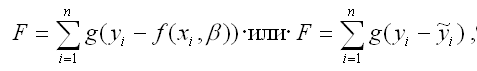
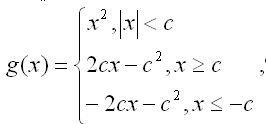
где с – ограничения функции.
Данный критерий определения наилучших оценок коэффициентов модели регрессии β0…βn является попыткой объединения достоинств двух предыдущих критериев. Основное преимущество данного критерия заключается в том, что оценки неизвестных коэффициентов, найденные с его помощью, являются более устойчивыми к случайным выбросам в исходных данных, чем оценки, полученные методом наименьших квадратов.
Для определения оптимальных значений коэффициентов β0…βn необходимо минимизировать функционал F по данным параметрам:
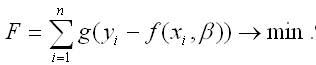
12. Оценивание неизвестных коэффициентов модели регрессии методом наименьших квадратов. Теорема Гаусса – Маркова
Определение коэффициентов модели регрессии осуществляется на третьем этапе схемы построения эконометрической модели. В результате этой процедуры рассчитываются оценки (приближенные значения) неизвестных коэффициентов спецификации модели.
Спецификация линейной эконометрической модели из изолированного уравнения с гомоскедастичными возмущениями имеет вид:
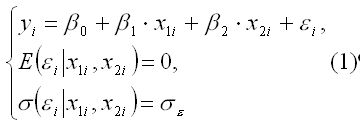 Рассмотрим метод наименьших квадратов на примере оценивания эконометрических моделей в виде моделей парной регрессии (изолированных уравнений с двумя переменными).
Рассмотрим метод наименьших квадратов на примере оценивания эконометрических моделей в виде моделей парной регрессии (изолированных уравнений с двумя переменными).
Если уравнение модели содержит две экономические переменные – эндогенную yiи предопределенную xi, то модель имеет вид:
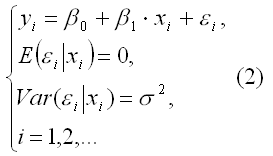 Данная модель называется моделью линейной парной регрессии и содержит три неизвестных параметра:
Данная модель называется моделью линейной парной регрессии и содержит три неизвестных параметра:
β0 , β1 , σ. (3)
Предположим, что имеется выборка: (х1, y1), (х2, y2),… (хn , yn) (4)
Тогда в рамках исследуемой модели данные величины связаны следующим образом:
y1 = a0 + a1 * x1 + u1,
y2 = a0 + a1 * x2 + u2, (5)
…
yn= a0 + a1 * x n + u n.
Данная система называется системой уравнений наблюдения объекта в рамках исследуемой линейной модели или схемой Гаусса-Маркова.
Компактная запись схемы Гаусса-Маркова:
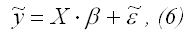 где
где
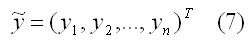 – вектор-столбец известных значений эндогенной переменной yiмодели регрессии;
– вектор-столбец известных значений эндогенной переменной yiмодели регрессии;
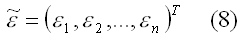 – вектор-столбец неизвестных значений случайных возмущений εi;
– вектор-столбец неизвестных значений случайных возмущений εi;
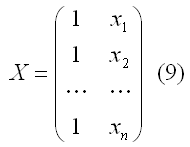 – матрица известных значений предопределенной переменной xi модели;
– матрица известных значений предопределенной переменной xi модели;
β = (β0 β1 )Т (10) – вектор неизвестных коэффициентов модели регрессии.
Обозначим оценку вектора неизвестных коэффициентов модели регрессии как
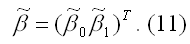 Данная оценка вычисляется на основании выборочных данных (7) и (9) с помощью некоторой процедуры:
Данная оценка вычисляется на основании выборочных данных (7) и (9) с помощью некоторой процедуры:
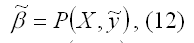 где P (X, ỹ) – символ процедуры.
где P (X, ỹ) – символ процедуры.
Процедура (12) называется линейной относительно вектора (7) значений эндогенной переменной yi, если выполняется условие:
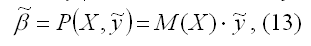 где
где
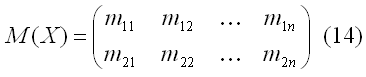 (14) – матрица коэффициентов, зависящих только от выборочных значений (9) предопределенной переменной хi.
(14) – матрица коэффициентов, зависящих только от выборочных значений (9) предопределенной переменной хi.
Теорема Гаусса-Маркова. Пусть матрица Х коэффициентов уравнений наблюдений (6) имеет полный ранг, а случайные возмущения (8) удовлетворяют четырем условиям:
E(ε1) = E(ε2) = … = E(εn) = 0, (15)
Var(ε1) = Var(ε2) = … = Var(εn) = σ2(16)
Cov(εi, εj) = 0 при i≠j(17)
Cov(xi,εj) = 0 при всех значениях i и j (18)
В этом случае справедливы следующие утверждения:
а) наилучшая линейная процедура (13), приводящая к несмещенной и эффективной оценке (11), имеет вид:
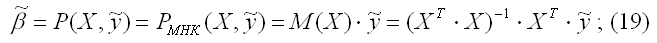 б) линейная несмещенная эффективная оценка (19) обладает свойством наименьших квадратов:
б) линейная несмещенная эффективная оценка (19) обладает свойством наименьших квадратов:
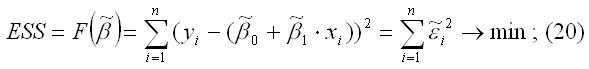 в) ковариационная матрица оценки (19) вычисляется по правилу:
в) ковариационная матрица оценки (19) вычисляется по правилу:
 г) несмещенная оценка параметра σ2 модели (2) находится по формуле:
г) несмещенная оценка параметра σ2 модели (2) находится по формуле:
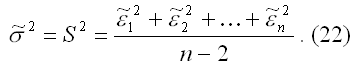 Следствие теоремы Гаусса-Маркова. Оценка
Следствие теоремы Гаусса-Маркова. Оценка
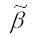 доставляемая процедурой (19) метода наименьших квадратов, может быть вычислена в процессе решения системы двух линейных алгебраических уравнений:
доставляемая процедурой (19) метода наименьших квадратов, может быть вычислена в процессе решения системы двух линейных алгебраических уравнений:
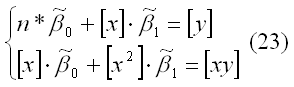 Данная система называется системой нормальных уравнений. Ее коэффициенты и свободные члены определяются по правилам:
Данная система называется системой нормальных уравнений. Ее коэффициенты и свободные члены определяются по правилам:
[x] = x1 + x2 +…+ xn,
[y] = y1 + y2 +…+ yn, (24)
x2] = x12 + x22 +…+ xn2,
[xy] = x1*y1 + x2*y2 + … + xn*yn.
Явный вид решения системы (23):
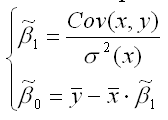
Спецификация линейной эконометрической модели из изолированного уравнения с гомоскедастичными возмущениями имеет вид:
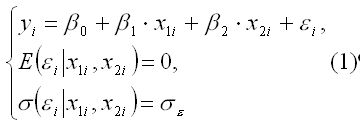
Если уравнение модели содержит две экономические переменные – эндогенную yiи предопределенную xi, то модель имеет вид:
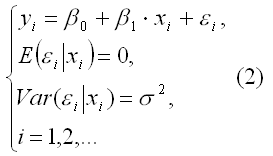
β0 , β1 , σ. (3)
Предположим, что имеется выборка: (х1, y1), (х2, y2),… (хn , yn) (4)
Тогда в рамках исследуемой модели данные величины связаны следующим образом:
y1 = a0 + a1 * x1 + u1,
y2 = a0 + a1 * x2 + u2, (5)
…
yn= a0 + a1 * x n + u n.
Данная система называется системой уравнений наблюдения объекта в рамках исследуемой линейной модели или схемой Гаусса-Маркова.
Компактная запись схемы Гаусса-Маркова:
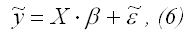
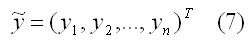
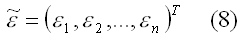
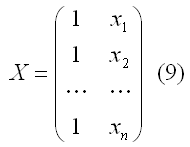
β = (β0 β1 )Т (10) – вектор неизвестных коэффициентов модели регрессии.
Обозначим оценку вектора неизвестных коэффициентов модели регрессии как
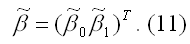
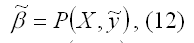
Процедура (12) называется линейной относительно вектора (7) значений эндогенной переменной yi, если выполняется условие:
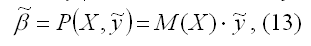
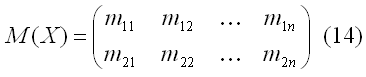
Теорема Гаусса-Маркова. Пусть матрица Х коэффициентов уравнений наблюдений (6) имеет полный ранг, а случайные возмущения (8) удовлетворяют четырем условиям:
E(ε1) = E(ε2) = … = E(εn) = 0, (15)
Var(ε1) = Var(ε2) = … = Var(εn) = σ2(16)
Cov(εi, εj) = 0 при i≠j(17)
Cov(xi,εj) = 0 при всех значениях i и j (18)
В этом случае справедливы следующие утверждения:
а) наилучшая линейная процедура (13), приводящая к несмещенной и эффективной оценке (11), имеет вид:
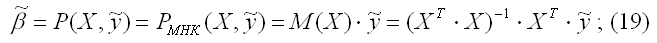
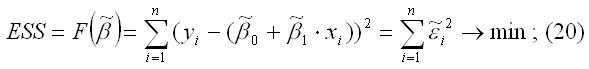

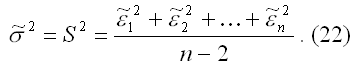
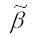
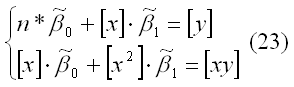
[x] = x1 + x2 +…+ xn,
[y] = y1 + y2 +…+ yn, (24)
x2] = x12 + x22 +…+ xn2,
[xy] = x1*y1 + x2*y2 + … + xn*yn.
Явный вид решения системы (23):
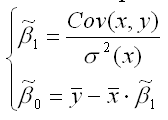
13. Система нормальных уравнений и явный вид ее решения при оценивании методом наименьших квадратов линейной модели парной регрессии
Предположим, что в ходе регрессионного анализа была установлена линейная взаимосвязь между исследуемыми переменными х и у, которая описывается моделью регрессии вида:
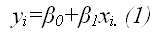 В результате оценивания данной эконометрической модели определяются оценки неизвестных коэффициентов. Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК).
В результате оценивания данной эконометрической модели определяются оценки неизвестных коэффициентов. Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК).
Метод наименьших квадратов позволяет получить такие оценки параметров β0 и β1, при которых сумма квадратов отклонений фактических значений результативного признака y от расчетных (теоретических) ỹ минимальна:
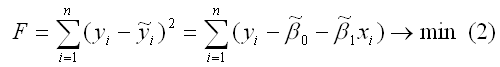 В процессе минимизации функции (1) неизвестными являются только значения коэффициентов β0 и β1, потому что значения результативной и факторной переменных известны из наблюдений. Для определения минимума функции двух переменных вычисляются частные производные этой функции по каждому из оцениваемых параметров и приравниваются к нулю. Результатом данной процедуры будет стационарная система уравнений для функции (2):
В процессе минимизации функции (1) неизвестными являются только значения коэффициентов β0 и β1, потому что значения результативной и факторной переменных известны из наблюдений. Для определения минимума функции двух переменных вычисляются частные производные этой функции по каждому из оцениваемых параметров и приравниваются к нулю. Результатом данной процедуры будет стационарная система уравнений для функции (2):
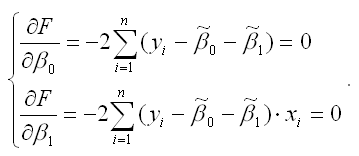 .
.
Если разделить обе части каждого уравнения системы на (-2), раскрыть скобки и привести подобные члены, то получим систему нормальных уравнений для функции регрессии вида yi=β0+β1xi:
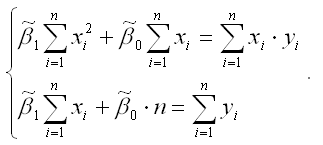 Если решить данную систему нормальных уравнений, то мы получим искомые оценки неизвестных коэффициентов модели регрессии β0 и β1:
Если решить данную систему нормальных уравнений, то мы получим искомые оценки неизвестных коэффициентов модели регрессии β0 и β1:
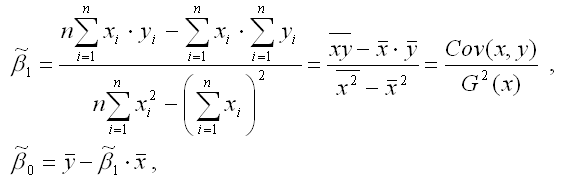 где
где
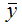 – среднее значение зависимой переменной;
– среднее значение зависимой переменной;
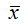 – среднее значение независимой переменной;
– среднее значение независимой переменной;
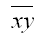 – среднее арифметическое значение произведения зависимой и независимой переменных;
– среднее арифметическое значение произведения зависимой и независимой переменных;
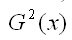 – дисперсия независимой переменной;
– дисперсия независимой переменной;
Gcov (x, y) – ковариация между зависимой и независимой переменными.
Таким образом, явный вид решения системы нормальных уравнений может быть записан следующим образом:
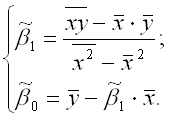
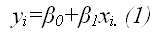
Метод наименьших квадратов позволяет получить такие оценки параметров β0 и β1, при которых сумма квадратов отклонений фактических значений результативного признака y от расчетных (теоретических) ỹ минимальна:
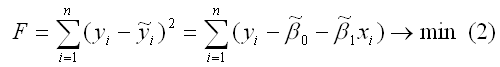
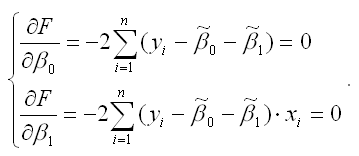
Если разделить обе части каждого уравнения системы на (-2), раскрыть скобки и привести подобные члены, то получим систему нормальных уравнений для функции регрессии вида yi=β0+β1xi:
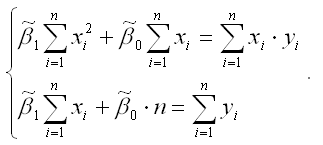
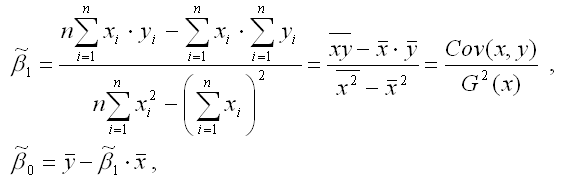
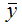
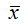
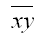
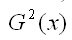
Gcov (x, y) – ковариация между зависимой и независимой переменными.
Таким образом, явный вид решения системы нормальных уравнений может быть записан следующим образом:
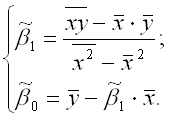
14. Оценка коэффициентов модели парной регрессии с помощью выборочного коэффициента регрессии
Помимо метода наименьших квадратов, с помощью которого в большинстве случаев определяются неизвестные параметры модели регрессии, в случае линейной модели парной регрессии осуществим иной подход к решению данной проблемы.
Линейная модель парной регрессии может быть записана в виде:
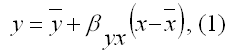 где у – значения зависимой переменной;
где у – значения зависимой переменной;
х – значения независимой переменной;
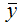 – среднее значение зависимой переменной, которое определяется на основании выборочных данных вычисленное по формуле средней арифметической:
– среднее значение зависимой переменной, которое определяется на основании выборочных данных вычисленное по формуле средней арифметической:
 уi– значения зависимой переменной,
уi– значения зависимой переменной,
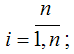 n – объём выборки;
n – объём выборки;
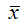 – среднее значение независимой переменной, которое определяется на основании выборочных данных вычисленное по формуле средней арифметической:
– среднее значение независимой переменной, которое определяется на основании выборочных данных вычисленное по формуле средней арифметической:
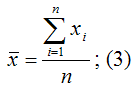 Параметр βyx называется выборочным коэффициентом регрессии переменной у по переменной х. Данный параметр показывает, на сколько в среднем изменится зависимая переменная у при изменении независимой переменной х на единицу своего измерения.
Параметр βyx называется выборочным коэффициентом регрессии переменной у по переменной х. Данный параметр показывает, на сколько в среднем изменится зависимая переменная у при изменении независимой переменной х на единицу своего измерения.
Выборочный коэффициент регрессии переменной у по переменной х рассчитывается по формуле:
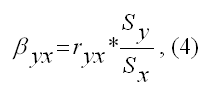 где ryx – это выборочный парный коэффициент корреляции между переменными у и х, который рассчитывается по формуле:
где ryx – это выборочный парный коэффициент корреляции между переменными у и х, который рассчитывается по формуле:
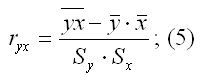
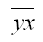 – среднее арифметическое значение произведения зависимой и независимой переменных:
– среднее арифметическое значение произведения зависимой и независимой переменных:
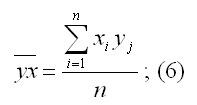 Sy – показатель выборочного среднеквадратического отклонения зависимой переменной у. Этот показатель характеризует, на сколько единиц в среднем отклоняются значения зависимой переменной у от её среднего значения. Он рассчитывается по формуле:
Sy – показатель выборочного среднеквадратического отклонения зависимой переменной у. Этот показатель характеризует, на сколько единиц в среднем отклоняются значения зависимой переменной у от её среднего значения. Он рассчитывается по формуле:
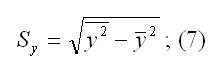
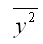 – среднее значение из квадратов значений зависимой переменной у:
– среднее значение из квадратов значений зависимой переменной у:
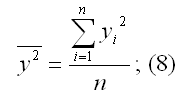
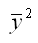 – квадрат средних значений зависимой переменной у:
– квадрат средних значений зависимой переменной у:
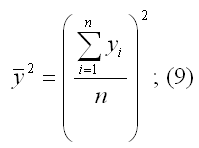 Sx – показатель выборочного среднеквадратического отклонения независимой переменной х. Этот показатель характеризует, на сколько единиц в среднем отклоняются значения независимой переменной х от её среднего значения. Они рассчитывается по формуле:
Sx – показатель выборочного среднеквадратического отклонения независимой переменной х. Этот показатель характеризует, на сколько единиц в среднем отклоняются значения независимой переменной х от её среднего значения. Они рассчитывается по формуле:
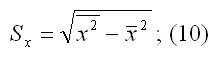
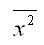 – среднее значение из квадратов значений независимой переменной х:
– среднее значение из квадратов значений независимой переменной х:
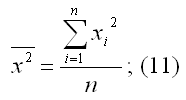
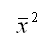 – квадрат средних значений независимой переменной х:
– квадрат средних значений независимой переменной х:
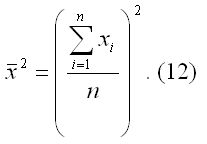 При использовании рассмотренного подхода оценивания неизвестных параметров линейной модели парной регрессии, следует учитывать что ryx=rxy, однако βyx≠βxy.
При использовании рассмотренного подхода оценивания неизвестных параметров линейной модели парной регрессии, следует учитывать что ryx=rxy, однако βyx≠βxy.
Линейная модель парной регрессии может быть записана в виде:
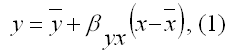
х – значения независимой переменной;
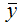
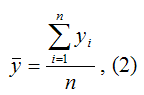
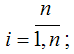
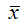
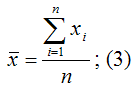
Выборочный коэффициент регрессии переменной у по переменной х рассчитывается по формуле:
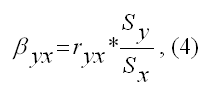
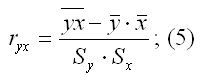
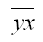
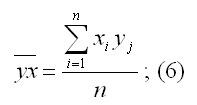
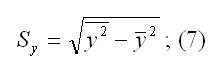
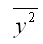
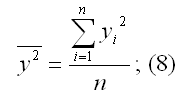
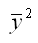
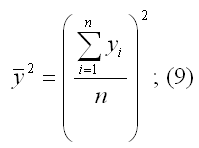
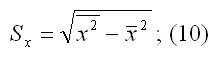
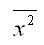
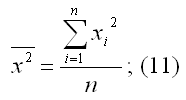
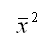

15. Оценка дисперсии случайной ошибки модели регрессии
При проведении регрессионного анализа основная трудность заключается в том, что генеральная дисперсия случайной ошибки является неизвестной величиной, что вызывает необходимость в расчёте её несмещённой выборочной оценки.
Несмещённой оценкой дисперсии (или исправленной дисперсией) случайной ошибки линейной модели парной регрессии называется величина, рассчитываемая по формуле:
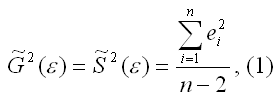 где n – это объём выборочной совокупности;
где n – это объём выборочной совокупности;
еi– остатки регрессионной модели:
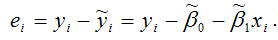 Для линейной модели множественной регрессии несмещённая оценка дисперсии случайной ошибки рассчитывается по формуле:
Для линейной модели множественной регрессии несмещённая оценка дисперсии случайной ошибки рассчитывается по формуле:
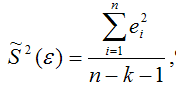 где k – число оцениваемых параметров модели регрессии.
где k – число оцениваемых параметров модели регрессии.
Оценка матрицы ковариаций случайных ошибок Cov(ε) будет являться оценочная матрица ковариаций:
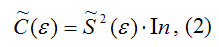 где In – единичная матрица.
где In – единичная матрица.
Оценка дисперсии случайной ошибки модели регрессии распределена по ε2(хи-квадрат) закону распределения с (n-k-1) степенями свободы.
Для доказательства несмещённости оценки дисперсии случайной ошибки модели регрессии необходимо доказать справедливость равенства
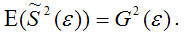 Доказательство. Примем без доказательства справедливость следующих равенств:
Доказательство. Примем без доказательства справедливость следующих равенств:
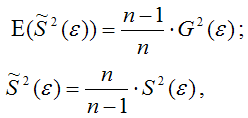 где G2(ε) – генеральная дисперсия случайной ошибки;
где G2(ε) – генеральная дисперсия случайной ошибки;
S2(ε) – выборочная дисперсия случайной ошибки;
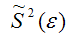 – выборочная оценка дисперсии случайной ошибки.
– выборочная оценка дисперсии случайной ошибки.
Тогда:
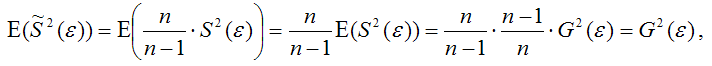 т. е.
т. е.
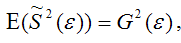 что и требовалось доказать.
что и требовалось доказать.
Следовательно, выборочная оценка дисперсии случайной ошибки
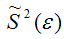 является несмещённой оценкой генеральной дисперсии случайной ошибки модели регрессии G2(ε).
является несмещённой оценкой генеральной дисперсии случайной ошибки модели регрессии G2(ε).
При условии извлечения из генеральной совокупности нескольких выборок одинакового объёма n и при одинаковых значениях объясняющих переменных х, наблюдаемые значения зависимой переменной у будут случайным образом колебаться за счёт случайного характера случайной компоненты β. Отсюда можно сделать вывод, что будут варьироваться и зависеть от значений переменной у значения оценок коэффициентов регрессии и оценка дисперсии случайной ошибки модели регрессии.
Для иллюстрации данного утверждения докажем зависимость значения МНК-оценки
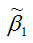 от величины случайной ошибки ε.
от величины случайной ошибки ε.
МНК-оценка коэффициента β1 модели регрессии определяется по формуле:
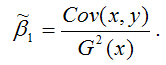 В связи с тем, что переменная у зависит от случайной компоненты ε (yi=β0+β1xi+εi), то ковариация между зависимой переменной у и независимой переменной х может быть представлена следующим образом:
В связи с тем, что переменная у зависит от случайной компоненты ε (yi=β0+β1xi+εi), то ковариация между зависимой переменной у и независимой переменной х может быть представлена следующим образом:
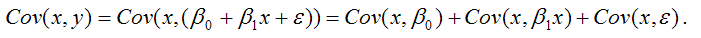 Для дальнейших преобразования используются свойства ковариации:
Для дальнейших преобразования используются свойства ковариации:
1) ковариация между переменной х и константой С равна нулю: Cov(x,C)=0, C=const;
2) ковариация переменной х с самой собой равна дисперсии этой переменной: Cov(x,x)=G2(x).
Исходя из указанных свойств ковариации, справедливы следующие равенства:
Cov(x,β0)=0 (β0=const);
Cov(x, β1x)= β1*Cov(x,x)= β1*G2(x).
Следовательно, ковариация между зависимой и независимой переменными Cov(x,y) может быть записана как:
Cov(x,y)= β1G2(x)+Cov(x,ε).
В результате МНК-оценка коэффициента β1 модели регрессии примет вид:
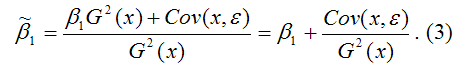 Таким образом, МНК-оценка
Таким образом, МНК-оценка
 может быть представлена как сумма двух компонент:
может быть представлена как сумма двух компонент:
1) константы β1, т. е. истинного значения коэффициента;
2) случайной ошибки Cov(x,ε), вызывающей вариацию коэффициента модели регрессии.
Однако на практике подобное разложение МНК-оценки невозможно, потому что истинные значения коэффициентов модели регрессии и значения случайной ошибки являются неизвестными. Теоретически данное разложение можно использовать при изучении статистических свойств МНК-оценок.
Аналогично доказывается, что МНК-оценка
 коэффициента модели регрессии и несмещённая оценка дисперсии случайной ошибки
коэффициента модели регрессии и несмещённая оценка дисперсии случайной ошибки
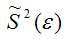 могут быть представлены как сумма постоянной составляющей (константы) и случайной компоненты, зависящей от ошибки модели регрессии ε.
могут быть представлены как сумма постоянной составляющей (константы) и случайной компоненты, зависящей от ошибки модели регрессии ε.
Несмещённой оценкой дисперсии (или исправленной дисперсией) случайной ошибки линейной модели парной регрессии называется величина, рассчитываемая по формуле:
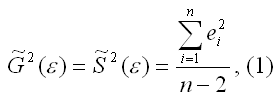
еi– остатки регрессионной модели:
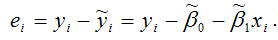
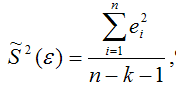
Оценка матрицы ковариаций случайных ошибок Cov(ε) будет являться оценочная матрица ковариаций:
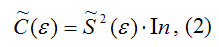
Оценка дисперсии случайной ошибки модели регрессии распределена по ε2(хи-квадрат) закону распределения с (n-k-1) степенями свободы.
Для доказательства несмещённости оценки дисперсии случайной ошибки модели регрессии необходимо доказать справедливость равенства
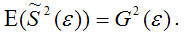
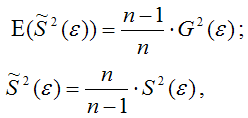
S2(ε) – выборочная дисперсия случайной ошибки;
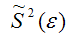
Тогда:
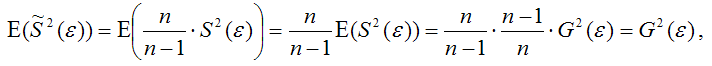
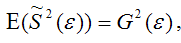
Следовательно, выборочная оценка дисперсии случайной ошибки
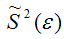
При условии извлечения из генеральной совокупности нескольких выборок одинакового объёма n и при одинаковых значениях объясняющих переменных х, наблюдаемые значения зависимой переменной у будут случайным образом колебаться за счёт случайного характера случайной компоненты β. Отсюда можно сделать вывод, что будут варьироваться и зависеть от значений переменной у значения оценок коэффициентов регрессии и оценка дисперсии случайной ошибки модели регрессии.
Для иллюстрации данного утверждения докажем зависимость значения МНК-оценки
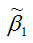
МНК-оценка коэффициента β1 модели регрессии определяется по формуле:
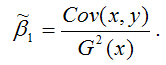
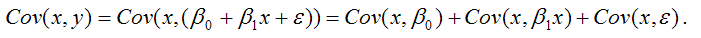
1) ковариация между переменной х и константой С равна нулю: Cov(x,C)=0, C=const;
2) ковариация переменной х с самой собой равна дисперсии этой переменной: Cov(x,x)=G2(x).
Исходя из указанных свойств ковариации, справедливы следующие равенства:
Cov(x,β0)=0 (β0=const);
Cov(x, β1x)= β1*Cov(x,x)= β1*G2(x).
Следовательно, ковариация между зависимой и независимой переменными Cov(x,y) может быть записана как:
Cov(x,y)= β1G2(x)+Cov(x,ε).
В результате МНК-оценка коэффициента β1 модели регрессии примет вид:
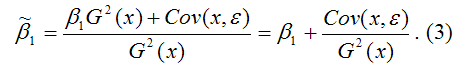
1) константы β1, т. е. истинного значения коэффициента;
2) случайной ошибки Cov(x,ε), вызывающей вариацию коэффициента модели регрессии.
Однако на практике подобное разложение МНК-оценки невозможно, потому что истинные значения коэффициентов модели регрессии и значения случайной ошибки являются неизвестными. Теоретически данное разложение можно использовать при изучении статистических свойств МНК-оценок.
Аналогично доказывается, что МНК-оценка
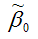
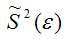
16. Состоятельность и несмещённость МНК-оценок
Предположим, что методом наименьших квадратов получена оценка
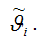 Для того, чтобы данная оценка могла быть принята за оценку параметра
Для того, чтобы данная оценка могла быть принята за оценку параметра
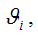 необходимо и достаточно выполнения трёх статистических свойств:
необходимо и достаточно выполнения трёх статистических свойств:
1) свойства несмещённости;
2) свойства состоятельности;
3) свойства эффективности.
Сделаем следующие предположения об отклонениях єi:
1) величина єiявляется случайной переменной;
2) математическое ожидание єiравно нулю: М (єi) = 0;
3) дисперсия є постоянна: D(єi) = D(єi) = s 2 для всех i, j;
4) значения єiнезависимы между собой, следовательно, справедливо следующее выражение:
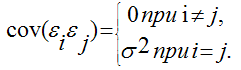 Если данные предпосылки выполняются, то оценки, найденные с помощью метода наименьших квадратов, обладают свойствами несмещённости, состоятельности и эффективности.
Если данные предпосылки выполняются, то оценки, найденные с помощью метода наименьших квадратов, обладают свойствами несмещённости, состоятельности и эффективности.
Если третье и четвёртое предположения не выполняются, т. е. дисперсия случайных компонент непостоянна и/или значения є коррелируют друг с другом, то свойства несмещенности и состоятельности сохраняются, но свойство эффективности – нет.
Величина
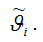 называется несмещённой оценкой параметра
называется несмещённой оценкой параметра
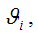 если её выборочное математическое ожидание равно оцениваемому параметру генеральной совокупности:
если её выборочное математическое ожидание равно оцениваемому параметру генеральной совокупности:
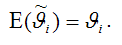 Отсюда следует, что
Отсюда следует, что
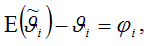 где φi – это величина смещения оценки.
где φi – это величина смещения оценки.
Рассмотрим свойство несмещённости МНК-оценок на примере модели парной регрессии.
Необходимо доказать, что оценка
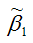 полученная методом наименьших квадратов, является несмещённой оценкой параметра β1 для нормальной линейной модели регрессии, т. е. необходимо доказать справедливость равенства
полученная методом наименьших квадратов, является несмещённой оценкой параметра β1 для нормальной линейной модели регрессии, т. е. необходимо доказать справедливость равенства
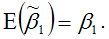 Доказательство. Проведём доказательство утверждения
Доказательство. Проведём доказательство утверждения
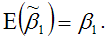 через ковариационную матрицу:
через ковариационную матрицу:
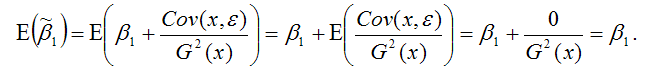 То же самое утверждение
То же самое утверждение
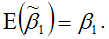 можно доказать в более развёрнутом виде:
можно доказать в более развёрнутом виде:
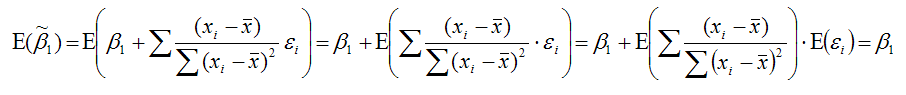 Следовательно, оценка
Следовательно, оценка
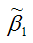 полученная методом наименьших квадратов, является несмещённой оценкой коэффициента β1 нормальной линейной модели парной регрессии.
полученная методом наименьших квадратов, является несмещённой оценкой коэффициента β1 нормальной линейной модели парной регрессии.
Свойство несмещённости оценки
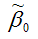 коэффициента β0нормальной линейной модели парной регрессии, полученной методом наименьших квадратов, доказывается аналогично.
коэффициента β0нормальной линейной модели парной регрессии, полученной методом наименьших квадратов, доказывается аналогично.
Для модели множественной регрессии доказательство свойства несмещённости оценок параметров βi, полученных методом наименьших квадратов, целесообразно провести в матричной форме:
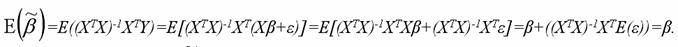 Следовательно, оценки
Следовательно, оценки
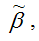 полученные методом наименьших квадратов, являются несмещёнными оценками коэффициентов βiнормальной линейной модели множественной регрессии.
полученные методом наименьших квадратов, являются несмещёнными оценками коэффициентов βiнормальной линейной модели множественной регрессии.
Величина
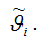 является состоятельной оценкой параметра
является состоятельной оценкой параметра
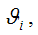 если она удовлетворяет закону больших чисел. Суть закона больших чисел состоит в том, что с увеличением выборочной совокупности значение оценки
если она удовлетворяет закону больших чисел. Суть закона больших чисел состоит в том, что с увеличением выборочной совокупности значение оценки
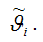 стремится к значению параметра
стремится к значению параметра
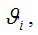 генеральной совокупности:
генеральной совокупности:
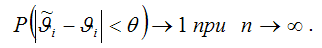 Условие состоятельности можно также записать через теорему Бернулли:
Условие состоятельности можно также записать через теорему Бернулли:
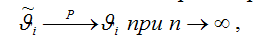 т. е. значение оценки
т. е. значение оценки
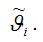 сходится по вероятности к значению параметра
сходится по вероятности к значению параметра
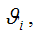 генеральной совокупности, при условии, что объём выборочной совокупности стремится к бесконечности.
генеральной совокупности, при условии, что объём выборочной совокупности стремится к бесконечности.
На практике оценка
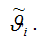 полученная методом наименьших квадратов, считается состоятельной оценкой параметра,
полученная методом наименьших квадратов, считается состоятельной оценкой параметра,
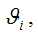 если выполняются два условия:
если выполняются два условия:
1) смещение оценки равно нулю или стремится к нему при объёме выборки, стремящемся к бесконечности:
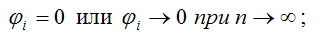 2) дисперсия оценки параметра
2) дисперсия оценки параметра
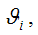 стремится к нулю при объёме выборки, стремящемся к бесконечности:
стремится к нулю при объёме выборки, стремящемся к бесконечности:
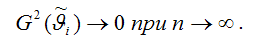 Рассмотрим свойство состоятельности МНК-оценок на примере модели парной регрессии.
Рассмотрим свойство состоятельности МНК-оценок на примере модели парной регрессии.
Необходимо доказать, что оценка
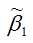 полученная методом наименьших квадратов, является состоятельной оценкой параметра β1для нормальной линейной модели регрессии.
полученная методом наименьших квадратов, является состоятельной оценкой параметра β1для нормальной линейной модели регрессии.
Доказательство. Докажем первое условие состоятельности для МНК-оценки
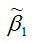
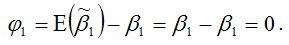 Докажем второе условие состоятельности для МНК-оценки
Докажем второе условие состоятельности для МНК-оценки
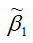
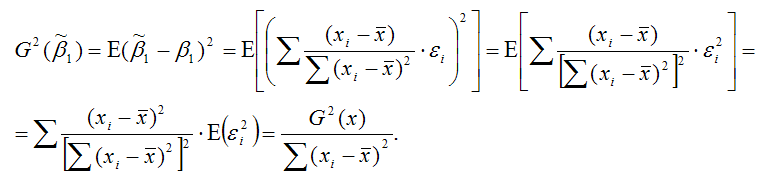 МНК-оценка
МНК-оценка
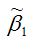 подчиняется нормальному закону распределения с математическим ожиданием β1 и дисперсией
подчиняется нормальному закону распределения с математическим ожиданием β1 и дисперсией
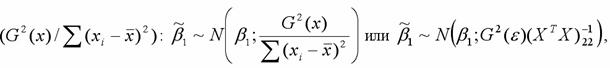 или
или
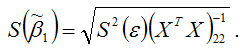 где индекс 22 указывает на расположение дисперсии параметра β1в матрице ковариаций.
где индекс 22 указывает на расположение дисперсии параметра β1в матрице ковариаций.
Свойство состоятельности оценки
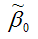 коэффициента β0 нормальной линейной модели парной регрессии, полученной методом наименьших квадратов, доказывается аналогично.
коэффициента β0 нормальной линейной модели парной регрессии, полученной методом наименьших квадратов, доказывается аналогично.
Оценка стандартной ошибки МНК-оценки
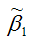 определяется по формуле:
определяется по формуле:
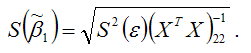 Для модели множественной регрессии доказательство свойства несмещённости оценок параметров βi, полученных методом наименьших квадратов, целесообразно провести в матричной форме:
Для модели множественной регрессии доказательство свойства несмещённости оценок параметров βi, полученных методом наименьших квадратов, целесообразно провести в матричной форме:
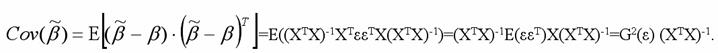 Следовательно, оценки
Следовательно, оценки
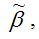 полученные методом наименьших квадратов, являются несмещёнными оценками коэффициентов βiнормальной линейной модели множественной регрессии.
полученные методом наименьших квадратов, являются несмещёнными оценками коэффициентов βiнормальной линейной модели множественной регрессии.
Эффективность МНК-оценок доказывается с помощью теоремы Гаусса-Маркова.
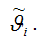
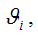
1) свойства несмещённости;
2) свойства состоятельности;
3) свойства эффективности.
Сделаем следующие предположения об отклонениях єi:
1) величина єiявляется случайной переменной;
2) математическое ожидание єiравно нулю: М (єi) = 0;
3) дисперсия є постоянна: D(єi) = D(єi) = s 2 для всех i, j;
4) значения єiнезависимы между собой, следовательно, справедливо следующее выражение:
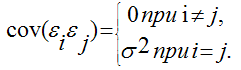
Если третье и четвёртое предположения не выполняются, т. е. дисперсия случайных компонент непостоянна и/или значения є коррелируют друг с другом, то свойства несмещенности и состоятельности сохраняются, но свойство эффективности – нет.
Величина
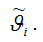
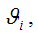
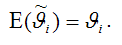
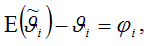
Рассмотрим свойство несмещённости МНК-оценок на примере модели парной регрессии.
Необходимо доказать, что оценка
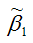
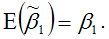
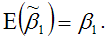
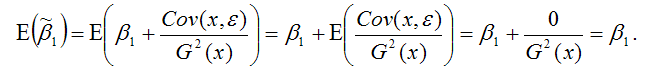
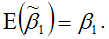
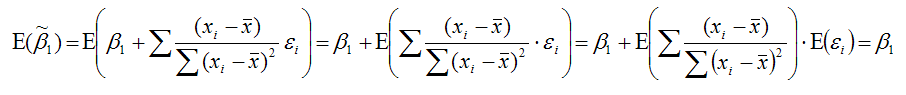
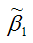
Свойство несмещённости оценки
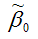
Для модели множественной регрессии доказательство свойства несмещённости оценок параметров βi, полученных методом наименьших квадратов, целесообразно провести в матричной форме:
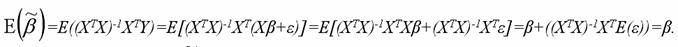
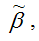
Величина
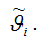
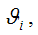
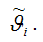
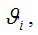
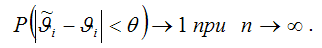
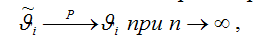
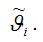
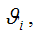
На практике оценка
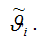
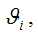
1) смещение оценки равно нулю или стремится к нему при объёме выборки, стремящемся к бесконечности:
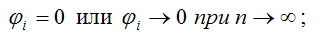
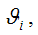
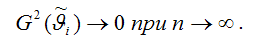
Необходимо доказать, что оценка
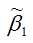
Доказательство. Докажем первое условие состоятельности для МНК-оценки
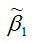
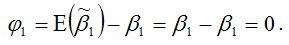
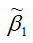
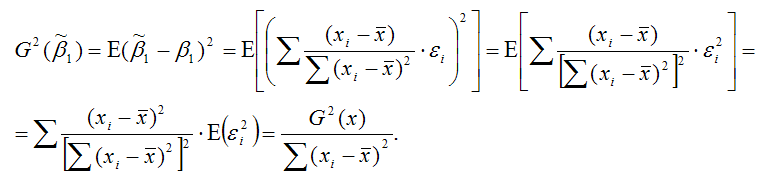
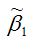
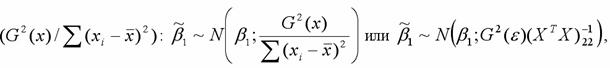
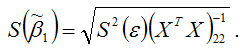
Свойство состоятельности оценки
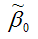
Оценка стандартной ошибки МНК-оценки
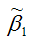
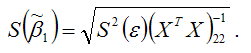
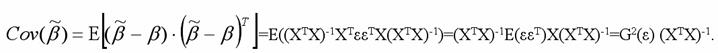
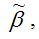
Эффективность МНК-оценок доказывается с помощью теоремы Гаусса-Маркова.
17. Эффективность МНК-оценок МНК
Свойство эффективности оценок неизвестных параметров модели регрессии, полученных методом наименьших квадратов, доказывается с помощью теоремы Гаусса-Маркова.
Сделаем следующие предположения о модели парной регрессии:
1) факторная переменная xi– неслучайная или детерминированная величина, которая не зависит от распределения случайной ошибки модели регрессии βi;
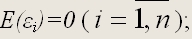 2) математическое ожидание случайной ошибки модели регрессии равно нулю во всех наблюдениях:
2) математическое ожидание случайной ошибки модели регрессии равно нулю во всех наблюдениях:
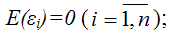 3) дисперсия случайной ошибки модели регрессии постоянна для всех наблюдений:;
3) дисперсия случайной ошибки модели регрессии постоянна для всех наблюдений:;
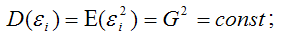 4) между значениями случайных ошибок модели регрессии в любых двух наблюдениях отсутствует систематическая взаимосвязь, т. е. случайные ошибки модели регрессии не коррелированны между собой (ковариация случайных ошибок любых двух разных наблюдений равна нулю):
4) между значениями случайных ошибок модели регрессии в любых двух наблюдениях отсутствует систематическая взаимосвязь, т. е. случайные ошибки модели регрессии не коррелированны между собой (ковариация случайных ошибок любых двух разных наблюдений равна нулю):
 Это условие выполняется в том случае, если исходные данные не являются временными рядами;
Это условие выполняется в том случае, если исходные данные не являются временными рядами;
5) на основании третьего и четвёртого условий часто добавляется пятое условие, заключающееся в том, что случайная ошибка модели регрессии – это случайная величина, подчиняющейся нормальному закону распределения с нулевым математическим ожиданием и дисперсией G2: εi~N(0, G2).
Если выдвинутые предположения справедливы, то оценки неизвестных параметров модели парной регрессии, полученные методом наименьших квадратов, имеют наименьшую дисперсию в классе всех линейных несмещённых оценок, т. е. МНК-оценки можно считать эффективными оценками неизвестных параметров β0 и β1.
Если выдвинутые предположения справедливы для модели множественной регрессии, то оценки неизвестных параметров данной модели регрессии, полученные методом наименьших квадратов, имеют наименьшую дисперсию в классе всех линейных несмещённых оценок, т. е. МНК-оценки можно считать эффективными оценками неизвестных параметров β0…βn.
Для обозначения дисперсий МНК-оценок неизвестных параметров модели регрессии используется матрица ковариаций.
Матрицей ковариаций МНК-оценок параметров линейной модели парной регрессии называется выражение вида:
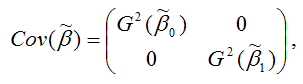 где
где
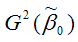 – дисперсия МНК-оценки параметра модели регрессии β0;
– дисперсия МНК-оценки параметра модели регрессии β0;
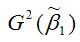 – дисперсия МНК-оценки параметра модели регрессии β1.
– дисперсия МНК-оценки параметра модели регрессии β1.
Матрицей ковариаций МНК-оценок параметров линейной модели множественной регрессии называется выражение вида:
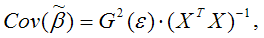 где G2(ε) – это дисперсия случайной ошибки модели регрессии ε.
где G2(ε) – это дисперсия случайной ошибки модели регрессии ε.
Для линейной модели парной регрессии дисперсии оценок неизвестных параметров определяются по формулам:
1) дисперсия МНК-оценки коэффициента модели регрессии β0:
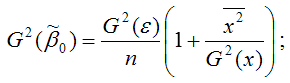 2) дисперсия МНК-оценки коэффициента модели регрессии β1:
2) дисперсия МНК-оценки коэффициента модели регрессии β1:
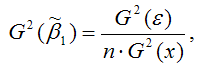 где G2(ε) – дисперсия случайной ошибки уравнения регрессии β;
где G2(ε) – дисперсия случайной ошибки уравнения регрессии β;
G2(x) – дисперсия независимой переменой модели регрессии х;
n – объём выборочной совокупности.
В связи с тем, что на практике значение дисперсии случайной ошибки модели регрессии G2(ε) неизвестно, для вычисления матрицы ковариаций МНК-оценок применяют оценку дисперсии случайной ошибки модели регрессии S2(ε).
Для линейной модели парной регрессии оценка дисперсии случайной ошибки определяется по формуле:
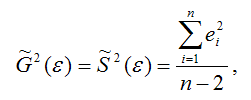 где
где
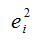 – это остатки регрессионной модели, которые рассчитываются как
– это остатки регрессионной модели, которые рассчитываются как
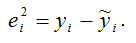 Тогда оценка дисперсии МНК-оценки коэффициента β0 линейной модели парной регрессии будет определяться по формуле:
Тогда оценка дисперсии МНК-оценки коэффициента β0 линейной модели парной регрессии будет определяться по формуле:
Сделаем следующие предположения о модели парной регрессии:
1) факторная переменная xi– неслучайная или детерминированная величина, которая не зависит от распределения случайной ошибки модели регрессии βi;
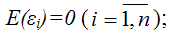
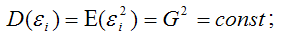
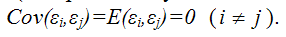
5) на основании третьего и четвёртого условий часто добавляется пятое условие, заключающееся в том, что случайная ошибка модели регрессии – это случайная величина, подчиняющейся нормальному закону распределения с нулевым математическим ожиданием и дисперсией G2: εi~N(0, G2).
Если выдвинутые предположения справедливы, то оценки неизвестных параметров модели парной регрессии, полученные методом наименьших квадратов, имеют наименьшую дисперсию в классе всех линейных несмещённых оценок, т. е. МНК-оценки можно считать эффективными оценками неизвестных параметров β0 и β1.
Если выдвинутые предположения справедливы для модели множественной регрессии, то оценки неизвестных параметров данной модели регрессии, полученные методом наименьших квадратов, имеют наименьшую дисперсию в классе всех линейных несмещённых оценок, т. е. МНК-оценки можно считать эффективными оценками неизвестных параметров β0…βn.
Для обозначения дисперсий МНК-оценок неизвестных параметров модели регрессии используется матрица ковариаций.
Матрицей ковариаций МНК-оценок параметров линейной модели парной регрессии называется выражение вида:
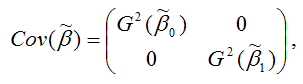
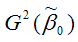
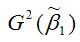
Матрицей ковариаций МНК-оценок параметров линейной модели множественной регрессии называется выражение вида:
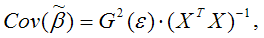
Для линейной модели парной регрессии дисперсии оценок неизвестных параметров определяются по формулам:
1) дисперсия МНК-оценки коэффициента модели регрессии β0:
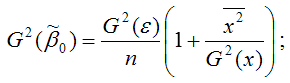
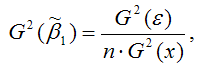
G2(x) – дисперсия независимой переменой модели регрессии х;
n – объём выборочной совокупности.
В связи с тем, что на практике значение дисперсии случайной ошибки модели регрессии G2(ε) неизвестно, для вычисления матрицы ковариаций МНК-оценок применяют оценку дисперсии случайной ошибки модели регрессии S2(ε).
Для линейной модели парной регрессии оценка дисперсии случайной ошибки определяется по формуле: